(全)初中数学|23种模型汇总
初中数学几何模型

全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是°、°、°、°及有一个角是°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇度旋度,造等边三角形遇度旋度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋度,造中心对称说明:IS 8模型变形BEFcEB说明:说明:nnnnnnnnnnnnnnnnnnnnnnn nnnnn口叩皿皿皿皿皿中点模型 边构诗中{fflt 逢阳点闵iS 中幽城 几何最值模型 VH *h 轴对称模型 对称最值 线mi 差模型 fflftffw 同侧"异侧两蜒段之利罐短视它 同侧、异删芮线投之羞媪小槐型 四边形周怏垠小根地 三角形眉长 必小檢哩三线穀之和 她知爬制过桥模取旋转最值说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
简拼模型三角形j四边形E 面积等分说明:说明:3045602说明:ACOCOAA 模型一:手拉手模型-旋转型全等<2)等濮的AA Mfr=血°拟述°均为等媵直甬M 册A 结险(DA (UCtAO^l>j 超乙他»③。
E 平分£忖了儿(1)―况> Sfr :LDW 牛底皿力能转至右囲检置A 皓论:> 右图中①bOCWMe\QAC AOSD 』 >⑨延氏M 交购于点G 必肖5氏-LBOA⑵特燥惜况>条件m 3MB ,厶伽■剜,将AXD 龍讳至右團位蛊a gife :右gcp fflAfJCD^iOJ^AC?JCiM£33②延长M 交加于点瓦愁有3EC -LUGA f BD 000B (5)-—--——=—-=tan ZlfX D®ACOCOA 3f^SDLAC.灘接也JC >临加*†g ・a+o>s ⑥矢"訐c&J 冊哒相垂直的四嬷)<3)任翦腰三角晤†辭,。
初中数学63个几何模型

初中数学63个几何模型
1. 点
2. 直线
3. 射线
4. 线段
5. 角
6. 直角
7. 钝角
8. 锐角
9. 平角
10. 三角形
11. 直角三角形
12. 等腰三角形
13. 等边三角形
14. 直线角平分线
15. 外角
16. 内角
17. 同位角
18. 对顶角
19. 同旁内角
20. 同旁外角
21. 三线合一定理
22. 利用同旁内角、三线合一求外角
23. 利用对顶角求角度
24. 正方形
25. 矩形
26. 平行四边形
27. 菱形
28. 梯形
29. 等腰梯形
30. 同底同高面积公式
31. 全等三角形
32. 相似三角形
33. 欧拉线
34. 垂线
35. 点到直线距离公式
36. 垂线段定理
37. 中线
38. 角平分线
39. 中垂线
40. 外心
41. 垂心
42. 重心
43. 内切圆
44. 外切圆
45. 位似比
46. 「半周角」公式
47. 内角和公式
48. 细分
49. 长度单位转换
50. 平面直角坐标系
51. 平移变换
52. 旋转变换
53. 对称变换
54. 条件语句
55. 循环语句
56. 取模 %
57. 迭代过程
58. Turtle库
59. 折线
60. 多边形
61. 圆
62. 起重机问题
63. 网格问题。
初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案) 初中数学几何模型大全及经典题型(含答案)全等变换平移:平行线段平移形成平行四边形。
对称:以角平分线、垂线或半角作轴进行对称,形成对称全等。
旋转:相邻等线段绕公共顶点旋转形成旋转全等。
对称半角模型通过翻折将直角三角形对称成正方形、等腰直角三角形或等边三角形。
旋转全等模型半角:相邻等线段所成角含1/2角及相邻线段。
自旋转:通过旋转构造相邻等线段的旋转全等。
共旋转:通过寻找两对相邻等线段构造旋转全等。
中点旋转:将倍长中点相关线段转换成旋转全等问题。
模型变形当遇到复杂图形找不到旋转全等时,先找两个正多边形或等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
几何最值模型对称最值:通过对称进行等量代换,转换成两点间距离及点到直线距离。
旋转最值:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
剪拼模型通过中点的180度旋转及平移改变图形的形状,例如将三角形剪拼成四边形或将矩形剪拼成正方形。
正方形的边长可以通过射影定理来求解。
假设正方形的边长为x,那么正方形的对角线长为x√2.将正方形分成两个等腰直角三角形,可以得到等腰直角三角形的斜边长为x√2/2.因此,根据射影定理,可以得到等腰直角三角形的高为x/2,进而得到正方形的边长为x=x√2/2.通过平移和旋转,可以将一个正方形变成另一个正方形。
这可以通过旋转相似模型来实现。
例如,两个等腰直角三角形可以通过旋转全等来实现形状的改变,而两个有一个角为300度的直角三角形可以通过旋转相似来实现形状的改变。
更一般地,两个任意相似的三角形可以通过旋转成一定角度来实现旋转相似,其中第三边所成夹角符合旋转“8”字的规律。
在相似证明中,需要注意边和角的对应关系。
相等的线段或比值在证明相似时可以通过等量代换来构造相似三角形。
另外,从三垂线到射影定理的演变,再到内外角平分线定理,需要注意它们之间的相同和不同之处。
初中数学常见几何模型大全

初中数学常见几何模型大全
以下是一些常见的初中数学几何模型大全:
1. 点(Point):没有大小和形状,用一个大写字母表示。
2. 直线(Line):由无限多个点组成,没有宽度和厚度。
3. 线段(Line Segment):直线上的两个点及其之间的部分。
4. 射线(Ray):起始于一个点,延伸至无穷远的部分。
5. 角(Angle):由两条射线共享一个端点而形成的图形。
6. 三角形(Triangle):由三条线段组成的图形。
7. 直角三角形(Right Triangle):一个角为直角(90度)的三角形。
8. 等腰三角形(Isosceles Triangle):具有两边长度相等的三角形。
9. 等边三角形(Equilateral Triangle):三条边都相等的三角形。
10. 平行四边形(Parallelogram):具有两对平行边的四边形。
11. 矩形(Rectangle):具有四个直角的平行四边形。
12. 正方形(Square):具有四个相等边和四个直角的矩形。
13. 梯形(Trapezoid):具有一对平行边的四边形。
14. 圆(Circle):由所有与圆心距离相等的点组成的图形。
15. 圆环(Annulus):由两个同心圆之间的区域组成。
16. 椭圆(Ellipse):平面上所有到两个给定点距离之和等于常数的点的轨迹。
17. 弧(Arc):圆上的一段连续的部分。
18. 扇形(Sector):圆心角及其对应的弧所围成的区域。
这些是初中数学中常见的几何模型,它们在解题和证明过程中起着重要的作用。
初中数学必背几何模型
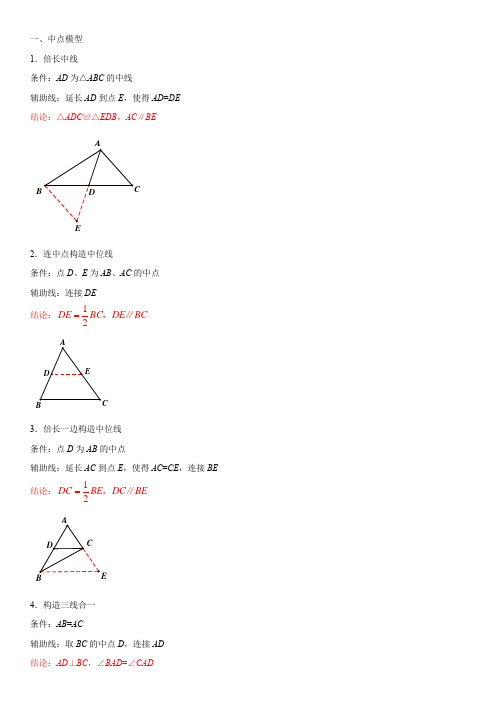
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。
初中数学四十八个几何模型

初中数学四十八个几何模型1. 直线与角直线是任意两点之间的最短路径。
角是由两条射线共享一个端点而形成的图形。
直线与角是几何学的基本概念。
线段是直线上两个点之间的部分。
线段具有长度,可以进行比较。
射线是由一个端点和延伸的直线组成的。
射线有起点,但没有终点,可以无限延伸。
4. 平面与平行线平面是一个没有边界的二维图形。
平行线是在同一个平面上,永远不会相交的直线。
三角形是由三条线段连接而成的图形。
三角形的内角和为180度。
6. 等腰三角形等腰三角形是具有两条边长度相等的三角形。
等腰三角形的底角也相等。
7. 直角三角形直角三角形是具有一个内角为90度的三角形。
直角三角形的斜边是其他两条边的平方和的开方。
8. 锐角三角形锐角三角形是所有内角都小于90度的三角形。
9. 钝角三角形钝角三角形是具有一个内角大于90度的三角形。
10. 正方形正方形是四条边相等且四个角都是直角的四边形。
11. 长方形长方形是具有两对相等且每一对内角都是直角的四边形。
12. 平行四边形平行四边形是具有两对平行边的四边形。
梯形是具有一对平行边的四边形。
梯形的非平行边也可以不等长。
菱形是具有四个边相等且对角线相等的四边形。
圆是具有相同半径的所有点的集合。
圆上任意两点与圆心构成的线段称为弦。
16. 圆心角圆心角是以圆心为顶点的角。
弧是圆上两个点之间的部分。
弦是圆上任意两点之间的线段。
切线是与圆只有一个交点的直线。
弧长是圆上一部分的长度。
扇形是以圆心为顶点的角所对应的圆上的区域。
22. 对称与相似对称是指一个图形通过某条线、点或平面进行折叠后与自身完全重合。
相似是指两个图形的形状相同但大小不同。
23. 二维几何体二维几何体包括平面图形。
24. 立体几何体立体几何体是具有实体和体积的图形。
25. 正方体正方体是六个面都是正方形的立体几何体。
26. 长方体长方体是六个面都是矩形的立体几何体。
27. 正圆柱体正圆柱体是圆和矩形结合形成的立体几何体。
初中数学模型23种(53张PPT)
等积变换模型
S△ACD=S△BCD
初二数学模型
八字模型
A B
E
C
D
角:∠A+ ∠B= ∠C+ ∠D 边:AD+BC>AB+CD
飞镖模型
A
D B
角:∠D = ∠B+ ∠C+ ∠A 边:AB+AC>BD+CD
C
内内角平分线模型
A
D
B
C
D 90 1 A 2
内外角平分线模型
A D
B
CE
D 1 A 2
外外角平分线模型
A
B E
D
C F
∠������=90°−
1 2
∠������
平行平分出等腰模型
E G A
C
H
M
F
B
HG=HM
D
等面积模型:D是BC的中点
A
h
B
a
D
b
C
������△������������������ ������△ ������������������
Smax
SOBM
S OAB
1 MN
2
max
OG
1 OA BG 2
1 4 4 1 5 4 18
2
2
M t, t2 5t
h
N t,t G
二次函数中等腰三角形存在性模型
A、B固定,找点C,使得△ABC是等腰三角形,C在两圆一线上
A
B
二次函数中直角三角形存在性模型
证明:DE2=BD2+CE2 △CEF为直角三角形
将军饮马模型
初中数学几何模型大汇总
初中数学几何模型大汇总几何模型是数学中的重要内容之一,对于初中数学学习来说,掌握并熟练运用各种几何模型是非常重要的。
下面是几何模型的大汇总,供初中学生学习参考。
一、平面图形的模型:1.直角三角形模型:直角三角形由两个直角边和一个斜边构成,可以利用直角三角形模型解决与直角三角形有关的问题。
2.等腰三角形模型:等腰三角形的底边两侧边相等,可以利用等腰三角形模型解决与等腰三角形有关的问题。
3.等边三角形模型:等边三角形的三边相等,可以利用等边三角形模型解决与等边三角形有关的问题。
4.平行四边形模型:平行四边形的对边平行且相等,可以利用平行四边形模型解决与平行四边形有关的问题。
5.矩形模型:矩形的四个角都是直角,可以利用矩形模型解决与矩形有关的问题。
6.正方形模型:正方形的四个边相等且都是直角,可以利用正方形模型解决与正方形有关的问题。
7.菱形模型:菱形的两对对边相等,可以利用菱形模型解决与菱形有关的问题。
8.圆形模型:圆形由中心点和半径构成,可以利用圆形模型解决与圆有关的问题。
二、立体图形的模型:1.正方体模型:正方体的六个面都是正方形,可以利用正方体模型解决与正方体有关的问题。
2.长方体模型:长方体的六个面有两个相等的长方形,可以利用长方体模型解决与长方体有关的问题。
3.球体模型:球体是由无数个半径相等的圆构成,可以利用球体模型解决与球体有关的问题。
4.圆柱模型:圆柱的底面是圆,可以利用圆柱模型解决与圆柱有关的问题。
5.圆锥模型:圆锥的底面是圆,可以利用圆锥模型解决与圆锥有关的问题。
6.圆台模型:圆台的底面是圆,可以利用圆台模型解决与圆台有关的问题。
7.正棱柱模型:正棱柱的底面是正多边形,可以利用正棱柱模型解决与正棱柱有关的问题。
8.正棱锥模型:正棱锥的底面是正多边形,可以利用正棱锥模型解决与正棱锥有关的问题。
9.正多面体模型:正多面体的面都是相等的正多边形,可以利用正多面体模型解决与正多面体有关的问题。
初中数学几何模型大全(精心整理)
三线八角同位角找F型内错角找Z型同旁内角找U型拐角模型1.锯齿形∠2=∠1+∠3 ∠1+∠2=∠3+∠42.鹰嘴型鹰嘴+小=大∠2=∠1+∠3 ∠2=∠1+∠33.铅笔头型∠1+∠2+∠3=360° ∠1+∠2+∠3+∠4=540°180×(n-1)等积变换模型S△ACD=S△BCD 八字模型∠A+∠B=∠C+∠DAD+BC>AB+CD飞镖模型∠D=∠B+∠C+∠AAB+AC>BD+CD内内角平分线模型∠A∠D=90°+12内外角平分线模型∠D=1∠A2外外角平分线模型∠D=90°-1∠A2平行平分出等腰模型HG=HM等面积模型 D是BC的中点S△ABD= S△ACD 倍长中线模型:D是BC的中点S△FBD= S△ECD角平分线构造全等模型角平分线垂直两边角平分线垂直中间角平分线构造轴对称以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,垂直也可以做为轴进行对称全等。
三垂模型拉手模型大小等边三角形虚线相等且夹角为60°大小等腰三角形顶角为a,虚线相等,且夹角为a大小等腰直角三角形虚线相等且夹角为90°大小正方形虚线相等,且夹角为90°半角模型正方形ABCD ∠EDF=45°得:EF=AE+CFCD=AD,∠ADC=90°,∠EDF=45°,∠A+∠C=180°得:EF=AE+CF∠BADAB=AD,∠B+∠D=180°,∠EAF=12得:EF=BE+DFAB=AC,∠BAC=90°,∠DAE=45°得:DE2=BD2+CE2△CEF为直角三角形上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
初中数学几何模型大全及解析
初中数学几何模型大全及解析一中点模型【模型1】倍长1、倍长中线;2、倍长类中线;3、中点遇平行延长相交【模型2】遇多个中点,构造中位线1、直接连接中点;2、连对角线取中点再相连【例】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE.(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.二角平分线模型【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形【例】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为 .三手拉手模型【例】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .四邻边相等的对角互补模型五半角模型六一线三角模型七弦图模型八最短路径模型【两点之间线段最短】1、将军饮马2、费马点【垂线段最短】【两边之差小于第三边】综合练习已知:如图1,正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.⑴求证:EG=CG且EG⊥CG;⑵将图1中△BEF绕B点逆时针旋转45º,如图2所示,取DF中点G,连接EG,CG.问⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.⑶将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(全)初中数学|23种模型汇总
1. 数列模型
数列模型是一组按照特定规律排列的数字,常见的数列有等差数列和等比数列。
在解题中,需要掌握其通项公式和求和公式。
2. 几何模型
几何模型是通过图形来表示问题,需要熟练掌握各种几何图形的性质和定理,如圆、三角形、直线等。
3. 等式模型
等式模型是通过等式来表示问题,需要掌握化简等式、配方、移项等技巧。
4. 方程模型
方程模型是通过方程来表示问题,需要掌握解方程的方法和技巧,如消元法、相似变形法、套公式法等。
5. 数据分析模型
数据分析模型需要对给定的数据进行处理和分析,如找出最大值、最小值、平均值等。
6. 概率模型
概率模型需要根据事件发生的可能性来计算概率,需要掌握概率的基本原理和计算方法。
8. 百分数模型
百分数模型需要将数值转化为百分数进行计算,需要掌握百分数的计算方法和应用。
9. 推理模型
推理模型需要根据已知的信息推出未知的结果,需要掌握逻辑思维和推理技巧,如分类讨论法、反证法等。
10. 图表模型
图表模型是通过图表来表示问题,需要掌握读图和解决图表问题的技巧。
11. 统计模型
统计模型需要对给定的数据进行统计分析,如频数分布、统计量计算等。
12. 函数模型
函数模型需要根据函数的定义和性质来计算未知量,需要掌握函数的基本概念和图像
变化规律。
13. 同余模型
同余模型需要根据同余关系来计算未知量,需要掌握同余关系的基本性质和计算方法,如模运算等。
14. 最优化模型
最优化模型需要找出满足特定条件下的最优解,需要掌握最优化方法和技巧,如最大
值最小值法、拉格朗日乘数法等。
16. 排列组合模型
排列组合模型需要计算不同元素之间的排列和组合方式,需要掌握排列组合的基本概
念和计算方法。
17. 质数模型
质数模型需要计算满足质数条件的解,需要掌握质数的基本性质和计算方法,如质因
数分解等。
23. 递推模型
递推模型需要利用递推公式来计算未知项,需要掌握递推公式的推导方法和递推问题
的解法。
