不等式试卷及答案

合集下载

高中试卷-2.2 基本不等式(含答案)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！2.2 基本不等式1. 利用基本不等式比较大小；2. 变形技巧：“1”的代换；3. 证明不等式；4. 不等式的证明技巧—字母轮换不等式的证法；5. 求参数的取值范围问题；6.求最大（小）值；7.均值不等式在实际问题中的应用一、单选题1．（2021·浙江高一单元测试）若0a B ．11a b>C ．222a b ab +>D ．a b +>-【答案】D 【解析】因为0a ->a b 所以a b >，11a b -<-即11a b>，故A ，B 正确.因为()20a b -³，所以222a b ab +³，所以222a b ab +>故C 正确.当 2,1a b =-=-时， +<-a b D 错误.故选：D2．（2021·全国高一课时练习）若0a b << ，则下列不等式一定成立的是（）A ．2a ba b +>>>B ．2a bb a +>>>C ．2a bb a +>>>D ．2a bb a +>>>【答案】C 【解析】因为0a b <<，所以2b a b >+，又由基本不等式可得：2a b +>，所以2a bb +>>，又2ab a >a >，因此2a bb a +>>>.故选：C.3．（2021·黑龙江南岗·哈师大附中高一期末）已知x ，y ＞0且x+4y=1，则11x y+的最小值为（）A ．8B ．9C ．10D ．11【答案】B 【解析】0x y Q ，＞且41x y += ，∴111144 1459x y x y x y x y y x +=++=+++³+（）（）．当且仅当1136x y ，==时，等号成立．∴11x y+的最小值为9．故选：B ．4．（2021·浙江高一单元测试）如图，某汽车运输公司刚买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y （单位：10万元）与营运年数x （x ∈N ）为二次函数关系，若使营运的年平均利润最大，则每辆客车应营运A ．3年B ．4年C ．5年D ．6年【答案】C 【解析】可设y=a(x －6)2+11，又曲线过(4，7)，∴7=a(4－6)2+11 ∴a=－1．即y=－x 2+12x －25，∴=12－(x+)≤12－2=2，当且仅当x=5时取等号. 故选C ．5．（2021·浙江鄞州·宁波华茂外国语学校高三一模）已知实数0a >，0b >，11111a b +=++，则2+a b 的最小值是（）A ．B ．C ．3D ．2【答案】B 【解析】∵0a >，0b >，11111a b +=++∴112(1)12(1)2(1)3[(1)2(1)](3[12]31111b a a b a b a b a b a b +++=+++-=+++×+-=+++-++++³-当且仅当2(1)111b a a b ++=++，即a =，b =.故选B6．（2021·全国高三课时练习（理））已知关于x 的不等式227x x a+³-在(,)x a Î+¥上恒成立，则实数a 的最小值为（）A ．1B ．52C ．2D ．32【答案】D 【解析】设2()2f x x x a=+-，,0x a x a >\->Q ， 227x x a+³-在(,)x a Î+¥上恒成立，需min ()7f x ³，22()22()222242f x x x a a a a x a x a=+=-++³´+=+--，当且仅当11x a x a -==-，即1x a =+时等号成立，3427,2a a \+³³.故选：D.7．（2021·广西兴宁·南宁三中高一期末）已知0a >，0b >，1ab =，且1m b a =+，1n a b=+，则m n +的最小值是（）A ．3B ．4C ．5D ．6【答案】B 【解析】由1ab =知，12m b b a =+=，12n a a b=+=，\()24m n a b +=+³=，当且仅当1a b ==时取等号.故m n +的最小值为4故选：B8．（2021·皇姑·辽宁实验中学高三其他（文））已知实数,x y 满足221x xy y -+=，则x y +的最大值为（）A ．1B ．2C ．3D ．4【答案】B 【解析】原式可化为：22()1313(2x y x y xy ++=+£+，解得22x y -£+£，当且仅当1x y ==时成立．所以选B.9．（2021·河南高二期末（理））设,,a b c 为任意正数．则111,,a b c b c a+++这三个数（）A ．都大于2B ．都小于2C ．至少有一个不小于2D ．至少有一个不大于2【答案】C 【解析】假设三个数均小于2，即1112,2,2a b c b c a +<+<+<，故1116a b c a b c+++++<，而1116a b c a b c +++++³++=，当1a b c ===时等号成立，这与1116a b c a b c+++++<矛盾，故假设不成立，故至少有一个不小于2，C 正确；取2a b c ===，计算排除BD ；取1a b c ===，计算排除A.故选：C.10．（2021·浙江金华·高一期末）已知x ，0y >，则41x y x y+++的最小值为（）A ．B ．6C ．D ．【答案】B 【解析】因为x ，0y >，由基本不等式可得，416x y x y +++³=，当且仅当2,1x y ==时等号成立．故选：B ．二、多选题11．（2021·浙江高一单元测试）已知函数11(0)y x x x=++<，则该函数的（）．A ．最小值为3B ．最大值为3C ．没有最小值D ．最大值为1-【答案】CD 【解析】0x <Q ，\函数111()111()y x x x x éù=++=--++-+=-êú-ëû…，当且仅当1x =-时取等号，\该函数有最大值1-．无最小值．故选：CD ．12．（2021·海南高二期末）已知实数a 、b 满足0a b >>，则下列不等式一定成立的有（）A ．22a b D ．a b ab+>【答案】BC 【解析】因为0a b >>，于是22a b >，A 项不成立；由0a b >>得a b -<-，B 项正确；由基本不等式可知2b a a b +³=，因为a b ¹，所以等号取不到，所以C 项正确；当3a =，2b =时，D 项不成立.故选：BC.13．（2021·山东德州·高三二模）若正实数a ，b 满足1a b +=则下列说法正确的是（）A ．ab 有最大值14BC ．11a b+有最小值2D ．22a b +有最大值12【答案】AB 【解析】对A,2211224a b ab +æöæö£==ç÷ç÷èøèø,当且仅当12a b ==时取等号.故A 正确.对B,22a b a b a b =++£+++=,+£,当且仅当12a b ==时取等号.故B 正确.对C,()1111224b a a b a b a b a b æö+=++=++³+è=ç÷ø.当且仅当12a b ==时取等号.所以11a b +有最小值4.故C 错误.对D, ()()2222222121a b a ab b a a bb+=Þ++=£+++,即2212a b +³,故22a b +有最小值12.故D 错误.故选：AB14．（2021·山东泰山·泰安一中高一期中）设0a >，0b >，给出下列不等式恒成立的是（）.A ．21a a+>B ．296a a+>C ．()114a b a b æö++³ç÷èøD ．114a b a b æöæö++³ç÷ç÷èøèø【答案】ACD 【解析】设0a >，0b >，22131024a a a æö+-=++>ç÷èø，A 成立，2296(3)0a a a +-=-…，B 不成立()111124b a a b a b a b æö++=+++³+=ç÷èø，当且仅当b a a b =即a b =时取等号，故C 成立，12a a +…，12b b +…，114a b a b æöæö\++³ç÷ç÷èøèø，当且仅当1a a =，1b b =即1a b ==时取等号，故D 成立，故选：ACD ．三、填空题15．（2021·浙江高一单元测试）已知04x <<，则414x x+-的最小值为______．【答案】94．【解析】用“1”的代换法配凑出定值，然后用基本不等式得最小值．4144114(4)95444444x x x x x x x x x x +--æöæöæö+=+=++ç÷ç÷ç÷---èøèøèø…，当且仅当4(4)4x x x x -=-，解得1288,3x x ==，又因为04x <<，所以83x =时等号成立．故答案为：94．16．（2021·全国高一）若0, 0a >b >，则“4a b +£”是 “4ab £”的_____条件【答案】充分不必要【解析】当0,0a b >>时，由基本不等式，可得a b +³，当4a b +£时，有4a b £+£，解得4ab £，充分性是成立的；例如：当1,4a b ==时，满足4ab £，但此时=5>4a+b ，必要性不成立，综上所述，“4a b +£”是“4ab £”的充分不必要条件.故答案为充分不必要条件.17．（2021·全国高一）若实数x ，y 满足xy=1，则x 2+4y 2的最小值为______．【答案】4【解析】若实数,x y 满足1xy=,则2242244x y x y xy +³××==,当且仅当2x y ==,上式取得最小值4故答案为：4四、双空题18．（2021·全国高一课时练习）若1x >，则1141x x ++-的最小值是______，此时x =______.【答案】9 32【解析】因为1x >，即10x ->所以1114=4(1)545911x x x x ++-++³+=--当且仅当14(1)1x x -=-即32x =时取等号．故第一空填9，第二空填3219．（2021·浙江鄞州·宁波诺丁汉附中高一期中）用一根长为12m 的铝合金条做成一个“目”字形窗户的框架（不计损耗），要使这个窗户通过的阳光最充足，则框架的宽为________m ；高为________m .【答案】323 【解析】设窗户的宽为x ，则其高为62x -，要使阳光充足，只要面积最大，()()()23962232[]22x x S x x x x +-=-=-£´=，当且仅当32x =时等号成立，这时高为3m .故答案为：(1).32(2). 3用基本不等式求最值问题:已知0,0x y >>，则：(1)如果积xy 是定值p ，那么当且仅当x y =时，x y +有最小值是 .(简记：积定和最小)(2)如果和x y +是定值p ，那么当且仅当x y =时，xy 有最大值是24p.(简记：和定积最大)20．（2021·浙江金华·高一期中）已知正数a ，b 满足a+b=1，则1b a b+的最小值等于__________ ，此时a=____________.【答案】3 12【解析】根据题意，正数a 、b 满足1a b +=，则1113b b a b b a a b a b a b ++=+=++³=，当且仅当12a b ==时，等号成立，故1b a b+的最小值为3，此时12a =.故答案为：3；12.21．（2017·北京人大附中高一期中）已知正数x 、y 满足1x y +=，则：（1）22xy +的最小值为________．（2）若14a x y+>恒成立，则实数a 的取值范围是______．【答案】12(),9-¥ 【解析】(1)因为正数x ､y 满足1x y +=,所以21()24x y xy +£=,当且仅当12x y ==时取等号,所以2221()2122x y x y xy xy =+-=-³+;(2)因为正数x ､y 满足1x y +=,14144()1459x y x y x y x y y x\+=++=+++³+=,当且仅当4x y y x =,即12,33x y ==时取等号,所以9a <;故答案为:()1;,92-¥五、解答题22．（2021·全国高一课时练习）已知a ，b ，c 为任意实数，求证：222a b c ab bc ca ++++…．【答案】见解析【解析】∵222a b ab +…，22222,2b c bc c a ca ++……，∴()22222()a b c ab bc ca ++++…．即222a b c ab bc ca ++++…．当且仅当a b c ==时，等号成立．23．（2021·全国）设a ，b ，c 都是正数，求证：bc ca ab a b c a b c++++…．【答案】详见解析【解析】证明：∵a ，b ，c 都是正数，∴由重要不等式可得：2bc ca c a b +³①，当且仅当bc ac a b =时等号成立，即a b =；2bc ab b a c +³②，当且仅当bc ab a c =时等号成立，即a c =；2ac ab a b c +³=③，当且仅当ac ab b c =时等号成立，即b c =；∴①+②+③得：22()bc ca ab a b c a b c æö++³++ç÷èø∴bc ca ab a b c a b c++++…；当且仅当a b c ==时等号成立.24．（2021·全国高一课时练习）已知a>0，b>0，a ＋b ＝1，求证：11119a b æöæö++³ç÷ç÷èøèø.【答案】证明见解析【解析】证明：法一：因为a>0，b>0，a ＋b ＝1，所以1＋1a ＝1＋a b a +＝2＋b a ，同理1＋1b ＝2＋a b，故11112252549b a b a a b a b a b æöæöæöæöæö++=++=++³+=ç÷ç÷ç÷ç÷ç÷èøèøèøèøèø.所以11119a b æöæö++³ç÷ç÷èøèø（当且仅当12a b ==时取等号）.法二：111111211111a b a b a b ab ab ab ab +æöæö++=+++=++=+ç÷ç÷èøèø，因为a ，b 为正数，a ＋b ＝1，所以ab≤2124a b +æö=ç÷èø，于是14ab ³，28ab ³，因此1111189a b æöæö++³+=ç÷ç÷èøèø（当且仅当12a b ==时取等号）.25．（2021·全国高一课时练习）用篱笆围一个面积为2100m 的矩形菜园，问这个矩形的长、宽各为多少时，所用篱笆最短，最短的篱笆是多少？【答案】矩形的长、宽都为10m 时，所用篱笆最短，最短篱笆为40m .【解析】设矩形菜园的长为m x ，宽为m y ，则100xy =，篱笆的长为()2x y m +.由基本不等式可得()2240x y +³´=，当且仅当10x y ==时，等号成立，因此，这个矩形的长、宽都为10m 时，所用篱笆最短，最短篱笆为40m .26．（2021·浙江高一单元测试）(1)已知x >3，求y =x +4x 3的最小值，并求取到最小值时x 的值；(2)已知x >0，y >0，x 2+y 3=2，求xy 的最大值，并求取到最大值时x 、y 的值．【答案】(1)当x =5时，y 的最小值为7．(2) x =2，y =3时，xy 的最大值为6．【解析】(1)已知x >3，则：x ―3>0，故：y =x +4x 3=x ―3+4x 3+3≥3=7，当且仅当：x ―3=4x3，解得：x =5，即：当x =5时，y 的最小值为7．(2)已知x >0，y >0，x 2+y 3=2，则：x 2+y 3≥解得：xy ≤6，即：x 2=y 3=1，解得：x =2，y =3时，xy 的最大值为6．27．（2021·浙江高一单元测试）已知0,0x y >>且191x y +=，求使不等式x y m +³恒成立的实数m 的取值范围．【答案】16m ….【解析】由191x y +=，则19()x y x y x y æö+=++ç÷èø910x y y x =++1016+=…．当且仅当169x y x y y x +=ìïí=ïî即412x y =ìí=î时取到最小值16．若x y m +…恒成立，则16m …．。

高中数学不等式经典题型专题训练试题(含答案)

高中数学不等式经典题型专题训练试题学校：___________姓名：___________班级：___________考号：___________说明：１、本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分100分。

考试时间120分钟。

２、考生请将第Ⅰ卷选择题的正确选项填在答题框内，第Ⅱ卷直接答在试卷上。

考试结束后，只收第Ⅱ卷第Ⅰ卷（选择题）一．单选题（共10小题，每题2分，共20分）1．设a=sin14°+cos14°，b=sin16°+cos16°，，则a，b，c大小关系（）A．a＜b＜c B．b＜a＜c C．c＜b＜a D．a＜c＜b2．已知实数x，y满足条件，则目标函数z=2x-y（）A．有最小值0，有最大值6B．有最小值-2，有最大值3C．有最小值3，有最大值6D．有最小值-2，有最大值63．若x是三角形的最小内角，则函数y=sinx+cosx+sinxcosx的最大值是（）A．-1B．C．D．4．不等式x2-|x|-2＜0的解集是（）A．{x|-2＜x＜2}B．{x|x＜-2或x＞2}C．{x|-1＜x＜1}D．{x|x＜-1或x＞1}5．若不等式f（x）=ax2-x-c＞0的解集为（-2，1），则函数y=f（x）的图象为（）A．B．C．D．6．设a=0.20.3，b=0.20.2，c=log20.4，则a，b，c的大小关系为（）A．c＜a＜b B．c＜b＜a C．a＜b＜c D．b＜c＜a7．设0＜b＜a＜1，则下列不等式中成立的是（）A．a2＜ab＜1B．C．ab＜b2＜1D．2b＜2a＜28．对任意的锐角α，β，下列不等关系中正确的是（）A．sin（α+β）＞sinα+sinβB．sin（α+β）＞cosα+cosβC．cos（α+β）＜sinα+sinβD．cos（α+β）＜cosα+cosβ9．若0＜m＜n，则下列结论正确的是（）A．B．2m＞2n C．D．log2m＞log2n10．设a＜b＜0，则下列不等式中不成立的是（）A．B．C．|a|＞-b D．二．填空题（共10小题，每题2分，共20分）11．已知x＞-1，y＞0且满足x+2y=2，则的最小值为______．12．已知a，b∈R+，且2a+b=1则的最大值是______．13．已知向量，若⊥，则16x+4y的最小值为______．14．若x＞0，y＞0，且+=1，则x+y的最小值是______．15、在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为______（m）．16．已知x＞-1，y＞0且满足x+2y=2，则的最小值为______．17．若实数a+b=2，a＞0，b＞0，则的最小值为______．18．若x，y满足约束条件，则z=3x-y的最小值是______．19．若a，b∈R，且4≤a2+b2≤9，则a2-ab+b2的范围是______．20．已知f（x）=，不等式f（x）≥-1的解集是______．三．简答题（共10小题，共60分）21．（6分）已知x＞0，y＞0，（1）若2x+y=1，求+的最小值．（2）若x+8y-xy=0，求xy的最小值．22．（6分）设a，b，c均为正数，且a+b+c=1，证明：（1）ab+bc+ca≤；（2）++≥1．23．（6分）已知a，b，c均为正实数，且满足abc=1，证明：（1）a+b+c≥；（2）a2+b2+c2≥24．（6分）设函数f（x）=|x+3|-|x-4|①解不等式f（x）＞3；②求函数f（x）的最小值．25．（6分）已知向量=（1+sin2x，sinx-cosx），=（1，sinx+cosx），函数f（x）=•．（Ⅰ）求f（x）的最大值及相应的x的值；（Ⅱ）在△ABC中，a，b，c分别是三个内角A，B，C所对边，若f（）=2，a=2，求△ABC 面积的最大值．26．（6分）27．（4分）已知：x，y，z∈R，x2+y2+z2=1，则x-2y-3z的最大值为______．28．（4分）若a，b，c∈R+，且++=1，求a+2b+3c的最小值．29．（10分）某工厂生产一种产品的成本费共由三部分组成：①原材料费每件50元；②职工工资支出7500+20x元；③电力与机器保养等费用为x2-30x+600元：其中x是该厂生产这种产品的总件数．（I）把每件产品的成本费p（x）（元）表示成产品件数x的函数，并求每件产品的最低成本费；（Ⅱ）如果该厂生产的这种产品的数量x不超过170件且能全部销售，根据市场调查，每件产品的销售价为Q（x）（元），且Q（x）=1240-．试问生产多少件产品，总利润最高？并求出最高总利润．（总利润=总销售额-总的成本）30．（6分）已知定义在R上的函数f（x）=|x-1|+|x+2|的最小值为a．（1）求a的值；（2）若m，n是正实数，且m+n=a，求+的最小值．参考答案一．单选题（共__小题）1．设a=sin14°+cos14°，b=sin16°+cos16°，，则a，b，c大小关系（）A．a＜b＜c B．b＜a＜c C．c＜b＜a D．a＜c＜b答案：D解析：解：由题意知，a=sin14°+cos14°==，同理可得，b=sin16°+cos16°=，=，∵y=sinx在（0，90°）是增函数，∴sin59°＜sin60°＜sin61°，∴a＜c＜b，故选D．2．已知实数x，y满足条件，则目标函数z=2x-y（）A．有最小值0，有最大值6B．有最小值-2，有最大值3C．有最小值3，有最大值6D．有最小值-2，有最大值6答案：D解析：解：画出不等式组表示的平面区域如图中阴影部分所示．当目标函数z=2x-y过直线x=3与直线y=0的交点（3，0），目标函数取得最大值6；当目标函数z=2x-y过直线x=0与直线x-y+2=0的交点（0，2）时，目标函数取得最小值-2．故选D．3．若x是三角形的最小内角，则函数y=sinx+cosx+sinxcosx的最大值是（）A．-1B．C．D．答案：D解析：解：y=sinx+cosx+sinxcosx=sinx（1+cosx）+1+cosx-1=（1+sinx）（1+cosx）-1≤[（1+sinx）2+（（1+cosx）2]-1（当且仅当1+sinx=1+cosx时成立，此时sinx=cosx=）即y（max）=+故选D4．不等式x2-|x|-2＜0的解集是（）A．{x|-2＜x＜2}B．{x|x＜-2或x＞2}C．{x|-1＜x＜1}D．{x|x＜-1或x＞1}答案：A解析：解：原不等式化为|x|2-|x|-2＜0因式分解得（|x|-2）（|x|+1）＜0因为|x|+1＞0，所以|x|-2＜0即|x|＜2解得：-2＜x＜2．故选A5．若不等式f（x）=ax2-x-c＞0的解集为（-2，1），则函数y=f（x）的图象为（）A．B．C．D．答案：B解析：解：∵不等式f（x）=ax2-x-c＞0的解集为（-2，1），∴a＜0，且-2，1是对应方程ax2-x-c=0的两个根，∴（-2，0），（1，0）是对应函数f（x）=ax2-x-c与x轴的两个交点，∴对应函数y=f（x）的图象为B．故选B．6．设a=0.20.3，b=0.20.2，c=log20.4，则a，b，c的大小关系为（）A．c＜a＜b B．c＜b＜a C．a＜b＜c D．b＜c＜a答案：A解析：解：∵函数y=0.2x是减函数，0.3＞0.2，故有a=0.20.3＜0.20.2=1，又a=0.20.3＞0，可得b＞a ＞0．由于函数y=log2x在（0，+∞）上是增函数，故c=log20.4＜log21=0，即c＜0．综上可得，b＞a＞c，故选A．7．设0＜b＜a＜1，则下列不等式中成立的是（）A．a2＜ab＜1B．C．ab＜b2＜1D．2b＜2a＜2答案：D解析：解：采用特殊值法，取a=，b=．则a2=，b2=，ab=，故知A，C错；对于B，由于函数y=是定义域上的减函数，∴，故B错；对于D，由于函数y=2x是定义域上的增函数，∴2b＜2a＜2，故D对．故选D．8．对任意的锐角α，β，下列不等关系中正确的是（）A．sin（α+β）＞sinα+sinβB．sin（α+β）＞cosα+cosβC．cos（α+β）＜sinα+sinβD．cos（α+β）＜cosα+cosβ答案：D解析：解：对于AB中的α，β可以分别令为30°，60°则知道A，B均不成立对于C中的α，β可以令他们都等于15°，则知道C不成立cos（α+β）=cosαcosβ-sinαsinβ＜cosα×1+cosβ×1=cosα+cosβ故选D9．若0＜m＜n，则下列结论正确的是（）A．B．2m＞2n C．D．log2m＞log2n 答案：C解析：解：观察B，D两个选项，由于底数2＞1，故相关的函数是增函数，由0＜m＜n，∴2m＜2n，log2m＜log2n，所以B，D不对．又观察A，C两个选项，两式底数满足0＜＜1，故相关的函数是一个减函数，由0＜m＜n，∴，所以A不对，C对．故答案为C．10．设a＜b＜0，则下列不等式中不成立的是（）A．B．C．|a|＞-b D．答案：D解析：解：∵a＜b＜0，∴，A正确，-a＞-b＞0，，B正确，|a|＞|b|=-b，C正确；，故D不正确．故选D．二．填空题（共__小题）11．已知x＞-1，y＞0且满足x+2y=2，则的最小值为______．答案：3解析：解：∵x＞-1，y＞0且满足x+2y=2，∴x+1＞0且x+1+2y=3，∴=（）（x+1+2y）=[5++]≥（5+2）=3，当且仅当=即x=0且y=1时取等号，故答案为：3．12．已知a，b∈R+，且2a+b=1则的最大值是______．答案：解析：解：∵2a+b=1，∴4a2+b2=1-4ab，∴S==4ab+2-1，令=t＞0，则S=4-，∵2a+b=1，∴1≥2⇒0＜t≤故当t=时，S有最大值为：故答案为：．13．已知向量，若⊥，则16x+4y的最小值为______．答案：8解析：解：∵∴4（x-1）+2y=0即4x+2y=4∵=当且仅当24x=22y即4x=2y=2取等号故答案为814．若x＞0，y＞0，且+=1，则x+y的最小值是______．答案：25解析：解：∵x＞0，y＞0，且+=1，∴x+y=（x+y）（+）=17++≥17+2=25当且仅当=，即x=5，y=20时取等号，∴x+y的最小值是25，故答案为：25．15、在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为______（m）．答案：20解析：解：设矩形高为y，由三角形相似得：=，且x＞0，y＞0，x＜40，y＜40，⇒40=x+y≥2，仅当x=y=20m时，矩形的面积s=xy取最大值400m2．故答案为：20．16．已知x＞-1，y＞0且满足x+2y=2，则的最小值为______．答案：3解析：解：∵x＞-1，y＞0且满足x+2y=2，∴x+1＞0且x+1+2y=3，∴=（）（x+1+2y）=[5++]≥（5+2）=3，当且仅当=即x=0且y=1时取等号，故答案为：3．17．若实数a+b=2，a＞0，b＞0，则的最小值为______．答案：解析：解：∵实数a+b=2，a＞0，b＞0，则=+=++≥+2=+，当且仅当b=a=4-2时取等号．故答案为：．18．若x，y满足约束条件，则z=3x-y的最小值是______．答案：-4解析：解：由约束条件作出可行域如图，化目标函数z=3x-y为y=3x-z，由图可知，当直线y=3x-z过点C（0，4）时直线在y轴上的截距最大，z有最小值为-4．故答案为：-4．19．若a，b∈R，且4≤a2+b2≤9，则a2-ab+b2的范围是______．答案：[2，]解析：解：∵a，b∈R，且4≤a2+b2≤9；∴设a=rcosθ，b=rsinθ，且2≤r≤3，∴s=a2-ab+b2=r2cos2θ-r2sinθcosθ+r2sin2θ=r2（1-sinθcosθ）=r2（1-sin2θ），由三角函数的图象与性质，得；当sin2θ取最大值1且r取最小值2时，s取得最小值2，当sin2θ取最小值-1且r取最大值3时，s取得最大值；综上，a2-ab+b2的范围是[2，]．故答案为：．20．已知f（x）=，不等式f（x）≥-1的解集是______．答案：{x|-4≤x≤2}解析：解：∵已知f（x）=，故由不等式f（x）≥-1可得①，或②．解①可得-4＜x≤0，解②可得0＜x≤2．综上可得，不等式的解集为{x|-4≤x≤2}，故答案为{x|-4≤x≤2}．三．简答题（共__小题）21．已知x＞0，y＞0，（1）若2x+y=1，求+的最小值．（2）若x+8y-xy=0，求xy的最小值．答案：解：（1）+=（+）（2x+y）=2+++1=3++≥3+2，当且仅当2x2=y2等号成立，∴+的最小值为3+2．（2）∵x+8y-xy=0，∴xy=x+8y≥2，当且仅当x=8y时等号成立．∴≥4，∴xy≥32，∴xy的最小值为32．解析：解：（1）+=（+）（2x+y）=2+++1=3++≥3+2，当且仅当2x2=y2等号成立，∴+的最小值为3+2．（2）∵x+8y-xy=0，∴xy=x+8y≥2，当且仅当x=8y时等号成立．∴≥4，∴xy≥32，∴xy的最小值为32．22．设a，b，c均为正数，且a+b+c=1，证明：（1）ab+bc+ca≤；（2）++≥1．答案：证明：（1）由a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca，可得a2+b2+c2≥ab+bc+ca，（当且仅当a=b=c取得等号）由题设可得（a+b+c）2=1，即a2+b2+c2+2ab+2bc+2ca=1，即有3（ab+bc+ca）≤1，则ab+bc+ca≤；（2）+b≥2a，+c≥2b，+a≥2c，故+++（a+b+c）≥2（a+b+c），即有++≥a+b+c．（当且仅当a=b=c取得等号）．故++≥1．解析：证明：（1）由a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca，可得a2+b2+c2≥ab+bc+ca，（当且仅当a=b=c取得等号）由题设可得（a+b+c）2=1，即a2+b2+c2+2ab+2bc+2ca=1，即有3（ab+bc+ca）≤1，则ab+bc+ca≤；（2）+b≥2a，+c≥2b，+a≥2c，故+++（a+b+c）≥2（a+b+c），即有++≥a+b+c．（当且仅当a=b=c取得等号）．故++≥1．23．已知a，b，c均为正实数，且满足abc=1，证明：（1）a+b+c≥；（2）a2+b2+c2≥．答案：证明：∵a，b，c∈R+∴a+b≥2，b+c≥2，a+c≥2∴2a+2b+2c≥2+2+2∴a+b+c≥++∵abc=1，∴a+b+c≥++；（2）∵a2+b2≥2ab，b2+c2≥2bc，a2+c2≥2ac，∴2a2+2b2+2c2≥2ab+2bc+2ac，∴a2+b2+c2≥ab+bc+ac，∵ab+bc+ac=≥=++，∴a2+b2+c2≥++．解析：证明：∵a，b，c∈R+∴a+b≥2，b+c≥2，a+c≥2∴2a+2b+2c≥2+2+2∴a+b+c≥++∵abc=1，∴a+b+c≥++；（2）∵a2+b2≥2ab，b2+c2≥2bc，a2+c2≥2ac，∴2a2+2b2+2c2≥2ab+2bc+2ac，∴a2+b2+c2≥ab+bc+ac，∵ab+bc+ac=≥=++，∴a2+b2+c2≥++．24．设函数f（x）=|x+3|-|x-4|①解不等式f（x）＞3；②求函数f（x）的最小值．答案：解：①不等式f（x）＞3，即|x+3|-|x-4|＞3．而|x+3|-|x-4|表示数轴上的x对应点到-3对应点和4对应点的距离之差，数轴上的2对应点到-3对应点和4对应点的距离之差为3，故不等式的解集为{x|x＞2}．…（3分）②f（x）=|x+3|-|x-4|表示数轴上的x对应点到-3对应点和4对应点的距离之差，可得函数f（x）的最小值为-7．（7分）解析：解：①不等式f（x）＞3，即|x+3|-|x-4|＞3．而|x+3|-|x-4|表示数轴上的x对应点到-3对应点和4对应点的距离之差，数轴上的2对应点到-3对应点和4对应点的距离之差为3，故不等式的解集为{x|x＞2}．…（3分）②f（x）=|x+3|-|x-4|表示数轴上的x对应点到-3对应点和4对应点的距离之差，可得函数f（x）的最小值为-7．（7分）25．已知向量=（1+sin2x，sinx-cosx），=（1，sinx+cosx），函数f（x）=•（Ⅰ）求f（x）的最大值及相应的x的值；（Ⅱ）在△ABC中，a，b，c分别是三个内角A，B，C所对边，若f（）=2，a=2，求△ABC 面积的最大值．答案：解：（Ⅰ）∵=（1+sin2x，sinx-cosx），=（1，sinx+cosx），∴f（x）=•=1+sin2x+sin2x-cos2x，=1+sin2x-cos2x，=1+sin（2x-），∴当2x-=2kπ+即x=+kπ，k∈Z时，函数取得最大值1+．（Ⅱ）由（I）知f（）=2时，sin（A-）=，∴A-=2kπ+或A-=2kπ+，即A=+2kπ或A=π+2kπ，k∈Z，∵A是三角形的一个内角，∴A=，即△ABC是直角三角形．∵a=2，∴b2+c2=4，∴S△ABC=bc≤=1（当且仅当b=c=时，取得最大值），∴△ABC面积的最大值为1．解析：解：（Ⅰ）∵=（1+sin2x，sinx-cosx），=（1，sinx+cosx），∴f（x）=•=1+sin2x+sin2x-cos2x，=1+sin2x-cos2x，=1+sin（2x-），∴当2x-=2kπ+即x=+kπ，k∈Z时，函数取得最大值1+．（Ⅱ）由（I）知f（）=2时，sin（A-）=，∴A-=2kπ+或A-=2kπ+，即A=+2kπ或A=π+2kπ，k∈Z，∵A是三角形的一个内角，∴A=，即△ABC是直角三角形．∵a=2，∴b2+c2=4，∴S△ABC=bc≤=1（当且仅当b=c=时，取得最大值），∴△ABC面积的最大值为1．26、解：由柯西不等式：（1+3+5）²≤（a+b+c）（）因为：a+b+c=12所以（1+3+5）²≤12*（）81≤12*（）≤当且仅当==时取等号即：最小值为27．已知：x，y，z∈R，x2+y2+z2=1，则x-2y-3z的最大值为______．答案：解：由已知x，y，z∈R，x2+y2+z2=1，和柯西不等式（a2+b2+c2）（e2+f2+g2）≥（ae+bf+cg）2则构造出[12+（-2）2+（-3）2]（x2+y2+z2）≥（x-2y-3z）2．即：（x-2y-3z）2≤14即：x-2y-3z的最大值为．故答案为．解析：解：由已知x，y，z∈R，x2+y2+z2=1，和柯西不等式（a2+b2+c2）（e2+f2+g2）≥（ae+bf+cg）2则构造出[12+（-2）2+（-3）2]（x2+y2+z2）≥（x-2y-3z）2．即：（x-2y-3z）2≤14即：x-2y-3z的最大值为．故答案为．28．若a，b，c∈R+，且，求a+2b+3c的最小值．答案：解：∵a，b，c∈R+，，∴=1+1+1，当且仅当a=2b=3c=3时取等号．即a+2b+3c≥9，∴a+2b+3c的最小值为9．解析：解：∵a，b，c∈R+，，∴=1+1+1，当且仅当a=2b=3c=3时取等号．即a+2b+3c≥9，∴a+2b+3c的最小值为9．29．某工厂生产一种产品的成本费共由三部分组成：①原材料费每件50元；②职工工资支出7500+20x元；③电力与机器保养等费用为x2-30x+600元：其中x是该厂生产这种产品的总件数．（I）把每件产品的成本费p（x）（元）表示成产品件数x的函数，并求每件产品的最低成本费；（Ⅱ）如果该厂生产的这种产品的数量x不超过170件且能全部销售，根据市场调查，每件产品的销售价为Q（x）（元），且Q（x）=1240-．试问生产多少件产品，总利润最高？并求出最高总利润．（总利润=总销售额-总的成本）答案：解：（I）P（x）=50++=+x+40．由基本不等式得P（x）≥2+40=220．当且仅当=x，即x=90时，等号成立．所以P（x）=+x+40．每件产品的最低成本费为220 元．（Ⅱ）设总利润为y=f（x）=xQ（x）-xP（x）=，f′（x）==（x-100）（x+120）当0＜x＜100时，f′（x）＞0，当x＞100时，f′（x）＜0．所以f（x）在（0，100）单调递增，在（100，170）单调递减，所以当x=100时，ymax=f（100）=故生产100件产品时，总利润最高，最高总利润为．解析：解：（I）P（x）=50++=+x+40．由基本不等式得P（x）≥2+40=220．当且仅当=x，即x=90时，等号成立．所以P（x）=+x+40．每件产品的最低成本费为220 元．（Ⅱ）设总利润为y=f（x）=xQ（x）-xP（x）=，f′（x）==（x-100）（x+120）当0＜x＜100时，f′（x）＞0，当x＞100时，f′（x）＜0．所以f（x）在（0，100）单调递增，在（100，170）单调递减，所以当x=100时，ymax=f（100）=故生产100件产品时，总利润最高，最高总利润为．30．已知定义在R上的函数f（x）=|x-1|+|x+2|的最小值为a．（1）求a的值；（2）若m，n是正实数，且m+n=a，求+的最小值．答案：解：（1）由|x-1|+|x+2|的几何意义表示了数轴上点x到点1与到点-2的距离之和，如图：则x在[-2，1]上时，函数f（x）=|x-1|+|x+2|取得最小值a=3．即a=3．（2）由题意，m+n=3，则+=+=+++=1++≥1+2=1+．（当且仅当=时，等号成立）．即+的最小值为1+．解析：解：（1）由|x-1|+|x+2|的几何意义表示了数轴上点x到点1与到点-2的距离之和，如图：则x在[-2，1]上时，函数f（x）=|x-1|+|x+2|取得最小值a=3．即a=3．（2）由题意，m+n=3，则+=+=+++=1++≥1+2=1+．（当且仅当=时，等号成立）．即+的最小值为1+．。

中考数学真题精选专题试卷不等式(含答案解析) (含答案解析)

不等式一．选择题（共15小题）1．（•怀化）下列不等式变形正确的是（）2．（•乐山）下列说法不一定成立的是（）3．（•黄石）当1≤x≤2时，ax+2＞0，则a的取值范围是（）4．（•南充）若m＞n，下列不等式不一定成立的是（）＞5．（•扬州）已知x=2是不等式（x﹣5）（ax﹣3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（）6．（•绥化）关于x的不等式组的解集为x＞1，则a的取值范围是（）解：因为不等式组7．（•桂林）下列数值中不是不等式5x≥2x+9的解的是（）8．（•嘉兴）一元一次不等式2（x+1）≥4的解在数轴上表示为（）B9．（•丽水）如图，数轴上所表示关于x的不等式组的解集是（）10．（•长沙）在数轴上表示不等式组的解集，正确的是（）B，再分别表示在数轴上即可得11．（•临沂）不等式组的解集，在数轴上表示正确的是（）．．．．，由①得，12．（•湖北）在数轴上表示不等式2（1﹣x）＜4的解集，正确的是（）B13．（•娄底）一元一次不等式组的解集在数轴上表示出来，正确的是（）．．．．14．（•南宁）不等式2x﹣3＜1的解集在数轴上表示为（）．．C．．15．（•河南）不等式的解集在数轴上表示为（）．．解：∴不等式的解集在数轴上表示为：二．填空题（共12小题）16．（•衢州）写出一个解集为x＞1的一元一次不等式：x﹣1＞0．17．（•茂名）不等式x﹣4＜0的解集是x＜4．18．（•吉林）不等式3+2x＞5的解集是x＞1．19．（•南充）不等式＞1的解集是x＞3．20．（•南昌）不等式组的解集是﹣3＜x≤2．21．（•湖州）解不等式组．22．（•黑龙江）不等式组的解集是2≤x＜4．，解①得23．（•乌鲁木齐）不等式组的解集为﹣2＜x＜1．解：，24．（•营口）不等式组的所有正整数解的和为6．﹣≤1不等式组不等式组25．（•安顺）不等式组的最小整数解是x=﹣3．＞﹣，＜，26．（•广安）不等式组的所有整数解的积为0．x，解不等式②得：27．（•天水）不等式组的所有整数解是0．，解不等式①得，，解不等式②得，x三．解答题（共3小题）28．（•南京）解不等式2（x+1）﹣1≥3x+2，并把它的解集在数轴上表示出来．29．（•安徽）解不等式：＞1﹣．30．（•自贡）解不等式：﹣x＞1，并把解集在数轴上表示出来．。

第5章一元一次不等式试卷2(含答案)

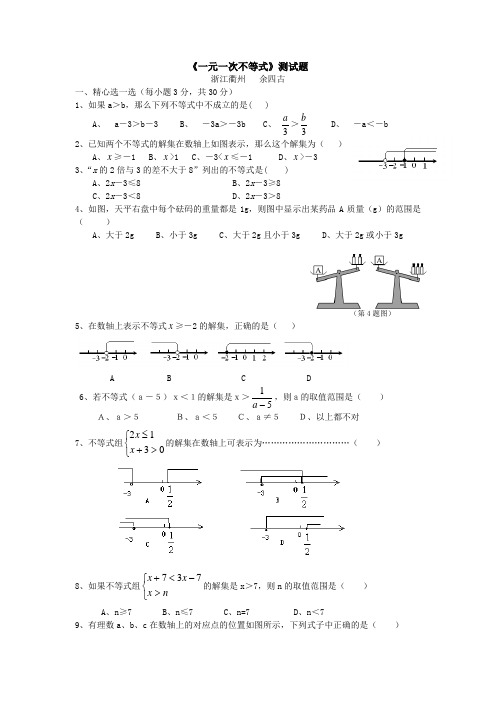
《一元一次不等式》测试题浙江衢州余四古一、精心选一选（每小题3分，共30分）1、如果a ＞b ，那么下列不等式中不成立的是( ) A 、 a ―3＞b ―3 B 、 ―3a ＞―3b C 、3a ＞3bD 、 ―a ＜―b2、已知两个不等式的解集在数轴上如图表示，那么这个解集为（）A 、x ≥－1B 、x >1C 、－3<x ≤－1D 、x >－3 3、“x 的2倍与3的差不大于8”列出的不等式是( )A 、2x －3≤8B 、2x －3≥8C 、2x －3＜8D 、2x －3＞84、如图，天平右盘中每个砝码的重量都是1g ，则图中显示出某药品A 质量（g ）的范围是（）A 、大于2gB 、小于3gC 、大于2g 且小于3gD 、大于2g 或小于3g（第4题图） 5、在数轴上表示不等式x ≥－2的解集，正确的是（）A B C D6、若不等式（ａ―５）ｘ＜１的解集是ｘ＞51-a ，则ａ的取值范围是（）Ａ、ａ＞５Ｂ、ａ＜５Ｃ、ａ≠５Ｄ、以上都不对 7、不等式组⎩⎨⎧>+≤0312x x 的解集在数轴上可表示为…………………………（）8、如果不等式组⎩⎨⎧>-<+n x x x 737的解集是x ＞7，则n 的取值范围是（）A 、n ≥7B 、n ≤7C 、n=7D 、n ＜79、有理数a 、b 、c 在数轴上的对应点的位置如图所示，下列式子中正确的是（）A 、b+c ＞0B 、a-b ＞a-cC 、ac ＞bcD 、ab ＞ac10、若abcd ＞0，a+b+c+d ＞0，则a 、b 、c 、d 中负数的个数至多有( )个A 、1B 、２Ｃ、３Ｄ、４二、耐心填一填（每小题3分，共30分） 1、用不等式表示：①、x 与2的和小于5____________．②、a 与b 的差是非负数___________． ②、a 的相反数的51不大于a 的3倍与15的和_________． 2、若x <y ，则x －2 y －2；若93ba -<-，则b 3a 。

高中数学专题复习基本不等式限时练习试卷与答案

高二数学专题复习（五）基本不等式1 限时练高二 ______班_____组学号：_______ 姓名：______________ 一、【基础过关】（大约35分钟）.225,0.1的最大值求已知xx x +<.19,1.2的最小值求已知-+>x x x.)41(,410.3的最大值求已知x x x -<<4.(2020·上海,13)下列不等式恒成立的是( )A.a 2+b 2≤2abB.a 2+b 2≥-2abC.a+b ≥2√|ab |D.a+b ≥-2√|ab |5.(2015·福建,理5)若直线x a +yb =1(a>0,b>0)过点(1,1),求a+b 的最小值.6.(2015·湖南,文)若实数a ,b 满足1a +2b =√ab ,则ab 的最小值为( )A.√2B.2C.2√2D.47.(2019·天津,文13)设x>0,y>0,x+2y=4,则(x+1)(2y+1)xy的最小值为 .8.(2019·天津,理13)设x>0,y>0,x+2y=5,则√xy的最小值为.9.(2014·重庆,文9)若log4(3a+4b)=log2√ab,则a+b的最小值是()A.6+2√3B.7+2√3C.6+4√3D.7+4√3二、【能力提升】（大约5分钟）10.(2015·重庆,文14)设a,b>0,a+b=5,则√a+1+√b+3的最大值为.高二数学专题复习（五）基本不等式1限时练答案1. 302. 73.641A.由基本不等式可知a2+b2≥2ab,故A不正确;B.a2+b2≥-2ab⇒a2+b2+2ab≥0,即(a+b)2≥0恒成立,故B正确;C.当a=-1,b=-1时,不等式不成立,故C不正确;D.当a=0,b=-1时,不等式不成立,故D不正确.故选B.∵直线xa+yb=1过点(1,1),∴1a+1b=1.又a,b均大于0,∴a+b=(a+b)(1a+1b)=1+1+ba+ab≥2+2√ba·ab=2+2=4.故选C.由已知1a+2b=√ab,可知a,b同号,且均大于0.由√ab=1a+2b≥2√2ab,得ab≥2√2.即当且仅当1a=2b,即b=2a时等号成立,故选C.(x+1)(2y+1)xy=2xy+x+2y+1xy=2xy+5xy=2+5xy.∵x+2y=4,∴4≥2√2xy,∴2xy≤4.∴1xy≥12.∴2+5xy≥2+52=92.先化简,利用√xy 的范围求解.√xy=√xy=√xy =2√xy √xy≥2·√2√xy ·6√xy =4√3.当且仅当√xy =√xy,即xy=3时等号成立.由log 4(3a+4b )=log 2√ab ,得12log 2(3a+4b )=12log 2(ab ),所以3a+4b=ab ,即3b +4a =1. 所以a+b=(a+b )(3b +4a )=3ab +4ba +7≥4√3+7,当且仅当3ab =4ba ,即a=2√3+4,b=3+2√3时取等号.故选D .10.(2015·重庆,文14,5分,难度★★)设a ,b>0,a+b=5,则√a +1+√b +3的最大值0,a+b=5,所以(a+1)+(b+3)=9.令x=a+1,y=b+3,则x+y=9(x>1,y>3),于是=√x +√y,而(√x +√y )2=x+y+2√xy ≤x+y+(x+y )=18,所以√x +√y ≤3√2 .此时x=y ,即a+1=b+3,结合a+b=5可得a=3.5,b=1.5,故当a=3.5,b=1.5时,√a +1+√b +3的最大值为3√2.。

高中试卷-2.2 基本不等式练习(1)(含答案)

第二章　一元二次函数、方程和不等式2.2等式性质与不等式性质（共2课时）（第1课时）一、选择题1．（2019·内蒙古集宁一中高一期末）下列不等式一定成立的是（）A ．a b2B ．a b 2≤C ．x +1x ≥2D ．x 2+1x 2≥2【答案】D【解析】当a ,b ,x 都为负数时，A,C 选项不正确.当a ,b 为正数时，B 选项不正确.根据基本不等式，有x 2+1x 2≥=2，故选D.2．（2019山东师范大学附中高一期中）已知x ＞0，函数9y x x=+的最小值是（）A ．2B ．4C ．6D ．8【答案】C【解析】∵x ＞0，∴函数96y x x =+³=，当且仅当x=3时取等号，∴y 的最小值是6．故选：C ．3.（2019广东高一期末）若正实数a ，b 满足a +b =1，则下列说法正确的是( )A ．ab 有最小值14BC ．1a +1b 有最小值4D ．a 2+b 2【答案】C【解析】∵a >0，b >0，且a +b =1；∴1=a +b ≥∴ab ≤14；∴ab 有最大值14，∴选项A 错误；=a +b =1+1+=2，∴B 项错误.1a+1b ==1ab ≥4，∴1a +1b 有最小值4，∴C 正确；a 2+b 2=(a +b )2―2ab =1―2ab ≥1―2×14=12,∴a 2+b 2的最小值是12，不是∴D 错误．4．（2019·柳州市第二中学高一期末）若x >―5，则x +4x 5的最小值为（）A ．-1B ．3C ．-3D ．1【解析】x +4x5=x +5+4x 5―5≥2×2―5=―1，当且仅当x =―3时等号成立，故选A.5．（2019吉林高一月考）若()12f x x x =+- (2)x >在x n =处取得最小值，则n =（）A ．52B ．3C ．72D ．4【答案】B 【解析】：当且仅当时,等号成立;所以,故选B.6．（2019·广西桂林中学高一期中）已知5x 2³,则f(x)= 24524x x x -+-有A ．最大值B ．最小值C ．最大值1D ．最小值1【答案】D【解析】()()()2211112122222x f x x x x -+éù==-+³=ê--ëû当122x x -=-即3x =或1（舍去）时， ()f x 取得最小值1二、填空题7．（2019·宁夏银川一中高一期末）当1x £-时，1()1f x x x =++的最大值为__________.【答案】-3.【解析】当1x £-时，()11[(1)111f x x x x x =+=--+--++又1(1)21x x -+-³+，()11[(1)1311f x x x x x =+=--+--£-++,故答案为：-38．（2019·上海市北虹高级中学高一期末）若0m >，0n >，1m n +=，且41m n+的最小值是___.【答案】9【解析】∵0m >，0n >，1m n +=，4()5414519n m m n m n m n m n æö\+=++=+++=ç÷èø…,当且仅当12,33n m == 时“=”成立，故答案为9.9．（2019·浙江高一期末）已知0a >，0b >，若不等式212ma b a b+³+恒成立，则m 的最大值为【答案】9.【解析】由212m a b a b +³+得()212m a b a b æö£++ç÷èø恒成立，而()212225a b a b a b b a æö++=++ç÷èø5549³+=+=，故9m £，所以m 的最大值为9.10．（2019·浙江高一月考）设函数24()(2)(0)f x x x x x=-++>．若()4f x =，则x =________．【答案】2【解析】因为2(2)0y x =-³，当2x =时，取最小值；又0x >时，44y x x=+³=，当且仅当06（，），即2x =时，取最小值；所以当且仅当2x =时，24()(2)f x x x x=-++取最小值(2)4f =.即()4f x =时，2x =.故答案为2三、解答题11．（2016·江苏高一期中）已知a ＞0，b ＞0，且4a ＋b ＝1，求ab 的最大值；（2）若正数x ，y 满足x ＋3y ＝5xy ，求3x ＋4y 的最小值；（3）已知x ＜54，求f （x ）＝4x －2＋145x -的最大值；【答案】（1）的最大值；（2）的最小值为5；（3）函数的最大值为【解析】（1）,当且仅当,时取等号，故的最大值为（2），当且仅当即时取等号（3）当且仅当,即时,上式成立,故当时,函数的最大值为.12．（2019·福建高一期中）设0,0,1a b a b >>+= 求证：1118a b ab++³ 【答案】可以运用多种方法。

一元二次函数、方程和不等式检测试卷及答案

一元二次函数、方程和不等式检测试卷及答案1.不等式x^2+x-6>0的解集为（B）{x|x2}。

2.若a>b>0，则不等式c^2/(a-b)>0一定成立，因为分母为正数。

3.已知不等式ax^2+bx+2>0的解集是(-1,2)，则a+b的值为（D）-2.4.若不等式组{x-1>a/2.x-43.5.已知关于x的不等式kx^2-6kx+k+8≥0对任意x∈XXX成立，则k的取值范围是（A）[0,1]。

6.已知不等式(x+y)/(1+xy)≥9对任意实数x、XXX成立，则实数a的最小值为（D）2.7.已知a1>a2>a3>0，则使得(1-a1x)<1、(1-a2x)<1和(1-a3x)<1都成立的x取值范围是（B）0<x<(a2/a3)。

8.某汽车运输公司刚买了一批豪华大客车投入营运，每辆客车营运的总利润y（单位：10万元）与营运年数x（x∈N）为二次函数关系，若使营运的年平均利润最大，则每辆客车应营运（C）5年。

9.已知-π/2≤α<β≤π/2，则(α-β)^2的范围是（A）(-π^2/4,0]。

10.已知正实数a,b,c,d满足a>b,c>d，则不等式ac>bd不正确，因为b和c可能很小，导致右边小于左边。

11.对任意实数x，不等式(a-2)x+2(a-2)x-4<XXX成立，则a的取值范围是（C）a<-2或a≥2.该选项成立；对于选项C，a b0,a b,所以a c b c，该选项成立；对于选项D，a b,c20，但无法确定ac和bc的大小关系，所以该选项不一定成立。

故答案为B。

3.若函数f x x2ax b的图象过点1,0，且有两个不同的实数x1，x2满足f x1f x21，则a，b的值应该是（）A.a2，b 1B.a2，b 1C.a1，b 2D.a1，b 2答：C由题意可得：f1b0，f x1f x2x1x2a，x1x2b0，又因为x1，x2不相等，所以x10，x2a，代入x1x20可得a0或b0，但因为f x1f x21，所以a0，故b0，代入x1x2a可得a1，故a，b的值应该是a1，b0，即选项C。

024-期末复习卷3不等式(含答案)

期末复习卷2（不等式）一、单选题1.(2021河南高二期末)设a=x2-2x+2,b=1-x,则实数a与b的大小关系为()A.a>bB.a=bC.a<bD.与x有关2.不等式2+x-x2<0的解集为()A.(-∞,-1)∪(2,+∞)B.(-2,1)C.(-1,2)D.(-∞,-2)∪(1,+∞)3.(2021福建泉州高一期末)若不等式ax2+bx-1≥0的解集是x-12≤x≤-13,则a=()A.-6B.-5C.65D.64.(2021安徽黄山高一期末)下列不等式正确的是()A.若a<b,则a2<b2B.若a>b,则ac>bcC.若a>b>0,c>d>0,e>f>0,则ace>bdfD.若a>b>c>0,d>e>f>0,则>>5.已知>0，则=2−4r1的最小值为()A.−2B.12C.1D.26.(2021云南高三期末)如果两个正方形的边长分别为x,y,且x+y=1,那么它们的面积之和的最小值是()A.14B.12C.1D.27.(2021湖北高三一模)已知正数a,b是关于x的函数y=x2-(m2+4)x+m的两个零点,则1+1的最小值为()A.2B.22C.4D.428.设>0，>0，+=1，则下列说法错误的是．()A.B的最大值为14B.2+2的最小值为12C.4+1的最小值为9D.+的最小值为2二、多选题9.若1<1<0,则下列说法正确的是()A.a<bB.a>bC.a2<b2D.ab<b210.(2021湖北高三月考)若非零实数a,b满足a>b,则下列结论正确的是()A.a+b≥2BB.a2+b2>2abC.|a+b|<2(2+2)D.(a+b)1+1>411.(2020广东高一期中)已知y=ax2+bx+c,不等式ax2+bx+c>0的解集是{x|1<x<3},下列说法正确的是()A.a>0B.a+b+c=0C.关于x的不等式cx2+bx+a>0的解集是x13<x<1D.如果am2+bm+c>0,则a(m+2)2+b(m+2)+c<012.已知正数，，则下列不等式中恒成立的是()A.+≥22B.(+p(1+1)≥4 C.≥2B D.2B r>B三、填空题13.(2021山东日照高一期末)不等式-1>0的解集为.14.(2020天津,14)已知a>0,b>0,且ab=1,则12+12+8r的最小值为.15.(2021上海黄浦格致中学高一期末)定义区间[a,b](a<b)的长度为b-a,若关于x的不等式x2-4x+m≤0的解集的区间长度为2,则实数m的值为.16.某校要建一个面积为200 2的长方形花园，并且在四周要修建出宽为2 和4 的小路(如图所示).要使得花园和小路占地总面积最小，则花园的长应为；最小面积为2．四、解答题17.(10分)解下列不等式：(1)2+3−22>0．(2)o3−p≤o+2)−1．(3)2−2+3>0．18.(12分)(2021吉林高一期末)已知x>0,y>0,且x+4y=40.(1)求xy的最大值;(2)求1+1的最小值.19.(12分)(2021云南昆明高二期末)已知函数y=x+1-1(x≠1).(1)解不等式(x-1)x+1-1>3;(2)当x>1时,求x+1-1的最小值.20.(12分)如图，某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形生态种植园.设生态种植园的长为B，宽为B．(1)若生态种植园面积为722，则，为何值时，可使所用篱笆总长最小?(2)若使用的篱笆总长度为30，求1+2的最小值．21.(12分)(2021山东济宁高一期末)设函数y=ax2+(b-2)x+3.(1)若不等式ax2+(b-2)x+3>0的解集为(-1,1),求实数a,b的值;(2)若b=-a-1,且存在x∈R,使ax2+(b-2)x+3>4成立,求实数a的取值范围.22.(12分)(2021云南曲靖第二中学高一期末)设y=x2-(a-1)x+a-2(a∈R).(1)若不等式x2-(a-1)x+a-2≥-2对一切实数x恒成立,求实数a的取值范围;(2)解关于x的不等式x2-(a-1)x+a-2<0.期末复习卷2（不等式）参考答案1a-b=x2-x+1=x-122+34>0恒成立,所以a>b.故选A.2x2-x-2>0,即(x-2)(x+1)>0,解得x<-1或x>2,所以不等式2+x-x2<0的解集为(-∞,-1)∪(2,+∞).故选A.3不等式ax2+bx-1≥0的解集为x-12≤x≤-13,∴-12,-13为方程ax2+bx-1=0的两个根,∴根据根与系数的关系可得-12×-13=-1,解得a=-6.故选A.4A,若a=-3,b=2,则a2>b2,错误;对于B,若c=0,则ac=bc,错误;对于C,若a>b>0,c>d>0,e>f>0,由不等式的基本性质可得ace>bdf,正确;对于D,若a=3,b=2,c=1,d=3,e=2,f=1,则===1,错误.故选C.5.【答案】A解：>0，则=2−4r1=+1−4≥4=−2，当且仅当=1，即=1时，等号成立，则=2−4r1的最小值为−2．故选A．6x2+y2≥2xy,所以2(x2+y2)≥x2+y2+2xy=(x+y)2=1,所以x2+y2≥12,当且仅当x=y=1时,等号成立.因此,两个正方形的面积之和x2+y2的最小值为12.故选B.7,正数a,b是关于x的方程x2-(m2+4)x+m=0的两根,可得a+b=m2+4,ab=m>0,则1+1=r B=m+4≥4,当且仅当m=4,即m=2时等号成立.经检验知当m=2时,方程x2-(m2+4)x+m=0有两个正实数解.所以1+1的最小值为4.故选C.8.【答案】D【解析】解：由题意，对各选项依次进行分析：对，因为正实数，满足+=1，所以1=+≥2B，当且仅当==12时等号成立，所以B≤14，当且仅当==12时等号成立，故B有最大值14，故A 正确;对，因为(+p2=2+2+2B=1，所以2+2=1−2B≥1−2×112，当且仅当==12时等号成立，所以2+2有最小值12，故B正确．对，利用基本不等式，有4+1=+=4++5=9=1=，即=23=13时等号成立，故4+1有最小值9，故C正确；对，由题意，得(+p2=++2B=1+2B≤1+=2，故+≤2，当且仅当==12时等号成立，即+有最大值2，故D错误．故选D．9.答案BCD解析因为1<1<0,故a<0,b<0,b<a,即b<a<0,故B正确,A错误.对于C,a2-b2=(a-b)(a+b),而a+b<0,a-b>0,故a2-b2<0,即a2<b2,故C正确.对于D,ab-b2=b(a-b)<0,故ab<b2,故D正确.故选BCD.10.答案BC解析对于A,若a,b均为负数,则不等式显然不成立,故A错误;对于B,显然成立,故B正确;对于C,在a2+b2>2ab两边同时加上a2+b2,得2(a2+b2)>(a+b)2,则|a+b|<2(2+2)成立,故C正确;对于D,取a=2,b=-1,则(a+b)1+1=(2-1)×12+1-1=-12<4,则(a+b)1+1>4不成立,故D错误.故选BC.11.答案BCD解析对于A,ax2+bx+c>0的解集是{x|1<x<3},则a<0,故A不正确;对于B,由题意知x=1是方程ax2+bx+c=0的一个实数根,故a+b+c=0,故B正确;对于C,由题意知x=1和x=3是方程ax2+bx+c=0的两个实数根,则由根与系数的关系得=-4,=3,则不等式cx2+bx+a>0变为x2+x+1<0,即3x2-4x+1<0,解不等式得x的取值范围为x13<x<1,故C正确;对于D,如果am2+bm+c>0,则1<m<3,故3<m+2<5,则a(m+2)2+b(m+2)+c<0,故D正确.故选BCD.12.【答案】ABC【解析】解：因为，均为正数，所以++1B≥2B+1B≥22，当且仅当==22时，等号成立，A正确;因为，均为正数，所以(+p(1+1)=++2≥2·+2=4，当且仅当=时，等号成立，B正确;因为，均为正数，所以2+2≥2B>0，∴2+2B≥2B，当且仅当=时，等号成立，C正确;因为，均为正数，所以+≥2B，∴2B r≤1，所以2B r≤B，当且仅当=时，等号成立，不正确．故选ABC．13.(2021山东日照高一期末)不等式-1>0的解集为.答案(-∞,0)∪(1,+∞)解析由-1>0,解得x<0或x>1,即原不等式的解集为(-∞,0)∪(1,+∞).14.(2020天津,14)已知a>0,b>0,且ab=1,则12+12+8r的最小值为.答案4解析∵ab=1,∴b=1.∴12+12+8r=12+2+8r1=121++8r1.令1+a=t>0,则原式=2+8≥22·8=24=4.当且仅当t2=16,即t=4时,等号成立,此时1+a=4.15.(2021上海黄浦格致中学高一期末)定义区间[a,b](a<b)的长度为b-a,若关于x的不等式x2-4x+m≤0的解集的区间长度为2,则实数m的值为.答案3解析设x1,x2是方程x2-4x+m=0的两个根,则x1+x2=4,x1x2=m,∴|x1-x2|=(1+2)2-412=16-4=2,解得m=3.16.某校要建一个面积为200 2的长方形花园，并且在四周要修建出宽为2 和4 的小路(如图所示).要使得花园和小路占地总面积最小，则花园的长应为；最小面积为2．【答案】20,392解：设花园的长为B，则花园的宽为200，又设花园占地面积为B2，依题意，得=(+ 8)(200+4)=232+4(+400)⩾232+4×2b400=392，当且仅当=400，即=20时取“=”．所以花园的长为20，宽为10时，占地总面积最小为392 2．故答案为20；392．17.(10分)解下列不等式：(1)2+3−22>0．(2)o3−p≤o+2)−1．(3)2−2+3>0．【答案】解：(1)原不等式可化为22−3−2<0，所以(2+1)(−2)<0，故原不等式的解集是{U−12< <2}．(2)原不等式可化为22−−1≥0．所以(2+1)(−1)≥0，故原不等式的解集为{U≤−12或≥1}．(3)由2−2+3=(−1)2+2>0对任意的∈恒成立，故原不等式的解集是．18.(12分)(2021吉林高一期末)已知x>0,y>0,且x+4y=40.(1)求xy的最大值;(2)求1+1的最小值.解(1)因为x>0,y>0,所以40=x+4y≥24B=4B(当且仅当x=4y,即x=20,y=5时,等号成立).所以xy≤100,因此xy的最大值为100.(2)因为x+4y=40,即140(x+4y)=1,所以1+1=140(x+4y)1+1=1405+4+≥1405+24·=940当且仅当x=2y,即x=403,y=203时,等号成立.所以1+1的最小值为940.19.(12分)(2021云南昆明高二期末)已知函数y=x+1-1(x≠1).(1)解不等式(x-1)x+1-1>3;(2)当x>1时,求x+1-1的最小值.解(1)由(x-1)x+1-1>3,得x2-x-2>0.又x≠1,所以解得x>2或x<-1,即原不等式的解集为(-∞,-1)∪(2,+∞). (2)当x>1时,x-1>0,y=x+1-1=x-1+1-1+1≥2+1=3,当且仅当x-1=1-1,即x=2或x=0(舍)时,等号成立.所以x+1-1的最小值是3.20.(12分)如图，某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形生态种植园.设生态种植园的长为B，宽为B．(1)若生态种植园面积为722，则，为何值时，可使所用篱笆总长最小?(2)若使用的篱笆总长度为30，求1+2的最小值．【答案】解：(1)由已知可得B=72，其中>0，>0，篱笆总长为(+2p．又因为+2≥22B=24，当且仅当=2，即=12，=6时等号成立．所以当=12，=6时，可使所用篱笆总长最小．(2)由已知得+2=30，>0，>0，又因为(1+2)(+2p=5+2+2≥5+=9，所以1+2≥310，当且仅当2=2，即=，即=10，=10时等号成立．所以1+2的最小值是310．21.(12分)(2021山东济宁高一期末)设函数y=ax2+(b-2)x+3.(1)若不等式ax2+(b-2)x+3>0的解集为(-1,1),求实数a,b的值;(2)若b=-a-1,且存在x∈R,使ax2+(b-2)x+3>4成立,求实数a的取值范围.由题意可知,方程ax2+(b-2)x+3=0的两根是-1,1,=0,1,解得=-3,=2.(2)存在x∈R,使ax2+(b-2)x-1>0成立,将b=-a-1代入上式可得ax2-(a+3)x-1>0成立.当a≥0时,显然存在x∈R使得上式成立;当a<0时,需使方程ax2-(a+3)x-1=0有两个不相等的实根,所以Δ=(a+3)2+4a>0,即a2+10a+9>0,解得a<-9或-1<a<0.综上可知,a的取值范围是(-∞,-9)∪(-1,+∞).22.(12分)(2021云南曲靖第二中学高一期末)设y=x2-(a-1)x+a-2(a∈R).(1)若不等式x2-(a-1)x+a-2≥-2对一切实数x恒成立,求实数a的取值范围;x的不等式x2-(a-1)x+a-2<0.由题意,不等式x2-(a-1)x+a-2≥-2对于一切实数x恒成立,等价于x2-(a-1)x+a≥0对于一切实数x恒成立.所以Δ=(a-1)2-4a≤0,解得3-22≤a≤3+22.故实数a的取值范围为[3-22,3+22].(2)不等式x2-(a-1)x+a-2<0,即[x-(a-2)](x-1)<0.当a-2>1,即a>3时,不等式的解集为{x|1<x<a-2};当a-2=1,即a=3时,不等式的解集为⌀;当a-2<1,即a<3时,不等式的解集为{x|a-2<x<1}.综上所述,当a<3时,不等式的解集为{x|a-2<x<1};当a=3时,不等式的解集为⌀;当a>3时,不等式的解集为{x|1<x<a-2}.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

新课标人教版必修5高中数学第3章不等式单元检测试卷1．设a b <，c d <，则下列不等式中一定成立的是（）A ．d b c a ->-B ．bd ac >C ．d b c a +>+D ．c b d a +>+2． “0>>b a ”是“222b a ab +<”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件3．不等式b ax >的解集不可能是（）A ．φB ．RC ．),(+∞a bD ．),(ab --∞ 4．不等式022>++bx ax 的解集是)31,21(-，则b a -的值等于（） A ．－14 B ．14 C ．－10 D ．105．不等式||x x x <的解集是（） A ．{|01}x x < 6．若011<<ba ，则下列结论不正确的是（） A ．22b a +ba ab D ．||||||b a b a +>+7．若13)(2+-=x x x f ，12)(2-+=x x x g ，则)(x f 与)(x g 的大小关系为（）A ．)()(x g x f >B ．)()(x g x f =C ．)()(x g x f <D ．随x 值变化而变化 8．下列各式中最小值是2的是（）A ．y x ＋x yB ．4522++x x C ．tan x ＋cot x D ． x x -+229．下列各组不等式中，同解的一组是（）A ．02>x 与0>xB ．01)2)(1(<-+-x x x 与02<+xC ．0)23(log 21>+x 与123<+x D ．112≤--x x 与112≤--x x 10．如果a x x >+++|9||1|对任意实数x 总成立,则a 的取值范围是（）A. }8|{<a aB. }8|{>a aC. }8|{≥a aD. }8|{≤a a 11．若+∈R b a ,，则b a 11+与ba +1的大小关系是 .12．函数121lg+-=x xy 的定义域是 . 13．某公司一年购买某种货物400吨，每次都购买x 吨，运费为4万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费用之和最小，则x = 吨.14. 已知0()1,0x x f x x ≥⎧=⎨-<⎩，, 则不等式3)2(≤+x f 的解集___ _ ____.15．已知()f x 是奇函数，且在（－∞，０）上是增函数，(2)0f =，则不等式()0xf x <的解集是___ _ ____. 16．解不等式：21582≥+-x x x17．已知1<a ，解关于x 的不等式12>-x ax．18．已知0=++c b a ，求证：0≤++ca bc ab 。

19．对任意]1,1[-∈a ，函数a x a x x f 24)4()(2-+-+=的值恒大于零，求x 的取值范围。

20．如图所示，校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。

已知喷水器的喷水区域是半径为5m 的圆。

问如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？21．已知函数b ax x x f ++=2)(.（1）若对任意的实数x ，都有a x x f +≥2)(，求b 的取值范围；（2）当]1,1[-∈x 时，)(x f 的最大值为M ，求证：1+≥b M ；（3）若)21,0(∈a ，求证：对于任意的]1,1[-∈x ，1|)(|≤x f 的充要条件是.142a b a -≤≤-§不等式单元测试; ; ; ; ; ; ; ; ; ;11.b a b a +>+111; 12.)21,1(-; 13. 20 ; 14. ]1,(-∞;15．{|20,}x x -<<或0<x<2;16．解：原不等式等价于：0158301720158301720215822222≤+-+-⇔≥+--+-⇔≥-+-x x x x x x x x x x x3250)5)(3()52)(6(<≤⇔≤----⇔x x x x x 或65≤<x ∴原不等式的解集为]6,5()3,25[Y17．解：不等式12>-x ax 可化为022)1(>-+-x x a ．∵1<a ，∴01<-a ，则原不等式可化为0212<---x a x ，故当10<<a 时，原不等式的解集为}122|{ax x -<<；当0=a 时，原不等式的解集为φ；当0<a 时，原不等式的解集为}212|{<<-x ax ． 18．证明：法一（综合法）0=++c b a Θ， 0)(2=++∴c b a展开并移项得：02222≤++-=++c b a ca bc ab 0≤++∴ca bc ab法二（分析法）要证0≤++ca bc ab ，0=++c b a Θ，故只要证2)(c b a ca bc ab ++≤++ 即证0222≥+++++ca bc ab c b a ，也就是证0])()()[(21222≥+++++a c c b b a ，而此式显然成立，由于以上相应各步均可逆，∴原不等式成立。

法三：0=++c b a Θ，b a c +=-∴222223()()[()]024b b ab bc ca ab b a c ab a b a b ab a ∴++=++=-+=---=-++≤0≤++∴ca bc ab法四：,222ab b a ≥+Θ bc c b 222≥+，ca a c 222≥+∴由三式相加得：ca bc ab c b a ++≥++222两边同时加上)(2ca bc ab ++得：)(3)(2ca bc ab c b a ++≥++0=++c b a Θ， ∴0≤++ca bc ab19．解：设22)2()2(24)4()(-+-=-+-+=x a x a x a x a g ，则)(a g 的图象为一直线，在]1,1[-∈a 上恒大于0，故有⎩⎨⎧>>-0)1(0)1(g g ，即⎩⎨⎧>+->+-02306522x x x x ，解得：1<x 或3>x ∴x 的取值范围是),3()1,(+∞⋃-∞20．解：设花坛的长、宽分别为xm ，ym ，根据要求，矩形花坛应在喷水区域内，顶点应恰好位于喷水区域的边界。

依题意得：25)2()4(22=+y x，（0,0>>y x ）问题转化为在0,0>>y x ，100422=+y x 的条件下，求xy S =的最大值。

法一：100)2(2222=+≤⋅⋅==y x y x xy S Θ，由y x=2和100422=+y x 及0,0>>y x 得：25,210==y x 100max =∴S法二：∵0,0>>y x ，100422=+y x ， 41002x x xy S -==∴=10000)200(41)4100(2222+--=-⋅x x x∴当2002=x ，即210=x ，100max =S由100422=+y x 可解得：25=y 。

答：花坛的长为m 210，宽为m 25，两喷水器位于矩形分成的两个正方形的中心，则符合要求。

21．解：（1）对任意的R x ∈，都有⇔+≥a x x f 2)(对任意的R x ∈，0)()2(2≥-+-+a b x a x 0)(4)2(2≤---=∆⇔a b a)(1412R a b a b ∈≥⇔+≥⇔Θ ∴),1[+∞∈b .（2）证明：∵,1)1(M b a f ≤++=,1)1(M b a f ≤+-=-∴222+≥b M ，即1+≥b M 。

（3）证明：由210<<a 得，0241<-<-a ∴)(x f 在]2,1[a --上是减函数，在]1,2[a-上是增函数。

∴当1||≤x 时,)(x f 在2ax -=时取得最小值42a b -，在1=x 时取得最大值b a ++1.故对任意的]1,1[-∈x ，.1414111|)(|22a b a a b b a x f -≤≤-⇔⎪⎩⎪⎨⎧-≥-≤++⇔≤。