人教版九年级数学上册 23.1---23.2随堂练习题含答案
人教版九年级数学上册 第23章 23.1.2 《旋转作图和应用》 同步测试(含答案)

人教版九年级数学上册第23章旋转23.1.2旋转的作图及应用同步测试题号一二三总分得分第Ⅰ卷(选择题)一、选择题(共10小题,3*10=30)1.下列各图中,可看作是由下面矩形顺时针方向旋转90°而成的是( )2.1.等边三角形绕着它的中心旋转一周,可与原图形重合的次数是()A.1 B.2C.3 D.43.有一种平面图形,它绕着中心旋转,不论旋转多少度,所得到的图形都与原图形完全重合,你觉得它可能是()A.三角形B.等边三角形C.正方形D.圆4. 右图是一个旋转对称图形,要使它旋转后与自身重合,至少应将它绕中心逆时针方向旋转的度数为()A.30°B.60°C.120° D.180°5.将下面的直角梯形绕直线L旋转一周,可以得到右边立体图形的是()6.如图,将正方形ABCD 绕点C 按顺时针方向旋转120°后,得到正方形D C B A ''',则∠BC D '等于( ) A .120°B .130°C .140°D .150°7. 如图,将等边△ABC 绕点C 顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD ⊥AC;③四边形ACED 是菱形.其中正确的个数是( ) A.0 B.1 C.2 D.38. 如图,△ABC 绕着点O 按顺时针方向旋转90°后到达了△CDE 的位置,下列说法中不正确的是( ) A.线段AB 与线段CD 互相垂直 B.线段AC 与线段CE 互相垂直 C.点A 与点E 是两个三角形的对应点 D.线段BC 与线段DE 互相垂直9. 如图,将等边△ABC 绕点C 顺时针旋转120°得到△EDC ,连接AD ,BD.则下列结论:①AC =AD ;②BD ⊥AC ;③四边形ACED 是菱形.其中正确的个数是( ) A .0个 B .1个 C .2个 D .3个10.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2 018次得到正方形OA2 018B2 018C2 018,如果点A的坐标为(1,0),那么点B2 018的坐标为( )A.(1,1) B.(0,2)C.(-2,0)D.(-1,1)第Ⅰ卷(非选择题)二.填空题(共8小题,3*8=24)11.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心一定是_____.12. 在△ABC中,∠C=90°,AB=5cm,BC=3cm,把这个三角形在平面内绕点C逆时针旋转60°至△A′B′C′,那么AA′的长度是______cm.(不取近似值)13. 如图,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕点A旋转180°,点C落在C’处,则CC’的长为___________.14.如果两个图形可通过旋转而相互得到,则下列说法中:①对应点连线的中垂线必经过旋转中心.②这两个图形大小、形状不变.③对应线段一定相等且平行.④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.其中正确的有________个15.如图用等腰直角三角板画∠AOB=45º,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22º,则三角板的斜边与射线OA的夹角α为______度.16.如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转900得到月牙②,则点A的对应点A’的坐标为.17.已知直线y=-2x+4,若该直线绕原点顺时针旋转1800,则旋转后得到的直线解析式是.18.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论中:①∠CDF=α;②A1E=CF;③DF=FC;④AD=CE;⑤A1F=CE.其中正确的有___________________(写出正确结论的序号).三.解答题(共7小题,46分)19.(6分) 如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(-6,12),B(-6,0),C(0,6),D(-6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°.(1)画出旋转后的小旗A′C′D′B;(2)写出点A′,C′,D′的坐标;(3)求出线段BA旋转到BA′时所扫过的扇形的面积.20. (6分) 如图是由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A,B,C,D 均在格点上,在网格中将点D按下列步骤移动:第一步:点D绕点A顺时针旋转180°得到点D1;第二步:点D1绕点B顺时针旋转90°得到点D2;第三步:点D2绕点C顺时针旋转90°回到点D.(1)请用圆规画出点D→D1→D2→D经过的路径;(2)所画图形是轴对称对称图形;(3)求所画图形的周长(结果保留π).21. (6分)如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA',求点A'的坐标.22.(6分) 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;(3)判断以O,A1,B为顶点的三角形的形状.(无需说明理由)23.(6分) 如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH ⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,求AH的长.24.(8分)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;25.(8分) ) 通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.原题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.(1)思路梳理∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.∵∠ADC=∠B=90°,∴∠FDG=180°,点F,D,G共线.根据______,易证△AFG≌_______,得EF=BE+DF;(2)类比引申如图②,在四边形ABCD中,AB=AD,∠BAD=90°,点E,F分别在边BC,CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系__________________时,仍有EF=BE+DF;(3)联想拓展如图③,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,猜想BD,DE,EC应满足的等量关系,并写出推理过程.∠B+∠D=180°参考答案 1-5ACDBB 6-10 DDCDD 11. 点B 12. 4 13. 414. 3 15. 22° 16. (2,4) 17. y=-2x-4 18. ①②⑤ 19. 解:(1)图略(2)点A′(6,0),C′(0,-6),D′(0,0)(3)∵点A 的坐标为(-6,12),点B 的坐标为(-6,0), ∴AB =12,∴线段BA 旋转到BA′时所扫过的扇形的面积=14π×122=36π20. 解:(1)点D→D 1→D 2→D 经过的路径如图所示(3)周长=8π21. 解:如图,过点A 作AB ⊥x 轴于点B,过点A'作A'B'⊥x 轴于点B',由题意知OA=OA',∠AOA'=90°, ∴∠A'OB'+∠AOB=90°, ∵∠AOB+∠OAB=90°, ∴∠OAB=∠A'OB',在△AOB 和△OA'B'中,{∠OAB =∠A 'OB ',∠ABO =∠OB 'A ',OA =A 'O ,∴△AOB≌△OA'B'(AAS),∴OB'=AB=4,A'B'=OB=3,∴点A'的坐标为(-4,3).22. 解:(1)如图所示,△A1B1C1即为所求(2)如图所示,△A2B2C2即为所求(3)三角形的形状为等腰直角三角形,OB=OA1=16+1=17,A1B=25+9=34,即OB2+OA12=A1B2,∴三角形的形状为等腰直角三角形23.解:由旋转的性质可知AF=AG,∠DAF=∠BAG.∵四边形ABCD为正方形,∴∠BAD=90°.又∵∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠BAG+∠BAE=45°,∴∠GAE=∠FAE.在△GAE和△FAE中,AG=AF,∠GAE=∠FAE,AE=AE,∴△GAE≌△FAE.∵AB⊥GE,AH⊥EF,∴AB=AH,GE=EF=5.设正方形的边长为x,则EC=x-2,FC=x-3.在Rt△EFC中,由勾股定理得EF2=EC2+FC2,即(x-2)2+(x-3)2=25.解得x=6(x=-1舍),∴AB=6,∴AH=6.24. 解:(1)证明;根据旋转的性质知,∠OCD=60°,CO=CD,∴△COD是等边三角形(2)当α=150°,即∠BOC=150°时,△AOD是直角三角形.理由如下:由旋转的性质可知,△BOC≌△ADC,∴∠ADC=∠BOC=150°.又∵△COD是等边三角形,∴∠ODC=60°,∴∠ADO=∠ADC-∠ODC=90°,人教版九年级数学上册第23章23.1.2《旋转作图和应用》同步测试(含答案)即△AOD是直角三角形25解:(1)SAS,△AFE(2)∠B+∠D=180°(3)猜想:DE2=BD2+EC2.证明:把△AEC绕点A顺时针旋转90°得到△AE′B,连接DE′,∴△AEC≌△AE′B,∴BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,在Rt△ABC中,∵AB=AC,∴∠ABC=∠C=45°,∴∠ABC+∠ABE′=90°,即∠E′BD=90°,∴E′B2+BD2=E′D2,又∵∠DAE=45°,∴∠BAD+∠EAC=45°,∴∠E′AB+∠BAD=45°,即∠E′AD=∠EAD=45°,又AD=AD,∴△AE′D≌△AED(SAS),∴DE=DE′,∴DE2=BD2+EC211/ 11。
人教版九年级数学上册23.2 中心对称 随堂练习 (1)

人教版九年级上册数学23.2 中心对称随堂练习-1一、选择题1.下列结论错误的是( )A. 平行四边形既是中心对称又是轴对称图形B. 菱形的四条边相等C. 正方形的对角线互相垂直平分且相等D. 矩形的四个角相等2、下列图形中,既是轴对称图形又是中心对称图形的有( )A. 1个B. 2个C. 3个D. 4个3、已知下列命题:(1)关于中心对称的两个图形一定不全等;(2)关于中心对称的两个图形是全等形;(3)两个全等的图形一定关于中心对称;其中真命题的个数是()A、0B、1C、2D、34. 下列说法中正确的是()A、能重合的图形一定是成轴对称图形B、成中心对称的图形一定是重合的图形C、两个会重合的三角形一定关于某一点成中心对称D、两个成中心对称的图形的对称点连线不一定过对称中心5、把下列每个字母都看成一个图形,那么中心对称图形有( )A. 1个B. 2个C. 3个D. 4个6、如图所示,已知△ABC和△A'B'C'关于点O成中心对称,则下列结论错误的是()A. ∠AOC=∠A'OC'B. ∠ABC=∠A'B'C'C.AB=A'B'D.OA=OC'7. 下列图形中不是轴对称而是中心对称图形的是()A、等边三角形B、平行四边形C、菱形D、矩形8.下列命题中的真命题是()A、中心对称图形都是轴对称图形B、关于中心对称的两个图形全等C、面积相等两个图形是中心对称图形D、轴对称图形都是中心对称图形9.下列给出的函数中,其图象是中心对称图形的是( )①函数y=x;②函数y=x2;③函数y=1.xA. ①②B. ②③C. ①③D. 都不是10、下列说法正确的是()A.旋转后能重合的两个图形成中心对称 B.成中心对称的两个图形必须能完全重合C.全等的两个图形成中心对称 D.成中心对称的两个图形不一定全等11、若两个图形成中心对称,则下列说法:①对应点的连线一定经过对称中心;②这两个图形的形状和大小完全相同;③这两个图形的对应线段一定互相平行;④将一个图形围绕对称中心旋转180∘后必与另一个图形重合.其中正确的有()A. 1个B. 2个C. 3个D. 4个12、如图,四边形ABCD是正方形,△ADE绕着点A旋转90°后到达△ABF的位置,连接EF,则△AEF的形状是()A、锐角三角形B、等腰三角形C、等腰直角三角形D、等边三角形二、填空题13、在平面坐标系中,若点P(m, 2)与点Q(3, n)关于原点对称,则m+n=________.14、关于中心对称的两个图形对应线段________.15. 如图,△A1B1C1是△ABC关于点O成中心对称的图形,点A的对称点是点A1,已知AO=4cm,那么AA1=cm.16、下列两个电子数字成中心对称的是________.17、二次函数y = x2-2x-2的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5个单位后图象对应的二次函数解析式为___________.三、解答题18、如图,已知四边形ABCD,画四边形A1B1C1D1,使它与四边形ABCD关于C点中心对称.19.如图,在△ABC中,D为BC上任一点,DE//AC交AB于点E,DF//AB交AC于点F,求证:点E,F关于AD的中点对称.20、如图,平面直角坐标系中,每个小正方形边长都是1.(1)按要求作图:①△ABC关于原点O逆时针旋转90°得到△A1B1C1;②△A1B1C1关于原点中心对称的△A2B2C2.(2)△A2B2C2中顶点B2坐标为.21、如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.22.已知如图所示,与关于点成中心对称,连接,.(1)求证:四边形是平行四边形;(2)若的面积为15 ,求四边形的面积.23、如图,已知两个字母“F”成中心对称,请你画出对称中心O.答案1. A2、 B 3、 B 4. B 5、 B 6、 D 7. B 8. B 9. C 10、 B 11、 C 12、 C 13、−5 14、平行且相等 15. 8. 16、①④ 17、y=-(x+2)2+2 18、四边形A1B1C1D1如图所示.19. 证明:如图,连接EF交于点O.∵DE//AC交AB与E,DF//AB交AC于F,∴四边形AEDF是平行四边形,∴点E,F关于AD的中点对称.20、解:(1)①△A1B1C1如图所示;②△A2B2C2如图所示;(2)B2(1,6).故答案为:(1,6).21、解:如下图所示.22.(1)证明:∵与关于点成中心对称,∴即四边形的对角线互相平分,∴四边形是平行四边形.(2)解:记底边上的高为h ,那么平行四边形ABCD底边AB上的为2h ,因为的面积为15,所以,所以2ABh=60,所以平行四边形ABCD的面积为60.23、如图,连接AB,CD,EF交于点O,点O即为所求.。
(含答案)九年级数学人教版上册课时练第23章《23.1 图形的旋转》

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!课时练第23章旋转23.1图形的旋转一、选择题1.如图,在△ABC 中,AB =AC ,∠BAC =50°,将△ABC 绕着点A 顺时针方向旋转得△ADE ,AB ,CE 相交于点F ,若AD ∥CE 时,则∠BAE 的大小是()A .20°B .25°C .30°D .35°2.如图,在等边△ABC 中,AC =9,点O 在AC 上,且AO =3,P 是AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,若使点D 恰好落在BC 上,则线段AP 的长是()A .4B .5C .6D .83.如图,以正方形ABCD 的顶点A 为坐标原点,直线AB 为x 轴建立直角坐标系,对角线AC 与BD 相交于点E ,P 为BC 上一点,点P 坐标为(,)a b ,则点P 绕点E 顺时针旋转90°得到的对应点P 的坐标是()A .(,)a b a -B .(,)b aC .(,0)a b -D .(,0)b 4.如图,在△ABC 中,∠CAB =70°,将△ABC 在平面内绕点A 旋转到△AB ′C ′的位置,使CC ′∥AB ,则旋转角的度数为()A.35°B.40°C.50°D.70°5.如图,在△ABC中,∠CAB=∠ACB=25°,将△ABC绕点A顺时针进行旋转,得到△AED.点C恰好在DE的延长线上,则∠EAC的度数为()A.75°B.90°C.105°D.120°6.已知直角梯形ABCD中,AB⊥BC,AD∥BC,AD=2,BC=3,将其中腰CD绕点D逆时针旋转90°至DE,连接AE,那么△ADE的面积为()A.1B.2C.3D.67.如图,△ABC为等边三角形,AB=4,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边在下方作等边△CEF,连接DF,则线段DF的最小值为()A.2B C.32D.18.如图,已知△AB C与△ADE都是以A为直角顶点的等腰直角三角形,△ADE绕顶点A旋转,连接BD,CE.以下四个结论:①BD=CE;②∠AEC+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是()A.1B.2C.3D.49.如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB'C'的位置,使得C'C∥AB,则∠B'AC等于()A .30°B .20°C .10°D .15°10.如图,将Rt △ABC 绕其直角顶点C 按顺时针方向旋转90°后得到Rt △DEC ,连接AD ,若∠B =55°,则∠ADE 等于()A .5°B .10°C .15°D .20°二、填空题11.如图,ABC 是等腰直角三角形,BC 是斜边,P 为ABC 内一点,将ABP △绕点A 逆时针旋转后与'ACP 重合,如果3AP =,那么线段'PP 的长等于________.12.如图,在Rt △ABC 中,∠ACB =90°,将△ABC 绕顶点C 逆时针旋转得到△A ′B ′C ,M 是BC 的中点,N 是A ′B ′的中点,连接MN ,若BC =4,∠ABC =60°,则线段MN 的最大值为___.13.如图,在Rt ABC △中,90ACB Ð=°,2AC BC ==,点P 是AB 上一动点,以点C 为旋转中心,将ACP △顺时针旋转到BCQ △的位置,则PQ 的最小值为________.14.如图,△ABC 中,AB =AC ,∠A =80°,将△ABC 绕着点B 旋转,使点A 落在直线BC 上的点A '处,点C 落在点C '处,那么∠BCC '=___度.15.如图,ABC 中,90ACB Ð=°,AC BC a ==,点D 为AB 边上一点(不与点A ,B 重合),连接CD ,将线段CD 绕点C 逆时针旋转90°得到CE ,连接AE .下列结论:①BDC D ≌AEC D ;②四边形AECD 的面积是2a ;③若105BDC Ð=°,则AD =;④2222AD BD CD +=.其中正确的结论是_____.(填写所有正确结论的序号)三、解答题16.如图,已知正方形ABCD 的边长为5,点E ,F 分别在BC 和CD 边上,分别连接AE ,AF ,EF ,若45EAF Ð=°,求CEF △的周长.17.如图,P 是等边三角形ABC 内的一点,且PA =6,PB =8,PC =10.若将△PAC 绕点A 逆时针旋转后,得到△P AB¢(1)点P 与点P ’之间的距离;(2)∠APB 的度数.18.如图,在△ABC 中,AB =AC ,∠BAC =100°,D 是BC 的中点.在射线AD 上任意取一点P ,连接PB .将线段PB 绕点P 逆时针方向旋转80°,点B 的对应点是点E ,连接BE 、CE .(1)如图1,当点E 落在射线AD 上时,①∠BEP =°;②直线CE 与直线AB 的位置关系是.(2)如图2,当点E落在射线AD的左侧时,试判断直线CE与直线AB的位置关系,并证明你的结论.19.把两个等腰直角△ABC和△ADE按如图1所示的位置摆放,将△ADE绕点A按逆时针方向旋转,如图2,连接BD,EC,设旋转角α(0°<α<360°).(Ⅰ)当DE⊥AC时,旋转角α=度,AD与BC的位置关系是,AE与BC的位置关系是;(Ⅱ)当点D在线段BE上时,求∠BEC的度数;(Ⅲ)当旋转角α=时,△ABD的面积最大.20.如图1,将三角板ABC与三角板ADE摆放在一起,其中∠ACB=30°,∠DAE=45°,∠BAC =∠D=90°.固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转(如图2),记旋转角∠CAE=α(0°<α<180°).(1)当α为度时,AD∥BC;(2)当旋转角0°<α<45°时,试探究∠CAD与∠BAE之间的关系,并说明理由;(3)若△ADE旋转速度为5°/秒时,设旋转的时间为t,当DE边与△ABC的某一边平行(不共线)时,直接写出时间t的所有值.21.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A 位于时,线段AC 的长取得最大值,且最大值为(用含a ,b 的式子表示);(2)应用:点A 为线段BC 外一动点,且BC =3,AB =1,如图2所示,分别以AB ,AC 为边,作等边三角形ABD 和等边三角形ACE ,连接CD ,BE ;找出图中与BE 相等的线段,并说明理由;求线段BE 长的最大值.(3)拓展:如图3,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(5,0),点P 为线段AB 外一动点,且PA =2,PM =PB ,∠BPM =90°,求线段AM 长的最大值及此时点P 的坐标.22.如图,直线122y x =-+交y 轴于点A ,交x 轴于点C ,抛物线214y x bx c =-++经过点A 与点C ,且交x 轴于另一点B .(1)求此抛物线的解析式及点B 的坐标;(2)在直线AC 上方的抛物线上有一点M ,求ACM △面积的最大值及此时点M 的坐标;(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段''O A ,若线段''O A 与抛物线只有一个公共点,请结合函数图象,直接写出m 的取值范围.23.在平面直角坐标系中,O 为原点,点(3,0)A ,点(0,4)B ,把ABO D 绕点A 顺时针旋转,得AB O ¢¢D ,点B ,O 旋转后的对应点为B ¢,O .(1)如图①,当旋转角为90°时,求BB ¢的长;(2)如图②,当旋转角为120°时,求点O ¢的坐标;(3)在(2)的条件下,边OB 上的一点P 旋转后的对应点为P ¢,当O P AP ¢¢+取得最小值时,求点P ¢的坐标_______.(直接写出结果即可)参考答案1.C 2.C 3.D 4.B 5.C 6.A 7.D 8.C 9.D 10.B11.12.613.214.65°或15.①③④16.CEF △的周长为10.17.(1)6;(2)150°18.(1)①50;②CE ∥AB ;(2)CE ∥AB .19.(Ⅰ)45;垂直;平行;(Ⅱ)90BEC Ð=°;(Ⅲ)90°或270°20.(1)15;(2)∠BAE -∠CAD =45°;(3)t =3或9或21或27或30.21.(1)CB 的延长线上,a +b ;(2)CD BE =,线段BE 长的最大值为4;(3),AM 长的最大值为,此时点P 的坐标是(2或(222.(1)211242y x x =-++,(-2,0);(2)2,(2,2);(3)34m -££-或32m -+££23.(1)BB ¢=;(2)9(,22O';(3)27(,)55。
人教版数学九年级上册随堂练习题:23.2 中心对称

中心对称一、填空题1.点A(-6,m)与点A′(n,3)关于原点中心对称,则m+n的值是____ .2.在平面坐标系中,若点与点关于原点对称,则________.3、给出以下4个图形:①平行四边形,②正方形,③等边三角形,④圆.其中,既是轴对称图形又是中心对称图形的是.(填写序号)4.在平面直角坐标系中,点关于原点对称的点的坐标是________.5、下列两个电子数字成中心对称的是________.6.已知点P(x+2y,﹣3)和点Q(4,y)关于原点对称,则x+y=_____.二、选择题7.如图是一个以点为对称中心的中心对称图形,若,,,则的长为( )A. 2B.4C. .D.88.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.9、如图所示,已知△ABC和△A'B'C'关于点O成中心对称,则下列结论错误的是()A.∠ABC=∠A'B'C'B.∠AOC=∠A'OC'C.AB=A'B'D.OA=OC'10. 下列几组几何图形中,既是轴对称图形,又是中心对称图形,完全正确的一组是().A.正方形、菱形、矩形、平行四边形 B.正三角形、正方形、菱形、矩形C.正方形、矩形、菱形 D.平行四边形、正方形、等腰三角形11.若点关于原点对称点的坐标为,则点的坐标是()A. B. C. D.12.下列图形中,是中心对称图形但不是轴对称图形的是()A .等边三角形B .圆C .矩形D .平行四边形13.已知点A (1x ,1y )与点B (2x ,2y )关于原点对称,若112x y +=,则22x y +的值为( )A .2B .12C .12-D .2-14.如图, , ,若画一条直线将这个图形分成面积相等的两个部分,则符合要求的直线可以画( )A. 条B. 条C. 条D.无数条15.下列说法正确的是( )A .全等的两个图形成中心对称B .成中心对称的两个图形必须能完全重合C .旋转后能重合的两个图形成中心对称D .成中心对称的两个图形不一定全等16、下列说法正确的是 ( )A .线段绕着它的中点旋转180°后与原线段重合,那么线段是中心对称图形B .等边三角形绕着它的三边中线的交点旋转120°后与原图形重合,那么等边三角形是中心对称图形C .正方形绕着它的对角线交点旋转90°后与原图形重合,那么正方形是中心对称图形D .正五角星绕着它的中心旋转72°后与原图形重合,那么正五角星是中心对称图形三、解答题17.在平面直角坐标系中,ABC △三个顶点的坐标分别是()3,1A -,()1,4B -,()0,1C .(1)将ABC △绕点C 旋转180︒,请画出旋转后对应的11A B C ;(2)将11A B C 沿着某个方向平移一定的距离后得到222A B C △,已知点1A 的对应点2A 的坐标为()3,1-,请画出平移后的222A B C △;(3)若ABC △与222A B C △关于某一点中心对称,则对称中心的坐标为_____.18、如图,平面直角坐标系中,每个小正方形边长都是1.(1)按要求作图:①△ABC关于原点O逆时针旋转90°得到△A1B1C1;②△A1B1C1关于原点中心对称的△A2B2C2.(2)△A2B2C2中顶点B2坐标为.19.用六根一样长的小棒搭成如图所示的图形,试移动、这两根小棒,使六根小棒成为中心对称图形;若移动、这两根,能不能也达到要求呢?(画出图形)20. 如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:CE的值.21.如图,已知两个字母“F”成中心对称,请你画出对称中心O.22、如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180°得到△DEC.(1)试猜想AE与BD有何关系?并且直接写出答案.(2)若△ABC的面积为4cm2,求四边形ABDE的面积;(3)请给△ABC添加条件,使旋转得到的四边形ABDE为矩形,并说明理由.答案一、1.3 12. 3. ②④ 4. 5、①④ 6.-7 二、7-16 B D D C B B D D B A三、17.(1)△A 1B 1C 1如图所示;(2)△A 2B 2C 2,如图所示;(3)∵()3,1A -,()1,4B -,()0,1C ,()23,1A -,()21,4B -,()20,1C - ∴ABC △与222A B C △关于原点对,对称中心坐标为()0,0,18.解:(1)①△A 1B 1C 1如图所示;②△A 2B 2C 2如图所示;(2)B 2(1,6).故答案为:(1,6).19.解: 能,20. 解:如答图所示.作已知图形的中心对称图形,以E为对称中心.令BF=a,FG=b,GE=c.因为M′C∥AM,N′C∥AN 所以a:(2b+2c)=BM:MC=1:2所以a=b+c,而(a+b):2c=BN:NC=2:1所以:a+b=4c,所以a=c,b=c.所以BF:FG:GE=5:3:2.21.如图,连接AB,CD,EF交于点O,点O即为所求.22、解:(1)AE∥BD,且AE=BD;(2)四边形ABDE的面积是:4×4=16;(3)AC=BC.理由是:∵AC=CD,BC=CE,∴四边形ABDE是平行四边形.∵AC=BC,∴平行四边形ABDE是矩形.。
2020年秋人教版九年级数学上册随堂练——23章图形的旋转单元学情练习
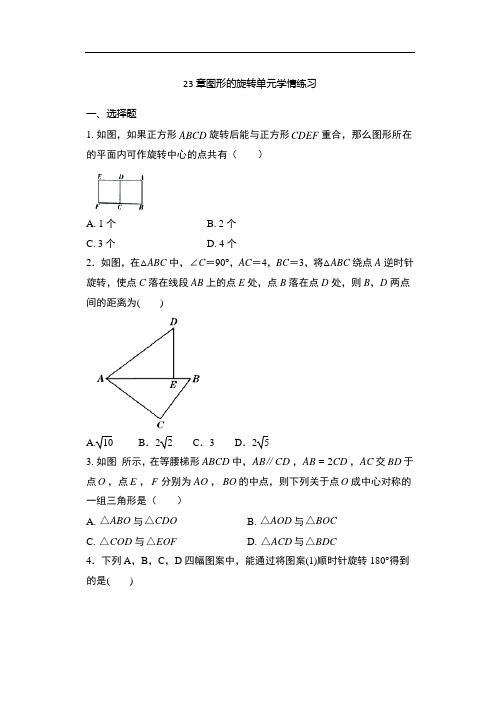
23章图形的旋转单元学情练习一、选择题1.如图,如果正方形ABCD 旋转后能与正方形CDEF 重合,那么图形所在的平面内可作旋转中心的点共有( )A .1个B .2个C .3个D .4个 2.如图,在△ABC 中,∠C =90°,AC =4,BC =3,将△ABC 绕点A 逆时针旋转,使点C 落在线段AB 上的点E 处,点B 落在点D 处,则B ,D 两点间的距离为( )A.10 B .2 2 C .3 D .2 53.如图 所示,在等腰梯形ABCD 中,AB CD ∥,2AB CD ,AC 交BD 于点O ,点E ,F 分别为AO ,BO 的中点,则下列关于点O 成中心对称的一组三角形是( )A .ABO △与CDO △B .AOD △与BOC △ C .COD △与EOF △ D .ACD △与BDC △4.下列A ,B ,C ,D 四幅图案中,能通过将图案(1)顺时针旋转180°得到的是( )5.如图 ,将AOB △绕点O 按逆时针方向旋转45︒后得到''A OB △,若15AOB ∠=︒,则'AOB ∠的度数是( )A .25︒B .30︒C .35︒D .40︒6.如图,将ABC △绕点B 逆时针旋转α,得到EBD △,若点A 恰好在ED 的延长线上,则CAD ∠的度数为( )A .90α︒-B .αC .180α︒-D .2α 7.如图,△OAB 绕点O 逆时针旋转75°到△OCD 的位置,已知∠AOB =40°,则∠AOD 等于( )A .55°B .45°C .40°D .35°8.如图 ,Rt AOB △放置在平面直角坐标系中,点A 的坐标是1,0(),点B 的坐标是0,2(),把Rt AOB △绕点A 按顺时针方向旋转90︒后,得到''Rt AO B △,则点'B 的坐标是( )A .()1,2B .()1,3C .()2,3D .()3,19.如图,将等边ABC △绕点C 顺时针旋转120︒得到EDC △,连接AD ,BD .则下列结论:①AC AD =;②BD AC ⊥;③四边形ACED 是菱形。
人教版数学九年级上册 23.1---23.3同步测试题含答案)

23.1图形的旋转一.选择题1.如图所示的是正十二角形体,因为其独特的对称美,所以2019年在英国举办的第60界国际数学奥林匹克的会标,就选用了正十二角形体,若将它绕自身中心旋转一定角度后能与原图重合,则这个角度不可能是()A.60°B.90°C.120°D.180°2.如图,△OAB绕某点旋转到△OCD的位置,则旋转中心是()A.点A B.点B C.点O D.无法确定3.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是()A.75°B.45°C.60°D.30°4.如图,是一个纸折的小风车模型,将它绕着旋转中心旋转下列哪个度数后不能与原图形重合()A.90°B.135°C.180°D.270°5.如图,用左面的三角形连续的旋转可以得到右面的图形,每次旋转()度.A.60B.90C.120D.1506.下列图形中,绕某个点旋转72度后能与自身重合的是()A.B.C.D.7.如图,在Rt△AOB中,∠O=90°,以点A为旋转中心,把△ABO顺时针旋转得△ACD,记旋转角为α,∠ABO为β,当旋转后满足BC∥OA时,α与β之间的数量关系为()A.α=βB.α=2βC.α+β=90°D.α+2β=180°8.如图,在正方形网格中,格点△ABC绕某点顺时针旋转α度(0<α<180),得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α的值为()A.50B.60C.90D.1209.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC;其中一定正确的是()A.①②B.②③C.③④D.②③④10.如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C 为旋转中心把△CBD旋转到△CAE,则下列结论:①D、A、E三点共线;②DC平分∠BDA;③∠E=∠BAC;④DC=DB+DA.其中正确的有()A.4个B.3个C.2个D.1个二.填空题11.如图,已知点D为等边三角形ABC的AC边的中点,BC=4,点B绕着点D顺时针旋转180°的过程中,点B的对应点为点B',连接B'C、B'D,当△B'DC的面积为时,∠B'DB为.12.等边△EBC中,EC=BC=6cm,点O在BC上,且OC=4cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.则当点F运动s时,点F恰好落在射线EB上.13.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任何一个角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O 点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=78°,则∠AOB等于度.14.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是度.15.如图,△ABP是由△ACD按顺时针方向旋转某一角度得到的,若∠BAP=60°,则在这转过程中,旋转中心是,旋转的角度为.三.解答题16.如图,在平面直角坐标系中,A(﹣3,0),点B是y轴正半轴上一动点,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,连接OP,求OP的最小值.17.如图,正方形ABCD内一点E,△ADE绕点A顺时针旋转能与△ABF重合,若AE=3.(1)求∠EAF的度数;(2)求EF的长.18.如图,△ABC中,∠B=19.11°,∠ACB=40.89°,AB=6,△ABC逆时针旋转一定角度后能与△ADE重合,且点C恰好为AD的中点.(1)指出旋转中心,并求出旋转的度数;(2)求出∠BAE的度数和AE的长.19.已知△ABC为等边三角形.(1)如图,P为△ABC外一点,∠BPC=120°,连接P A,PB,PC,求证:PB+PC=P A;(2)如图,P为△ABC内一点,若P A=12,PB=5,PC=13,求∠APB的度数.参考答案与试题解析一.选择题1.【解答】解:∵正十二角形体的中心角为30°,∴观察图象可知,旋转角是30°的偶数倍数时,可以与本身重合,故选:B.2.【解答】解:由题意得△OAB绕某点旋转到△OCD的位置,则旋转中心是点O.故选:C.3.【解答】解:如图,由题意及旋转变换的性质得:∠AOC=∠BOD=45°,∵∠AOB=15°,∴∠AOD=45°+15°=60°,故选:C.4.【解答】解:图案可以被平分成四部分,因而每部分被分成的圆心角是90°,并且圆具有旋转不变性,因而旋转90度的整数倍,就可以与自身重合,故选:B.5.【解答】解:根据图形可得出:这是一个由基本图形绕着中心连续旋转3次,每次旋转120度角形成的图案.故选:C.6.【解答】解:A.旋转90°后能与自身重合,不合题意;B.旋转72°后能与自身重合,符合题意;C.旋转60°后能与自身重合,不合题意;D.旋转45°后能与自身重合,不合题意;故选:B.7.【解答】解:∵把△ABO顺时针旋转得△ACD,∴△AOB≌△ADC,∠BAC=∠OAD=α,∴AB=AC,∠BAO=∠CAD,在△ABC中,∠ABC=(180°﹣α),∵BC∥OA,∴∠OBC=180°﹣∠O=180°﹣90°=90°,∴β+(180°﹣α)=90°,整理得,α=2β.故选:B.8.【解答】解:如图,连接AA1,CC1,作AA1,CC1的垂直平分线交于点O,∵CC1,AA1的垂直平分线交于点O,∴点O是旋转中心,由图形可得:∠AOA1=90°∴旋转角α度=90°故选:C.9.【解答】解:∵将△ABC绕点C顺时针旋转得到△DEC,∴AC=CD,BC=CE,AB=DE,故①错误,③正确;∴∠ACD=∠BCE,∴∠A=∠ADC=,∠CBE=,∴∠A=∠EBC,故④正确;∵∠A+∠ABC不一定等于90°,∴∠ABC+∠CBE不一定等于90°,故②错误.故选:C.10.【解答】解:如图,①设∠1=x度,则∠2=(60﹣x)度,∠DBC=(x+60)度,故∠4=(x+60)度,∴∠2+∠3+∠4=60﹣x+60+x+60=180度,∴D、A、E三点共线;故①正确;②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE,∴CD=CE,∠DCE=60°,∴△CDE为等边三角形,∴∠E=60°,∴∠BDC=∠E=60°,∴∠CDA=120°﹣60°=60°,∴DC平分∠BDA;故②正确;③∵∠BAC=60°,∠E=60°,∴∠E=∠BAC.故③正确;④由旋转可知AE=BD,又∵∠DAE=180°,∴DE=AE+AD.∵△CDE为等边三角形,∴DC=DB+BA.故④正确;故选:A.二.填空题(共5小题)11.【解答】解:如图,若点B'在AC的左侧时,过点B'作BN⊥AC,交CA于点N,∵△ABC是等边三角形,∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC=4,又∵点D是CD的中点,∴BD⊥AC,CD=AD=2,BD=CD=2,∵△B'DC的面积为,∴×CD×B'N=,∴×2×B'N=,∴B'N=,∵点B绕着点D顺时针旋转180°,∴B'D=BD=2,∴DN===,∴DN=B'N=,∴∠NDB'=∠DB'N=45°,∴∠BDB'=45°,在点B'在AC的右侧时,∠B''DA=45°,∴∠BDB''=135°,综上所述:∠B'DB=45°或135°,故答案为:45°或135°.12.【解答】解:如图,∵由旋转知,OP=OF,∵△BCE是等边三角形,∴∠CBE=∠BCE=60°,∴∠OCP=∠FBO=120°,∠CPO+∠COP=60°,∵∠POF=120°,∴∠COP+∠BOF=60°,∴∠CPO=∠BOF,在△BOF和△PCO中,,∴△BOF≌△PCO(AAS),∴CP=OB,∵EC=BC=6cm,OC=4cm,∴OB=BC﹣OC=2(cm),∴CP=2cm,∴EP=CE+CP=8(cm),∴点P运动的时间t=8÷2=4(s),故答案为:4.13.【解答】解:∵OC=CD=DE,∴∠O=∠CDO,∠DCE=∠DEC,∵∠DCE=∠O+∠CDO=2∠O,∴∠DEC=2∠O,∵∠BDE是△ODE的外角,∴∠BDE=∠O+2∠DEC=3∠O=78°,∴∠AOB=26°,故答案为:26.14.【解答】解:∵时针从上午的6时到10时共旋转了4个格,每相邻两个格之间的夹角是30°,∴时针旋转的旋转角=30°×4=120°.故答案为:120.15.【解答】解:旋转中心为点A,旋转角为∠BAC=∠BAP+∠P AC=60°+30°=90°;故答案为A,90°.三.解答题(共4小题)16.【解答】解:如图,以OA为对称轴作等边△ADE,连接EP,并延长EP交x轴于点F,∴∠AED=60°,∴AO=OE=3,∴OE=,∵△ADE和△ABP是等边三角形,∴AB=AP,AD=AE,∠BAP=∠DAE=60°,∴∠BAD=∠P AE,在△ADB和△AEP中,∴△AEP≌△ADB(SAS),∴∠AEP=∠ADB=120°,∴∠OEF=60°,∴OF=OE=3,∠OFE=30°,∴点P在直线EF上运动,当OP⊥EF时,OP最小,∴OP=OF=,则OP的最小值为,17.【解答】解(1)∵△ADE绕点A顺时针旋转能与△ABF重合,∴∠DAB=∠EAF=90°;(2)∵△ADE绕点A顺时针旋转能与△ABF重合,∴AE=AF=3,∠EAF=90°,∴EF=AE=3.18.【解答】解:(1)∠BAC=180°﹣∠B﹣∠ACB=180°﹣19.11°﹣40.89°=120°,即∠BAD=120°,所以旋转中心为点A,旋转的度数为120°;(2)∵△ABC逆时针旋转一定角度后与△ADE重合,∴∠EAD=∠BAC=120°,AE=AC,AD=AB=6,∴∠BAE=360°﹣120°﹣120°=120°,∵点C恰好成为AD的中点,∴AC=AD=3,∴AE=3.19.【解答】证明:(1)如图1,延长BP至点E,使得PE=PC,连接CE,∵∠BPC=120°,PE=PC,∴∠CPE=60°,∴△CPE为等边三角形,∴CP=PE=CE,∠PCE=60°,∵△ABC是等边三角形,∴AC=BC,∠BCA=60°,∴∠ACB=∠ECP,∴∠ACB+∠BCP=∠ECP+∠BCP,即:∠ACP=∠BCE,在△ACP和△BCE中,,∴△ACP≌△BCE(SAS),∴AP=BE,∵BE=BP+PE=BP+PC,∴PB+PC=P A;(2)如图2,将△ABP绕点B顺时针方向旋转60°,得到△CBP',连接PP',由旋转知,△APB≌△CP′B,∴∠BP A=∠BP′C,P′B=PB=5,P′C=P A=12,∠PBP'=∠ABC=60°,又∵P′B=PB=5,∴△PBP′是等边三角形,∴∠PP′B=60°,PP′=523.3课时学习图案设计一.选择题1.如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有()A.1个B.2个C.3个D.4个2.下列是国内几所知名大学的图标,若不考虑图标上的文字、字母和数字,其中既可以通过翻折变换,又可以通过旋转变换得到的图形是()A.清华大学B.浙江大学C.北京大学D.中南大学3.一个图形无论经过平移变换,还是经过旋转变换,下列说法:a.对应线段平行,b.对应线段相等,c.图形的形状和大小都没有发生变化,d.对应角相等,其中正确的是()A.a.b.c.B.b.c.d.C.a.b.d.D.a.c.d.4.如图,点A,B在方格纸的格点位置上,若要再找一个格点C,使它们所构成的三角形为轴对称图形,则这样的格点C在图中共有()A.4个B.6个C.8个D.10个5.如图,在正方形方格中,阴影部分是涂黑7 个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有()A.4 种B.3 种C.2 种D.1 种6.“飞流直下三千尺”、“坐地日行八万里(只考虑地球自转)”如果只从数学角度看,它们分别蕴含的图形变换是()A.平移、对称B.对称、旋转C.平移、旋转D.旋转、对称7.将如图所示“你最棒”的微信图案通过平移后可以得到的图案是()A.B.C.D.8.如图的四个图形中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有()个.A.1B.2C.3D.49.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.10.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有20×20的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是()A.13B.14C.15D.16二.填空题11.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有种.12.图中能通过基本图形旋转得到的有(请填写序号)13.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要在其余13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形,这样的白色小方格有个,请在图中设计出一种方案.14.如图,这个图形是由“基本图案”ABCDE绕着点顺时针依次旋转次得到的,则每次旋转的角度为.15.如图,在网格图中,平移图A,使它与图B拼合成一个长方形,应将图A向(填“左”或“右”)平移格;再向(填“上”或“下”)平移格.三.解答题16.如图,△ABC的三个顶点在网格上(1)画出三角形关于原点O的中心对称图形△A1B1C1;(2)直接写出点A1的坐标为.17.如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点AB的坐标分别是A(3,2),B(1,3).将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并直接写出这时点A2的坐标.18.如图,图中每个小方格都是边长为1个单位长度的正方形,△ABC在方格纸中的位置如图所示.(1)请在图中建立平面直角坐标系,使得A,B两点的坐标分别为A(2,﹣1),B(1,﹣4),并写出C点坐标;(2)在图中作出△ABC绕坐标原点旋转180°后的△A1B1C1,并写出A1,B1,C1的坐标:(3)在图中作出△ABC绕坐标原点顺时针旋转90°后的△A2B2C2,并写出A2,B2,C2的坐标.19.阅读下列材料,完成相应学习任务旋转对称把正n边形绕着它的中心旋转°的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有°的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.任务:(1)如图2,正六边形关于其中心O有的旋转对称,中心对称图形关于其对称中心有的旋转对称;(2)图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转与原图形重合;(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.参考答案与试题解析一.选择题1.【解答】解:如图所示:,共3个,故选:C.2.【解答】解:A、是既可以通过翻折变换,又可以通过旋转变换得到的图形,正确;B、可以通过翻折变换,但不可以通过旋转变换得到的图形,错误;C、可以通过翻折变换,但不可以通过旋转变换得到的图形,错误;D、不可以通过翻折变换,但可以通过旋转变换得到的图形,错误;故选:A.3.【解答】解:a、经过旋转变换对应线段不一定平行,b、无论经过平移变换,还是经过旋转变换,对应线段相等,c、无论经过平移变换,还是经过旋转变换,图形的形状和大小都没有发生变化,d、无论经过平移变换,还是经过旋转变换,对应角相等,综上所述,说法正确的是b、c、d.故选:B.4.【解答】解:如图所示,这样的格点C在图中共有10个,故选:D.5.【解答】解:在1,2,3处分别涂黑都可得一个轴对称图形.故选:B.6.【解答】解:根据平移和旋转定义可知:“飞流直下三千尺”是平移;“坐地日行八万里”是旋转.故选:C.7.【解答】解:将如图所示“你最棒”的微信图案通过平移后可以得到的图案是,故选:C.8.【解答】解:图形①可以分别旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;图形②可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;图形③可以旋转180°得到,不可以经过轴对称得到,故此选项错误;图形④可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合.故既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有3个.故选:C.9.【解答】解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,故选:B.10.【解答】解:如图1,连接AC,CF,则AF=3,∴两次变换相当于向右移动3格,向上移动3格,又∵MN=20,∴20÷3=,(不是整数)∴按A﹣C﹣F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处,∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是10+4=14次,故选:B.二.填空题(共5小题)11.【解答】解:如图,有三种方案,故答案为3.12.【解答】解:四幅图中,能通过基本图形旋转得到的有:(1)(2)(3)(4).故答案为:(1)(2)(3)(4).13.【解答】解:如图所示,有4个位置使之成为轴对称图形.故答案为:4.14.【解答】解:根据旋转的性质,可知:在点D处有6个角,故360°÷6=60°,所以它的旋转角为60°.即这个图形是由“基本图案”ABCDE绕着点D顺时针依次旋转5次得到的,则每次旋转的角度为60°.故答案为:D、5、60°.15.【解答】解:∵A图形在B图形的左边可知应先向右平移图形A,点C距点D4个格,∴应先向右平移4个格,此时点C与点D重合,∵点D距点E2个格,∴向上平移2格.故答案为:右,4,上,2.三.解答题(共4小题)16.【解答】解:(1)如图,△A1B1C1为所作;(2)点A1的坐标为(1,﹣3).故答案为(1,﹣3).17.【解答】解:如图所示:A2(﹣2,3);.18.【解答】解:(1)坐标系如图所示,C(3,﹣3);(2)△A1B1C1如图所示,A1(﹣2,1),B1(﹣1,4),C1(﹣3,3);(3)△A2B2C2如图所示,A(﹣1,﹣2),B(﹣4,﹣1),C2(﹣3,﹣3).19.【解答】解:(1)正六边形关于其中心O有60°的旋转对称,中心对称图形关于其对称中心有180°的旋转对称;故答案为:60°;180°;(2)∵360°÷5=72°。
人教版九年级数学上册同步测试 23.1 --23.3 基础知识检测题含答案
人教版九年级数学上册同步测试23.1 --23.3 基础知识检测题含答案23.1 图形的旋转一、选择题(共18小题)1.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为()A.4,30°B.2,60°C.1,30°D.3,60°2.如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=()A.90°B.100°C.110°D.120°3.如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是()A.15°B.60°C.45°D.75°4.如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB 绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为()A.B.15 C.3 D.5.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是()A.21°B.45°C.42°D.24°6.如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=,则CG的长是()A.1.5 B.1.6 C.1.8 D.27.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为()A.56°B.50°C.46°D.40°8.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于()A.55°B.60°C.65°D.80°9.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B.C. D.π10.如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA()A.顺时针旋转90°B.顺时针旋转45°C.逆时针旋转90°D.逆时针旋转45°11.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB.6πC.3πD.1.5π12.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70°B.65°C.60°D.55°13.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是()A.AE∥BC B.∠ADE=∠BDCC.△BDE是等边三角形D.△ADE的周长是914.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()A.0.5 B.1.5 C.D.115.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为()A.10°B.20°C.7.5°D.15°16.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30°B.60°C.90°D.150°17.如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为()A.π﹣2 B.πC.πD.π﹣218.如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC 相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A.2﹣B. +1 C.D.﹣1二、填空题(共6小题)19.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是.20.如图,在△ABC中,∠B=50°,在同一平面内,将△ABC绕点A逆时针方向旋转到△AB′C′的位置,使得AB′⊥BC,连接CC′,则∠AC′C=度.21.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为.22.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是.23.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为.24.如图,在△ABC中,AC=BC=8,∠C=90°,点D为BC中点,将△ABC绕点D逆时针旋转45°,=.得到△A′B′C′,B′C′与AB交于点E,则S四边形ACDE三、解答题(共6小题)25.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.26.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.27.将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.(1)求∠ADE的度数;(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断的值是否随着α的变化而变化?如果不变,请求出的值;反之,请说明理由.28.已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME ⊥m于E,CF⊥m于F.(1)当直线m经过B点时,如图1,易证EM=CF.(不需证明)(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.29.在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.小明做了如下操作:将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.30.两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD 绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).(2)当α=45°时(如图③),求证:四边形MHND为正方形.参考答案一、选择题(共18小题)1.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为()A.4,30°B.2,60°C.1,30°D.3,60°【考点】旋转的性质;平移的性质.【分析】利用旋转和平移的性质得出,∠A′B′C=60°,AB=A′B′=A′C=4,进而得出△A′B′C是等边三角形,即可得出BB′以及∠B′A′C的度数.【解答】解:∵∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,∴∠A′B′C=60°,AB=A′B′=A′C=4,∴△A′B′C是等边三角形,∴B′C=4,∠B′A′C=60°,∴BB′=6﹣4=2,∴平移的距离和旋转角的度数分别为:2,60°.故选:B.2.如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=()A.90°B.100°C.110°D.120°【考点】旋转的性质.【分析】由旋转的性质可知AC=EC,BC=DC,∠BCD=∠ACE=40°,在△BCD中,由内角和定理求∠1,根据外角定理可求∠2.【解答】解:在△BCD中,∠BCD=∠ACE=40°,BC=CD,∴△BCD为等腰三角形,∴∠1=(180°﹣40°)=70°,∵∠BEC为△ACE的外角,∴∠2+∠DEC=∠ACE+∠A,而∠DEC与∠A为对应角,∴∠2=∠ACE=40°,∴∠1+∠2=70°+40°=110°,故选C.3.如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是()A.15°B.60°C.45°D.75°【考点】旋转的性质.【分析】根据∠AOD=∠DOB﹣∠AOB求解.【解答】解:∵将△AOB绕点O按逆时针方向旋转60°后得到△COD,∴∠BOD=60°,∵∠AOB=15°,∴∠AOD=∠DOB﹣∠AOB=60°﹣15°=45°.故选:C.4.如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB 绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为()A.B.15 C.3 D.【考点】旋转的性质;平移的性质.【专题】网格型.【分析】首先作出线段A1B1和A2B2,确定线段AB,A1B1,A2B2的中点,作出三角形,利用三角形的面积公式求解.【解答】解:三角形的面积是:×3×5=.故选A.5.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是()A.21°B.45°C.42°D.24°【考点】旋转的性质.【分析】如图,首先运用旋转变换的性质求出∠BOB′的度数,结合∠AOB=21°,即可解决问题.【解答】解:如图,由题意及旋转变换的性质得:∠BOB′=45°,∵∠AOB=21°,∴∠AOB′=45°﹣21°=24°,故选D.6.如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=,则CG的长是()A.1.5 B.1.6 C.1.8 D.2【考点】旋转的性质;勾股定理;相似三角形的判定与性质.【专题】计算题.【分析】先根据正方形的性质得AB=AD=CD=3,再根据旋转的性质得AF=AE=,则可根据勾股定理计算出DF=2,所以CF=CD﹣DF=1,然后证明△CGF∽△DAF,再利用相似比可计算出CG.【解答】解:∵四边形ABCD是正方形,∴AB=AD=CD=3,∵△ABE绕点A逆时针旋转90°,得到△ADF,∴AF=AE=,在Rt△ADF中,∵AD=3,AF=,∴DF==2,∴CF=CD﹣DF=3﹣2=1,∵AD∥CG,∴△CGF∽△DAF,∴=,即=,∴CGF=1.5.故选A.7.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为()A.56°B.50°C.46°D.40°【考点】旋转的性质;等腰三角形的性质.【专题】几何图形问题.【分析】利用旋转的性质以及等腰三角形的性质得出∠AC′C=∠AC′B′=67°,进而得出∠B′C′B的度数.【解答】解:∵将△ABC绕点A顺时针旋转后,得到△AB′C′,∴AC′=AC,∴∠C=∠AC′C=67°,∴∠AC′B=180°﹣67°=113°,∵∠AC′C=∠AC′B′=67°,∴∠B′C′B=∠AC′B﹣∠AC′B′=113°﹣67°=46°.故选:C.8.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于()A.55°B.60°C.65°D.80°【考点】旋转的性质.【分析】利用直角三角形斜边上的中线等于斜边的一半,进而得出△ABB1是等边三角形,即可得出旋转角度.【解答】解:∵在Rt△ABC中,∠BAC=90°,将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处,∴AB1=BC,BB1=B1C,AB=AB1,∴BB1=AB=AB1,∴△ABB1是等边三角形,∴∠BAB1=60°,∴旋转的角度等于60°.故选:B.9.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B.C. D.π【考点】旋转的性质;弧长的计算.【专题】几何图形问题.【分析】利用锐角三角函数关系得出BC的长,进而利用旋转的性质得出∠BCB′=60°,再利用弧长公式求出即可.【解答】解:∵在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,∴cos30°=,∴BC=ABcos30°=2×=,∵将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,∴∠BCB′=60°,∴点B转过的路径长为:=π.故选:B.10.如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA()A.顺时针旋转90°B.顺时针旋转45°C.逆时针旋转90°D.逆时针旋转45°【考点】旋转的性质.【专题】几何图形问题.【分析】因为四边形ABCD为正方形,所以∠COD=∠DOA=90°,OC=OD=OA,则△COD绕点O 逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,据此可得答案.【解答】解:∵四边形ABCD为正方形,∴∠COD=∠DOA=90°,OC=OD=OA,∴△COD绕点O逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,故选:C.11.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB.6πC.3πD.1.5π【考点】旋转的性质;弧长的计算.【专题】计算题.【分析】根据弧长公式列式计算即可得解.【解答】解:的长==1.5π.故选:D.12.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70°B.65°C.60°D.55°【考点】旋转的性质.【专题】几何图形问题.【分析】根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.【解答】解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,∴AC=A′C,∴△ACA′是等腰直角三角形,∴∠CAA′=45°,∴∠A′B′C=∠1+∠CAA′=20°+45°=65°,由旋转的性质得∠B=∠A′B′C=65°.故选:B.13.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是()A.AE∥BC B.∠ADE=∠BDCC.△BDE是等边三角形D.△ADE的周长是9【考点】旋转的性质;平行线的判定;等边三角形的性质.【专题】几何图形问题.【分析】首先由旋转的性质可知∠EBD=∠ABC=∠C=60°,所以看得AE∥BC,先由△ABC是等边三角形得出AC=AB=BC=5,根据图形旋转的性质得出AE=CD,BD=BE,故可得出AE+AD=AD+CD=AC=5,由∠EBD=60°,BE=BD即可判断出△BDE是等边三角形,故DE=BD=4,故△AED的周长=AE+AD+DE=AC+BD=9,问题得解.【解答】解:∵△ABC是等边三角形,∴∠ABC=∠C=60°,∵将△BCD绕点B逆时针旋转60°,得到△BAE,∴∠EAB=∠C=∠ABC=60°,∴AE∥BC,故选项A正确;∵△ABC是等边三角形,∴AC=AB=BC=5,∵△BAE△BCD逆时针旋旋转60°得出,∴AE=CD,BD=BE,∠EBD=60°,∴AE+AD=AD+CD=AC=5,∵∠EBD=60°,BE=BD,∴△BDE是等边三角形,故选项C正确;∴DE=BD=4,∴△AED的周长=AE+AD+DE=AC+BD=9,故选项D正确;而选项B没有条件证明∠ADE=∠BDC,∴结论错误的是B,故选:B.14.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()A.0.5 B.1.5 C.D.1【考点】旋转的性质.【分析】解直角三角形求出AB,再求出CD,然后根据旋转的性质可得AB=AD,然后判断出△ABD 是等边三角形,根据等边三角形的三条边都相等可得BD=AB,然后根据CD=BC﹣BD计算即可得解.【解答】解:∵∠B=60°,∴∠C=90°﹣60°=30°,∵AC=,∴AB=AC•tan30°=×=1,∴BC=2AB=2,由旋转的性质得,AB=AD,∴△ABD是等边三角形,∴BD=AB=1,∴CD=BC﹣BD=2﹣1=1.故选:D.15.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为()A.10°B.20°C.7.5°D.15°【考点】旋转的性质;全等三角形的判定与性质;等腰直角三角形.【分析】根据直角三角形两锐角互余求出∠DCE=60°,旋转的性质可得∠BCE1=15°,然后求出∠BCD1=45°,从而得到∠BCD1=∠A,利用“边角边”证明△ABC和△D1CB全等,根据全等三角形对应角相等可得∠BD1C=∠ABC=45°,再根据∠E1D1B=∠BD1C﹣∠CD1E1计算即可得解.【解答】解:∵∠CED=90°,∠D=30°,∴∠DCE=60°,∵△DCE绕点C顺时针旋转15°,∴∠BCE1=15°,∴∠BCD1=60°﹣15°=45°,∴∠BCD1=∠A,在△ABC和△D1CB中,,∴△ABC≌△D1CB(SAS),∴∠BD1C=∠ABC=45°,∴∠E1D1B=∠BD1C﹣∠CD1E1=45°﹣30°=15°.故选:D.16.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30°B.60°C.90°D.150°【考点】旋转的性质.【专题】几何图形问题.【分析】根据直角三角形两锐角互余求出∠A=60°,根据旋转的性质可得AC=A′C,然后判断出△A′AC 是等边三角形,根据等边三角形的性质求出∠ACA′=60°,然后根据旋转角的定义解答即可.【解答】解:∵∠ACB=90°,∠ABC=30°,∴∠A=90°﹣30°=60°,∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上,∴AC=A′C,∴△A′AC是等边三角形,∴∠ACA ′=60°,∴旋转角为60°.故选:B .17.如图,Rt △ABC 中,∠ACB=90°,AC=BC=2,在以AB 的中点O 为坐标原点,AB 所在直线为x 轴建立的平面直角坐标系中,将△ABC 绕点B 顺时针旋转,使点A 旋转至y 轴正半轴上的A ′处,则图中阴影部分面积为( )A .π﹣2B .πC .πD .π﹣2【考点】旋转的性质;扇形面积的计算.【分析】根据等腰直角三角形的性质求出AB ,再根据旋转的性质可得A ′B=AB ,然后求出∠OA ′B=30°,再根据直角三角形两锐角互余求出∠A ′BA=60°,即旋转角为60°,再根据S 阴影=S 扇形ABA ′+S △A ′BC ′﹣S △ABC ﹣S 扇形CBC ′=S 扇形ABA ′﹣S 扇形CBC ′,然后利用扇形的面积公式列式计算即可得解. 【解答】解:∵∠ACB=90°,AC=BC ,∴△ABC 是等腰直角三角形,∴AB=2OA=2OB=AC=2,∵△ABC 绕点B 顺时针旋转点A 在A ′处,∴BA ′=AB ,∴BA ′=2OB ,∴∠OA ′B=30°,∴∠A ′BA=60°,即旋转角为60°,S 阴影=S 扇形ABA ′+S △A ′BC ′﹣S △ABC ﹣S 扇形CBC ′,=S 扇形ABA ′﹣S 扇形CBC ′, =﹣,=π﹣π,=π.故选C.18.如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC 相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A.2﹣B. +1 C.D.﹣1【考点】旋转的性质;四点共圆;线段的性质:两点之间线段最短;等边三角形的性质;勾股定理;相似三角形的判定与性质.【专题】压轴题.【分析】取AC的中点O,连接AD、DG、BO、OM,如图,易证△DAG∽△DCF,则有∠DAG=∠DCF,从而可得A、D、C、M四点共圆,根据两点之间线段最短可得BO≤BM+OM,即BM≥BO﹣OM,当M在线段BO与该圆的交点处时,线段BM最小,只需求出BO、OM的值,就可解决问题.【解答】解:AC的中点O,连接AD、DG、BO、OM,如图.∵△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,∴AD⊥BC,GD⊥EF,DA=DG,DC=DF,∴∠ADG=90°﹣∠CDG=∠FDC,=,∴△DAG∽△DCF,∴∠DAG=∠DCF.∴A、D、C、M四点共圆.根据两点之间线段最短可得:BO≤BM+OM,即BM≥BO﹣OM,当M在线段BO与该圆的交点处时,线段BM最小,此时,BO===,OM=AC=1,则BM=BO﹣OM=﹣1.故选:D.二、填空题(共6小题)19.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是.【考点】旋转的性质;扇形面积的计算.【专题】计算题.【分析】根据含30度的直角三角形三边的关系得到AB=2AC=2,BC=AC=,根据互余得到∠CAB=60°,再根据旋转的性质得到AC′=AC=1,AB′=AB=2,B′C′=BC=,∠B′AB=30°,∠C′AB′=∠CAB=60°,则∠C′AD=∠C′AB′∠BAB′=30°,接着在Rt△AC′D中,利用∠C′AD=30°可得C′D=AC′=,所以B′D=B′C′﹣C′D=,然后根据三角形面积公式、扇形面积公式和图中阴影部分的面积=S﹣S△ADB′进行计算即可.扇形BAB′【解答】解:∵∠C=90°,∠ABC=30°,∴∠CAB=60°,AB=2AC=2,BC=AC=,∵Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,∴AC′=AC=1,AB′=AB=2,B′C′=BC=,∠B′AB=30°,∠C′AB′=∠CAB=60°,∴∠C′AD=∠C′AB′∠BAB′=30°,在Rt△AC′D中,∵∠C′AD=30°,∴C′D=AC′=,∴B′D=B′C′﹣C′D=﹣=,∴图中阴影部分的面积=S﹣S△ADB′扇形BAB′=﹣××1=.故答案为:.20.如图,在△ABC中,∠B=50°,在同一平面内,将△ABC绕点A逆时针方向旋转到△AB′C′的位置,使得AB′⊥BC,连接CC′,则∠AC′C=70度.【考点】旋转的性质.【分析】首先证明∠CAC′=40°然后证明∠ACC′=∠AC′C;然后运用三角形的内角和定理求出∠AC′C=70°即可解决问题.【解答】解:∵∠B=50°,AB′⊥BC,∴∠B′AB=40°,∴旋转角为40°,∴∠CAC′=40°,由题意得:AC=AC′,∴∠ACC′=∠AC′C;∴∠AC′C=70°,故答案为7021.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为2﹣.【考点】旋转的性质.【专题】几何图形问题.【分析】利用正方形和旋转的性质得出A′D=A′E,进而利用勾股定理得出BD的长,进而利用锐角三角函数关系得出DE的长即可.【解答】解:由题意可得出:∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD中,AD=1,∴AB=A′B=1,∴BD=,∴A′D=﹣1,∴在Rt△DA′E中,DE==2﹣.故答案为:2﹣.22.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是2π.【考点】旋转的性质.【分析】首先计算出圆的面积,根据图示可得阴影部分面积为半圆的面积,进而可得答案.【解答】解:∵AB=4,∴BO=2,∴圆的面积为:π×22=4π,∴阴影部分的面积是:×4π=2π,故答案为:2π.23.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为6.【考点】旋转的性质;相似三角形的判定与性质.【专题】几何图形问题.【分析】利用平行线的性质以及旋转的性质得出△CAD∽△B′A′C,再利用相似三角形的性质得出AD的长,进而得出BD的长.【解答】解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,∵CB′∥AB,∴∠B′CA′=∠D,∴△CAD∽△B′A′C,∴=,∴=,解得AD=8,∴BD=AD﹣AB=8﹣2=6.故答案为:6.24.如图,在△ABC中,AC=BC=8,∠C=90°,点D为BC中点,将△ABC绕点D逆时针旋转45°,=28.得到△A′B′C′,B′C′与AB交于点E,则S四边形ACDE【考点】旋转的性质.【专题】几何图形问题.=S△ACB﹣S△BDE求出即【分析】利用旋转的性质得出∠B=∠BDE=45°,BD=4,进而由S四边形ACDE可.【解答】解:由题意可得:∠B=∠BDE=45°,BD=4,则∠DEB=90°,∴BE=DE=2,∴S△BDE=×2×2=4,∵S△ACB=×AC×BC=32,=S△ACB﹣S△BDE=28.∴S四边形ACDE故答案为:28.三、解答题(共6小题)25.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.【考点】旋转的性质;含30度角的直角三角形;直角三角形斜边上的中线;菱形的判定.【专题】几何图形问题.【分析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.【解答】解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,∴AC=DC,∠A=60°,∴△ADC是等边三角形,∴∠ACD=60°,∴n的值是60;(2)四边形ACFD是菱形;理由:∵∠DCE=∠ACB=90°,F是DE的中点,∴FC=DF=FE,∵∠CDF=∠A=60°,∴△DFC是等边三角形,∴DF=DC=FC,∵△ADC是等边三角形,∴AD=AC=DC,∴AD=AC=FC=DF,∴四边形ACFD是菱形.26.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.【考点】旋转的性质;正方形的判定;平移的性质.【专题】几何图形问题.【分析】(1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.【解答】(1)解:FG⊥ED.理由如下:∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,∵CG∥EB,∴∠BCG=∠CBE=90°,∴四边形BCGE是矩形,∵CB=BE,∴四边形CBEG是正方形.27.将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.(1)求∠ADE的度数;(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断的值是否随着α的变化而变化?如果不变,请求出的值;反之,请说明理由.【考点】旋转的性质;相似三角形的判定与性质.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC﹣∠EDF计算即可得解;(2)根据同角的余角相等求出∠PDM=∠CDN,再根据然后求出△BCD是等边三角形,根据等边三角形的性质求出∠BCD=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°,从而得到∠CPD=∠BCD,再根据两组角对应相等,两三角形相似判断出△DPM和△DCN 相似,再根据相似三角形对应边成比例可得=为定值.【解答】解:(1)∵∠ACB=90°,点D为AB的中点,∴CD=AD=BD=AB,∴∠ACD=∠A=30°,∴∠ADC=180°﹣30°×2=120°,∴∠ADE=∠ADC﹣∠EDF=120°﹣90°=30°;(2)∵∠EDF=90°,∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°,∴∠PDM=∠CDN,∵∠B=60°,BD=CD,∴△BCD是等边三角形,∴∠BCD=60°,∵∠CPD=∠A+∠ADE=30°+30°=60°,∴∠CPD=∠BCD,在△DPM和△DCN中,,∴△DPM∽△DCN,∴=,∵=tan∠ACD=tan30°=,∴的值不随着α的变化而变化,是定值.28.已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME ⊥m于E,CF⊥m于F.(1)当直线m经过B点时,如图1,易证EM=CF.(不需证明)(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.【考点】旋转的性质;全等三角形的判定与性质;梯形中位线定理.【专题】证明题.【分析】(1)利用垂直于同一直线的两条直线平行得出ME∥CF,进而利用中位线的性质得出即可;(2)根据题意得出图2的结论为:ME=(BD+CF),图3的结论为:ME=(CF﹣BD),进而利用△DBM≌△KCM(ASA),即可得出DB=CK,DM=MK即可得出答案.【解答】解:(1)如图1,∵ME⊥m于E,CF⊥m于F,∴ME∥CF,∵M为BC的中点,∴E为BF中点,∴ME是△BFC的中位线,∴EM=CF.(2)图2的结论为:ME=(BD+CF),图3的结论为:ME=(CF﹣BD).图2的结论证明如下:连接DM并延长交FC的延长线于K又∵BD⊥m,CF⊥m∴BD∥CF∴∠DBM=∠KCM在△DBM和△KCM中,∴△DBM≌△KCM(ASA),∴DB=CK,DM=MK由题意知:EM=FK,∴ME=(CF+CK)=(CF+DB)图3的结论证明如下:连接DM并延长交FC于K 又∵BD⊥m,CF⊥m∴BD∥CF∴∠MBD=∠KCM在△DBM和△KCM中,∴△DBM≌△KCM(ASA)∴DB=CK,DM=MK,由题意知:EM=FK,∴ME=(CF﹣CK)=(CF﹣DB).29.在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.小明做了如下操作:将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.【考点】旋转的性质;平行四边形的判定;菱形的判定.【专题】几何综合题.【分析】(1)根旋转的性质得AB=DF,BD=FA,由于AB=BD,所以AB=BD=DF=FA,则可根据菱形的判定方法得到四边形ABDF是菱形;(2)由于四边形ABDF是菱形,则AB∥DF,且AB=DF,再根据旋转的性质易得四边形ABCE为平行四边形,根据平行四边形的性质得AB∥CE,且AB=CE,所以CE∥FD,CE=FD,所以可判断四边形CDEF是平行四边形.【解答】(1)解:四边形ABDF是菱形.理由如下:∵△ABD绕着边AD的中点旋转180°得到△DFA,∴AB=DF,BD=FA,∵AB=BD,∴AB=BD=DF=FA,∴四边形ABDF是菱形;(2)证明:∵四边形ABDF是菱形,∴AB∥DF,且AB=DF,∵△ABC绕着边AC的中点旋转180°得到△CEA,∴AB=CE,BC=EA,∴四边形ABCE为平行四边形,∴AB∥CE,且AB=CE,∴CE∥FD,CE=FD,∴四边形CDEF是平行四边形.30.两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD 绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).(2)当α=45°时(如图③),求证:四边形MHND为正方形.【考点】旋转的性质;全等三角形的判定与性质;矩形的性质;正方形的判定.【专题】几何综合题.【分析】(1)由全等三角形的判定定理SAS证得:△AED≌△GCD(如图②);(2)通过判定四边形MHND四个角是90°,且邻边DN=NH来判定四边形MHND是正方形.【解答】证明:(1)如图②,∵由题意知,AD=GD,ED=CD,∠ADC=∠GDE=90°,∴∠ADC+∠CDE=∠GDE+∠CDE,即∠ADE=∠GDC,在△AED与△GCD中,,∴△AED≌△GCD(SAS);(2)如图③,∵α=45°,BC∥EH,∴∠NCE=∠NEC=45°,CN=NE,∴∠CNE=90°,∴∠DNH=90°,∵∠D=∠H=90°,∴四边形MHND是矩形,∵CN=NE,∴DN=NH,∴矩形MHND是正方形.23.2 中心对称一、选择题1. 下列图形中,一定既是轴对称图形又是中心对称图形的是()A.等边三角形B.直角三角形C.平行四边形D.正方形2. 如图,在△ABC中,AB=AC,△ABC与△FEC关于点C对称,连接AE,BF,当∠ACB=______时,四边形ABFE为矩形()A.90°B.60°C.45°D.30°3. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为()A.A2P的中点B.A1B2的中点C.A1O的中点D.PO的中点4. 把△ABC各点的横坐标都乘-1,纵坐标都乘-1,符合上述要求的图是()5. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为()A.2 B.3 C.4 D.1.56. 如图,已知菱形ABCD与菱形EFGH关于直线BD上的某个点中心对称,则点B的对称点是()A .点EB .点FC .点GD .点H7. 2019·襄阳期末 如图,在正方形网格中,格点三角形ABC 绕某点顺时针旋转α度(0<α<180),得到格点三角形A 1B 1C 1,点A 与点A 1,点B 与点B 1,点C 与点C 1是对应点,则α的值为( )A .50B .60C .90D .1208. 若点P (-a ,a -3)关于原点对称的点是第二象限内的点,则a 满足( )A .a >3B .0<a ≤3C .a <0D .a <0或a >39. 在如图所示的平面直角坐标系中,△OA 1B 1是边长为2的等边三角形,作△B 2A 2B 1与△OA 1B 1关于点B 1对称,再作△B 2A 3B 3与△B 2A 2B 1关于点B 2对称……如此作下去,则△B 2n A 2n +1B 2n +1(n 是正整数)的顶点A 2n +1的坐标是( )A .(4n -1,3)B .(2n -1,3)C .(4n +1,3)D .(2n +1,3)10. 2020·河北模拟 如图所示,A 1(1,3),A 2(32,32),A 3(2,3),A 4(3,0).作折线OA 1A 2A 3A 4关于点A 4中心对称的图形,得折线A 8A 7A 6A 5A 4,再作折线A 8A 7A 6A 5A 4关于点A 8中心对称的图形……以此类推,得到一个大的折线.现有一动点P 从原点O 出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t 秒.当t =2020时,点P 的坐标为( )A.(1010,3) B.(2020,3 2)C.(2016,0) D.(1010,3 2)二、填空题11. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.12. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.13. 已知▱ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.14. 如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.15. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.。
九年级数学上册第23章同步习题
2014人教版九年级数学上册第23章 23.1《图形的旋转》同步练习1带答案一、选择题1.在26个英文大写字母中,通过旋转180°后能与原字母重合的有().A.6个 B.7个 C.8个 D.9个2.从5点15分到5点20分,分针旋转的度数为().A.20° B.26° C.30° D.36°3.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,•将△ABC 旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于().A.70° B.80° C.60° D.50°(1) (2) (3)二、填空题.1.在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.2.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,•点E•在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.3.如图3,△ABC为等边三角形,D为△ABC•内一点,•△AB D•经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)•旋转角度是________;•(•3)•△ADP•是________三角形.三、综合提高题.1.阅读下面材料:如图4,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.如图5,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.(4) (5) (6) (7)如图6,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,•其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.回答下列问题如图7,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=12 AB.(1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,•使△ABE移到△ADF的位置?(2)指出如图7所示中的线段BE与D F之间的关系.BADE2.一块等边三角形木块,边长为1,如图,•现将木块沿水平线翻滚五个三角形,那么B 点从开始至结束所走过的路径长是多少?答案:一、1.B 2.C 3.B二、1.旋转 旋转中心 旋转角 2.A 45° 3.点A 60° 等边 三、1.(1)通过旋转,即以点A 为旋转中心,将△AB E 逆时针旋转90°.(2)BE=•DF ,BE ⊥DF2.翻滚一次 滚120° 翻滚五个三角形,正好翻滚一个圆,所以所走路径是2.2014人教版九年级数学上册第23章 23.1《图形的旋转》同步练习2带答案【知识回顾】1、下列说法正确的是( )A 、平移不改变图形的形状和大小,而旋转则改变图形的形状和大小B 、平移和旋转的共同点是改变图形的位置C 、图形可以向某方向平移一定距离,也可以向某方向旋转一定距离D 、在平移和旋转图形中,对应角相等,对应线段相等且平行2、将一图形绕着点O 顺时针方向旋转700后,再绕着点O 逆时针方向旋转1200,这时如果要使图形回到原来的位置,需要将图形绕着点O 什么方向旋转多少度?( ) A 、顺时针方向,500B 、逆时针方向,500C 、顺时针方向,1900D 、逆时针方向,1903、如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是( ) A 、300B 、600C 、900D 、1204、如图,在正方形ABCD 中,E 为DC 边上的点,连结BE ,将△BCE 绕点C 顺时针方向旋转B'C'AB900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为()A、100B、150C、200D、2505、等边三角形至少旋转__________度才能与自身重合。
人教版 九年级数学上册 23.1--23.3知识检测题含答案
人教版九年级数学上册23.1--23.3知识检测题含答案23.1 图形的旋转一、选择题1. 如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是△ABC经过怎样的图形变换得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是()A.①④B.②③C.②④D.③④2. 如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是()A.4 cm B.3 cmC.2 3 cm D.(4-3)cm3. 如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB 边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B′的坐标是()A.(-1,2) B.(1,4)C.(3,2) D.(-1,0)4. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为()A.4 B.2 5C.6 D.2 65. 如图,Rt△OCB的斜边在y轴上,OC=3,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是()A.(3,-1) B.(1,-3)C.(2,0) D.(3,0)6. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是()A.AC=AD B.AB⊥EBC.BC=DE D.∠A=∠EBC7. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为()A.90°-αB.αC.180°-αD.2α8. 2019·河南如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△O AB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为()A.(10,3) B.(-3,10) C.(10,-3) D.(3,-1 0)二、填空题9. 如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.10. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C 逆时针旋转90°,那么点B的对应点B′的坐标是________.11. 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.12. 如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为________.13. 如图,在四边形ABCD 中,AB =AD ,∠BAD =∠BCD =90°,连接AC.若AC =6,则四边形ABCD 的面积为________.14. 2018·陕西如图,点O 是平行四边形ABCD 的对称中心,AD >AB ,E ,F是AB 边上的点,且EF =12AB ;G ,H 是BC 边上的点,且GH =13BC.若S 1,S 2分别表示△EOF 和△GOH 的面积,则S 1与S 2之间的等量关系是S 1S 2=________.15. 如图,AB ⊥y轴,将△ABO 绕点A 逆时针旋转到△AB 1O 1的位置,使点B的对应点B 1落在直线y =-33x 上,再将△AB 1O 1绕点B 1逆时针旋转到△A 1B 1O 2的位置,使点O 1的对应点O 2落在直线y =-33x 上,依次进行下去……若点B 的坐标是(0,1),则点O 12的纵坐标为________.三、解答题16. 如图,P为正方形ABCD 内一点,若PA =a ,PB =2a ,PC =3a(a >0).(1)求∠APB 的度数; (2)求正方形ABCD 的面积.17. 如图,在等边三角形ABC内有一点P,且PA=2,PB=3,PC=1.求∠BPC 的度数和等边三角形ABC的边长.18. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD. 求证:BD2=AB2+BC2.23.1 图形的旋转答案一、选择题1. 【答案】D[解析] 先将△ABC绕着B′C的中点旋转180°,再将所得的三角形绕着B′C′的中点旋转180°,即可得到△A′B′C′;先将△ABC沿着B′C的垂直平分线翻折,再将所得的三角形沿着B′C′的垂直平分线翻折,即可得到△A′B′C′.故选D.2. 【答案】B[解析] ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.在△OB′B中,∵∠B′=60°,OB′=OB,∴△OB′B是等边三角形,∴BB′=OB=1 cm,∴A′B=A′B′-BB′=4-1=3(cm).3. 【答案】C4. 【答案】D[解析] 由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=25.∵DE=2,∴在Rt△ADE中,AE=AD2+DE2=2 6.故选D.5. 【答案】A6. 【答案】D[解析] 由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.7. 【答案】C[解析] 由题意可得∠CBD=α,∠C=∠EDB.∵∠EDB+∠ADB=180°,∴∠C+∠ADB=180°.由四边形的内角和定理,得∠CAD+∠CBD=180°.∴∠CAD=180°-∠CBD=180°-α.故选C.8. 【答案】D二、填空题9. 【答案】47210. 【答案】(1,0)11. 【答案】20[解析] ∵AB=AB′,∠BAB′=40°,∴∠ABB′=70°.∵B′C′⊥AB,∴∠BB′C′=20°.12. 【答案】15°[解析] 由旋转的性质可知AB=AD,∠BAD =150°,∴∠B =∠ADB =12×(180°-150°)=15°.13. 【答案】18[解析] 如图.∵∠BAD =∠BCD =90°,∴∠B +∠ADC =180°.又∵AB =AD ,∴将△ABC 绕点A 逆时针旋转90°后点B 与点D 重合,点C 的对应点E 落在CD 的延长线上,∴AE =AC =6,∠CAE =90°,∴S 四边形ABCD =S △ACE =12AC·AE =12×6×6=18.14. 【答案】32 [解析] ∵S 1S △AOB =EF AB =12,S 2S △BOC =GH BC =13,∴S 1=12S △AOB ,S 2=13S △BOC . ∵点O 是▱ABCD 的对称中心,∴S △AOB =S △BOC =14S 平行四边形ABCD ,∴S 1S 2=32.15. 【答案】9+33 [解析] 将y =1代入y =-33x ,解得x =- 3.∴AB =3,OA =2,且直线y =-33x 与x 轴所夹的锐角是30°.由图可知,在旋转过程中每3次一循环,其中OO 2=O 2O 4=O 4O 6=O 6O 8=O 8O 10=O 10O 12=2+3+1=3+ 3. ∴OO 12=6×(3+3)=18+6 3. ∴点O 12的纵坐标=12OO 12=9+3 3.三、解答题16. 【答案】解:(1)将△ABP 绕点B 顺时针旋转90°得到△CBQ ,连接PQ ,如图,则∠APB=∠BQC,PB⊥QB,PB=QB=2a,AP=QC=a,∴PQ=2 2a.在△PQC中,∵PC2=9a2,PQ2+QC2=9a2,∴PC2=PQ2+QC2,∴△PQC为直角三角形且∠PQC=90°.∵△PBQ是等腰直角三角形,∴∠BPQ=∠BQP=45°,故∠APB=∠CQB=90°+45°=135°.(2)连接AC.∵∠APQ=∠APB+∠BPQ=135°+45°=180°,∴A,P,Q三点在同一条直线上.在Rt△AQC中,AC2=AQ2+QC2=(a+2 2a)2+a2=(10+4 2)a2,∴正方形ABCD的面积S=AB2=AC22=(5+2 2)a2.17. 【答案】解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).连接PP′,由旋转的性质知△BPP′为等边三角形,AP′=PC=1,∴PP′=PB=3,∠BPP′=∠BP′P=60°.在△APP′中,∵AP′2+PP′2=12+(3)2=22=PA2,∴△APP′是直角三角形,且∠AP′P=90°,∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,∴∠BPC=∠BP′A=150°.在Rt△APP′中,∵PA=2,AP′=1,∴∠APP′=30°.又∵∠BPP′=60°,∴∠APB=90°,∴在Rt△ABP中,AB=PA2+PB2=22+(3)2=7,即等边三角形ABC的边长为7.18. 【答案】证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.又∵∠ADC=60°,∴∠BDE=60°,∴△DBE是等边三角形,∴BD=BE.又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,∴△ECB是直角三角形,∴BE2=CE2+BC2,即BD2=AB2+BC2.23.2 中心对称一、选择题(本大题共12道小题)1. 如图所示电视台的台标中,是中心对称图形的是()2. 如图,如果甲、乙两图关于点O对称,那么乙图中不符合题意的一块是()3. 如图,在△ABC中,AB=AC,△ABC与△FEC关于点C对称,连接AE,BF,当∠ACB=______时,四边形ABFE为矩形()A.90°B.60°C.45°D.30°4. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形菱形OA′B′C′,再作菱形OA′B′C′关于点O的中心对称图形菱形OA″B″C″,则点C的对应点C″的坐标是()图25-K-1A.(2,-1) B.(1,-2)C.(-2,1) D.(-2,-1)5. 如图,四边形ABCD与四边形FGHE关于一个点中心对称,则这个点是()A.O1B.O2C.O3D.O46. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为()A.A2P的中点B.A1B2的中点C.A1O的中点D.PO的中点7. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为()A.2 B.3 C.4 D.1.58. 如图,已知菱形ABCD与菱形EFGH关于直线BD上的某个点中心对称,则点B的对称点是()A.点E B.点FC.点G D.点H9. 如图示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图两个阴影部分的面积S1,S2之间的关系是()A.S1<S2B.S1>S2C.S1=S2D.不确定10. 2018·潍坊在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取一定点O 称为极点;从点O 出发引一条射线Ox 称为极轴;线段OP 的长度称为极径.点P 的极坐标就可以用线段OP 的长度以及从Ox 转动到OP 的角度(规定逆时针方向转动角度为正)来确定,即P (3,60°)或P (3,-300°)或P (3,420°)等,则与点P 关于点O 对称的点Q 的极坐标表示不正确的是( )A .Q (3,240°)B .Q (3,-120°)C .Q (3,600°)D .Q (3,-500°)11. 在如图所示的平面直角坐标系中,△OA 1B 1是边长为2的等边三角形,作△B 2A 2B 1与△OA 1B 1关于点B 1对称,再作△B 2A 3B 3与△B 2A 2B 1关于点B 2对称……如此作下去,则△B 2n A 2n +1B 2n +1(n 是正整数)的顶点A 2n +1的坐标是( )A .(4n -1,3)B .(2n -1,3)C .(4n +1,3)D .(2n +1,3)12. 2020·河北模拟如图所示,A 1(1,3),A 2(32,32),A 3(2,3),A 4(3,0).作折线OA 1A 2A 3A 4关于点A 4中心对称的图形,得折线A 8A 7A 6A 5A 4,再作折线A 8A 7A 6A 5A 4关于点A 8中心对称的图形……以此类推,得到一个大的折线.现有一动点P 从原点O 出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t 秒.当t =2020时,点P 的坐标为( )A .(1010,3)B .(2020,32)C.(2016,0) D.(1010,3 2)二、填空题(本大题共6道小题)13. 王老师、杨老师两家所在的位置关于学校对称.如果王老师家距学校2千米,那么他们两家相距________千米.14. 若点A(x+3,2y+1)与点A′(y-5,1)关于原点对称,则点A的坐标是________.15. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O 为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.16. 如图,将等边三角形AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是________.17. 在平面直角坐标系中,若点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,则代数式x2-y2的值为________.18. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.三、解答题(本大题共3道小题)19. 如图,正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称.已知A ,D 1,D三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标;(2)写出顶点B ,C ,B 1,C 1的坐标.20. 2018·眉山在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC 的顶点都在格点上,请解答下列问题:(1)作出△ABC 向左平移4个单位长度后得到的△A 1B 1C 1,并写出点C 1的坐标; (2)作出△ABC 关于原点O 对称的△A 2B 2C 2,并写出点C 2的坐标;(3)已知△ABC 关于直线l 对称的△A 3B 3C 3的顶点A 3的坐标为(-4,-2),请直接写出直线l 的函数解析式.21. [材料阅读]在平面直角坐标系中,以任意两点P (x 1,y 1),Q (x 2,y 2)为端点的线段的中点坐标为⎝ ⎛⎭⎪⎫x 1+x 22,y 1+y 22.[运用](1)已知点A (-2,1)和点B (4,-3),则线段AB 的中点坐标是________;已知点M (2,3),线段MN 的中点坐标是(-2,-1),则点N 的坐标是________.(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.23.2 中心对称答案一、选择题(本大题共12道小题)1. 【答案】A2. 【答案】C[解析]3. 【答案】B[解析] ∵△ABC与△FEC关于点C对称,∴AC=FC,BC=EC,∴四边形ABFE是平行四边形.当AC=BC时,四边形ABFE是矩形,∴BC=AC=AB,∴∠ACB=60°.故选B.4. 【答案】A[解析] ∵点C的坐标为(2,1),∴点C′的坐标为(-2,1),∴点C″的坐标为(2,-1).故选A.5. 【答案】A[解析] 如图,连接HC和DE交于点O1.6. 【答案】D[解析] 因为P,O是对称点,所以PO的中点是对称中心.7. 【答案】A[解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.8. 【答案】D[解析] 由于点B,D,F,H在同一条直线上,根据中心对称的定义可知,只能是点B和点H是对称点,点F和点D是对称点.故选D.9. 【答案】C [解析] ∵P 是半圆AC 的中点,∴半圆关于直线OP 对称,且点D ,E 关于圆心O 对称,因而S 1,S 2在直径AC 上面的部分面积相等.∵OD =OE ,∴CD =AE .∵△CDB 的底边CD 与△AEB 的底边AE 相等,高相同,∴它们的面积相等,∴S 1=S 2.10. 【答案】D[解析] ∵P (3,60°)或P (3,-300°)或P (3,420°),由点Q 与点P 关于点O 中心对称可得,点Q 的极坐标为(3,240°)或(3,-120°)或(3,600°)等.11. 【答案】C[解析] A 1(1,3),A 2(3,-3),A 3(5,3),A 4(7,-3),…,∴点A n 的坐标为⎩⎨⎧(2n -1,3)(n 为奇数),(2n -1,-3)(n 为偶数).∵2n +1是奇数,∴点A 2n +1的坐标是(4n +1,3).故选C.12. 【答案】A二、填空题(本大题共6道小题)13. 【答案】4 [解析] ∵王老师、杨老师两家所在的位置关于学校对称, ∴王老师、杨老师两家到学校的距离相等. ∵王老师家距学校2千米, ∴他们两家相距4千米. 故答案为4.14. 【答案】(6,-1) [解析] 依题意,得⎩⎨⎧x +3=-(y -5),2y +1=-1,解得⎩⎨⎧x =3,y =-1.∴点A 的坐标为(6,-1).15. 【答案】25 [解析] ∵△ABC 绕AC 的中点O 旋转了180°,∴OB =OB′,∴BB′=2OB. 又∵OC =OA =12AC =1,BC =2,∴在Rt △OBC 中,OB =OC 2+BC 2=12+22=5,∴BB′=2OB =2 5.16. 【答案】(-23,-2) [解析] 过点B 作BH ⊥y 轴于点H ,如图.∵△OAB为等边三角形,A(0,4),∴OH =AH =2,∠BOA =60°,∴BH =3OH =2 3,∴点B 的坐标为(2 3,2).∵将△AOB 绕点O 顺时针旋转180°得到△A′OB′,∴点B′的坐标是(-2 3,-2).17. 【答案】5[解析] ∵点A (x +1,2y +1)与点A ′(y -2,x )关于原点O 对称,∴⎩⎨⎧x +1+y -2=0,2y +1+x =0,解得⎩⎨⎧x =3,y =-2. 故x 2-y 2=9-4=5. 故答案为5.18. 【答案】(-a ,-b +2)[解析] 如图,过点A 作AD ⊥y 轴于点D ,过点A′作A′D′⊥y 轴于点D′,则△ACD ≌△A′CD′,∴A′D′=AD =a ,CD′=CD =-b +1,∴OD′=-b +2,∴点A′的坐标为(-a ,-b +2).三、解答题(本大题共3道小题)19. 【答案】解:(1)∵点D 和点D 1是对称点, ∴对称中心是线段DD 1的中点, ∴对称中心的坐标是(0,52).(2)B(-2,4),C(-2,2),B 1(2,1),C 1(2,3).20. 【答案】解:(1)如图,△A 1B 1C 1为所作,C 1(-1,2). (2)如图,△A 2B 2C 2为所作,C 2(-3,-2).(3)因为点A 的坐标为(2,4),点A 3的坐标为(-4,-2), 所以直线l 的函数解析式为y =-x .21. 【答案】解:(1)(1,-1) (-6,-5) (2)12(3)设点D 的坐标为(x ,y).若以AB 为对角线,AC ,BC 为邻边的四边形为平行四边形,则AB ,CD 的中点重合,∴⎩⎪⎨⎪⎧1+x 2=-1+32,4+y 2=2+12,解得⎩⎨⎧x =1,y =-1;若以BC 为对角线,AB ,AC 为邻边的四边形为平行四边形,则AD ,BC 的中点重合,∴⎩⎪⎨⎪⎧-1+x 2=3+12,2+y 2=1+42,解得⎩⎨⎧x =5,y =3;若以AC 为对角线,AB ,BC 为邻边的四边形为平行四边形,则BD ,AC 的中点重合,∴⎩⎪⎨⎪⎧3+x 2=-1+12,1+y 2=2+42,解得⎩⎨⎧x =-3,y =5.综上可知,点D 的坐标为(1,-1)或(5,3)或(-3,5).23.3图形的旋转一.选择题1.下列说法正确的是( ) A .平移前后图形大小可能改变B .平移和旋转的共同之处是改变了图形的位置和大小C .对应点到旋转中心的距离相等D .由旋转得到的图形一定可以通过平移得到2.如图,在△ABC 中,∠CAB =62°,将△ABC 绕点A 旋转到△AB 'C '的位置,使得CC '∥AB ,则∠BAB '的大小为( )A .64°B .52°C .62°D .56°3.如图,在△ABC 中,∠CAB =65°,现将△ABC 绕着点A 逆时针旋转一定角度α(0<α<180°)△AB 'C ′,并且使AC '⊥AB ,那么旋转角的度数α为( )A .65°B .25°C .35°D .40°4.如图,已知在正方形ABCD 中,AD =4,E ,F 分别是CD ,BC 上的一点,且∠EAF =45°,EC =1,将△ADE 绕点A 沿顺时针方向旋转90°后与△ABG重合,连接EF,则以下结论:①DE+BF=EF,②BF=,③AF=,④S=中正确的是()△AEFA.①②③B.②③④C.①③④D.①②④5.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为24,DE=2,则AE的长为()A.4 B.2C.2D.26.如图,若△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合,则∠AB1B =()A.50°B.55°C.60°D.65°7.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C'使各顶点仍在格点上,则其旋转角的度数是()A.52°B.64°C.77°D.90°8.下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是()A.等边三角形B.平行四边形C.正八边形D.圆及其一条弦9.将图中可爱的“小鸭子”图片按顺时针方向旋转90°后得到的图片是()A.B.C.D.10.如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC二.填空题11.时钟从上午8时到中午12时,时针沿顺时针方向旋转了度.12.如图,将△ABC绕着点C顺时针旋转一定角度后得到△A′B′C,若∠A=45°.∠B′=110°,则∠ACB的度数是.13.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为.14.如图,O是等边△ABC内一点,OA=1,OB=,OC=2,将线段BO绕点B逆时针旋转60°得到线段BO′,连接AO'①点O与O′的距离为2;②∠AOB=135°;③四边形AOBO′的面积为;④△ABC的边长为;其中正确的结论为.(填正确的番号)15.如图,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE.交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,DE的长为.三.解答题16.如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,求BE的长.17.如图,将Rt△ABC的斜边BC绕点B顺时针旋转90°得边BD,过点D作AB的垂线,交AB延长线于点E,求证:△EDB≌△ABC.18.如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC按逆时针方向旋转一定角度后与△ADE重合,且点C恰好成为AD的中点,①指出旋转中心,并求出旋转的度数;②求出∠BAE的度数和AE的长.19.如图,正方形ABCD中,E、F分别在边BC、CD上,且∠EAF=45°,连接EF,这种模型属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路.例如图中△ADF与△ABG可以看作绕点A旋转90°的关系.这可以证明结论“EF=BE+DF”,请补充辅助线的作法,并写出证明过程.(1)延长CB到点G,使BG=,连接AG;(2)证明:EF=BE+DF.参考答案与试题解析一.选择题1.【解答】解:A、平移不改变图形的大小,所以A选项错误;B、平移和旋转的共同之处是改变图形的位置,不改变图形的形状,所以B选项错误;C、对应点到旋转中心的距离相等,所以C选项正确;D、由旋转得到的图形不一定可以通过平移得到,所以D选项错误.故选:C.2.【解答】解:∵CC'∥AB,∴∠CAB=∠C'CA=62°,∵将△ABC绕点A旋转到△AB'C'的位置,∴AC=AC',∠CAC'=∠BAB',∴∠AC'C=∠ACC'=62°,∴∠CAC'=56°=∠BAB',故选:D.3.【解答】解:如图,∵△ABC绕着点A逆时针旋转到△AB'C',∴旋转角等于∠CAC′,∵AC'⊥AB,∴∠C′AB=∠CAC′+∠CAB=90°∵∠CAB=65°,∴∠CAC′=90°﹣65°=25°.故选:B.4.【解答】解:∵将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,∴AG=AE,∠DAE=∠BAG,DE=BG,∵∠EAF=45°,∴∠DAE+∠BAF=45°=∠GAB+∠BAF=∠GAF=45°,∵AG=AE,∠F AE=∠F AG=45°,AF=AF,∴△AFE≌△AFG(SAS),∴EF=FG,∵DE=BG,∴EF=FG=BG+FB=DE+BF,故①正确,∵BC=CD=AD=4,EC=1,∴DE=3,设BF=x,则EF=x+3,CF=4﹣x,在Rt△ECF中,(x+3)2=(4﹣x)2+12,解得x=,∴BF=,AF===,故②正确,③错误,∴GF=3+=,∴S△AEF =S△AGF=AB×GF=,故④正确,故选:D.5.【解答】解:∵把△ADE绕点A顺时针旋转90°到△ABF的位置,∴△ADE≌△ABF,∴S△ADE =S△ABF,∴四边形AECF的面积=正方形ABCD的面积,∴AD2=24,∵AE2=AD2+DE2=24+4=28,∴AE=2,故选:D.6.【解答】解:∵△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合,∴AB=AB1,∠BAB1=50°,∴∠AB1B=(180°﹣50°)=65°.故选:D.7.【解答】解:根据旋转角的概念:对应点与旋转中心连线的夹角,可知∠BOB′是旋转角,且∠BOB′=90°,故选:D.8.【解答】解:A、最小旋转角度==120°;B、最小旋转角度==180°;C、最小旋转角度==45°;D、不是旋转对称图形;综上可得:旋转一定角度后,能与原图形完全重合,且旋转角度最小的是C.故选:C.9.【解答】解:如图所示:“小鸭子”图片按顺时针方向旋转90°后得到的图片是:.故选:C.10.【解答】解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故应补充“AB=CD”,故选:B.二.填空题11.【解答】解:从上午8时到中午12时,时针就从指向8,旋转到指向12,共顺时针转了3个“大格”,而每个“大格”相应的圆心角为30°,所以,30°×4=120°,故答案为:120°.12.【解答】解:∵△ABC绕着点C顺时针旋转一定角度后得到△A′B′C′,∴∠B=∠B′=110°,在△ABC中,∠ACB=180°﹣∠A﹣∠B=180°﹣45°﹣110°=25°,故答案为:25°.13.【解答】解:∵把△ADE顺时针旋转△ABF的位置,∴△ADE的面积=△ABF的面积,∴四边形AECF的面积等于正方形ABCD的面积等于25,∴AD=DC=5,∵DE=2,∴Rt△ADE中,AE===,故答案为:.14.【解答】解:如图,连接OO',过点B作BM⊥AO,交AO的延长线于M,∵△ABC是等边三角形,∴∠ABC=60°,AB=BC,∵将线段BO绕点B逆时针旋转60°得到线段BO′,∴BO=BO'=,∠OBO'=60°,∴△BOO'是等边三角形,∴OO'=BO=,∠BOO'=60°,故①错误,∵∠OBO'=∠ABC=60°,∴∠ABO'=∠CBO,在△BOC和△BO'A中,,∴△BOC≌△BO'A(SAS),∴O'A=OC=2,∵AO'2=4,AO2+O'O2=3+1=4,∴AO'2=AO2+O'O2,∴∠AOO'=90°,∴∠AOB=150°,故②错误,+S△AO'O,∵四边形AOBO′的面积=S△O'BO∴四边形AOBO′的面积=×3+×1×=,故③正确,∵∠BOM=180°﹣∠AOB=30°,∴BM=BO=,OM=BM=,∴AM=AO+OM=,∴AB===,故④正确,故答案为:③④.15.【解答】解:∵△ABC是等边三角形,BM平分∠ABC,∴∠ABD=30°,∵以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,∴BE=BD,∠DBE=60°,∴∠EBF=30°,∴AB垂直平分DE,∴AE=AD,EF=DF,又∵AF=AF,∴△AEF≌△ADF(SSS),如图1中,当点D在线段BM上时,由题意:AF=AM=CM=BF=2在Rt△BEF中,∵∠BFE=90°,EF=BF tan30°=,∴DE=2EF=;②如图2中,当点D在线段BM的延长线上时,同法可得DE=2EF=4;③如图3﹣3中,当点D在线段BM的延长线上,△ADM≌△AFD时,可得DE=4,综上所述,满足条件的DE的值为或4或4.三.解答题16.【解答】解:将DE绕点E逆时针旋转60°得到EF,连接AF、DF,如图所示:则∠AEF=∠DEF+∠AED=60°+30°=90°,由旋转的性质得:DE=EF,∴△DEF是等边三角形,∴DF=DE,∠EDF=60°,∵△ABD是等边三角形,∴AD=BD,∠ADB=60°,∴∠ADF=∠BDE,在Rt△AEF中,由勾股定理得:AF===,在△ADF和△BDE中,,∴△ADF≌△BDE(SAS),∴BE=AF=.17.【解答】证明:∵BC绕点B顺时针旋转90°得边BD,∴BC=BD,∠DBC=90°=∠CAB,∴∠ABC+∠ACB=90°,∠ABC+∠DBE=90°,∴∠ACB=∠DBE,又∵∠CAB=∠DEB=90°,∴△EDB≌△ABC(AAS).18.【解答】①∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点,∴旋转中心是点A,根据旋转的性质可知:∠CAE=∠BAD=180°﹣∠B﹣∠ACB=140°,∴旋转角度是140°;②由旋转可知:△ABC≌△ADE,∴AB=AD,AC=AE,∠BAC=∠EAD=140°,∴∠BAE=360°﹣140°×2=80°,∵C为AD中点,∴AC=AE=AB=×4=2cm.19.【解答】解:(1)∵△ADF与△ABG可以看作绕点A旋转90°的关系.∴延长CB到点G,使BG=DF,连接AG,故答案为:AG;(2)证明:由(1)得GB=DF,∵AD=AB,∠ABG=∠ADF=90°,∴△ADF≌△ABG(SAS),∴AF=AG,∠DAF=∠BAG,∵四边形ABCD为正方形,∴∠BAD=90°,∵∠EAF=45°。
人教版九年级数学上册 23.1.2 旋转作图和应用 同步测试(含答案)
人教版九年级数学上册第23章旋转23.1.2旋转的作图及应用同步测试题号一二三总分得分第Ⅰ卷(选择题)一、选择题(共10小题,3*10=30)1. 如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是( ) A.(1,1) B.(1,2) C.(1,3) D.(1,4)2.观察下列图形,其中可以看成是由“基本图案”通过旋转形成的有( ) A.1个B.2个C.3个D.4个3.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )4.如图,由一个矩形沿顺时针方向旋转90°后所形成的图形是( )A.①④B.②③C.①②D.②④5. 如图所示,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2,将Rt△ABC 先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是( ) A.(2,2) B.(1,2) C.(-1,2) D.(2,-1)6. 如图,该图形围绕点O按下列角度旋转后,不能与其自身重合的是( )A.72°B.108°C.144°D.216°7. 将等腰直角三角形AOB按如图所示位置放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B 的横坐标为2,则点A′的坐标为( )A.(1,1) B.(2,2)C.(-1,1) D.(-2,2)8. 如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为( )A.(0,4) B.(1,1) C.(1,2) D.(2,1)9. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( ) A.(0,1) B.(1,-1)C.(0,-1) D.(1,0)10.如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将边CD以点D为旋转中心逆时针旋转90°至ED,连接AE,则△ADE的面积是( )A.1 B.2C.3 D.不能确定第Ⅰ卷(非选择题)二.填空题(共8小题,3*8=24)11. 如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心一定是_______.12. 如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按顺时针方向旋转而得到的,则旋转的角度为_______.13.如图,正方形OEFG的一个顶点与正方形ABCD的对角线交点O重合,且正方形ABCD与正方形OEFG的边长都为2 cm,则图中阴影部分的面积为___cm2.14. 在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为_____________.15.如图,在等边三角形ABC中,AC=9,点O在AC上,且AO=3,点P在AB上,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长为____.16. 如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=4,将腰CD以D为中心逆时针旋转90°到DE,连接AE,CE,△ADE的面积为12,则BC的长为____.17.如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是__________.18. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去.若点A(1.5,0),B(0,2),则点B2 018的坐标为___________三.解答题(共7小题,46分)19.(6分) 如图所示,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,画出旋转后的△AB′C′.20. (6分) 在一次黑板报的评选中,九(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点C按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案.21. (6分)在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:(1)将四边形ABCD先向左平移4个单位长度,再向下平移6个单位长度,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;(2)将四边形A1B1C1D1绕点A1逆时针旋转90°,得到四边形A1B2C2D2,画出旋转后的四边形A1B2C2D2,并写出点C2的坐标.22. (6分)如图,四边形ABCD绕点O旋转后,顶点A的对应点为点E,试确定B,C,D的对应点的位置以及旋转后的四边形.23.(6分) 如图,在平面直角坐标系中,△ABC的顶点坐标是A(-7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,-1),E(-1,-7).(1)试说明如何平移线段AC,使其与线段ED重合;(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.24.(8分) 如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.(1)写出旋转角的度数;(2)求证:∠A1AC=∠C1.25.(8分) 将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.(1)如图,当点E在BD上时.求证:FD=CD;(2)当α为何值时,GC=GB?画出图形,并说明理由.参考答案1-5 BDDBA6-10 BCCBA11. 点B12. 90°13. 114. (-4,3)15. 616. 1017. 2+618. (6 054,2).19. 解:如图所示,△AB′C′即为所求三角形20.解:如图所示:21.解:(1)如图,四边形A1B1C1D1即为所求(2)四边形A1B2C2D2即为所求,C2(1,-2)22.解:如图.B,C,D的对应点分别是F,G,H,四边形EFGH是四边形ABCD旋转后得到的四23.解:(1)将线段AC先向右平移6个单位长度,再向下平移8个单位长度(或将线段AC先向下平移8个单位长度,再向右平移6个单位长度)(2)F(-1,-1)(3)画出如图所示的图形24. 解:(1)60°(2)由旋转的性质知△ABC≌△A1BC1,∴∠ABC=∠A1BC1=120°,AB=A1B,∠C=∠C1,∵∠A1BA+∠A1BC1=180°,∴∠A1BA=60°,∴△A1BA为等边三角形,∴∠A1AB=60°,∵∠A1AB+∠ABC=180°,∴AA1∥BC,∴∠C=∠A1AC,∴∠A1AC=∠C125.解:(1)由旅转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD, ∴∠AEB=∠ABE.又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,∴∠EDA=∠DEF.又∵DE=ED,∴△AED≌△FDE(SAS),∴DF=AE,又∵AE=AB=CD,∴CD=DF(2)如图,当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:①当点G 在AD右侧时,取BC的中点H,连接GH交AD于M,∵GC=GB,.GH⊥BC,∴四边形ABEHIM 是矩形,∴GM垂直平分AD,∴GD=GA=DA, ∴△ADG是等边三角形,∴∠DAG=60°,∴旋转角a=60°;②当点G在AD左侧时,同理可得△ADG是等边三角形,∴∠DAG=60°,∴旋转角a=360°-60°=300°时,GC=GB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23.1 图形的旋转一.选择题1.在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有()个.A.1B.2C.3D.42.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上的点G处,连接CE,则点B到CE的距离是()A.B.C.D.3.如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E 与点C对应),连接AD,若AD∥BC,则∠ABE的度数为()A.25°B.30°C.35°D.40°4.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD =2,BD=3,则CD的长为()A.B.4C.D.5.如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠ADE的大小为()A.60°B.50°C.45°D.40°6.如图,等边三角形ABC与等边三角形EFB共端点B,BC=2,BF=,△EFB绕点B 旋转,∠BCF的最大度数()A.30°B.45°C.60°D.90°7.如图,将△ABC绕顶点A顺时针旋转一个角度后,恰好AB′∥BC,若∠B=30°,则△ABC旋转了()A.10°B.20°C.30°D.35°8.在△ABC中,∠ACB=90°,∠B=65°.在同一平面内,将△ABC绕点C旋转到△A'B'C,若B'恰好落在线段AB上,连接AA',则下列结论中错误的是()A.∠B'A'C=25°B.AC=AA'C.∠ACA'=50°D.AB⊥AA'9.如图,△ABC中,∠ACB=90°,AC=3.将△ABC绕点B逆时针旋转得到△A'BC′,点C的对应点C'落在AB边上,A'B=5,连接AA′.则AA'长为()A.2B.C.3D.410.如图所示的是正十二角形体,因为其独特的对称美,所以2019年在英国举办的第60界国际数学奥林匹克的会标,就选用了正十二角形体,若将它绕自身中心旋转一定角度后能与原图重合,则这个角度不可能是()A.60°B.90°C.120°D.180°11.将图绕其中心旋转某一角度后会与原图形重合,这个角不能是()A.90°B.120°C.180°D.270°12.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q的坐标为()A.(﹣4,5)B.(4,﹣5)C.(﹣5,4)D.(5,﹣4)13.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O 逆时针旋转60°,则旋转后点B的对应点B′的坐标为()A.(﹣,)B.(﹣1,)C.(﹣,)D.(﹣,)14.在直角坐标系中,点O为坐标原点,点A(3,4),把线段OA绕点O顺时针旋转90°得到线段OA',则点A'的坐标为()A.(4,3)B.(4,﹣3)C.(﹣4,3)D.(3,﹣4)15.在平面直角坐标系中,点A的坐标为(﹣1,﹣2),将OA绕原点O逆时针旋转90°得到OA′,点A′的坐标为(a,b),则a+b等于()A.1B.﹣1C.3D.﹣3二.填空题16.时钟从上午8时到中午12时,时针沿顺时针方向旋转了度.17.在正方形ABCD中,AB=6,点P为边AB上的一动点,连接PC,以PC为边向下作等边△PCQ,连接BQ,则BQ的最小值是.18.如图,在正方形ABCD中,点E在边DC上,DE=5,EC=3,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为.19.如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点B旋转得△A′BC′,点A 的对应点为点A′,点C的对应点为点C′.当点A,B,C′三点共线时,点C和点C′之间的距离为.20.如图,已知∠EAD=34°,△ADE绕着点A旋转50°后能与△ABC重合,则∠BAE=度.21.如图,O是等边△ABC内一点,OA=1,OB=,OC=2,将线段BO绕点B逆时针旋转60°得到线段BO′,连接AO'①点O与O′的距离为2;②∠AOB=135°;③四边形AOBO′的面积为;④△ABC的边长为;其中正确的结论为.(填正确的番号)22.正方形绕着它的中心至少旋转度可以与它自身重合;五角星的最小旋转角是度.23.如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B(﹣1,2),第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1;第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,……按此规律,经过第五次旋转得到的点A5坐标为.24.在平面直角坐标系中,将点P(﹣3,2)绕点Q(﹣1,0)顺时针旋转90°,所得到的对应点P′的坐标为.25.如图,在平面直角坐标系中,有Rt△AOB,∠AOB=30°,∠OBA=90°,OA边在x 轴正半轴,且A(,0),现将其中的OB边绕原点O每次按逆时针方向旋转30°,并且每旋转一次长度增加一倍,点B对应点依次为B1、B2、B3、…,按照此规律,点B100的坐标为.三.解答题26.已知△ABC为等边三角形.(1)如图,P为△ABC外一点,∠BPC=120°,连接P A,PB,PC,求证:PB+PC=P A;(2)如图,P为△ABC内一点,若P A=12,PB=5,PC=13,求∠APB的度数.27.如图,图1等腰△BAC与等腰△DEC,共点于C,且∠BCA=∠ECD,连结BE、AD,若BC=AC、EC=DC.(1)求证:BE=AD;(2)若将等腰△DEC绕点C旋转至图2、3、4情况时,其余条件不变,BE与AD还相等吗?为什么?(请你用图2证明你的猜想)28.如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,求BE的长.29.如图,边长为1的方格纸中建立直角坐标系,△OAB旋转得到△OA'B′,观察图形并回答问题:(1)请将作图过程补充完整;并说明△OAB是如何旋转得到△OA'B'.(2)填空:△OAA′的形状是.30.如图,在平面直角坐标系中,有Rt△ABC,∠ACB=90°,∠BAC=30°,点A、B均在x轴上,边AC与y轴交于点D,连接BD,且BD是∠ABC的角平分线,若点B的坐标为(,0).(1)如图1,求点C的横坐标;(2)如图2,将Rt△ABC绕点A逆时针旋转一个角度α(0°≤α≤180°)得到Rt△AB'C',直线AC'交直线BD于点P,直线AB'交y轴于点Q,是否存在点P、Q,使△APQ为等腰三角形?若存在,直接写出∠APQ的度数;若不存在,请说明理由.参考答案一.选择题1.C.2.A.3.B.4.A.5.D.6.C.7.C.8.B.9.B.10.B.11.B.12.C.13.A.14.B.15.C.二.填空题16.120°.17.3.18.3或13.19.或.20.16.21.③④.22.90,72.23.(9,2).24.(1,2).25.(﹣299•,299).三.解答题26.证明:(1)如图1,延长BP至点E,使得PE=PC,连接CE,∵∠BPC=120°,PE=PC,∴∠CPE=60°,∴△CPE为等边三角形,∴CP=PE=CE,∠PCE=60°,∵△ABC是等边三角形,∴AC=BC,∠BCA=60°,∴∠ACB=∠ECP,∴∠ACB+∠BCP=∠ECP+∠BCP,即:∠ACP=∠BCE,在△ACP和△BCE中,,∴△ACP≌△BCE(SAS),∴AP=BE,∵BE=BP+PE=BP+PC,∴PB+PC=P A;(2)如图2,将△ABP绕点B顺时针方向旋转60°,得到△CBP',连接PP',由旋转知,△APB≌△CP′B,∴∠BP A=∠BP′C,P′B=PB=5,P′C=P A=12,∠PBP'=∠ABC=60°,又∵P′B=PB=5,∴△PBP′是等边三角形,∴∠PP′B=60°,PP′=5,在△PP′C中,PC=13,PP′=5,P′C=12,∴PC2=PP′2+P′C2,即∠PP′C=90°,∴∠APB=∠BP′C=60°+90°=150°.27.(1)证明:∵∠BCA=∠ECD,∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,∴∠BCE=∠ACD,在△BCE和△ACD中,,∴△BCE≌△ACD(SAS),∴BE=AD;(2)解:图2、图3、图4中,BE=AD,理由如下:∵∠BCA=∠ECD,∴∠BCA﹣∠ECA=∠ECD﹣∠ECA,∴∠BCE=∠ACD,在△BCE和△ACD中,,∴△BCE≌△ACD(SAS),∴BE=AD.28.解:将DE绕点E逆时针旋转60°得到EF,连接AF、DF,如图所示:则∠AEF=∠DEF+∠AED=60°+30°=90°,由旋转的性质得:DE=EF,∴△DEF是等边三角形,∴DF=DE,∠EDF=60°,∵△ABD是等边三角形,∴AD=BD,∠ADB=60°,∴∠ADF=∠BDE,在Rt△AEF中,由勾股定理得:AF===,在△ADF和△BDE中,,∴△ADF≌△BDE(SAS),∴BE=AF=.29.解:(1)如图,△OA'B'即为所求.(2)△AOA′是等腰直角三角形.理由:∵OA=OA′=5,AA′=5,∴AO2+OA′2=AA′2,∴∠AOA′=90°,∴△AOA′是等腰直角三角形.故答案为:等腰直角三角形.30.解:(1)如图1中,过点C作CH⊥AB于H.∵∠ABC=90°,∠CAB=30°,∴∠ABC=90°﹣30°=60°,∵BD平分∠ABC,∴∠ABD=∠ABC=30°,∴∠DAB=∠DBA=30°,∴DA=DB,∵DO⊥AB,∴OA=OB,∵B(,0),∴OA=OB=,∴AB=2,∴BC=AB=,∵CH⊥AB,∴∠CHB=90°,∴BH=BC=,CH=BH=,∴OH=OB﹣BH=,∴C(,).(2)①当旋转角小于90°时,P在y轴左侧,Q在y轴正半轴上,对应∠APQ=75°和120°的情况.②当旋转角度大于90°小于120°时,P在y轴左侧,Q在y轴负半轴上,此时∠P AQ=150°,此时要形成等腰三角形∠APQ=15°.③当旋转角度大于120°小于180°时,P在y轴右侧,Q在y轴负半轴上,对应∠APQ=30°的情况.所以总共有四个情况,15°、30°、75°、120°.综上所述,满足条件的∠APQ的值为15°或30°或75°或120°.23.2中心对称一.选择题1.下列图形,既是中心对称图形又是轴对称图形的是()A.B.C.D.2.在等边三角形,圆,菱形,正方形,正五边形,正六边形中是中心对称的图形有()A.3个B.4个C.5个D.6个3.在平面直角坐标系中,点(2,0)关于原点对称的点的坐标为()A.(-2,0)B(0,-2)C.(0,2)D(1,2)4.下列汽车标志中,是中心对称图形的是()A.B.C.D.5.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O 逆时针旋转60°,则旋转后点B的对应点B′的坐标为()A.(﹣,)B.(﹣1,)C.(﹣,)D.(﹣,)6.如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是()A.B.C.D.7.如图,线段OA,OB分别从与x轴和y轴重合的位置出发,绕着原点O顺时针转动,已知OA每秒转动45°,OB的转动速度是每秒转动30°,则第2020秒时,OA与OB之间的夹角的度数为()A.90°B.145°C.150°D.165°8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2020次得到正方形OA2020B2020C2020,如果点A 的坐标为(1,0),那么点B2020的坐标为()A.(﹣1,1)B.C.(﹣1,﹣1)D.9.如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段P A绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是()A.3B.5C.D.210.在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,0)、B(5,0)、C(5,1),将△ABC绕点A逆时针旋转90°得到△AB'C',则点C′的坐标为()A.C.二.填空题11.已知点A(a,3)与点B(2,﹣3)关于原点对称,则a=.12.在平面直角坐标系中,将点P(﹣3,2)绕点Q(﹣1,0)顺时针旋转90°,所得到的对应点P′的坐标为.13.关于原点对称,则n﹣m的值为.14.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是.15.如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B(﹣1,2),第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1;第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,……按此规律,经过第五次旋转得到的点A5坐标为.三.解答题16.如图,在平面直角坐标系中,点A(2,0),点B在第一象限,AB⊥OA,AB=OA,将△OAB绕点O按逆时针方向旋转105°得到△OA'B',连接BB'.(Ⅰ)求∠OBB'的度数;(Ⅱ)求出点B'的坐标.17.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:(1)若点P在第三象限,则a的取值范围为;(2)若点P在y轴上,则a的值为;(3)当a=2时,点P关于y轴对称的点的坐标为点P关于原点对称的点的坐标为.19.如图,在平面直角坐标系中,有Rt△ABC,∠ACB=90°,∠BAC=30°,点A、B均在x轴上,边AC与y轴交于点D,连接BD,且BD是∠ABC的角平分线,若点B的坐标为(,0).(1)如图1,求点C的横坐标;(2)如图2,将Rt△ABC绕点A逆时针旋转一个角度α(0°≤α≤180°)得到Rt△AB'C',直线AC'交直线BD于点P,直线AB'交y轴于点Q,是否存在点P、Q,使△APQ为等腰三角形?若存在,直接写出∠APQ的度数;若不存在,请说明理由.参考答案与试题解析一.选择题1.【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不符合题意;B.不是轴对称图形,是中心对称图形,故此选项不符合题意;C.既是中心对称图形,又是轴对称图形,故此选项符合题意;D.是轴对称图形,不是中心对称图形,故此选项不符合题意;故选:C.2.【解答】解:在等边三角形,圆,菱形,正方形,正五边形,正六边形中是中心对称的图形有圆,菱形,正方形,正六边形共4个.故选:B.3.【解答】解:点(2,0)关于原点对称的点的坐标为(﹣2,0).故选:A.4.【解答】解:A、不是中心对称图形,故本选项不合题意;B、不是中心对称图形,故本选项不合题意;C、是中心对称图形,故本选项符合题意;D、不是中心对称图形,故本选项不合题意;故选:C.5.【解答】解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.∵A(1,0),∴OA=1,∵△AOB是等边三角形,BH⊥OA,∴OH=AH=OA=,BH=OH=,∴B (,),∵∠AOB =∠BOB ′=60°,∠JOA =90°,∴∠BOJ =∠JOB ′=30°,∵OB =OB ′,∴BB ′⊥OJ ,∴BJ =JB ′,∴B ,B ′关于y 轴对称,∴B ′(﹣,),故选:A .6.【解答】解:如图,连接OA ,OB ,OC .设平行四边形的面积为4s .∵点O 是平行四边形ABCD 的对称中心,∴S △AOB =S △BOC =S 平行四边形ABCD =s ,∵EF =AB ,GH =BC ,∴S 1=s ,S 2=s , ∴==,故选:B .7.【解答】解:设t 秒第一次相遇.由题意:270+30t =45t ,解得t =18,相遇后设m 秒第二次相遇,则有45t ﹣30t =360,解得t =24,以后每过24秒相遇一次,(2020﹣18)÷24=83…10,∴2020秒时,10×45°﹣10×30°=150°,故选:C.8.【解答】解:∵四边形OABC是正方形,且OA=1,∴B(1,1),连接OB,由勾股定理得:OB=,由旋转得:OB=OB1=OB2=OB3=…=,∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,∴B1(0,),B2(﹣1,1),B3(﹣,0),B(﹣1,﹣1),…,发现是8次一循环,所以2020÷8=252…4,∴点B2020的坐标为(﹣1,﹣1)故选:C.9.【解答】解:∵A(2,0),∴OA=2,设P(0,m),则OP=m,作QM⊥y轴于M,∵∠APQ=90°,∴∠OAP+∠APO=∠APO+∠QPM,∴∠OAP=∠QPM,∵∠AOP=∠PMQ=90°,P A=PQ,∴△AOP≌△PMQ(AAS),∴MQ=OP=m,PM=OA=2,∴Q(m,m+2),∵B(4,0),∴BQ==,∴当m=1时,BQ有最小值3,故选:A.10.【解答】解:∵△ABC三个顶点的坐标分别为A(2,0)、B(5,0)、C(5,1),将△ABC绕点A逆时针旋转90°得到△AB'C',如图所示:则点C′的坐标为(1,3).故选:B.二.填空题11.【解答】解:∵点A(a,3)与点B(2,﹣3)关于原点对称,∴a=﹣2,故答案为:﹣2.12.【解答】解:如图,观察图象可知,P′(1,2).故答案为(1,2).13.【解答】解:∵点(m,3n)与点(﹣4,9)关于原点对称,∴3n=﹣9,m=4,∴n=﹣3,∴n﹣m=﹣3﹣4=﹣7.故答案为:﹣7.14.【解答】解:如图,旋转中心M即为所求.M(1,﹣1).故答案为(1,﹣1).15.【解答】解:∵点B(﹣1,2),∴A(﹣1,0),OA=BC=1,AB=OC=2,∵第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1,且A1O=AO=1,OC1=OC=2,第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,且B2O =C1O+B1C1=3…,依此规律,∴A1(0,1),A2(3,2),A3(5,0),A4(6,1),A5(9,2),故答案为(9,2).三.解答题(共4小题)16.【解答】解:(Ⅰ)∵△OAB≌△OA′B′,∴OB=OB′,又∠BOB′=105°,∴∠OBB′=∠OB′B=(180°﹣105°)=37.5°.(Ⅱ)过点B′作B′C垂直于x轴,垂足为C.∵OA=AB=2,∠OAB=90°,∴∠AOB=45°,OB=OA=2,∴∠COB′=180°﹣105°﹣45°=30°,在Rt△OCB′中,B′C=OB′=,∴OC=CB′=,∴B′(﹣,).17.【解答】解:∠B与∠F相等,理由如下:∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,∴∠B=∠DEC,∵AF∥BE,∴∠F=∠DEC,∴∠B=∠F.18.【解答】解:(1)∵点P(a,﹣1),点P在第三象限,∴a<0;故答案为:a<0;(2)∵点P(a,﹣1),点P在y轴上,∴a=0;故答案为:0;(3)当a=2时,点P(a,﹣1)的坐标为:(2,﹣1)关于y轴对称的点的坐标为:(﹣2,﹣1),点P关于原点对称的点的坐标为:(﹣2,1).故答案为:(﹣2,﹣1),(﹣2,1).19.【解答】解:(1)如图1中,过点C作CH⊥AB于H.∵∠ABC=90°,∠CAB=30°,∴∠ABC=90°﹣30°=60°,∵BD平分∠ABC,∴∠ABD=∠ABC=30°,∴∠DAB=∠DBA=30°,∴DA=DB,∵DO⊥AB,∴OA=OB,∵B(,0),∴OA=OB=,∴AB=2,∴BC=AB=,∵CH⊥AB,∴∠CHB=90°,∴BH=BC=,CH=BH=,∴OH=OB﹣BH=,∴C(,).(2)如图2中,∵△P AQ是是等腰三角形,∠P AQ=30°。
