布尔代数入门
布尔代数的基本公式和定律

布尔代数的基本公式和定律布尔代数是数学中的一个重要概念,在计算机科学、电子工程等领域都有着广泛的应用。
对于咱们从小学到高中的学习来说,虽然不会深入到特别复杂的层面,但了解其基本公式和定律,对于培养逻辑思维可是大有益处的。
先来说说布尔代数中的基本公式。
就比如说,A + 0 = A ,这就好像你兜里已经有了一些糖果 A ,别人再给你 0 颗糖,你兜里还是只有原来的那些糖果 A 。
再比如,A · 1 = A ,这就好比你有一个书包 A ,里面装满了书,然后你又把一整个图书馆的书(1)都装进去,可实际上书包还是只能装下原来的那些书 A 。
还有 A + 1 = 1 ,想象一下,你正在参加一个比赛,已经有了自己的一些分数 A ,然后比赛规则说,不管你之前多少分,只要你完成了某个超级难的任务就能直接得到满分 1 ,那最终你的成绩就是满分 1 啦。
布尔代数的定律也很有趣。
交换律,A + B = B + A ,这就好像你和朋友交换礼物,不管谁先给谁,结果都是一样的,都完成了礼物的交换。
结合律,(A + B) + C = A + (B + C) ,就像你们三个人排队,不管是你先和第二个排好,再一起和第三个排,还是第二个和第三个先排好,你再加入,最终的队伍顺序都是一样的。
我还记得之前给学生们讲布尔代数的时候,有个小同学一脸迷糊地问我:“老师,这布尔代数到底有啥用啊?”我笑着回答他:“就像你搭积木,每一块积木都有自己的位置和作用,布尔代数就是帮你找到这些位置和作用的工具呀。
”他似懂非懂地点点头,然后在接下来的练习中,努力地去理解和运用这些公式和定律。
分配律,A · (B + C) = A · B + A · C ,这就好像你有一堆水果,一部分是苹果(B ),一部分是香蕉(C ),然后你要把它们分别装在几个盒子(A )里,不管是先把水果混合再分装,还是先分开再分别装,最终装在盒子里的水果数量都是一样的。
布尔代数基础

布尔代数基础和布尔函数的化简和实现布尔代数是分析和设计数字逻辑电路的数学工具。
因此这里从应用的角度向读者介绍布尔代数,而不是从数学的角度去研究布尔代数。
一、布尔代数的基本概念1、布尔代数的定义域和值域都只有“0”和“1”。
布尔代数的运算只有三种就是“或”(用+表示),“与”(用·表示)和“非”(用 ̄表示,以后用’表示)。
因此布尔代数是封闭的代数系统,可记为B=(k,+,·, ̄,0,1),其中k表示变量的集合。
2、布尔函数有三种表示方法。
其一是布尔表达式,用布尔变量和“或”、“与”和“非”三种运算符所构成的式子。
其二是用真值表,输入变量的所有可能取值组合及其对应的输出函数值所构成的表格。
其三是卡诺图,由表示逻辑变量所有可能取值组合的小方格所构成的图形。
3、布尔函数的相等可以有两种证明方法,一种是从布尔表达式经过演绎和归纳来证明。
另一种就是通过列出真值表来证明,如两个函数的真值表相同,则两个函数就相等。
二、布尔代数的公式、定理和规则1、基本公式有交换律、结合律、分配律、0—1律、互补律、重叠律、吸收律、对合律和德·摩根律。
值得注意的是分配律有两个是:A·(B+C)=A·B+A·C和A+B·C=(A+B)·(A+C),另外就是吸收律,A+AB=A;A+A’B=A+B它们是代数法化简的基本公式。
2、布尔代数的主要定理是展开定理(教材中称为附加公式)。
3、布尔代数的重要规则有对偶规则和反演规则。
三、基本逻辑电路1、与门F=A·B2、或门F=A+B3、非门F=A’(为了打字的方便,以后用单引号“’”表示非运算,不再用上划线表示非运算)4、与非门F=(A·B)’5、或非门F=(A+B)’6、与或非门F=(A·B+C·D)’7、异或门F=A’B+AB’=A⊕B8、同或门F=A’B’+AB=A⊙B四、布尔函数的公式法化简同一个布尔函数可以有许多种布尔表达式来表示它,一个布尔表达式就相应于一种逻辑电路。
布尔代数的基本规则

布尔代数的基本规则布尔代数是一种逻辑计算的方法,它主要运用于电子电路和计算机领域。
在布尔代数中,只存在两种逻辑值,即真和假。
这两种逻辑值可以通过一系列运算得出相应的结果。
在布尔代数中,存在一些基本的规则和定律,这些规则和定律对于求解逻辑运算非常关键。
以下是布尔代数的基本规则:1. 与运算规则与运算也称为“乘法”,表示为“∩”。
对于任意两个逻辑变量A 和 B,有以下运算规则:真∩真=真真∩假=假假∩真=假假∩假=假2. 或运算规则或运算也称为“加法”,表示为“∪”。
对于任意两个逻辑变量A 和 B,有以下运算规则:真∪真=真真∪假=真假∪真=真假∪假=假3. 非运算规则非运算也称为“取反”,表示为“~”。
对于任何逻辑变量 A,有以下运算规则:~真=假~假=真4. 吸收律吸收律是指在与运算或或运算中,对于一个变量进行两次操作等于一次操作的规律。
吸收律有以下两个定律:A∩(A∪B)=AA∪(A∩B)=A5. 分配律分配律指在与运算或或运算中,一个变量与一组变量的运算结果与一个变量与这组变量中每个变量的运算结果的和之间等效的规律。
分配律有以下两个定律:A∩(B∪C)=(A∩B)∪(A∩C)A∪(B∩C)=(A∪B)∩(A∪C)6. 结合律结合律是指在同种运算规则下,先运算任意两个变量得到的结果与其中一个变量与剩余变量运算之后得到的结果是相等的规律。
结合律有以下两个定律:(A∩B)∩C=A∩(B∩C)(A∪B)∪C=A∪(B∪C)7. 常数运算布尔代数中出现的“1”表示真,“0”表示假。
对于任何逻辑变量 A,有以下常数规则:A∪1=1A∩0=0通过以上基本规则,我们可以对逻辑运算有着深入的认识并用于实际应用中。
当我们设计电子电路或者编写计算机程序时,十分需要严格遵守这些规则,以便确保逻辑的正确性。
同时,这些规则在逻辑思维和分析问题的能力的提升方面也具有重要的指导意义。
离散数学9-格与布尔代数

17
定理4: 设<A, ∨, ∧>是格,对任意a, b, cA,有 (1)若a≤b和c≤d,则a∧c≤b∧d,a∨c≤b∨d (2)若a≤b,则a∧c≤b∧c,a∨c≤b∨c
18
证明:(1)如果a≤b,又b≤b∨d, 由传递性得 a≤b∨d, 类似由c≤d, d≤b∨d,由传递性得 c≤b∨d,这说明b∨d是{a, c}的上界,而a∨c是{a, c}的最小上界,所以a∨c≤b∨d。类似可证 a∧c≤b∧d。
则称b是a的补元,记为a′。若b是a的补元,则a也是b的补 元,即a与b互为补元。 一般说来,一个元素可以有其补元 ,未必唯一,也可能无补元。0′=1和1′=0。
37
定义12: 在有界格中,如果每个元素都有补元,则称格是有 补格。
由于补元的定义是在有界格中给出的,可知,有补格一定是 有界格。
38
定理11: 在有界分配格中,如果某元素有补元,则补元是唯 一的。
34
定理9: 设<A, ∧,∨, 0, 1>是有界格,则对于A中任意元素 a 都有 a∨1 = 1 a∧1 = a a∨0 = a a∧0 = 0
1称为全上界或最大元,0称为全下界或最小元。
图9-6中(a)(b)(c)都有最大元和最小元,所以都是有界格。
35
定理10: 有限格必定是有界格。
36
定义11: 设<A,∨,∧>是有界格,aA,如果存在bA使得 a∨b = 1 a∧b = 0
31
定义8: 设<A,∨,∧>是格,如果A中存在元素a,使得对于A中 任意元素x 都有a≼x,则称a为格(A , ≤)的全下界,用0表 示。如果L中存在元素 a, 使得对于L中任意元素 x 都有 x≼a则称a为格(A , ≤)的全上界,用1表示。全下界即是格 的最小元,是唯一的。全上界即是格的最大元,是唯一的 。
a'b'c'+ab'+a'b+abc'的最简布尔代数

a'b'c'+ab'+a'b+abc'的最简布尔代数中文内容:布尔代数是数学的一种分支,它使用变量和逻辑运算符来表示逻辑关系。
它是计算机技术的主要基础,可以用来解决各种问题。
介绍1、什么是布尔代数布尔代数是数学的一个重要分支,它主要用于表示和分析逻辑关系。
它是一种重要的形式语言,可以用来表示利用逻辑运算的条件来解决复杂的问题。
它使用算术表达式来表示逻辑关系,它可以用来表示真或假的结论。
2、布尔代数的基本结构布尔代数是由布尔变量,逻辑运算符和联结词以及命题变量组成的一种形式语言,它由布尔变量,即T还有F两个变量组成,T代表True,F代表False,它们用来表示逻辑关系的真或假。
另外,布尔代数还有七种逻辑运算符,包括and(且)、or(或)、not(非)、xor(非全等)、nor(非或)、xnor(全等)以及implies (构成)等。
3、求解“a'b'c'+ab'+a'b+abc'”的最简布尔代数由公式可知,最简布尔代数可以化简为:a'b + ab + bc'。
用and(且)符号可化为:a'b * ab * bc'。
即求解上述布尔代数的最简式为:a'b * ab * bc'。
总结布尔代数是一种数学的重要分支,它用变量和逻辑运算符来表示和分析逻辑关系,它主要由布尔变量及七种逻辑运算符组成。
由实例可知,求解“a'b'c'+ab'+a'b+abc'”的最简布尔代数为:a'b * ab * bc'。
布尔代数pdf

布尔代数pdf布尔代数(Boolean algebra)是数学中一种代数结构,由乔治·布尔(George Boole)于19世纪中叶提出。
它主要关注逻辑运算和关系,并在计算机科学、电子工程和信息技术等领域中得到广泛应用。
以下是一些基本概念:●布尔变量(Boolean Variables):布尔代数的基本单位是布尔变量,它只能取两个值,通常表示为0和1。
这两个值分别代表逻辑中的"假"和"真"。
●布尔运算(Boolean Operations):布尔代数包含一系列基本的逻辑运算,如与(AND)、或(OR)、非(NOT)等。
这些运算用于处理布尔变量,产生新的布尔值。
1.与运算(AND):如果所有输入都是1,结果为1;否则结果为0。
2.或运算(OR):如果至少有一个输入是1,结果为1;否则结果为0。
3.非运算(NOT):对输入取反,即1变为0,0变为1。
●布尔表达式(Boolean Expression):由布尔变量、常数和布尔运算符构成的代数表达式。
布尔表达式可用于描述逻辑函数。
●卡诺图(Karnaugh Map):一种图形工具,用于简化布尔表达式。
通过填写卡诺图中的1和0,可以直观地找到布尔表达式的最简形式。
逻辑门(Logic Gates):在电子和计算机领域,布尔代数被应用于设计逻辑电路。
逻辑门是实现布尔运算的电子元件,如与门、或门、非门等。
布尔代数在计算机科学中的应用是深远的,因为计算机内部的信息表示和处理都涉及到布尔逻辑。
逻辑电路和布尔代数的理论奠定了计算机硬件和软件设计的基础。
布尔代数的基本运算与性质

布尔代数的基本运算与性质布尔代数是一种逻辑代数,用于对逻辑表达式进行运算和分析。
它是以数学符号和运算为基础,对逻辑关系进行描述和计算的一种工具。
在计算机科学和电子工程等领域,布尔代数被广泛应用于数位逻辑电路和逻辑编程等方面。
本文将介绍布尔代数的基本运算与性质。
一、布尔代数的基本运算1. 与运算(AND)与运算是布尔代数中最基本的运算之一,它采用逻辑与操作符“∧”表示。
与运算的规则是:只有在两个变量同时为真时,结果才为真;否则结果为假。
例如,变量A和变量B的与运算可以表示为 A ∧ B。
2. 或运算(OR)或运算是布尔代数中另一个基本运算,它采用逻辑或操作符“∨”表示。
或运算的规则是:只要两个变量中有一个为真,结果就为真;否则结果为假。
例如,变量A和变量B的或运算可以表示为 A ∨ B。
3. 非运算(NOT)非运算是布尔代数中最简单的运算,它采用逻辑非操作符“¬”表示。
非运算的规则是:翻转变量的取值,如果原来为真,则结果为假;如果原来为假,则结果为真。
例如,变量A的非运算可以表示为 ¬A。
二、布尔代数的性质1. 结合律布尔代数的运算满足结合律,即运算的结果与运算的先后顺序无关。
例如,对于与运算,A ∧ (B ∧ C) 的结果和 (A ∧ B) ∧ C 的结果相同。
2. 分配律布尔代数的运算满足分配律,即一个运算符在有两个不同的运算符作用时,结果相同。
对于与运算和或运算,有以下两个分配律:- A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C)- A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)3. 吸收律布尔代数的运算满足吸收律,即一个变量与该变量的运算结果相同。
例如,A ∨ (A ∧ B) 的结果和A的结果相同。
4. 对偶性原理布尔代数的运算满足对偶性原理,即一个布尔代数式子中的与运算(∧)与或运算(∨),变量的取反(¬)可以互换。
例如,对于布尔表达式 A ∧ B ∨ C,可以通过对偶性原理转换为 A ∨ B ∧ ¬C。
布尔代数
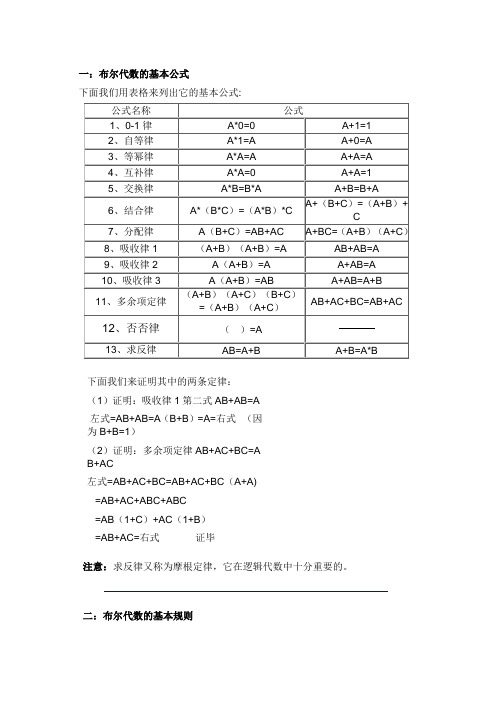
一:布尔代数的基本公式下面我们用表格来列出它的基本公式:下面我们来证明其中的两条定律:(1)证明:吸收律1第二式AB+AB=A左式=AB+AB=A(B+B)=A=右式(因为B+B=1)(2)证明:多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC(A+A)=AB+AC+ABC+ABC=AB(1+C)+AC(1+B)=AB+AC=右式证毕注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
我们可以看出基本公式是成对出现的,二都互为对偶式。
反演法则有原函数求反函数就称为反演(利用摩根定律),我们可以把反演法则这样描述:将原函数F中的“*”换成“+”,“+”换成“*”,“0”换成“1”,“1”换成“0”;原变量换成反变量,反变量换成原变量,长非号即两个或两个以上变量的非号不变,就得到原函数的反函数。
的基本公式下面我们用表格来列出它的基本公式:下面我们来证明其中的两条定律:(1)证明:吸收律1第二式AB+AB=A左式=AB+AB=A(B+B)=A=右式(因为B+B=1)(2)证明:多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC(A+A)=AB+AC+ABC+ABC=AB(1+C)+AC(1+B)=AB+AC=右式证毕注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
布尔代数入门
布尔代数是计算机的基础。
没有它,就不会有计算机。
布尔代数发展到今天,已经非常抽象,但是它的核心思想很简单。
本文帮助你理解布尔代数,以及为什么它促成了计算机的诞生。
我依据的是《编码的奥妙》的第十章。
这是一本好书,强烈推荐。
一、数理逻辑的起源
19世纪早期,英国数学家乔治·布尔(George Boole,1815-1864)突发奇想:人的思想能不能用数学表达?
此前,数学只用于计算,没有人意识到,数学还能表达人的逻辑思维。
两千年来,哲学书都是用文字写的。
比如,最著名的三段论:
所有人都是要死的,
苏格拉底是人,
所以,苏格拉底是要死的。
乔治·布尔认为,这种推理可以用数学表达,也就是说,哲学书完全可以用数学写。
这就是数理逻辑的起源。
二、集合论
乔治·布尔发明的工具,叫做"集合论"(Set theory)。
他认为,逻辑思维的基础是一个个集合(Set),每一个命题表达的都是集合之间的关系。
比如,所有人类组成一个集合R,所有会死的东西组成一个集合D。
所有人都是要死的
集合论的写法就是:
R X D = R
集合之间最基本的关系是并集和交集。
乘号(X)表示交集,加号(+)表示并集。
上面这个式子的意思是,R与D的交集就是R。
同样的,苏格拉底也是一个集合S,这个集合里面只有苏格
拉底一个成员。
苏格拉底是人
// 等同于
S X R = S
上面式子的意思是,苏格拉底与人类的交集,就是苏格拉底。
将第一个式子代入第二个式子,就得到了结论。
S X (R X D)
= (S X R) X D
= S X D
= S
这个式子的意思是,苏格拉底与会死的东西的交集,就是苏格拉底,即苏格拉底也属于会死的东西。
三、集合的运算法则
前面的三段论比较容易,一眼就能看出结论。
但是,有些三段轮比较复杂,不容易立即反应过来。
请看下面这两句话。
"鸭嘴兽是卵生的哺乳动物。
鸭嘴兽是澳洲的动物。
"
你能一眼得到结论吗?
鸭嘴兽X 卵生= 鸭嘴兽
鸭嘴兽x 澳洲= 鸭嘴兽
将第一个式子代入第二个,就会得到:
鸭嘴兽X 卵生x 澳洲= 鸭嘴兽
// 相当于
卵生x 澳洲= 鸭嘴兽+ 其他
因此,结论就是"有的卵生动物是澳洲的动物",或者"有的澳洲的动物是卵生动物"。
还有更不直观的三段论。
"哲学家都是有逻辑头脑的,一个没有逻辑头脑的人总是很顽固。
"
请问结论是什么?
这道题会用到新的概念:全集和空集。
集合A和所有不属于它的元素(记作-A)构成全集(I),这时A和-A的交集就是一个空集(0)。
A + (-A) = I
A X (-A) = 0
因此,有下面的公式。
B
= B X I
= B X (A + -A)
= B X A + B X (-A)
回到上面那道题。
哲学家X 逻辑= 哲学家
无逻辑X 顽固= 无逻辑
根据第一个命题,可以得到下面的结论。
哲学家X 无逻辑
= (哲学家X 逻辑) X 无逻辑
= 哲学家X (逻辑X 无逻辑)
= 哲学家X 0
= 0
即哲学家与没有逻辑的人的交集,是一个空集。
根据第二个命题,可以得到下面的结论。
无逻辑X 顽固
= 无逻辑X 顽固X (哲学家+ 非哲学家)
= 无逻辑X 顽固X 哲学家+ 无逻辑X 顽固X 非哲学家
= 0 X 顽固+ 无逻辑X 顽固X 非哲学家
= 无逻辑X 顽固X 非哲学家
= 无逻辑
也就是说,最终的结论如下。
无逻辑X 顽固X 非哲学家= 无逻辑
// 相当于
顽固X 非哲学家= 无逻辑+ 其他
结论就是顽固的人与非哲学家之间有交集。
通俗的表达就是:一些顽固的人,不是哲学家,或者一些不是哲学家的人,很顽固。
由此可见,集合论可以帮助我们得到直觉无法得到的结论,保证推理过程正确,比文字推导更可靠。
四、集合论到布尔代数
既然命题可以用集合论表达,那么逻辑推导无非就是一系列集合运算。
由于集合运算的结果还是集合,那么通过判断个体是否属于指定集合,就可以计算命题的真伪。
一名顾客走进宠物店,对店员说:"我想要一只公猫,白色或黄色均可;或者一只母猫,除了白色,其他颜色均可;或者只要是黑猫,我也要。
"
这名顾客的要求用集合论表达,就是下面的式子。
公猫X (白色+ 黄色)
+ 母猫X 非白色
+ 黑猫
店员拿出一只灰色的公猫,请问是否满足要求?
布尔代数规定,个体属于某个集合用1表示,不属于就用0表示。
灰色的公猫属于公猫集合,就是1,不属于白色集合,就是0。
上面的表达式变成下面这样。
1 X (0 + 0)
+ 0 X 1
+ 0
= 0
因此,就得到结论,灰色的公猫不满足要求。
这就是布尔代数:计算命题真伪的数学方法。
五、布尔代数的运算法则
布尔代数的运算法则与集合论很像。
交集的运算法则如下。
1 X 1 = 1
1 X 0 = 0
0 X 0 = 0
并集的运算法则如下。
1 + 1 = 1
1 + 0 = 1
0 + 0 = 0
集合论可以描述逻辑推理过程,布尔代数可以判断某个命题是否符合这个过程。
人类的推理和判断,因此就变成了数学运算。
20世纪初,英国科学家香农指出,布尔代数可以用来描述电路,或者说,电路可以模拟布尔代数。
于是,人类的推理和判断,就可以用电路实现了。
这就是计算机的实现基础。
六、布尔代数的局限
虽然布尔代数可以判断命题真伪,但是无法取代人类的理性思维。
原因是它有一个局限。
它必须依据一个或几个已经明确知道真伪的命题,才能做出判断。
比如,只有知道"所有人都会死"这个命题是真的,才能得出结论"苏格拉底会死"。
布尔代数只能保证推理过程正确,无法保证推理所依据的前提是否正确。
如果前提是错的,正确的推理也会得到错误的结果。
而前提的真伪要由科学实验和观察来决定,布尔代数无能为力。
(完)。
