开环对数频率特性和时域指标.
开环频率特性与时域响应的关系

负幅值裕度
dB
dB
0
w
0
w
- 90?
- 90?
- 180?
w
- 180?
w
- 270?
- 270?
正相角裕度
负相角裕度
稳定系统
不稳定系统
(最γ小>0相,位Lh系>B0统od)e图中稳定裕度的γ定<0,义Lh<0
4
第五章 习题课
一、基本要求
1、掌握频率特性的实质,能够应用频率特性计算系 统的稳态响应;
§5-4 稳定裕度
一、相位裕度、相角裕度
1、截止频率ωc
A( jc ) G( jc )H( jc ) 1 或:L(c ) 20lg G( jc )H( jc ) 0
2、相角裕度 g: g 180 G( jc )H ( jc )
Nyquist图:负实轴与模值等于1的矢量的夹角。 Bode图:L(ω) =0处的相频φ (ω ) 与-π的角度差。 3、相角裕度的含义是:对于闭环稳定系统,如果开环相
P 2
2 2
1
所以系统不稳定
14
Im
Im
Im
1 0 Re
Re
1
Re
0
1 0
0
0
0
P0
P0
P0
R R 1 1 P 00 22
所以系统稳定
R R 0 1
P 2
0 2
0
所以系统不稳定
R R 1 1
P 2
0 2
0
所以系统稳定
15
求:系统的稳态输出。
【分析】cs (t ) A0 ( j ) sin(t ( j ))
G(s)H (s) (s) ( j ) ( j ) e j( j )
自动控制原理--频率特性与时域指标的关系及三频段分析法的应用

2 2
2.相位裕量: 180 (c ) arctan
2
1 4 4 2 2
5-17 5-18 5-19
Saturday, August 17当, 0< <0.6时, 100*
2024
1
3.与超调量的关系
e( / 1 2 ) p
p
4.与调整时间的关系
ts
3
n
3
2024
3
5.6.3闭环频率特性及其特征量
对于单位反馈系统其闭环传递函数为:
对应的频率特性为:
M (s) G(s) 1 G(s)
M ( j ) G( j ) M ( )e j () 1 G( j)
(5-21) (5-22)
对于非单位反馈系统,如图5-3(a)所示。
R(s)
+ -
C(s) G(s)
Saturday, August 17,
2024
15
某最小相位系统的对数幅频特性如图所示, 求 系统的开环传递函数 计算系统的相位裕量和幅值裕量 判断系统的稳定性
L(w)
-20 A
46
B 6
-40 C
W1
W2
10
100
-60
Saturday, August 17,
2024
16
解;1)低频段渐进线的斜率为-20dB,所以是1型系统(延长
当0< <0.707时, 二阶振荡环节的幅频特性曲线位于相应的渐近 线上方,系统存在峰值Mr 。对应的频率ωr为谐振频率。
r n 1 2 2
Mr
2
1
1 2 2
(5-24 )
2.截止频率和频带宽度
自控理论 4-6频域指标与时域指标的关系

2 −40
ω
作业
4 - A -14、 4 -B - 4 、
K s(Ts + 1)
c(t)
例:已知最小相位系统的开环对数幅频特 性曲线,试求: 性曲线,试求:
L(ω)
(1) 开环传递函数 开环传递函数G(s); ; (2) 剪切频率 ωc ; (3) 相角裕量 γ(ωc); (4) r(t)=(1/4)t2 时的 ess 。
6 0
−40 −20 0.5
ωc
令 G ( jω c ) = 1,
解得
ω c = ω n − 2ζ 2 + 4ζ 4 + 1
γ = 180 + ϕ (ω c ) = tg
0 −1
(4 − 30)
(4 − 31)
求γ
2ζω n
ωc
将式(4-30)代入式 代入式(4-31)得 将式 代入式 得
求γ
γ = 180 + ϕ (ω c ) = tg
2.
r(t)
25 s( s + 6)
c(t)
ωn2 =25 得 ζ =0.6 ωn=5
2ζ = 59.2 0
γ = tg
−1
− 2ζ 2 + 4ζ 4 + 1
ω c = ω n − 2ζ 2 + 4ζ 4 + 1 = 3.58
3.
Mr =
1 2ζ 1 − ζ
2
= 1.04
ω r = ω n 1 − 2ζ 2 = 2.65
结论
8 t sω c = tgγ
(4 − 36)
( 2) ω c与ζ、ω n 都有关,当ζ 一定,ω c ↑→ ω n ↑→ t s ↓ 一定,
开环频率特性与系统时域指标的关系PPT文档共24页

1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 பைடு நூலகம்8、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
开环频率特性与系统时域指标的关系
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
自动控制原理-频率特性与系统性能的关系
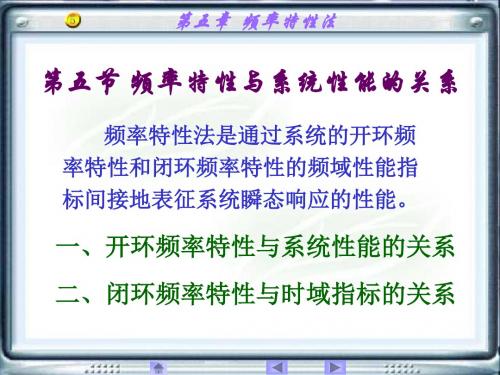
A(ω)= ω
1
ω 2ζωn
第四节 频率特性与系统性能的关系
二阶系统的开环对数频率特性曲线
时域法中:
L(ω)/dB
σ%—系统的平稳性
-20dB/dec
ts —系统的快速性
0
ωc
Φ(ω)
2ξ ωn
ω
频域法中:
0
-40dB/dec
ω
ωc
-90
—系统的快速性 -180
第五章 频率特性法
第五节 频率特性与系统性能的关系
频率特性法是通过系统的开环频 率特性和闭环频率特性的频域性能指 标间接地表征系统瞬态响应的性能。
一、开环频率特性与系统性能的关系 二、闭环频率特性与时域指标的关系
第四节 频率特性与系统性能的关系
一 、开环频率特性与系统性能的关系
常将开环频率特性分成低、中、高 三个频段。
第四节 频率特性与系统性能的关系
(2)中频段的斜率与动态性能的关系 频段较Φ设(宽s系)=,统1可+G中G(近频s()s似)段=认斜1+为率ωSωS整2c为22c2个-=4曲0Sd2ω+线Bωc/2是dce2 c一,条且斜中 率为-40系dB统/d处ec的于直临线界。稳定状态。
开环传递函数:
L(ω)/dB
2. 中频段
穿越频率ωc附近的区段为中频段。它 反映了系统动态响应的平稳性和快速性。
(1)穿越频率ωc与动态性能的关系 设系统中频段斜率为20dB/dec且中频
段比较宽,如图所示。可近似认为整个曲 线是一条斜率为-20dB/dec的直线。
第四节 频率特性与系统性能的关系
中频段对数幅频特性曲线
开环传递函数:
G解对(设 ωj:tωt应g性1g:)-的(-1=11ωω的的ωω)变ωcjω3c2曲频关ω--3c化tt(g线=率系g1ω-ω范K-+111如3特。3jc(21围=ω==ω性图+73110j2ω8):ω~o(o12ω+) j2ωω,0可3L-)2(求ω0ωd)B1得//dd-ω4Be0:c2dBω/d-4ec0cdBω/d3ec ω
控制工程(自动控制)第十八课 频率特性与时域指标

闭环频率特性主要性能指标
带宽频率ω 带宽频率ωb:当闭环幅频特性下降到频率为零时的分 贝值以下3分贝时,对应的频率称为带宽频率ω 贝值以下3分贝时,对应的频率称为带宽频率ωb . 频率范围(0,ωb)称为系统的带宽. 频率范围( 称为系统的带宽.
ω > ωb
20 lg Φ ( jω ) < 20 lg Φ ( j 0) 3
πζ / 1ζ 2
ζ =
1 1 1 2 Mr 2
π
2 M r M r 1 2 M r + M r 1
σ% = e
× 100%
ts =
3.5
ζωn
( = 0.05, 0 < ζ < 0.9)
因此,若知道频域指标中的任两个, 因此,若知道频域指标中的任两个,就可解算 从而求出时域指标.反之, 出ζ和ωn,从而求出时域指标.反之,给出时域指 标的任两个,就可确定闭环频域指标. 标的任两个,就可确定闭环频域指标.
高阶系统
1 Mr = ( 35 ° ≤ γ ≤ 90 ° ) sin γ σ = 0 . 16 + 0 . 4 ( M r 1) (1 ≤ M ts = kπ ≤ 1 .8 )
r
ωc
(1 ≤ M
r
k = 2 + 1 . 5 ( M r 1) + 2 . 5 ( M r 1) 2
≤ 1 .8 )
2 b 2 2 n
1 = 20 lg 2
ω jα ( ω ) Φ ( jw) = = M (ω )e 2 2 ( jω ) + 2ζω n ( jω ) + ωn
2 n
M (ω ) =
1
ωb2 2 ωb 2 [1 2 ] + [2ζ ] ωn ωn
开环频率特性与系统时域指标的关系PPT文档24页

61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
开环频率特性与系统时域指标的关系
16、人民类对于不公正的行为加以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
谢谢!
开环频率特性与系统时域指标的关系

系统相角裕量为:? = 1800 +? (wc )
-40dB/dec -20dB/dec
w2 w0 wc
= arctan wc ? arctan wc
w2
lw2
最小相位滞后? (w)发生在:
wm = w2w3
此时可得到最大相角裕量:
?m
= arcsin l ? 1 l +1
w
w3
-40dB/dec
10
a、增加开环放大系数K; b、提高系统的型号数;
单位加速 度输入
r(t) = Rt 2 2
?
? R Ka
2
开环对数幅频特性的第一个转折频率 w1以前的区段称为低 频段。该段取决于系统开环增益K 和开环积分环节的数目v。
低频段决定了系统稳态精度。
低频起始段
L0 (w) = 20lg
K
wv
= 20lg
以-20dB/dec穿过0dB线。开环截止频率wc反映了系统响应的 快速性。
? (wc )与? 的关系图
?(wc )与? % 的关系图
8
? (wc )与 ts 的关系图
tswc
=
3
?
4? 4 + 1 ? 2? 2
9
高阶系统
G(s)
=
K (T2s s2 (T3s
+1) +1)
设中频段长度为: l = w3 w2
K
?
v20lg w
0型系统
结论:0型系统对数幅频特性
曲线低频段的斜率为0;高度
为20lg K ,其中KP即为该系 统的稳态位置误差系数。
20lg Kp
0
w1
? 20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-6 开环对数频率特性和时域指标
根据系统开环对数频率特性对系统性能的不同影响,将系统开环对数频率特性分为三个频段。
即低频段、中频段和高频段。
一、 低频段
低频段通常是指开环对数幅频特性的渐近曲线在第一个交接频率以前的频段,这一频段完全由开环传递函数中的积分环节和放大环节所决定。
低频段的对数幅频为
ωωωωlg 20lg 20lg 20)()(lg 20⨯-==v K K
j H j G v (5-32)
式中v 为开环传递函数中的积分环节数。
根据式(5-32)及积分环节数,就可作出开环对数幅频特性曲线的低频段,如图5-39所示。
若已知低频段的开环对数幅频特性曲线,则很容易得到K 值和积分环节数v ,故低频段的频率特性决定了系统的稳态性能。
二、中频段
中频段是指开环对数幅频特性曲线截止频率c ω附近的频段。
这决定系统的稳定程度,即决定系统的动态性能。
设有二个系统,均为最小相位系统,它们的开环对数幅频特性曲线除中频段的斜率不同(即一个为20-dB/dec,另一个为40-dB/dec) 之外, 其余低频、 高频段均相同。
并且中频段相当长,如图5-40 所示。
显然,系统(a)有将近90°的相裕量,而系统(b)则相裕量很小。
假定另有二个系统, 均为最小相位系统, 开环对数幅频特性曲线除中频段 (斜率为 -20 dB/dec ) 线段的长度不同外, 其余部分完全相同, 如图 5-41 所示。
显然, 中频段线段较长的系统 (a) 的相裕量将大于中频段线短的系统(b)。
可见,开环对数幅频特性中频段斜率最好为20-dB/dec ,而且希望其长度尽可能长些,以确保系统有足够的相角裕量。
如果中频段的斜率为40-dB/dec 时,中频段占据的频率范围不宜过长,否则相裕量会很小;若中频段斜率更小(如60-dB/dec),系统就难以稳定。
另外,截止频率c ω越高,系统复现信号能力越强,系统快速性也就越好。
三、 高频段
高频段是指开环对数幅频特性曲线在中频段以后的频段(一般c ωω10>的频段)。
这部分特性是由系统中时间常数很小的部件所决定。
由于它远离截止频率c ω,一般幅值分贝数较低,故对系统动态性能(相裕量)影响不大。
另外,由于高频段的开环幅值较小,故对单位反馈系统有
()()
1()G j j G j ωΦωω=
+
)(ωj G ≈
该式表明,闭环幅值近似等于开环幅
值。
因此,系统开环对数幅频特性在高频段
的幅值,直接反映了系统对输入端高频干扰
的抑制能力。
所以,高频段的分贝数值愈低,系统的抗干扰能力愈强。
图5-42为典型的一型高阶系统开环对数幅频特性曲线的三个频段的划分。
应当指出,三个频段的划分并没有严格的确定准则,但是三个频段的概念为直接运用开
环频率特性来判别、估算系统性能指出了方向。
四、 从相裕量γ估算时域指标
相裕量γ是在频域内描述系统稳定程度的指标,而系统的稳定程度直接影响时域指标%σ和s t ,因此,γ必定与%σ和s t 存在内在联系。
1、 二阶系统的时域指标 二阶系统的相裕量与时域指标间有确定的关系。
分析图5-43所示二阶系统,其开环传递函数
)
2()(2n n s s s G ξωω+= )121
(2+=
s s n n ξωξω
其开环对数幅频特性曲线如图5-44所示。
二阶系统的结构参量ξ、n ω,在时域分析中已建立了与时域指标间的关系式,即
%100%21/⨯=--ξξπσe
n s t ξω5.3=
21ξωπ
-=n p t
式中自然频率n ω可从渐近对数幅频曲线上确定。
在图5-44中,斜率为40-dB/dec 的线段(或其延
长线)与零分贝的交点即为n ω。
因为该点频率恰好
是ξ2n ω和n ω/ξ2频率的几何平均值。
下面求解γ与ξ的关系式:
根据相裕量的定义
式,即
c c c j G ξωωωγ2arctan 90)(180-︒=∠+︒= (5-33)
当开环幅频等于1。
即()1c G j ω=,得
24241ξξωω-+=n
c
将上式代入(5-33)式,得 242412arctan ξξξ
γ-+= (5-34)
根据式(5-34)绘制ξγ-曲线,如图5-45所示。
由图可见,γ越大,ξ也越大;γ越小,ξ就越小。
要想得到满意的动态过程,一般γ取值范围在︒︒70~30之间。
由开环对数幅频特性求时域指标的方法:首先从开环对数幅频特性曲线上求得n ω和γ值,然后根据γ值查图5-45获得ξ值,最后由ξ值查图3-14便可得到%σ;将n ω、ξ值代入式(3-16)和(3-18)分别求得p t 和s t 。
2
对于高阶系统,γ毕竟只是比较简单的一项指标,它不能
完全概括千变万化的频率特性形状。
γ相同的系统,频率特性
未必完全相同,因此时域指标也不会一样。
所以在高阶系统中,
γ与时域指标之间没有确定的函数关系。
但是,通过对大量系
统的研究。
可归纳出下面两个近似的计算公式 ,1sin 14.016.0⎪⎪⎭⎫
⎝⎛-+=γσp ︒≤≤︒9035γ
(5-35)
⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+=21sin 15.21sin 15.12γγωπc s t
(5-36)
根据以上公式绘制成曲线如图5-46所示。
应当指出,根据计算公式或查图5-46所得结果,当γ较小时,比较接近实际系统,即准确度就高;而当γ较大时,近似程度较差,准确度就低。
