地球物理计算方法课件:习题课3
地球物理流体力学课件

地球物理流体力学课件
地球物理流体力学是研究地球内部和大气、海洋等自然界流体运动规律的学科。
其课件内容一般包括以下几个方面:
1. 流体力学基础知识,介绍流体的性质、流体静力学、动力学基本方程、连续性方程、动量方程和能量方程等基础知识,为后续地球物理流体力学的学习打下基础。
2. 地球内部流体运动,介绍地球内部的物质运动规律,包括地幔对流、地核运动等,探讨地球内部流体对地壳构造和地震等地质现象的影响。
3. 大气和海洋流体运动,探讨大气和海洋中的气流和洋流等运动规律,包括环流系统、季风、厄尔尼诺现象等,以及它们对气候和天气的影响。
4. 地球物理流体力学模型,介绍地球物理流体力学模型的建立和应用,包括数值模拟方法、地球系统模型等,以及这些模型在地球科学研究中的作用和意义。
在课件中,通常会结合理论知识和实际案例进行讲解,以便帮助学生更好地理解地球物理流体力学的理论和应用。
同时,课件中可能还会包括一些实验、观测数据和计算方法,以及相关的学习资源和参考文献,以便学生能够深入学习和研究地球物理流体力学的领域。
地球物理计算方法课件:第二章_数值积分 3

R
I
S n
ba 180
h 4
2
f
(4) ( )
b a h4 2880
f
(4) ( ),
(a,b).
n , h4 0, R 0
具有相应的收敛性和稳定性.
10
复化求积公式的截断误差
复化梯形公式的截断误差:
RT ( f )
b
f (x)dx T
a
n
h3 12
nf
(
)
ba 12
h2
f
(
)
I S2n 1 I Sn 16
移项整理,知
I
16 15
S
2n
1 15
Sn
16
1
这个值正好是科特斯公式的结果。也可写为 Cn 15 S2n 15 Sn
Cn (1 )S2n Sn
1
15
3、Romberg公式
重复同样的手续,依据柯特斯法的误差公式可进一步导出下列 龙贝格公式:
Rn
64 63 C2n
1 63 Cn
这个公式也可写为
Rn (1 )C2n Cn
1
63
18
一般递推公式:
k次二分得到得到的m次加速值,龙贝格一般公式
T (k) m
4m 4m
1
T (k m1
1)
1 4m 1
T( m1
k
)
.k
1,2,....
19
4、 Romberg算法的实现
计算流程见P70,实现步骤:
① 用梯形公式计算积分近似值
xk a kh(k 0,1,, n),
由定积分性质知
I
b
n1
f (x)dx
地球物理解释基础ppt课件

第19章介绍AVO方法
• 什么是AVO?——研究CMP道集内相对振幅,称作振幅随炮检
距变化的分析(AVO)。研究相对振幅随反射角的变化,这种方法称 作振幅随入射角变化的分析(AVA)
• AVO分析能解决什么地质问题 —碎屑岩气藏直接烃类指示 —在碳酸盐油藏中可能识别孔隙发育带
• 随炮检距变化的反射系数 ——AVO的计算
地球物理解释基础 (2)
第14章解释与盐构造有关的圈闭
• 许多重要油田 和盐圈闭联系在一起——著名的墨西哥湾、美国几
个洲、加拿大、北海、北非、德国 、里海地区 都存在盐圈闭。塔里木盆 地的克拉2气田也和盐圈闭有关
• 盐与众不同 ——有较低的密度和较高的地震速度 • “漂浮”状侵入到沉积物之下——侵入体产生各种盐体形状 ,盐
层析成像技术
• 层析的目标是求解每个面元的速度 • 层析成像方法的第一步是从未叠加的地震资料上或直接从野
外观测值拾取旅行时 • 建立初始模型作射线追踪,由初始模型计算的波至时间与观
测值进行比较 • 根据模型值与观测值之差对模型进行修改 • 拾取旅行时-建立模型-模型正演-测量时间差-修改模型——这
正演模拟和反演的关系
正演模拟——用一个数学关系式,对给
出的一组模型参数合成地下响应。
反演或“反演模拟” ——与正演 模拟
“相反”的过程。对一个给出的数据集, 寻
求定义一个与观测数据相符的地质模型
从数学上讲,反问题由于比方程式更多 未知数的存在,能够引起不确定性,产生 多解,所以反演的多解性是固有的
反演的多解性(非唯一性、不确定性)
1D, 2D, 3D需要将物理模 型材料校正为成比例的模 型
当非均质体的尺度与 Fresnel带相比很大时, 一般是可以应用的。通
物 理 大 地 测 量 学3
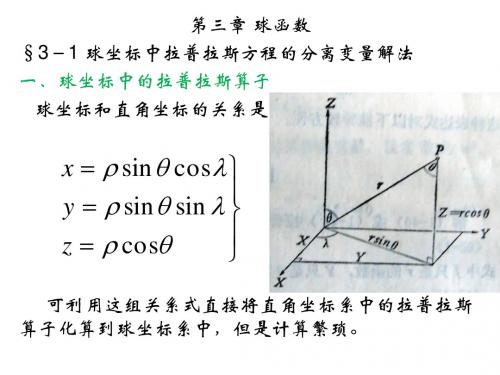
分离变量法就是将方程的解分解为依赖于不同自变量 的函数之积 令 v( , , ) f ( )Y ( , ) 代入上式,可得
d df ( ) f () Y ( , ) f ( ) 2Y ( , ) y ( , ) [ 2 ] [sin ] 0 2 2 d d sin sin
两边同除以 f ( )Y ( , ) 然后将后两项移到等号右边,得
1 d 2 df ( ) [ ] f ( ) d d 1 1 Y ( , ) 1 2Y ( , ) { [sin ] } 2 2 Y ( , ) sin sin
1 1 d dB( ) 1 1 d 2 L( )) [sin ] } a 0 2 2 B( ) sin d d L( ) sin d
上式两边同乘以sin2θ,然后将第二项移到等号 右边,得
sin d dB( ) 1 d 2 L( )) 2 [sin ] a sin B( ) d d L( ) d2
0 i 0
i
可以解出计算系数的递推公式
Ci 2
i(i 1) Ci (i 2)(i 1)
勒让得方程是一个二阶奇次常微分方程,它有两个线 性无关的解。若取C0≠0且C1=0,则C2i+1 =0 ;若取C0=0 且C1≠0,则C2i =0,则这两个线性无关的解可以写成
B ( x ) C2 i x i 0 0 2 i 1 B2 ( x) C2i 1 x i 0
2 将 k 代入分离变量的连带勒让德方程和勒让德方程, 得
d 2 dB ( x) 0 [(1 x ) ] B ( x) 0 dx dx
地球物理计算方法 第三章_微分方程差分法1

yn p y(xn ) phk1
k2 f (xn p , yn p )
(2)将近似值代入公式作迭代计算:
ky1n
1
yn f(
xn
h[(1 , yn )
)k1
k2
]
k2 f (xn p , yn phk1)
38
定理: 当 p 1 时,Runge-Kuta格式具有二阶精度。
2
采用精度分析方法:对y=x2能够精确成立。
yn )
f
( xn 1 ,
yn
hf
(xn ,
yn ))]
于是:
yn1
yn
h 2 [k1
k2 ]
其中预报-校正
k1 f (xn , yn ) k2 f (xn1, yn hk1)
Runge-Kutta算法 在区间 [xn , xn1] 上取几个点的斜率,然后计算它们的平均斜率 k*,以此可以构造出更高精度的格式,这就是Runge-Kutta 算法 的基本思想。
y(xn )
hy(xn )
(2)将近似值代入梯形公式作迭代计算:
y ( n 1) n1
yn
h[ f 2
(xn ,
yn )
f
( xn1 ,
y(n) )] n1
23
只用一次迭代计算即可。显式与隐式的结合建立的预报-校正系统:
预报 校正
yn1 yn hf (xn , yn )
h
yn1
yn
[ 2
特别地,当 p 1, 1 时,有
2
yn1
yn
h 2 [k1
k2 ]
k1 f (xn , yn )
k2 f (xn1, yn hk1)
地球物理计算方法课件:绪论2

(x)
1 10l1
2(1 1)
则x至少具有l位有效数字(即至少精确到它的第l位)。
例: 当用3.1416来表示 的近似值时,它的相对误差是多少?
例 为了使 x 20 的近似值x的相对误差小于0.1%,问至少
取几位有效数字?
误差的传播与估计
误差的传播
两个近似数x1与x2,其误差限分别为ε(x1) 及ε(x2), 它们进行加、减、乘、除运算得到的误差限分别为
解为 x1=-6.222…, x2=38.25…, x3=-33.65…,
误差来源
用计算机解决科学计算问题(地球物理)的过程如下:
修修改改处处理理
地地质问质题 问题
物物理理模 模型型
数数学学模 模型型
数数值值计 算计算
否否
计足计要算算求结果结是否果满 是否满足
要求
是是 地地质质解 解释释
模型 误差
Cp越大,病态越严重.
避免误差危害的若干原则
1. 要避免除数绝对值远远小于被除数绝对值的除法 用绝对值小的数作除数舍入误差会增大,如计算 x
y
若0 y , 则x 可能对计算结果带来严重影响,应 尽量避免.
2. 要避免两相近数相减
在数值计算中两相近数相减有效数字会严重损失. 例如, x 532.65, 都y 具5有32五.5位2有效数字, 但 x y 只0.有13两位有效数字. 这说明必须尽量避免出现这类运算. 最好是改变计算方法, 防止这种现象产生.
a1 为0整, m数,取l
x x * 1 10ml. 2
0ln
有效数字与绝对误差限的关系
对 取3位和5位有效数字,他们的误差限是多少?
3* 0.002, 5* 0.000008,
计算地球物理课件 第2章 地球物理中常用数值解法的基本原理-2

某一位置 u x ,计算它的位能(W 1 T 2, 为伸缩率):
2
应变位能 外力作功
第二节 偏微分方程的有限元解法
2.2 两点边值问题——弦的平衡 总位能
根据极小位能原理, u* u* x 是下列变分问题的解:
J
u*
min u
J
u
第二节 偏微分方程的有限元解法
几个概念
测度:有界开集和有界闭集的测度是区间长度的直接
推广。
E 是有界集 存在常数 M ,使对任意的 x (x1, x2, , xn ) E ,都有| xi | M (i 1, 2, , n) .
有界集
E
的外测度——
m*E
inf
Ii
,
Ii E , inf 表
i 1
i 1
示最左边的意思。
有界集 E 的内测度——有界集 E 所包含的一切有界闭
第二节 偏微分方程的有限元解法
有限元法的基本问题可归纳为: (1)把问题转化成变分形式; (2)选定单元的形状,对求解域作剖分; (3)构造基函数或单元形状函数; (4)形成有限元方程(Ritz-Galerkin方程); (5)提供有限元方程的有效解法; (6)收敛性及误差估计。
第二节 偏微分方程的有限元解法
x y z x y z (结合律);
2)对任何 , k , x, y X ,定义数乘,即 x X ,且满足
x x x ; x x ; x y x y ; 1 x x ;
3)在 X 中存在零元素,记为“0”,它满足
x0 x 4)对每个 x X ,存在 x 的加法逆元素,记为“-x” X ,使 x x 0
正定:设A是n阶实系 数对称矩阵,如果对 任何非零向量x都有 xTAx>0,就称A正定。
地球物理计算方法第一章

地球物理计算方法第一章地球物理学是研究地球内部构造、物质组成、能量交换以及地球与其他天体相互作用的一门学科。
地球物理计算方法是地球物理学中使用的数学方法和计算技术,为解决地球物理问题提供了强大的工具。
第一章介绍了地球物理计算方法的概念和基本原理。
地球物理计算方法是基于数学模型来描述地球物理现象,并通过计算技术来求解这些模型。
地球物理学中常用的计算方法包括正演模拟、反演和数据处理等。
正演模拟是地球物理计算的一种基本方法,它通过已知的地质模型和物理参数来计算预期观测数据。
正演模拟可以帮助地球物理学家理解地球内部的物理过程,并对地球内部结构和物质组成进行研究。
反演是地球物理计算的另一种重要方法,它通过观测数据来推断地下的物理性质和地质结构。
反演过程中,需要建立一个数学模型来描述地球物理问题,然后利用观测数据来对模型进行约束,从而求解模型中的未知参数。
反演方法在地球物理勘探和地震学等领域中被广泛应用。
数据处理是地球物理计算的第三种常用方法,它主要针对观测数据进行处理和分析。
地球物理观测数据往往存在噪声和干扰,需要通过数据处理方法来滤除这些干扰,以便更准确地获取地质信息和定量分析。
地球物理计算方法的应用广泛,涵盖了地球物理学的各个领域。
例如,在地球物理勘探中,地球物理计算方法可以用来预测地下矿产资源的分布和储量,帮助勘探人员确定最佳的钻探位置。
在地震学研究中,地球物理计算方法可以用来模拟地震波的传播路径和速度,帮助科学家更好地理解地震灾害的发生机制。
除了在地球物理学领域中的应用,地球物理计算方法也被广泛应用于其他科学领域。
例如,在地质学中,地球物理计算方法可以用来重建地壳变形的历史,推断地球演化的过程。
在气象学研究中,地球物理计算方法可以用来模拟大气环流和气候变化。
综上所述,地球物理计算方法是地球物理学研究中不可或缺的工具。
它通过数学模型和计算技术,为解决地球物理问题和揭示地球内部的奥秘提供了有效的手段。
