反比例函数的性质-k的几何意义及应用课件
合集下载
反比例函数中K的几何意义课件

总结词
k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中,k值决定了图 像的形状和位置。当k>0时,图像出 现在第一象限和第三象限;当k<0时 ,图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时,图像分布在第一象限和第三象限;当k<0时,图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展,反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域,如经济学、生物学等,以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念,与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系,以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小,反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用,如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解,但仍有许多未知的性质等待我们去发 现和研究。例如,反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质:当 x 增大时,y 值会减小;当 x 减小 时,y 值会增大。这是因为 xy =
k 的关系。
在图像上,反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的,且无限接近于坐标轴
。
Part
02
k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中,k值决定了图 像的形状和位置。当k>0时,图像出 现在第一象限和第三象限;当k<0时 ,图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时,图像分布在第一象限和第三象限;当k<0时,图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展,反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域,如经济学、生物学等,以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念,与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系,以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小,反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用,如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解,但仍有许多未知的性质等待我们去发 现和研究。例如,反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质:当 x 增大时,y 值会减小;当 x 减小 时,y 值会增大。这是因为 xy =
k 的关系。
在图像上,反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的,且无限接近于坐标轴
。
Part
02
人教版数学九年级下册26.1.1反比例函数中K的几何意义课件

,求$k$的值。
利用K值解决实际问题
例题3:某工厂生产A、B两种配套产品 ,其中每天生产$x$吨A产品,需生产 $y$吨B产品。已知生产A产品的成本与 产量的平方成正比。经测算,生产1吨 A产品需要4万元,而B产品的成本为每
吨8万元。求
(1)生产A、B两种配套产品的平均成本 的最小值;
(2)若原料供应商对这种小型工厂供货 办法使得该工厂每天生产A产品的产量 $x$在$0 < x leqslant 2$的范围内, 那么在这种情况下,该工厂应生产A产
当$K < 0$时,距离公式同样适用, 只是图像位于第二、四象限。
K值与角度关系
对于反比例函数图像上任意一点,其与原点连线的倾斜角$theta$与该点 的横坐标$x$和纵坐标$y$满足关系:$tantheta = frac{y}{x} = frac{K}{x^2}$。
当$K > 0$时,$theta$为锐角或直角;当$K < 0$时,$theta$为钝角或 直角。
随着$|K|$的增大,倾斜角$theta$也逐渐增大,但始终不会超过直角。
05
典型例题解析
求反比例函数中K值
01
例题1
已知反比例函数$y = frac{k}{x}$的图像经过点 $A(2,3)$,求$k$的值。
02
例题2
已知反比例函数$y = frac{k}{x}$的图像经过点 $B(m,n)$和$C(p,q)$,且$mn = 6$,$pq = 8$
06
课堂小结与拓展延伸
课堂小结
反比例函数$y = frac{k}{x}$($k neq 0$)中,比例系数$k$的几 何意义:过双曲线上任意一点引 $x$轴、$y$轴垂线,所得矩形面
积为$|k|$。
利用K值解决实际问题
例题3:某工厂生产A、B两种配套产品 ,其中每天生产$x$吨A产品,需生产 $y$吨B产品。已知生产A产品的成本与 产量的平方成正比。经测算,生产1吨 A产品需要4万元,而B产品的成本为每
吨8万元。求
(1)生产A、B两种配套产品的平均成本 的最小值;
(2)若原料供应商对这种小型工厂供货 办法使得该工厂每天生产A产品的产量 $x$在$0 < x leqslant 2$的范围内, 那么在这种情况下,该工厂应生产A产
当$K < 0$时,距离公式同样适用, 只是图像位于第二、四象限。
K值与角度关系
对于反比例函数图像上任意一点,其与原点连线的倾斜角$theta$与该点 的横坐标$x$和纵坐标$y$满足关系:$tantheta = frac{y}{x} = frac{K}{x^2}$。
当$K > 0$时,$theta$为锐角或直角;当$K < 0$时,$theta$为钝角或 直角。
随着$|K|$的增大,倾斜角$theta$也逐渐增大,但始终不会超过直角。
05
典型例题解析
求反比例函数中K值
01
例题1
已知反比例函数$y = frac{k}{x}$的图像经过点 $A(2,3)$,求$k$的值。
02
例题2
已知反比例函数$y = frac{k}{x}$的图像经过点 $B(m,n)$和$C(p,q)$,且$mn = 6$,$pq = 8$
06
课堂小结与拓展延伸
课堂小结
反比例函数$y = frac{k}{x}$($k neq 0$)中,比例系数$k$的几 何意义:过双曲线上任意一点引 $x$轴、$y$轴垂线,所得矩形面
积为$|k|$。
反比例函数中k的几何意义-优质课公开课课件一等奖

坐标轴围成的矩形的面积,发现,无论图像
上的点如何移动,矩形的面积却始终不变,
且刚好为 。接着,我们发现双曲线上的点
||
与坐标轴围成的三角形的面积始终为 ,可
2
见值常常与图形的面积相联系。
PPT模板:/moban/
PPT素材:/sucai/
PPT背景:/beijing/
3
相交于、两
点,过作 ⊥ 轴,过作 ⊥ 轴,则
图中阴影部分的面积为( )
A、2
B、3
C、4
D、6
3
点和点都在反比例函数 = 的图像上
⊥ 轴, ⊥ 轴
△ = △
3
=
2
阴影部分的面积就是两个三角形面积之和,为3
正确答案是选项B。
我们通过探究反比例函数图像上的点与
历史课件:/kejian/lishi/
PPT背景:/beijing/
PPT图表:/tubiao/
PPT下载:/xiazai/
PPT教程: /powerpoint/
资料下载:/ziliao/
数学课件:/kejian/shuxue/
英语课件:/kejian/yingyu/
美术课件:/kejian/meishu/
科学课件:/kejian/kexue/
物理课件:/kejian/wuli/
PPT图表:/tubiao/
PPT下载:/xiazai/
PPT教程: /powerpoint/
A、2
B、4
C、6
D、8
两个矩形的面积相等,且都为比例系数4。
1 = 矩形 − 阴影矩形 = 4 − 1 = 3
2 = 矩形 − 阴影矩形 = 4 − 1 = 3
上的点如何移动,矩形的面积却始终不变,
且刚好为 。接着,我们发现双曲线上的点
||
与坐标轴围成的三角形的面积始终为 ,可
2
见值常常与图形的面积相联系。
PPT模板:/moban/
PPT素材:/sucai/
PPT背景:/beijing/
3
相交于、两
点,过作 ⊥ 轴,过作 ⊥ 轴,则
图中阴影部分的面积为( )
A、2
B、3
C、4
D、6
3
点和点都在反比例函数 = 的图像上
⊥ 轴, ⊥ 轴
△ = △
3
=
2
阴影部分的面积就是两个三角形面积之和,为3
正确答案是选项B。
我们通过探究反比例函数图像上的点与
历史课件:/kejian/lishi/
PPT背景:/beijing/
PPT图表:/tubiao/
PPT下载:/xiazai/
PPT教程: /powerpoint/
资料下载:/ziliao/
数学课件:/kejian/shuxue/
英语课件:/kejian/yingyu/
美术课件:/kejian/meishu/
科学课件:/kejian/kexue/
物理课件:/kejian/wuli/
PPT图表:/tubiao/
PPT下载:/xiazai/
PPT教程: /powerpoint/
A、2
B、4
C、6
D、8
两个矩形的面积相等,且都为比例系数4。
1 = 矩形 − 阴影矩形 = 4 − 1 = 3
2 = 矩形 − 阴影矩形 = 4 − 1 = 3
反比例函数中K的几何意义 上课ppt课件

别向x轴、y轴作垂线
⑴若P的坐标是(-1,3)则PM=__3__,PN=_1___
⑵若F的坐标是(0.5,-6),则FB=_6___,FA=_0_.5__
⑶若P的坐标是(x,y),则PM=__y__,PN=__x__ y
P
N
B
x
M0
平面直角坐标系内任意一点P(x,y)
.
AF
P到x轴的距离是这点纵坐标的绝对值即是 y
1
1.理解并掌握反比例函数中 ∣K∣的几何意义; 2.能灵活运用∣K∣的几何 意义求图形面积; 3.能根据图形面积求出K值
2
概念回顾
定义
形如__y_=__kx___(k≠0,k为常数)的函数叫 做反比例函数
关系式
防错 提醒
y k 或y=kx-1或xy=k(k≠0) x
(1)k≠0;(2)自变量x≠0;(3)函数值y≠0
5 2
B
D
x
14
变式练习
y 6
已知:如图,反比例函数
与x一次函数
y=kx+1的图像交于A、B两点,点A的纵坐标是3.
(1)求这个一次函数的解析式 (2)求△AOB的面积.
解
:
(2)
y
6 x
,
y x 1.
解得xy
3,2或xy
2, 3.
A(2,3),B(3,2).
为什么?数缺形时少直觉, 形少数时难入微.
21
反比例函数 y kx上一点P(x0,y0),过点P 分别作PA⊥y轴,PB⊥X轴,垂足分别为A、
B,则矩形AOBP的面积为 k ;
且S△AOP= S△BOP = k
第26章 反比例函数——反比例函数中k的几何意义课件

6
拓展3 : A(x1,y1)在反比例函数y= (>)图像上
2
(3) 如图 ,点B(x2,y2 )为反比例函数y=- (x <0)图像上一点.求△OAB的面积.
补
E
S△AOB= S梯形ABEF-S△AOF-S△BOE
=S梯形ABEF-3-1
=S梯形ABEF-4
| −
|(| |+| | )
2
(1) 如图,点B(x2,y2 )为反比例函数y= (x>0)图像上一点.
若A,B为两函数同一象限的点,求 △ OAB的面积.
S△AOE≠S△BOF
S△AOB= S梯形AEFB+S△AOE-S△BOF
=S梯形AEFB+3-1
=S梯aAEFB+2
E
F
| − |(| |+| | )
=
等底等高,
面积不变
N
x
利用平行转化解决面积问题
变形
等底等高,
面积不变
变形
利用平行转化解决面积问题
1、如图6, P是反比例函数y=(x>0)图象上的一点,PM⊥y,点Q,N在x轴
4
上,QN∥PM,且QN=PM,四边形PMQN的面积为4,则k=____________.
6
D
2、如图,已知点A在反比例函数y=
6
1、如图,反比例函数y= 的图像经过A(1,6),B(3,2)两点,求△AOB 的面积
.
F
方法2: S△AOB= S△AOE-S△BOE
或S△AOB= S△OBF-S△OAF
补
E
F
G
E
方法3: S△AOB= S矩形OEGF-S△BOE-S△ABG- S△OAF
拓展3 : A(x1,y1)在反比例函数y= (>)图像上
2
(3) 如图 ,点B(x2,y2 )为反比例函数y=- (x <0)图像上一点.求△OAB的面积.
补
E
S△AOB= S梯形ABEF-S△AOF-S△BOE
=S梯形ABEF-3-1
=S梯形ABEF-4
| −
|(| |+| | )
2
(1) 如图,点B(x2,y2 )为反比例函数y= (x>0)图像上一点.
若A,B为两函数同一象限的点,求 △ OAB的面积.
S△AOE≠S△BOF
S△AOB= S梯形AEFB+S△AOE-S△BOF
=S梯形AEFB+3-1
=S梯aAEFB+2
E
F
| − |(| |+| | )
=
等底等高,
面积不变
N
x
利用平行转化解决面积问题
变形
等底等高,
面积不变
变形
利用平行转化解决面积问题
1、如图6, P是反比例函数y=(x>0)图象上的一点,PM⊥y,点Q,N在x轴
4
上,QN∥PM,且QN=PM,四边形PMQN的面积为4,则k=____________.
6
D
2、如图,已知点A在反比例函数y=
6
1、如图,反比例函数y= 的图像经过A(1,6),B(3,2)两点,求△AOB 的面积
.
F
方法2: S△AOB= S△AOE-S△BOE
或S△AOB= S△OBF-S△OAF
补
E
F
G
E
方法3: S△AOB= S矩形OEGF-S△BOE-S△ABG- S△OAF
反比例函数中K的几何意义及其应用复习课名师公开课获奖课件百校联赛一等奖课件
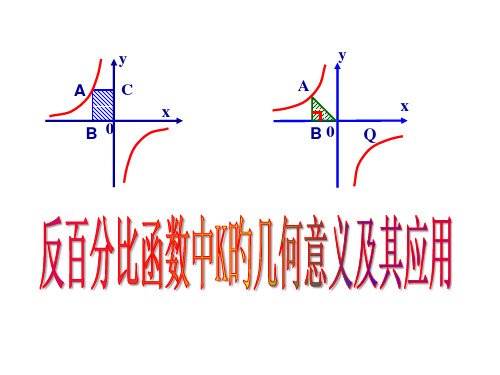
xy
y
AC
A
x B0
B0 Q
x
S矩形 K
K S △2
注意(1)面积与点A旳位置无关 (2)在没图旳前提下, 须分类讨论
数形结合思想
“数无形,少直观,形无数,难入 微”。 “数形结合”是数学中最主 要旳,也是最基本旳思想措施之一, 是处理许多数学问题旳有效思想。利 用“数形结合”可使所要研究旳问题 化难为易,化繁为简,使抽象变得直 观。
y
AC x
B0
y
A B0
x Q
一、知识回忆
1、如图所示,四边形
是矩形,反百分比函数y
-
6 x
过点A ,则S矩形ABOC=
;
2、若连接AO,则
S= RtABO
;
y
AC B Ox
y k (k 0) xy
AC x
B0
y A
B0 Q
x
S矩形 K
K S △2
一、基础应用
1、如旳图面,积若为反4,百则分k比= 函数y .kx
旳图象上一点,点B是函数
y k (x 0) 上旳图象上一点,且
x
4
OB⊥OA,若OA :OB=3:2 , 则k 旳值为 3 .
y CA
O
x DB
思绪措施小结
有关反百分比函数与几何综合旳问题 旳处理思绪: 从关键点入手.经过关键点坐标和横 平竖直线段长旳相互转化,结合 K旳 几何意义,可将函数特征与几何特征 综合在一起进行研究. 对函数特征和几何特征进行转化、组 合,列方程求解.
k2 x
(x>0)
旳图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,
且OA⊥OB,S△AOC=
人教版初三数学9年级下册 第26章(反比例函数)反比例函数k的几何意义 课件(17张ppt)
(3)若点(a,y)在该函数图象上,且a>-2,求y的取值范围.
7.【例 4】如图,在平面直角坐标系中,反比例函数 y=k(k>0)的
x
图象经过点 A(2,m),过点 A 作 AB⊥x 轴于点 B,且△AOB 的面积
为 5. (1)求k和m的值; (2)当x≥8时,求函数值y的取值范围.
解:(1)∵A(2,m),
第二十六章 反比例函数 与反比例函数有关的面积问题
k 的几何意义及应用
函数
图象形状 图象位置 增减性 延伸性 对称性
y
函数图象的 在每一支
双曲线既
k>0
两支分支分 曲线上,y 双曲线向 是轴对称
O x 别位于第一、都随x的增 四边无限 图形(对称
三象限
大而减小 延伸,与 轴:y=±x),
y 函数图象的 在每一支 坐标轴没 又是中心
自主归纳
y
P(m,n) B
oA
x
K与图形面积
S矩形OAPB OA• AP
m•n
k
反比例函数图像上任意一点向x轴和y轴作垂线,
得到矩形的面积为 S矩形OAPB k
如图:连接OP,则
SOAP
1 • OA • AP 2
y
1 m•n
2
P(m,n) B
oA
x
1 k 2
反比例函数图像上任意一点向x轴或y轴作垂线,
5.若D、E、F是此反比例函数在第三象限图像上的三个点,
过D、E、F分别作x轴的垂线,垂足分别为M,N、K,连接
OD、OE、OF,设△ ODM、△OEN、 △OFK 的面积分别
为S1、S2、S3,则下列结论成立的是( D )
y A(1,4)A S1﹤S2 Nhomakorabea﹤ S3
《反比例函数图像性质-k的几何意义》课件
随着x的增大或减小,曲线会逐渐靠近 坐标轴,但永远不会与坐标轴相交。
曲线形状
图像是由两支分别位于第一和第三象 限的曲线组成,这两支曲线关于原点 对称。
k<0时图像特征
1 2
图像位于第二、四象限
当k<0时,反比例函数的图像会出现在第二和第 四象限。
曲线形状
图像同样是由两支分别位于第二和第四象限的曲 线组成,这两支曲线也关于原点对称。
图像的性质。
总结
反比例函数的图像性质与 $k$ 的 正负有关。当 $k > 0$ 时,图像 位于第一、三象限;当 $k < 0$
时,图像位于第二、四象限。
涉及综合应用问题
01
例题5
已知反比例函数 $y = frac{k}{x}$ 的图像与一次函数 $y = ax + b$ 的
图像交于点 $M(2,1)$ 和 $N(-1,-2)$,求这两个函数的解析式。
反比例函数的极限与连续性问题
讨论反比例函数在特定点的极限行为,以 及在定义域内的连续性。
反比例函数与其他函数的复合问 题
研究反比例函数与其他基本函数(如幂函 数、三角函数等)的复合性质及图像特征 。
THANK YOU
06
总结回顾与拓展延伸
重点知识点总结回顾
反比例函数图像的基本性质
反比例函数图像为双曲线,当k>0时,图像位于第一、三象限;当k<0时,图像位于第二 、四象限。
k的几何意义
k的绝对值表示双曲线与坐标轴所围成的矩形的面积。当k>0时,矩形在第一象限;当 k<0时,矩形在第二象限。
反比例函数图像的对称性
通过中心对称性,我们可以更好 地理解反比例函数的性质和行为 ,以及它在解决实际问题中的应
反比例函数图象性质及应用复习课件
04
反比例函数的实际应用案 例
电流与电阻的关系
总结词
电流与电阻成反比关系,当电阻增大时,电流减小;反之亦然。
详细描述
在电路中,电流与电阻之间的关系表现为反比例关系。当电路中的电压保持恒定时,电阻的阻值增大,会导致电 流减小;反之,如果电阻的阻值减小,电流则会增大。这一关系在电子设备和电路设计中具有重要应用。
答案解析
针对每个练习题,提供 详细的答案解析,帮助 学生理解解题思路和过
程。
感谢您的观看
THANKS
表达式
一般形式为 y = k/x,其中 k 是 常数且 k ≠ 0。
图像特点
双曲线
反比例函数的图像是双曲线,分布在两个象限内。
渐近线
图像分别渐近于 x 轴和 y 轴。
变化趋势
随着 x 的增大或减小,y 的值会无限接近于 0 但永远不会等于 0。
渐近线与对称性
渐近线
对于反比例函数 y = k/x (k > 0),其图像在第一象限和第三象限内,当 x 趋于正无穷 或负无穷时,y 值趋于 0,因此渐近于 x 轴;当 y 趋于正无穷或负无穷时,x 值趋于 0 ,因此渐近于 y 轴。对于 k < 0 的情况,图像在第二象限和第四象限内,渐近线为 y
反比例函数图象性质及 应用复习ppt课件
目录 CONTENT
• 反比例函数的基本性质 • 反比例函数的图像绘制 • 反比例函数的应用场景 • 反比例函数的实际应用案例 • 反比例函数与其他知识点的关联 • 复习与巩固
01
反比例函数的基本性质
定义与表达式
定义
反比例函数是指形如 y = k/x (k ≠ 0) 的函数,其中 x 是自变量, y 是因变量。
人教版初三数学9年级下册 26.1.2反比例函数的图象和性质反比例函数k的几何意义 课件(17张)
变式练习:
(1)(娄底中考数学)已知:如图,点M是反比例 函数 (x>0)的图象上任意一点,MN丄y轴于点
N,点P是x(轴1) 上的一个动点,则△MNP的面积
是
1。
(2)( 永州中考)
3 2
S△AOB =S△AOC -S△BOC
C
=6 3
22
=3 2
(3)(苏州)如图:点A是反比例函数
(y x<x6 0)的图象上的
课题:反比例函数k的几何意义
科目:数学 年级:初三年级 主讲人:
反比例函数K的几何意义
(一)基本图形1及其应用:
(x,y)
例1:如图,点A在双曲线
y
4 xபைடு நூலகம்
上,点B在双曲线y
k
x(k≠0)
上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,
若矩形ABCD的面积是8,则k的值为 1__2__。
• 解:∵双曲线 y (k k≠0)在第一象限,∴k
>0,
x
• 延长线段BA,交y轴于点E,
• ∵AB∥x轴,
E
• ∴AE⊥y轴,
• ∴四边形AEOD是矩形,
• ∵点A在双曲线上,
• ∴S矩形AEOD=4, • 同理S矩形OCBE=k, • ∵S矩形ABCD=S矩形OCBE-S矩形AEOD=k-4=8, • ∴k=12.
一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在
y轴上,则平行四边形ABCD的面积为( )C
A.1 B.3 C.6 D.12
(二)基本图形2及其应用:
图中面积相等的图形有哪些?
例2:如图,点A、B、是双曲线
y3 x
上的点,分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于A、B两点,连接OA、OB,则△AOB的面积为( A)
A. 3
B.2
C.3
D.1
2
C
PPT学习交流
9
趁热打铁,大显身手(提高篇)
3.(2012湖北孝感) 如图,点A在双曲线 y 1 上,点B在双曲线 y 3上,且AB∥x轴,C、 x D在x轴上,若四边形ABxCDy形OP(A1,Py)B的面积=6____ B
BB
AO A
P(3,y) P(5,y)
A Ax
结论:从双曲线上任意一点向x、y轴分别作垂线段,两 条垂线段与两坐标轴所围成的矩形的面积=︱k︱.
PPT学习交流
2
推广:反比例函数与三角形面积
过P作x轴的垂线,垂足为A,则它与坐标轴形成的 三角形的面积是不变的,为:
AP⊥x轴于点P,已知△AOP的面积3,则k的值是( B )
A. 6 C.-3
B. -6 D. 3
y AP
♦像这样的图形变换叫等积变换
CP O
x
PPT学习交流
8
趁热打铁,大显身手(提高篇)
y 2.(2012辽宁)反比例函数
y
6 x
与
3 x
在第一象限
的图象如图所示,作一条平行于x轴的直线分别交双曲线
S OA 1 2 P OA A P 1 2|m |•|n|1 2|k|
y
P(m,n)
oA
x
PPT学习交流
3
一 千里之行 始于足下
1.如图,点P是反比例函数 y 图2象上的一
x
点,PD⊥x轴于D.则△POD的面积为 1.
y
P
oD
x
PPT学习交流
4
2.如图,点A,B是双曲线 y 上3 的点,过点A
轴的垂线,图中所构成的阴影部分的面积从左到右依次为
S1,S2,S3 ,则
y
3
S1S2 S3 2 .
y 2 (x>0) x
P1
思考:1.你能求出S2和S3的值吗?
11
P2
36
P3
P4
2.S1呢? 1
O
x
1 23 4
PPT学习交流
7
二、趁热打铁,大显身手
1. 已知点A是反比例函数y k 上的点,过点A作 x
x
、B两点分别向x轴、y轴作垂线,若S阴影
=1,则S1+4S2=
y
A
S1 B
S2
O
x
PPT学习交流
5
4.如图 ,在y1(x0)的图像上有A,三 B,C点 , x
经过三点分x轴 别引 向垂,交 线x轴于 A1,B1,C1三点 ,
边结 OA,OB,OC,记OA1A,OB1B,OC1C的
面积分别 S1,为 S2,S3,则有_A_.
A
△ABC的面积是1____
△ABD的面积是224____
OC
四边形ADBE
♦对称性
反比例函数的图象 是关于原点成中心
x 对称的图形
的 48
B
D
面积是____
PPT学习交流
12
四.中考题型精选
PPT学习交流
13
PPT学习交流
14
课堂小结
反比例函数中的面积问题
以形助数 用数解形
一个性质:反比例函数的面积不变性
两种思想:分类讨论和数形结合
PPT学习交流
15
作业布置
1 若A(m,n)是反比例函数图象上的一动点,其中0<m<3, 点B的坐标(3,2),过点A作直线AC∥x轴,交y轴于点C;过 点B作直线BD∥y轴交x轴于点D,交直线AC于点E,当四边形 OBEA的面积为6时,请判断线段AC与AE的大小关系,并说明
PPT学习交流
10
趁热打铁,大显身手(提高篇)
4.(2011年陕西)如图,过y轴正半轴上的任意一点P,作x
轴的平行线,分别与反比例函数y=- 4 和y= 2 图象交于点
x
x
A和点B.若点C 是x轴上任意一点,连接AC、BC,则△ABC的面
积为 ( A )
A.3
B.4
C.5
D.6
PPT学习交流
11
想一想
反比例函数中“k”的几何意义
y
B P(m,n)
oA x
y
y
P(m,n)
E
C
B
F
oA x
x
O
A
PPT学习交流
1
反比例函数与矩形面积
如图,是y=6/x的图象,点P是图象上的一个动点。
1、若P(1,y),则矩形OAPB的面积=___6______ 2、若P(3,y),则矩形OAPB的面积=____6_____ 3、若P(5,y),则矩形OAPB的面积=____6_____
1、如图反比例函数y=12/x与正比例函数y=kx相交于点A、点B。
(1)点A与点B关于点___O__对称,相等的线段有_O__A__=___。
(2)若点A的坐标是(a,b),则点B的坐标是_(_-_aO_,_-B_b_)__
(3)AC⊥x轴,则△OAC的面积是6
(4)_连___接BC,则
y
△OBC的面积是6____,E
理由。
y
2、已知反比例函数y=12/x与 一次函数y=kx-7的图象都经 过点 P(m,2),函数y=kx-7的
AE C
图象交y轴于点Q.试求这个一
B
次函 数的解析式及△OPQ的 面积。
o
D
x
PPT学习交流
16
教师寄语
•悟性的高低取决于有无悟“心”,其 实,人与人的差别就在于你是否去思 考, 去发现,去总结。
y
A.S1 = S2 = S3 B. S1 < S2 < S3 C. S3 < S1 < S2 D. S1 > S2 >S3
A
S1
B C
S2 S3
o A1 B1 C1
x
PPT学习交流
6
4.如图,在反比例函数y
2 x(x>0)
的图象上,有点 P1,P2,P3,P4
,它们的横坐标依次为1,2,3,4.分别过这些点作 x轴与 y
PPT学习交流
17
