第3章 分离过程中的动力学汇总
第三章 玻璃分相与析晶汇总

· 特点:由成核剂或二液相的界面可使界面能降低, 从而影响临界形核功G *, 较小的过冷度就能成核
非均匀成核临界成核位垒 GK* 与接触角的关系。
GK* G*. f ( ) 液体
f ( ) (2 cos )(1 cos )2
· 定义:在宏观均匀的玻璃体中,没有外来物质参与, 在基质内部而与相界、缺陷等无关的成核过程。(自发 成核、本征成核)
· 热力学条件 G<0
假设晶核为球。 G=4/3 r3G+4r2 体积自由能:形成晶核所释放出的能量,使体系自由 能减小。 G 单位体积自由能变量 形成新相所需界面能(克服表面张力)
四、分相的原因
结晶化学理论:
分相的原因是 :玻璃结构中阳离子对氧的争夺
M或I的配位结构与F不同,高场强离子较多时易分相。
不同阳离子的离子势:
Cs+ 0.61
1700
Rb+ 0.67
℃
K+
0.75
1650
Na+ 1.02
Li+ 1.28
1600
Ba2+ 1.40
1550
Sr2+ 1.57
Ca2+ 1.89
分相范围 亚稳分相区范围:自 由焓-组成曲线的各 切点轨迹相连范围; 不稳分相区:各曲线 的拐点轨迹相连的范 围。
4 亚稳定区与不 稳区的分相机理
(2G/C2)T、P 判断由于过 冷液相(熔 融体)的分 相是亚稳的 还是不稳的。
当( 2G/C2) T、P>0时,系统单相液相对微小的组 成起伏是亚稳的,分相如同析晶中的成核-生长, 需要克服一定的成核能垒才能形成稳定的核,而后 新相继续扩大。如果系统不足以提供此能垒,系统 将不分相而呈亚稳态。 当(2G/C2) T、P<0时,系统单相液相对微小的组成 起伏是不稳定的,组成起伏由小逐渐增大,初期新 界面弥散,因而不需克服任何能垒,分相是必然发 生的。
第三章化学动力学初步

限速步骤(定速步骤):在一连串的反应中,较慢的基元反应限 制 了整个反应的速率,这一步骤称为限速步骤。
4
3.2 反应速率理论简介 速率理论简介 论简
3.2.1有效碰撞理论
1.反应速率正比于反应物分子的碰撞次数υ∝Z0c(NO)c(O3) 2.反应物分子必须定向碰撞才可能发生反应 有效碰撞
无效碰撞
υ∝PZ0c(NO)c(O3)
10
3.4 反应速率与温度的关系
3.4.1 范特霍夫 范特霍夫(Van’t Hoff)近似规则 近似规则 近似
反应体系的温度每升高10 K,化学反应速率将增加到原来的 k T + n ⋅10 2~4倍。 k T + 10 =γn =γ
kT
kT
γ:温度系数;一般为2~4,k:各温度下的反应速率常数。
9
表3.2 cA和cB及反应速率v
∴根据实验结果可知:m = 2,n = 1 反应的速率方程为υ =kcA
2c D
反应的级数:m + n =
3
说明 (1)常见反应级数:零、一、二级反应,三级反应少见,三级以上 反应无。 (2)反应级数可为零、正整数、分数, 反应级数不同K的单位不同。 (3)复合反应可由限速步骤写出速率方程。
单位是J·mol-1 。
上式两边取自然对数,得:
Ea ln k = ln A − RT
Ea lg k = lg A − (3.6) 2.303RT
【例3-1】对下列反应C2H5Cl(g)→C2H4(g) + HCl(g),已知 A=1.6×1014,Ea=246.9 KJ·mol-1,求700 K时的速率常数。如果 反应温度升高到710 K时,计算速率常数,并与700 K时的速率常 数做比较。
第三章 化学反应动力学的计算
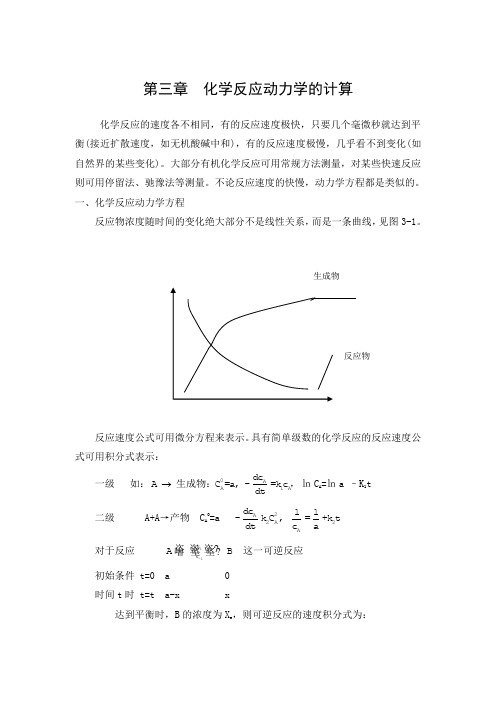
第三章 化学反应动力学的计算化学反应的速度各不相同,有的反应速度极快,只要几个毫微秒就达到平衡(接近扩散速度,如无机酸碱中和),有的反应速度极慢,几乎看不到变化(如自然界的某些变化)。
大部分有机化学反应可用常规方法测量,对某些快速反应则可用停留法、驰豫法等测量。
不论反应速度的快慢,动力学方程都是类似的。
一、化学反应动力学方程反应物浓度随时间的变化绝大部分不是线性关系,而是一条曲线,见图3-1。
反应速度公式可用微分方程来表示。
具有简单级数的化学反应的反应速度公式可用积分式表示:一级 如:0AA1Adc A C =a, -=k c dt 生成物:,㏑C A =㏑a –K 1t 二级 A+A →产物 C A 0=a 2A 2A 2A d c 11-k C , =+k t d t c a对于反应 1-1k k A B 这一可逆反应初始条件 t=0 a 0 时间t 时 t=t a-x x达到平衡时,B 的浓度为X e ,则可逆反应的速度积分式为: 级数:1-1 1-10k A A e e 1A -1B k 0e 0C =a dc x xA B=-k C +k C : =kt dt a x -xC =0ln 1-21-10Ak0A e e e B 1A -1B C k e e 0CC =a dc x ax +x(a-x )A B+C C =0=-k C +k C C : =kt dt 2a-x a(x -x)C =0ln 二、常微分方程的解化学反应动力学方程是用微分方程表示的,对于简单的反应,可直接求得微分方程的解。
微分方程:()(1)(,,,......)......(1)n n y f x y y y -'=在区间a<x<b 的解,是指()y x ϕ=,这样一个函数,在所述区间内存在导数()(),(),......()n x x x ϕϕϕ'''。
且对于区间a<x<b 内的每一个x ,等式(1)都成立。
《化工原理》第3章 非均相物系的分离

20
第3章 非均相物系的分离
图3-15表示分配头的结构。此分配头由一随转鼓转动的 转动盘和一固定盘所组成。
1.转动盘 2.固定盘 3.与真空管路相通的孔隙 4.与洗涤液贮槽相通的孔隙 5、6.与压缩空气管路相通的孔隙 7.转动盘上的小孔 图3-15 分配头
21
图3-17 气体在旋风分离器中的运动情况
25
第3章 非均相物系的分离
2.旋液分离器 旋液分离器是一种利用 离心力的作用分离悬浮液的 设备。其结构和原理和旋风 分离器相似。如图3-18所示, 设备主体是由圆筒和圆锥两 部分构成。
1.悬浮液入口管 2.圆筒 3.锥形筒 4.底流出口 5.中心溢流管 6.溢流出口管 图3-18 旋液分离器
我们从过滤速率式出发,求出过滤的推动力和阻力,然后 对上式进行积分即可得到滤液量V与过滤时间τ之间的关 系,即过滤基本方程式。
13
第3章 非均相物系的分离
2.恒压过滤方程式 过滤操作可以在恒压、恒速,先恒速后恒压等不同条件 下进行,其中恒压过滤是最常见的过滤方式。连续过滤机上 进行的过滤都是恒压过滤,间歇过滤机上进行的过滤也多为 恒压过滤,因此,我们重点讨论恒压过滤方程式。 恒压过滤时滤液体积与 过滤时间的关系为一抛物线 方程,如图3-8所示。
第3章 非均相物系的分离
3.1 概述 3.2 重力沉降 3.3 过滤 3.4 离心分离
第3章 非均相物系的分离
3.1 概述
在化工生产中,经常遇到混合物的分离过程。混合物可 分为两大类,即均相混合物(或均相物系)和非均相混合物 (或非均相物系)。 若物系内各处组成均匀且不存在相界面,则称为均相混 合物(或均相物系)。如溶液及混合气体都属于均相物系。 均相物系的分离可采用蒸发、精馏、吸收等方法。若物系内 有相界面存在且界面两侧的物质的性质截然不同,这类物系 称为非均相混合物(或非均相物系)。如含尘气体和含雾气 体属于气态非均相物系;悬浮液、乳浊液、泡沫液等属于液 态非均相物系。
第3章-药物代谢动力学

D:用药总量。
绝对生物利用度:同一制剂,不同给药途径的AUC
(五)体内屏障
1. 血-脑屏障
脑组织毛细血管内皮细胞间连接紧密,外 表面几乎全部为星形胶质细胞所包围。许多 分子量大、极性高的药物不能穿透,脂溶性 高或分子量小的药物可透过。
Blood-brain barrier limits drug access to brain
(五)体内屏障:
2. 胎盘屏障
2.易化扩散
顺差转运 不消耗能量
需要载体 具有饱和性 具有竞争性
第二节 药物的体内过程
吸收(Absorption) 分布(Distribution) 代谢(Metabolism) 排泄(Excretion)
LOCUS OF ACTION
“RECEPTORS”
Bound
Free
TISSUE RESERVOIRS
药物的影响而出现增强或减弱现象。
药酶诱导药:凡能够增强药酶活性的 药物(巴比妥类、苯妥英钠、利福平 等)。合用时,使其他药效力下降,并 可产生耐受性,应增加其他药的剂量。
药酶抑制药:凡能够减弱药酶活性的 药物(异烟肼、西咪替丁、保泰松等)。 合用时,使其他药效力增强,并可产生 中毒,应减少其他药的剂量。
简单扩散
顺差转运 不消耗能量
无需载体 无饱和性 无竞争性
简单扩散的条件:脂溶性、解离度、浓度差。
绝大多数药物为弱酸性或弱碱性,均有解离型
与非解离型,后者脂溶性高。
现以弱酸性药物为例说明(H-H方程)
HA
H+ + A-
Ka = [H+][A-]
[HA]
- lgKa= -lg [H+][A-] [HA]
分离工程期末知识总结

思考题
1. 什么叫泡点,什么叫露点? 2. 精馏塔塔顶的温度和塔釜的温度分别是什么? 3. 简述求解泡露点的思路? 4. 对于泡点温度,∑Kixi <1,应如何调整温度? 5. 怎样判断闪蒸问题在给定的T、P下是否成立? 6. 等温闪蒸的通用闪蒸方程(Rachford-Rice方程
)的形式。
第三章 多组分精馏
特点:★F=D=W=0
★ L=V;L/V=1
★操作线方程: yn1 ,i xn,i
★板效率 最高
由于全回流,用 N m表示N,省去“均”:
Nm
lg([
x x
A B
)D
(
x x
A B
)W
lg AB
]
(3 8)
— — Fenske方程
最少理论板数只与分离要求有关,与进料组成无关。
多组分精馏
分离工程
第一章 绪论
分离过程基本概念 定义:将一混合物转变为组成不相同的两种或 两种以上产物的操作。
分离工程示意图
分离剂 (物质或能量)
原料物流 (一股或几股)
分离装置
产品1 (组成不同的物流) 产品2
第一章 绪论
分离过程的分类
分离过程分为机械分离过程和传质分离过程两大 类。
机械分离过程是指分离装置所接受的是多于一个 相的非均相进料,只要简单地分相就可以。如过 滤、沉降、固-液分离和气-液分离器等。
no yes
T,yi
第二章 单级平衡过程
露点计算
平衡常数与组成无关的露点计算 ki f (T , P) 露点方程: f (T ) iC1Kyii 1.0 0 (2 60)
f (P) iC1Kyii 1.0 0 (2 61)
化工分离过程__第3章 第一讲 设计变量的确定

进料变量数: 2(C+2) 压力等级数: 1 +) 2C+5
F1 F2 QW
塔内无压降
N
u a
分配器数: 1 侧线采出: 1
传热单元: 2 串级数: 4 8
+)
34
3.2 多组分精馏 Multicomponent Distillation
3.2.1 多组分精馏过程分析 (Process Analysis)
自学p66例3-2双塔共沸精馏流程
28
例2. 双塔共沸精馏流程
Nx
进料变量数: 压力等级数:
原料 蒸汽
4+3 1 8
+)
N
u a
分配器数: 侧线采出: 传热单元: 串级数:
0 0
2
3 5 +)
29
5个可调设计变量的选择
情况(1): 三个串级各自的级数 3; 再沸器的蒸发速率 1; 冷凝器的过冷温度 1。 情况(2): 异丙醇塔釜液中异丙醇的摩尔分数 1; 水塔釜液中异丙醇的摩尔分数 1; 异丙醇塔的最适进料位置 1; 再沸器的蒸发速率 1; 冷凝器的过冷温度 1。
N =N +N
e D e x
e a
固定设计变量Nx 可调设计变量Na =ND-Nx
L1
L L2
Nx
= 进料物流变量数+系统的压力
分配器
固定设计变量Nx = 进料+压力=(C+2)+1
分配比
可调设计变量Na = ND-Nx=(C+4)-(C+3)=1
13
例2. 产物为两相的全凝器 NVe
出入物流变量数: 3(C+2) 能量交换数: 1 +) Nv = 3C+7
环境工程学(王玉恒)重点-第3章 第2(2)节 活性污泥系统生物过程动力学

回流污泥:R——污泥回流比;XR— 回流污泥浓度(MLVSS);
剩余污泥: Qw—剩余污泥排放量;
出水:Xe——出流水中带走的微生物浓度;
S、X 稳定不变。
2021/6/18
5Hale Waihona Puke 劳伦斯-麦卡蒂数学模型※污泥泥龄:又称微生物平均停留时间,是指反应 系统(曝气池)内的微生物全部更新一次所用的时间, 在工程上,就是指反应系统内总的活性污泥质量与每日 排出的活性污泥质量之比。以θC表示,单位为d。
Qw,Se,XR
C
XV
(QQw)Xe QwXR
在一般条件下,Xe值可以忽略不计,上式可简化为:
※※
XV
C Qw XR
XV X
应用时注意 污泥浓度单位的统一
2021/6/18
7
【例】某活性污泥系统曝气池容积1000m3, 污泥浓度
MLSS=3000mg/L。若该系统污泥泥龄为10d,排放剩余污泥含
(1+R)Q S,X
回流污泥
二沉池
出水 (Q-QW),S,Xe
剩余污泥
RQ,XR
Qw,XR
进水:Q —进水流量; S0—进水有机底物浓度;X0—进水微生物浓度 曝气池:S—曝气池有机底物浓度;X—曝气池中微生物浓度(注意:挥发性
悬浮固体浓度, MLVSS); V—曝气池体积;
进入二沉池中的混合液物质组成与曝气池中混合液一致;
1
c
Y
1 d S
X dtu
Kd
(2)
Y— 活性污泥产率系数,kgVSS/kgBOD;
Kd—内源代谢系数; dS — 底物降解速率,kgBOD/(m3 d)。
dt u
2021/6/18
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式(3.13)即为普朗克 - 爱因斯坦(Planck - Einstein)方程,有:
J =- RT dc =-D dc f dx dx
(3.14)
式(3.14)即为费克(Fick)第一扩散定律,是早在1855年就
已发表的描述分子扩散的基本方程。费克第一扩散定律
的通式可以写成:
J (x)=-A dy dx
生物分离工程-第2章:分离过程的动力学
第3章 分离过程中的动力学
分子迁移-费克第一扩散定律 流体的迁移与扩散 带的迁移-费克第二扩散定律 有流存在下的溶质输运
生物分离工程-第2章:分离过程的动力学
一个体系在达到平衡之前,体系内存在各种梯度,有外场 作用下的梯度,如压力梯度、浓度梯度、电位梯度和温度 梯度,也有体系内部的分子间相互作用引起的化学势梯度;
生物分离工程-第2章:分离过程的动力学
与宏观物体的机械运动相比,溶质分了在溶液中的运动 加速度几乎为零(几乎是立即达到稳态)。因此,处理分子 运动时可以认为其平均加速度为零,即:
d2 x M dt2 =0 由分子运动方程可得:
d2 x d d x
M
dt 2
=- - f dx
dt
=0
分子运动的平均速度为:
J =- c d =- c d(ext + +RT ln c)
f dx f
dx
=-
c f
d ext
dx
+
d
dx
+
RT c
dc dx
c d ext d RT dc
=-
f
dx
+
dx
f
dx
生物分离工程-第2章:分离过程的动力学
如果定义:
Y
=-
c f
d ext
dx
+
d
dx
物质的扩散运动也是在梯度(浓度梯度)驱动下,物质分子 自发输运的过程;
扩散速度的差异可使某些组分达到分离,但也会使组分的 谱带展宽;
无论是定向迁移还是非定向扩散,涉及的都是物质分子的 迁移,因此分子迁移的表征是研究分离过程的基础
生物分离工程-第2章:分离过程的动力学
机械运动是指宏观物体的运动,其运动规律可以用牛顿流体
摩擦系数f 的加和,即 f =NA f。 所有分离过程都在不同程度上对物质(溶质)进行输运, 分离所需时间与输运时间有关,因而也与摩擦系数有关。
Stokes定律描述了分子运动摩擦系数与其它因素的关系,
即:f =6 NAr
(3.8)
式中,f 为摩尔摩擦系数;NA为阿伏加德罗常数;r为球形
溶质分子的半径;为介质黏度。
在分离过程中,溶质分子在外场或内部化学势作用下趋于 平衡的方向定向迁移,在空间上重新分配;
与此同时,溶质分子的随机运动又会使溶质分子从高浓度 区域向四周低浓度区域扩散,使分离开的溶质又趋向重新 混合;
定向迁移与非定向扩散,即分离与混合,是两种相伴而生 的趋势;
分离过程中动力学的研究内容就是物质在输运过程中运动 规律,即分离体系中组分迁移和扩散的基本性质和规律。
(3.6)
如果将宏观物体运动的方程用来描述分子运动,则得到
分子运动方程为:
d2 x d dx
M
dt 2
=- - f dx
dt
(3.7)
生物分离工程-第2章:分离过程的动力学
上式中以1mol物质计,M 为物质的摩尔质量;x表示整个
1mol分子(粒子)运动的位移平均值;f 表示每摩尔运动着 的分子的阻力常数,即摩尔摩擦系数,它是所有分子的
U = dx =- 1 d
(3.9)
dt f dx
生物分离工程-第2章:分离过程的动力学
因为分子或离子的运动速度难于测定,所以人们提出了
一个易于测定的物理量-流密度(J )-来反应分子在液体中 的运动速度。流密度是指单位时间内Βιβλιοθήκη 过单位面积的物 质的量(mol)。
当分子运动的平均速度U的单位为cm/s,溶质的浓度c的 单位取mol/cm3时,有下列关系式:
路径上的位置。
生物分离工程-第2章:分离过程的动力学
宏观物体的机械运动规律可以用牛顿定律来描述。根据
牛顿运动规律,力F与加速度的关系为:
F
=
F1
+
F2
=
m
d2 dt
x
2
(3.3)
这个微分方程可以被积分并可表示物体在不同时间的瞬
间位置。式中,m为物体的质量;d2 dt
x
2
为加速度,F1为
机械推动力,其大小由物体的位置决定,F2为摩擦力,
J =Uc
(3.10)
将式(3.9)代入(3.10)中得:
J =- c d
f dx
(3.11)
生物分离工程-第2章:分离过程的动力学
在低浓度下(假定 =c),化学势可以写成
= ext + +RT ln c
式中, ext为外场作用于分子(粒子)上的化学势; 为
体系的标准化学势;c为溶质浓度,假定其在扩散方向 不随时间变化,于是有:
定律描述;分子迁移是指分子的运动,研究其运动规律不是
研究单个分子的运动规律,而是研究大量分子(粒子)在统计学
上的规律,这两种运动的共同点在于他们对力的响应以及数学
表达式相似:
机械运动推动力= dp
(3.1)
dx
分子运动推动力= d
(3.2)
dx
式中,p为势能;为化学势,且p和具有相同的量纲;x为迁移
(3.15)
式中,J(x)表示沿x轴方向的流;A为比例系数;dy 指在x轴 dx
方向上的梯度。当y为浓度c时,dc 为x轴方向上的浓度梯度。 dx
生物分离工程-第2章:分离过程的动力学
3.1 分子迁移-费克第一扩散定律
所有溶质的迁移都是朝着趋向平衡的方向进行的,平衡控 制着组分的迁移方向。但仅用平衡的观点无法准确回答组 分的迁移速度和迁移性质的问题,而迁移速度与整个分离 速度是密切相关的;
物质的输运过程是指在适当的介质中,在化学势梯度的驱 动下物质分子发生相对位移的过程;
其大小与摩擦系数f 成比例,在运动速度较低时,与 dx dt
成正比,故以负号表示。
生物分离工程-第2章:分离过程的动力学
F1
=-
dp dx
(3.4)
F2 =-f
dx dt
(3.5)
将式(3.4)和(3.5)代入(3.3)。得到宏观物体基本运动方程:
d2 x dp dx
m dt2
=- -f dx
dt
Y是外场和内部物理化学作用的总化学势产生的迁移
速度。将Y代入公式有:
J =Yc- RT dc f dx
(3.12)
当外场和内部作用势能梯度为零(Y = 0)时,就只存在
扩散运动了,此时有:
J =- RT dc f dx
定义扩散系数D为:
D= RT f
(3.13)
生物分离工程-第2章:分离过程的动力学
