第2章(分离过程动力学)
化工分离工程第2章 单级平衡过程

FLGC
• 活度系数法通式
fˆi L
i
xi
fiL
i
xi
is
Pi s
expVi L
(P RT
Pi s
)
yiˆiv
P
i
xiis Pi s
expVi L
(P RT
Pi s
)
i 1,2,, N
低压至中压
expVi
L
(P RT
Pi
s
)
1
yiˆiv P
xi
s
ii
Pi
s
i 1,2,, N
(2-7)
11
FLGC
两种常用的汽液相平衡关系表达式:
(2-5)式和(2-6)式代入(2-4),得 ˆiV yi p ˆiL xi p (2-5)式和(2-7)式代入(2-4),得 ˆiV yi p i xi fiOL
12
FLGC
二、相平衡关系的表示方法:
1. 相图 yi
主要用来表示二元组分体系的相 平衡关系,包括恒压下的t-x图和 y-x图,以及恒温下的p-x图。
i
④判定 | 1 S y | 是否接近0,是,得到Tb=T和Ki;否,按以下方式调整
T。
⑤ S y 1,T偏大,调小; S y 1,T偏小,调大;调整后返回②。
FLGC
一、泡点温度的计算
1. Ki与组成无关: Ki f (T, P)
泡点方程:
f
T
C
Ki xi
1
0
i 1
假定T
已知P 得到Ki 调整T
3
FLGC
• 相平衡,是研究多相平衡体系的状态如何随温度、 压力、组成的变化的科学。
第0章(绪论)

分离方法分类(按分离过程实质)
3.反应分离过程—促进化学反应达到分离
反应分离操作
反应体 再生型 有反应体 一次性 反应类型 可逆的或平衡交换反应 不可逆反应分离 分离反应 (螯合)离子交换反应、反 应萃取、反应吸收 反应吸收、反应晶析、中 和沉淀、氧化还原
生物体
无反应体 电化学反应
活性污泥
湿式精炼
浓缩
纯化
0.1-0.9
>0.9
分离科学(separation science)
研究从混合物中分离、纯化或富集某些组分以获 得相对纯物质的过程的规律、仪器制造技术及其 应用的一门学科。 分离科学已成为一门独立的新学科
(分离科学系、分离科学专业、分离科学杂志)
分离的目的
确认对象物质或准确测定其含量; 获取单一纯物质或某类物质以作它用; 浓缩(富集)某个或某类物质; 消除干扰,提高分析方法选择性和灵敏度。
分离的两种形式
1. 组(族)分离—将性质相近的一类组分一起分离 石油炼制中的轻重油分离; 中药有效部位的分离。 2. 单一分离—将某一组分以纯物质形式分离出来 工业上纯物质的制备; 化学标准品的制备;
药物对映异构体的分离。
单一分离的结果
相互完全分离
(a,b,c,……) (a) + (b) + (c) + ……
利用混合物中各组分在物理或化学性质上的差异,通过 适当的装置或方法,使各组分分配至不同的空间区域或 者在不同的时间依次分配至同一空间区域的过程。
富集(concentration)
通过分离过程,使目标物质在某空间区域的浓度增大。
从大量基体物质中将欲测量的组分集中到一较小体积的 溶液中,从而提高检测灵敏度。
分离过程的分类

第一章 绪论分离过程的分类:机械分离、传质分离机械分离:处理两相以上的混合物如过滤、沉降、离心分离等 传质分离:处理均相混合物传质分离可分为:平衡分离过程如精馏、吸收、萃取、结晶、吸附等,借助分离剂使均相混合物系统变成两相系统,再利用混合物中各组分在处于相平衡的两相中的不等同分配而实现分离。
速率分离过程如微滤、超滤、反渗透、电渗析等,在某种推动力(浓度差、压力差、温度差、电位差等)的作用下,利用各组分扩散速率的差异实现分离。
分离媒介:能量媒介ESA 、质量媒介MSA第二章 单级平衡过程相平衡关系:混合物所形成的若干相保持物理平衡而共存的状态。
热力学:整个物系的自由能最小。
动力学:相间表观传递速率为零。
相平衡条件(准则):各相的温度相等、压力相等,每个组分的化学位相等。
相平衡常数:i i i x y K /= 分离因子:ji j i j i ij K K/x x /y y ==α,平衡分离过程,常采用分离因子表示平衡关系。
相对挥发度对温度和压力变化不敏感,常视为常数,简化计算。
分离因子与1的偏离程度表示组分间分离的难易程度。
相平衡方程:C 个 C 1,2,...,i ==i i i x K y 摩尔分率加和方程:2个0.11=∑=Cii x0.11=∑=Cii y汽液平衡常数关联式: C 个 C 1,2,...,i ),,,(==y x P T f K i 泡点方程: ()011=-=∑=Ciii x K Tf泡点压力的计算:泡点方程: ()011=-=∑=Ciii x K pf露点方程:()0.1/1=∑=cii i K y 闪蒸过程:连续单级蒸馏过程。
它使进料混合物部分汽化或冷凝得到含易挥发组分较多的蒸汽和含难挥发组分较多的液体。
物料衡算—M 方程 C 个 ,...C ,i Vy Lx Fz i i i 21=+= 相平衡—E 方程 C 个 C i x K y i i i ,...2,1== 摩尔分率加和式—S 方程 2个11=∑=Cii x11=∑=Cii y热量平衡式— H 方程 1个 L V F LH VH Q FH +=+设计前需预先给定数值的变量称为设计变量。
大学物理学第2章 动力学

受力分析涉及变力的情况
例1 如图长为 l 的轻绳,一端系质量为 m 的小球,
另有一水端平系 速于 度定v0点,o求,小t球在0任时意小位球置位的于速最率低及位绳置的,张并力具.
解 FT mg cos ma n
mg sin ma
FT mg cos mv2 / l
mm
1.图中A为定滑轮,B为动滑轮,三个物体的质量分
别 为 m1=200g , m2=100g , m3=50g , 滑 轮 及 绳 的 质 量 以及摩擦均忽略不计。求:
(1)每个物体的加速度;
(2)两根绳子的张力T1与T2。
A
T T 求a1:
a1 T1
a1
m1g (m2 m3 )g m1 m2 m3 a1 m1
直角坐标系:
F Fxi Fy j Fzk
a
axi
a
y
j
az
k
Fx max
Fy may Fz maz
Fx
max
m dvx dt
d2x m dt2
Fy ma y
m dvy dt
m
d2 dt
y
2
Fz
ma z
m dvz dt
(a) F=(m+M)g
(b) F>(m+M)g
F
(c) F=0
(d) F<(m+M)g
(d)
m M
如图所示,一只质量为m的猫,抓住一根竖直悬吊的 质量为M的直杆。当悬线突然断开时,猫沿杆竖直向 上爬,以保持它离天花板的高度不变。在此情况中, 杆具有的加速度应是下面的哪一个答案?
3--第二章色谱分析理论基础
当待分离组分随着载气进入色谱柱,组分就开始在两相间进行 分配,平衡后,再随着载气进入下一个塔板进行分配,平衡后 再进入下一个塔板。以此类推,从而不断达到分配平衡。
1.塔板理论基本假设
(1)在色谱柱中的每一小段长度H内,组分迅速达到分 配平衡,这一小段色谱柱称为理论塔板,其长度称为理论 塔板高度,简称板高,记为H; (2)载气不是连续通过色谱柱,而是脉冲式,每次进气 量为一个板体积; (3)试样开始时都加在0号塔板上,且试样沿柱纵向扩 散忽略不计; (4)分配系数在各塔板上是常数; (5)塔板与塔板之间不连续。
结论: 分配系数K是色谱分离中的一个重要参数。 两组分分配系数K相差越大,两峰分离的就越好。 不同物质的分配系数K相同时,组分不能分离。因此是色 谱分离依据。
3.分配比k
又叫容量比、容量因子。
在一定温度、压力下,在两相间达到分配平衡时,组分在 两相之间的质量比值,以k表示。
组分在固定相中的质量
k=
分子扩散大。
3.传质阻力项C
组分在气相和液相两相间进行反复分配时,遇到阻力。传质阻 力C包括气相传质阻力Cg和液相传质阻力CL 。液相传质阻力 大于气相传质阻力。
C =(Cg + CL)
气相传质过程是指试样组分从气相移动到固定相表面的过程。
这一过程中试样组分将在两相间进 行质量交换,即进行浓度分配。有 的分子还来不及进入两相界面,就 被气相带走;有的则在进入两相界 面后又来不及返回气相。这样,使 得试样在两相界面上不能瞬间达到 分配平衡,引起滞后现象,从而使 色谱峰变宽。
(3)对于某确定的色谱分配体系,组分的分离最终决定于 组分在每相中的相对量,而不是决定于组分在每相中的相对 浓度,因此分配比是衡量色谱柱对组分保留能力的重要参数。 k越大,组分保留时间越长,k=0,组分的保留时间为死时间。
中山大学-化工分离新技术-第二章:分离基础

● 速度差分离过程
● 反应分离
利用重力梯度、温度梯度、电位梯度等场 中,各组分的移动速度差进行分离
▲ 化学反应,如水中重金属沉淀,离子交换反应 ▲ 电化学反应,如电沉积 ▲ 生物反应,如BOD
可见,分离科学是一门综合学科!
2.2 分离过程与分离方法
一、分离过程
力学能:机械能、流体动能、位能、 热能
一种新型的分析技术
2.1 概述
要求:正确把握分离的概念 分离:字面解释清楚 科学定义难
人们对“分离”一词的反应是强烈的,比如亲人间、朋 友间的分离大多是痛苦的。因此人类社会的分离要考虑是 否有必要。
物质分离也要考虑是否有必要,因为它是需要付出代 价的。
作为物质分离,在科学研究和工业生产 中遇到,在日常生活中也无处不在。。
nB nA nB
)]
分离----负熵的生成:
蒸馏过程 d(S) Q( 1 1 ) 0
dt
T1 T2
T1:液面蒸汽 T2 :冷凝管入口
分离的理论耗能量(最小功):
Wmin, T
RT[n A
ln(
n
nA A n
B
)
n
B
ln( nB nA nB
)]
三、 分离方法的分类
● 平衡分离过程
利用相间平衡 ▲相平衡:在分离过程中形成新相 ▲分布平衡:分离前引入第二相,
3)分离因子(Separation Factor)
QB
SB/ A
QA QB0
Q
0 A
RB RA
A+B?
A+B
分离因子(分离系数)表示两种组分分离的难易程度, 显然当SB/A<<1或SA/B>>1时,两者越易分离。
《化工分离工程》PPT课件-第4讲分离过程
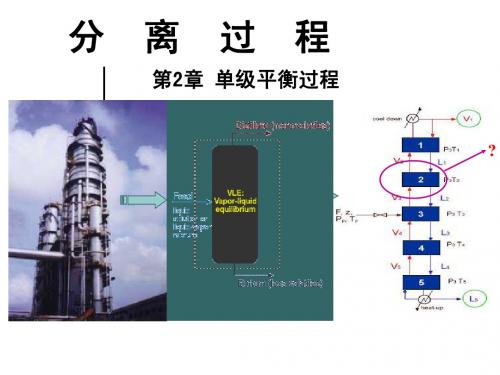
(k )
f T (k ) − f ′ T (k )
( ) ( )
f (T ) = ∑ K i xi − 1
2. Ki与组成有关: 与组成有关:
已知: 已知: x 、p 计算: 计算: y 、T 已知: 已知: x 、T 计算: y 、p 计算: 泡点方程: 泡点方程:
f (T ) =
பைடு நூலகம்泡点温度计算 泡点压力计算
pb = ∑ pis xi
y i = K i xi
C
i = 1,2,..., C
C
(2)摩尔分率加和方程: 2个 摩尔分率加和方程:
∑x
i =1
i
= 1 .0
∑y
i =1
i
= 1.0
2C+ 2C+2 C个
(3)汽液平衡常数关联式: 汽液平衡常数关联式:
Ki = f (T , P, x, y)
i = 1,2,...,C
变量数: 变量数:
∑K
i =1
C
i
xi − 1 = 0
K i = f T , P , x, y
(
)
由状态方程法或活度系数法求取K 由状态方程法或活度系数法求取 i :
K
i
φˆ i L = φˆ iV
K
i
yi γ i Pi sφ = = xi φˆ iV P
s i
v iL ( P − P i s ) exp RT
已知条件
开始
输入p 及有关参数 输入 ,x及有关参数
活 度 系 数 法 计 算 泡 点 温 度 的 框 图
设T并令φiV=1,作第一次迭代 并令 ,
L Vm,i p − pis pisϕis Ki = )V exp RT ϕi p
分离工程期末知识总结

思考题
1. 什么叫泡点,什么叫露点? 2. 精馏塔塔顶的温度和塔釜的温度分别是什么? 3. 简述求解泡露点的思路? 4. 对于泡点温度,∑Kixi <1,应如何调整温度? 5. 怎样判断闪蒸问题在给定的T、P下是否成立? 6. 等温闪蒸的通用闪蒸方程(Rachford-Rice方程
)的形式。
第三章 多组分精馏
特点:★F=D=W=0
★ L=V;L/V=1
★操作线方程: yn1 ,i xn,i
★板效率 最高
由于全回流,用 N m表示N,省去“均”:
Nm
lg([
x x
A B
)D
(
x x
A B
)W
lg AB
]
(3 8)
— — Fenske方程
最少理论板数只与分离要求有关,与进料组成无关。
多组分精馏
分离工程
第一章 绪论
分离过程基本概念 定义:将一混合物转变为组成不相同的两种或 两种以上产物的操作。
分离工程示意图
分离剂 (物质或能量)
原料物流 (一股或几股)
分离装置
产品1 (组成不同的物流) 产品2
第一章 绪论
分离过程的分类
分离过程分为机械分离过程和传质分离过程两大 类。
机械分离过程是指分离装置所接受的是多于一个 相的非均相进料,只要简单地分相就可以。如过 滤、沉降、固-液分离和气-液分离器等。
no yes
T,yi
第二章 单级平衡过程
露点计算
平衡常数与组成无关的露点计算 ki f (T , P) 露点方程: f (T ) iC1Kyii 1.0 0 (2 60)
f (P) iC1Kyii 1.0 0 (2 61)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如:在300K时,使1mol普通溶质以0.1mm/s的速度通
过溶剂运动时,要克服25000吨的阻力。 因此,溶质分子在溶液中的运动加速度几乎为零(几 乎是立即达到稳态)。
平均速度
因为加速度几乎为零,即:
d 2x M 2 0 dt
分子运动方程:
d 2x d ~ dx M 2 f dx dt dt
代入
dc dJ dt dx
得: dc dC d RT dC Y ( ~ ) dt dx dx f dx
(输运方程)
Fick第二定律
2 dc dc d RT dc dc d c 输运方程: Y ( ~ ) Y D 2 dt dx dx f dx dx dx
其中扩散系数D ~ f 即只有扩散
热力学的局限
所有溶质的迁移都是朝着趋向平衡的方向进行的,是
平衡控制着组分的迁移方向。但仅用平衡的观念(热
力学)无法准确回答组分的迁移速率和迁移性质等问 题。而迁移速率与整个分离速度又是密切相关的,因
此需要从动力学的角度研究溶质的迁移。
无论是定向迁移还是非定向扩散,涉及的都是物质分 子的迁移,因此分子迁移的表征是研究分离过程动力 学的基础。
dx 1 du ~ 所以,分子运动平均速度: U dt f dx
2.2 Fick第一定律
1. 流密度(J) 因为分子的运动速度难于测定,所以人们提出一个易于 测定的物理量(流密度)来反映分子在流体中的运动速
度。
流密度—单位时间内通过单位面积的物质的摩尔数。 当分子的平均运动速度 U 的单位为cm/s,溶质的浓度单 位取mol/cm3时,有下列关系式:
C 为溶质浓度,假定其在扩散方向上不随时间变化,
(接下页)
2. Fick第一定律
于是有:
C du C d (u ext u 0 RT ln C ) J ~ ~ f dx f dx C du du RT dC ~( ) f dx dx C dx C du ext du 0 RT dC ~( ) ~ f dx dx f dx
RT
当既无外场梯度,也无内部化学势梯度时,Y=0,
所以: Fick第二定律(一维扩散)
dc d 2c D 2 dt dx
多维扩散情况下的Fick第二定律
一维扩散:
dc d 2c D dt dx 2
dc 2c 2c 二维扩散: D( 2 2 ) dt x y dc 2c 2c 2c 三维扩散: D( 2 2 2 ) dt x y z
2.3 Fick第二定律和输运方程
Fick第一定律的假设:
溶质浓度C在扩散方向上不随时间变化。
Fick第二定律的条件:
考虑溶质浓度C在扩散方向上随时间变化的实际情况。 为简单起见,先只考虑一维扩散的情形。
2.3 Fick第二定律和输运方程
根据质量守恒定律,单位 时间内在x处因扩散而进入 到小体积元dx的物质流减
有流时的输运方程:
dc dc d 2c Y D 2 dt dx dx dc dc d 2c (Y V ) D 2 dt dx dx
dx dm ( J x J x dx ) 1 dx dt dm dx dx dc dc dx dx dt dt dt
J x J x dx
dc dx dt
2.3 Fick第二定律和输运方程
将Jx+dx在dx附近按Taylor级数展开,并略去高次项,得:
和p的差别:比p包含更多的内容。
力学运动的规律
根据牛顿运动定律、力F与加速度的关系:
d 2x F F1 F2 m 2 dt
力学推动力:F1 dp
dx
阻力: F2 f
dx dt
2 d x dp dx 基本力学运动方程:m 2 f dx dt dt
分子运动规律
费克第一定律的通用公式
费克第一定律的通用式可以写成:
J ( x) A dy dx
J(x)表示沿x轴方向的流,A为比例系数,-dy/dx指在x
轴方向上的梯度。 当y为浓度C时,dC/dx为x轴方向上的浓度梯度,J(x) 就是沿x轴方向的质量流(扩散)。 如果y为温度T时, dT/dx为x轴方向上的温度梯度,J(x) 就是沿x轴方向的热流。
(接下页)
ext
0
2. Fick第一定律
ext 0 1 du du 定义: Y ( ) ~ f dx dx
Y是外场和内部物理化学作用的总化学势产生的位移速度
将Y代入前面的公式:
RT dC J YC ~ f dx
当外场和内部作用势能梯度为零(Y=0)时:
RT dC J ~ f dx
力学输运与分子输运
目前还只能通过物质的机械运动和分子统计学间的相互关 系来了解迁移过程的规律 力学运动研究的对象:宏观物体的运动轨迹。 分子运动研究的对象:大量分子在统计学上的运动规律。 共性:对力的响应以及数学表达式相似。 力学推动力=-dp/dx 分子推动力=-d/dx (p为势能,x为坐标) (为化学势)
分子运动除受使宏观物体运动的所有力的约束外,每个 分子还与邻近分子发生激烈的碰撞作用。 分子运动的推动力为化学势梯度,阻力是分子碰撞的摩 擦阻力。 d 2x d ~ dx M f 分子运动方程: 2 dx dt dt M为物质的分子量; x表示整个1摩尔分子运动位移平均值;
~ f 表示每摩尔运动着的分子的阻力常数。
(接下页)
2. Fick第一定律
定义扩散系数D: 于是有:
RT D ~ f RT dC dC J ~ D f dx dx
Planck-Einsten方程 Fick第一定律
这是早在1855年就已发表的描述分子扩散的基本方程。 Fick第一定律的物理意义:扩散系数一定时,单位时间 扩散通过单位截面积的物质的摩尔数与浓度梯度成正比, 负号表示扩散方向与浓度梯度方向相反。
J U C
( J的单位为mol/scm2 )
2.菲克(Fick)第一定律
1 du 将 U ~ f dx C du 代入 J U C 中,得:J ~ f dx
在低浓度下(假定=C),化学势可以写成: = ext + 0 +RT lnC 式中 ext 为外场作用于分子(粒子)上的化学势; 0 为体系的标准化学势。
研究生课程
分离方法基础与技术
第2章 分离过程动力学
第2章 分离过程动力学
2.1 分离过程中物质的输运
2.2 Fick第一定律
2.3 Fick第二定律和输运方程
2.4 在有流存在下的输运
2.1 分离过程中物质的输运
一个体系达到平衡之前,体系内存在外场作用下的梯 度(如压力梯度、浓度梯度),也有体系内部的分子 间相互作用引起的化学势梯度。 定向迁移:溶质分子在外场或内部化学势作用下向趋 于平衡的方向定向迁移,在空间上重新分配。 非定向扩散:与定向迁移同时,溶质分子的随机运动 又会使溶质从高浓度区域向四周低浓度区域扩散,使 分离开的溶质又趋向重新混合。 定向迁移与非定向扩散总是相伴而生,分离过程就是 强化定向迁移,尽量减小非定向扩散。
S S
设截面积为1个单位,即:S=1
去在x+dx处扩散出来的物
质流,等于单位时间内体 积元dx中积累的物质量。
Jx x Jx+dx x+dx x
dm ( J x J x dx ) S dt
2.3 Fick第二定律和输运方程
公式变形:
dm ( J x J x dx ) S dt J x J x dx
J x dx
将此式代入公式
dJ Jx dx dx J x J x dx dc dx dt
得:
dJ dc Jx Jx dx dx dx dt
dJ dc dx dt
2.3 Fick第二定律和输运方程
浓度随时间变化情况下得输运方程 将
RT dC J YC ~ f dx
摩擦系数
所有分离过程都在不同程度上对物质(溶质)进行输 运,分离所需时间与输运时间有关,因而也与摩擦系 数有关。
Stokes定律—分子运动的摩擦系数与其他因素的关系
~ f 6Leabharlann Af 为摩尔摩擦系数;NA为Avogadro常数;为球 式中 ~
形溶质分子的半径;为介质粘度。
摩擦系数
分子运动的特点与平均速度 特点:与力学运动相比,分子运动的摩擦阻力(分子碰 撞)要大得多。
2.1 分离过程中物质的输运
分离过程动力学的研究内容: 物质在输运过程中的运动规律,即分离体系中组分迁移 和扩散的基本性质和规律 。 扩散有时也被用于分离: 利用物质扩散速度的差异可使某些组分达到分离,如等
温扩散法就可以用来制备高纯的挥发性酸。但在色谱分
离过程中扩散会使组分的谱带展宽,是要设法减小的。
无流时的流密度公式:
RT dC J YC ~ f dx
有流时的流密度公式:
RT dC J (Y V )C ~ f dx
此式为考虑外场和内部化学作用存在时,同时有介 质流动情况下一维输运的一般方程。
2.4 在有流存在下的输运
无流时的输运方程: 考虑溶质浓度随时间变化的情况
dc dJ dt dx
2.4 在有流存在下的输运
在前面的讨论中,只考虑了溶质本身的位移,即假设介 质(气体或溶剂)是不流动的。
很多分离体系(如色谱)中,载带溶质的介质也流动。
有流:有介质流动存在。设介质的流速为V,介质对溶 质输运所产生的流密度为:
J=VC
考虑有流存在时的流密度: J U C V C
2.4 在有流存在下的输运
