c语言实现cic梳状滤波__理论说明
CIC滤波器的原理与设计
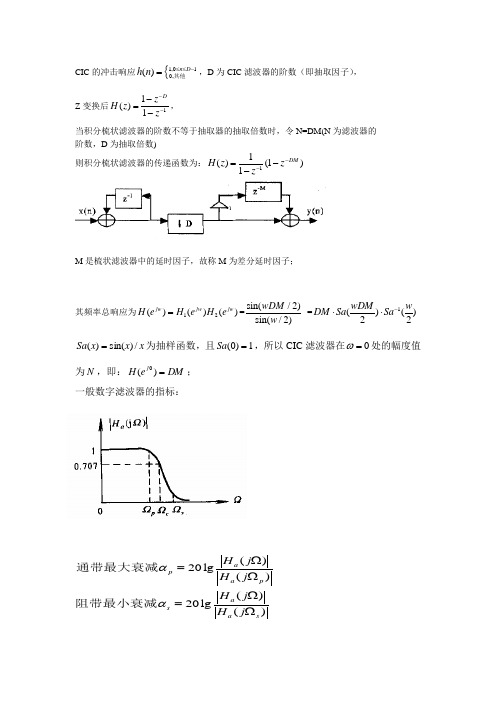
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带容差(通带衰减),即,在通带,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽,红线到绿线,信号给CIC 滤 波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带幅值容差不能太大,否则会引起高频失真;设该带容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带容差也会增大;由上面分析可知,阻带衰减和带容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带的混叠就越小,但Q越大,通带主瓣衰减也越大,所以Q不可太大,不宜超过5级。
cic滤波器原理详解

级联积分梳状(Cascade Integrator Comb,CIC)[1]滤波器结构简单、标准化,是高速抽取器中十分简单有效的抗混叠滤波单元,已被广泛使用于多抽样率信号处理系统中。
其组成只有积分器、加法器、寄存器,没有乘法器,使得CIC滤波器非常适合在具有较强实时性和并行处理能力的FPGA 上实现。
但是其阻带衰减和通带波纹的相互抑制限制了其滤波性能。
锐化级联积分梳状滤波器[2]、CIC 滤波器的部分锐化[3]、在CIC 滤波器级联分解的基础上级联一级余弦滤波器[4]、二级补偿CIC 滤波器( TSC -CIC)[5]、内插二阶多项式级联积分梳状滤波器(ISOP-CIC)[6]都是用来进行CIC滤波器改进的技术。
但上述CIC 滤波器的改进或只是降低了通带衰减,或只是提高了阻带衰减,或同时降低通带衰减、提高阻带衰减,但是占用硬件逻辑资源较多。
手把手教系列之梳状滤波器设计实现

⼿把⼿教系列之梳状滤波器设计实现[导读]:前⾯⼀篇⽂章关于IIR/移动平均滤波器设计的⽂章。
本⽂来聊⼀聊陷波滤波器,该滤波器在混⼊谐波⼲扰时⾮常有⽤,算法简单,实现代价低。
本⽂来⼀探其在机理、应⽤场景。
注:尽量在每篇⽂章写写摘要,⽅便阅读。
信息时代,⼤家时间都很宝贵,如此亦可节约粉丝们的宝贵时间。
前⽂所说学习的倡导2W1H原则,思来想来并不全⾯,本⽂决定从What Why Where When How⼏个维度展开。
我称之为4W1H学习法,借鉴管理学领域中的5W1H,起源于1932年,美国政治学家拉斯维尔提出“5W分析法”,后延伸出5W1H法。
有兴趣的可以找来阅读,题外话技术⼈员读⼀些⽅法论管理学⽅⾯的书籍于做⼈做事个⼈认为是⾮常有益的。
梳状滤波器之What?在信号处理中,梳状滤波器是通过向其⾃⾝添加信号的延迟⽽实现的,从⽽造成增强或削弱⼲扰的滤波器。
梳状滤波器的频率响应由⼀系列规则间隔的凹⼝组成,从⽽呈现出梳状外观。
其⼤体拓扑形式如下:梳状滤波器有着⼤量不同形式的传递函数,其作⽤是对周期性信号增强或削弱周期性信号,本⽂主要介绍其中⼀种形式的Z传递函数H(Z)=b1−Z−N 1−ρN−N其中:b=1+ρ2其信号流图如下:梳状滤波器英⽂称为comb(梳⼦) filter,这个名字真是⽆与伦⽐的绝!为何?谈到滤波器⼀定会重点关注其对幅频响应曲线,梳状滤波器,正是描述其幅频响应的。
⽽幅频响应从本质上讲是描述系统各频率能量的放⼤或者衰减。
本⽂中谈到的滤波器就是⼀个系统,对其输⼊能量按频率不同进⾏放⼤或者衰减,从⽽起到过滤作⽤。
梳状滤波器之Why?前⾯说到梳状滤波器其幅频响应样⼦和梳⼦长的很像,为啥长的像,来⼀探究竟:其频率响应为:H(e jω)=b1−e jωN 1−ρe jωN现以采样率20000Hz,10阶,阻带带宽50Hz为例。
其幅频响应曲线如下:相频响应曲线为:从幅频响应曲线可看出,其形状真是如梳⼦形状,当阶数越⼤,其齿数越多。
CIC滤波器的原理及FPGA实现

com ber: p rocess (clk_ com b) b eg in if (clk_ com b’even t and clk_ com b= ’1’) then
x ≤x_ in; - - x_ in 是 8 位输入 i0 ≤i0+ conv_ in teger (sx tx) ; i1 ≤i1+ i0; - - 累加 i2 ≤i2+ i1; i3 ≤i3+ i2; - - i3 为第四级积分器输出
……… End if; End p rocess in tegra to r;
大。鉴于此, 当前的专用DDC 芯片中, 都采用了一种 高 效的滤波器—— C IC 滤波器 (C IC 滤 波 器 是 由 Hogenauer E. B. 于 1981 年提出的, 因此又被称为 Hogenauer 滤波器) 作为第一级滤波器, 实现抽取、 低 通滤波; 第二级则采用一般的 F IR 或者 F IR 实现 的特殊滤波器 (如半带滤波器) , 此时它们工作在较 低的频率下, 且滤波器的参数得到了优化, 因此更容 易以较低的阶数实现, 节省资源, 降低功耗。 本文在研究C IC 滤波器基本原理的基础上, 对 其进行了 FPGA 仿真、综合, 并最终应用在工程中, 达到了设计要求。
resou rces and can p lay w ell in h igher frequency. B a sed on the theo ry of C IC filter, I have
cic滤波器原理

cic滤波器原理
CIC滤波器是一种数字滤波器,其原理基于累加器和差分器组成的级联结构。
CIC滤波器的工作原理如下:
1. 累加器阶段:输入信号经过累加器,累加器将输入信号进行递增操作,得到一个累加的输出。
2. 差分器阶段:累加器的输出信号经过差分器,差分器进行减法运算,得到相邻两个时间点上的差分输出。
3. 重采样阶段:差分器的输出信号经过重采样,根据重采样比率进行下采样操作,得到最终的输出信号。
CIC滤波器的特点:
1. CIC滤波器具有很高的差分非线性,可以有效抑制高频分量。
2. CIC滤波器在频率域上具有矩形频率响应,可以实现理想的低通滤波器功能。
3. CIC滤波器的实现简单,运算量少,适用于实时处理和硬件实现。
4. CIC滤波器具有固定频率响应,不需要频率域上的运算,适用于离散时间系统。
CIC滤波器的应用:
1. 信号预处理:用于消除高频噪声和干扰,提高信号的质量。
2. 降采样:用于降低采样率,减少数据存储和处理的开销。
3. 高通滤波:用于提取输入信号中的高频部分。
4. 低通滤波:用于去除输入信号中的高频部分。
总之,CIC滤波器通过累加器和差分器的级联结构,实现了一种简单有效的数字滤波器,其原理基于累加和差分操作,适用于信号预处理、降采样和频率域滤波等应用。
(完整版)CIC滤波器的原理与设计
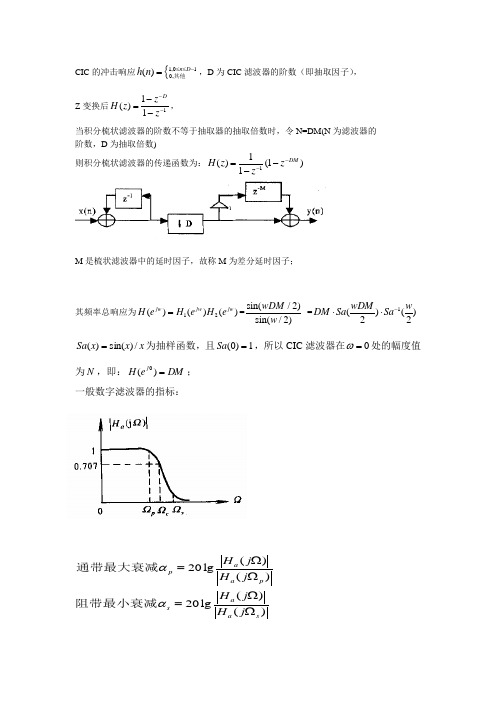
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
cic滤波器原理详解

cic滤波器原理详解
级联积分梳状(Cascade Integrator Comb,CIC)[1]滤波器结构简单、标准化,是高速抽取器中十分简单有效的抗混叠滤波单元,已被广泛使用于多抽样率信号处理系统中。
其组成只有积分器、加法器、寄存器,没有乘法器,使得CIC滤波器非常适合在具有较强实时性和并行处理能力的FPGA 上实现。
但是其阻带衰减和通带波纹的相互抑制限制了其滤波性能。
锐化级联积分梳状滤波器[2]、CIC 滤波器的部分锐化[3]、在CIC 滤波器级联分解的基础上级联一级余弦滤波器[4]、二级补偿CIC 滤波器( TSC -CIC)[5]、内插二阶多项式级联积分梳状滤波器(ISOP-CIC)[6]都是用来进行CIC滤波器改进的技术。
但上述CIC 滤波器的改进或只是降低了通带衰减,或只是提高了阻带衰减,或同时降低通带衰减、提高阻带衰减,但是占用硬件逻辑资源较多。
CIC滤波器的原理及设计
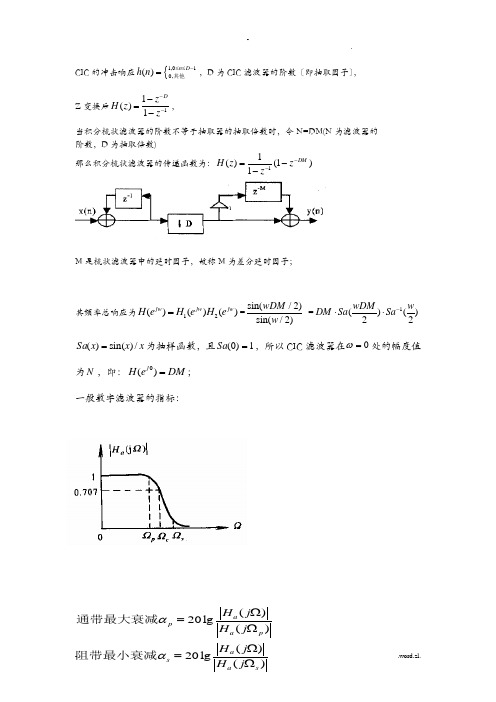
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数〔即抽取因子〕,Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)那么积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jw H e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM w DM Sa Sa -⋅⋅ x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()a p a p H j H j αΩ=Ω通带最大衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 〔用dB 数表示〕为:dB A DM s 46.1323lg 20lg201===πα 00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制dB Q Q A DM Q Q s )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减〕,即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进展滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,那么在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/〔fs/DM 〕, B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,那么w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; 〔假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能到达40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否那么会引起高频失真;设该带内容差为s δ,那么,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b b s ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减表2:大抽取因子下的阻带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c语言实现cic梳状滤波理论说明
1. 引言
1.1 概述
CIC(Cascade Integrator-Combinator)梳状滤波器是一种常见的数字滤波器,广泛应用于信号处理领域。
它具有简单的结构和高效的运行特性,在数字信号处理中发挥着重要作用。
本文将介绍CIC梳状滤波器的原理和C语言实现原理,并讨论其在不同领域中的应用。
1.2 文章结构
本文分为五个部分。
引言部分介绍了文章的背景和结构安排。
第二部分讲解了CIC梳状滤波器的原理以及C语言实现原理,并对相关算法进行了介绍。
第三部分探讨了CIC梳状滤波器在不同领域中的应用场景,包括数字信号处理、实时数据处理和音频信号处理等方面。
第四部分详细解释了如何使用C语言来实现CIC梳状滤波器,包括硬件平台准备、基本组件搭建与初始化配置以及数据输入与处理流程设计等方面内容。
最后,第五部分将对实验结果进行分析并展示其效果,并对整篇文章进行总结与展望。
1.3 目的
本文的目的是介绍CIC梳状滤波器的原理和C语言实现原理,并探讨其在不同
领域中的应用场景。
通过详细解释C语言实现CIC梳状滤波器的步骤,读者可以加深对该滤波器的理解,并了解如何将其应用于具体项目中。
最后,通过对实验结果进行分析与总结,读者可以评估CIC梳状滤波器在不同场景下的性能表现,并对其未来发展进行展望。
2. 理论基础:
2.1 CIC梳状滤波器原理
CIC(Cascade Integrator-Comb)梳状滤波器是一种常用的数字信号处理滤波器,用于对离散时间序列进行低通滤波。
它由级联部分积分器和组合部分组成。
CIC梳状滤波器的输入信号首先经过M个阶数为R的积分级,在每一级中累加了M个输入样本,然后被一个差分延时线延时M/R个采样周期。
延时后的信号经过一个减法运算,乘以一个增益因子D,并通过R级组合部分,其中每一级包含一个差分延时线和一个减法运算单元。
最终输出结果是经过R级积分之后的信号。
2.2 C语言实现原理
在C语言中实现CIC梳状滤波器需要定义相应的数据结构和函数来实现不同模块之间的连接和数据处理。
首先需要定义积分阶数、增益因子等参数,并初始化这些参数。
然后根据输入信号向前传递并计算输出结果。
在每一步中,根据不同阶数和延时时间进行相关运算,并将结果保存或输出至下一级。
2.3 相关算法介绍
在CIC梳状滤波器中,最主要的算法包括积分运算和组合运算。
积分运算使用简单的加法累加输入样本,并根据阶数和延时时间进行数据处理。
组合运算则通过差分延时线和减法运算单元对累加结果进行相应操作,并输出至下一级。
这些算法需要根据具体场景和需求进行调整和优化。
以上是对CIC梳状滤波器理论基础的详细说明,包括原理、C语言实现原理以及相关的算法介绍。
这些基础知识将为后续章节中的应用场景和具体步骤设计提供必要的背景知识。
3. CIC梳状滤波的应用场景
3.1 数字信号处理中的应用
CIC梳状滤波器在数字信号处理中有广泛的应用。
它主要用于对离散时间信号进行滤波和降采样,可以有效地提取出所需的频率成分,并且能够大幅度降低数据采样率。
因此,在音频、语音和视频等领域中,CIC滤波器常被用于预处理过程中以提高系统性能。
另外,在无线通信系统和雷达信号处理等方面,CIC滤波器也具有重要的应用价值。
3.2 实时数据处理中的应用
实时数据处理是指对连续输入数据进行及时响应和处理的过程,而CIC梳状滤波器在实时数据处理中具有很多优势。
由于其简单的结构和高效的运算方式,CIC滤波器可以实现快速、准确地对实时数据进行滤波和降采样,在无人车导航、
医疗设备监测等领域发挥着重要作用。
3.3 音频信号处理中的应用
在音频信号处理方面,CIC梳状滤波器被广泛应用于音频编解码、音频增强和音频分析等领域。
例如,在数字音频播放器中,CIC滤波器可以用于对音频信号进行降噪和去混叠处理,以提升音质效果。
此外,在声源定位和语音识别等应用中,CIC滤波器也能够提供有效的信号预处理。
综上所述,CIC梳状滤波器在数字信号处理、实时数据处理和音频信号处理等多个领域都有广泛的应用。
其高效的运算方式和优秀的滤波性能使得它成为了许多系统中必不可少的组件。
随着科技的不断发展,相信CIC梳状滤波器将会有更广阔的应用前景,并为各行业的技术创新带来更大的推动力量。
4. C语言实现CIC梳状滤波器步骤详解
CIC(Cascade Integrator-Comb)梳状滤波器是一种用于数字信号处理的高效滤波器结构。
它通过级联的积分器和组合器构成,具有高低通特性和高通增益特性,可以在消除直流偏移、降低采样率和抑制噪声等方面有很好的应用。
本节将详细介绍如何使用C语言来实现CIC梳状滤波器。
下面是具体的步骤:
4.1 硬件平台准备
首先,需要准备一个适当的硬件平台来进行CIC梳状滤波器的实现。
可以选择使用一款开发板或者单片机等设备作为硬件平台,在上面进行程序编写和测试。
确保所选硬件平台能够支持C语言编程,并提供相应的IO接口用于输入输出操作。
4.2 基本组件搭建与初始化配置
在C语言中,可以使用结构体来表示CIC梳状滤波器的基本组件,例如积分器和组合器。
我们需要定义这些结构体,并初始化其相关参数。
首先,创建一个名为"integrator"的结构体,用于表示积分器。
该结构体应包含输入、输出和状态变量等参数。
例如,可以定义一个整型变量"input"用于表示输入数据,一个整型变量"output"用于表示输出数据,以及一个整型变量"state"用于保存积分器的状态。
接下来,创建一个名为"combiner"的结构体,用于表示组合器。
同样地,该结构体应包含输入、输出和状态变量等参数。
在这个结构体中,我们需要定义一个整型变量数组"inputs[]"用于存储不同级别的积分器的输出值,和一个整型变量"output"用于表示组合器的输出。
完成结构体的定义后,根据实际需求对这些结构体进行初始化配置。
例如,可以设置初始状态为0,并指定适当的增益值。
4.3 数据输入与处理流程设计
在CIC梳状滤波器中,数据输入和处理是循环进行的。
首先,需要通过硬件平台提供的IO接口读取输入数据,并将其存储到积分器中。
然后,在每个时钟周期内进行处理操作。
首先,在积分器中对输入数据进行累加操作,并更新状态变量。
累加结束后,将得到的结果存储到组合器对应级别的输入数组中。
接下来,在组合器中对各个级别积分器的输出值进行相加,并计算出最终的输出结果。
然后,将该结果通过硬件平台提供的IO接口进行输出。
最后,重复上述步骤以处理连续的输入数据流,并不断更新梳状滤波器的状态,实现持续的滤波操作。
通过以上步骤,我们可以在C语言中实现CIC梳状滤波器。
这种滤波器结构简单高效,在数字信号处理和实时数据处理等领域有着广泛的应用。
在具体应用场景中,我们可以根据需求调整相关参数和配置,以达到更好的滤波效果。
5. 结果分析与总结:
在本文中,我们详细介绍了C语言实现CIC梳状滤波器的步骤和应用场景。
在完成了硬件平台准备、基本组件的搭建与初始化配置以及数据输入与处理流程设
计后,我们进行了一系列实验,并对实验结果进行了分析。
首先,我们对于数字信号处理中的应用进行了测试。
通过将需要处理的数字信号输入到CIC梳状滤波器中,我们观察到该滤波器能够有效地降低信号中的高频噪声和混叠效应,从而提高信号质量。
这可以在图表中清晰地看出来,图表展示了使用CIC梳状滤波器前后信号的频谱变化情况。
实验证明,在适当配置下,CIC梳状滤波器可以有效去除不想要的高频噪声。
其次,在实时数据处理中的应用方面,我们将一系列实时采集到的数据输入到CIC梳状滤波器进行处理,并对输出结果进行了观察和比较。
通过对比原始数据和经过CIC梳状滤波器处理后的数据,我们发现滤波器能够有效地提取其中感兴趣的信号,并滤除一些噪声和干扰。
这对于实时数据处理应用非常重要,可以大大提高数据分析和决策的准确性。
最后,在音频信号处理中的应用上,我们进一步验证了CIC梳状滤波器的效果。
通过将音频信号输入到滤波器中,并与未经滤波处理的音频进行对比,我们观察到CIC梳状滤波器能够有效地减少背景噪声、混响等不必要的声音成分,从而使得音频更加清晰、纯正。
这对于音频设备和语音识别等领域具有重要意义。
综上所述,CIC梳状滤波器在数字信号处理、实时数据处理以及音频信号处理等多个应用场景中都起到了积极的作用。
通过本文所介绍的C语言实现原理和步骤详解,读者可以对于如何使用C语言编写并应用该滤波器有一个清晰且全面
的认识。
此外,本文还对于实验结果进行了分析,并总结了CIC梳状滤波器在不同应用场景下的效果。
未来,在进一步优化算法和硬件配置方面还存在着一些挑战,但我们对于CIC梳状滤波器的应用前景充满了信心,并期待着更多的研究和实践。
