(完整版)CIC滤波器的原理与设计
CIC滤波器的原理与设计
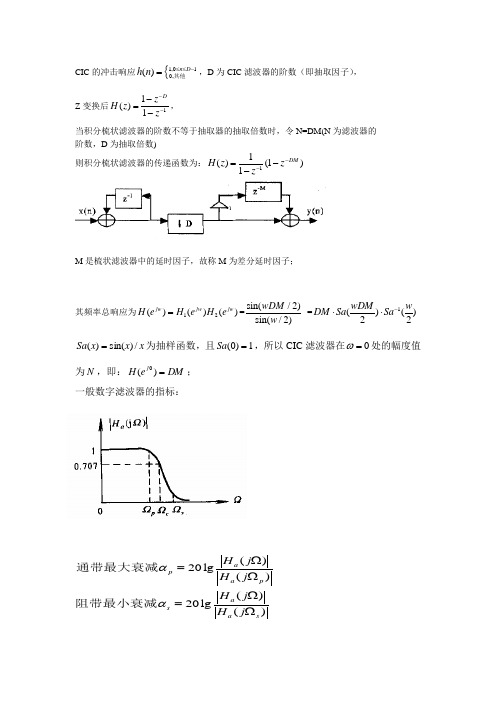
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带容差(通带衰减),即,在通带,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽,红线到绿线,信号给CIC 滤 波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带幅值容差不能太大,否则会引起高频失真;设该带容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带容差也会增大;由上面分析可知,阻带衰减和带容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带的混叠就越小,但Q越大,通带主瓣衰减也越大,所以Q不可太大,不宜超过5级。
累积梳状(CIC)滤波器分析与设计
累积梳状(CIC )滤波器分析与设计1、累积梳状(CIC )滤波器的分析所谓累积梳状滤波器,是指该滤波器的冲激响应具有如下形式: ⎩⎨⎧-≤≤=其它,010,1)(N n n h (1)式中N 为梳状滤波器的系数长度(后面将会看到这里的N 也就是抽取因子)。
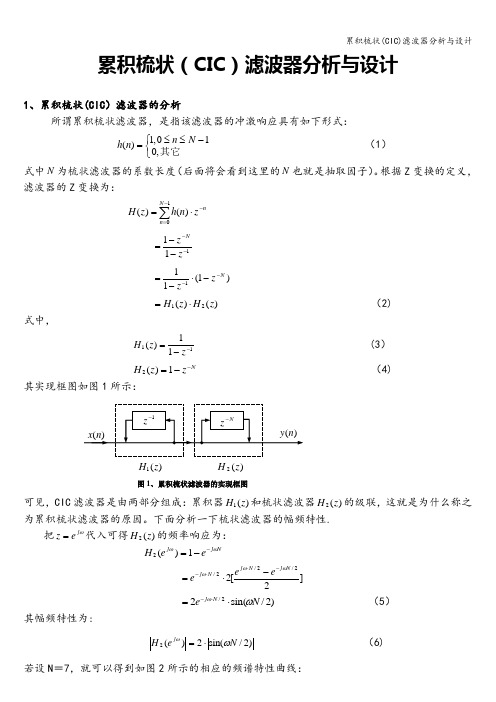
根据Z 变换的定义,滤波器的Z 变换为:∑-=-⋅=10)()(N n n z n h z H111----=z z N)1(111Nz z---⋅-=)()(21z H z H ⋅= (2) 式中,1111)(--=zz H (3) N z z H --=1)(2 (4) 其实现框图如图1所示:可见,CIC 滤波器是由两部分组成:累积器)(1z H 和梳状滤波器)(2z H 的级联,这就是为什么称之为累积梳状滤波器的原因。
下面分析一下梳状滤波器的幅频特性.把ωj e z =代入可得)(2z H 的频率响应为: N j j e e H ωω--=1)(2 ]2[22/2/2/N j N j N j e e eωωω-⋅⋅--⋅=)2/sin(22/N e N j ωω⋅=⋅- (5) 其幅频特性为:)2/sin(2)(2N e H j ωω⋅= (6) 若设N =7,就可以得到如图2所示的相应的频谱特性曲线:)(2z H)(1z H图1、累积梳状滤波器的实现框图由图2可以清楚地看到:)(2ωj e H 的形状犹如一把梳子,故把其形象地称之为梳状滤波器。
同样可以求得累积器)(1z H的频率响应为:ωj e z H --=11)(112/2/2/]2[2---=ωωωj j j e e e 12/)2(sin 2-⋅=ωωj e (7) 故CIC 滤波器的总频率响应为:)()()(21ωωωj j j e H e H e H ⋅= )2/sin(/)2/sin(ωωN = )2()2(1ωω-⋅⋅=Sa NSa N (8)式中,x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:N e H j =)(0 (9)CIC 滤波器的幅频特性如图3所示:在)~0(π区间上称)/2~0(N π的区间为CIC 滤波器的主瓣,而其它区间称为旁瓣。
cic滤波器原理详解

级联积分梳状(Cascade Integrator Comb,CIC)[1]滤波器结构简单、标准化,是高速抽取器中十分简单有效的抗混叠滤波单元,已被广泛使用于多抽样率信号处理系统中。
其组成只有积分器、加法器、寄存器,没有乘法器,使得CIC滤波器非常适合在具有较强实时性和并行处理能力的FPGA 上实现。
但是其阻带衰减和通带波纹的相互抑制限制了其滤波性能。
锐化级联积分梳状滤波器[2]、CIC 滤波器的部分锐化[3]、在CIC 滤波器级联分解的基础上级联一级余弦滤波器[4]、二级补偿CIC 滤波器( TSC -CIC)[5]、内插二阶多项式级联积分梳状滤波器(ISOP-CIC)[6]都是用来进行CIC滤波器改进的技术。
但上述CIC 滤波器的改进或只是降低了通带衰减,或只是提高了阻带衰减,或同时降低通带衰减、提高阻带衰减,但是占用硬件逻辑资源较多。
cic滤波器原理

cic滤波器原理
CIC滤波器是一种数字滤波器,其原理基于累加器和差分器组成的级联结构。
CIC滤波器的工作原理如下:
1. 累加器阶段:输入信号经过累加器,累加器将输入信号进行递增操作,得到一个累加的输出。
2. 差分器阶段:累加器的输出信号经过差分器,差分器进行减法运算,得到相邻两个时间点上的差分输出。
3. 重采样阶段:差分器的输出信号经过重采样,根据重采样比率进行下采样操作,得到最终的输出信号。
CIC滤波器的特点:
1. CIC滤波器具有很高的差分非线性,可以有效抑制高频分量。
2. CIC滤波器在频率域上具有矩形频率响应,可以实现理想的低通滤波器功能。
3. CIC滤波器的实现简单,运算量少,适用于实时处理和硬件实现。
4. CIC滤波器具有固定频率响应,不需要频率域上的运算,适用于离散时间系统。
CIC滤波器的应用:
1. 信号预处理:用于消除高频噪声和干扰,提高信号的质量。
2. 降采样:用于降低采样率,减少数据存储和处理的开销。
3. 高通滤波:用于提取输入信号中的高频部分。
4. 低通滤波:用于去除输入信号中的高频部分。
总之,CIC滤波器通过累加器和差分器的级联结构,实现了一种简单有效的数字滤波器,其原理基于累加和差分操作,适用于信号预处理、降采样和频率域滤波等应用。
(完整版)CIC滤波器的原理与设计
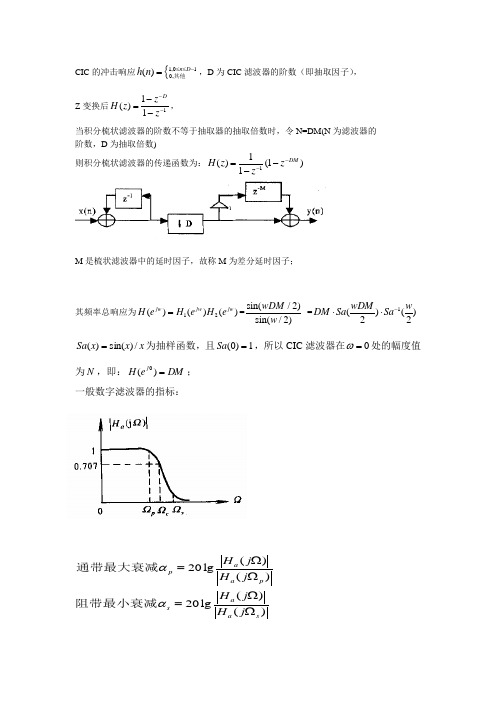
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计1.原理概述CIC滤波器由差分器、积分器和组合器三部分组成,可有效实现信号的重采样和滤波功能。
其基本原理是将输入信号通过差分器进行差分运算,然后经过积分器进行累积运算,最后通过组合器实现滤波和重采样。
CIC滤波器的特点是具有高的通带增益和截止频率,且不需要乘法器和存储器,适合在FPGA中实现。
2.设计步骤(1)确定CIC滤波器的设计参数,包括增益因子、积分阶数、截止频率等。
(2)根据设计参数计算滤波器的结构参数,包括输入和输出数据宽度、积分器的阶数和阶间差值等。
(3)根据计算结果,设计CIC滤波器的硬件结构,包括差分器、积分器和组合器的实现方法。
(4) 使用HDL语言(如Verilog或VHDL)编写FPGA的CIC滤波器的代码,同时进行功能仿真和波形仿真。
(5)在FPGA开发板上进行综合、布局布线和验证,实现CIC滤波器的硬件设计。
3.设计关键技术(1)差分器设计:差分器实现差分运算,可以简单采用异或门或加减器实现。
需要注意输入信号的幅度范围和差分器的输出范围。
(2)积分器设计:积分器实现累积运算,需要考虑积分阶数、数据宽度和溢出等问题。
可以采用寄存器与加法器的串行或并行结构实现。
(3)组合器设计:组合器实现滤波和重采样功能,需要根据设计参数确定组合器的截止频率和增益系数。
可以采用多级组合器结构实现。
(4)输入输出接口设计:FPGA的CIC滤波器需要与外部系统进行数据交换,因此需要设计合适的输入输出接口,包括数据接口、时钟接口和控制接口等。
4.实现优化技术(1)折叠积分器:为了减少资源占用和延迟,可以采用折叠积分器结构,将多级积分器合并为一个积分器实现。
(2)级联结构:为了增加滤波器的阶数和降低截止频率,可以采用级联结构,将多个CIC滤波器级联实现。
(3)变系数设计:为了实现可调节的滤波参数,可以设计可变系数的CIC滤波器,在运行时动态调整增益因子和积分阶数。
综上所述,FPGA的CIC滤波器设计是一项复杂的数字信号处理任务,需要深入理解CIC滤波器的原理和设计方法,结合FPGA的硬件实现技术进行设计和优化。
c语言实现cic梳状滤波__理论说明

c语言实现cic梳状滤波理论说明1. 引言1.1 概述CIC(Cascade Integrator-Combinator)梳状滤波器是一种常见的数字滤波器,广泛应用于信号处理领域。
它具有简单的结构和高效的运行特性,在数字信号处理中发挥着重要作用。
本文将介绍CIC梳状滤波器的原理和C语言实现原理,并讨论其在不同领域中的应用。
1.2 文章结构本文分为五个部分。
引言部分介绍了文章的背景和结构安排。
第二部分讲解了CIC梳状滤波器的原理以及C语言实现原理,并对相关算法进行了介绍。
第三部分探讨了CIC梳状滤波器在不同领域中的应用场景,包括数字信号处理、实时数据处理和音频信号处理等方面。
第四部分详细解释了如何使用C语言来实现CIC梳状滤波器,包括硬件平台准备、基本组件搭建与初始化配置以及数据输入与处理流程设计等方面内容。
最后,第五部分将对实验结果进行分析并展示其效果,并对整篇文章进行总结与展望。
1.3 目的本文的目的是介绍CIC梳状滤波器的原理和C语言实现原理,并探讨其在不同领域中的应用场景。
通过详细解释C语言实现CIC梳状滤波器的步骤,读者可以加深对该滤波器的理解,并了解如何将其应用于具体项目中。
最后,通过对实验结果进行分析与总结,读者可以评估CIC梳状滤波器在不同场景下的性能表现,并对其未来发展进行展望。
2. 理论基础:2.1 CIC梳状滤波器原理CIC(Cascade Integrator-Comb)梳状滤波器是一种常用的数字信号处理滤波器,用于对离散时间序列进行低通滤波。
它由级联部分积分器和组合部分组成。
CIC梳状滤波器的输入信号首先经过M个阶数为R的积分级,在每一级中累加了M个输入样本,然后被一个差分延时线延时M/R个采样周期。
延时后的信号经过一个减法运算,乘以一个增益因子D,并通过R级组合部分,其中每一级包含一个差分延时线和一个减法运算单元。
最终输出结果是经过R级积分之后的信号。
2.2 C语言实现原理在C语言中实现CIC梳状滤波器需要定义相应的数据结构和函数来实现不同模块之间的连接和数据处理。
一种短波数字化电台CIC抽取滤波器的设计

D
0 罄 害 罄 咨 t 2 罄 ^ ,
图1 00 波 器 幅频 特 性 1滤
Ⅳ
图1 区间 f 丌 中, D 称为CC I滤波器 的主瓣 , 其余区间称 为旁瓣。由图可见 , 随着频率 的增大 , 旁瓣 电平不 断减 小。 阻 但 带抑制 比较小, 一般采 用多级 CC I 滤波器级联 的方 法来增大 阻 带抑制。
字滤波器 , 广泛 应用于数字下变频器前级处理 中, 是数 字下变
根据式 () 4可得单级带内容差:
t { r
≈ 2 5X1 . 0
‘
~
.
:
= := : :
根据式 () 6 可计算无用边带的抑制为:
a 11
.
。
3 .d 35 B
8 h .
^
I矗 . 妻 .
采 用单 级C C I抽取滤 波器 时, 其无 用边带抑制为3 .d , 35 B 无 法满足 系统 9 d 的要求 。 0B 所以, 需求采用3 I抽取滤波器进 级CC
数。 ( z 专是积 分器 , (=— 是梳妆滤波器, ) = z I ) z 所以,
命名为级联积分一 梳状 滤波器。 CC I抽取滤波器 的幅频公式 为:
带内容差。 以, I 滤波器 的级数不宜太长。 所 CC
4 CI C抽取 滤 波器 的设 计
根 据此短 波 电台项 目要求 ,电台数字 化在 中频5 0 H 上 0K z 进行。 收时, 接 首先对 5 0 H 中频信号进 行采样 , 0K z 采样 速率为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CIC 的冲击响应{
1,010,()n D h n ≤≤-=
其他
,D 为CIC 滤波器的阶数(即抽取因子),
Z 变换后
1
1()1
D
z H z z ---=-,
当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)
则积分梳状滤波器的传递函数为:)1(11
)(1
DM z z
z H ----=
M 是梳状滤波器中的延时因子,故称M 为差分延时因子;
其频率总响应为12()()()jw jw jw
H e H e H e ==
sin(/2)sin(/2)wDM w =1()()22
wDM w
DM Sa Sa -⋅⋅
x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值
为N ,即:DM e H j =)(0; 一般数字滤波器的指标:
()20lg
()()20lg ()
a p
a p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减
即:
CIC 幅频特性响应曲线图
由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为
21.51
()
sin(3/2)/sin(3/2)sin(3/2)
j DM
H e DM DM ωπωπππ=⋅
==
,
旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.132
3lg 20lg
201===π
α 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣
电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:
)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Q
j Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦
⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Q
s )46.13(2
3lg 20)lg(
201⨯=⋅==π
α 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线
来分析:
00()20lg ()
()20lg
()
p
s j a p jw a j a s jw a H e H e
H e H e αα==
1、
设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;
且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤
波器带来的混叠就可以忽略,计算此时阻带衰减:
)
2/sin()
2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·
引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;
2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设
该带内容差为s δ,则,)()(lg 201
0jw j s e H e H =δ将w1带入可简化得)
sin(lg 20b b
s ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,D
f B
b s /=
,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:
表1:大抽取因子下的通带衰减
由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
显然,级数Q和差分延时因子M具有类似的作用,但它们完成这一作用所采取的方法却不一样,提高级数N 来减小混叠,其实质是通过加大阻带衰减来实现,而增加差分延时因子M来减少混叠,其实质是通过增大延时,改变混叠区域来实现的。
假设该信号工作在1M-30M 的频段,由带通采样定理,得fs=62MHz;假如中心频率为f0=10MHz;
假设要求把带宽为400kHz 、采样率为80MHz 的10MHz 的正弦信号降低为采样
率为800kHz 的信号,抽取因子为D=100=25*2^2; b=8
1
125.025/80400/====
M k D f B b s ;
设计带宽比例因子b=1/8;通带衰减可忽略;则CIC 滤波器可根据要求 通带衰减最大不得超过3dB ,阻带衰减不得低于60dB 。
由以上公式及上表查出,最好级联5级,差分延迟为1,可完成25倍抽取;半带滤波器完成级联2级的2倍抽取,完成4倍抽取;然后经过FIF 滤波器进行整形;下面是仿真:
下面是我假设的一个模型:
10M 的正弦信号+噪声
10M 的正弦信号
5级CIC ;抽取系数为25
Fs=80M
2级HB ,每级抽取系数为2
Fs=3.2MHz
FIR 低通滤波器
Fs=800kHz
数字基带信号。
