CIC滤波器的原理及FPGA实现
基于FPGA的CIC滤波器的设计与实现

设输 入序列 为 ( m) , 输 出序 列为 Y ( m) , 若输 入
采样 率为_ 厂 =1 / T , 输 出采 样率为_ 厂 = , / 。内插后 的序
列为
以单级 C I C抽 取 滤 波器 为例 , 积分 部 分 的积 分
程 为
I R滤波器 , 并且反 馈系数为 1 , 状态 方 y ( m ) : f ( 予 ) , , = 0 , ± , , ± 2 , , … ( ) 器是单 级点 的 I
符合设计 的要 求 。故 在 系统 中根据 需要 而设 计信 号 的速率非常重 要 , 而通 过 内插 和抽取 就可 以改变数 字 信号 的速率 , 故研 究 内插 和抽 取 对 于 软 件 无 线 电 的
设计 非常 有 必 要 。运 用 内插 和抽 取 的 就是 多 速 率 滤波 器 … , 这 种 常 用 的多 速 率 滤 波 器 有 C I C 滤 波 器、 H B滤 波 器 、 F I R滤 波器 。本 文设 计 的是 C I C滤
■
( G u i l i n U n i v e r s i t y o f E l e c t r o n i c T e c h n o l o g y , G u i l i n G u a n g x i 5 4 1 0 0 4, C h i n a )
【 A b s t r a c t 】 T h e d e s i g n a n d i m p l e m e n t ar a t o r c o m b( C I C ) i f l t e r a r e d e s c r i b e d . T h e v e i f l o g l a n g u a g e
2 内插 理论
CIC插值滤波器的FPGA设计与实现

CIC插值滤波器的FPGA设计与实现摘要:基于多速率信号处理原理,设计了用于下变频的CIC插值滤波器,由于CIC 滤波器结构只用到加法器和延迟器,没有乘法器,很适合用FPGA来实现,所以本文分析了CIC滤波器的原理,性能及影响参数,借助MATLAB设计符合系统要求CIC 滤波器,并利用Modelsim软件建模仿真,验证CIC滤波器性能是否达到要求。
(一)CIC滤波器基本原理A.CIC滤波器的基本单元CIC滤波器主要由积分滤波Integrator和梳状滤波Comb两个基本单元部分构成。
典型的CIC滤波器的结构,它由两个基本单元I(积分滤波器)和C(梳状滤波器)级联构成。
本设计主要针对插值滤波器,所以插值滤波器的结构示意图如图1-1所示:图 1-1 3级级联的CIC插值滤波器结构示意图积分器和梳状滤波器之间是一个采样率转换器,对于CIC插值器而言,它完成在每一个样值后补上R-1个0值的工作,,对于CIC抽取器来说,它完成在实际的抽取工作,每R个样值中取样一个。
R(插值倍数),M(延迟因子,一般取1或者2)以及N(级联级数)是影响CIC 滤波器的三个参数,它们的值需根据通带性能的需求而设定。
(二)CIC插值滤波器的设计流程根据CIC滤波器的原理,本设计的流程如图2-1所示:图2-1 CIC 插值滤波器的设计流程图(三)模型的建立和测试A .位宽策略对于数字滤波器,一个不得不考虑的问题是为防止溢出每一级所需的位宽。
对于抽取器来说,CIC 滤波器的输出增益为(*)NG R M = (3-1)所以,在全精度的情况下,最后一级输出的位宽为2log (*)out in B B N R M =+ (3-2)其中in B 表示输入数据的宽度,为了保证精度,每一个积分器和梳状滤波器的输入输出位宽都为out B 。
对于插值器而言,输出增益为212,1,2,....2(*)/,1, 2......2i i N i N i N G R M R i N N N --⎛⎫== ⎪ ⎪=++⎝⎭ (3-3)因此,第i 级为避免溢出所需要的位宽为2log ()i in i W B G =+ (3-4)最后一级输出位宽为22log (*)log out in B B N R M R =+- (3-5)在实际当中,当差分延时M=1时,为保证稳定,所有积分器的位宽在理论值的基础上加一。
改进型CIC抽取滤波器设计与FPGA实现

改进型CIC抽取滤波器设计与FPGA实现张杰;戴宇杰;张小兴;吕英杰【摘要】为了改善级联积分梳状(CIC)滤波器通带不平和阻带衰减不足的缺点,给出一种改进型CIC滤波器.该滤波器在采用COSINE滤波器提高阻带特性的基础上,级联了一个SINE滤波器,补偿了其通带衰减.硬件实现时,采用新的多相分解方法结合非递归结构,不仅大大减少了存储单元数量,还使电路结构更加规则.经仿真和FPGA 验证,改进型CIC滤波嚣使用较少硬件,实现了阻带衰减100.3 dB,通带衰减仅为0.000 1 dB.【期刊名称】《现代电子技术》【年(卷),期】2009(032)010【总页数】3页(P22-24)【关键词】CIC抽取滤波器;COSINE滤波器;SINE滤波器;设计优化;FPGA【作者】张杰;戴宇杰;张小兴;吕英杰【作者单位】南开大学,南开大学微电子所,天津,300071;南开大学,南开大学微电子所,天津,300071;南开大学,南开大学微电子所,天津,300071;南开大学,南开大学微电子所,天津,300071【正文语种】中文【中图分类】TP368.1抽取滤波器是Σ-Δ模/数转换器中的重要组成部分,积分梳状滤波器经常作为第一级滤波器,用以实现抽取和低通滤波[1]。
其优点是实现时不需要乘法器电路,且系数为整数,不需要电路来存储系数,同时通过置换抽取可以使部分电路工作在较低频率,与相同滤波性能的其他FIR滤波器相比,节约了硬件开销[2]。
经过仿真,抽取率为32的一阶积分梳状滤波器第一旁瓣相对于主瓣的衰减最大约为15 dB,这样的阻带衰减根本达不到实用滤波器的设计要求。
为了改变滤波性能,一般采用级联积分梳状滤波器(CIC)[3]。
但经过CIC降频滤波系统降频后会产生信号混叠现象,并且主瓣曲线不平,需要用新的算法或新结构来修正改善这些特性。
1 CIC抽取滤波器原理经典的抽取滤波器为Hogenauer [3]CIC滤波器,其传输函数表达式为:(1)式中:参数M为降频因子,决定了CIC的通带大小;K为滤波器的阶数,对阻带衰减起到加深作用。
cic滤波器的fpga实现

cic滤波器的FPGA实现发布时间:2016-01-26 15:07:21技术类别:CPLD/FPGA一、关于多采样率数字滤波器很明显从字面意思上可以理解,多采样率嘛,就是有多个采样率呗。
前面所说的FIR,IIR滤波器都是只有一个采样频率,是固定不变的采样率,然而有些情况下需要不同采样频率下的信号,具体例子我也不解释了,我们大学课本上多速率数字信号处理这一章也都举了不少的例子。
按照传统的速率转换理论,我们要实现采样速率的转换,可以这样做,假如有一个有用的正弦波模拟信号,AD采样速率是f1,现在我需要用到的是采样频率是f2的信号,传统做法是将这个经过f1采样后的信号进行DA转换,再将转换后的模拟信号进行以f2采样频率的抽样,得到采样率为f2的数字信号,至此完成采样频率的转换但是这样的做法不仅麻烦,而且处理不好的话会使信号受到损伤,所以这种思想就被淘汰了,现在我们用到的采样率转换的方法就是抽取与内插的思想。
二、抽取先来总体来解释一下抽取的含义:前面不是说,一个有用的正弦波模拟信号经采样频率为f1的抽样信号抽样后得到了数字信号,很明显这个数字信号序列是在f1频率下得到的,现在,假如我隔几个点抽取一个信号,比如就是5吧,我隔5个点抽取一个信号,是不是就是相当于我采用了1/5倍f1的采样频率对模拟信号进行采样了?所以,抽取的过程就是降低抽样率的过程,但是我们知道,这是在时域的抽样,时域的抽样等于信号在频域波形的周期延拓,周期就是采样频率,所以,为了避免在频域发生频谱混叠,抽样定理也是我们要考虑的因素下面来具体来介绍如上图所示,假如上面就是某一有用信号经采样频率f1抽样得到的频谱,假设这时候的采样频率为8Khz ,可以通过数格子得到,从0到F1处有8个空格,每个空格代表1Khz,有些朋友可能会问,这不是在数字频域吗,单位不是π吗,哪来的hz?是的,这里是数字频域,采样频率F1处对应的是2π,这里只是为了好解释,我们用模拟频率来对应数字频率。
cic滤波器原理详解

级联积分梳状(Cascade Integrator Comb,CIC)[1]滤波器结构简单、标准化,是高速抽取器中十分简单有效的抗混叠滤波单元,已被广泛使用于多抽样率信号处理系统中。
其组成只有积分器、加法器、寄存器,没有乘法器,使得CIC滤波器非常适合在具有较强实时性和并行处理能力的FPGA 上实现。
但是其阻带衰减和通带波纹的相互抑制限制了其滤波性能。
锐化级联积分梳状滤波器[2]、CIC 滤波器的部分锐化[3]、在CIC 滤波器级联分解的基础上级联一级余弦滤波器[4]、二级补偿CIC 滤波器( TSC -CIC)[5]、内插二阶多项式级联积分梳状滤波器(ISOP-CIC)[6]都是用来进行CIC滤波器改进的技术。
但上述CIC 滤波器的改进或只是降低了通带衰减,或只是提高了阻带衰减,或同时降低通带衰减、提高阻带衰减,但是占用硬件逻辑资源较多。
cic滤波器原理

cic滤波器原理
CIC滤波器是一种数字滤波器,其原理基于累加器和差分器组成的级联结构。
CIC滤波器的工作原理如下:
1. 累加器阶段:输入信号经过累加器,累加器将输入信号进行递增操作,得到一个累加的输出。
2. 差分器阶段:累加器的输出信号经过差分器,差分器进行减法运算,得到相邻两个时间点上的差分输出。
3. 重采样阶段:差分器的输出信号经过重采样,根据重采样比率进行下采样操作,得到最终的输出信号。
CIC滤波器的特点:
1. CIC滤波器具有很高的差分非线性,可以有效抑制高频分量。
2. CIC滤波器在频率域上具有矩形频率响应,可以实现理想的低通滤波器功能。
3. CIC滤波器的实现简单,运算量少,适用于实时处理和硬件实现。
4. CIC滤波器具有固定频率响应,不需要频率域上的运算,适用于离散时间系统。
CIC滤波器的应用:
1. 信号预处理:用于消除高频噪声和干扰,提高信号的质量。
2. 降采样:用于降低采样率,减少数据存储和处理的开销。
3. 高通滤波:用于提取输入信号中的高频部分。
4. 低通滤波:用于去除输入信号中的高频部分。
总之,CIC滤波器通过累加器和差分器的级联结构,实现了一种简单有效的数字滤波器,其原理基于累加和差分操作,适用于信号预处理、降采样和频率域滤波等应用。
(完整版)CIC滤波器的原理与设计
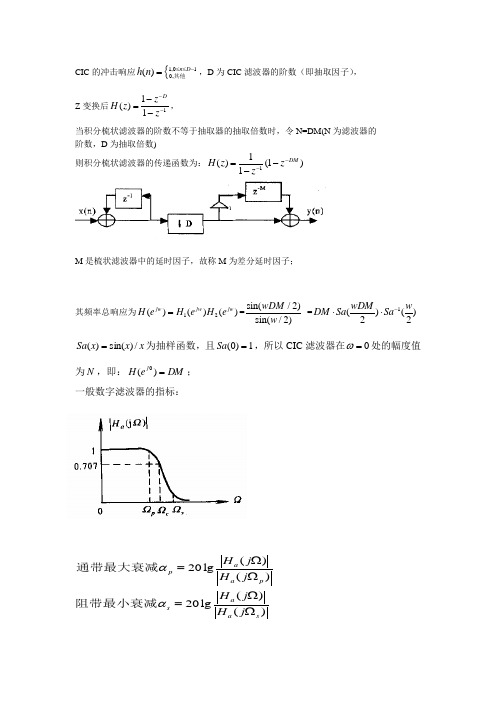
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计1.原理概述CIC滤波器由差分器、积分器和组合器三部分组成,可有效实现信号的重采样和滤波功能。
其基本原理是将输入信号通过差分器进行差分运算,然后经过积分器进行累积运算,最后通过组合器实现滤波和重采样。
CIC滤波器的特点是具有高的通带增益和截止频率,且不需要乘法器和存储器,适合在FPGA中实现。
2.设计步骤(1)确定CIC滤波器的设计参数,包括增益因子、积分阶数、截止频率等。
(2)根据设计参数计算滤波器的结构参数,包括输入和输出数据宽度、积分器的阶数和阶间差值等。
(3)根据计算结果,设计CIC滤波器的硬件结构,包括差分器、积分器和组合器的实现方法。
(4) 使用HDL语言(如Verilog或VHDL)编写FPGA的CIC滤波器的代码,同时进行功能仿真和波形仿真。
(5)在FPGA开发板上进行综合、布局布线和验证,实现CIC滤波器的硬件设计。
3.设计关键技术(1)差分器设计:差分器实现差分运算,可以简单采用异或门或加减器实现。
需要注意输入信号的幅度范围和差分器的输出范围。
(2)积分器设计:积分器实现累积运算,需要考虑积分阶数、数据宽度和溢出等问题。
可以采用寄存器与加法器的串行或并行结构实现。
(3)组合器设计:组合器实现滤波和重采样功能,需要根据设计参数确定组合器的截止频率和增益系数。
可以采用多级组合器结构实现。
(4)输入输出接口设计:FPGA的CIC滤波器需要与外部系统进行数据交换,因此需要设计合适的输入输出接口,包括数据接口、时钟接口和控制接口等。
4.实现优化技术(1)折叠积分器:为了减少资源占用和延迟,可以采用折叠积分器结构,将多级积分器合并为一个积分器实现。
(2)级联结构:为了增加滤波器的阶数和降低截止频率,可以采用级联结构,将多个CIC滤波器级联实现。
(3)变系数设计:为了实现可调节的滤波参数,可以设计可变系数的CIC滤波器,在运行时动态调整增益因子和积分阶数。
综上所述,FPGA的CIC滤波器设计是一项复杂的数字信号处理任务,需要深入理解CIC滤波器的原理和设计方法,结合FPGA的硬件实现技术进行设计和优化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C IC 滤波器的原理及 F PGA 实现
盖鹏翱, 赵笛 (山东航天电子技术研究所, 烟台 264000)
摘要: 在数字下变频 (DDC) 中, C IC (级联积分梳状) 滤波器起着重要的作用。 它主要用于 采样速率的抽取, 同时具有低通滤波的作用。C IC 滤波器的主要特点是, 仅利用加法器、减法器 和寄存器 (无需乘法器) , 因此占用资源少、实现简单且速度高。本文在分析C IC 滤波器原理的 基础上, 用V HDL 语言在 FPGA 上进行了仿真、综合, 并成功的应用于DDC 芯片的开发中。 关键词: 数字下变频; FPGA ; C IC 抽取滤波器; V HDL 中图分类号: TN 713+ . 6 文献标识码: A 文章编号: 100328329 (2005) 0420052204
个极点。RM 个零点是由 (1 - z - RM ) 产生的, 处于
2Π (RM ) (或 f s RM 频率) 弧度处, 圆心起始于 z =
1。每个不同的零点都重复 N 次。H (z ) 的 N 个极点
位于 z = 1 处, 可以看出这些极点已经被C IC 滤波器
的N 个零点抵消掉了。其最大动态范围增长出现在
frequency. Second ly , it can be u sed a s a low p a ss filter. T he C IC filter is a flex ib le,
m u lt ip lier2free filter w h ich includes adders, sub t racters and reg isters, so it u ses less
2. 2 C IC 内插滤波器 通过改变 C IC 抽取滤波器的结构, 可以实现 C IC 内插滤波器, 应用在数字上变频中。 如图 4 所 示, 在 C IC 内插滤波器中, 梳状滤波器工作在低的 f s R , 积 分 器 工 作 在 高 的 f s 频 率 下, 内 插 器 ( In terpo la tion) 将最后一级梳妆滤波器的输出数据 速率从 f s R 升到 f s 。
resou rces and can p lay w ell in h igher frequency. B a sed on the theo ry of C IC filter, I have
sim u la ted and syn thesized the filter w ith the FPGA , and rea lized it in the circu it of DDC
p ackage da ta_ vecto r_ 28 is sub typ e w o rd28 is in teger range 0 to 23 3 28- 1; - 设置 28 位的数据变量 end p ackage da ta_ vecto r_ 28; - - 对输入进行符号扩展 Signa l sx tx : std_ logic_ vecto r (27 dow n to 0) ; A : p rocess (x) b eg in sx tx < = sx t (x, 28) ; end p rocess A ; - - 4 级积分器 in tegra to r: p rocess (clk) b eg in if (clk’even t and clk= ’1’) then
抽取滤波器的频率响应。
《无线通信技术》2005 年第 4 期
— 53 —
图 5 C IC 抽取滤波器的频率响应
3 C IC 抽取滤波器的 F PGA 实现
对于一个 R = 32、M = 1、N = 4 的C IC 抽取滤 波器来说, 它包括一个四阶积分器和一个四阶梳状 滤波器, 并且采样速率降低了32 倍。用FPGA 实现, 首先要实现所有的积分器, 然后是抽取器, 最后是实 现梳状部分。 3. 1 积分器的 FPGA 实现 由式 (1) 推出单级积分器的差分方程 y (n) = x (n) + y (n - 1) , 可以看出用累加器即可实现。对 于一个8 位输入的4 阶C IC 滤波器, 为了保证运行时 间不会产生溢出, 需要的内部字宽为 W = B in + B grow = 8 + 4lo g232 × 1 = 28 位, 因此需要将输入进 行符号扩展。V HDL 代码示例如下:
- - - - - - - signa l coun t: in teger range 0 to 31; - - 计数器 signa l clk_ com b: std_ logic; - - 梳状部分时钟 - - - - - - - if (coun t > 8) and (coun t < 16) then clk_ com b≤ ’1’; e lse clk_ com b≤’0’; end if;
Ξ 作者简介: 盖鹏翱, 男, 1975 年 12 月生, 工程师, 中国空间技术研究院在读硕士研究生。 主要研究方向: 中频数字化、嵌入式系统。
— 52 —
《无线通信技术》2005 年第 4 期
2 C IC 滤波器的基本原理
2. 1 C IC 抽取滤波器 N 级C IC 抽取滤波器的基本框图如图 1 所示。 从图中可知, C IC 抽取滤波器主要由 N 级积分器 ( In teg ra to r)、抽取器 (D ecim a t ion) 和N 级梳状滤波 器 (Com b F ilter) 三部分组成。其中, N 级积分器工 作在高采样频率 f s 下。每级积分器都是一个反馈系 数为 1 的单极点 IIR 滤波器, 其传递函数为:
Abstract: T he filter of ca scaded in teg ra to r com b is becom ing m o re im po rtan t in the
app lica t ion of d ig ita l dow n converter (DDC ). F irst ly, it is u sed to decim a te the sam p le
3. 2 抽取器的 FPGA 实现 实现抽取器的最简单的一种方法是, 从 x (n) 中 每 R 个采样点抽取一个, 重新组成一个新的序列 x ’(n) , 即
x ’(n) = x (R n) , n = - ∞~ + ∞ 因此, 可以通过分频的方法用 FPGA 实现。V HDL 代码示例如下:
H l (z ) =
1 1 - z- 1
(1)
单级积分器基本实现框图如图 2 所示。
图 1 N 级C IC 抽取滤波器基本框图
图 2 单级积分器的基本实现框图
C IC 抽取滤波器的梳状部分工作在较低的频率 f s R (R 是整数倍的频率变换因子)。梳状部分由 N 级梳状滤波器组成, 以 f s R 为参照, 每级微分延迟 M 个样本。M 影响滤波器频率响应, 工程实现中一 般取值为 1 或 2。以 f s 为参照, 单级梳状滤波器的传 递函数为
successfu lly.
Key words: DDC; FPGA ; the decim a t ion filter of C IC; V HDL
1 前 言
在软件无线电中, 数字下变频器接收经过高速 采样的中频数字信号, 将所需的频带下变到基带。它 一般位于信号处理链的前端, 靠近A D。它主要由数 字振荡器、数字乘法器、数字滤波器三部分组成。 DDC 中数字滤波器的主要作用是抽取、低通滤 波, 一般由F IR 滤波器实现。但F IR 滤波器需要大量 的乘法器, 且一般DDC 中的采样速率很高, 因此F IR 滤波器需要工作在很高的频率, 使用资源多、功耗
T he R ea liza t ion of Ca scaded In teg ra to r Com b F ilter W ith FPGA
GA I Peng2ao, ZHAO D i (Shandong A ero sp ace E lect ron ic T echno logy In st itu te, Shandong Yan ta i 264000, Ch ina)
大。鉴于此, 当前的专用DDC 芯片中, 都采用了一种 高 效的滤波器—— C IC 滤波器 (C IC 滤 波 器 是 由 Hogenauer E. B. 于 1981 年提出的, 因此又被称为 Hogenauer 滤波器) 作为第一级滤波器, 实现抽取、 低 通滤波; 第二级则采用一般的 F IR 或者 F IR 实现 的特殊滤波器 (如半带滤波器) , 此时它们工作在较 低的频率下, 且滤波器的参数得到了优化, 因此更容 易以较低的阶数实现, 节省资源, 降低功耗。 本文在研究C IC 滤波器基本原理的基础上, 对 其进行了 FPGA 仿真、综合, 并最终应用在工程中, 达到了设计要求。
H c (z ) = 1 - z - RM
(2)
当M = 1, 以 f s R 为参照时, 传递函数为
H c (z ) = 1 - z - 1
(3)
单级梳状滤波器基本实现框图如图 3 所示。
图 3 单级梳状滤波器的基本实现框图
在积分器和梳状滤波器之间是一个速率转换器 (抽取器) , 转换器将最后一级积分器的输出数据速 率从 f s 降到 f s R (将多余的样本丢弃)。
3. 3 梳状滤波器的 FPGA 实现 由式 (3) 推出单级梳状滤波器的差分方程 y (n) = x (n) - y (n - 1) , 可以看出用减法器即可实现。 对于C IC 滤波器来说, 正常的输出字宽一般都明显 比W 小, 比如 9 位。V HDL 代码示例如下:
com ber: p rocess (clk_ com b) b eg in if (clk_ com b’even t and clk_ com b= ’1’) then
