(新课标)2020版高考物理大二轮复习专题强化训练11带电粒子在复合场中的运动
高考物理带电粒子在复合场中的运动技巧(很有用)及练习题含解析

一、带电粒子在复合场中的运动专项训练1.扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆.其简化模型如图:Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直,相距为L ,磁场方向相反且垂直纸面.一质量为m ,电量为-q ,重力不计的粒子,从靠近平行板电容器MN 板处由静止释放,极板间电压为U ,粒子经电场加速后平行于纸面射入Ⅰ区,射入时速度与水平和方向夹角30θ=︒(1)当Ⅰ区宽度1L L =、磁感应强度大小10B B =时,粒子从Ⅰ区右边界射出时速度与水平方向夹角也为30︒,求B 0及粒子在Ⅰ区运动的时间t 0(2)若Ⅱ区宽度21L L L ==磁感应强度大小210B B B ==,求粒子在Ⅰ区的最高点与Ⅱ区的最低点之间的高度差h(3)若21L L L ==、10B B =,为使粒子能返回Ⅰ区,求B 2应满足的条件(4)若12B B ≠,12L L ≠,且已保证了粒子能从Ⅱ区右边界射出.为使粒子从Ⅱ区右边界射出的方向与从Ⅰ区左边界射出的方向总相同,求B 1、B 2、L 1、、L 2、之间应满足的关系式.【来源】2011年普通高等学校招生全国统一考试物理卷(山东) 【答案】(1)32lm t qU π=(2)2233h L ⎛⎫=- ⎪⎝⎭(3)232mU B L q >(或232mUB L q≥)(4)1122B L B L =【解析】图1(1)如图1所示,设粒子射入磁场Ⅰ区的速度为v ,在磁场Ⅰ区中做圆周运动的半径为1R ,由动能定理和牛顿第二定律得212qU mv =①211v qvB m R = ②由几何知识得12sin L R θ= ③联立①②③,带入数据得012mUB L q=④设粒子在磁场Ⅰ区中做圆周运动的周期为T ,运动的时间为t12R T v π= ⑤ 22t T θπ=⑥ 联立②④⑤⑥式,带入数据得32Lmt qUπ=⑦ (2)设粒子在磁场Ⅱ区做圆周运动的半径为2R ,有牛顿第二定律得222v qvB m R = ⑧由几何知识得()()121cos tan h R R L θθ=+-+ ⑨联立②③⑧⑨式,带入数据得2233h L ⎛⎫=- ⎪⎝⎭⑩图2(3)如图2所示,为时粒子能再次回到Ⅰ区,应满足()21sin R L θ+<[或()21sin R L θ+≤] ⑾联立①⑧⑾式,带入数据得232mU B L q >(或232mUB L q≥) ⑿图3图4(4)如图3(或图4)所示,设粒子射出磁场Ⅰ区时速度与水平方向得夹角为α,有几何知识得()11sin sin L R θα=+ ⒀ [或()11sin sin L R θα=-]()22sin sin L R θα=+ ⒁[或]()22sin sin L R θα=- 联立②⑧式得1122B R B R = ⒂联立⒀⒁⒂式得1122B L B L = ⒃【点睛】(1)加速电场中,由动能定理求出粒子获得的速度.画出轨迹,由几何知识求出半径,根据牛顿定律求出B 0.找出轨迹的圆心角,求出时间;(2)由几何知识求出高度差;(3)当粒子在区域Ⅱ中轨迹恰好与右侧边界相切时,粒子恰能返回Ⅰ区,由几何知识求出半径,由牛顿定律求出B 2满足的条件;(4)由几何知识分析L 1、L 2与半径的关系,再牛顿定律研究关系式.2.如图1所示,宽度为d 的竖直狭长区域内(边界为12L L 、),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为0E ,0E >表示电场方向竖直向上。
(物理)带电粒子在复合场中的运动练习题含答案及解析

解得: <0.63%
5.如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为
d ,两侧为相同的匀强磁场,方向垂直纸面向里.一质量为 m 、带电量 q 、重力不计的 带电粒子,以初速度 v1 垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然
后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动.已知粒子第二次在磁场中 运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推.求:
由题知 vm=kym
若 E=0 时,粒子以初速度 v0 沿 y 轴正向入射,有 qv0B=m v02 R0
在最高处有 v0=kR0
联立解得 vm
E B
(
E B
)2
v02
考点:带电粒子在符合场中的运动;动能定理.
2.在 xOy 平面的第一象限有一匀强电磁,电场的方向平行于 y 轴向下,在 x 轴和第四象限 的射线 OC 之间有一匀强电场,磁感应强度为 B,方向垂直于纸面向里,有一质量为 m,带 有电荷量+q 的质点由电场左侧平行于 x 轴射入电场,质点到达 x 轴上 A 点,速度方向与 x 轴的夹角为 φ,A 点与原点 O 的距离为 d,接着,质点进入磁场,并垂直与 OC 飞离磁场, 不计重力影响,若 OC 与 x 轴的夹角为 φ.求:
(3)由以上分析可得:R = 设 m/为铀 238 离子质量,由于电压在 U±ΔU 之间有微小变化,铀 235 离子在磁场中最大半 径为:Rmax=
铀 238 离子在磁场中最小半径为:Rmin=
这两种离子在磁场中运动的轨迹不发生交叠的条件为:Rmax<Rmin
即:
<
得:
<
< 其中铀 235 离子的质量 m = 235u(u 为原子质量单位),铀 238 离子的质量 m,= 238u 则: <
高考复习(物理)专项练习:带电粒子在复合场中的运动【含答案及解析】

专题分层突破练9带电粒子在复合场中的运动A组1.(2021湖南邵阳高三一模)如图所示,有一混合正离子束从静止通过同一加速电场后,进入相互正交的匀强电场和匀强磁场区域Ⅰ。
如果这束正离子束在区域Ⅰ中不偏转,不计离子的重力,则说明这些正离子在区域Ⅰ中运动时一定相同的物理量是()A.动能B.质量C.电荷D.比荷2.(多选)(2021辽宁高三一模)劳伦斯和利文斯设计的回旋加速器如图所示,真空中的两个D形金属盒间留有平行的狭缝,粒子通过狭缝的时间可忽略。
匀强磁场与盒面垂直,加速器接在交流电源上,A处粒子源产生的质子可在盒间被正常加速。
下列说法正确的是()A.虽然逐渐被加速,质子每运动半周的时间不变B.只增大交流电压,质子在盒中运行总时间变短C.只增大磁感应强度,仍可能使质子被正常加速D.只增大交流电压,质子可获得更大的出口速度3.(2021四川成都高三二模)如图所示,在第一、第四象限的y≤0.8 m区域内存在沿y轴正方向的匀强电场,电场强度大小E=4×103 N/C;在第一象限的0.8 m<y≤1.0 m区域内存在垂直于坐标平面向外的匀强磁场。
一个质量m=1×10-10 kg、电荷量q=1×10-6 C的带正电粒子,以v0=6×103 m/s的速率从坐标原点O沿x轴正方向进入电场。
不计粒子的重力。
(1)求粒子第一次离开电场时的速度。
(2)为使粒子能再次进入电场,求磁感应强度B的最小值。
4.(2021河南高三二模)如图所示,在平面直角坐标系xOy内有一直角三角形,其顶点坐标分别为d),(d,0),三角形区域内有垂直于纸面向里的匀强磁场,磁感应强度大小为B,x轴下方有沿(0,0),(0,√33着y轴负方向的匀强电场,电场强度大小为E。
一质量为m、电荷量为-q的粒子从y轴上的某点M 由静止释放,粒子第一次进入磁场后恰好不能从直角三角形的斜边射出,不计粒子重力。
(1)求M点到O点的距离。
2020届高考回归复习—电学选择之带电微粒在复合场中的运动含答案
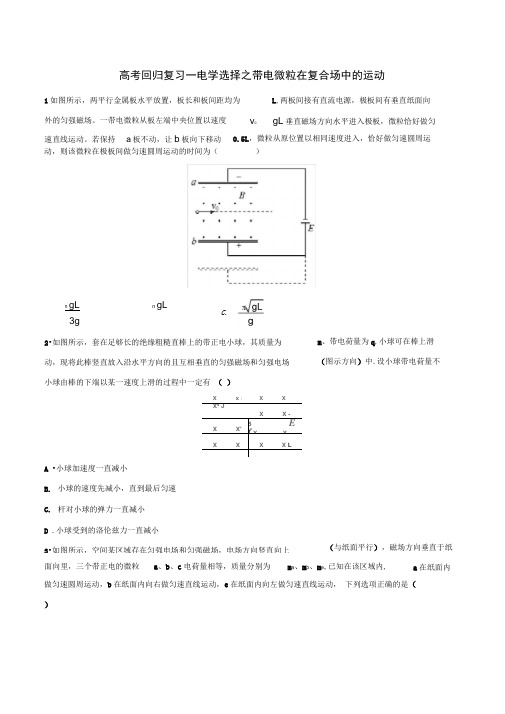
高考回归复习一电学选择之带电微粒在复合场中的运动1如图所示,两平行金属板水平放置,板长和板间距均为L ,两板间接有直流电源,极板间有垂直纸面向外的匀强磁场。
一带电微粒从板左端中央位置以速度v 0gL 垂直磁场方向水平进入极板,微粒恰好做匀动,则该微粒在极板间做匀速圆周运动的时间为( )做匀速圆周运动,b 在纸面内向右做匀速直线运动,e 在纸面内向左做匀速直线运动, 下列选项正确的是( )速直线运动。
若保持 a 板不动,让b 板向下移动 0.5L ,微粒从原位置以相同速度进入,恰好做匀速圆周运ngL 3gngL2•如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为 动,现将此棒竖直放入沿水平方向的且互相垂直的匀强磁场和匀强电场 小球由棒的下端以某一速度上滑的过程中一定有 ( )m 、带电荷量为q ,小球可在棒上滑 (图示方向)中.设小球带电荷量不Xx iXXX s JXX -X X' 5 Ef XX XXXX LA •小球加速度一直减小B. 小球的速度先减小,直到最后匀速C. 杆对小球的弹力一直减小 D .小球受到的洛伦兹力一直减小3•如图所示,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上 (与纸面平行),磁场方向垂直于纸面向里,三个带正电的微粒a 、b 、c 电荷量相等,质量分别为 m a 、m b 、m e ,已知在该区域内,a 在纸面内C .X1X JX 1 」 X 1X左只X X X X右XXXXXB . m b m a m eD . m e m b m a4.如图所示,环形塑料管半径为R ,竖直放置,且管的内径远小于环的半径,ab 为该环的水平直径,环的mgab 及其以下部分有水平向左的匀强电场,电场强度的大小E,管的内壁光滑。
现将一质量为 m ,电q荷量为+q 的小球从管中a 点由静止开始释放,则()A .小球到达b 点时速度为零,并在 adb 间往复运动 B. 小球每周的运动过程中最大速度在圆弧 ad 之间的某一位置C.小球第一次和第二次经过最高点 e 时对管壁的压力之比为 1:5D .小球第一次经过最低点 d 和最高点e 时对管壁的压力之比为 4:15. 如图所示,质量为 m ,带电荷量为q 的微粒以速度v 与水平方向成45。
高中物理带电粒子在复合场中的运动题20套(带答案)

一、带电粒子在复合场中的运动专项训练1.小明受回旋加速器的启发,设计了如图1所示的“回旋变速装置”.两相距为d 的平行金属栅极板M 、N ,板M 位于x 轴上,板N 在它的正下方.两板间加上如图2所示的幅值为U 0的交变电压,周期02mT qBπ=.板M 上方和板N 下方有磁感应强度大小均为B 、方向相反的匀强磁场.粒子探测器位于y 轴处,仅能探测到垂直射入的带电粒子.有一沿x 轴可移动、粒子出射初动能可调节的粒子发射源,沿y 轴正方向射出质量为m 、电荷量为q (q >0)的粒子.t =0时刻,发射源在(x ,0)位置发射一带电粒子.忽略粒子的重力和其它阻力,粒子在电场中运动的时间不计.(1)若粒子只经磁场偏转并在y =y 0处被探测到,求发射源的位置和粒子的初动能; (2)若粒子两次进出电场区域后被探测到,求粒子发射源的位置x 与被探测到的位置y 之间的关系【来源】【省级联考】浙江省2019届高三上学期11月选考科目考试物理试题【答案】(1)00x y = ,()202qBy m(2)见解析【解析】 【详解】(1)发射源的位置00x y =, 粒子的初动能:()2002k qBy Em=;(2)分下面三种情况讨论: (i )如图1,002k E qU >由02101mv mv mvy R R Bq Bq Bq===、、,和221001122mv mv qU =-,222101122mv mv qU =-, 及()012x y R R =++, 得()()22002224x y yqB mqU yqB mqU qBqB=++++;(ii )如图2,0002k qU E qU <<由020mv mv y d R Bq Bq--==、, 和220201122mv mv qU =+, 及()032x y d R =--+,得()222023)2x y d y d q B mqU qB=-++++(;(iii )如图3,00k E qU <由020mv mv y d R Bq Bq--==、, 和220201122mv mv qU =-, 及()04x y d R =--+, 得()222042x y d y d q B mqU qB=--+-2.如图所示,在无限长的竖直边界NS 和MT 间充满匀强电场,同时该区域上、下部分分别充满方向垂直于NSTM 平面向外和向内的匀强磁场,磁感应强度大小分别为B 和2B ,KL 为上下磁场的水平分界线,在NS 和MT 边界上,距KL 高h 处分别有P 、Q 两点,NS 和MT 间距为1.8h ,质量为m ,带电荷量为+q 的粒子从P 点垂直于NS 边界射入该区域,在两边界之间做圆周运动,重力加速度为g.(1)求电场强度的大小和方向;(2)要使粒子不从NS边界飞出,求粒子入射速度的最小值;(3)若粒子能经过Q点从MT边界飞出,求粒子入射速度的所有可能值.【来源】【全国百强校】2017届浙江省温州中学高三3月高考模拟物理试卷(带解析)【答案】(1)mgqE=,方向竖直向上(2)min(962)qBhv-=(3)0.68qBhvm=;0.545qBhvm=;0.52qBhvm=【解析】【分析】(1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,电场力与重力合力为零;(2)作出粒子的运动轨迹,由牛顿第二定律与数学知识求出粒子的速度;(3)作出粒子运动轨迹,应用几何知识求出粒子的速度.【详解】(1)粒子在磁场中做匀速圆周运动,电场力与重力合力为零,即mg=qE,解得:mgqE=,电场力方向竖直向上,电场方向竖直向上;(2)粒子运动轨迹如图所示:设粒子不从NS边飞出的入射速度最小值为v min,对应的粒子在上、下区域的轨道半径分别为r 1、r 2, 圆心的连线与NS 的夹角为φ,粒子在磁场中做匀速圆周运动,由牛顿第二定律得:2v qvB m r=,解得,粒子轨道半径:v r qBπ=, min1v r qBπ=,2112r r =, 由几何知识得:(r 1+r 2)sin φ=r 2,r 1+r 1cos φ=h ,解得:min 962)qBhv m=(﹣; (3)粒子运动轨迹如图所示,设粒子入射速度为v ,粒子在上、下区域的轨道半径分别为r 1、r 2, 粒子第一次通过KL 时距离K 点为x , 由题意可知:3nx =1.8h (n =1、2、3…)3(962)2h x -≥()2211x r h r =-- 解得:120.361)2hr n =+(,n <3.5, 即:n =1时, 0.68qBhv m=,n=2时,0.545qBh vm=,n=3时,0.52qBhvm=;答:(1)电场强度的大小为mgqE=,电场方向竖直向上;(2)要使粒子不从NS边界飞出,粒子入射速度的最小值为min962)qBhvm=(﹣.(3)若粒子经过Q点从MT边界飞出,粒子入射速度的所有可能值为:0.68qBhvm=、或0.545qBhvm=、或0.52qBhvm=.【点睛】本题考查了粒子在磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹是正确解题的前提与关键,应用平衡条件、牛顿第二定律即可正确解题,解题时注意数学知识的应用.3.如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向里的有界矩形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场。
高二物理专题练习-带电粒子在复合场中的运动大题专题(详细解答)
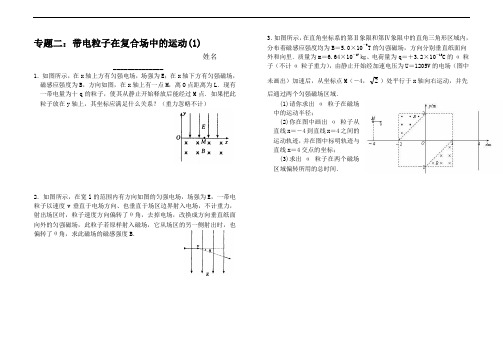
专题二:带电粒子在复合场中的运动(1)姓名______________1.如图所示,在x轴上方有匀强电场,场强为E;在x轴下方有匀强磁场,磁感应强度为B,方向如图,在x轴上有一点M,离O点距离为L.现有一带电量为十q的粒子,使其从静止开始释放后能经过M点.如果把此粒子放在y轴上,其坐标应满足什么关系?(重力忽略不计)2.如图所示,在宽l的范围内有方向如图的匀强电场,场强为E,一带电粒子以速度v垂直于电场方向、也垂直于场区边界射入电场,不计重力,射出场区时,粒子速度方向偏转了θ角,去掉电场,改换成方向垂直纸面向外的匀强磁场,此粒子若原样射入磁场,它从场区的另一侧射出时,也偏转了θ角,求此磁场的磁感强度B.3.如图所示,在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内,分布着磁感应强度均为B=5.0×10-3T的匀强磁场,方向分别垂直纸面向外和向里.质量为m=6.64×10-27㎏、电荷量为q=+3.2×10-19C的α粒子(不计α粒子重力),由静止开始经加速电压为U=1205V的电场(图中未画出)加速后,从坐标点M(-4,2)处平行于x轴向右运动,并先后通过两个匀强磁场区域.(1)请你求出α粒子在磁场中的运动半径;(2)你在图中画出α粒子从直线x=-4到直线x=4之间的运动轨迹,并在图中标明轨迹与直线x=4交点的坐标;(3)求出α粒子在两个磁场区域偏转所用的总时间.专题二:带电粒子在复合场中的运动(4)姓名______________1.如图所示,竖直平面xOy 内存在水平向右的匀强电场,场强大小E=10N/c ,在y ≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T 一带电量0.2C q =+、质量0.4kg m =的小球由长0.4m l =的细线悬挂于P 点小球可视为质点,现将小球拉至水平位置A 无初速释放,小球运动到悬点P 正下方的坐标原点O 时,悬线突然断裂,此后小球又恰好能通过O 点正下方的N 点.(g=10m /s 2),求: (1)小球运动到O 点时的速度大小;(2)悬线断裂前瞬间拉力的大小; (3)ON 间的距离2.两块平行金属板MN 、PQ 水平放置,两板间距为d 、板长为l ,在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC 与PQ 在同一水平线上,顶点A 与MN 在同一水平线上,如图所示.一个质量为m 、电量为+q 的粒子沿两板中心线以初速度v 0水平射入,若在两板间加某一恒定电压,粒子离开电场后垂直AB 边从D 点进入磁场,BD=41AB ,并垂直AC 边射出(不计粒子的重力).求: (1)两极板间电压;(2)三角形区域内磁感应强度; (3)若两板间不加电压,三角形区域内的磁场方向垂直纸面向外.要使粒子进入磁场区域后能从AB 边射出,试求所加磁场的磁感应强度最小值.专题二:带电粒子在复合场中的运动——参考答案(1)1、解析:由于此带电粒子是从静止开始释放的,要能经过M点,其起始位置只能在匀强电场区域.物理过程是:静止电荷位于匀强电场区域的y轴上,受电场力作用而加速,以速度v进入磁场,在磁场中受洛仑兹力作用作匀速圆周运动,向x轴偏转.回转半周期过x轴重新进入电场,在电场中经减速、加速后仍以原速率从距O点2R处再次超过x轴,在磁场回转半周后又从距O点4R处飞越x轴如图所示(图中电场与磁场均未画出)故有L=2R,L=2×2R,L=3×2R即 R=L/2n,(n=1、2、3……)……………①设粒子静止于y轴正半轴上,和原点距离为h,由能量守恒得mv2/2=qEh……②对粒子在磁场中只受洛仑兹力作用而作匀速圆周运动有:R=mv/qB………③解①②③式得:h=B2qL2/8n2mE (n=l、2、3……)2、解析:粒子在电场中运行的时间t= l/v;加速度 a=qE/m;它作类平抛的运动.有tgθ=at/v=qEl/mv2………①粒子在磁场中作匀速圆周运动由牛顿第二定律得:qvB=mv2/r,所以r=mv/qB 又:sinθ=l/r=lqB/mv………②由①②两式得:B=Ecosθ/v 3、解析:(1)粒子在电场中被加速,由动能定理得221mvqU=α粒子在磁场中偏转,则牛顿第二定律得rvmqvB2=联立解得2102.312051064.62005.01211927=⨯⨯⨯⨯==--qmUBr(m)(2)由几何关系可得,α粒子恰好垂直穿过分界线,故正确图象为(3)带电粒子在磁场中的运动周期qBmvrTππ22==α粒子在两个磁场中分别偏转的弧度为4π,在磁场中的运动总时间631927105.6105102.321064.614.3241----⨯=⨯⨯⨯⨯⨯⨯===qBmTtπ(s)OM2-22-4 4 x/my/m-2vBB (4,2-)(4) 1、解:(1)小球从A 运到O 的过程中,根据动能定理:212mv mgl qEl =- ① 则得小球在O 点速度为:2/s v m == ② (2)小球运到O 点绳子断裂前瞬间,对小球应用牛顿第二定律:2v F T mg f m l=-==向洛 ③f Bvq =洛 ④由③、④得:28.2mv T mg Bvq N l=++= ⑤ (3)绳断后,小球水平方向加速度25/s x F Eq a m m===电 ⑥ 小球从O 点运动至N 点所用时间0.8t s aυ∆== ⑦ON 间距离21 3.2m 2h gt == ⑧2、 解:⑴垂直AB 边进入磁场,由几何知识得:粒子离开电场时偏转角为30°∵0.v lmd qu v y =0v v tg y=θ ∴qlmdv u 332= 由几何关系得:030cos dl AB =在磁场中运动半径d l r AB 23431==∴ 121r mv qv B = ︒=30cos 0v v∴qdmv B 3401= 方向垂直纸面向里⑶当粒子刚好与BC 边相切时,磁感应强度最小,由几何知识知粒子的运动半径r 2为:42d r = ………( 2分 ) 2202r mv qv B = ∴qd mv B 024=即:磁感应强度的最小值为qdmv 0422(12分)如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。
物理带电粒子在复合场中的运动练习题20篇

一、带电粒子在复合场中的运动专项训练1.如图,绝缘粗糙的竖直平面MN 左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E ,磁场方向垂直纸面向外,磁感应强度大小为B .一质量为m 、电荷量为q 的带正电的小滑块从A 点由静止开始沿MN 下滑,到达C 点时离开MN 做曲线运动.A 、C 两点间距离为h ,重力加速度为g .(1)求小滑块运动到C 点时的速度大小v c ;(2)求小滑块从A 点运动到C 点过程中克服摩擦力做的功W f ;(3)若D 点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D 点时撤去磁场,此后小滑块继续运动到水平地面上的P 点.已知小滑块在D 点时的速度大小为v D ,从D 点运动到P 点的时间为t ,求小滑块运动到P 点时速度的大小v p .【来源】2015年全国普通高等学校招生统一考试物理(福建卷带解析) 【答案】(1)E/B (2)(3)【解析】 【分析】 【详解】小滑块到达C 点时离开MN ,此时与MN 间的作用力为零,对小滑块受力分析计算此时的速度的大小;由动能定理直接计算摩擦力做的功W f ;撤去磁场后小滑块将做类平抛运动,根据分运动计算最后的合速度的大小;(1)由题意知,根据左手定则可判断,滑块在下滑的过程中受水平向左的洛伦兹力,当洛伦兹力等于电场力qE 时滑块离开MN 开始做曲线运动,即Bqv qE = 解得:E v B=(2)从A 到C 根据动能定理:2102f mgh W mv -=- 解得:2212f E W mgh m B=-(3)设重力与电场力的合力为F ,由图意知,在D 点速度v D 的方向与F 地方向垂直,从D 到P 做类平抛运动,在F 方向做匀加速运动a=F /m ,t 时间内在F 方向的位移为212x at =从D 到P ,根据动能定理:150a a +=,其中2114mv 联立解得:()22222()P Dmg qE v t v m+=+ 【点睛】解决本题的关键是分析清楚小滑块的运动过程,在与MN 分离时,小滑块与MN 间的作用力为零,在撤去磁场后小滑块将做类平抛运动,根据滑块的不同的运动过程逐步求解即可.2.如图,空间存在匀强电场和匀强磁场,电场方向为y 轴正方向,磁场方向垂直于xy 平面(纸面)向外,电场和磁场都可以随意加上或撤除,重新加上的电场或磁场与撤除前的一样.一带正电荷的粒子从P (x =0,y =h )点以一定的速度平行于x 轴正向入射.这时若只有磁场,粒子将做半径为R 0的圆周运动;若同时存在电场和磁场,粒子恰好做直线运动.现在,只加电场,当粒子从P 点运动到x =R 0平面(图中虚线所示)时,立即撤除电场同时加上磁场,粒子继续运动,其轨迹与x 轴交于M 点.不计重力.求: (1)粒子到达x =R 0平面时速度方向与x 轴的夹角以及粒子到x 轴的距离; (2)M 点的横坐标x M .【来源】磁场 【答案】(1)20122R H h at h =+=+;(2)22000724M x R R R h h =++- 【解析】 【详解】(1)做直线运动有,根据平衡条件有:0qE qB =v ①做圆周运动有:200qB m R =v v ②只有电场时,粒子做类平抛,有:qE ma =③00R t =v ④ y v at =⑤解得:0y v v =⑥ 粒子速度大小为:22002y v v v v =+=⑦速度方向与x 轴夹角为:π4θ=⑧ 粒子与x 轴的距离为:20122R H h at h =+=+⑨(2)撤电场加上磁场后,有:2v qBv m R=⑩解得:02R R =⑾. 粒子运动轨迹如图所示圆心C 位于与速度v 方向垂直的直线上,该直线与x 轴和y 轴的夹角均为4π,有几何关系得C 点坐标为:02C x R =⑿02C R y H R h =-=-⒀ 过C 作x 轴的垂线,在ΔCDM 中:02CM R R ==⒁2C R CD y h ==-⒂) 解得:22220074DM CM CD R R h h =-=+- M 点横坐标为:22000724M x R R R h h =+-3.利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC 边足够长)中存在垂直于纸面的匀强磁场,A 处有一狭缝.离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA 边且垂直于磁场的方向射入磁场,运动到GA 边,被相应的收集器收集.整个装置内部为真空.已知被加速的两种正离子的质量分别是m 1和m 2(m 1>m 2),电荷量均为q .加速电场的电势差为U ,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用.(1)求质量为m 1的离子进入磁场时的速率v 1;(2)当磁感应强度的大小为B 时,求两种离子在GA 边落点的间距s ;(3)在前面的讨论中忽略了狭缝宽度的影响,实际装置中狭缝具有一定宽度.若狭缝过宽,可能使两束离子在GA 边上的落点区域交叠,导致两种离子无法完全分离.设磁感应强度大小可调,GA 边长为定值L ,狭缝宽度为d ,狭缝右边缘在A 处.离子可以从狭缝各处射入磁场,入射方向仍垂直于GA 边且垂直于磁场.为保证上述两种离子能落在GA 边上并被完全分离,求狭缝的最大宽度.【来源】2011年普通高等学校招生全国统一考试物理卷(北京)【答案】(112qU m 21228Um m qB (3)d m 12122m m m m --L【解析】(1)动能定理 Uq =12m 1v 12 得:v 1=12qUm …① (2)由牛顿第二定律和轨道半径有:qvB =2mv R,R = mv qB 利用①式得离子在磁场中的轨道半径为别为(如图一所示):R 1=122mU qB ,R 2=222 m U qB …② 两种离子在GA 上落点的间距s =2(R 1−R 2)=1228()Um m qB- …③ (3)质量为m 1的离子,在GA 边上的落点都在其入射点左侧2R 1处,由于狭缝的宽度为d ,因此落点区域的宽度也是d (如图二中的粗线所示).同理,质量为m 2的离子在GA 边上落点区域的宽度也是d (如图二中的细线所示).为保证两种离子能完全分离,两个区域应无交叠,条件为2(R 1-R 2)>d…④ 利用②式,代入④式得:2R 1(1−21m m >d R 1的最大值满足:2R 1m =L-d 得:(L −d )(1−21m m >d 求得最大值:d m 12122m m m m --L4.如图1所示,宽度为d 的竖直狭长区域内(边界为12L L 、),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为0E ,0E >表示电场方向竖直向上。
2020届高三高考物理复习专题突破:带电粒子在组合场中的运动

带电粒子在组合场中的运动1.(2018·河南省驻马店市第二次质检)如图所示,平面直角坐标系的第二象限内存在着垂直纸面向外、磁感应强度大小为2B 的匀强磁场,第三象限内存在着垂直纸面向里、磁感应强度大小为B 的匀强磁场.一带负电的粒子从原点O 以某一速度沿与y 轴成30°角方向斜向上射入磁场,且在第二象限运动时的轨迹圆的半径为R ,已知带电粒子的质量为m ,所带电荷量为q ,且所受重力可以忽略.则( )A.粒子在第二象限和第三象限两磁场中运动的轨迹圆半径之比为1∶2B.粒子完成一次周期性运动的时间为2πm 3qBC.粒子从O 位置入射后第二次经过x 轴时的位置到坐标原点的距离为33RD.若仅将粒子的入射速度大小变为原来的2倍,则粒子完成一次周期性运动的时间将减少2.(多选)(2019·山西省晋城市第一次模拟)足够大的空间内存在着竖直向上的匀强磁场和匀强电场,有一带正电的小球在电场力和重力作用下处于静止状态.现将磁场方向顺时针旋转30°,同时给小球一个垂直磁场方向斜向下的速度v (如图2所示),则关于小球的运动,下列说法正确的是( )A.小球做类平抛运动B.小球在纸面内做匀速圆周运动C.小球运动到最低点时电势能增加D.整个运动过程中机械能不守恒3.(2019·江西省十所省重点高中二模)如图所示,在纸面内有两个磁感应强度大小均为B 、方向相反的匀强磁场,虚线等边三角形ABC 为两磁场的理想边界.已知三角形ABC 边长为L ,虚线三角形内为方向垂直纸面向外的匀强磁场,三角形外部的足够大空间为方向垂直纸面向里的匀强磁场.一电荷量为+q 、质量为m 的带正电粒子从AB 边中点P 垂直AB 边射入三角形外部磁场,不计粒子的重力和一切阻力,试求:(1)要使粒子从P 点射出后在最短时间内通过B 点,则从P 点射出时的速度v 0为多大?(2)满足(1)问的粒子通过B后第三次通过磁场边界时到B的距离是多少?(3)满足(1)问的粒子从P点射入外部磁场到再次返回到P点的最短时间为多少?画出粒子的轨迹并计算.4.(2019·河南省商丘市模拟)如图所示,在xOy坐标系的第二象限内有水平向右的匀强电场,第四象限内有竖直向上的匀强电场,两个电场的场强大小相等,第四象限内还有垂直于纸面的匀强磁场,让一个质量为m、带电荷量为q 的粒子在第二象限内的P(-L,L)点由静止释放,结果粒子沿直线运动到坐标原点并进入第四象限,粒子在第四象限内运动后从x轴上的Q(L,0)点进入第一象限,重力加速度为g,求:(1)粒子从P点运动到坐标原点的时间;(2)匀强磁场的磁感应强度的大小和方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题强化训练(十一)一、选择题1.(多选)(2019·广西桂林、百色和崇左市第三次联考)如右图所示,在第二象限内有水平向右的匀强电场,在第一、第四象限内分别存在如图所示的匀强磁场,磁感应强度大小相等.在该平面有一个质量为m 、带正电q 的粒子以初速度v 0垂直x 轴,从x 轴上的P 点进入匀强电场,恰好与y 轴成45°角射出电场,再经过一段时间恰好垂直于x轴进入下面的磁场,已知OP 之间的距离为d ,不计粒子重力,则( )A .磁感应强度B =2mv 04qdB .电场强度E =mv 202qdC .自进入磁场至在磁场中第二次经过x 轴所用时间为t =72πd2v 0D .自进入磁场至在磁场中第二次经过x 轴所用时间为t =7πd2v 0[解析] 粒子的轨迹如图所示:带电粒子在电场中做类平抛运动,水平方向做匀加速运动,竖直方向做匀速运动,由题得知,出电场时,v x =v y =v 0,根据:x =v x2t ,y =v y t =v 0t ,得y =2x =2d ,出电场时与y 轴交点坐标为(0,2d ),设粒子在磁场中运动的半径为R ,则有R sin(180°-β)=y =2d ,而β=135°,解得:R =22d ,粒子在磁场中运动的速度为:v =2v 0,根据R =mvqB ,解得B=mv 02qd ,故A 错误;根据v x =at =qE m t =v 0,x =v x 2t ,联立解得:E =mv 202qd,故B 正确;在第一象限运动时间为:t 1=135°360°T =38T ,在第四象限运动时间为:t 2=12T ,所以自进入磁场至在磁场中第二次经过x 轴所用时间为:t =t 1+t 2=78T =7πd2v 0,故D 正确,C 错误.[答案] BD2.(多选)(2019·昆明质检)某型号的回旋加速器的工作原理图如下图所示.回旋加速器的核心部分为D 形盒,D 形盒置于真空容器中,整个装置放在电磁铁两极之间的磁场中,磁场可以认为是匀强磁场,且与D 形盒盒面垂直.两盒间狭缝很小,带电粒子穿过的时间可以忽略不计.质子从粒子源A 处进入加速电场的初速度不计,从静止开始加速到出口处所需的时间为t ,已知磁场的磁感应强度大小为B ,质子质量为m 、电荷量为+q ,加速器接一高频交流电源,其电压为U ,可以使质子每次经过狭缝都能被加速,不考虑相对论效应和重力作用,则下列说法正确的是( )A .质子第一次经过狭缝被加速后,进入D 形盒运动轨迹的半径r =1B2mU qB .D 形盒半径R =2Ut πBC .质子能够获得的最大动能为2q 2BUtπmD .加速质子时的交流电源频率与加速α粒子的交流电源频率之比为1∶1 [解析] 设质子第1次经过狭缝被加速后的速度为v 1,由动能定理得qU =12mv 21,①由牛顿第二定律有qv 1B =m v 21r 1,②联立①②式解得r 1=1B2mUq,故A 正确;设质子从静止开始加速到出口处运动了n圈,质子在出口处的速度为v ,则2nqU =12mv 2,③qvB =m v 2R,④质子做圆周运动的周期T =2πmqB,⑤质子运动的总时间t =nT ,⑥ 联立③④⑤⑥式解得R =2Ut πB ,故B 正确;根据qvB =m v 2R ,解得v =BRqm,质子射出加速器时的动能E k =12mv 2=B 2R 2q 22m =BUq 2t πm ,故C 错误;根据圆周运动的周期T =2πmqB ,由于质子与α粒子的电荷量之比为1∶2,而质子与α粒子的质量之比为1∶4,因此它们周期之比为1∶2,那么频率之比为2∶1,故D 错误.[答案] AB3.(2019·洛阳高三适应性测试)如下图所示,某种带电粒子由静止开始经电压为U 1的电场加速后,射入水平放置、电势差为U 2的两导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场中,则粒子射入磁场和射出磁场的M 、N 两点间的距离d 随着U 1和U 2的变化情况为(不计重力,不考虑边缘效应)( )A .d 随U 1变化,d 与U 2无关B .d 与U 1无关,d 随U 2变化C .d 随U 1变化,d 随U 2变化D .d 与U 1无关,d 与U 2无关[解析] 带电粒子在电场中做类平抛运动,可将射出电场的粒子速度v 分解成初速度方向与加速度方向,设出射速度与水平夹角为θ,则有:v 0v=cos θ,而在磁场中做匀速圆周运动,设运动轨迹对应的半径为R ,由几何关系得,半径与直线MN 夹角正好等于θ,则有:d2R=cos θ,所以d =2Rv 0v ,又因为半径公式R =mv Bq ,则有d =2mv 0Bq =2B2mU 1q.故d 随U 1变化,d 与U 2无关,故A 正确,B 、C 、D 错误.[答案] A4.(多选)(2019·杭州学军中学月考)如右图所示是选择密度相同、大小不同的纳米粒子的一种装置.待选粒子带正电且电荷量与其表面积成正比,待选粒子从O 1进入小孔时可认为速度为零,加速电场区域Ⅰ的板间电压为U ,粒子通过小孔O 2射入正交的匀强电场和匀强磁场区域Ⅱ,其中匀强磁场的磁感应强度大小为B ,左右两极板间距为d ,区域Ⅱ的出口小孔O 3与O 1、O 2在同一竖直线上,若半径为r 0、质量为m 0、电荷量为q 0的纳米粒子刚好能沿该直线通过,不计纳米粒子的重力,则( )A .区域Ⅱ的电场的场强大小与磁场的磁感应强度大小比值为 2q 0Um 0B .区域Ⅱ左右两极板的电势差U 1=Bdq 0Um 0C .若密度相同的纳米粒子的半径r >r 0,则它进入区域Ⅱ时仍将沿直线通过D .若密度相同的纳米粒子的半径r >r 0,它进入区域Ⅱ时仍沿直线通过,则区域Ⅱ的电场强度与原电场强度之比为r 0r[解析] 设半径为r 0的粒子加速后的速度为v ,则有q 0U =12m 0v 2,设区域Ⅱ内电场强度为E ,由题意可知洛伦兹力与电场力等大反向,即q 0vB =q 0E ,联立解得E =B 2q 0Um 0,则E B=2q 0Um 0,区域Ⅱ左右两极板的电势差为Ed =Bd2q 0Um 0,故A 正确,B 错误;若纳米粒子的半径r >r 0,设半径为r 的粒子的质量为m 、带电荷量为q 、加速后的速度为v ′,则m=⎝ ⎛⎭⎪⎫r r 03m 0,而q =⎝ ⎛⎭⎪⎫r r 02q 0,由12mv ′2=qU ,解得v ′=2q 0Ur 0m 0r=r 0rv <v ,故粒子进入区域Ⅱ后受到的洛伦兹力变小,粒子向左偏转,故C 错误;由于v ′=r 0rv ,由E =Bv 得,区域Ⅱ的电场与原电场的电场强度之比为r 0r,故D 正确. [答案] AD5.(2019·惠州莆田中学一模)如右图所示的金属导体,长l 、宽d 、高h ,导体中通有沿x 轴正方向的恒定电流I ,空间存在沿z 轴负方向的匀强磁场,磁感应强度为B ,已知金属导体中单位体积内自由电子数为n ,电子电荷量为e ,则下列说法正确的是( )A .金属导体的M 面带正电B .金属导体中电荷定向移动速率为I nehdC .增加导体高度h ,M 、M ′两面间的电压将增大D .M 、M ′两面间的电势差为IB ned[解析] 根据左手定则知,电子向M 面偏转,则导体的M 面带负电,为负极,M ′面带正电,为正极;自由电子做定向移动,视为匀速运动,设定向移动速率为v ,则时间t 内某一截面内电子前进的距离为vt ,对应体积为vthd ,此体积内含有的电子个数为nvthd ,电荷量为nevthd ,则电流I =nevthd t =nevhd ,电荷定向移动速率为v =Inehd;电子受电场力和洛伦兹力平衡,有e U h=Bev ,可得电势差U =Bhv =IBned,可知M 、M ′两面间的电压与导体高度h 无关;因M 面电势低,则M 、M ′两面间的电势差为-IBned.所以B 正确,A 、C 、D 错误. [答案] B 二、非选择题6.(2019·江西名校联盟质检)如右图所示,OD 在平面直角坐标系xOy 第四象限的角平分线上,D 点的坐标为(l ,-l ),直角三角形OAD 区域内有垂直于纸面向里的匀强磁场,磁感应强度大小为B ,直角三角形OCD 区域内有沿x 轴负方向的匀强电场,电场强度大小为E ,其中OC 和CD 为荧光屏(能吸收打到屏上的粒子).现有一束质量均为m 、电荷量均为q 的带正电粒子从原点O 沿y 轴负方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为v ≤qBl m .已知E =qB 2l 12m,不计带电粒子的重力和粒子之间的相互作用.求:(1)带电粒子从O 点射入到第一次进入电场的时间; (2)能打到荧光屏CD 上的带电粒子的最小入射速度; (3)荧光屏CD 、OC 上形成亮线的长度.[解析] (1)带电粒子在磁场中运动的周期T =2πm Bq,当粒子从OD 边离开磁场时,因∠AOD =45°,则粒子运动轨迹所对应的圆心角为90°,故粒子从原点O 射入后第一次在磁场中运动的时间为t 0=T 4=πm 2Bq.(2)带电粒子射入匀强磁场中在洛伦兹力作用下做匀速圆周运动,经14圆周到达OD 边,然后水平向右进入匀强电场,在电场力的作用下做匀减速直线运动.由题意知,带电粒子到达CD 的速度恰好为零时对应的入射速度最小,设为v 0,并设该粒子在磁场中的运动轨迹半径为r ,由牛顿第二定律可得,Bqv 0=mv 20r,由动能定理可得qE (l -r )=12mv 20,联立解得r =13l ,v 0=qBl3m .(3)速率大于qBl 3m 的带电粒子直接打在荧光屏CD 上,其中入射速度为qBl m的粒子在磁场中运动的轨迹半径为l ,即该粒子将直接打到D 点,故荧光屏CD 上亮线的长度为x 1=l -r =l-13l =23l ,速率小于qBl3m的带电粒子,进入电场后不能到达荧光屏CD ,从电场中返回后又在磁场中运动了34个周期,刚好垂直电场进入,在电场中做类平抛运动.当粒子以v 0=qBl3m的速度射入磁场时,粒子从P 点进入电场,然后做类平抛运动,如图所示,则有y =l -13l =v 0t ,x =12·qE m t 2,可得x =l NM =16l ,荧光屏OC 上亮线的长度为x 2=l OM =23l -16l =12l .[答案] (1)πm 2Bq (2)qBl3m(3)荧光屏CD 上亮线的长度为23l ,荧光屏OC 上亮线的长度为12l7.(2019·新疆乌鲁木齐诊断)如图所示,在平面直角坐标系中,AO 是∠xOy 的角平分线,x 轴上方存在水平向左的匀强电场,下方存在竖直向上的匀强电场和垂直纸面向里的匀强磁场,两电场的电场强度大小相等.一质量为m 、带电荷量为+q 的质点从OA 上的M 点由静止释放,质点恰能沿AO 运动而通过O 点,经偏转后从x 轴上的C 点进入第一象限内并击中AO 上的D 点(C 、D 均未画出).已知OD =34OM ,匀强磁场的磁感应强度大小为B =m q(T),重力加速度g 取10 m/s 2.求:(1)两匀强电场的电场强度E 的大小; (2)OM 的长度L ;(3)质点从M 点出发到击中D 点所经历的时间t .[解析] (1)质点在第一象限内受重力和水平向左的电场力作用,沿AO 做匀加速直线运动,所以有mg =qE ,即E =mgq.(2)质点在x 轴下方,重力与电场力平衡,质点做匀速圆周运动,从C 点进入第一象限后做类平抛运动,其轨迹如图所示.有qvB =m v 2R,由运动学规律可知v 2=2aL ,a =2g ,设粒子从C 点运动到D 点所用时间为t 3,由类平抛运动规律知:R =vt 3,R -3L 4=12at 23,联立解得L =20 2 m 或2029m.(3)质点做匀加速直线运动有L =12at 21,得t 1=2 s 或23 s ;质点做匀速圆周运动有t 2=34×2πm qB=4.71 s ;质点做类平抛运动有R =vt 3,得t 3=1 s ;质点从M 点出发到击中D 点所经历的时间为t =t 1+t 2+t 3=7.71 s 或6.38 s.[答案] (1)mg q (2)20 2 m 或2029m (3)7.71 s 或6.38 s。
