《全等三角形》单元测试题(含答案)
最经典《全等三角形》单元测试题卷(含答案)

最经典《全等三角形》单元测试题卷(含答案)全等三角形单元测试题一、选择题(每小题3分,共30分)1.下列说法错误的是()A。
全等三角形的对应边相等B。
全等三角形的对应角相等C。
全等三角形的周长相等D。
全等三角形的高相等2.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是()A。
∠1=∠2B。
AC=CAC。
AB=ADD。
∠B=∠D3.如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是()A。
AB=DEB。
∠B=∠EXXX=BCD。
EF∥BC4.长为3cm、4cm、6cm、8cm的木条各两根,XXX与XXX分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为()A。
一个人取6cm的木条,一个人取8cm的木条B。
两人都取6cm的木条C。
两人都取8cm的木条D。
B、C两种取法都可以5.△ABC中,AB=AC,三条高AD、BE、CF相交于O,那么图中全等的三角形有()A。
5对B。
6对C。
7对D。
8对6.下列说法中,正确的有()①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;③两角、一边相等的两个三角形全等;④两边、一角对应相等的两个三角形全等。
A。
1个B。
2个C。
3个D。
4个7.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A。
B。
4C。
D。
58.如图,ABC中,AD是它的角平分线,AB=4,AC=3,那么△ABD与△ADC的面积比是()A。
1:1B。
3:4C。
4:3D。
不能确定二、填空题(每小题3分,共24分)11.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=7.12.如图,∠1=∠2,CD=BD,可证△ABD≌△ACD,则依据是SSS。
13.在四边形ABCD中,已知CB=CD,∠XXX∠ADC=90°,∠BAC=35°,求∠BCD的度数。
全等三角形》单元测试题(含答案)

全等三角形》单元测试题(含答案)全等三角形》单元测试题姓名。
班级:得分:一、填空题(4×10=40分)1、在△ABC中,AC>BC>AB,且△ABC≌△DEF,则在△DEF中,DE>EF>DF。
2、已知:△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,AB=15cm,则∠C′=70°,A′B′=15cm。
3、如图1,△ABD≌△BAC,若AD=BC,则∠BAD的对应角是∠XXX。
4、如图2,在△ABC和△FED,AD=FC,AB=FE,当添加条件BD=CE时,就可得到△ABC≌△FED。
5、如图3,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形4对。
6、如图4,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是BD=EC。
7、如图5,△ABC中,∠C=90°,CD⊥XXX于点D,AE是∠BAC的平分线,点E到AB的距离等于3cm,则CF=6cm。
8、如图6,在△ABC中,AD=DE,AB=BE,∠A=80°,则∠CED=50°。
9、P是∠AOB平分线上一点,CD⊥OP于F,并分别交OA、OB于C、D,则CD=PD,P点到∠AOB两边距离之和等于AO或BO。
10、AD是△ABC的边BC上的中线,AB=12,AC=8,则中线AD的取值范围是6≤AD≤8.二、选择题:(每小题5分,共30分)11、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等。
其中真命题的个数有2个。
12、如图7,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有△ABD≌△AFDB、△AFE≌△ADC。
13、下列条件中,不能判定△ABC≌△A′B′C′的是∠B=∠B′。
八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)

八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题:(本题共8小题,每小题5分,共40分.)1.下列可以判定两个直角三角形全等的条件是( )A .斜边相等B .面积相等C .两对锐角对应相等D .两对直角边对应相等2.到三角形三边的距离相等的点是( )A .三角形三内角平分线的交点;B .三角形三边中线的交点;C .三角形三边高的交点;D .三角形三边中垂线的交点。
3.如图,ABC ≌△DEC ,B 、C 、D 在同一直线上,且CE=5,AC=7,则BD 长( )A .12B .7C .2D .144.如图,在ABC 中,AD 平分BAC ∠,DE AB ⊥于点E ,再添加一个条件仍然不能证明△ADC ≌△ADE 的是( )A .90ACB ∠=︒ B .∠ADC =∠ADE C .AC AE =D .DC DE =5.如图,在△ABC 中,∠A=90°,AB=AC=6,点D 是BC 中点,点E 、F 分别在AB 、AC 上,且BE=AF ,则四边形AEDF 的面积为( )A .6B .7C .D .96.如图,在ABC 中90A ∠=︒,AB =2,BC =5,BD 是ABC ∠的平分线,设ABD 和BDC 的面积分别是1S 和2S ,则S 1:S 2的值为( )A .5:2B .2:5C .12:D .1:5 7.如图,∠A=∠B ,AE=BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O ,若∠1=38°,则∠BDE 的度数为( )A .71°B .76°C .78°D .80°8.如图所示,点 ,A B 分别是 ,NOF MOF ∠∠ 平分线上的点, AB OF ⊥ 于点 E , BC ⊥MN 于点 C , AD ⊥MN 于点 D ,下列结论错误的是( )A .90AOB ∠= B .AD +BC =ABC .点 O 是 CD 的中点 D .图中与 ∠CBO 互余的角有两个二、填空题:(本题共5小题,每小题3分,共15分.)9.如图,在△ABC 和△DEF 中,已知CB =DF ,∠C =∠D ,要使△ABC ≌△EFD ,还需添加一个条件,那么这个条件可以是 .10.在Rt △ABC 中,∠ACB=90°,BC=2cm ,CD ⊥AB ,在AC 上取一点E ,使EC=BC ,过点E 作EF ⊥AC 交CD 的延长线于点F ,若EF=5cm ,则AE= cm.11.如图,AC 平分∠DCB ,CB =CD ,DA 的延长线交BC 于点E ,若∠BAE =80°,则∠EAC 的度数为 .12.如图,有一个直角三角形ABC ∠C =90° , AC=10 , BC=5 ,一条线段PQ=AB ,P 、Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AX 上运动,动点P 从C 点以2个单位秒的速度出发,问P 点运动 秒时(不包括点C ),才能使△ABC ≌△QPA .13.如图,已知ABC ∆的周长是 21 ,OB ,OC 分别平分ABC ∠和ACB ∠,OD BC ⊥于D ,且OD =4,ABC ∆ 面积是 .三、解答题:(本题共5题,共45分)14.如图,△ABO ≌△CDO ,点B 在CD 上,AO ∥CD ,∠BOD=30°,求∠A 的度数.15.如图,在ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE 于E ,AD CE ⊥于D ,AD =2.5cm ,DE =1.7cm ,求BE 的长.16.如图,DE AC ⊥于点E ,BFAC ⊥于点F .AB =CD ,AE =CF ,BD 交AC 于点M ,求证:MB =MD .17.如图所示,已知 AD//BC , 点 E 为 CD 上一点,AE 、BE 分别平分∠DAB 、∠CBA ,BE 交 AD 的延长线于点 F.求证:(1)△ABE ≌△AEF ;(2) AD+BC=AB18.如图,在△ABC 中,∠B =60°,AD 平分∠BAC ,CE 平分∠BCA ,AD 、CE 交于点F ,CD =CG ,连结FG.(1)求证:FD =FG ;(2)线段FG 与FE 之间有怎样的数量关系,请说明理由;(3)若∠B ≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由参考答案:1.D 2.A 3.A 4.D 5.D 6.B 7.A 8.D9.AC =ED 或∠A =∠FED 或∠ABC =∠F .10.311.50°12.2.513.4214.解:∵△ABO ≌△CDO∴OB=OD ,∠ABO=∠D∴∠OBD=∠D=12(180°﹣∠BOD )=12×(180°﹣30)=75° ∴∠ABC=180°﹣75°×2=30°∴∠A=∠ABC=30°.15.解:∵90ACB ∠=︒∴90BCE ACD ∠+∠=︒∵AD CE BE CE ⊥⊥,∴9090ADC CEB CAD ACD ∠=∠=︒∠+∠=︒, ∴CAD BCE ∠∠=在ACD 与CBE 中{∠ADC =∠CEB∠BCE =∠CAD AC =BC∴()AAS ACD CBE ≌∴BE CD CE AD ==,∴ 2.5 1.70.8cm BE CD CE DE AD DE ==-=-=-=. 答:BE 的长为0.8cm .16.证明:∵AE =CF∴AE +EF =CF +EF ,即AF =CE∵DE ⊥AC 于点E ,BF AC ⊥于点F∴ABF 和CDE 是直角三角形在Rt ABF 和Rt CDE 中{AB =CD AF =CE∴Rt △ABF ≌Rt △CDE(HL),∴BF =DE ;在DEM 和△BFM 中{∠DEM =∠BFM =90°∠DME =∠BMF DE =BF∴△DEM ≌△BFM(AAS),∴MB =MD .17.(1)证明:如图,∵AE 、BE 分别平分∠DAB 、∠CBA∴∠1=∠2,∠3=∠4∵AD∥BC∴∠2=∠F,∠1=∠F在△ABE和△AFE中∴△ABE≌△AFE(AAS)(2)证明:∵△ABE≌△AFE∴BE=EF在△BCE和△FDE中∴△BCE≌△FDE(ASA)∴BC=DF∴AD+BC=AD+DF=AF=AB即AD+BC=AB.18.(1)证明:∵EC平分∠ACB ∴∠FCD=∠FCG∵CG=CD,CF=CF∴△CFD≌△CFG(SAS)∴FD=FG.(2)解:结论:FG=FE.理由:∵∠B=60°∴∠BAC+∠BCA=120°∵AD平分∠BAC,CE平分∠BCA∴∠ACF+∠FAC=12(∠BCA+∠BAC)=60°∴∠AFC=120°,∠CFD=∠AFE=60°∵△CFD≌△CFG∴∠CFD=∠CFG=60°∴∠AFG=∠AFE=60°∵AF=AF,∠FAG=∠FAE∴△AFG≌△AFE(ASA)∴FG=FE.(3)解:结论:(1)中结论成立.(2)中结论不成立. 理由:①同法可证△CFD≌△CFG(SAS)∴FD=FG.②∵∠B≠60°∴无法证明∠AFG=∠AFE∴不能判断△AFG≌△AFE∴(2)中结论不成立。
全等三角形单元测试题(含答案)

全等三角形单元测试题一、填空题(每小题4分,共32分).1.已知:///≌,/ABC A B C∆∆∠=∠,70B B∠=∠,/A A=,则AB cmC∠=︒,15 /∠=_________,//CA B=__________.∆中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角2.如图1,在ABC形_______对.图1 图2 图33.已知△AB C≌△A′B′C′,若△ABC的面积为10 cm2,则△A′B′C′的面积为______ cm2,若△A′B′C′的周长为16 cm,则△AB C的周长为________cm.4.如图2所示,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是________________(只添一个条件即可).5.如图3所示,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还需补充一个条件________,依据是________________.6.三角形两外角平分线和第三个角的内角平分线_____一点,且该点在三角形______部.7.如图4,两平面镜α、β的夹角θ,入射光线AO平行于β,入射到α上,经两次反射后的出射光线CB平行于α,则角θ等于________.图4 图5 图68.如图5,直线AE ∥BD ,点C 在BD 上,若AE =4,BD =8,△ABD 的面积为16,则ACE △ 的面积为______.二、选择题(每小题4分,共24分)9.如图6,AE =AF ,AB =AC ,EC 与B F 交于点O ,∠A =600,∠B =250,则∠EOB 的度数为( )A 、600B 、700C 、750D 、85010.△ABC ≌△DEF ,且△ABC 的周长为100 cm ,A 、B 分别与D 、E 对应,且AB =35 cm ,DF =30 cm ,则EF 的长为( )A .35 cmB .30 cmC .45 cmD .55 cm11.图7是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在________两点上的木条.( )A .A 、FB .C 、E C .C 、AD .E 、F12.要测量河两岸相对的两点A 、B 的距离,先在AB 的垂线BF 上取两点C 、D ,使CD =•BC ,再定出BF的垂线DE ,使A 、C 、E 在一条直线上,可以证明△EDC ≌△ABC ,•得到ED =AB ,因此测得ED 的长就是AB 的长(如图8),判定△EDC ≌△ABC 的理由是( )A .边角边公理B .角边角公理;C .边边边公理D .斜边直角边公理13.如图9,在△ABC 中,∠A :∠B :∠C =3:5:10,又△MNC ≌△ABC ,则∠BCM :∠BCN 等于( )A .1:2B .1:3C .2:3D .1:414.如图10,P 是∠AOB 平分线上一点,CD ⊥OP 于F ,并分别交OA 、OB 于CD ,则CD _____P 点到∠AOB N A M C B 图7 图8 图9 图10两边距离之和.( )A.小于B.大于C.等于D.不能确定三、解答题(共46分)中,∠ACB=90°,延长BC至B',使15.已知如图11,ABCC B'=BC,连结A B'.求证:△AB B'是等腰三角形.参考答案。
苏科版八年级数学上册试题 第1章 全等三角形 单元测试卷(含详解)

第1章《 全等三角形》单元测试卷一、单选题(本大题共10小题,每小题3分,共30分)1.下列说法正确的是( )A .两个等边三角形一定全等B .腰对应相等的两个等腰三角形全等C .形状相同的两个三角形全等D .全等三角形的面积一定相等2.已知与全等,A 、B 、C 的对应点分别为D 、E 、F ,且E 点在AE 上,B 、F 、C 、D 四点共线,如图所示若,,则下列叙述何者正确?( )A .,B .,C .,D .,3.如图,在△ABC 中,AB =BC ,点D 为AC 上的点,连接BD ,点E 在△ABC 外,连接AE ,BE ,使得CD =BE ,∠ABE =∠C ,过点B 作BF ⊥AC 交AC 点F ,若∠BAE =21°,∠C =28°,则∠FBD =( )A .49°B .59°C .41°D .51°4.如图,有一块边长为4的正方形塑料模板,将一块足够大的直角三角板的直角顶点落在点,两条直角边分别与交于点F ,与延长线交于点E .则四边形的面积是( )ABC V DEF V .=40A ∠︒=35CED ∠︒=EF EC =AE FC=EF EC AE FC ≠EF EC ≠=AE FC EF EC ≠AE FC≠ABCD A CD CB AECFA .4B .6C .10D .165.如图,在的网格中,每一个小正方形的边长都是1,点,,,都在格点上,连接,相交于,那么的大小是( )A .B .C .D .6.△ABC 中,AB =AC ,∠ABC =72°,以B 为圆心,以任意长为半径画弧,分别交BA 、BC 于M 、N ,再分别以M 、N为圆心,以大于MN 为半径画弧,两弧交于点P ,射线BP 交AC 于点D ,则图中与BC 相等的线段有( )A .BD B .CD C .BD 和AD D .CD 和AD7.如图,在Rt △ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AB 、AC 于点M 、N ,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,射线AP 交边BC 于点D .下列说法错误的是( )33⨯A B C D AC BD P APB ∠80︒60︒45︒30︒1212A .B .若,则点D 到AB 的距离为2C .若,则D .8.如图,长方形中,点为上一点,连接,将长方形沿着直线折叠,点恰好落在的中点上,点为的中点,点为线段上的动点,连接、,若、、,则的最小值是( )A .B .C .D .9.如图,点在线段上,于,于.,且,,点以的速度沿向终点运动,同时点以的速度从开始,在线段上往返运动(即沿运动),当点到达终点时,,同时停止运动.过,分别作的垂线,垂足为,.设运动时间为,当以,,为顶点的三角形与全等时,的值为( )A .1或3B .1或C .1或或 D .1或或510.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )CAD BAD ∠=∠2CD =30B ∠=CDA CAB ∠=∠2ABD ACDS S =V V ABCD E AD CE ABCD CE D AB F G CF P CE PF PG AE a =ED b =AF c =PF PG +a c b +-2b c +2a b c ++a b+C BD AB BD ⊥B ED BD ⊥D 90ACE ∠=︒5cm AC =6cm CE =P 2cm/s A C E →→E Q 3cm/s E EC E C E C →→→→⋅⋅⋅P P Q P Q BD M N s t P C M QCN △t 115115235115ABC V 60A ∠=︒ABC ∠ACB ∠BD CE O BD AC D CE AB E ABC V 207BC =:4:3AE AD =AEA. B . C . D .4二、填空题(本大题共8小题,每小题4分,共32分)11.如图,已知正方形中阴影部分的面积为3,则正方形的面积为 .12.数学课上,老师出示如下题目:“已知:.求作:.”如图是小宇用直尺和圆规的作法,其中的道理是作出△,根据全等三角形的性质,得到.△的依据是 .13.如图,已知,,,直线与,分别交于点,,且,,则的度数为 .14.如图,在△ABC 中,点D 是AC 的中点,分别以AB ,BC 为直角边向△ABC 外作等腰直角三角形ABM 和等腰直角三角形BCN ,其中∠ABM =NBC =∠90°,连接MN ,已知MN =4,则BD = .187247267AOB ∠A O B AOB '''∠=∠ΔC O D COD ''≅'A O B AOB '''∠=∠ΔC O D COD ''≅'AB AD =AC AE =BC DE =BC AD DE F G 65DGB ∠=︒120EAB ∠=︒CAD ∠15.如图,为的平分线,为上一点,且于点,,给出下列结论:①;②;③;④;⑤四边形的面积是面积的2倍,其中结论正确的个数有 .16.如图,把两块大小相同的含45°的三角板ACF 和三角板CFB 如图所示摆放,点D 在边AC 上,点E 在边BC 上,且∠CFE =13°,∠CFD =32°,则∠DEC 的度数为 .17.如图,在中,,,,有下列结论:①;②;③连接,;④过点作交于点,连接,则.其中正确的结论有 .18.如图,在Rt △ABC 中,∠C =90°,两锐角的角平分线交于点P ,点E 、F 分别在边BC 、AC 上,且都不与点C 重合,若∠EPF =45°,连接EF ,当AC =6,BC =8,AB =10时,则△CEF的BN MBC ∠P BN PD BC ⊥D 180APC ABC ∠+∠=︒MAP ACB ∠=∠PA PC =2BC AB CD -=BP AC =BAPC PBD △ABC V AD BC ⊥AD BD =BF AC =ADC BDF △≌△BE AC ⊥DE 135AED ∠=︒D DM AB ∥AC M FM BF AM MD =+周长为 .三、解答题(本大题共6小题,共58分)19.(8分)如图,,点E 在BC 上,且,.(1) 求证:;(2) 判断AC 和BD的位置关系,并说明理由.BD BC =BE AC =DE AB =ABC EDB V V ≌20.(8分)如图,在五边形中,,.(1) 请你添加一个条件,使得,并说明理由;(2) 在(1)的条件下,若,,求的度数.21.(10分)在复习课上,老师布置了一道思考题:如图所示,点M ,N 分别在等边的边上,且,,交于点Q .求证:.同学们利用有关知识完成了解答后,老师又提出了下列问题:(1) 若将题中“”与“”的位置交换,得到的是否仍是真命题?请你给出答案并说明理由.ABCDE AB DE =AC AD =ABC DEA △△≌66CAD ∠=︒110B ∠=︒BAE ∠ABC V ,BC CA BM CN =AM BN 60BQM ∠=︒BM CN =60BQM ∠=︒(2) 若将题中的点M ,N 分别移动到的延长线上,是否仍能得到?请你画出图形,给出答案并说明理由.22.(10分)如图1,点P 、Q 分别是边长为4cm 的等边三角形ABC 的边AB 、BC 上的动点,点P 从顶点A ,点Q 从顶点B 同时出发,且它们的速度都为1cm/s .(1)连接AQ 、CP 交于点M ,则在P ,Q 运动的过程中,证明≌;(2)会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;(3)P 、Q 运动几秒时,是直角三角形?,BC CA 60BQM ∠=︒ABQ ∆CAP ∆CMQ ∠PBQ ∆(4)如图2,若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动,直线AQ 、CP 交点为M ,则变化吗?若变化说明理由,若不变,则求出它的度数。
八年级数学上册《第十二章 全等三角形》单元测试卷及答案(人教版)
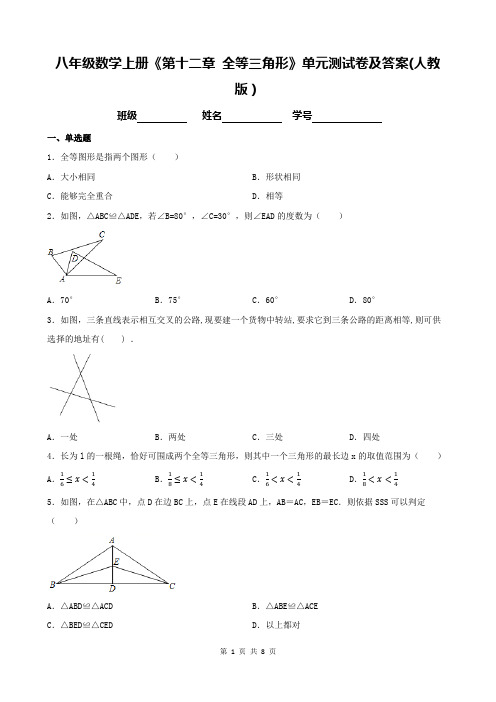
八年级数学上册《第十二章全等三角形》单元测试卷及答案(人教版)班级姓名学号一、单选题1.全等图形是指两个图形()A.大小相同B.形状相同C.能够完全重合D.相等2.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为()A.70°B.75°C.60°D.80°3.如图,三条直线表示相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) .A.一处B.两处C.三处D.四处4.长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为()A.16≤x<14B.18≤x<14C.16<x<14D.18<x<145.如图,在△ABC中,点D在边BC上,点E在线段AD上,AB=AC,EB=EC.则依据SSS可以判定()A.△ABD≌△ACD B.△ABE≌△ACEC.△BED≌△CED D.以上都对6.如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是()A.2α+∠A=180°B.α+∠A=90°C.2α+∠A=90°D.α+∠A=180°7.如图,点O在△ABC内,且到三边的距离相等,∠A=64°,则∠BOC的度数为()A.58°B.64°C.122°D.124°8.如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是()A.②③④B.①②C.①④D.①②③④二、填空题9.已知△ABC≌△DEF,若∠B=40°,∠D=30°,则∠F=10.如图,已知B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件,可以判断△ABF≌△DCE.11.如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC= cm.12.如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面AC•BD.正确的是(填写所有正确结论的序号)积S= 1213.如图,在△ABC中AC=BC,∠ACB=50°,AD⊥BC于点D,MC⊥BC于点C,MC=BC点E,点F分别在线段AD,AC上CF=AE,连接MF,BF,CE.(1)图中与MF相等的线段是;(2)当BF+CE取最小值时∠AFB=°三、解答题14.将Rt△ABC的直角顶点C置于直线l上AC=BC,分别过点A、B作直线l的垂线,垂足分别为点D、E连接AE若BE=3,DE=5求△ACE的面积.15.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.16.如图,已知AC∥BD、EA、EB分别平分∠CAB和△DBA,CD过点E,则线段AB与AC、BD有什么数量关系?请说明理由.17.如图,已知B,C,E三点在同一条直线上AC//DE,AC=CE,∠ACD=∠B .求证:△ABC≌△EDC .18.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.19.已知:AD=BC,AC=BD.(1)如图1,求证:AE=BE;(2)如图2,若AB=AC,∠D=2∠BAC,在不添加任何辅助线的情况下,请直接写出图2中四个度数为36°的角.参考答案 1.C 2.A 3.D 4.A 5.D 6.A 7.C 8.B 9.110° 10.AB=DC 11.5 12.①④ 13.(1)EC (2)9514.解:∵AD ⊥CE ,BE ⊥CE ∴∠ADC =∠CEB =90° ∵∠ACB =90°∴∠ACD =∠CBE =90°−∠ECB 在 △ACD 与 △CBE 中{∠ADC =∠CEB∠ACD =∠CBE AC =BC∴△ACD ≌△CBE (AAS) ∴CD =BE =3 AD =CE ∵CE =CD +DE =3+5=8 ∴AD =8 .S △ACE =12CE ·AD =12×8×8=32 . 15.证明:∵CE ∥DF ∴∠ACE=∠D 在△ACE 和△FDB 中{AC=FD ∠ACE=∠D EC=BD∴△ACE≌△FDB(SAS)∴AE=FB.16.解:AB=AC+BD理由是:在AB上截取AC=AF,连接EF∵AE平分∠CAB∴∠CAE=∠BAE在△CAE和△FAE中{AC=AF∠CAE=∠BAE AE=AE∴△CAE≌△FAE(SAS)∴∠C=∠AFE∵AC∥BD∴∠C+∠D=180°∴∠AFE+∠D=180°∵∠EFB+∠AFE=180°∴∠D=∠EFB∵BE平分∠ABD∴∠DBE=∠FBE在△BEF和△BED中{∠D=∠EFB∠FBE=∠DBEBE=BE∴△BEF≌△BED(AAS)∴BF=BD∵AB=AF+BF,AC=AF,BF=BD ∴AB=AC+BD.17.证明:∵AC//DE∴∠BCA =∠E ∠ACD =∠D . 又∵∠ACD =∠B ∴∠B =∠D .在 △ABC 和 △EDC 中{∠B =∠D∠BCA =∠E AC =EC∴△ABC ≌△EDC .18.解:过点D 作DE ⊥AB 于点E ,DF ⊥BC 于点F . ∴∠DEB =∠DFB =90°. 又∵BD 平分∠ABC ∴DE =DF .∵∠BMD+∠DME =180°,∠BMD+∠BND =180° ∴∠DME =∠BND . 在△EMD 和△FND 中{∠DEM =∠DFN∠EMD =∠FND DE =DF∴△EMD ≌△FND (AAS ). ∴DM =DN .19.(1)证明:在△ABD 和△BAC 中:{AB =BAAD =BC BD =AC∴△ABD ≌△BAC (SSS ) ∴∠ABD=∠BAC ∴AE=BE ;(2)∠BAC ,∠ABD ,∠DAC ,∠DBC。
八年级数学上册《全等三角形》单元测试题(含答案解析)

八年级数学上册《全等三角形》单元测试题(含答案解析)一、选择题(每题4分,共40分)1. 在三角形ABC中,AB=AC,点D是边BC上的一个点,且BD=DC。
以下结论正确的是()A. AD平分∠BACB. AD垂直平分BCC. AD平分∠BD. AD平分∠C【答案】B【解析】因为AB=AC,所以三角形ABC是等腰三角形,∠B=∠C。
又因为BD=DC,所以AD垂直平分BC。
2. 如果两个三角形的两边和它们夹角分别相等,那么这两个三角形()A. 相似B. 全等C. 不一定全等D. 以上都对【答案】B【解析】根据SAS全等定理,如果两个三角形的两边和它们夹角分别相等,那么这两个三角形全等。
3. 在全等三角形ABC和DEF中,如果∠A=40°,∠B=50°,那么∠E的度数是()A. 40°B. 50°C. 60°D. 90°【答案】C【解析】因为三角形ABC和DEF全等,所以∠A=∠D,∠B=∠E。
所以∠E=∠B=50°。
又因为三角形内角和为180°,所以∠E=180°-∠A-∠D=60°。
4. 如果两个三角形的两边及其中一边的对角分别相等,那么这两个三角形()A. 相似B. 全等C. 不一定全等D. 以上都对【答案】C【解析】这种情况不能确定两个三角形全等,因为可能存在两种情况:一种是两个三角形全等,另一种是两个三角形不全等但相似。
5. 在全等三角形ABC和DEF中,如果AB=5cm,BC=8cm,AC=10cm,那么DE的长度是()A. 5cmB. 8cmC. 10cmD. 13cm【答案】C【解析】因为三角形ABC和DEF全等,所以对应边相等,即AB=DE,所以DE=5cm。
6. 如果两个三角形的三个角分别相等,那么这两个三角形()A. 相似B. 全等C. 不一定全等D. 以上都对【答案】C【解析】如果两个三角形的三个角分别相等,那么这两个三角形不一定全等,但一定相似。
全等三角形单元测试(含答案)

全等三角形单元测试(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列作图属于尺规作图的是A.用量角器画出∠AOB,使∠AOB等于已知角αB.用圆规和直尺作线段AB,使AB等于已知线段αC.用刻度尺作出线段AB等于2倍的已知线段mD.用三角板作45°的角2.如图,某同学不小心把一块三角形玻璃打碎成三块,现在要到玻璃店配一块与原来完全相同的玻璃,最省事的方法是A.带①和②去B.只带②去C.只带③去D.都带去3.山脚下有A、B两点,要测出A、B两点间的距离.在地上取一个可以直接到达A、B点的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB,连接DE.可以证△ABC≌△DEC,得DE=AB,因此,测得DE的长就是AB的长,判定△ABC≌△DEC的理由是A.SSS B.ASA C.SAS D.AAS4.下列条件中,能判定△ABC≌△DEF的是A.AB=DE,BC=EF,∠A=∠E B.∠A=∠E,AB=EF,∠B=∠DC.∠A=∠D,∠B=∠E,∠C=∠F D.∠A=∠D,∠B=∠E,AC=DF5.如图,AB=CD,AD=CB,那么下列结论中错误的是A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD6.如图,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定7.如图,AB∥CD,BC∥AD,AB=CD,AE=CF,其中全等三角形共有对A.5 B.3 C.6 D.48.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF ≌△CDE;③点D在∠BAC的平分线上.正确的是A.①B.②C.①②D.①②③9.如图,在等边△ABC中,D,E分别是BC,AC上的点,且BD=CE,AD与BE相交于点P,则∠1+∠2的度数是A.45°B.55°C.60°D.75°10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DA平分∠CDE;②∠BAC=∠BDE ;③DE 平分∠ADB ;④BE +AC =AB ,其中正确的有A .4个B .3个C .2个D .1个二、填空题(本大题共10小题,每小题3分,共30分)11.若△ABC ≌△A ′B ′C ′,AB =3,∠A ′=30°,则A ′B ′=__________,∠A =__________°.12.如图,OC 为AOB ∠的平分线,CM OB ⊥,3CM =,则点C 到射线OA 的距离为__________.13.已知△ABC ≌△DEF ,且△ABC 的三边长分别为3,4,5,则△DEF 的周长为__________.14.如图,△ABC 的两条高AD ,BE 相交于点F ,请添加一个条件,使得△ADC ≌△BEC (不添加其他字母及辅助线),你添加的条件是__________.15.如图,在Rt △ABC 中,∠ACB =90°,BC =2 cm ,CD ⊥AB ,在AC 上取一点E ,使EC =BC ,过点E 作EF ⊥AC 交CD 的延长线于点F .若EF =8 cm ,则AE =__________cm .16.如图,△ABC 中,D 是AB 的中点,DE ⊥AB ,∠ACE +∠BCE =180°,EF ⊥AC 交AC 于F ,AC =12,BC =8,则AF =________.17.如图,Rt △ABC 中,∠C =90°,BD 平分∠ABC 交边AC 于点D ,CD =4,△ABD 的面积为10,则AB 的长是__________.18.如图,AB =AC ,AD =AE ,∠BAC =∠DAE ,点D 在线段BE 上.若∠1=25°,∠2=30°,则∠3=__________.19.如图,五边形ABCDE 中,∠B =∠E =90°,AB =CD =AE =BC +DE =2,则这个五边形ABCDE 的面积是__________.20.如图,Rt △ABC 中,9083C AC BC ∠=︒==,,,AE AC P Q ⊥,,分别是AC AE ,上的动点,且PQ AB =,当AP =__________时,才能使ABC △和PQA △全等.三、解答题(本大题共8小题,共60分.解答应写出文字说明、证明过程或演算步骤) 21.如图,已知∠1=∠2,∠B =∠D ,求证:CB =CD .22.如图,点E ,F 在AB 上,CE 与DF 交于点G ,AD =BC ,∠A =∠B ,AE =BF .求证:GE =GF .23.如图,12AC AE AB AD =∠=∠=,,.求证:BC DE =.24.如图,在Rt △ABC 中,∠C =90°.作∠BAC 的平分线AP 交边BC 于点D .(保留作图痕迹,不写作法).若∠BAC =28°,求∠ADB 的度数.25.如图,AD 是BAC ∠的平分线,点E 在AB 上,且AE AC =,EF BC ∥交AC 于点F .试说明:EC平分DEF ∠.26.如图,在△BCE 中,AC ⊥BE ,AB =AC ,点A 、点F 分别在BE 、CE 上,BE 、CF 相交于点D ,BD =CE .求证:AD =AE .27.如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BA C.(1)求证:∠ABD=∠ACD;(2)若∠ACB=65°,求∠BDC的度数.28.如图,△ABC是边长为5 cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿射线AB,BC运动,且它们的速度都为2 cm/s.设点P的运动时间为t(s).(1)当t为何值时,△ABQ≌△CBP;(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.3.【答案】C【解析】因为CD=CA,CE=CB,ACB DCE∠=∠,所以△ABC≌△DEC(SAS).故选C.4.【答案】D【解析】A.AB=DE,BC=EF,∠A=∠E,SSA不能确定全等;B.∠A=∠E,AB=EF,∠B=∠D,AB和EF不是对应边,不能确定全等;C.∠A=∠D,∠B=∠E,∠C=∠F,AAA不能确定全等;D.∠A=∠D,∠B=∠E,AC=DF,根据AAS,能判断△ABC≌△DEF.故选D.5.【答案】B【解析】∵在△ABD和△CDB中,AB CD AD CB BD BD=⎧⎪=⎨⎪=⎩,∴△ABD≌△CDB,∴∠ADB=∠CBD,∠ABD=∠CDB,∠A=∠C,∴AD∥BC,AB∥CD,∴A、C、D选项正确.故选B.6.【答案】A【解析】∵AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,PA=PB,∠CPA=∠DPB,∴△CPA≌△∠DPB(AAS),∴PC=PD,∴∠1=∠2,故选A.7.【答案】B【解析】根据AB=CD,AE=CF,∠BAE=∠DCF可得:△ABE≌△CDF;根据CE=AF,∠DAF=∠BCE,∠DFA=∠BEC可得:△ADF≌△CBE;根据∠DAC=∠BCA,∠BAC=∠DCA,AC=CA可得:△ACD≌△CAB,共有3对全等三角形,故选B.8.【答案】D∵△ABE≌△ACF,∴AE=AF,∵△BDF≌△CDE,∴DF=DE,∵在△AFD和△AED中,AF AE AD AD DF DE=⎧⎪=⎨⎪=⎩,∴△AFD≌△AED(SSS),∴∠FAD=∠EAD,∴AD平分∠BAC,即点D在∠BAC的平分线上.综上所述,在本题给出的结论中,正确的是①②③.故选D.9.【答案】C【解析】∵在等边△ABC中,∠ABC=∠C=60°,AB=BC,BD=CE,∴△ABD≌△BCE,∴∠CBE=∠1,而∠CBE+∠2=60°,∴∠1+∠2=60°.故选C.10.【答案】B【解析】根据题中条件,结合图形及角平分线的性质得到:∵AD平分∠BAC,∴∠DAC=∠DAE,∵∠C=90°,DE⊥AB,∴∠C=∠E=90°,∵AD=AD,∴△DAC≌△DAE,∴∠CDA=∠EDA,∴①AD 平分∠CDE正确;无法证明∠BDE=60°,∴③DE平分∠ADB错误;∵BE+AE=AB,AE=AC,∴BE+AC=AB,∴④BE+AC=AB正确;∵∠BDE=90°-∠B,∠BAC=90°-∠B,∴∠BDE=∠BAC,∴②∠BAC=∠BDE正确.故选B.11.【答案】3;30【解析】由对应角相等,对应边相等,A′B′=AB ,∠A =30°.故答案为:3;30. 12.【答案】3【解析】如图,过C 作CF ⊥AO .∵OC 为∠AOB 的平分线,CM ⊥OB ,∴CM =CF .∵CM =3,∴CF =3.故答案为:3.角的余角相等),在△FCE 和△ABC 中,90ECF BEC BC ACB FEC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴△ABC ≌△FCE (ASA ),∴AC =EF ,∵AE =AC -CE ,BC =2 cm ,EF =8 cm ,∴AE =8-2=6 cm ,故答案为:6. 16.【答案】10【解析】如图,连接AE ,BE ,过E 作EG ⊥BC 于G ,∵D是AB的中点,DE⊥AB,∴DE垂直平分AB,∴AE=BE,∵∠ACE+∠BCE=180°,∠ECG+∠BCE=180°,∴∠ACE=∠ECG,又∵EF⊥AC,EG⊥BC,∴EF=EG,∠FEC=∠GEC,∵CF⊥EF,CG⊥EG,∴CF=CG,在Rt△AEF和Rt△BEG中,AE BEEF EG=⎧⎨=⎩,∴Rt△AEF≌Rt△BEG(HL),∴AF=BG,设CF=CG=x,则AF=AC-CF=12-x,BG=BC+CG=8+x,∴12-x=8+x,解得x=2,∴AF=12-2=10.故答案为:10.17.【答案】5【解析】如图,过点D作DE⊥AB于点E.∵BD平分∠ABC.又∵DE⊥AB,DC⊥BC,∴DE=DC=4.∵△ABD的面积=12·AB·DE=12×AB×4=10,∴AB=5.故答案为:5.20.【答案】3或8【解析】分为两种情况:①当AP=3时,∵BC=3,∴AP=BC,∵∠C=90°,AE⊥AC,∴∠C=∠QAP=90°,∴在Rt △ABC 和Rt △QAP 中,AB PQ BC AP =⎧⎨=⎩,∴Rt △ABC ≌Rt △PQA (HL ); ②当AP =8时,∵AC =8,∴AP =AC ,∵∠C =90°,AE ⊥AC ,∴∠C =∠QAP =90°,∴在Rt △ABC 和Rt △QAP中,AB PQ AC AP =⎧⎨=⎩,∴Rt △ABC ≌Rt △QAP (HL ),故答案为:3或8.22.【解析】∵AE =BF ,∴AE +EF =BF +EF ,∴AF =BE ,在△ADF 与△BCE 中,=AD BC A B AF BE =⎧⎪⎨⎪=⎩∠∠,∴△ADF ≌△BCE (SAS ),∴∠CEB =∠DFA ,∴GE =GF .23.【解析】∵12∠=∠,∴12BAE BAE ∠+∠=∠+∠,即BAC DAE ∠=∠,在BAC △和DAE △中,AC AE BAC DAE AB AD =⎧⎪∠=∠⎨⎪=⎩,∴BAC △≌DAE △(SAS ),∴BC DE =.24.【解析】(1)如下图所示,AD 为所求的角平分线:(2)∵∠BAC 的平分线AP ,∠BAC =28°, ∴∠CAD =BAD =14°,又∵∠C =90°,∠ADB =∠C +∠CAD ,∴∠ADB =90°+14°=104°.26.【解析】∵AC ⊥BE ,∴∠BAD =∠CAE =90°,在Rt △ABD 和Rt △ACE 中,BD CE AB AC =⎧⎨=⎩, ∴Rt △ABD ≌Rt △ACE (HL ),∴AD =AE .27.【解析】(1)∵∠BAC =∠EAD ,∴∠BAC -∠EAC =∠EAD -∠EAC ,即:∠BAE=∠CAD,在△ABE和△ACD中,AB ACBAE CAD AE AD=⎧⎪∠=∠⎨⎪=⎩,28.【解析】(1)∵△ABQ≌△CBP,∴BQ=BP,∴2t=5-2t,∴t=54,∴t=54s时,△ABQ≌△CBP,(2)结论:∠CMQ=60°不变,理由:∵△ABC是等边三角形,∴∠ABQ=∠CAP,AB=CA,又∵点P,Q运动速度相同,∴AP=BQ,在△ABQ与△CAP中,AB CAABQ CAP AP BQ=⎧⎪∠=∠⎨⎪=⎩,∴△ABQ≌△CAP(SAS),∴∠BAQ=∠ACP,∵∠QMC=∠ACP+∠MAC,∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《全等三角形》单元测试题
姓名 班级 得分
一、填空题(4×10=40分)
1、在△ABC 中,AC>BC>AB ,且△ABC ≌△DEF ,则在△DEF 中,______>______>_______(填边)。
2、已知:△ABC ≌△A ′B ′C ′,∠A=∠A ′,∠B=∠B ′,∠C=70°,AB=15cm ,则∠C ′=_________,A ′B ′=__________。
3、如图1,△ABD ≌△BAC ,若AD=BC ,则∠BAD 的对应角是________。
4、如图2,在△ABC 和△FED ,AD=FC ,AB=FE ,当添加条件__________时,就可得到△ABC ≌△FED 。
(只需填写一个你认为正确的条件)
5、如图3,在△ABC 中,AB=AC ,AD ⊥BC 于D 点,E 、F 分别为DB 、DC 的中点,则图中共有全等三角形________对。
6、如图4,BE ,CD 是△ABC 的高,且BD =EC ,判定△BCD ≌△CBE 的依据是 .
7、如图5,△ABC 中,∠C=90°,CD ⊥AB 于点D ,AE 是∠BAC 的平分线,点E 到AB 的距离等于3cm ,则CF= cm.
8、如图6,在△ABC 中,AD =DE ,AB =BE ,∠A =80°,则∠CED =_____.
9、P 是∠AOB 平分线上一点,CD ⊥OP 于F ,并分别交OA 、OB 于CD ,则CD_____P 点到∠AOB 两边距离之和。
(填“>”,“<”或“=”)
10、AD 是△ABC 的边BC 上的中线,AB =12,AC =8,则中线AD 的取值范围是
二、选择题:(每小题5分,共30分)
11、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等, 其中真命题的个数有( )
A 、3个
B 、2个
C 、1个
D 、0个
12、如图7,已知点E 在△ABC 的外部,点D 在BC 边上,
A
D E
C
B
图4
A
B
D
E 图1 图2 图3
图5
图6
DE 交AC 于F ,若∠1=∠2=∠3,AC=AE ,则有( ) A 、△ABD ≌△AFD B 、△AFE ≌△ADC
C 、△AEF ≌△DFC
D 、△ABC ≌△ADE
13、下列条件中,不能判定△ABC ≌△A ′B ′C ′的是( ) A 、AB=A ′B ′,∠A=∠A ′,AC=A ′C ′
B 、AB=A ′B ′,∠A=∠A ′,∠B=∠B ′
C 、AB=A ′B ′,∠A=∠A ′,∠C=∠C ′
D 、∠A=∠A ′,∠B=∠B ′,∠C=∠C ′
14、如图8所示,90E F ∠=∠=,B C ∠=∠,AE AF =,结论:①EM FN =;②CD DN =;③FAN EAM ∠=∠;④ACN ABM △≌△.其中
正确的有( )
A .1个
B .2个
C .3个
D .4个
15、全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三
角形与镜面合同三角形,假设△ABC 和△A 1B 1C 1是全等(合同)三角形,点A 与点A 1对应,点B 与点B 1对应,点C 与点C 1对应,当沿周界A →B →C →A ,及A 1→B 1→A 1环绕时,若运动方向相同,则称它们是真正合同三角形(如图9),若运动方向相反,则称它们是镜面合同三角形(如图10),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°(如图11),下列各组合同三角形中,是镜面合同三角形的是( )
16、如图12,在△ABC 中,∠C=90°,AD 平分∠BAC 交BC 于D , 若BC=64,且BD :CD=9:7,则点D 到AB 边的距离为( ) A 、18 B 、32 C 、28 D 、24
三、解答下列各题:(17-18题各8分,19-2280分)
17、如图13,点A 、B 、C 、D AB=DC ,AE//DF ,AE=DF ,求证:EC=FB
18、如图14,AE 是∠BAC 的平分线,AB=AC 。
⑴若点D 是AE 上任意一点,则△ABD ≌△ACD ;⑵若点D 是AE 反向延长线上一点,结论还成立吗?试说明你的猜想。
A
C
D
B
图12
E
C
B D F
A
图7
图8
图13
19、如图15,在一次军事演习中,红方侦察员发现蓝方指挥部在A 区内,到铁路到公路的距离相等,且离铁路与公路交叉处B 点700米,如果你是红方的指挥员,请你在图16所示的作战图上标出蓝方指挥部的位置,并简要说明画法和理由。
20、如图17,A 、B 两建筑物位于河的两岸,要测得它们之间的距离,可以从B 点出发沿河岸画一条射线BF ,在BF 上截取BC=CD ,过D 作DE ∥AB ,使E 、C 、A 在同一直线上,则DE 的长就是A 、B 之间的距离,请你说明道理。
21、如图18,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是282
cm ,
AB=20cm ,AC=8cm ,求DE 的长。
B A C
D
E
A
A
B
图14 图16
图15 图17
22、如图19,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC
23、如图20,AB=CD,AD=CB,求证:∠B=∠D
E C
A
图18 图19
图20
24、如图21,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF
⑴求证:BG=CF
⑵请你判断BE+CF与EF的大小关系,并说明理由。
图21
参考答案:
一、⑴DF EF DE ⑵70°15cm ⑶∠ABC ⑷∠A=∠F
⑸4 ⑹150°(7)3 (8)80°(9)大于(10)2<AD<10
二、⑾C ⑿D (13)D (14)C (15)B (16)C
三、(17) 略
(18)①△ABD≌△ACD ∵AB=AC ∠BAC=∠CAD AD=AD
②无论D在AE上或AE的反向延长线上,结论都成立,证明过程如①
(19)在两条路所夹角的平分线上,由比例尺算出到B点的距离为3.5cm。
(20)DE=AE 由△ABC≌△EDC可知
(21)DE=2cm
(22)AD平分∠BAC DE⊥AB于E,DF⊥AC于F,∴DE=DF
又∵DB=DC ∴Rt△DBE≌Rt△DCF(HL) ∴EB=FC
(23)提示:连接BD。
(24)①∵AC∥BG ∴∠GBD=∠C,在△GBD与△FCD中,∠GBD=∠C
BD=CD ∠BDG=∠CDF ∴△GBD≌△FCD ∴BG=CF
②BE+CF>EF,又∵△GBD≌△FCD(已证) ∴GD=FD,在△GDE与△FDE中,GD=FD,∠GDE=∠FDE=90°DE=DE ∴△GDE≌△FDE(SAS)
∴EG=EF ∵BE+BG>GE ∴BE+CF>EF。
