异步电机转子磁链闭环观测方法及仿真
异步电动机转子磁链观测方法的比较与研究

异步电动机转子磁链观测方法的比较与研究转子磁链、观测方法、比较、矢量控制、直接转矩控制1 引言在异步电动机变频调速控制系统中,矢量控制技术和直接转矩控制技术得以有效实现的一个重要基础是在于异步电动机磁链信息的准确获取,这就需要知道磁链的幅值和相位。
根据三相异步电动机在两相任意转速旋转坐标系下的数学模型可知,定子、转子和气隙磁链的方程式为:定子磁链:(1)转子磁链:(2)气隙磁链:(3)从以上方程式不难看出定子、转子和气隙磁链三者只要有一个获得,另外两个就可推导而出。
因此异步电动机就有三种与之相对应的磁场定向方法,分别是按定子磁场定向、按转子磁场定向和按气隙磁场定向。
不过按定子、气隙磁场定向方法未能实现iM和iT的完全解耦,因此按转子磁场定向是目前主要采用的方法,它可以实现磁通电流分量、转矩电流分量的完全解耦。
下面就对转子磁链观测的方法进行一些比较研究,从而为实际应用时选择合适的观测器提供依据。
转子磁链的观测最初是采用直接检测气隙磁链的方法,就是在电机定子内表面装贴霍尔元件或其他磁敏元件,或者在电机槽内埋设探测线圈。
利用被测量的气隙磁通,由式(2)、(3)就可得到转子磁通。
从理论上讲,该方法应该比较准确,但实际上埋设探测线圈和装贴磁敏元件都会遇到不少工艺和技术上的问题,在一定程度上破坏了电机的机械鲁棒性。
同时由于齿槽影响,使检测信号中含有较大的脉动分量,越到低速时越严重。
因此在实用的系统中,多采用间接计算的办法,即利用容易测量的电压、电流或转速等信号,借助转子磁链观测模型,实时计算磁链的模值和空间位置。
2 转子磁链的间接获取方法根据实测信号的不同组合,可以有多种转子磁链观测模型,总的说来可以分为两大类:开环观测模型和闭环观测模型。
2.1 开环观测模型(1)电流模型法根据描述磁链与电流关系的磁链方程来计算转子磁链,所得出的模型叫做电流模型,它可以在不同的坐标系下获得。
● 在两相静止坐标系α-β下转子磁链的电流模型由实测的三相定子电流经过Clarke变换很容易得到两相静止坐标系上的电流isα和isβ。
带转矩内环的转速、磁链闭环矢量控制系统的仿真

带转矩内环的转速、磁链闭环矢量控制系统的仿真1、 仿真模型1.5psir*psiS2psiSDiscrete,Ts = 1e-005 s.pow ergui1400n*nisabcg A BC+-inverteriabc*iSqiSdi0dq0sin_cosabcdq0_to_abcatr asrapsirTe TLmis_abcphis_qd wm TeMachines Demuxi*abc iabcpulsesGeneration-K-2*0.0693*u(1)*u(2)/0.071FcnDemuxDC 510viabcwr psir ist sincosCurrent modelTm mABC Asynchronous MachineSI Unitspsir*psirism*ApsiRTe*1Teist*ATRn*nTe*ASR各个子模块的仿真模型 ①转矩调节器的模型②转速调节器的模型③磁链调节器的模型④按转子磁链定向的转子磁链电流模型2、控制原理带转矩内环的转速、磁链闭环矢量控制系统的仿真模型中,其中直流电源DC、逆变器inverter、电动机motor和电动机测量模块的主电路,逆变器的驱动信号由滞环脉冲发生器模块产生。
三个调节器ASR、ATR和ApsiR均是带输出限幅的PI调节器。
转子磁链观测使用二相同步旋转坐标系上的磁链模型,函数模块Fcn用于计算转矩,dq0-to-abc 模块用于2r/3s的坐标转换。
在控制电路中,在转速环后增加了转矩控制内环,转速调节器ASR的输出是转矩调节器ATR的给定Te*,而转矩的反馈信号Te,则通过矢量控制方程得到。
调机器参数参考值3、仿真的输出结果00.10.20.30.40.50.60.70.80.9150010001500t/sn /(r /m i n )转速响应00.10.20.30.40.50.60.70.80.91-2020406080100120t/s电动机输出转矩0.10.20.30.40.50.60.70.80.91-1-0.8-0.6-0.4-0.200.20.40.60.81t/s isd0.10.20.30.40.50.60.70.80.91-1-0.8-0.6-0.4-0.200.20.40.60.81t/sisq00.10.20.30.40.50.60.70.80.912468101214t/s磁链调节器ApsiR 的输出0.10.20.30.40.50.60.70.80.91-20-1001020304050607080t/s转速调节器输出00.10.20.30.40.50.60.70.80.91-10102030405060t/s转矩调节器输出00.10.20.30.40.50.60.70.80.91-80-60-40-20020406080t/s电流isa 的输出00.10.20.30.40.50.60.70.80.91-80-60-40-20020406080t/s电流ia*的输出定子磁链轨迹转矩-转速曲线4、仿真总结由于电力系统的运行过程中的各个参数不能直接观测,为了跟好的了解系统各个参数的变化及其走向,能更好的做到控制。
基于转子磁链定向d-q坐标的异步电机控制系统仿真

基于转子磁链定向d-q坐标的异步电机控制系统仿真
朱里红;黄喜恒
【期刊名称】《测控技术》
【年(卷),期】2016(035)010
【摘要】为了解决异步电机在调速过程中强耦合性的问题,实现定子电流转换成在d-q坐标系下的转子磁链,并保证其同步,通过矢量算法建立磁链电流模型,计算出电动机转子磁链Ψ,,并且在磁链闭环控制下保持不变.根据转差率间接求解方法实现了速度闭环控制,保证了系统在复杂环境下稳定运行.
【总页数】4页(P62-65)
【作者】朱里红;黄喜恒
【作者单位】成都理工大学工程技术学院,四川乐山614000;成都理工大学工程技术学院,四川乐山614000
【正文语种】中文
【中图分类】TN301.2
【相关文献】
1.基于MATLAB的异步电机转子磁场定向矢量控制系统仿真 [J], 常伟
2.按转子磁链定向的矢量控制系统仿真研究 [J], 郭瑞;王庆贤
3.按转子磁链定向的异步电机转差型矢量控制系统仿真研究 [J], 张燕燕;张宝栋;王爱华;高楠楠;刘朝阳;李培;杨巍巍
4.基于BP神经网络的异步电机转子磁链定向矢量复合控制 [J], 李海侠;林继灿;符士宾;张晖东
5.基于定子电流矢量定向的异步电机转子磁链估计器及其应用研究 [J], 张春朋;林飞;宋文超;高龙;陈寿孙
因版权原因,仅展示原文概要,查看原文内容请购买。
一种闭环磁链观测器的仿真研究

可见 ,5 式就是定 子磁链 的 一i 测模型 。现在 主要 的问题 是 () 观
如何配 置观测器 的极点 以保证观测误差 的快速收 敛。借鉴 一 观 测 模型 中的电流调节器概念 , 复杂 的极点配置工 作简化为 P 参数 的确 将 I 定问题 。在 这里 , 电流 调节 器的作用是强迫 电机状态 观测器的 电流 与 实际 的电机 电流相等 , 如果 观测器所得 电流与实际测量 的电机 电流不 相等 , 产生一个差值送 到P 电流调 节器 的输入端 , 就会 I 电流调节器就会 输出补偿信号加到积分项 以修正 和 , 直到 与 i 相等 , 与 相 等, 这时电流调节器才停止工作 。此时 , 观测的定子磁链就和实 际定子
的问题 , 究了闭环磁链观测 器的构成 , 研 仿真验证 了其对定子磁链观 测的准确性 。 [ 关键词 ] 直接转矩控制 定子磁链 闭环磁链观测 器
1前 言 .
直接转矩控制是 目前 异步电动机 的一种 高性能控制方法。它一方 面实现转 矩的直 接控制 , 另一方 面实现定子磁链 的直接控制 。为了实 现对定 子磁链 的闭环 控制 , 需要将 其检测 出来 。由于直接检测定 子磁 链存 在着 制造 工 艺 、 使用 环境 以及 成本等 问题 , 在实际 系统 中很 少使 用 。一般通过易 于测量 的电机其 他物 理量如定子电压 、 电流 、 转速等建 立定子磁 链的观测模 型 , 在控制 中实时地计算 出定 子磁链 的幅值 和相 位 。若磁 链实际值 观测不准 , 将会 导致 电动机 的实际定子磁链过饱 和 或者处 于欠磁状态 , 有可能会引起 电动机的发热 、 振动等 , 导致 电机的
按照转子磁链定向的矢量控制系统仿真
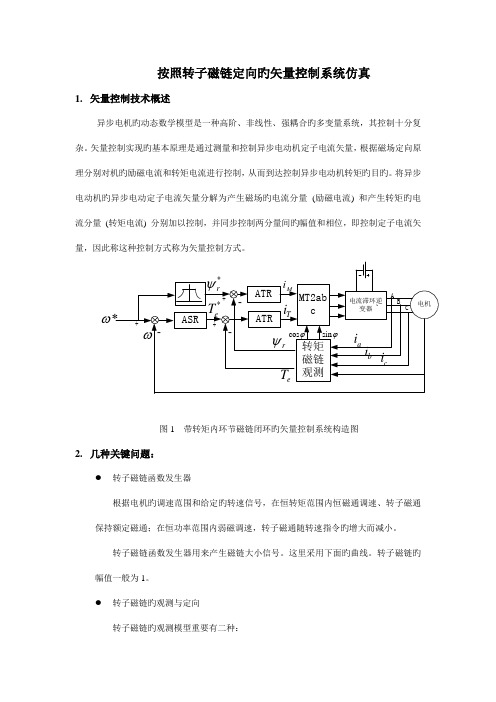
按照转子磁链定向旳矢量控制系统仿真1.矢量控制技术概述异步电机旳动态数学模型是一种高阶、非线性、强耦合旳多变量系统,其控制十分复杂。
矢量控制实现旳基本原理是通过测量和控制异步电动机定子电流矢量,根据磁场定向原理分别对机旳励磁电流和转矩电流进行控制,从而到达控制异步电动机转矩旳目旳。
将异步电动机旳异步电动定子电流矢量分解为产生磁场旳电流分量(励磁电流) 和产生转矩旳电流分量(转矩电流) 分别加以控制,并同步控制两分量间旳幅值和相位,即控制定子电流矢量,因此称这种控制方式称为矢量控制方式。
ω图1 带转矩内环节磁链闭环旳矢量控制系统构造图2.几种关键问题:●转子磁链函数发生器根据电机旳调速范围和给定旳转速信号,在恒转矩范围内恒磁通调速、转子磁通保持额定磁通;在恒功率范围内弱磁调速,转子磁通随转速指令旳增大而减小。
转子磁链函数发生器用来产生磁链大小信号。
这里采用下面旳曲线。
转子磁链旳幅值一般为1。
●转子磁链旳观测与定向转子磁链旳观测模型重要有二种:(1) 在两相静止坐标系上旳转子磁链模型电机旳定子电压和电流由传感器测得后,通过3S/2S 变换,再根据异步电机在两项静止坐标系下旳数学模型,计算转子磁链旳大小。
()r αm s αr r βr 11L i T T p ψωψ=-+ ()r βm s βr r αr 11L i T T p ψωψ=++ (2) 按磁场定向两相旋转坐标系上旳转子磁链模型三相定子电流 iA 、 iB 、iC 经3/2变换变成两相静止坐标系电流 is α 、 is β ,再经同步旋转变换并按转子磁链定向,得到M ,T 坐标系上旳电流 ism 、ist ,运用矢量控制方程式m st1s r rL i T ωωωψ-==mr smr 1L i T p ψ=+可以获得 ψr 和 ωs 信号,由ωs 与实测转速 ω 相加得到定子频率信号ω1,再经积分即为转子磁链旳相位角ϕ ,它也就是同步旋转变换旳旋转相位角。
磁链观测方案

异步电机矢量控制方案论证一,概述三相异步电机具有结构简单,牢固,维修方便,价格便宜等特点,目前在工业领域中得到广泛应用。
早期的变频调速采用变压变频(VVVF)速度开环的方式,基频以下为恒压频比控制,在低速时,提高电压以补偿定子阻抗压降。
这种调速方法的控制结构简单,成本低,适用于风机等对调速系统动态特性要求不高的场合,但是对于动态和静态性能要求高的场合,这种开环系统就无法提供足够的保障。
1971年德国西门子公司的F.Blashke等革命性地提出了“感应电机磁场定向控制原理(Fieldorientation)”,即矢量控制技术,使交流传动的转矩静动态特性取得质的改善,完全可与直流调速系统相媲美。
矢量控制的实质是利用美国A.A.Clark提出的“感应电机定子电压的坐标变换控制”原理。
经过不断的实践和改进,形成了现已得到普遍应用的矢量控制变频调速技术。
矢量控制通过引入坐标变换,把复杂的异步电机等效为简单的模型,在保证磁场准确定向的情况下,可以实现励磁电流和转矩电流的解耦,使得交流电机的转矩控制性能可以与直流电机相比拟,这无疑是交流传动控制理论上的一个质的飞跃。
转子磁场的定向控制就是在将旋转坐标系放在同步旋转磁场上,将电机的转子磁通作为旋转坐标系的直轴。
若忽略由反电动势引起的交叉耦合,检测出定子电流的直轴分量,就可以观测转子磁通幅值,但转子磁通恒定电磁转矩与定子电流的交轴分量成正比,通过控制定子电流的交轴分量就实现对电磁转矩的控制,此时称定子电流的直轴分量为励磁分量,定子电交轴分量为转矩分量。
可由电压方程的直轴分量控制转子磁通,交轴分量控制转矩从而实现磁通和转矩的解耦控制。
转子磁场定向的最大的优点是达到了完全解耦,无需增加解耦器,控制方式简单,具有良好的动态性能和控制精度。
在异步电机矢量控制中,要实现准确的解耦,必须要知道转子磁链准确的相位角。
而在直接矢量控制中,为了实现磁链的反馈控制,还要知道转子磁链准确的幅值。
异步电动机仿真指导书

异步电动机按转子磁链定向的矢量控制系统仿真指导书一、实验目的:⒈深入理解异步电动机的矢量控制策略。
⒉了解基于MATLAB 仿真实现异步电动机矢量控制变频调速系统的构成。
⒊掌握异步电动机矢量控制系统的分析、设计、调试方法。
二、实验开发设计原理:(1)本实验的异步电机FOC 交流调速控制系统总框图如下图所示:图1异步电机FOC 交流调速控制系统框图采用双闭环结构,空间矢量脉宽调制(SVPWM )控制策略,内环是调节电流的电流环,外环是调节转速的转速环,都采用PI 控制调节。
(2)程序设计内容本实验的程序设计主要包含以下模块:Clark-Park 变换模块;转子磁链位置计算模块(磁通观测定向);速度PI 调节器模块;转矩电流PI 调节器模块;励磁电流PI 调节器模块;磁链PI 调节器模块;Park 逆变换模块;svpwm 模块。
三、仿真设计举例:鼠笼异步电动机铭牌数据为:额定功率kW P N 3=,额定电压V 380=N U ,额定电流A 9.6=N I ,额定转速min 1400r n N =,额定频率z f N H 50=,定子绕组Y 联接。
由实验测得定子电阻Ω=85.1s R ,转子电阻Ω=658.2r R ,定子漏感H 0102.0=ls L ,电感H 294.0=s L ,转子漏感H 006.0=lr L ,转子自感H 2898.0=r L ,定、转子互感H 2838.0=m L ,转子参数已折合到定子侧,系统的转动惯量21284.0m kg J ⋅=,初始转差率s=1。
设计三相电流闭环控制的矢量控制系统。
用MATLAB 仿真软件,建立异步电动机的仿真模型(参考exercise6_4_0)。
解:由题知:额定转速min 1400r n N =,额定频率z f N H 50=,则电动机极对数2=p n ,额定转速)(6.146602s rad n Nm ==πω;)(2.293s rad n m p ==ωω; 设三相正弦对称电流)100sin(758.9)2sin(t t f I i N m A ππ==、)32100sin(758.9)322sin(ππππ-=-=t t f I i N m B 、 )32100sin(758.9)322sin(ππππ+=+=t t f I i N m C ,转子电磁时间常数)(109.0658.22898.0s R L T r r r ===, 电动机稳定运行在额定工作状态时αβββααψωψψωψr r s m r r r s m r T i L T i L +=-=,得1、ACR (电流调节器)按典型I 型系统设计由课本《运动控制系统》P179式(6-81)知异步电动机的传递函数为:1s L s Xσ+。
三相异步电动机按转子磁链定向的矢量控制系统仿真

摘要本文对三相异步电动机按转子磁链定向的矢量控制系统进行了计算机仿真研究,运用Matlab/Simulink和SimPowerSystem工具箱及面向系统电气原理结构图的仿真方法,实现了带转矩内环的转速、磁链闭环矢量控制系统的建模与仿真;重点介绍了调速系统的建模和调节器参数的设置,给出了矢量交流调速系统的仿真模型和仿真结果非常接近实际情况,说明了仿真模型的正确性。
关键词:异步电动机;交流调速;矢量控制目录摘要 (I)1概述 (1)2总系统设计 (2)3子系统设计 (6)3.1 转速控制器 (6)3.2 定向控制器 (6)4三相异步电动机磁场定向矢量控制系统仿真 (8)4.1参数给定 (8)4.2系统仿真 (10)总结 (12)参考文献 (13)附录 (14)1概述交流调速技术在工业领域的各个方面应用很广,对于提高电力传动系统的性能有着重要的意义,由于电力传动系统的复杂性和被控对象的特殊性,使得对它的建模与仿真一直是研究的热点。
对其仿真研究不能像控制系统那样可用各环节简化传递函数来表示,这样会有很多重要环节被忽略,完全体现不了交流调速系统的整体结构和各个环节点上的信号状态。
对电气传动系统的建模仿真力求达到与实际系统相一致,Matlab提供的Simulink中的电力系统工具箱(SimPowerSystems)能很好地满足这一要求。
以往对电气传动系统的仿真研究主要集中在电机的建模和仿真,最近,许多对复杂电力传动系统的建模仿真方法已提出,主要有运用仿真工具箱对电力传动系统建模仿真和将电力传动系统的功能单元模块化的仿真建模。
由于三相异步电动机是一个多变量、强耦合非线性系统,存在着高性能上难以控制的问题。
矢量控制技术有按转子磁链定向和按定子磁链定向的控制等策略。
按转子磁链定向矢量控制给出了交流电动机的基本解耦控制方法。
在设计调速系统过程中,利用Matlab按转子磁链定向矢量控制的交流调速系统仿真,正确的应用坐标变换模块是建立转子磁链模型的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f4 =
Lm Rr isβ Lr
未知模型: Lm ∆Rr L ( R + ∆Rr ) LL ϖ3 = ψ rα − ωrψ r β = isα − m r − r σ ϖ1 Lr Lr Lm
m r ϖ4 = isβ −
L ∆R Lr
Lm ( Rr + ∆Rr ) LL ψ r β + ωrψ rα = − r σ ϖ2 Lr Lm
∧ ∧
通过电流的扩张状态观测器,观测出ϖ 1 ,ϖ 2 而后计算得到ϖ 3 ,ϖ 4
∧ ∧
,
• ∧ ∧ ∧ L2 R + L2 R ∧ L R ∧ L 1 isα = − m r2 r s isα + 2m r ψ rα + m ωr ψ r β + usα + ϖ 1 + b1∆isα Lr Lσ Lr Lσ Lr Lσ Lσ • ∧ ∧ ∧ L2 R + L2 R ∧ L R ∧ L 1 usβ + ϖ 2 + b1∆isβ − m r2 r s isβ + 2m r ψ r β − m ωr ψ rα + isβ = σ σ σ σ L L L L L L L r r r • ∧ ∧ R ∧ R ∧ ψ rα Lm r isα − r ψ rα − ωr ψ r β + ϖ 3 + b2 ∆isα = L L r r • ∧ ∧ ∧ ∧ R R ψ r β = Lm r isβ − r ψ r β + ωr ψ rα + ϖ 4 + b2 ∆isβ Lr Lr • = ϖ 1 b3 . fal (∆isα , α , δ ) • = ϖ 2 b3 . fal (∆isβ , α , δ )
于 ∀ε > 0 , ∃ f − f < ε , x2 = x(t )
' ^
^
^
。如果对
时,可以认为原系统 , x3 = f 。将变量
被改造为了一个线性、确定的系统。 令 x1 = x(t )
x3 作为一个状态变量扩张到原系统中,则系统状态
方程可写成如下形式:
• x1 = x2 • x= x3 + b0u 2 • x = f' 3 y = x1
∧
(5)
1 ∧ χ α3 | x1 − x1 |<| | lim β3 t →∞ α1 ∧ χ α 3 − < β lim | x x | . | | t →∞ 2 2 1 β 3 α2 ∧ χ lim | x3 − f |< β 2 . | |α3 β3 t →∞
由上述扩张系统构造相应的状态观测器:
• ∧ ∧ ∧ x1 = x 2 − β1. f1 ( x1 − x1 ) • ∧ ∧ ∧ x 2 =x 3 − β 2 . f 2 ( x1 − x1 ) + b0u • ∧ ∧ − β . ( x f x 3 = 3 3 1 − x1 )
异步电机转子磁链闭环观测方法及仿真
李红波 张凯 熊健 康勇
华中科技大学 电力电子与电气传动系 武汉 430074 Emai:llihongbo3457@
摘 要 : 本文基于自抗扰技术中的扩张状态观测器(Extended State Observer, ESO) ,提出一种闭环磁链观测模型。该模
其中, 校正函数。
β1
、 β2
、 β3
均为正; f i (ε )
为
期望所构造状态观测器的各状态分别跟踪被扩张的状 态变量,即 xi (t ) → xi (t ), (i = 1, 2,3) 。 将(1)式和(2)式相减可得:
∧
• ε 2 − β1. f1 (ε1 ) 1 ε= • ε 3 − β 2 . f 2 (ε1 ) ε= 2 • −b − β3 . f3 (ε1 ) ε 3 =
未知模型为:
L 2 ∆R L 2 ( R + ∆Rr ) Lω ϖ1 = ψ rα + m r ψ r β − m 2 r isα + m r2 Lr Lσ Lr Lσ Lr Lσ
L 2 ∆R L 2R Lω ϖ2 = − m 2 r isβ + m2 r ψ r β − m r ψ rα Lr Lσ Lr Lσ Lr Lσ
(15)
其中,
, 将其代替ϖ 3 ,ϖ 4
带入到(13)
式中,即可得到磁链的观测值。 观察上述未知模型,除有转子电阻的摄动以外, 还包含了未知量转子磁链,使得系统的不确定性范围 较大。如果将磁链的观测值带入模型中,可以减少系 统未知模型的不确定范围,减轻观测模型的负担。同 时上述磁链模型包含有纯积分环节,且是开环结构, 不能解决直流偏移和误差等问题。 为得到更好的观测效果,将上述观测模型做如下 调整:
磁链方程改写为:
−
• = ψ rα • ψ r= β
f3 + ϖ 3 f4 +ϖ 4
ωr
0 0
(13)
1 0 LL − r σ Lm 0 0 0
'
为方便说明将上述模型写成方程组的形式:
其中,已知模型:
f3 =
Lm Rr isα Lr
• x A(ωr ) x + Bu = y = Cx
b= f
'
。
由 (3) 式可知,对于在一定范围内变化的函数 b , 选择合适的函数 f i (ε1 ), (i = 1, 2,3) 可使得系统 (5)
稳定在原点附近区域。进而系统(4)就能跟踪系统(3)的 扩张状态 xi , (i = 1, 2,3) 。 因此系统(4)被称为系统(3) 的扩张状态观测器。值得注意的是扩张状态观测器(4) 与系统 (3) 中的不确定成分和外扰 f 无关,而仅和
构造电流的扩张状态观测器 • ∧ ∧ isα = ϖ 1 − b1. fal (isα − isα , α1 , δ ) + f1 + 1 usα Lσ • ∧ ∧ −b2 . fal (isα − isα , α 2 , δ ) ϖ1 =
• ∧ ∧ isβ = ϖ 2 − b1. fal (isβ − isβ , α1 , δ ) + f 2 + 1 usβ Lσ • ∧ ∧ −b2 . fal (isβ − isβ , α 2 , δ ) ϖ2 =
ε 2 − β1 fal (ε1 , α1 , δ ) 1 ε= • ε 3 − β 2 . fal (ε1 , α 2 , δ ) 2 ε= • − f ' − β3 . fal (ε1 , α 3 , δ ) ε 3 =
•
(7)
• i = f1 + ϖ 1 + 1 usα Lσ sα • isβ = f 2 + ϖ 2 + 1 usβ Lσ
a0 , a1 不确定, b0 为 b 的已知部分,则原系
统可以写成如下形式:
'' x= f + b0u
(2)
可 值,
其中, f =
a0 x + a1 x + (b − b0 )u + ω 。 f
'
^
以看做系统的总扰动。 ESO 目的就是通过观测 f
进而改造原来系统的结构。原系统可进一步改写为:
x '' = ( f − f ) + u0 ,其中 u = b0u + f 0
(6)
1 Lσ B= 0
0 1 Lσ
0 0 0 0
1 0 0 0 C= 0 1 0 0
将 (6) 式带入 (5) 式,得到误差状态方程:
电机运行时,转子侧电阻容易产生摄动。设其变 化量为 ∆Rr ,则实际电阻为 Rr + ∆Rr 。分别将电 流方程和磁链方程的未知和已知模型分离。 电流方程改写为:
0 b2
0
b3 0 0 b3
Lm Rr Lr 2 Lσ − Lmωr Lr Lσ Rr Lr
'
Lmωr Lr Lσ Lm Rr Lr 2 Lσ −ωr − Rr Lr 0 0 −
1 0 Lr Lσ Lm 0 0 0
−
Lm 2 Rr + Lr 2 Rs Lr 2 Lσ 0 Lm Rr Lr 0 0
1 Lδ B= 0
(11)
0 1 Lδ
0 0 0 0 0 0 0 0
'
'
1 0 0 0 0 0 C= 0 1 0 0 0 0
b 0 b2 H = 1 0 b1 0
(12)
Lm 2 Rr + Lr 2 Rs − Lr 2 Lσ 0 Lm Rr A(ωr ) = Lr 0 0 0
(3)
2.扩张状态观测器(ESO)原理
【2】
状态观测器本质是根据已知输入和测量输出重构 出系统状态。假设二阶系统
(4)
x '' = a0 x ' + a1 x + bu + ω
其中 u ,x
(1)
为
分别是系统的输入、 输出;ω
系统的外加扰动。 在实际系统中,除外加扰动、测量误差外,还 常出现参数的摄动以及未建模动态等情况。 假定
就 是 传 统 的 Luenberger 观 测 器 【 4,5 】。 如 果 取 fi (ε ) = ε + ki sign(ε ), ki > 0 ,则观测器就是变结 构观测器。在 ESO 中一般选择 fal 数,其定义如下:
α
函数作为校正函
ωr
