批量流水线调度问题的混合离散蛙跳算法
【计算机应用研究】_蛙跳算法_期刊发文热词逐年推荐_20140723
2012年 序号 1 2 3 4 5
科研热词 选择和变异机制 蛙跳算法 聚类分析 模糊c-均值聚类 数据挖掘
推荐指数 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2013年 科研热词 混合蛙跳算法 逆转变异 蛙跳策略 生存周期 混洗蛙跳算法 混沌优化策略 无线传感器网络 收敛性 多样性 反向学习 分簇路由协议 函数优化 作业调度 人工智能 matlab map-reduce 推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
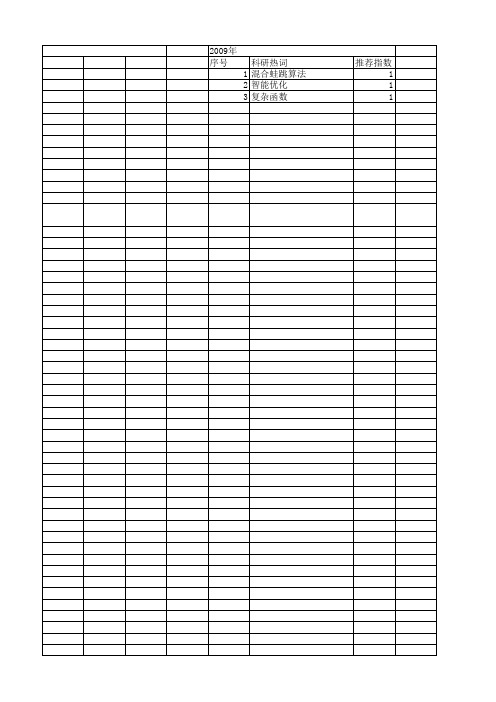
2009年 序号
科研热词 1 混合蛙跳算法 2 智能优化 3 复杂函数
推荐指数 1 1 1
2010年 序号 1 2 3 4 5 6
科研热词 蛙跳算法 混合蛙跳算法 模糊c均值 批量无等待流水线调度 快速局部搜索 交通状态判别
推荐指数 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 蛙跳算法 混合蛙跳算法 车辆路径问题 自适应差分扰动 自适应变异 混沌序列 混沌局部搜索 混沌变异 混沌 无约束连续优化问题 数字水印 改进型蛙跳算法 批量无等待流水线调度问题 微粒群优化算法 图像置乱 全局收敛性
推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1
改进的混合蛙跳算法及其多目标优化的应用研究
改进的混合蛙跳算法及其多目标优化的应用研究改进的混合蛙跳算法及其多目标优化的应用研究摘要：蛙跳算法（Frog Leap Algorithm, FLA）作为一种基于群体智能的优化算法，在解决单目标优化问题上具有较好的效果。
然而，传统的FLA在处理多目标优化问题时存在一些不足之处，如过早收敛和缺乏全局搜索能力。
为了克服这些问题，本文提出了一种改进的混合蛙跳算法（Improved Hybrid Frog Leap Algorithm, IHFLA），并通过实验证明其在多目标优化问题上的应用效果。
引言：随着计算机技术的迅猛发展，多目标优化问题在各个领域中得到越来越广泛的关注。
多目标优化问题是指在多个目标函数的约束下，寻找最优解空间中的非劣解集合。
针对多目标优化问题，传统的单目标优化算法效果不佳，因此需要开发新的算法来解决这一问题。
本文将基于群体智能的优化算法——蛙跳算法，进行改进，以提高其在多目标优化问题上的性能。
1.蛙跳算法的原理及不足蛙跳算法是一种基于仿生学的启发式优化算法，模拟了青蛙在寻找食物过程中的行为。
其基本思想是通过模拟蛙类的跳跃行为来搜索最优解。
每个蛙个体都含有一组决策变量，通过不断迭代调整这些变量，以达到最优解。
然而，传统的FLA在多目标优化问题中存在一些问题：（1）易陷入局部最优解，过早收敛；（2）缺乏全局搜索能力。
2.改进的混合蛙跳算法(IHFLA)为了克服传统FLA中的问题，本文提出了一种改进的混合蛙跳算法（IHFLA）。
该算法在传统FLA的基础上引入了局部搜索和全局搜索的策略，以提高其多目标优化问题的能力。
具体步骤如下：（1）初始化种群：根据问题的约束条件，随机生成一定数量的蛙个体作为初始种群。
（2）目标函数计算：计算种群中每个蛙个体的目标函数值。
（3）更新个体位置：根据当前种群中每个蛙个体的目标函数值，更新其位置。
（4）局部搜索：对每个个体进行局部搜索，以增加探索空间。
（5）全局搜索：通过引入全局搜索策略，使蛙个体具有更好的全局搜索能力。
蛙跳算法
（三）混洗蛙跳算法研究许多研究人员致力于研究模拟生物群体活动，并且取得很多研究成果。如鸟群算法、鱼群算法都是模拟生物在群体活动中表现出的行为。在寻找食物过程中，群体中个体可以从其他个体上获得经验；但是在资源难以预测分布时，这种群体行为就具有决定性意义。正是基于种群间信息互享这一思想，使混洗蛙跳算法具有理论基础。这一理论的发展方向主要有：（1）个体研究小组采用不同的方法解决相同问题；（2）一些研究人员提出新的方法，并且与其他的方法进行对比；（3）大型的团队可能改变一些规范标准。但是这些研究人员有共同的研究特点都是从其他的设计中获得更好信息，反复逐步提高技术。
2.模因与基因的比较。Meme和Gene之间也具有很有相似的特点，如建立可能解，通过某种策略选择可能解，与其他的解相结合产生后代等。Meme和Gene的最根本的区别是在群体中采用不同的传播机制。在种群中通过选择Meme增强种群间的交流能力（如混合蛙跳算法中的青蛙个体）。而选择gene是为了繁殖后代。（1）Meme进化更具有灵活性，能在种群中任意个体之间进行传播策略；Gene仅可以在具有亲缘关系的个体之间进行信息传递。（2）进化速度不同。由于Gene在N代中传递，所以需要更多的时间进行传播。而meme仅需要分级速度传播。（3）变异率不同。在神经网络系统中，Meme更容易产生变异。而以双螺旋稳定结构为基础的染色体中，Gene的变异率会很低。综合以上的分析，得出结论是以Meme为传播单元比以Gene的传播速度快。
蛙跳步长更新：Si=rand()×(Pb-Pw)（1）位置更新：Pw(k+1)=Pw(k)+Si（2）Smax≥Si≥-Smax，其中rand()∈[0，1](k=1，2，?，n)，S是最大步长。如果计算后新的解较优，则用其替代最差个体。并且通过求全局最优解Pg。如果得到的解没有改进，那么随机生成新解取代所求个体的解，算法继续迭代直至迭代次数完毕。混洗蛙跳算法的参数：青蛙群体数P，族群数m，混合操作前族群内更新代数和混合迭代次数。3.算法流程随机产生P solutions(individuals);For each individuali E P:Sort the whole population P in descending order of theirfitness;根据每个个体的适应度按降序排列Divide the population P into m memeplexes;For each memeplex;Determine the best and worst individuals;Improve the worst individual position using Eqs.1 and2;Repeat for a specific number of iterations;End;Combine the evolved memeplexes;Sort the population P in descending order of theirfitness;Check if termination=true;End;
混洗蛙跳算法的研究
混洗蛙跳算法的研究作者：王晓笛,何灿来源：《电脑知识与技术》2011年第19期摘要：混洗蛙跳算法是一种基于启发式搜索的算法，通过启发函数进行搜索，从而找到组合优化问题的解。
该文介绍了混洗蛙跳算法的产生发展以及基本原理和流程，并对以后做了展望。
关键词：混洗蛙跳算法；局部搜索；全局信息交换中图分类号：TP18 文献标识码：A文章编号：1009-3044(2011)19-4661-04智能优化算法通过模拟或揭示某种自然现象或者过程发展而来，具有鲁棒性、通用性强，全局的、并行高效的优化性能这些鲜明的特点[1]。
群体智能优化算法是如今在优化计算领域中的一个研究热点。
人们研究不同的群体智能算法如蚁群算法、粒子群算法等等，通过改善这些算法的不同参数如蚁群算法中的信息素挥发度、蚁群数量、启发因子；粒子群算法中的惯性权重、领域拓扑结构、学习因子等等不同的方法来改进这些算法，或者探索新的群体智能算法，以求能更好地求解优化问题尤其是多目标约束下的优化问题。
混洗蛙跳算法就是近年来人们探索新算法的成果之一。
2000年，Eusuff以及Lansay最初不过是设想模拟青蛙的觅食过程，但在后来的研究中发现，这一过程可以作为一种不错的优化工具，并将其最初应用于水资源网络分配问题。
此后，经过不断的探索，2003年，Eusuff和Lansay在文献[2]中正式提出混洗蛙跳算法，成为智能优化算法家族和模因算法家族的一名新成员。
混洗蛙跳算法是一种基于启发式搜索的算法，通过启发函数进行搜索，从而找到组合优化问题的解。
这个算法受以遗传算法为基础的自然模因算法的启示，结合了以社会行为为基础的粒子群优化算法的优点。
1 模因算法Moscato于1989年第一次系统地使用计算机语言提出模因算法（Memetic Algorithm，MA）。
“memetic”来自于单词“meme”[3]，meme就是寄存在人或动物的大脑中，能指导他们行为并且能够传播的信息。
批量流水线调度问题的混合离散蛙跳算法
批量流水线调度问题的混合离散蛙跳算法潘玉霞;潘全科;桑红燕【摘要】研究了以提前/拖后惩罚指标为目标的批量流水线调度问题,给出了该问题的数学模型以及小批量的调整策略.根据蛙跳算法的原理,采用基于工序的编码方式并利用两点交叉操作设计了新的位置生成公式,提出了解决该问题的离散蛙跳算法.为进一步增强算法的开发能力和效率,结合扰动策略、模拟退火概率接受准则和插入邻域搜索对该算法进行改进.对随机生成的实例进行了广泛的试验,结果表明了所提算法的高效性.【期刊名称】《计算机集成制造系统》【年(卷),期】2010(016)006【总页数】7页(P1265-1271)【关键词】批量流水线;调度;蛙跳算法;模拟退火;插入邻域搜索;数学模型【作者】潘玉霞;潘全科;桑红燕【作者单位】海南大学三亚学院,公共基础部,海南,三亚,572022;聊城大学计算机学院,山东,聊城,252059;聊城大学计算机学院,山东,聊城,252059【正文语种】中文【中图分类】TP180 引言批量流水线调度问题(Lot-streaming Flowshop Scheduling Problem，LFSP)是许多工业生产的简化模型[1]，已被证明属于NP完全问题。
精确求解方法如穷举法、整数规划法和分支定界法只能解决很小的问题。
由于组合的复杂性和时间的约束，多数大型问题只能用试探法来求解。
近年来提出的构造式启发算法[2]和智能优化算法[3]成为求解调度问题的主要方法。
文献[4]的离散微粒群优化(Discrete Particle Swarm Optimization，DPSO)算法和文献[5]中的混合遗传算法(Hybrid Genetic Algorithm，HGA)取得了至今最好的研究结果。
蛙跳算法(Shuffled Frog-Leaping Algorithm，SFLA)是一种模拟群体青蛙觅食特性产生的智能算法。
该算法结合了以遗传为基础的Memetic算法和以社会行为为基础的微粒群优化算法的优点[6]，具有概念简单、参数少、计算速度快、全局寻优能力强和易于实现的特点。
混合蛙跳算法 基本原理
混合蛙跳算法基本原理
嘿，朋友们！今天咱们来聊聊超有意思的混合蛙跳算法的基本原理！
你想想啊，就好比一群青蛙在一个大大的池塘里蹦跶（这就像算法中各种可能的解）。
它们有的蹦得远，有的蹦得近，但是它们都在努力寻找最好的位置。
混合蛙跳算法呢，就是让这些青蛙们分成小组（可以类比为不同的解集群）。
每个小组里的青蛙们会一起交流，互相学习，然后各自根据学到的东西蹦一蹦（调整解）。
比如说，有一只青蛙发现旁边那只蹦得挺不错，它就会跟人家学学，也试着往那个方向多蹦一点。
然后呢，各个小组之间还会交换信息（这就像是不同解集群之间的交互）！哎呀，这多棒啊！这样就可以让大家都能知道其他小组找到的好地方，都朝着更好的方向去努力。
就好像一群小伙伴一起玩游戏，互相分享经验，然后一起进步！
那这个算法到底有啥用呢？这么说吧，假如你要规划一条最优的物流路线，那它就能帮你找到最合适的那条路，能省好多时间和成本呢！这不就像你找路的时候有人给你指了一条明路一样吗？
再比如，在设计一个复杂的系统时，它能让你快速找到最佳的参数组合。
这不就相当于有个超级聪明的助手帮你把一切都安排得妥妥当当嘛！
我觉得混合蛙跳算法真的太神奇了，就像给我们打开了一扇通往高效解决问题的大门。
它让我们能在各种复杂的情况下都能找到最好的办法，难道不是很了不起吗？朋友们，你们说呢！
观点结论：混合蛙跳算法是一种非常有创意和实用的算法，能帮助我们高效地解决各种问题，具有很大的价值和潜力。
基于离散蛙跳算法的零空闲流水线调度问题求解
第36卷第1期2010年1月北京工业大学学报J OURN AL OF BE IJI NG UNI VERS I TY OF TEC HNOLOG YVo.l 36No .1Jan .2010基于离散蛙跳算法的零空闲流水线调度问题求解王亚敏1,2,冀俊忠1,潘全科2(11北京工业大学多媒体与智能软件技术北京市重点实验室,北京 100124;21聊城大学计算机学院,山东聊城 252059)摘 要:针对零空闲流水线调度问题,提出了一种新的离散化蛙跳求解算法.该算法借助蛙跳算法优化机理,采用基于工件序列的编码方式和新的个体产生方法扩展了传统蛙跳算法的求解模型,并结合简化邻域搜索算法给出了3种改进策略.仿真实验表明了所提算法及策略的有效性.关键词:零空闲流水线调度;离散蛙跳算法;邻域搜索中图分类号:TP 18文献标志码:A文章编号:0254-0037(2010)01-0124-07收稿日期:2008205226.基金项目:北京市自然科学基金资助项目(4083034),北京市教育委员会科技发展资助项目(KM 200610005020).作者简介:王亚敏(1979)),女,山东菏泽人,讲师.车间调度问题的求解及其优化技术是制造业实现生产过程合理化、自动化、集成化的基础和关键.其中,零空闲流水线调度(no -idle fl o w shop ,记为N I FS)是一类组合优化问题[1];Baptiste 等[2]提出了解决N I FS 问题的分枝限界法;K alcz ynski 等[3]提出了解决N I FS 问题的构造式启发方法;Bzraz 等[4]提出了有效的改进贪心算法;一些基于离散粒子群优化算法[5]、差分进化算法[6]等相继被提出;Eusu f f 等[7]首次提出了蛙跳算法(shu f fled frog leap i n g algorith m,记为SFL A ),并应用于水管网络扩充中管道尺寸最小化问题的求解.由于蛙跳算法能结合生物种群的遗传行为和群落间信息交流的社会行为,是解决组合优化问题的有效工具[8].本文提出了基于离散蛙跳算法的N I FS 问题的求解方法.采用基于工件序列的编码方式和新的个体产生方法扩展了传统蛙跳算法的求解模型,提出了解决N I FS 问题的蛙跳算法,并给出了3种提高性能的改进策略.1 N IFS 问题描述及邻域搜索算法111 N IFS 问题描述n 个工件在m 台机器上流水加工,每个工件在机器上的加工顺序相同,同时,约定每个工件在每台机器上只加工1次,而在同一机器上加工的相邻工件之间没有等待时间,且机器之间存在无限缓冲区.在已知各工件在各台机器上所需加工时间的前提下,问题的求解目标是得到满足上述约束条件的可行调度,使得最大完工时间最短.文献[5]提出了通过完工时间差或开工时间差来计算最大完工时间的方法.给定单个工件的排序P ={P 1,P 2,,,P n },而P e (i)={P 1,P 2,,,P i }和P j(i)={P i ,P i +1,,,P n }表示其中的2个部分排序.令F (P e(i),j ,j +1)表示排序P e(i)中机器j 和j +1的完工时间差,E (P f(i),j ,j +1)表示排序P f(i)中机器j 和j +1的开工时间差,而p(P i ,j)表示工件P i 在机器j 上的加工时间.如图1(a )所示,当从前往后依次增加工件时最大完工时间F (P e(1),j ,j +1)=p(P 1,j +1),j =1,2,,,m -1(1)第1期王亚敏,等:基于离散蛙跳算法的零空闲流水线调度问题求解F (P e(i),j ,j +1)=max {F (P e(i -1),j ,j +1)-p (P i ,j),0}+p (P i ,j +1) i =2,3,,,n,j =1,2,,,m -1(2)从前往后计算方式排列P 的最大完工时间为C m ax (P )=Em-1j=1F (P ,j ,j +1)+Eni=1p (P i ,1)(3)如图1(b )所示,当从后往前依次增加工件时最大完工时间E (P f(n),j ,j +1)=p(P n ,j), j =1,2,,,m -1(4)E (P f(i),j ,j +1)=max {E (P f(i +1),j ,j +1)-p (P i ,j +1),0}+p(P i ,j) i =n -1,n -2,,,1,j =1,2,,,m -1(5)图1 最大完工时间计算方法示意F ig .1 Sketch m ap of co mputi ng the m ax i m u m co mp l etio n ti m e for bot h cases从后往前计算方式排列P 的最大完工时间C m ax (P )=Em-1j=1E (P ,j ,j +1)+Eni=1p (P i ,m )(6)求最大完工时间的复杂度为O (mn).如图1(b )所示,在一个排列之前增加工件时完工时间差F (P f(n),j ,j +1)=p(P n ,j +1),j =1,2,,,m -1(7)F (P f(i),j ,j +1)=max {p(P i ,j +1)-E (P f(i +1),j ,j +1),0}+F (P f(i +1),j ,j +1)i =n -1,n -2,,,1,j =1,2,,,m -1(8)112 邻域搜索算法在排列P 中,随机选择不同的2个位置k 、j ,将j 处的零件移动到k 处,称为插入移动v(j ,k),其中j ,k I {1,2,,,n }.由移动可以得到原排列的一个邻居.所有这样的邻居构成插入邻域,则该邻域的规模为n (n -1),评价该邻域的时间复杂度为O (mn 3).如果将排列P 看作是2个排列P 1和P 2合并在一起得到的排列,其中P 2在P 1之后,如图2所示.则图2 2个排列合并在一起的最大完工时间计算方法示意F ig .2 Sketch m ap of co mputi ng the m axi m u m co m pletio n ti m e for co m bi natio n t w o per muta ti onsF (P ,j ,j +1)=max {F (P 1,j ,j +1)-E (P 2,j ,j +1),0}+F (P 2,j ,j +1) j =1,2,,,m -1(9)125北京工业大学学报2010年若记排列P进行插入移动v(j,k)之后的新排列为P c,对比P c和P可得到邻域搜索算法.第1步,按照式(1)和(2)从前往后依次求出每个P e(i)的完工时间差,按照式(4)、(5)和(7)、(8)从后往前依次求出每个P f(i)的完工时间差和开工时间差,进而得到排列P的C m ax(P).第2步,取出P中的第j个工件,将其依次插入P的k处,其中k=1,2,,,n,且k X j.得到新P c,则此时P c可以看作由k之前的P e(k-1)、k之后的P f(k+1)和k处的工件j3部分组成.第3步,在P e(k-1)后面增加工件j得到P c的P c e(k),由式(2)可以求出P c e(k)的完工时间差;P c的另一部分P c j(k+1)与P f(k+1)相同.由式(9)可求出P c的完工时间差F(P c,j,j+1),由式(3)得P c的C max(P c).第4步,重复第2和第3步,直到将排列P的插入邻域搜索一遍.上述算法中,第2步和第3步的时间复杂度为O(mn).所以整个算法的时间复杂度为O(mn2).2蛙跳算法SFLA蛙跳算法是一种新的元启发式的搜索算法[6],通过模拟青蛙群体在觅食过程中所体现出的协同行为来完成对问题的求解.这种算法按照族群分类进行信息传递,并将全局信息的交换与局部进化搜索相结合.在蛙跳算法中,种群由很多青蛙组成,每只青蛙代表1个解.种群被分成了多个子群,每个子群包括一定数量的青蛙,称为1个me meplex.在每个子群内分别执行局部搜索.每只青蛙都受自己和其他青蛙想法的影响,并通过m e m etic进化来调整位置.经过一定数量的进化后,不同子群间的青蛙通过跳跃过程来传递信息.这种局部进化和跳跃过程相间进行,直到满足收敛的条件为止.首先,由随机初始化一组解组成青蛙的初始种群,然后,将所有青蛙按照它们的适配值降序排列,并分别放入各个me mep lex中,用P b和P w分别表示该子群中位置(适应值)最好和最坏的青蛙.另外,用P g表示整个种群中最好的青蛙.在每一轮的进化中,通过与PS O算法近似的方法改善最坏青蛙P w的位置.青蛙移动的距离D i=rand()*(P b-P w)(10)新的位置P w=P w(当前位置)+D i,(D m ax\D i\-D m ax)(11)式中,rand()为0到1之间的随机数;D max为允许青蛙移动的最大距离.如果这个过程能产生一个较好解,那么就用新位置的青蛙取代原来的青蛙P w;否则,用P g代替P b,重复上述过程.如果上述方法仍不能生成更好的青蛙,那么就随机生成一个新解取代原来最坏的青蛙P w.按照这种方法执行一定次数的进化.最后,将所有的青蛙重新排序、子群划分,继续进化、跳跃,重复上述过程直到收敛为止.3N IFS问题的离散蛙跳求解算法DSFLA311个体矢量编码建立个体矢量与调度方案之间的映射关系.对于零空闲流水线编码方案就的个体矢量的每一维表示1个工件.这样,个体本身就表示所有工件的一个排列.表1为个体矢量与调度方案之间的对应关系.表1个体矢量及对应的工件排列Tab le1Ind ivi dua l vector and cor r espond i ng job perm u ta tions个体矢量维数个体矢量工件序列133211个体矢量维数个体矢量工件序列322444个体矢量维数个体矢量工件序列566655126第1期王亚敏,等:基于离散蛙跳算法的零空闲流水线调度问题求解127 312个体矢量的更新青蛙所代表的解向量在连续解空间跟踪其局部极值或全局极值的向量运算.换句话说,式(10)、(11)表示P w向P b学习逼近的过程,其中rand()表示学习的程度,将式(10)、(11)合并可知P w=P w(当前位置)+rand()*(P b-P w(当前位置))(12)式中,rand()代表青蛙P w从局部极值P b的信息继承度,反映了对P b信息的置信指标.当rand()=1时,P w=P b,当rand()=0时,P w=P w(当前位置).定义f(P w,P b)为P w向P b的学习过程,该过程可以通过交叉操作实现.1)在P b中随机选择1个交叉区域,其中rand()决定着交叉区域的大小.2)将P b的交叉区域加到P w的前面或后面,并删除P w中已在P b的交叉区中出现过的数字.采用这种更新策略,子串能继承父串的有效模式,实现了从局部极值P b获得更新信息的目的.313工序编码的DSLFA调度算法Step0初始化.选择M和N,M表示me meplex的数量,即子群的数量,N表示每个m e m eplex中青蛙的个数.那么,整个种群的数量F=M@N.Step1生成初始种群.在可行解空间8<R n,生成F个青蛙U(1),U(2),,,U(F),其中n为工件数量.每个青蛙(Fr og)原本代表青蛙的当前位置,对于N I FS问题则表示解空间的1个候选解.第i个青蛙可以表示为U(i)=(U1i,U2i,,,U n i).计算出工件序列U(i)的最大完工时间makespan,用f(i)表示.则f(i)的值越小,表示该解的适应度越高.Step2对青蛙划分等级.将F只青蛙按照适应度的降序排列,生成数组X={U(i),f(i),i=1,2, ,,F},这样的话,i=1表示这只青蛙的位置(适应度)最好,记录下种群中位置最好青蛙P g=U(1).Step3将青蛙分组,放入不同的me mep lex.将数组X分成M个me m eplex:Y1,Y2,,,Y M.每个me meplex中包含N只青蛙,即:Y k={U(j)k,f(j)k|U(j)k=U(k+M(j-1)),f(j)k=f(k+M(j-1)),j=1, ,,N},其中k=1,2,,,M;比如M=3,那么第1只青蛙属于子群me m eplex1,第2只青蛙属于子群me meplex2,第3只青蛙属于子群me mep lex3,第4只青蛙属于子群me mep lex1,等等.Step4在每个me mep l e x中执行me metic进化.在每个me meplex中,每只青蛙受到其他青蛙想法的影响,通过me metic进化,使得各个青蛙朝目标位置逼近.Step4-0设i M=0,i M表示对me mep lex的计数,在0到M之间变化,与m e m eplex的数量M比较.设i N=0,i N表示进化次数,与每个m e m eplex中允许的最大进化次数N max比较.用P b和P w分别表示每个me meplex中位置(适应度)最好的和最坏的青蛙,用P g表示整个种群中最好的青蛙.在每轮的进化中,改善最坏青蛙P w的位置,注意,并非对所有的青蛙都优化.Step4-1i M=i M+1.Step4-2i N=i N+1.Step4-3采用式(12)调整最坏青蛙的位置.Step4-4如果Step4-3能使得青蛙有一个更好的位置,即能产生一个更好的解,那么就用新位置的青蛙取代原来的青蛙,执行step4-6;否则,用P g代替P b,利用式(12)计算f(P w,P g),如果能产生一个更好的解,取代原来的青蛙,执行step4-6.Step4-5随机生成一个新解取代原来最坏的青蛙P w.Step4-6如果i N<N max,那么执行4-2.Step4-7如果i M<M,那么执行4-1,否则执行Step5.Step5青蛙在me mep l e x之间跳跃移动.在每个me m eplex中执行了一定次数的m e m etic进化之后,将各个子群Y1,Y2,,,Y M合并到X,即X={Y k,k=1,2,,,M}.将X重新按降序排列,并更新种群中最好的青蛙P g.Step6检查终止条件.如果迭代终止条件满足,则停止.否则,重新执行step3.一般情况下,当执北 京 工 业 大 学 学 报2010年行了一定次数的循环进化,代表最好解的青蛙不再改变的时候,算法停止.有时也定义最大进化次数作为停止标准.314 蛙跳算法的改进31411 引入邻域搜索算法的改进策略蛙跳算法中青蛙从局部极值或全局极值中获得更新信息,其信息共享机制中信息的流动是单向的,信息流动的目的性更强,效率更高.同时,搜索过程受局部极值P b 以及全局极值P g 的影响较大.加强P b 和P g 的局部探测能力可提高算法性能.改进SFL A 的方法是在每组me mep lex 进化过程中,对P b 执行简化插入邻域搜索算法,如果搜索之后发现更好的解,则用该解代替原来的P b ,如果新得到的P b 优于P g ,更新P g .并且在整个种群的每次迭代中,对P g 也执行简化邻域搜索算法.通过对P b 和P g 的细搜索,使得整个种群能更快的向最优解移动,有利于增加算法的收敛速度,记为DSFL A1.31412 增加随机扰动的改进策略DSFL A 1虽然增强了局部搜索能力,但细搜索范围仅限于P b 和P g 的最近邻居,范围较小,有可能使P b 和P g 长时间/徘徊0在若干旧状态上,容易陷入局部最优.为了增强算法跳出局部最优的能力,可以在1次邻域搜索之后,对P b 和P g 执行1次随机插入移动,对所得结果再执行邻域搜索算法,如此将随机插入和邻域搜索过程重复几次,即通过增加扰动来扩大细搜索的范围.虽然细搜索的时间有所增加,有利于优化过程中状态的局部小范围趋化性移动,从而增强了算法在解空间的探索能力和效率.记为DS FL A2.31413 结合模拟退火机理的改进策略正是因为种群进化受P b 和P g 影响,一旦为局部最优,青蛙将难以摆脱局部极值,其信息将覆盖整个邻域种群,导致该种群以较大概率陷入局部收敛.由此,还可以借鉴模拟退火中的概率接收[9]准则优化P b 和P g ,即在DSFL A2的基础上,在对P b 和P g 进行多次邻域搜索后,如果找到更好的解,那么就接受这个解,如果找不到更好的解,就以一定概率接受次优解.这种在DSFL A2中S A 的嵌入,赋予优化过程在各状态具有可控的概率突跳特性,尤其在高温时使得算法具有较大的突跳性,是避免P b 和P g 陷入局部极小和算法/早熟收敛0的有力手段,记为DSFL A 3.4 仿真试验采用包含120个流水线调度的Ta ill a rd Benchmar k 问题作为实例,每个实例计算5次,求算法所得解的平均相对偏差(PRD)和平均方差(SD).设种群规模为20,因算法受初始解情况的影响,如果初始解先通过某种智能优化算法优化生成,算法的收敛性及其他性能会有所提高.但是,为了检验该算法的鲁棒性,初始解采用随机生成的方法.对局部极值P b 和全局极值P g 执行3次随机插入移动和邻域搜索,模拟退火接受标准的温度系数t =0105E ni=1Emj=1P ij /(mn ).并与基于离散粒子群优化DPS O 算法进行了比较.实验的运行环境为:操作系统W i n dows XP ,CP U 为P Ô115G H z ,内存为256MB ,算法用C++语言编程.各算法采用相同的终止条件,即最大运行时间为10ms .结果如表2所示.DSFL A 算法所得的平均相对偏差和平均方差近似于DPSO 算法,由此表明具有信息共享、协同进化机制的DSFL A 能在较短时间内较快得向最优解逼近,是一种有效的解决N I FS 问题的方法.由DSFL A 和DSFL A 1、DSFL A2和DSFL A3各个算法的对比分析可以看出,通过简化邻域搜索算法提高局部极值和全局极值之后,平均偏差减少,解的质量有所提高,尤其是加入随机扰动对算法性能提高有很大作用.并可以看出,DSFL A2和DSFL A3的平均方差明显减少,表明这2种改进策略使得算法的稳定性有所提高.原因在于P b 和P g 对种群的进化搜索过程起着引导作用,其性能对算法结果影响很大,所以DS FL A 和DS FL A1算法性能对P b 和P g 的依赖性较大,而对于改进策略DS FL A2和DSFL A3,由于在对P b 和P g 邻域搜索时增加了扰动,扩大了搜索范围,从而使得算法在每一代进化过程中对P b 和P g 的初始性能的依赖性降低,进而使得算法的稳定性提高.128第1期王亚敏,等:基于离散蛙跳算法的零空闲流水线调度问题求解表2 不同算法的比较Tab le 2 C o m pa r ison of d iffer ent a lgor ithm sInstance DPSODSFL A DSFL A1DSFL A2DSFLA3n @m PRD SD PRD SD PRD S D PRD SD PRD SD 20@59171151915611919166212514111215136114820@102319221712316421962313521441513811615168117120@2048149211749132183491163133371352157381411950@561941169713211445199113331701953153111650@1022182212423185211920195212917104210916161119650@20551243134551931245012131534117231614016312100@54115110141751112301881195018911810174100@102010521292110121111612611451317116413121166100@204616921634818521640107310335152197341452187200@10151131111161031129111311146101091121101241122200@2038116115540132118301312176291831195281572112500@202612511092719111252312111323169113723131113分别选取一个50@20的中等规模和大规模的N I FS 问题进行分析,各算法的进化过程如图3所示.图3(a )为50@20的中等规模N I FS 问题Ta051的各算法进化曲线.对于中等规模的问题,DSFL A 具有较好的计算性能和较强的全局搜索能力.与DSFL A 相比较,DSFL A1明显加快了简化邻域搜索的收敛速度,由于P b 和P g 搜索范围不大,易陷入局部最优,进而整个种群也更易陷入局部极值.加入随机扰动后的DSFL A2和DSFL A3,扩大了P b 和P g 的搜索范围,不仅收敛速度更快,而且易于跳出局部极值,并且融合了模拟退火机理的改进策略对于跳出局部最优也有一定作用.由此可以看出,DS FL A2和DSFL A3在搜索广度和深度上能达到较好的均衡,是解决N I FS 这类组合优化问题的有效工具.图3(b )为500@20的大规模N I FS 问题Ta111的各算法进化曲线.对于大规模问题,虽然DSFL A 收敛速度比DPSO 稍慢一些,但是从试验中看出相对不易陷入局部极值,依然是一种解决N I FS 问题的有效工具.这是由于DSFL A 中对于较差解可能有变异操作,这对保持种群多样性可以起到一定的作用,能在一定程度上减少陷入局部极值的可能.而对于3种改进策略,尽管较大规模问题的邻域搜索算法本身需要占用较多的时间,对整体的收敛进度依然起到了极大的促进作用,使得收敛速度有较大提高.图3 各算法进化曲线比较F i g .3 Evol utio n curves of different algorith m s129130北京工业大学学报2010年5结论蛙跳算法结合了粒子群优化算法的社会特性和m e m etic算法的遗传特性,具有连续性和较强的全局搜索能力.本文基于该算法的优化机理,提出了适合于解决零空闲流水线调度问题的离散蛙跳算法,并研究了几种改进策略,仿真试验表明,离散蛙跳算法是解决零空闲流水线调度问题的有效方法,几种改进策略都有助于改善解的质量和提高算法的收敛速度.参考文献:idle/cmax proble m[J].[1]S AADA N I N E I,GUI NET A,MOAL A M.A trave li ng sa les m an approach to sol ve the f/no-European Journa l of Ope ratio n R esearch,2005,161:11220.[2]S AADA N I N E H,BAPTIS ETE P,MOALL A M.The si m p le F2M C m ax w ith forb i ddden tasks i n first or last positi on:Aproble m more co mp l ex t han i t see m s[J].Eur J Oper R es,2005,161:21231.[3]KALCZ YNS K I P J,KA MBURO WSKI J.A heuristic f or m i n i m i zing the m akespan i n no2idle pe r muta tion flo w s hop[J].Co mput Ind Eng,2005,49:1462154.[4]BZ RAZ D,MOS HEIO V G.A note on a greedy heuristi c for t he fl o w2shop makespan m i n i m izati on with no m achi ne idle2ti m e[J].Eur J Ope r R es,2008,184(2):8102813.[5]PA N Quan2ke,WANG L i ng.No2i dle per muta ti on fl o w shop schedu li ng based on a hybr i d d i scre te particle s war m o pti m izati ona l gor it hm[J].The Inte rnati onal Journa l of Advanced M anu fact ur i ng Technol ogy,2008,39(728):7962807.[6]PA N Quan2ke,WAN G L i ng.A novel diff e renti a l evol utio n a l gor it hm for no2i dle per m utatio n flo w2shop scheduli ng prob l em s[J].European J.of Industrial Engi nee ri ng,2008,2(3):2792297.[7]EUS UFF M M,LA NSEY K E.Opti m i zati on ofwate r distributi on net work desig n usi ng t he shu ffl ed fro g leap i ng algor i th m[J].W ater R esour P lan M anage,2003,129(3):2102225.[8]EL BELT AG I E,HEGAZ Y T,GR IER S ON D.Co m parison among fi ve evol utio nary2based opti m izati on algorith m[J].AdvancedEngineer i ng In f or m atics,2005,19(1):43253.[9]王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001,10.An Algor ithm Based on Discrete Shuffled Frog L eap i ng forNo-Id le Per m uta ti on F lo w Shop Sc hedu li ng Proble mWANG Y a2m in1,2,JI Jun2zhong1,P AN Quan2ke2(11Be iji ng Munic i pal Key Laboratory ofM ulti m edia and Intelli gent Soft w are Technol ogy,Be iji ng Un i versity of Technol ogy,B eiji ng100124;21College of Co mpu ter Sc i ence,L i aocheng Un i versity,Liaocheng,252059,Ch i na)Abstr act:A D iscrete Shuffled Frog Leap i n g A l g orit h m(DS FL A)is proposed to solve the No-Idle per m utati o n F l o w Shop schedu ling proble ms(N I FS).I n the li g ht of the opti m ization m echan is m of genera l SFL A,the algorithm adopts an encoding sche me based on job per m utation and a ne w method of indivi d ual producti o n to extend the trad itionalmodel of SFL A,and e mp l o ys the si m ple neighbor hood search to present t h ree i m pr ove ment strategi e s.The experi m en tal resu lts sho w that the proposed algorithm and its stra tegies are eff ective and e f ficient i n d iff erent scale bench m ar ks ofN I FS.K ey w ord s:no-idle flo w shop;discrete shu f fled frog leapi n g a l g orit h m;neighbor hood search(责任编辑张士瑛)。
蛙跳算法与批量无等待流水线调度问题的优化
蛙跳算法与批量无等待流水线调度问题的优化
谢圣献;潘全科;潘玉霞;贾保先
【期刊名称】《计算机应用研究》
【年(卷),期】2010(027)008
【摘要】针对以makespan为指标的批量无等待流水线调度问题,提出了一种有效的离散蛙跳算法.首先采用基于工序的编码方式使蛙跳算法直接应用于调度问题;其次采用基于NEH与改进NEH和随机产生相结合的初始化方法,保证了初始解的高质量和分布性;再次采用交叉或变异方法产生新解,保持了种群的优越性和多样性;最后对全局最优解执行快速局部搜索,有效地降低了算法的时间复杂度,平衡算法的全局和局部开发能力.对随机生成不同规模的实例进行广泛的实验,通过仿真实验结果的比较,表明所得蛙跳算法的有效性和高效性.
【总页数】4页(P2909-2912)
【作者】谢圣献;潘全科;潘玉霞;贾保先
【作者单位】聊城大学,计算机学院,山东,聊城,252059;聊城大学,计算机学院,山东,聊城,252059;海南大学,三亚学院,海南,三亚,572022;聊城大学,计算机学院,山东,聊城,252059
【正文语种】中文
【中图分类】TP18
【相关文献】
1.无等待流水线调度问题的混合优化算法 [J], 刘敏
2.批量流水线调度问题的混合离散蛙跳算法 [J], 潘玉霞;潘全科;桑红燕
3.批量无等待调度问题的微粒群蛙跳混合优化算法 [J], 潘玉霞;谢光;潘全科
4.蛙跳优化算法求解多目标无等待流水线调度 [J], 潘玉霞;潘全科;李俊青
5.求解无等待Flow shop调度问题的改进蛙跳算法 [J], 吴永明;王亚昆;张晗;赵旭东;陈琳升;史海鹏
因版权原因，仅展示原文概要，查看原文内容请购买。
解决批量流水线调度问题的离散微粒群算法
第 ３期
潘 玉 霞等 ： 决批 量 流 水线 调度 问题 的离 散 微 粒 群 算 法 解
９ １
工件 ．被划分 成 ｓ 个小 批量 ， 『 Ｊ Ｉ 是工 件 Ｊ的小 批量在 机床 ｉ 的加 工时 间 ， ， ｔ 上 Ｓ 为工件 在机床 ｉ 上 的开始加 工 时间 ， 为工 件 在机床 ｉ 的完 成时 间． ＥＴ 上 则
潘玉霞 潘全科 桑红燕 武 磊
（ 聊城 大 学 计 算 机 学 院 ， 山东 聊 城 ２２ ５ ） ５ ０ ９
摘
要
提 出了解决 以 ｍａ ｅｐ ｎ为 目标 的批 量 流水 线调 度 问题 的 离散 微 粒群 优 化 算 法． ｋ ｓａ 该算
法采用 了基 于工序 的编码 方 式， 设计 了新 的粒 子 生成 公式 ， 过局 部 搜 索 来提 高 算 法的 开发 能 通
Ｓ ． Ｔ１ １— ０ ，
一
Ｓ ， Ｔ， １一 Ｓ — ． Ｔ １ １＋ ／ｆ１ ｆ１ ｔ一 ． １× 一 ，
（ ｘ［ Ｓ １ Ｊ １ ，Ｓ ，ｌ ＋ Ｉ － × ５ １ ， Ｊ ｍａ （ Ｔ ． ＋ ， ） （ Ｔ ＿ ｔ ｌ ｊ ］ Ｉ ， 卜 卜 ， ， — ｔ ≥ ， ， 卜ｌ
１ ０ ２ ０ ３ ０ ４ ０ ５ ０ ６ ０ ７ ０ ８ ０ ９ ０
效果 ， 故采用 小批量 的等 量分 配原则 ． 个工 件 各 的小批 量加工 完成后 就能 被传送 到下一 台机 床
图１ ＬＳ Ｆ Ｐ调 度 模 型
上加工 ， 所有 小批量 的加工顺 序都相 同． 每个 工件在每 台机床 上加 工完 成后 ， 不影 响 各工 件最 后 一个 小 在
较好 的优 化性能 ， 根据 Ｐ Ｏ 的优 化原理 ， 出了一种离 散微 粒群 算法 （ ｉｃｅｅＰ Ｏ，Ｄ Ｓ 来 解 决批 量 Ｓ 提 Ｄ ｓｒｔ Ｓ Ｐ Ｏ） 流水 线调 度问题 ． 同时 ， 合基 于 Ｐ ｉ ｓ 局部搜 索来平衡 算法 的全 局开发 和局 部搜 索 能力． 真 试验 表 结 ａｒ ｅ ｗｉ 仿
一种多智能体混合蛙跳算法
一种多智能体混合蛙跳算法王联国;代永强【期刊名称】《计算机工程》【年(卷),期】2013(039)007【摘要】This paper proposes a Multi-agent Shuffled Frog Leaping Algorithm(MSFLA) by introducing the multi-agent system to the Shuffled Frog Leaping Algorithm(SFLA).This algorithm fixes the agent on grid,with the competition and cooperation with its neighbors,and combining the evolution mechanism of the SFLA.Each agent unceasingly senses local environment,and gradually affects the whole agent grid,so that it enhances its adaptiveness to the environment.The agent also makes self-study by using its knowledge to enhance its adaptiveness to the environment.By the test of high dimension benchmark functions,the results illustrate this algorithm this algorithm can effectively maintain the diversity of the population,increase the precision of optimization,simultaneously,efficiently restrain the prematurity,and has higher optimization performance in the field of high dimension functions optimization.%提出一种多智能体混合蛙跳算法.将智能体固定在智能体网格上,每个智能体通过与其邻居的竞争与合作,结合混合蛙跳算法的进化机制,不断感知局部环境,并逐渐影响整个智能体网格,以提高自身对环境的适应能力.为更好地适应环境,智能体也可以利用自身的知识进行自学习.仿真实验结果表明,该算法能有效地维持种群的多样性,提高优化精度,同时抑制早熟现象,在高维函数优化方面具有较高的优化性能.【总页数】6页(P265-269,287)【作者】王联国;代永强【作者单位】甘肃农业大学信息科学技术学院,兰州730070;甘肃农业大学信息科学技术学院,兰州730070【正文语种】中文【中图分类】TP301.6【相关文献】1.一种新的领域智能体:免疫智能体 [J], 马笑潇;黄席樾;柴毅;黎昱2.未来网络的一种新范式:网络智能体和城市智能体(特邀) [J], 余少华3.一种智能多功用一体化助老购物代步车的设计 [J], 蔡文明;崔有正;范翔铃;段成承;王博;陈领枢4.一种基于神经网络的多智能体建模技术 [J], 张增辉;唐平;马若雯5.一种新的GIS智能分析框架——GIS智能体 [J], 沙宗尧;胡自锋因版权原因，仅展示原文概要，查看原文内容请购买。
求解混合流水线调度问题的离散人工蜂群算法
（ １ ． 聊城大学 计算机学 院， 山东 聊 城 ２ ５ ２ ０ ５ ９；２ ． 东 北 大 学 流 程 工 业 综 合 自动 化 国 家 重 点 实验 室 ， 辽宁 沈 阳 １ １ ０ ８ １ ９；３ ． 北 京 邮 电大 学 经 济 管 理 学 院 ， 北京 １ ０ ０ ８ ７ ６ ）
ｔ ｈ ｅ ｐ ｏ ｐ ｕ ｌ ａ ｔ ｉ ｏ ｎ ｓ ｅ ｔ ，ｔ ｏ ｃ ｏ ｍｐ ｌ ｅ ｔ ｅ ｔ ｈ ｅ ｌ ｏ ｃ ａ ｌ ｓ ｅ ａ ｒ ｃ ｈ ｔ ａ ｓ ｋ ｗｉ ｔ ｈ ａ ｄｅ ｔ ａ ｉ ｌ ｅ ｄ ｄ ｅ ｓ ｉ ｇ ｎ ｅ ｄ ｌ ｏ ｃ ａ ｌ ｓ ｅ ａ ｒ ｃ ｈ ａ ｐ ｐ ｒ ｏ ａ ｃ ｈ． Ｏｎ ｌ ｏ ｏ ｋ ｅ ｒ ｂ ｅ ｅ ｓ ｒ ａ ｎ ｄ ｏ ｍｌ ｙ ｆ ｅ ｔ ｃ ｈ ｔ ｗｏ ｕ ｐ ｄａ ｔ ｅ ｄ ｓ ｏ ｌ ｕｔ ｉ ｏ ｎ ｓ ａ ｎｄ ｓ ｅ ｌ ｅ ｃ ｔ ｔ ｈ ｅ ｂｅ ｔ ｔ ｅ ｒ ｏ ｎ ｅ ａ ｓ ｔ ｈｅ ｃ ｕ ｒ ｒ ｅ ｎ ｔ ｓ ｏ ｌ ｕ ｔ ｉ ｏ ｎ，ａ ｎ ｄ ｔ ｈｅ ｎ ｃ ｏ ｍｐ ｌ ｅ ｔ ｅ ａ
ｔ ｈ ｅ ｔ ｉ ｃ ａ ｌ Ａ ｕ ｔ ｏ ｍａ ｔ ｉ ｏ ｎ ｆ ｏ ｒ Ｐ ｒ ｏ ｃ ｅ ｓ ｓ Ｉ ｎ ｄ ｕ ｓ ｔ ｒ ｉ ｅ ｓ ， Ｎ ｏ ｒ ｔ ｈ ｅ ａ ｓ ｔ ｅ ｒ ｎ Ｕ ｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ ，Ｓ ｈ ｅ ｎ ｙ ａ ｎ ｇ １ １ ０ ８ １ ９ ，Ｃ ｈ ｉ ｎ ａ ； ３ ．Ｓ ｃ ｈ ｏ ｏ ｌ ｆ ｏ Ｅ ｃ ｏ — ｎ ｏ ｍｉ ｃ ｓ ａ ｎ ｄ Ｍａ ｎ ａ ｇ ｅ ｍ ｅ ｎ ｔ ， Ｂ ｅ ｉ ｊ ｉ ｎ ｇ Ｕ ｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ ｆ ｏ Ｐ ｏ ｓ ｔ ｓ ａ ｎ ｄ Ｔ ｅ ｌ ｅ ｃ ｏ ｍ ｍｕ ｎ ｉ ｃ ａ ｔ ｉ ｏ ｎ ｓ ， Ｂ ｅ ｉ ｊ ｉ ｎ ｇ １ ０ ０ ８ ７ ６， Ｃ ｈ ｉ ｎ ａ ）
改进二进制-实数编码混合蛙跳算法在水电机组短期发电调度中的应用
改进二进制-实数编码混合蛙跳算法在水电机组短期发电调度中的应用杨哲;杨侃;吴云;夏怡;齐伟擎;张天衍;仲晓林【摘要】本文将改进实数编码混合蛙跳算法(IR-SFLA)和二进制编码的(IB-SFLA)方法分别应用到水电站经济负荷分配(ELD)和机组组合(UC)问题,提出解决STHGS 问题的IBR-SFLA方法.实数编码版本IR-SFLA利用混沌学遍历性、随机性特征生成初始种群,采用更新的局部搜索和位置更新策略实现青蛙更新换代,并在迭代后期通过自适应青蛙激活机制重新激发青蛙搜索能力;在二进制编码IB-SFLA中引入改良青蛙子种群分组方式,将青蛙种群分为领导蛙、追随蛙和变异蛙3类蛙群,各类蛙群分别基于正态云模型的精英进化策略、改进的局部搜索机制和混沌理论的蛙群变异操作进行更新迭代.运行结果显示IBR-SFLA相较对比算法,在低、中、高水头下最高缩减耗水量1.14×107、1.22×107、7.52×106 m3,有效提升水能资源利用效率;在保证运算精度、稳定性的同时,平均运行时间最高缩减178、173和172 s,进一步,改进策略性能分析显示,各改进策略可有效增强搜索性能,提升精度,且耗时增幅较小,在较小种群规模下便可获取较高质量的解,为解决大规模机组短期电力调度优化课题提供有效了新思路.【期刊名称】《天津大学学报》【年(卷),期】2019(052)009【总页数】11页(P979-989)【关键词】水电站机组短期发电调度(STHGS);自适应青蛙激活机制;改良子种群分组方式;云模型精英进化策略;混沌蛙群变异【作者】杨哲;杨侃;吴云;夏怡;齐伟擎;张天衍;仲晓林【作者单位】河海大学水文水资源学院,南京 210098;河海大学水文水资源学院,南京 210098;山西水利职业技术学院,运城 044004;河海大学水文水资源学院,南京210098;河海大学水文水资源学院,南京 210098;河海大学水文水资源学院,南京210098;扬州市勘测设计研究院有限公司,扬州 225000【正文语种】中文【中图分类】TM612水电站机组短期发电调度(STHGS)问题的研究旨在满足水电站电网发电要求前提下，寻求最小的发电和机组启停水量消耗．通常STHGS可划分为两个子问题，一是水电站机组组合(unit commitment，UC)优化，决定运行时段内机组启停的时序组合，典型0～1规划问题；二是机组经济负荷分配(economic load distribution，ELD)，为连续空间约束问题，旨在对每台机组进行最优负荷分配．对机组组合和负荷分配优化可有助提升水能资源利用效率，增发电量，保证电网系统运行稳定．STHGS问题研究历经由传统数学到智能算法优化的过渡，传统数学方法以混合整数非线性规划、拉格朗日松弛法(LR)、二次规划(QP)和动态规划(DP)为主，以DP为例，此方法可以求出理论最优解，但面对较大规模机组组合易陷入“维数灾”，虽然传统方法取得了不同程度的优化效果，但在面对大规模机组发电优化问题时的运算效率和精度难以得到保证．随着人工智能的兴起，诸如萤火虫算法、万有引力算法(GSA)、烟花算法[1-3]等方法被应用到复杂水电站发电优化调度问题．与传统方法相比，智能算法不受约束条件的限制，凭借灵活的搜索策略和强大的收敛性能，可在较短时间内获取高质量的优化结果．与此同时，为进一步增强搜索和收敛性能，由两种或多种算法组合的混合方法被应用到STHGS问题优化．然而，上述方法在收敛性能和搜索精度等方面仍有提升空间．例如万有引力算法，虽然加入混沌理论来增强局部搜索能力，但整体效率、鲁棒性仍有待提升和改善；蚁群算法随着机组数目的增多，搜索效率显著下降，且参数设置可能会导致结果早熟．总体来说，对于STHGS问题，迫切寻求更高效的优化方法和工具．混合蛙跳算法(SFLA)子种群内部信息交流和全局蛙群信息共享可有效引导算法向全局最优方向快速收敛，但仍存在“早熟”收敛弊端．为此，学者针对混合蛙跳算法进行改进，并应用于水资源、交通、电力系统等领域[4]．本文首先构建水电站机组短期发电模型，包含机组组合和负荷分配子模块；进而在传统SFLA基础上加以改进分别提出二进制编码IB-SFLA和实数编码IR-SFLA．前者用于解决UC子问题，改进策略为引入云模型和混沌理论，将蛙群分为3类子种群，每类子种群按各自搜索方式进行更新；后者被应用到经济负荷分配子问题，改进策略为基于改进Logistic映射的种群初始化和启发式青蛙激活机制，以及改良的蛙群局部搜索公式，从而提出二进制及实数编码混合蛙跳算法(improved binary and real-coded shuffled frog leaping algorithm，IBR-SFLA)．在三峡大规模水电站机组短期发电调度优化的应用，验证了算法在解决高维、非线性、离散发电调度问题中的高效性和适用性，为此类问题优化提供有效新方法．经济负荷分配作为短期水电站发电调度子问题，旨在以最小水量消耗完成发电目标，目标函数为式中：为第台机组的启停状态；为机组数；、分别为第台机组分配的负荷和当前状态下的水头；即为在水头下第台机组分配负荷消耗的流量．机组组合问题是寻求机组开启和关闭的最优时序安排，减少发电和机组开启、关闭时水量的消耗．相应目标函数可描述为式中：为总耗水量；代表流量与水量的换算系数；表示运行期间隔，设为1h；为总运行期；、为启停机组消耗的部分流量；代表第台机组在时刻水头；为第台机组在时刻负荷；为时刻第台机组对应、时的耗流量；取值0或1，代表第台机组时刻为开启或关闭状态．(1) 功率平衡约束为式中为时刻水电站的发电要求．(2) 旋转备用约束为式中表示时刻旋转备用容量．(3) 水电机组发电负荷约束为式中和分别代表第台机组最小和最大发电负荷．(4) 禁止运行区约束为式中：为禁止运行区总数量；为计数变量；和分别表示台发电机组、第和第禁止运行区上限和下限．(5) 最小启停时间约束为式中：、分别为最小的启动和关闭时间；和分别表示台机组到时刻时的累计开启和关闭时间．(6) 水电站调蓄和下泄流量约束为式中：、分别为水电站最小和最大蓄水容量；和分别为下泄流量的下限和上限．(7) 水量平衡约束为式中：为时刻水库蓄存的水量；和分别为入库和出库流量；为调度期间隔．混合蛙跳算法(SFLA)是结合了确定性和随机性方法的基于群体智能的后启发式全局优化算法，该算法融合了模因演化和基于群体行为的粒子群算法的优点，具有参数少、理论概念易于理解等特点[5]．有关SFLA的更新和种群分组策略参阅文献[6]．2.2.1 青蛙子种群分组策略传统SFLA分组策略首先将种群内各只青蛙按适应度好坏排序，此分组方式往往把适应相对较差的青蛙分在靠后的群组中，使得该组青蛙更新效率远不如前面的群组，导致青蛙的学习更新效果不佳．为此，本文将整个蛙群划分为领导蛙、追随蛙、变异蛙3类蛙群，各类蛙群根据各自青蛙特点按相应更新机制进行迭代，从而提高更新效率．具体分组方法如下．首先求解所有子群中最佳个体适应度值的平均值，然后得到优于和劣于的所有子群内最优青蛙适应度的平均值和；最佳青蛙适应度优于的子蛙群设定为领头蛙群组，次于的子蛙群是变异蛙群组，追随蛙子种群即为(为种群规模)．2.2.2 追随蛙蛙群局部搜索策略由于机组组合优化非线性0～1规划问题，因而首先对青蛙位置进行离散化处理，编码方式为0、1二进制编码，在此编码方式下，青蛙位置的更新采用具有概率性质的方程，跳跃步长决定青蛙位置为0或1的概率，采用改进的Sigmoid函数(式(10))建立步长与位置转换概率间的关系．相应Sigmoid函数见图1．式中：和分别为次迭代前后第只青蛙对应第台机组的状态；rand为[0，1]随机数；为第只青蛙对应台机组在次迭代跳跃步长．传统蛙跳算法中，子群中最差个体首先参照内部最优青蛙进行更新，若适应度无法提升，则根据全局最优青蛙进行更新；因而青蛙更新过程中并没有同时利用子种群、全局最优个体携带信息，导致蛙群子种群内部局部搜索机制存在局限性．本文对局部搜索方式进行改良，同时利用子种群内最优个体和全局最优个体来引导最差青蛙进行跳跃步长、觅食位置更新，其更新公式为式中：为更新后的青蛙跳跃步长；和分别为最优、最差青蛙位置；表示当前全局最优青蛙位置；和具有与[0，1]随机数相同的含义．改进策略首先对子种群最差青蛙按照传统策略进行位置更新，若新位置劣于原位置，则将用替换，按传统位置更新公式进行搜索，若仍无法获取优秀位置，则依照式(11)更新最差青蛙．2.2.3 基于云模型的领头蛙蛙群精英进化策略云模型可完成定性概念和定量描述间不确定转换，构建一种定量和定性间的映射，具有随机性和稳定倾向性的特点[7]．云模型的引入可在小范围内搜寻潜在的最优解，从而显著提升算法局部优化性能．期望、熵和超熵为云模型用以描述所生成云滴的3个数字特征．云滴的生成是由正态云发生器，通过产生两次正态随机数来实现．各数字特征含义、功能及云滴具体生成方法可参考文献[6，8]．基于云模型的精英进化策略在对领导蛙子种群最差个体进行位置更新的同时，对最优青蛙采用云模型进行局部“发掘”探索，搜寻潜在的优秀个体．将最优个体作为，生成一系列具有与子种群青蛙相同数目的正态云滴(，，)，若这组云滴(青蛙)中存在更优位置则进行替换．2.2.4 基于混沌理论变异蛙蛙群变异策略变异蛙蛙群往往都是种群中较差个体，学习和交流能力远不如领导蛙和追随蛙蛙群，对此，本文根据混沌学理论遍历、随机、规律性等特征，运用改进后Logistic映射(式(12))生成混沌变量[9]，对青蛙进行混沌变异操作，在算法陷入迭代停滞时，在收敛域以外空间进行跳跃性“开拓”，寻找游离在可行域中的“有利突变”个体．式中：和均为更新前后混沌变量；为当前更新数；为总更新数．通过Logistic映射生成的各混沌变量由式(13)映射到青蛙跳跃步长，跳跃步长与机组启停状态的概率转换由式(10)实现．式中和分别为步长上、下限值．变异蛙更新后的位置如果优于当前全局范围内最优青蛙位置，原位置即被取代，若无法得到提升则保留原位置，继续按变异策略搜索直至触发终止条件.2.3.1 混沌理论初始种群生成机制初始种群生成方式直接影响种群多样性和整体质量，相比随机生成的初始种群，利用第2.2节阐述的混沌原理遍历性、随机性进行蛙群初始化，可有效提升种群多样性、分布均匀性．由于IR-SFLA优化变量为实数编码的机组负荷，因而对混沌变量映射到优化变量的方式进行调整，其公式为式中和分别为优化变量机组负荷的下边界和上边界．在IR-SFLA中，青蛙位置更新参照标准蛙跳算法，进而计算适应度，若新位置优于上一代青蛙位置，则将上一代青蛙进行替换，并记录新青蛙为初始青蛙种群的一员．2.3.2 改进的局部搜索和位置更新策略在IB-SFLA中提到，传统SFLA没有充分利用子种群内部和全局最优青蛙的引导作用，对此，本文进一步改良IR-SFLA中更新策略(式(15)和式(16))，充分利用两个最优个体更新最差青蛙位置．此外，引入改进动态惯性权重因子，在迭代开始时取较大值，使蛙群具有强大的全局和子群体局部搜索能力，在迭代后期，蛙群搜索速度放缓，此时值相应缩小使蛙群在局部可行域进行精细搜索．式中：为t＋1代跳跃步长；、分别为子种群青蛙最优、最差位置；为当前全局最优位置；、为[0，1]随机数．式中：为当前全局迭代数；为全局总迭代数；为局部总迭代数；为权重系数；和分别表示迭代初、末惯性权重．2.3.3 启发式青蛙激活机制随着迭代的进行，将出现这样的情况：子种群最佳青蛙位置和种群最佳位置非常相近，导致青蛙更新变得缓慢甚至停滞．为此提出启发式青蛙激活机制，淘汰逐渐失去竞争力的青蛙[9]，生成新青蛙位置来激活搜索能力的公式为式中：为判定阈值，若在指定迭代次数内均满足，则激活式(17)；为[0，1]随机数；为调节因子，引入反正切函数使其动态变化[10]，在迭代初期，为增强局部搜索性能，取较大值；在迭代后期，为降低不确定影响，缩小取值．式中：和分别为调节因子初始、结束值；为控制因子．将经济负荷分配模型与机组组合模型分别作为内、外层子模块，外层模块通过调用IR-SFLA制定的最优负荷分配表，对开启发电机组分配最优机组出力，进而计算相应总发电耗水量．内外层模块进行耗水量信息交流反馈，将信息传到UC子模块，利用提出IB-SFLA搜寻更优机组组合方式．详细模型优化流程如图2所示．3.1.1 编码结构及初始化UC子问题中的青蛙个体是按二进制0～1进行编码，分别代表第台机组在时刻关机、开机状态．因而针对UC问题的模型编码结构可表述为矩阵形式，矩阵中均为0和1整数，具体结构为式中：为机组编号；j为运行时刻，h；代表第台机组在时刻的启停状态(0或1)，具体通过式(20)进行相应机组在每一运行时刻初始化二进制编码．3.1.2 约束条件处理策略1) 旋转备用约束修补策略在某时刻机组组合方案确定后，需判定其是否满足旋转备用约束(见式(4))．若不满足需要启动备用容量补充方案，在启动额外机组满足旋转备用约束时，可能出现新增开机机组过多，导致备用容量偏大而额外增加一部分耗水量，此时需通过修复策略关闭部分机组．引入机组启停优先顺序表来对合理安排机组启停时序，优先顺序表依照各类型机组在满负荷状态下的平均耗水率升序排列．机组满负荷耗水率[11] (m³/MW)定义为式中和分别为第发电机组对应水头最大的输出功率和消耗的水量．(1) 容量补充方案．当稳定运行条件下所有启动机组的总输出上限小于当时水电站的装载计划和备用容量之和时，以机组开启和关闭优先顺序，依次关闭已达到最小启动时间的机组，直到满足约束条件．(2) 修复策略．当稳定运行条件下所有启动机组的最小输出总和大于当时水电站的装载计划和备用容量之和时，以机组启停优先顺序的相反顺序依次关闭满足最小启动时间的机组，直到满足系统备用容量约束．2) 开启、关闭时间修补策略算法在寻优过程中设置两个数组变量和，按式(22)分别记录第只青蛙时刻第台机组的开、关机持续时间，机组若没有达到最小开启和关闭时间，则时刻仍保持－1时刻的开启或关闭状态，若满足约束则依据式(10)选择各青蛙对应机组在时刻的启停状态．最优负荷分配表的制定在机组全部开启基础上，且考虑机组稳定运行区约束，保证机组的安全高效运行．制定好的机组最优负荷分配表存入数据库中以备调用．定义为机组组合中开机机组数目，计数变量表示最优负荷分配表中的第行，可根据各时刻发电负荷计划定位到表中某一行，进行机组出力最优分配；若无法直接定位，可采用线性内插获得[12]．基于IR-SFLA的负荷分配计算式可描述为式中：为初始状态边界条件；定义为机组累计负荷；表示在水头总出力为时的发电耗水量；为最优青蛙个体．为验证IBR-SFLA在解决复杂、连续和离散空间优化耦合的STHGS问题的适用性和寻优性能，本文以三峡水电站大型发电机组短期发电优化为例，选取左、右岸26台发电机组，调度周期为24h．4.1.1 算法主要参数设置为避免频繁启停对机组造成的损耗，选定机组最小启停时间和为4h，IBR-SFLA需要控制的参数较少，分别选取蛙群规模、子蛙群数目为80和10，对应子蛙群青蛙数目＝8；青蛙跳跃步长上、下限分别为＝4和＝－4；惯性权重w的初值和分别为0.85和0.40；调节因子和分别为0.90和0.40；自适应激活机制判定阈值＝10-3；局部更新次数和全局更新次数分别为10和50．4.1.2 机组稳定运行区、发电负荷要求不同机组流量特性曲线各有不同，在不同水头下都有各自稳定运行区，图3为75m、88m和107m平均水头下各类型机组(1#～26#)稳定、限制运行区的分布情况；水电站依照电力部门的用电计划，制定的发电机组各时段负荷要求如图4所示．4.1.3 计算结果与讨论针对三峡水电站26台发电机组在75m(低)、88m(中)和107m(高)平均水头下分别独立运算20次，机组分配负荷表、开启和关闭时序组合参见表1；图5为20次运算中最优发电耗水量的迭代曲线，描述了∶群中最优耗水量、平均耗水量迭代过程．从图5可以看出，迭代初期IBR-SFLA在领头蛙蛙群领导下，算法依靠云模型在局部的深度搜索能力可以快速向最小耗水量不断逼近；与此同时追随蛙在改进搜索策略引导下不断向最小耗水量逼近；随着迭代深入，蛙群开拓能力开始下降，搜索可能趋于稳定停滞状态，即局部最优，变异蛙蛙群结合混沌理论随机性和遍历性特征，可在收敛停滞区域以外可行搜寻空间“开拓”更优解，有助蛙群及时跳出局部最优，摆脱“早熟”迹象，向更优耗水量收敛，而在迭代后期，IBR-SFLA稳定收敛到最优解．由表1可知，基于IBR-SFLA求解的机组短期发电调度经济负荷分配和机组组合可满足最小开启和关闭时间、禁止运行区域等约束；有效保证机组在各自稳定运行区运行，避免频繁启停对机组寿命的不利影响，实现发电机组安全高效运行．为进一步验证IBR-SFLA在解决短期电力调度问题的高效性，选取改进遗传算法(LAGA)、扩展蚁群(EACO)、混沌引力搜索算法(CGSA)、烟花算法(FA)和改进蜂群算法(IBCO)作为对照，初始种群规模和进化代数均保持一致，各方法独立运行20次，发电总耗水量迭代曲线如图6所示．由图6可以看出，与对比算法相比，IBR-SFLA求解精度得到有效提升，可获取更小发电耗水量；LAGA收敛的最优解相对较差，与其交叉、变异参数不确定性有很大关联，IBR-SFLA需控制参数较少，一定程度降低算法不确定性；IBCO陷入搜索停滞状态时的局部深度“开拓”能力不如IBR-SFLA，导致其中后期搜索进程放缓，过早收敛到局部最优解．为进一步对比各算法结果的分布和离散情况，将3种水头下20次运行耗水量整理成箱形图(图7).图中各算法对应箱形图左侧为数据点，右侧为数据分布“箱子”．由图7可以看出，IBR-SFLA对应低、中和高水头的最优耗水量精度均优于其他算法，体现在IBR-SFLA获取的“箱子”位于最低位置；20次运行结果围绕中位数分布密集，离散程度较低，可由IBR-SFLA相对扁平的“箱子”和较短“胡须”(箱子上下的延伸线)验证，它表明IBR-SFLA在解决稳定性和准确性方面更加出色．对于高水头工况，虽然IBR-SFLA对应“箱子”高度并不占据优势，但其20次运算结果的分布位置均优于对比算法，较短的“胡须”表明不存在与中位数相距较远的“离群解”．上述迭代曲线和箱形图验证了IBR-SFLA在求解精度和可靠性方面的高效性，但并未体现IBR- SFLA运算速度优势，IBR-SFLA整体性能(精度、可靠性和运算速度)优势如表2所示，表中“平均”、“最优”分别为20次运行平均和最优解．分析表2数据可得以下结论．(1)求解精度方面，IBR-SFLA相比LAGA、EACO、CGSA、FA以及IBCO有显著提升，以低水头为例，20次运行“平均”耗水缩减量分别为1.14×107、5.32×106、4.32×106、3.68×106和2.99×106m3，缩减率分别为1.06%、0.50%、0.40%、0.35%和0.28%，可以看出对SFLA的改进策略使得求解精度显著提升．(2) 求解速度方面，青蛙子种群只更新组内最差或最优青蛙，因而1次迭代可能只需计算1次，最多也只需3次运算，充分压缩每次迭代所需时间，提升算法寻优和收敛速度．(3) 稳定可靠性方面，IBR-SFLA20次运行所得结果的标准差显著降低，图8中扁平的箱形图和较短的“胡须”表明解分布较为密集，离散程度较小，整体质量可得到保证，从而验证了IBR-SFLA良好的求解稳定性．为进一步验证种群规模、4种改进策略对算法性能的影响，体现本文方法的有效性和优势，设计了多组方案进行计算，各方案寻优过程、计算时间对比如图8所示．从单一改进策略来看，4种策略较传统 SFLA均可不同程度改善短期发电调度耗水量；将各策略进行耦合所得优化结果最为明显．计算时间方面，加入改进策略的SFLA会有所增加，但增幅较小；从不同种群规模结果可知，改变种群规模对本文方法的提升有限，同时会显著增加计算时间．综上所述，所提出的改进策略可有效地提高算法搜索性能，显著提升运行效率，在牺牲一定计算时间的前提下可获取更高质量的结果．针对机组组合和经济负荷分配子问题组成的水电站短期发电调度问题，本文首先提出改进的二进制IB-SFLA和实数编码IR-SFLA，对于UC子问题，IB-SFLA将青蛙种群分组为3类，各类子种群基于云模型理论、改进的局部搜索公式、混沌学原理分别进行领头蛙、追随蛙和变异蛙蛙群的进化、更新、变异操作；经济负荷分配作为连续空间优化问题，由基于混沌理论的初始种群生成策略、改进的局部搜索与位置更新公式和启发式青蛙激活机制的IR-SFLA进行优化，进而提出基于二进制-实数编码IBR-SFLA方法．改进后的IBR-SFLA应用到大规模机组短期电力调度优化问题，削减了水电站发电耗水量，实现水能资源高效利用；算法在保证运行稳定性前提下进一步提高求解精度，缩减运行时间，为STHGS优化问题提供切实有效新方法．【相关文献】［1］石季英，薛飞，李雅静，等. 基于免疫二进制萤火虫算法的主动配电网低碳目标网架规划[J]. 天津大学学报:自然科学与工程技术版，2017，50(5)：507-513.Shi Jiying，Xue Fei，Li Yajing，et al. Active distribution system planning for low-carbon objective using immune binary firefly algorithm[J]. Journal of Tianjin Univer-sity：Science and Technology，2017，50(5)：507-513(in Chinese).［2］沈冬梅. 基于改进引力搜索算法的电力系统机组组合问题的研究[D]. 上海：东华大学，2016.Shen Dongmei. Research on Unit Commitment Problems in Power System Based on Improved Gravitational Search Algorithm[D]. Shanghai：Donghua University，2016(in Chinese).［3］ Srikanth R K，Panwar L K，Kumar R，et al. Binary fireworks algorithm for profit based unit commitment(PBUC)problem[J]. International Journal of Electrical Power& Energy Systems，2016，83：270-282.［4］ Hidalgo-P A，Vega-Rodríguez M A，Ferruz J，et al. MOSFLA-MRPP：Multi-objective shuffled frog-leaping algorithm applied to mobile robot path planning[J]. Engineering Applications of Artificial Intelligence，2015，44：123-136.［5］赵付青，陈自豪. 基于自适应变异因子策略的混合蛙跳算法[J]. 甘肃科学学报，2016，28(1)：6-11.Zhao Fuqing，Chen Zihao. Shuffled frog-leaping algorithm based on the theory of adaptive mutation factors[J]. Journal of Gansu Sciences，2016，28(1)：6-11(in Chinese). ［6］杨哲，杨侃，夏怡，等. 考虑不同生态流量要求梯级水库群生态调度及其算法[J]. 天津大学学报：自然科学与工程技术版，2018，51(12)：1266-1277. Yang Zhe，Yang Kan，Xia Yi，et al. Optimal ecological operation of cascade reservoirs and the algorithm considering different ecological flow demand[J]. Journal of Tianjin University：Science and Technology，2018，51(12)：1266-1277(in Chinese).［7］李德毅，孟海军，史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展，1995，32(6)：15-20.Li Deyi，Meng Haijun，Shi Xuemei. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development，1995，32(6)：15-20(in Chinese).［8］黄海鹏，徐镇凯，李诒路. 基于云模型的河流健康多层次模糊综合诊断——以赣江南昌段为例[J]. 长江流域资源与环境，2015，24(增1)：62-69.Huang Haipeng，Xu Zhenkai，Li Yilu. River health based on cloud model of multilevel fuzzy comprehensive diagnosis—In Nanchang section of ganjiang river[J]. Resources and Environment in the Yangtze Basin，2015，24(Suppl 1)：62-69(in Chinese).。
蛙跳算法-详解
蛙跳算法-详解目录• 1 什么是蛙跳算法• 2 蛙跳算法的原理• 3 蛙跳原理的特点• 4 蛙跳原理的数学模型什么是蛙跳算法蛙跳算法是一种全新的启发式群体进化算法，具有高效的计算性能和优良的全局搜索能力。
对混合蛙跳算法的基本原理进行了阐述，针对算法局部更新策略引起的更新操作前后个体空间位置变化较大，降低收敛速度这一问题，提出了一种基于阈值选择策略的改进蛙跳算法。
通过不满足阈值条件的个体分量不予更新的策略，减小了个体空间差异，从而改善了算法的性能。
数值实验证明了该改进算法的有效性，并对改进算法的阈值参数进行了率定。
蛙跳算法的原理蛙跳算法的思想是：在一片湿地中生活着一群青蛙。
湿地内离散的分布着许多石头，青蛙通过寻找不同的石头进行跳跃去找到食物较多的地方。
每只青蛙个体之间通过文化的交流实现信息的交换。
每只青蛙都具有自己的文化。
每只青蛙的文化被定义为问题的一个解。
湿地的整个青蛙群体被分为不同的子群体，每个子群体有着自己的文化，执行局部搜索策略。
在子群体中的每个个体有着自己的文化，并且影响着其他个体，也受其他个体的影响，并随着子群体的进化而进化。
当子群体进化到一定阶段以后，各个子群体之间再进行思想的交流（全局信息交换）实现子群体间的混合运算，一直到所设置的条件满足为止。
蛙跳原理的特点蛙跳原理是由Eusuff和Lansey为解决组合优化问题于2003年最先提出。
作为一种新型的仿生物学智能优化算法，SFLA 结合了基于模因（meme）进化的模因演算法（MA，memeticalgorithm）和基于群体行为的粒子群算法（PSO,particle swarm optimization）2 种群智能优化算法的优点。
该算法具有概念简单，调整的参数少，计算速度快，全局搜索寻优能力强，易于实现的特点。
混合蛙跳算法主要应用于解决多目标优化问题，例如水资源分配、桥墩维修、车间作业流程安排等工程实际应用问题。
蛙跳原理的数学模型算法参数与其他优化算法一样，SFLA亦具有一些必要的计算参数，包括F：蛙群的数量；m：族群的数量；n：族群中青蛙的数量；Smax：最大允许跳动步长；Px：全局最好解；Pb：局部最好解；Pw：局部最差解；q：子族群中青蛙的数量；LS：局部元进化次数以及SF：全局思想交流次数等。
混合蛙跳算法及其应用研究
混合蛙跳算法及其应用研究
混合蛙跳算法是一种基于蛙跳算法和遗传算法的混合优化算法。
该算法结合了蛙跳算法的局部搜索能力和遗传算法的全局搜索能力，可以在一定程度上提高算法的搜索效率。
在混合蛙跳算法中，首先使用蛙跳算法进行局部搜索，以寻找最优解的邻域。
然后，使用遗传算法对局部搜索得到的最优解进行全局搜索，以扩大最优解的搜索范围。
混合蛙跳算法在很多领域都有应用，如：
1. 函数优化：混合蛙跳算法可以用于求解多维函数的最小值问题，通过不断迭代和优化，最终得到最优解。
2. 组合优化：混合蛙跳算法可以用于解决一些组合优化问题，如旅行商问题、背包问题等。
3. 机器学习：混合蛙跳算法可以用于支持向量机、神经网络等机器学习模型的参数优化，以提高模型的分类或回归性能。
4. 数据挖掘：混合蛙跳算法可以用于聚类分析、关联规则挖掘等数据挖掘任务，以发现数据中的模式和规律。
5. 路径规划：混合蛙跳算法可以用于解决机器人或车辆的路径规划问题，以找到最优或次优路径。
总之，混合蛙跳算法是一种有效的优化算法，具有广泛的应用前景。
基于新型蛙跳算法的带阻塞流水线调度问题
基于新型蛙跳算法的带阻塞流水线调度问题
韩炜;崔喆;顾幸生
【期刊名称】《华东理工大学学报（自然科学版）》
【年(卷),期】2014(040)001
【摘要】针对目标函数为最小化Makespan的带阻塞流水线问题,提出了一种新型的蛙跳算法(New Modified Shuffled Frog Leaping Algorithm,NMSFLA)并对其求解.在蛙跳算法的局部搜索步骤中引入带约束的交叉变异思想,针对调度问题对青蛙的跳跃规则做出了改进,有效地解决了传统蛙跳算法局部搜索易出现不合法解从而导致算法效率不高的问题.仿真实验结果验证了NMSFLA解决带阻塞的Flow Shop问题的有效性.
【总页数】5页(P86-90)
【作者】韩炜;崔喆;顾幸生
【作者单位】华东理工大学化工过程控制与优化技术教育部重点实验室,上海200237;华东理工大学化工过程控制与优化技术教育部重点实验室,上海200237;华东理工大学化工过程控制与优化技术教育部重点实验室,上海200237
【正文语种】中文
【中图分类】TP31
【相关文献】
1.基于离散蛙跳算法的零空闲流水线调度问题求解 [J], 王亚敏;冀俊忠;潘全科
2.批量流水线调度问题的混合离散蛙跳算法 [J], 潘玉霞;潘全科;桑红燕
3.基于蛙跳算法的零空闲流水线调度问题优化 [J], 王亚敏;潘全科;冀俊忠;包云
4.蛙跳算法与批量无等待流水线调度问题的优化 [J], 谢圣献;潘全科;潘玉霞;贾保先
5.求解随机阻塞批量流水线调度问题的改进人工蜂群算法 [J], 韩玉艳;巩敦卫;张勇因版权原因，仅展示原文概要，查看原文内容请购买。
离散微粒群算法求解批量流水线调度问题
摘
要 ： 出了解决批量流水线调度问题 的离散 微粒群优化算法。 算法采用 了基于工序的编码方式 ， 提 该 设计 了新的粒子生成公 式，
从 而使微粒群 算法可以直接应 用于调 ， 将其与模拟退 火算法结合 ， 得到 了 改进的微粒群优化算法。仿真 实验 表明了上述算法的有效性 。
Ｅ ｍａ ｌｐ ｎ ｕ ｉ２ ０ ＠１ ． ｎ － ｉ： ａ ｙ ｘ ａ ｏ ８ ６ ｃ ３ ｏ
Ｐ Ｎ Ｙ — ｉ． Ａ ａ － ｅ Ｓ Ｎ Ｈｏ ｇ ｙ ｕ ｅ ａ．ｉ ｒｔ ｐ ｒ ｃｅｓ ａｍ ｐ ｍｉａ ｏ ｌｏｉ ｍ ｏ ｔｓ ｅｍｉｇｆ ｗ Ａ ｕ ｘａ Ｐ Ｎ Ｑｕ ｎ ｋ 。Ａ Ｇ ｎ － ａ ，ｔ Ｉ ｓ ｅｅ ａｔ ｌ ｗ ｒ ｏ ｔ ｚｔ ｎ ａｇ ｒ ｈ ｆｒｌ －ｔ ａ ｎ ｏ Ｄ ｃ ｉ ｉ ｉ ｔ ｏ ｒ ｌ
批量流水线调度 问题 （ ｔｓｅ ｍｎ ｌ ｓｏ ｃｅ ｕ ｎ ｏ Ｌ —ｔ ａ ｉｇＦｏ ｈｐ Ｓ ｈｄ ｌ ｇ ｒ ｗ ｉ Ｐｏｌ Ｌ Ｓ ） 许多实际 问题的简化模 型 ， ｒｂ ｍ，Ｆ Ｐ 是 ｅ 具有 广泛的工程 应用背景。 目前 ， 解决 Ｌ Ｓ Ｆ Ｐ的算法可大致 区分为构造式启发 算法ｌｌ 智能优化算 法［ １； ．ｆ ２Ⅱ ３ １ 。优先分配规则等构造式方 法虽然能 快速求解 ， 但是解的质量往往不高。 因此 ， 能在合理时间内求得 满意解的智能优化算法就成为求解调度 问题的主要 方法 。 微粒 群优化 （ ａ ｉ ｅＳ ａ ｐｉ ｚｔ ｎ Ｐ Ｏ） Ｐｒｃ ｗ ｒ Ｏ ｔ ａｉ ，Ｓ 算法源 于对鸟群 或 ｔｌ ｍ ｍｉ ｏ
关键词 ： 批量流水线调度 ； 微粒群算法； 模拟退 火算法 ＤＯ ：０３ ７￣ｉ ｎ１０ — ３ １ ０ ０ ６ １ 文章编号 ：０２ ８ ３ （０ ０ ０ — ０ ２ ０ 文献标识码 ： 中图分类￣ ： Ｐ ８ Ｉ １． ８ ．ｓ．０ ２ ８ ３ ． １． ． ５ ７ ｓ ２ ００ １０ — ３ １２ １ ）６ ０ ５ — ４ Ａ ＇ １１ Ｔ
求解混合流水车间调度问题的离散布谷鸟算法
1引言车间调度问题是指在有限的资源条件下，如何合理地安排车间生产任务，以满足或优化一个或多个性能指标。
该问题的性能指标种类繁多，如常用的生产效率指标[1]和近年来提出的绿色化指标[2]。
混合流水车间是一种常见的流水作业生产车间，具备一般流水车间和并行求解混合流水车间调度问题的离散布谷鸟算法罗函明1，罗天洪2，吴晓东1，陈科百11.重庆交通大学机电与车辆工程学院，重庆4000742.重庆文理学院智能制造工程学院，重庆402160摘要：为求解混合流水车间调度问题，提出一种离散布谷鸟算法。
针对常规解码方法难以获得最优解的缺点，提出一种改进的解码方法，基于工件数与并行机数，按概率随机分配机器；根据标准布谷鸟算法中莱维飞行和巢寄生行为两种位置更新策略的核心思想，提出基于位置交叉和个体距离的离散莱维飞行，设计基于最优插入和最优交换的巢寄生策略。
最后算例对比实验结果显示，采用基于改进解码方法的离散布谷鸟算法求解所得结果的平均值最小，验证了改进解码方法能提高解的质量；实例测试所得结果均获得了当前最优解，验证了离散布谷鸟算法求解该类问题的优越性。
关键词：混合流水车间调度；布谷鸟算法；解码方法；最小化最大完工时间文献标志码：A中图分类号：TH165；TP391doi：10.3778/j.issn.1002-8331.1908-0443罗函明，罗天洪，吴晓东，等.求解混合流水车间调度问题的离散布谷鸟算法.计算机工程与应用，2020，56（22）：264-271. LUO Hanming,LUO Tianhong,WU Xiaodong,et al.Discrete cuckoo search algorithm for solving hybrid flow-shop scheduling puter Engineering and Applications,2020,56（22）：264-271.Discrete Cuckoo Search Algorithm for Solving Hybrid Flow-Shop Scheduling ProblemLUO Hanming1,LUO Tianhong2,WU Xiaodong1,CHEN Kebai11.School of Mechanotronics&Vehicle Engineering,Chongqing Jiaotong University,Chongqing400074,China2.School of Mechanotronics Engineering,Chongqing University of Arts and Sciences,Chongqing402160,ChinaAbstract：To solve the hybrid flow-shop scheduling problem,an improved discrete cuckoo search algorithm is proposed. Aiming at the disadvantage that conventional decoding method is difficult to obtain the optimal solution,an improved decoding method is proposed,which is based on the number of workpieces and parallel machines,and assigns machines ran-domly according to the probability.According to the core ideas of two kinds of location update strategies of Lévy flight and brood parasitic behavior in standard cuckoo algorithm,the discrete Lévy flight based on position crossover and indi-vidual distance is proposed,and the brood parasitic strategy based on optimal insertion and optimal exchange is designed. Finally,the comparison results of the examples show that the average value of the results obtained from the discrete cuckoo algorithm based on the improved decoding method is the minimum,which verifies that the improved decoding method can generate better solutions.All the test results of the examples obtain the current optimal solutions,which verifies the superi-ority of the improved discrete cuckoo algorithm in solving this kind of problem.Key words：hybrid flow-shop scheduling;cuckoo search;decoding method;minimizing makespan基金项目：重庆市技术创新与典型应用重点项目（No.cstc2018jszx-cyzdX0175）；重庆市研究生教育创新基金（No.CYS18223）。
求解无等待Flow shop调度问题的改进蛙跳算法
No.7Jul.2020第7期2020年7月组合机床与自动化加工技术Modular Machine Tool & Automatic Manufacturing Techninue文章编号：1001 -2265（2020）07 -0081 -04DOI # 10.13462/j. cnki. mmtamt. 2020. 07. 018求解无等待Flow shop 调度问题的改进蛙跳算法%吴永明，王亚昆，张啥,赵旭东，陈琳升，史海鹏（贵州大学现代制造技术教育部重点实验室，贵阳550025）摘要：无等待Flow shop 调度一直是研究的热点问题，为减少无等待流水车间调度总完工时间，文章 提出了一种结合高斯变异和扰动因子的蛙跳算法。
在蛙群更新策略中引入扰动因子，平衡了蛙跳算法搜索的深度，利用高斯变异产生子代新蛙代替随机产生子代新蛙，增强了蛙跳算法的寻优速度；同时引入交叉操作，增加蛙群的多样性，提高蛙群中所有青蛙的局部搜索能力以及全局搜索能 力。
研究了无等待Flow shop 调度算例，将蛙跳算法与遗传算法的求解结果进行了对比，结果验证 了该文改进蛙跳算法在解决无等待流水车间调度问题的有效性和可行性。
关键词：Flow shop ;蛙跳算法；调度中图分类号:TH162: TG506 文献标识码：AImprovedFrog Leapnng Algornrhm forSolvnng No-wanrnng Flow ShopSchedulnng ProblemWU Yong-ming , WANG Ya-kun ,ZHANG Han ,ZHAO Xu-dong ,CHEN Lin-sheng ,SHI Hai-peng(Key Laboratoc of Adranced ManufCcturing Technology , Minista of Education , Guizhou University , Guiy- ang 550025 , China )AbhracU The no-waiting Flow shop scheduling has always been a hot issue. In this paper , a frog leaping algorithm combining Gaussian vakabiWy and dcWrbance factor is proposed to reducc the total completion hme of the no-waiting fow shop. In the fog group updatt strategy , the di.stwbance factor is introduced tobalancc the depth of the leapfog algorithm search. The Gaussian mutation is used to generatt the new gen eration of the frog instead of the random generation of the new frog , which enhances the speed of the leap frog algorithm. Crossover operation is inhoduced , which increases the frog group diversity , the locclsearch ability and global search ability of all frogs in the frog group. The no-waiting Flow shop scheduling example is studied. The result obtained by the leapfrog algorithm is compared with that obtained by the ge netic algorithm , which verifies the effachvens s and fasibility of the improved leapfrog algoathm in sol ving the problem of no-wait fow shop scheduling.Key wort ： fow shop ；fog hopping algorithm ；scheduling0引言Flow shop 车间调度问题是一类经典的组合优化 问题,Rock H ［1］证明，当机器数大于2时，Flow shop 车间问题已被证明属于NP-难问题。
基于混洗蛙跳算法的农用机械调度方法[发明专利]
![基于混洗蛙跳算法的农用机械调度方法[发明专利]](https://img.taocdn.com/s3/m/65577ed60912a2161579291e.png)
专利名称：基于混洗蛙跳算法的农用机械调度方法专利类型：发明专利
发明人：徐磊,刁爱军
申请号：CN202010135766.6
申请日：20200302
公开号：CN111353647A
公开日：
20200630
专利内容由知识产权出版社提供
摘要：本发明公开了基于混洗蛙跳算法的农用机械调度方法。
该方法包括以下步骤：步骤1，任务请求点通过WIFI发送位置信号至控制中心；步骤2，控制中心通过贪婪算法思想确定各请求点对应的调配中心；步骤3，利用混洗蛙跳算法确定各调配站局部最优的调配方案；步骤4，以各局部最优解作为总的调配方案优化的初始值，并利用混洗蛙跳算法得出全局最优解，即最佳的调配方案；步骤5，通过WIFI将最佳的调配方案发送至各个调配站；步骤6，各调配站执行任务，任务执行完后农用机械返回调配站。
本发明提出了一种基于混洗蛙跳算法的农用机械调度方法，能够快速有效的规划农用机械最佳的调度方案，不仅降低了使用成本，同时提高了生产效率，具有良好的实际应用价值。
申请人：南京机电职业技术学院
地址：211135 江苏省南京市江宁区沧波门宝善寺路56号
国籍：CN
代理机构：南京众联专利代理有限公司
代理人：刘趁新
更多信息请下载全文后查看。
求解混合流水线调度问题的离散人工蜂群算法
求解混合流水线调度问题的离散人工蜂群算法李俊青;潘全科;王法涛【摘要】In this paper , we propose a hybrid discrete artificial bee colony ( HDABC ) algorithm for solving the hybridflow-shopscheduling(HFS)problems.In the hybrid algorithm, each solution is coded by a job-permuta-tion mechanism .Four neighborhood structures are designed .The employed bees are assigned to each solution in the population set , to complete the local search task with a detailed designed local search approach .Onlooker bees randomly fetch two updated solutions and select the better one as the current solution , and then complete a further exploitation process .The scouts help the algorithm jump out of the local best by applying three different approaches .Then, the proposed algorithm is tested on the 34 identical parallel machines HFS and two un-related parallel machines HFS problems .The performance comparisons with other efficient algorithms are provided .It is concluded that the proposed algorithm is competitive to the compared existing algorithms for the problem consid -ered, in terms of searching quality , diversity, robustness and convergence ability .%本文给出了一种离散的人工蜂群算法（ HDABC）用于求解混合流水车间调度（ HFS）问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
假设工件按机床 1 到 m 的顺序加工 , 给定一个 δ δ 工序 π = (δ 1 , 2 , …, n ) , 工件 j 被划分成 s j 个小批 量 , lt ij 是工件 j 的小批量在机床 i 上的加工时间 , d j 是工件 j 的交货期 , ct ij k 为工件 j 第 k 个小批量在 机床 i 上的完成时间 , cj 为工件 j 的完成时间 , Ej 和 T j 分别是工件 j 的提前完成时间和拖后完成时间 , α j 和β j 分别是提前惩罚因子和拖后惩罚因子 。则 L FSP 的数学模型为 : ( 1) ct 1 ,δ1 , 1 = lt 1 ,δ1 ; ( 2) ct i ,δ1 , 1 = ct i- 1 ,δ1 , 1 + lt i ,δ1 , i = 2 , …, n; ( 3) ct 1 ,δ = ct 1 ,δ + lt 1 ,δ1 , k = 2 , …, sδj ; 1 ,k 1 , k- 1
潘玉霞1 ,潘全科2 ,桑红燕2
(1. 海南大学三亚学院 公共基础部 ,海南 三亚 572022 ; 2. 聊城大学 计算机学院 ,山东 聊城 252059)
摘 要 : 研究了以提前/ 拖后惩罚指标为目标的批量流水线调度问题 ,给出了该问题的数学模型以及小批量的 调整策略 。根据蛙跳算法的原理 ,采用基于工序的编码方式并利用两点交叉操作设计了新的位置生成公式 , 提出 了解决该问题的离散蛙跳算法 。为进一步增强算法的开发能力和效率 , 结合扰动策略 、 模拟退火概率接受准则和 插入邻域搜索对该算法进行改进 。对随机生成的实例进行了广泛的试验 ,结果表明了所提算法的高效性 。 关键词 : 批量流水线 ; 调度 ; 蛙跳算法 ; 模拟退火 ; 插入邻域搜索 ; 数学模型 中图分类号 : TP18 文献标志码 :A
60874075 ,70871065) , t he State Key Laboratory of Digital Manufact uring Equip ment & Technology of Huazhong Universit y of Sci2 ence & Technology ,China ,and t he China Po st doctoral Science Foundation ,China ( No . 20070410791) .
式 ( 1) 代表第一个工件第一个小批量在第一台 机床上的完成时间 ; 式 ( 2) 代表第一个工件第一个小 批量在第 i 台机床上的完成时间 ; 式 ( 3 ) 代表第一个 工件第 k 个小批量在第一台机床上的完成时间 ; 式 ( 4 ) 代表第 j 个工件第一个小批量在第一台机床上 的完成时间 ; 式 ( 5) 代表第 j 个工件第 k 个小批量在 第一台机床上的完成时间 ; 式 ( 6) 代表第 j 个工件第 一个小批量在第 i 台机床上的完成时间 ; 式 ( 7 ) 代表 第 j 个工件第 k 个小批量在第 i 台机床上的完成时 间 ; 式 ( 8) 求出工件的提前和拖后完成时间 。调度的 目标是求最小 E/ T 指标 ,即
j- 1
ct i ,δj , k = max{ ct i- 1 ,δj , k , ct i ,δj , k- 1 } + lt i ,δj ,
( 7) ( 8)
Ej = max ( 0 , d j - cj ) ; T j = max ( 0 , cj - d j ) 。
1 批量流水线调度数学模型
传统流水线调度要求每个工件加工完成后 , 才 能被传送到下一台机床上加工 。而 L FSP 还要把每 个工件分成若干个小批量 , 使得各个工件的小批量 加工完成后 ,就能被传送到下一台机床上加工 。这 样能有效地减小调度的提前/ 拖后惩罚 ( Earliness/ Tardiness Penalties , E/ T ) 指标 。批量的分配原则 对调度的性能有重要影响 , 常见的批量分配原则有 等量分配 、 一致分配和可变分配 。调查表明 [ 4 ] ,等量 分配原则在应用中取得了较好效果 , 故采用小批量 的等量分配原则 。所有小批量的加工顺序都相同 , 在不影响各工件最后一个小批量在最后一台机器上 开始加工时间的条件下 , 推迟加工各台机床上的各 个小批量 ,使得同一机床上同一工件的相邻两个小 批量之 间 没 有 等 待 时 间 。最 终 调 度 模 型 如 图 1 所示 。
Hybrid discrete shuffled frog2leaping algorithm f or lot2streaming flowshop schedul ing problem
PA N Y u2x i a , PA N Quan2ke , S A N G Hon g2y an
1 2 2
) = min f (π
j =1
6
n
(α j E j +β j T j) 。
( 9)
为了使目标函数值最小 , 用批量移动受益 ( Net Benefit of Movement , NBM ) [ 4 ] 算法决定每个小批 量的开始加工时间和完成时间 。其中当第 k 个工件 的最后一个小批量被移动一个时间单元时 , 净受益 目标函数值计算如下 : α ( K) , E( k) > 0 ; ( 10) UB ( K) = -β ( K) , 其他 。 式中 r 代表当小批量移动时连续影响的工件的 个数 ,则所有受影响工件的单元净受益目标函数值 计算如下 :
1266
计算机集成制造系统
第 16 卷
特点 。SFL A 在成品油管网设计[ 7 ] 、 贴片机贴装顺 [8 ] [9 ] 序 、 含风电场电力系统动态优化 等方面得到成 功应用 。鉴于 SFL A 的优点 ,本文采用 SFL A 来解 决此类调度问题 。首先根据该算法的优化原理 , 提 出了离散蛙跳算法 ,使 SFL A 能够解决 L FSP ,进而 结合扰动策略 、 模拟退火概率接受准则和插入邻域 搜索算法提出了三种改进的混合算法 。实验研究表 明 ,所提算法优于文献 [ 4 ] 的D PSO 和文献 [ 5 ] 的 H GA ,尤其是改进的算法更具有良好的寻优特性和 较高的运算效率 。
第 16 卷第 6 期 2 0 1 0 年6月
计算机集成制造系统
Computer Integrated Manufact uring Systems
Vol. 16 No. 6 J une 2 0 1 0
文章编号 :1006 - 5911 ( 2010) 06 - 1265 - 07
批量流水线调度问题的混合离散蛙跳算法
的主要方法 。文献 [ 4 ] 的离散微粒群优化 ( Discrete Particle Swarm Optimizatio n , DPSO ) 算 法 和 文 献 [ 5 ] 中的混合遗传算法 ( Hybrid Genetic Algo rit hm , H GA ) 取 得 了 至 今 最 好 的 研 究 结 果 。蛙 跳 算 法 ( Shuffled Frog2Leaping Algorit hm , SFL A ) 是一种 模拟群体青蛙觅食特性产生的智能算法 。该算法结 合了以遗传为基础的 Memetic 算法和以社会行为 为基础的微粒群优化算法的优点 [ 6 ] ,具有概念简单 、 参数少 、 计算速度快 、 全局寻优能力强和易于实现的
收稿日期 :2009207227 ; 修订日期 :2009209217 。Received 27 J uly 2009 ;accepted 17 Sep1 2009. 基金项目 : 国家自然科学基金资助项目 (60874075 ,70871065) ; 华中科技大学数字制造装备与技术国家重点实验室开放课题资助项目 ; 博士后 科学基金资助项目 ( 20070410791) 。Foundation items : Project supported by t he National Nat ural Science Foundation , China ( No .
( 1. Depart ment of Elementary Co urses , Hainan U niversity Sanya College ,Sanya 572022 ,China ; 2. School of Co mp uter Science , Liaocheng U niversity , Liaocheng 252059 ,China) Abstract : The lot2st reaming flow shop scheduling p ro blem to minimize t he total Earliness / Tardiness ( E/ T) penalty was st udied. Acco rding to t he p rinciple of f rog2leaping algorit hm , a novel allocation f unction was designed by adop2 ting sequence2based coding met hod and two2point cro ssover operator. Then , a novel discrete Shuffled Frog2Leaping Algo rit hm ( SFL A ) was p ut forward to solve t he p roblem. To f urt her enhance develop ment capability and efficiency of t he algorit hm , t he p ropo sed SFL A was imp roved wit h pert urbatio n tactic , simulated annealing acceptance criteria and inserting neighbo rhood search. Extensive experiment s based on t he rando mly generated instances were conduc2 ted. Co mp utational result s and comparison verified t he effectiveness of t he p ropo sed algo rit hm. Key words : lot2st reaming flow shop ; scheduling ; shuffled f rog2leaping algo rit hm ; simulated annealing ; insert neigh2 bo rhood search ; mat hematical models