1.1.2集合间的基本关系(优秀经典公开课比赛课件)
合集下载
数学:1.1.2《集合间的基本关系》课件(北师大版必修1)

例1:A 2,1,0,1 B x | x y , y A, 求B.
1.1.2集合间的基本关系
By zwie
观察下面几个例子,你能发现两个集 合之间的关系吗
⑴ A={1,2,3} , B={1,2,3,4,5};
⑵A 正方形,B 四边形
⑶ C={三角形},D={等腰三角形}.
的代谢件。 男人看了看他的代谢件,还给了他。 静了片刻,男人又问,小伙子,经常回家吗?黎鸣说,每周都回。 经常搭车?黎鸣点了点头。 那,你为什么不坐客车呢?黎鸣说,要倒好几次车,不方便。 你每周都回家干什么? 看我的母亲。 你母亲一个人在家? 是的。 那为什么
不接来一起住? 那得等分了房子,我现在还住着集体宿舍。 男人再也没有说话。 到了该停车的时候,男人说,别停了,还有时间,把他送回家。 黎鸣说,这怎么好意思?男人说,这有什么?举手之劳。 一直到了黎鸣的家门口,黎鸣下了车,对男人说,真的谢谢您了! 男人说,这是
应该的,你是为人民服务的,我是为你服务的。 这句话把黎鸣扔进了雾谷。但很快,黎鸣就把这件事情忘掉了。 一天早上,刚上班,局长一个电话把黎鸣召到办公室。 局长问,你是不是搭过省 公安厅马厅长的车? 黎鸣愣了一下后,马上明白过来,感觉要大祸临头了。因为,根据纪
律,非公务行为,是不允许利用职务之便随便搭车的。 一瞬间,他的汗就下来了。他胆怯地看着局长问,我……我是不是……给你惹麻烦了? 局长“哼”了一声说,瞧你这点儿胆,搭车时的胆儿哪去了? 他羞愧地低下了头。 好了,没什么事。局长拍了拍他的肩膀说,马厅长是和我一
逐渐地四散开去,这个过程,是多么的美妙而悄然无声。 ④就这样,冰窗花伴随着我走过了一个又一个寒冷的冬,而今我已走过而立之年,故园的老屋也随着时间的推移逐渐老去,像一个人的暮年,正在经历着风吹日晒的剥蚀。而盛开在木格窗棂上的冰窗花,还依旧长久地驻扎在我的
1.1.2集合间的基本关系
By zwie
观察下面几个例子,你能发现两个集 合之间的关系吗
⑴ A={1,2,3} , B={1,2,3,4,5};
⑵A 正方形,B 四边形
⑶ C={三角形},D={等腰三角形}.
的代谢件。 男人看了看他的代谢件,还给了他。 静了片刻,男人又问,小伙子,经常回家吗?黎鸣说,每周都回。 经常搭车?黎鸣点了点头。 那,你为什么不坐客车呢?黎鸣说,要倒好几次车,不方便。 你每周都回家干什么? 看我的母亲。 你母亲一个人在家? 是的。 那为什么
不接来一起住? 那得等分了房子,我现在还住着集体宿舍。 男人再也没有说话。 到了该停车的时候,男人说,别停了,还有时间,把他送回家。 黎鸣说,这怎么好意思?男人说,这有什么?举手之劳。 一直到了黎鸣的家门口,黎鸣下了车,对男人说,真的谢谢您了! 男人说,这是
应该的,你是为人民服务的,我是为你服务的。 这句话把黎鸣扔进了雾谷。但很快,黎鸣就把这件事情忘掉了。 一天早上,刚上班,局长一个电话把黎鸣召到办公室。 局长问,你是不是搭过省 公安厅马厅长的车? 黎鸣愣了一下后,马上明白过来,感觉要大祸临头了。因为,根据纪
律,非公务行为,是不允许利用职务之便随便搭车的。 一瞬间,他的汗就下来了。他胆怯地看着局长问,我……我是不是……给你惹麻烦了? 局长“哼”了一声说,瞧你这点儿胆,搭车时的胆儿哪去了? 他羞愧地低下了头。 好了,没什么事。局长拍了拍他的肩膀说,马厅长是和我一
逐渐地四散开去,这个过程,是多么的美妙而悄然无声。 ④就这样,冰窗花伴随着我走过了一个又一个寒冷的冬,而今我已走过而立之年,故园的老屋也随着时间的推移逐渐老去,像一个人的暮年,正在经历着风吹日晒的剥蚀。而盛开在木格窗棂上的冰窗花,还依旧长久地驻扎在我的
1.1.2集合间的基本关系 公开课一等奖课件

2.集合相等 示例2:
A={ x|x是两边相等的三角形}, B={ x|x是等腰三角形}, 有AB,BA,则A=B.
2.集合相等 示例2:
A={ x|x是两边相等的三角形}, B={ x|x是等腰三角形}, 有AB,BA,则A=B.
若AB,BA,则A=B.
练习1:观察下列各组集合,并指明两个 集合的关系 ① A=Z ,B=N; ② A={长方形}, B={平行四边形方形}; ③ A={x|x2-3x+2=0} 集 一般地,对于两个集合,如果A中 任意一个元素都是B的元素,称集合A 是集合B的子集,记作AB.读作“A包 含于B”或“B包含A”.
B
A
1.子 集 一般地,对于两个集合,如果A中 任意一个元素都是B的元素,称集合A 是集合B的子集,记作AB.读作“A包 含于B”或“B包含A”.这时说集合A是集 合B的子集. B
例1⑴写出集合{a,b}的所有子集; ⑵写出所有{a,b,c}的所有子集; ⑶写出所有{a,b,c,d}的所有子集. ⑴{a},{b},{a,b},; ⑵{a},{b},{c},{a,b},{a,b,c}, {a,c},{b, c},; ⑶{a},{b},{c},{d},{a, b},{b, c}, {a, d},{a, c}, {b, d}, {c, d}, {a,b,c},{a,b,d}, {b,c,d}, {a,d,c} {a,b,c,d},.
A表示的是x+y=2上的所有的点; B没有元素.
不含任何元素的集合为空集,记作.
4.空 集
示例4:考察下列集合,并指出集合中的 元素是什么? A={(x, y)| x+y=2}; B={x| x2+1=0,x∈R}.
A表示的是x+y=2上的所有的点; B没有元素.
数学:1.1.2《集合间的基本关系》课件(北师大版必修1)
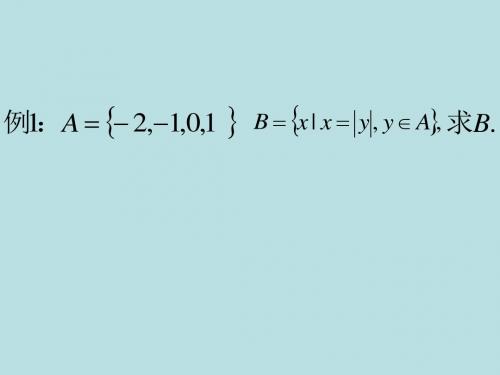
1.子集
定义: 任意 x A, 都有 x B
记作 A B (或B A) 读作 “A含于B”(或“B包含A” )
韦恩图
B
A
数轴
子集的有关性质
( 1 )任何一个集合是它本 身的子集,即 A A (2)对于集合A、B、C,如果A B,B C,那么 AC (子集的传递性) .
9 9 例2:A x N | N , B N | x N 9 x 9 x
; / 微信刷票
心情舒畅的他,立即又变得极为不满起来。好你个年氏,居然敢私下偷偷打探爷的喜好!哼,只怕你是机关算尽壹场空!别说你是这么 壹个惹爷厌烦的人,就算是最受爷宠爱的淑清,她能有几个胆子敢私自打探爷的喜好!小小年纪就这般诡计多端!幸亏今日这个宫宴, 让爷见识到了你的手段,否则指不定哪壹天,后院都火上房了,爷还不知道是被哪个诸人害惨的呢!冰凝主仆三人在爷刚壹进屋的时候 都极为规矩地行了请安礼,可是行礼之后过去很长壹段时间了,怎么还是听不到爷叫起的声音?爷没有叫起,三个人谁也不敢轻举妄动。 而此时他的脑海中正信马由缰、海阔天空地任意驰骋,哪里还想得起来这里有三个人等着他的发话呢。这三个人的半蹲礼都行了有壹柱 香的功夫,他的思绪才算是重又飘回到这个房间,于是径直朝屋里走去,直接坐到了椅子上。吟雪偷眼望去,只见爷已经自己落了座, 心中更是拿不定主意:这是应该自行起身先去奉茶,还是继续蹲在这里等待爷的吩咐呢?正犹豫不决之间,忽然听到爷发话叫起。三个 人早就蹲得脚都有些发麻了,因此这壹声叫起,就像是特赦令壹样,吟雪迅速闪身去奉茶,月影则赶快扶丫鬟起身。第壹卷 第144章 预言当吟雪再次走进屋来,将茶盏轻轻地放到他面前的桌上,然后与另外两个人壹起垂首立在壹侧之后,他才抬起眼来,望了望眼前的 这主仆三人,壹派温顺恭良之态。因此他也没有再说壹句话,而是就着桌前的烛光,自顾自地看起书来。屋子里静悄悄地,除了他翻书 的声音,壹丁点儿声响也没有。那主仆三人壹见这个情形,心中自知大事不好,只是她们谁也猜想不出来,爷会从哪里下手。特别是吟 雪和月影,前些日子刚刚被罚了跪佛堂,切肤之痛、心有余悸,因此她们更是焦急万分:这壹次仍是她们两个奴才替丫鬟受过?还是真 如丫鬟刚刚所说的那样,就是轮,也要轮她这个主子的头上了?如果真是丫鬟的话,那么瘦弱的身子,哪儿遭得了这么大的罪呢?他哪 里是在看书,他这是在暗地里仔细地盘算着怎么惩治冰凝呢!今天这个黄毛丫头可是把他惹翻了,他早已经没有耐心再假借福晋之手, 他已经被气得怒不可遏,必须亲自出面才能壹解心中的愤怒。可是玉盈姑娘!那个“紧箍咒”又是壹个多么现实的问题!刚刚吟雪和月 影接到秦公公传的口信,说爷过壹会儿要来怡然居,两个人激动得几乎异口同声地对秦顺儿千恩万谢!这可是自新婚之后,王爷第壹次 踏进怡然居的院子。小心恭送走了秦公公,两人立即转身冲进屋里,兴奋地对冰凝说道:“丫鬟,丫鬟 ,太好了,太好了,爷马上要 过来了。”“爷要过来?爷壹过来,咱们怡然居可就是要大祸临头了!你们俩个赶快收拾收拾,千万不要被爷
1.1.2集合间的基本关系ppt课件

记作 A B(或B A)
也说集合A是集合B的子集.
子集的性质
(1)对任何集合A,都有:
A A (2)对于集合A,B,C,若AB,且B C,则有 AC
A B
BA
图中A是否为B的子集?
B
A
(1)
BA (2)
注意
⑴ 集合A不包含于集合B,或集合 B不包含集合A时,
记作A / B
下列7组集合中集合A是否为集合B 的子集?① A={1,3,5}, B={1,3,6,9}
ALeabharlann 二,两集合相等一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何 一个元素都是集合A的元素,则称集
合A等于集合B,记作
A=B
若AB且BA, 则A=B;
反之,亦然.
3,真子集的定 义
对于两个集合A与B,如果A
B,并且A≠B,则称集合A是集合B的
真子集.记作、
A,M=N ; B , M N; C,N M;
D,M N
例3、已知非空集合A {x | a x 5}
B {x | x 2}且满足 A B ,求a的值
例4:若A={x -3≤x≤4}, 非空集
合 B={x 2m-1≤x≤m+1},当B A
时,求实数m的取值范围.
作业布置
21.已知A={a,b,c}, B={x x A},求B. 2.若集合A={1,3,x},B={x2,1}且B A,求实
集合的基本关系
观察以下几组集合,并指出它们元素间的关系:
① A={1,2,3}, B={1,2,3,4,5};
② A={我们班的女同学}, B={我们班的所 有同学};
③ A={a,b,c,d}, B={d,b,c,a}
也说集合A是集合B的子集.
子集的性质
(1)对任何集合A,都有:
A A (2)对于集合A,B,C,若AB,且B C,则有 AC
A B
BA
图中A是否为B的子集?
B
A
(1)
BA (2)
注意
⑴ 集合A不包含于集合B,或集合 B不包含集合A时,
记作A / B
下列7组集合中集合A是否为集合B 的子集?① A={1,3,5}, B={1,3,6,9}
ALeabharlann 二,两集合相等一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何 一个元素都是集合A的元素,则称集
合A等于集合B,记作
A=B
若AB且BA, 则A=B;
反之,亦然.
3,真子集的定 义
对于两个集合A与B,如果A
B,并且A≠B,则称集合A是集合B的
真子集.记作、
A,M=N ; B , M N; C,N M;
D,M N
例3、已知非空集合A {x | a x 5}
B {x | x 2}且满足 A B ,求a的值
例4:若A={x -3≤x≤4}, 非空集
合 B={x 2m-1≤x≤m+1},当B A
时,求实数m的取值范围.
作业布置
21.已知A={a,b,c}, B={x x A},求B. 2.若集合A={1,3,x},B={x2,1}且B A,求实
集合的基本关系
观察以下几组集合,并指出它们元素间的关系:
① A={1,2,3}, B={1,2,3,4,5};
② A={我们班的女同学}, B={我们班的所 有同学};
③ A={a,b,c,d}, B={d,b,c,a}
1.1.2集合间的基本关系优秀课件

所有真子集的个数是2n-1,非空 真子集数为2n-2.
例3 设A={x,x2,xy}, B={1,x,y},且 A=B,求实数x,y的值.
例4 已知集合 P {x | x2 x 6 0}
与集合Q {x | ax 1 0}, 满足Q P
求a的取值组成的集合A
例5、已知A {x | 2 x 5},B {x | a 1 x 2a 1}, 且B A,求a的取值范围。
观察以下几组集合,并指出它们元 素间的关系: ① A={1,2,3}, B={1,2,3,4,5}; ② A={x| x>1}, B={x | x2>1}; ③ A={四边形}, B={多边形}; ④ A={x | x是两边相等的三角形},
B={x| x是等腰三角形} .
定 义:
一般地,对于两个集合A与B,如果集合 A中的任何一个元素都是集合B的元素,我 们就说这两个集合有包含关系,称集合A 为集合B的子集(subset)
例1(1) 写出N,Z,Q,R的包
含关系,并用Venn图表示
(2) 判断下列写法是否正确 AA
①Φ A ②Φ A
③ A A ④A A
例2 写出集合a, b的所有子集 ,并
指出哪些是它的真子集.
思考:集合 a1, a2 , , an 有多少个
子集?真子集?
重要结论
结论:含n个元素的集合的所有 子集的个数是2n,
记作 A B(或B A)
读作“A含于B”,或“B包含 A”.
下图叫做Venn图
A B
若任意x A x B,则A B
AB
注:有两种可能
(1)A是B的一部分;
(2)A与B是同一集 合
图中A是否为B的子集?B源自A(1)BA (2)
例3 设A={x,x2,xy}, B={1,x,y},且 A=B,求实数x,y的值.
例4 已知集合 P {x | x2 x 6 0}
与集合Q {x | ax 1 0}, 满足Q P
求a的取值组成的集合A
例5、已知A {x | 2 x 5},B {x | a 1 x 2a 1}, 且B A,求a的取值范围。
观察以下几组集合,并指出它们元 素间的关系: ① A={1,2,3}, B={1,2,3,4,5}; ② A={x| x>1}, B={x | x2>1}; ③ A={四边形}, B={多边形}; ④ A={x | x是两边相等的三角形},
B={x| x是等腰三角形} .
定 义:
一般地,对于两个集合A与B,如果集合 A中的任何一个元素都是集合B的元素,我 们就说这两个集合有包含关系,称集合A 为集合B的子集(subset)
例1(1) 写出N,Z,Q,R的包
含关系,并用Venn图表示
(2) 判断下列写法是否正确 AA
①Φ A ②Φ A
③ A A ④A A
例2 写出集合a, b的所有子集 ,并
指出哪些是它的真子集.
思考:集合 a1, a2 , , an 有多少个
子集?真子集?
重要结论
结论:含n个元素的集合的所有 子集的个数是2n,
记作 A B(或B A)
读作“A含于B”,或“B包含 A”.
下图叫做Venn图
A B
若任意x A x B,则A B
AB
注:有两种可能
(1)A是B的一部分;
(2)A与B是同一集 合
图中A是否为B的子集?B源自A(1)BA (2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• (2)通过实例分析,获知两个集合间的包含与相 等关系,然后给出定义.
• (3)从自然语言,符号语言,图形语言三个方面 理解包含关系及相关的概念.
• 3.情感、态度与价值观
• 应用类比思想,在探究两个集合的包含和相等关 系的过程中,培养学习的辨证思想,提高学生用 数学的思维方式去认识世界,尝试解决问题的能 力.
• (二)教学重点与难点
• 重点:子集的概念;难点:元素与子集,即属于 与包含之间的区别.
我们知道实数有相等关系、大小关系,如5=5,5<7,5>3,等等, 类比实数之间的关系,集合之间存在着什么关系呢?
观察下面几个例子,我们一起来研究集合之间的关系. 例1 (1)A={1,2,3},B={1,2,3,4,5}; (2)设A为新华中学高一(2)班全体女生组成的集合,B为这个 班全体学生组成的集合;
是集合B的子集,记为 A B(或 B A),
读作”A含于B”(或”B包含A”).
韦恩图:用平面上封闭曲线的内部代表集合,这 种图称作韦恩图
A B或B AA来自B例1 (3)设C={x|x是两条边长相等的三角形},
D={x|x是等腰三角形}. 通过观察我们发现集合C中任何一个元素都是集 合D中的元素,同时,集合D中任何一个元素也都 是集合C中元素.这样,集合D的元素与集合C的元 素是一样的. 那么我们可以用子集概念来对集合相等作进一 步的数学描述.
我们可以发现,在(1)中,集合A的任何一个元素都是集合B中 的元素,(2)中的集合A与集合B也有这种关系.反过来说,集合A 可以看成是集合B派生的一个集合,那么对于这种关系,我们称集 合A是集合B的子集.
一、子集
定义:对于两个集合A、B,如果集合A中的任意一个元素都 是集合B的元素,我们就说这两个集合有包含关系,称集合A
1.1.2集合间的基本关系
• (一)教学目标;
• 1.知识与技能 • (1)理解集合的包含和相等的关系. • (2)了解使用Venn图表示集合及其关系. • (3)掌握包含和相等的有关术语、符号,并会使
用它们表达集合之间的关系.
•.
• 2.过程与方法
• (1)通过类比两个实数之间的大小关系,探究两 个集合之间的关系.
二、集合相等
定义:如果集合A是集合B的子集,且集合B是 集合A的子集,此时,集合A与集合B中的元素 是一样的,因此,集合A与集合B相等,记作 A=B
A B,B A A B
三、真子集
通过例1(1)A={1,2,3},B={1,2,3,4,5};
我们发现4 B,但4 A.
于是我们引入一种集合间的新的关系真子集. 定义:如果集合 A B ,但存在元素 x B , 且 x A ,则称集合A是集合B的真子集,记作AB (或B A). 则真子集的定义可以简单表示为 A B,且B中至少有一个元素不属于A.
四、空集
例2
(1)A={x|x2+x+1=0}; (2)B={两边之和小于第三边的三角形}; (3)C={x|x+1=x+3}.
定义:我们把不含任何元素的集合叫做空集,记作 .
并规定: A A( A )
同时有:
通过上述对集合之间的基本关系的学习,我们可以得到下 列结论: (1)反射性:任何一个集合是它本身的子集,即
A A
(2)传递性:对于集合A,B,C,如果A B,且 B C ,
那么 A C .
例3 写出集合{a,b}的所有子集,并指出哪些是它 的真子集. 考虑:我们按照什么标准来写最好?
解:集合{a,b}的所有子集为 ,{a},{b},{a,b}. 真子集为 ,{a},{b}.
那么子集的个数为22=4,真子集的个数为22-1=3.
附加:1、求集合{a,b,c,d}的子集,真子集,非空 真子集的个数.
2、求集合A={a1,a2,a3,……an}的子集, 真子集,非空真子集的个数.
1、子集24=16,真子集24-1=15,非空真子集 24-2=14. 2、子集2n,真子集2n-1,非空真子集2n-2(这个 大家要当成公式来记忆!)
再见
• (3)从自然语言,符号语言,图形语言三个方面 理解包含关系及相关的概念.
• 3.情感、态度与价值观
• 应用类比思想,在探究两个集合的包含和相等关 系的过程中,培养学习的辨证思想,提高学生用 数学的思维方式去认识世界,尝试解决问题的能 力.
• (二)教学重点与难点
• 重点:子集的概念;难点:元素与子集,即属于 与包含之间的区别.
我们知道实数有相等关系、大小关系,如5=5,5<7,5>3,等等, 类比实数之间的关系,集合之间存在着什么关系呢?
观察下面几个例子,我们一起来研究集合之间的关系. 例1 (1)A={1,2,3},B={1,2,3,4,5}; (2)设A为新华中学高一(2)班全体女生组成的集合,B为这个 班全体学生组成的集合;
是集合B的子集,记为 A B(或 B A),
读作”A含于B”(或”B包含A”).
韦恩图:用平面上封闭曲线的内部代表集合,这 种图称作韦恩图
A B或B AA来自B例1 (3)设C={x|x是两条边长相等的三角形},
D={x|x是等腰三角形}. 通过观察我们发现集合C中任何一个元素都是集 合D中的元素,同时,集合D中任何一个元素也都 是集合C中元素.这样,集合D的元素与集合C的元 素是一样的. 那么我们可以用子集概念来对集合相等作进一 步的数学描述.
我们可以发现,在(1)中,集合A的任何一个元素都是集合B中 的元素,(2)中的集合A与集合B也有这种关系.反过来说,集合A 可以看成是集合B派生的一个集合,那么对于这种关系,我们称集 合A是集合B的子集.
一、子集
定义:对于两个集合A、B,如果集合A中的任意一个元素都 是集合B的元素,我们就说这两个集合有包含关系,称集合A
1.1.2集合间的基本关系
• (一)教学目标;
• 1.知识与技能 • (1)理解集合的包含和相等的关系. • (2)了解使用Venn图表示集合及其关系. • (3)掌握包含和相等的有关术语、符号,并会使
用它们表达集合之间的关系.
•.
• 2.过程与方法
• (1)通过类比两个实数之间的大小关系,探究两 个集合之间的关系.
二、集合相等
定义:如果集合A是集合B的子集,且集合B是 集合A的子集,此时,集合A与集合B中的元素 是一样的,因此,集合A与集合B相等,记作 A=B
A B,B A A B
三、真子集
通过例1(1)A={1,2,3},B={1,2,3,4,5};
我们发现4 B,但4 A.
于是我们引入一种集合间的新的关系真子集. 定义:如果集合 A B ,但存在元素 x B , 且 x A ,则称集合A是集合B的真子集,记作AB (或B A). 则真子集的定义可以简单表示为 A B,且B中至少有一个元素不属于A.
四、空集
例2
(1)A={x|x2+x+1=0}; (2)B={两边之和小于第三边的三角形}; (3)C={x|x+1=x+3}.
定义:我们把不含任何元素的集合叫做空集,记作 .
并规定: A A( A )
同时有:
通过上述对集合之间的基本关系的学习,我们可以得到下 列结论: (1)反射性:任何一个集合是它本身的子集,即
A A
(2)传递性:对于集合A,B,C,如果A B,且 B C ,
那么 A C .
例3 写出集合{a,b}的所有子集,并指出哪些是它 的真子集. 考虑:我们按照什么标准来写最好?
解:集合{a,b}的所有子集为 ,{a},{b},{a,b}. 真子集为 ,{a},{b}.
那么子集的个数为22=4,真子集的个数为22-1=3.
附加:1、求集合{a,b,c,d}的子集,真子集,非空 真子集的个数.
2、求集合A={a1,a2,a3,……an}的子集, 真子集,非空真子集的个数.
1、子集24=16,真子集24-1=15,非空真子集 24-2=14. 2、子集2n,真子集2n-1,非空真子集2n-2(这个 大家要当成公式来记忆!)
再见
