苏科版九年级数学下册《第五章二次函数》单元检测试题(有答案)
苏科版九年级数学下册《第五章二次函数》单元测试卷(有答案)

苏科版九年级数学下册第五章二次函数单元测试卷学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(本题共计 10 小题,每题 3 分,共计30分,)1. 下列函数关系中是二次函数的是()A.正三角形面积S与边长a的关系B.直角三角形两锐角A与B的关系C.矩形面积一定时,长y与宽x的关系D.等腰三角形顶角A与底角B的关系2. 在平面直角坐标系中,二次函数y=a(x+ℎ)2的图象可能是()A. B.C. D.3. 苹果熟了,从树上落下所经过的路程s与下落时间t满足S=gt2(g=9.8),则s与t的函数图象大致是()A. B.C. D.4. 抛物线y=2(x−3)2+1的顶点坐标是()A.(−3, 1)B.(3, 1)C.(3, −1)D.(−3, −1)5. 对抛物线:y=−x2+2x−3而言,下列结论正确的是()A.与x轴有两个交点B.开口向上C.与y轴的交点坐标是(0, 3)D.顶点坐标是(1, −2)6. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=−1,且过点(−3, 0).下列说法:①abc<0;②2a−b=0;③4a+2b+c<0;④3a+c=0;其中说法正确的是()A.①②B.②③C.①②④D.②③④7. 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是()A.b2−4ac>0B.a−b+c<0精品 Word 可修改欢迎下载C.abc<0D.2a+b>08. 若A(−4, y1),B(−14, y2),C(3, y3)为二次函数y=(x+2)2−9的图象上的三点,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y29. 把抛物线y=−x2向右平移2个单位,再向下平移3个单位,即得到抛物线()A.y=−(x+2)2+3B.y=−(x−2)2+3C.y=−(x+2)2−3D.y=−(x−2)2−310. 如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(−1, −2)、(1, −2),点B的横坐标的最大值为3,则点A的横坐标的最小值为()A.−3B.−1C.1D.3二、填空题(本题共计 10 小题,每题 3 分,共计30分,)11. 抛物线y=−3x2+8向右平移5个单位的抛物线的函数关系式是________.12. 将函数y=2x2+1向上平移1个单位,再向左平移2个单位,得到抛物线的解析式________.13. 二次函数y=ax2+bx+c中,若a:b:c=1:4:3,且该函数的最小值是−3,则解析式为________.14. 已知二次函数y=(x−1)2+(x−3)2,当x=________时,函数达到最小值.15. 已知二次函数的图象如图所示,则 (1)这个二次函数的解析式是________;(2)当x=________时,y=3(3)当x的取值范围是________时,y>0.16. 二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=−1,x2=3;③a+b+c>0;④当x>1时,y 随x值的增大而增大;⑤当y>0时,−1<x<3.其中,正确的说法有________(请写出所有正确说法的序号).17. 已知二次函数y=−x2+4x+5,用配方法化成y=a(x+ℎ)2+k的形式为________.18. 将二次函数y=x2−4x+7化为y=(x−a)2+b的形式,如果直角三角形的两边长分别为a、b,那么第三边的长为________.19. 军事演习在平坦的草原上进行,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=−15x2+10x.经过________秒时间,炮弹落到地上爆炸了.20. 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(−2, 4),B(1, 1),则关于x的不等式ax2>bx+c的解集为________.精品 Word 可修改欢迎下载三、解答题(本题共计 6 小题,每题 10 分,共计60分,)21. 已知函数y=(m+3)x m2+m−4+(m+2)x+2.(1)当函数是二次函数时,求m的值;(2)当函数是一次函数时,求m的值.22. 已知抛物线的解析式为y=−12x2+4x−6(1)求抛物线的顶点坐标;(2)求出抛物线与x轴的交点坐标;(3)当x取何值时y>0?23. 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长a的变化而变化.(1)当矩形边长a为多少米时,矩形面积为200m2; (2)求出S关于a的函数关系式,并直接写出当a为何值时,场地的面积S最大.24. 如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.精品 Word 可修改欢迎下载25. 张经理到老王的果园里一次性采购一种水果,他俩商定:张经理的采购价y(元/吨)与采购量x(吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).(1)求y与x之间的函数关系式;(2)已知老王种植水果的成本是2 800元/吨,那么张经理的采购量为多少时,老王在这次买卖中所获的利润w最大?最大利润是多少?26. 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3, 0)(0, −3),抛物线的对称轴为x=1,D为抛物线的顶点.(1)求抛物线的解析式.(2)抛物线的对称轴上是否存在一点P,使△PCD为等腰三角形?若存在,写出点P点的坐标,若不存在,说明理由.(3)点E为线段BC上一动点,过点E作x轴的垂线,与抛物线交于点F,求四边形ACFB面积的最大值,以及此时点E的坐标.答案1. A2. D3. B4. B5. D6. C7. C8. B9. D10. A11. y=−3(x−5)2+8精品 Word 可修改欢迎下载12. y=2(x+2)2+213. y=3x2+12x+914. 215. 解:(1)观察图象得:此函数的顶点坐标为(1, −1),对称轴为x=1,与x轴的交点坐标为(0, 0),(2, 0),∴设此函数的解析式为y=a(x−1)2−1,将点(0, 0)代入函数解析式得a=1,∴这个二次函数的解析式是y=(x−1)2−1,即y=x2−2x;(2)当x2−2x=3时,y=3,解得x1=3,x2=−1,∴当x=3或−1时,y=3;(3)根据图象得,当x<0或x>2时,y>0.16. ①②④17. y=−(x−2)2+918. √1319. 5020. x>1或x<−221. 解:(1)依题意得:m2+m−4=2且m+3≠0.即(m−2)(m+3)=0且m+3≠0,解得m=2;(2)依题意得:m2+m−4=0或m2+m−4=1或m+3=0,解得m=2或m=1±√212或m=−3.22. 解:(1)y=−12x2+4x−6=−12(x−4)2+2,∴抛物线顶点坐标为(4, 2);(2)当y=0时,即y=−12x2+4x−6=0,∴x=2或x=6,∴抛物线与x轴的交点坐标为(2, 0)(6, 0);(3)∵抛物线的开口方向向下,且抛物线与x轴的交点坐标为(2, 0)(6, 0),∴当2<x<6时,y>0.23. 解:(1)由题意可得,a(30−a)=200,解得,a1=10,a2=20,即当矩形的边长a为10米或20米时,矩形面积为200m2;(2)由题意可得,S=a(30−a)=−a2+30a=−(a−15)2+225,∴当a=15时,场地面积S取得最大.24. 解:如图,∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,∴存在线段AB且AB的位置已经固定,当P和B重合时,x=4,即x≤4当x=2,P和A重合,即x≥2,∴x的取值范围是2≤x≤4,如图,S矩形PNDM=xy,且2≤x≤4,延长NP交EF于G,显然PG // BF,∴△AGP∽△AFB,∴PGBF=AGAF,即4−y1=x−22,∴y=−12x+5,精品 Word 可修改欢迎下载精品 Word 可修改 欢迎下载∴S =xy =−12x 2+5x , 即S =−12x 2+5x(2≤x ≤4).25. 解:(1)根据图象可知当0<x ≤20时, y =8000(0<x ≤20), 当20<x ≤40时,将B(20, 8000),C(40, 4000),代入y =kx +b ,得: {8000=20k +b 4000=40k +b , 解得:{k =−200b =12000,y =−200x +12000(20<x ≤40);(2)根据上式以及老王种植水果的成本是2 800元/吨, 由题意得:当0<x ≤20时, W =(8000−2800)x =5200x ,W 随x 的增大而增大,当x =20时,W 最大=5200×20=104000元, 当20<x ≤40时,W =(−200x +12000−2800)x =−200x 2+9200x , ∵a =−200, ∴函数有最大值, 当x =−b 2a =23时, W 最大=4ac−b 24a =105800元.故张经理的采购量为23吨时,老王在这次买卖中所获的利润W 最大,最大利润是105800元. 26. 解:(1)∵点B 和点C 的坐标分别为(3, 0)(0, −3),抛物线的对称轴为x =1, ∴{9a +3b +c =0c =−3−b 2a =1,解得{a =1b =−2c =−3, ∴抛物线解析式为y =x 2−2x −3;(2)∵y =x 2−2x −3=(x −1)2−4, ∴D(1, −4),且C(0, −3), ∵P 点为对称轴上的一点,∴可设P(1, t),∴PC =√12+(t +3)2=√t 2+6t +10,PD =|t −4|,CD =√12+(−4+3)2=√2, ∵△PCD 为等腰三角形,∴分PC =PD 、PC =CD 和PD =CD 三种情况,①当PC =PD 时,则√t 2+6t +10=|t −4|,解得t =37,此时P 点坐标为(1, 37);②当PC =CD 时,则√t 2+6t +10=√2,解得t =−2或t =−4(与D 点重合,舍去),此时P 点坐标为(1, −2);③当PD =CD 时,则|t −4|=√2,解得t =4+√2或t =4−√2,此时P 点坐标为(1, 4+√2)或(1, 4−√2);综上可知存在满足条件的P 点,其坐标为(1, 37)或(1, −2)或(1, 4+√2)或(1, 4−√2);(3)∵B(3, 0),C(0, −3),∴直线BC 解析式为y =x −3,∵E 点在直线BC 上,F 点在抛物线上, ∴设F(x, x 2−2x −3),E(x, x −3), ∵点F 在线段BC 下方,∴EF =x −3−(x 2−2x −3)=−x 2+3x ,∴S △BCF =12EF ⋅OB =12×3(−x 2+3x)=−32x 2+92x =−32(x −32)2+278,且S △ABC =12AB ⋅OC =12×4×3=6,精品 Word 可修改 欢迎下载∴S 四边形ACFB =S △ABC +S △BCF =−32(x −32)2+278+6=−32(x −32)2+758,∵−32<0,∴当x =32时,S 四边形ACFB 有最大值,最大值为758,此时E 点坐标为(32, −32), 综上可知四边形ACFB 面积的最大值758,此时点E 的坐标为(32, −32).。
苏科版九年级数学下册 第五章 二次函数 单元测试卷【含答案】

苏科版九年级数学下册第五章二次函数单元测试卷一、单选题(本大题共10题,每题3分,共30分)1.下列关系式中,属于二次函数的是()A. B. C. D.2.抛物线y=3x2向左平移4个单位,再向下平移2个单位,所得到的抛物线是()A. y=3(x﹣4)2+2B. y=3(x﹣4)2﹣2C. y=3(x+4)2﹣2D. y=3(x+4)2+23.抛物线y=x2–3x+5与坐标轴的交点个数为()A. 无交点B. 1个C. 2个D. 3个4.若是抛物线上的三个点,则、、的大小关系是()A. B. C. D.5.直线y=bx+c与抛物线y=ax2+bx+c(a>0)在同一坐标系中大致图象可能是()A. B. C. D.6.已知二次函数中,自变量x与函数y之间的部分对应值如表:x 0 1 2 3y 2 3 2在该函数的图象上有和两点,且,,与的大小关系正确的是()A. B. C. D.7.一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是()A. 此抛物线的解析式是y=- x2+3.5B. 篮圈中心的坐标是(4,3.05)C. 此抛物线的顶点坐标是(3.5,0)D. 篮球出手时离地面的高度是2m8.二次函数图象上部分点的坐标对应值列表如下:x … 0 1 2 3 …y … -2 -3 -2 …则下列说法错误的是()A. 抛物线开口向上.B. 抛物线的对称轴为直线C. 当时,随的增大而增大D. 方程有一个根小于9.如图,二次函数的图象与轴交于两点,,其中.下列四个结论:①;②;③;④,正确的个数是()A. 1B. 2C. 3D. 410.如图,在四边形ABCD 中,AD∥BC ,∠A=45°,∠C=90°,AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以cm/s 的速度沿AB 向终点B运动,点N以2cm/s 的速度沿折线AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为Scm²,则下列图象能大致反映S与t之间函数关系的是()A. B. C. D.二、填空题(本大题共8题每题2分,共16分)11.抛物线y=3(x-2)2+3的顶点坐标是________。
苏科版九年级数学下册 第五章 二次函数 单元检测试题(有答案)

第五章二次函数单元检测试题一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 下列函数属于二次函数的是()A. B. C. D.2. 如图,已知二次函数的图象如图,有下列个结论:①;②;③;④;⑤(的实数).其中正确结论的有()A.①②③B.①③④C.③④⑤D.②③⑤3. 抛物线的顶点坐标是( )A. B. C. D.4. 抛物线=的顶点坐标是()A. B. C. D.5. 已知,,在函数的图象上,则,,的大小关系是()A. B. C. D.6. 二次函数、、为常数,且中的与的部分对应值如下表:下列结论:①;②当时,的值随值的增大而减小;③是方程的一个根;④当时,;⑤.其中正确说法的序号是()A.①③④B.①③⑤C.②④⑤D.①②④⑤7. 已知,是抛物线上的两点,则,的大小关系为()A. B. C. D.8. 用配方法将二次函数写成形如的形式,则,的值分别是()A.,B.,C.,D.,9. 将二次函数配方成的形式,则它的顶点坐标为( )A. B. C. D.10. 如图是二次函数图象的一部分,直线是对称轴,下列结论:①;②若、是抛物线上两点,则;③;④将抛物线沿轴向右平移一个单位后得到的新抛物线的表达式为.其中正确的是()A.①②③B.①③④C.①②④D.①②③④二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 与抛物线关于轴对称的抛物线的解析式为________.12. 抛物线的顶点在,且经过点,这个函数解析式为________.13. 如图,有长为米的篱笆,一边利用墙(墙的最大可用长度为米),当花圃的宽为________米时,围成的花圃面积最大,最大面积为________平方米.14. 若把二次函数化为的形式,其中,为常数,则________.15. 已知二次函数的图象开口向下,且与轴的正半轴相交.请你写出一个满足条件的二次函数的解析式:________.16. 在一边靠墙的空地上,用砖墙围成三格的矩形场地,已知砖墙在地面上占地总长度,分隔墙在地面上的长度为________时,所围场地总面积最大.17. 如表是二次函数的自变量与函数值的对应关系,一元二次方程的一个解的取值范围是________.18. 已知有一条抛物线的形状(开口方向和开口大小)与抛物线相同,它的对称轴是直线. 当,时,这条抛物线的解析式为________;定义:如果点在抛物线上,则点叫做这条抛物线的不动点,中所求抛物线的所有不动点的坐标为________.19. 已知二次函数=的部分图象如图所示,则关于的一元二次方程=的解为________.20. 已知一次函数和二次函数的图象如图所示,它们有两个交点,,那么能够使得的自变量的取值范围是________.三、解答题(本题共计6 小题,共计60分,)21. 如图,用一段长为米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园,设边长为米,则菜园的面积(单位:米)与(单位:米)的函数关系式为多少?22. 已知二次函数的图象以为顶点,且过点.求该函数的关系式;求该函数图像与坐标轴轴的交点坐标和(点在点的左侧);当函数图象向右平移经过原点时,点与原点重合,因此抛物线向右平移了________个单位;直接写才出此时图象对应的函数解析式:________.23. 已知二次函数.求抛物线顶点的坐标;设抛物线与轴交于,两点,与轴交于点,求,,的坐标(点在点的左侧),并画出函数图象的大致示意图;根据图象,求不等式的解集.24. 某运动员在推铅球时,铅球经过的路线是抛物线的一部分(如图),落地点的坐标是,已知抛物线的函数解析式为,求的值;计算铅球距离地面的最大高度.25. 某电子商投产一种新型电子产品,每件制造成本为元,在销售过程中发现,每月销量(万件)与销售单价(元)之间关系如表所示:求每月的利润(万元)与销售单价(元)之间函数解析式;当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?26. 如图,已知抛物线的对称轴为,且抛物线经过、两点,与轴交于另一点.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴上求一点,使点到点的距离与到点的距离之和最小,并求出此时点的坐标.参考答案一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】C【解答】解:、是一次函数,错误;、分母中含有自变量,不是二次函数,错误;、符合二次函数的一般形式,是二次函数,正确;、被开方数中含自变量,不是二次函数,错误.选.2.【答案】C【解答】①由图象可知:,,,,故①错误;②当时,,即,故②错误;③由对称知,当时,函数值大于,即,故③正确;④当时函数值小于,,且,即,代入得,得,故④正确;⑤当时,的值最大.此时,,而当时,,所以,故,即,故⑤正确.综上所述,③④⑤正确.3.【答案】A【解答】解:∵抛物线,∴顶点坐标为:.故选.4.【答案】C【解答】∵抛物线=,∴该抛物线的顶点坐标是,5.【答案】B【解答】解:∵,∴图象的开口向上,对称轴是直线,关于直线的对称点是,∵,∴,故选.6.【答案】A【解答】解:将、,、,、代入,得,解得:,∴,∴,故①正确;当时,随的增大而减小,故②错误;方程可整理为方程,解得:或,∴是方程的一个根,故③正确;不等式可变形为,解得:,故④正确;由可知当时,取得最大值,即当时,,变形可得,故⑤错误;综上,正确的结论有①③④,故选:.7.【答案】A【解答】解:∵,∴抛物线的对称轴为直线,抛物线开口向下,∴当,随的增大而减小,∵,所以.故选.8.【答案】B【解答】解:∵,,∴将二次函数写成形如的形式后,,的值分别是、;故选.9.【答案】B【解答】解:∵,∴,∴它的顶点坐标为.故选.10.【答案】D【解答】∵开口向下,∴,∵抛物线与轴的正半轴相交,∴,∴,故①正确;∵对称轴为,当时,抛物线有最大值,距离有个单位长度,距离有个单位长度,∴,故②正确;∵对称轴,∴,当时,,∴,∴,∴,∴,故③正确;∵抛物线过,对称轴为,∴设抛物线的解析式为,将抛物线沿轴向右平移一个单位后得出平移后的解析式,∵,∴,∴将抛物线沿轴向右平移一个单位后得到的新抛物线的表达式为,故④正确;正确结论有①②③④;二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】【解答】解:∵的顶点坐标为,∴关于轴对称的抛物线顶点坐标为,且开口向下,∴所求抛物线解析式为:.故本题答案为:.【答案】【解答】解:设抛物线解析式为,把代入得,解得,所以抛物线解析式为.故答案为.13.【答案】,【解答】解:设的长度为米,面积为米,则∵墙的最大可用长度为米,∴,解得..∵,∴函数的开口方向向下,∴当时,.故答案是:;.14.【答案】【解答】解:把二次函数化为,所以,,所以.故答案为:.15.【答案】=,=等,答案不唯一【解答】二次项系数小于,顶点在轴的正半轴的二次函数就满足条件.如=,=等.16.【答案】,,【解答】解:设矩形的面积为,所围矩形的长为米,由题意,得,故当时,,且符合题意.则当所围矩形的长为、宽为时,能使矩形的面积最大,最大面积为,分隔墙在地面上的长度为,,时,所围场地总面积最大.故答案为:,,.17.【答案】【解答】解:由表格中的数据看出和更接近于,故应取对应的范围.故答案为.18.【答案】或【解答】解:设抛物线的解析式为,由已知可得,∴解得:,,∴抛物线的解析式为.故答案为:.设是抛物线的不动点,则,解得:,∴不动点.故答案为:或.19.【答案】=,=【解答】根据图象可知,二次函数=的部分图象经过点,所以该点适合方程=,代入,得=解得=①把①代入一元二次方程=,得=,②解②得=,=,20.【答案】【解答】解:的自变量的取值范围,从图上看就是一次函数图象在二次函数图象上方时,横坐标的取值范围,从图上看当时一次函数图象在二次函数图象上方,所以.三、解答题(本题共计6 小题,每题10 分,共计60分)21.【答案】解:∵边长为米,而菜园是矩形菜园,∴,菜园的面积,则菜园的面积(单位:米)与(单位:米)的函数关系式为:.【解答】解:∵边长为米,而菜园是矩形菜园,∴,菜园的面积,则菜园的面积(单位:米)与(单位:米)的函数关系式为:.22.【答案】解:∵此抛物线的顶点坐标为,∴设此抛物线的解析式为,又因此抛物线过点,∴,解得,∴此抛物线的解析式为:.∵抛物线的解析式为,令,得:,∴ ,∴抛物线与x轴的交点坐标为,,又因点在点的左侧,故点的坐标为,点的坐标为.,【解答】解:∵此抛物线的顶点坐标为,∴设此抛物线的解析式为,又因此抛物线过点,∴,解得,∴此抛物线的解析式为:.∵抛物线的解析式为,令,得:,∴ ,∴抛物线与x轴的交点坐标为,,又因点在点的左侧,故点的坐标为,点的坐标为.∵抛物线与轴的交点的坐标为,原点的坐标为,当函数图像向右平移经过原点,且点与原点重合,∴此抛物线向右平移个单位,根据平移的规律:左加右减,所以此时图像的函数解析式为,故答案为:;.23.【答案】解:)∵,∴抛物线顶点的坐标为;把代入得;把代入得,解得,,∴点坐标为、点坐标为、点坐标为;如图;当或时,,.【解答】解:)∵,∴抛物线顶点的坐标为;把代入得;把代入得,解得,,∴点坐标为、点坐标为、点坐标为;如图;当或时,,.24.【答案】将(10,0)代入,-+,-+,-+,.y=-+=-(-8+=-(+=-.离地面的最高距离为3m. 【解答】将(10,0)代入,-+,-+,-+,.y=-+=-(-8+=-(+=-.离地面的最高距离为3m.25.【答案】解:设,将,和,代入,得:,解得:,∴,则;∵,∴当时,(最大值).答:当销售单价为元时,厂商每月能够获得最大利润,最大利润是万元.【解答】解:设,将,和,代入,得:,解得:,∴,则;∵,∴当时,(最大值).答:当销售单价为元时,厂商每月能够获得最大利润,最大利润是万元.26.【答案】解:(1)设抛物线的解析式为,则有:,解得:,所以抛物线的解析式为;(2)令,解得,,所以点坐标为.设直线的解析式为,则,解得,所以直线解析式是.当时,.所以点的坐标为.【解答】解:(1)设抛物线的解析式为,则有:,解得:,所以抛物线的解析式为;(2)令,解得,,所以点坐标为.设直线的解析式为,则,解得,所以直线解析式是.当时,.所以点的坐标为.。
苏科版九年级数学下册《第五章二次函数》单元测试卷(有答案)
苏科版九年级数学下册第五章二次函数单元测试卷学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(本题共计 10 小题,每题 3 分,共计30分,)1. 下列函数关系中是二次函数的是()A.正三角形面积S与边长a的关系B.直角三角形两锐角A与B的关系C.矩形面积一定时,长y与宽x的关系D.等腰三角形顶角A与底角B的关系2. 在平面直角坐标系中,二次函数y=a(x+ℎ)2的图象可能是()A. B.C. D.3. 苹果熟了,从树上落下所经过的路程s与下落时间t满足S=gt2(g=9.8),则s与t的函数图象大致是()A. B.C. D.4. 抛物线y=2(x−3)2+1的顶点坐标是()A.(−3, 1)B.(3, 1)C.(3, −1)D.(−3, −1)5. 对抛物线:y=−x2+2x−3而言,下列结论正确的是()A.与x轴有两个交点B.开口向上C.与y轴的交点坐标是(0, 3)D.顶点坐标是(1, −2)6. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=−1,且过点(−3, 0).下列说法:①abc<0;②2a−b=0;③4a+2b+c<0;④3a+c=0;其中说法正确的是()A.①② B.②③C.①②④D.②③④7. 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是()A.b2−4ac>0B.a−b+c<0C.abc<0D.2a+b>08. 若A(−4, y1),B(−14, y2),C(3, y3)为二次函数y=(x+2)2−9的图象上的三点,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y29. 把抛物线y=−x2向右平移2个单位,再向下平移3个单位,即得到抛物线()A.y=−(x+2)2+3B.y=−(x−2)2+3C.y=−(x+2)2−3D.y=−(x−2)2−310. 如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(−1, −2)、(1, −2),点B的横坐标的最大值为3,则点A的横坐标的最小值为()A.−3B.−1C.1D.3二、填空题(本题共计 10 小题,每题 3 分,共计30分,)11. 抛物线y=−3x2+8向右平移5个单位的抛物线的函数关系式是________.12. 将函数y=2x2+1向上平移1个单位,再向左平移2个单位,得到抛物线的解析式________.13. 二次函数y=ax2+bx+c中,若a:b:c=1:4:3,且该函数的最小值是−3,则解析式为________.14. 已知二次函数y=(x−1)2+(x−3)2,当x=________时,函数达到最小值.15. 已知二次函数的图象如图所示,则(1)这个二次函数的解析式是________;(2)当x=________时,y=3(3)当x的取值范围是________时,y>0.16. 二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=−1,x2=3;③a+b+c>0;④当x>1时,y 随x值的增大而增大;⑤当y>0时,−1<x<3.其中,正确的说法有________(请写出所有正确说法的序号).17. 已知二次函数y=−x2+4x+5,用配方法化成y=a(x+ℎ)2+k的形式为________.18. 将二次函数y=x2−4x+7化为y=(x−a)2+b的形式,如果直角三角形的两边长分别为a、b,那么第三边的长为________.19. 军事演习在平坦的草原上进行,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足y=−15x2+10x.经过________秒时间,炮弹落到地上爆炸了.20. 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(−2, 4),B(1, 1),则关于x的不等式ax2>bx+c的解集为________.三、解答题(本题共计 6 小题,每题 10 分,共计60分,)21. 已知函数y=(m+3)x m2+m−4+(m+2)x+2.(1)当函数是二次函数时,求m的值;(2)当函数是一次函数时,求m的值. 22. 已知抛物线的解析式为y=−12x2+4x−6(1)求抛物线的顶点坐标;(2)求出抛物线与x轴的交点坐标;(3)当x取何值时y>0?23. 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长a的变化而变化.(1)当矩形边长a为多少米时,矩形面积为200m2;(2)求出S关于a的函数关系式,并直接写出当a为何值时,场地的面积S最大.24. 如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.25. 张经理到老王的果园里一次性采购一种水果,他俩商定:张经理的采购价y(元/吨)与采购量x(吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).(1)求y与x之间的函数关系式;(2)已知老王种植水果的成本是2 800元/吨,那么张经理的采购量为多少时,老王在这次买卖中所获的利润w最大?最大利润是多少?26. 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B和点C的坐标分别为(3, 0)(0, −3),抛物线的对称轴为x=1,D为抛物线的顶点.(1)求抛物线的解析式.(2)抛物线的对称轴上是否存在一点P,使△PCD为等腰三角形?若存在,写出点P点的坐标,若不存在,说明理由.(3)点E为线段BC上一动点,过点E作x轴的垂线,与抛物线交于点F,求四边形ACFB面积的最大值,以及此时点E的坐标.答案1. A2. D3. B4. B5. D6. C7. C8. B9. D10. A11. y=−3(x−5)2+812. y=2(x+2)2+213. y=3x2+12x+914. 215. 解:(1)观察图象得:此函数的顶点坐标为(1, −1),对称轴为x=1,与x轴的交点坐标为(0, 0),(2, 0),∴设此函数的解析式为y=a(x−1)2−1,将点(0, 0)代入函数解析式得a=1,∴这个二次函数的解析式是y=(x−1)2−1,即y=x2−2x;(2)当x2−2x=3时,y=3,解得x1=3,x2=−1,∴当x=3或−1时,y=3;(3)根据图象得,当x<0或x>2时,y>0.16. ①②④17. y=−(x−2)2+918. 1319. 5020. x>1或x<−221. 解:(1)依题意得:m2+m−4=2且m+3≠0.即(m−2)(m+3)=0且m+3≠0,解得m=2;(2)依题意得:m2+m−4=0或m2+m−4=1或m+3=0,解得m=2或m=1±212或m=−3.22. 解:(1)y=−12x2+4x−6=−12(x−4)2+2,∴抛物线顶点坐标为(4, 2);(2)当y=0时,即y=−12x2+4x−6=0,∴x=2或x=6,∴抛物线与x轴的交点坐标为(2, 0)(6, 0);(3)∵抛物线的开口方向向下,且抛物线与x轴的交点坐标为(2, 0)(6, 0),∴当2<x<6时,y>0.23. 解:(1)由题意可得,a(30−a)=200,解得,a1=10,a2=20,即当矩形的边长a为10米或20米时,矩形面积为200m2;(2)由题意可得,S=a(30−a)=−a2+30a=−(a−15)2+225,∴当a=15时,场地面积S取得最大.24. 解:如图,∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,∴存在线段AB且AB的位置已经固定,当P和B重合时,x=4,即x≤4当x=2,P和A重合,即x≥2,∴x的取值范围是2≤x≤4,如图,S矩形PNDM=xy,且2≤x≤4,延长NP交EF于G,显然PG // BF,∴△AGP∽△AFB,∴PG BF =AGAF,即4−y1=x−22,∴y=−12x+5,∴S=xy=−12x2+5x,即S=−12x2+5x(2≤x≤4).25. 解:(1)根据图象可知当0<x≤20时,y=8000(0<x≤20),当20<x≤40时,将B(20, 8000),C(40, 4000),代入y=kx+b,得:8000=20k+b4000=40k+b,解得:k=−200b=12000,y=−200x+12000(20<x≤40);(2)根据上式以及老王种植水果的成本是2 800元/吨,由题意得:当0<x≤20时,W=(8000−2800)x=5200x,W随x的增大而增大,当x=20时,W最大=5200×20=104000元,当20<x≤40时,W=(−200x+12000−2800)x=−200x2+9200x,∵a=−200,∴函数有最大值,当x=−b2a=23时,W最大=4ac−b24a=105800元.故张经理的采购量为23吨时,老王在这次买卖中所获的利润W最大,最大利润是105800元.26. 解:(1)∵点B和点C的坐标分别为(3, 0)(0, −3),抛物线的对称轴为x=1,∴9a+3b+c=0c=−3−b2a=1,解得a=1b=−2c=−3,∴抛物线解析式为y=x2−2x−3;(2)∵y=x2−2x−3=(x−1)2−4,∴D(1, −4),且C(0, −3),∵P点为对称轴上的一点,∴可设P(1, t),∴PC=12+(t+3)2= t2+6t+10,PD=|t−4|,CD=12+(−4+3)2=2,∵△PCD为等腰三角形,∴分PC=PD、PC=CD和PD=CD三种情况,①当PC=PD时,则 t2+6t+10=|t−4|,解得t=37,此时P点坐标为(1, 37);②当PC=CD时,则 t2+6t+10=2,解得t=−2或t=−4(与D点重合,舍去),此时P点坐标为(1, −2);③当PD=CD时,则|t−4|=2,解得t=4+2或t=4−2,此时P点坐标为(1, 4+2)或(1, 4−2);综上可知存在满足条件的P点,其坐标为(1, 37)或(1, −2)或(1, 4+2)或(1, 4−2);(3)∵B(3, 0),C(0, −3),∴直线BC解析式为y=x−3,∵E点在直线BC上,F点在抛物线上,∴设F(x, x2−2x−3),E(x, x−3),∵点F在线段BC下方,∴EF=x−3−(x2−2x−3)=−x2+3x,∴S△BCF=12EF⋅OB=12×3(−x2+3x)=−32x2+92x=−32(x−32)2+278,且S△ABC=12AB⋅OC=12×4×3=6,∴S四边形ACFB =S△ABC+S△BCF=−32(x−32)2+278+6=−32(x−32)2+758,∵−32<0,∴当x=32时,S四边形ACFB有最大值,最大值为758,此时E点坐标为(32, −32),综上可知四边形ACFB面积的最大值758,此时点E的坐标为(32, −32).。
完整版苏科版九年级下册数学第5章 二次函数含答案

苏科版九年级下册数学第5章二次函数含答案一、单选题(共15题,共计45分)1、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:其中正确的结论有()①abc>0;②8a+2b=-1;③4a+3b+c>0;④4ac+24c<b2A.1B.2C.3D.42、二次函数的图象如图所示,反比例函数与正比例函数在同一坐标系中的大致图象可能是()A. B. C. D.3、二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是()A.当x>2时,y随x增大而减小B.4a=bC.图象过点(﹣1,0) D.9a+3b+c>04、在平面直角坐标系中,如果抛物线y=2x2不动,而把x轴、y轴分别向上、向右平移3个单位,那么在新坐标系下抛物线的解析式是()A.y=2(x+3) 2-3B.y=2(x-3) 2+3C.y=2(x-3) 2-3D.y=2(x+3) 2+35、若关于x的方程|ax2+bx+c|=5有三个不相等的实数根,则二次函数y=ax2+bx+c有()A.最小值为5B.最大值为5C.最大值为5或最小值-5D.最大值-5或最小值56、如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点C是第四象限内抛物线上一点,连结AC,BC.下列所给条件中,能确定二次项系数a的值的是()A.A(2,0),B(6,0),AC=BCB.AB=2,C(3,-1)C.∠ACB=90°,点C的纵坐标为-2D.A(2,0),AB=2AC7、已知二次函数y=ax2+bx+c的图象如图所示,则a、b、c满足()A.a<0,b<0,c>0B.a<0,b<0,c<0C.a<0,b>0,c>0 D.a>0,b<0,c>08、已知二次函数y=ax2+bx+c(a≠0) 的图象如图所示,给出以下结论:① b2>4ac;②abc<0 ;③2a+b=0 ;④ 8a+c>0 ;⑤9a+3b+c<0,其中正确结论是().A.①②B.②③C.①③④D.①③④⑤9、二次函数(是常数,)的自变量与函数值的部分对应值如下表:…0 1 2 ………且当时,与其对应的函数值.有下列结论:① ;② 和3是关于的方程的两个根;③ .其中,正确结论的个数是()A.0B.1C.2D.310、将抛物线y=(x﹣2)2+1向上平移3个单位,得到新抛物线的顶点坐标是()A.(2,4)B.(﹣1,1)C.(5,1)D.(2,﹣2)11、已知,(m为任意实数),则P、Q的大小关系为()A. B. C. D.不能确定12、如图,是抛物线在第四象限的一点,过点分别向轴和轴作垂线,垂足分别为、,则四边形周长的最大值为()A. B. C. D.13、如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时.达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是()A.水流运行轨迹满足函数y=﹣x2﹣x+1B.水流喷射的最远水平距离是40米C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌14、如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c >0.其中正确的命题是()A.①②B.②③C.①③D.①②③④15、如图是二次函数y=ax2+bx+c(a≠0)的图象,下列结论正确的个数是()①顶点是(﹣1,4)②方程ax2+bx+c=0的解是x1=﹣3,x2=1③4a+2b+c>0④不等式ax2+bx+c>0的解为﹣2<x<0.A.1B.2C.3D.4二、填空题(共10题,共计30分)16、红光旅行社有100张床位,每床每日收费10元,客床可全部租出,若每床每日收费提高2元,则租出床位减少10张,若每床每日收费再提高2元,则租出床位再减少10张,以每提高2元的这种变化方法变化下去,每床每日提高________元可获最大利润。
苏科版九年级数学下册《第五章二次函数》单元检测试题(有答案)
2017-2018学年度第二学期苏科版九年级数学下册第五章二次函数单元检测试题考试总分: 120 分考试时间: 120 分钟姓名:__________考号:__________班级:__________学校:__________一、选择题(共 10 小题,每小题 3 分,共 30 分)1.下列函数中,二次函数是()A. B.C. D.2.如图,二次函数的图象的对称轴为,与轴交于点,,与轴交于点,则下列四个结论:①;②;③;④当时,或.其中正确的个数是()A. B. C. D.3.如图所示,当时,二次函数的图象大致为()A. B.C. D.4.已知抛物线如图所示,下列结论中,正确的是()A. B.C.时,抛物线是上升的D.抛物线有最高点5.已知,点,,都在函数的图象上,则()A. B.C. D.6.若把函数的图象用记,函数的图象用记,…则可以由怎样平移得到?()A.向上平移个单位B.向下平移个单位C.向左平移个单位D.向右平移个单位7.二次函数,,为常数,且中的与的部分对应值如下表:下列结论:;当时,的值随值的增大而减小.是方程的一个根;当时,.其中正确的个数为()A.个B.个C.个D.个8.若二次函数的图象经过原点,则的值必为()A.或B.C.D.9.抛物线的图象如图,则下列结论:①;② ;③;④ .其中正确的结论是()A.①②B.②③C.②④D.③④10.如图,在中,,,,动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,那么经过()秒,四边形的面积最小.A. B. C. D.二、填空题(共 10 小题,每小题 3 分,共 30 分)11.抛物线的顶点是,它与轴交于,两点,它们的横坐标是方程的两根,则________.,当时,的范围12.设,当取何值时最小,最小是多少?当时,________.,当时,的范围是________是________13.如图的一座拱桥,当水面宽为时,桥洞顶部离水面,已知桥洞的拱形是抛物线,以水平方向为轴,建立平面直角坐标系,若选取点为坐标原点时的抛物线解析式是.,则选取点为坐标原点时的抛物线解析式是________14.已知二次函数的图象过点,并且,试写出一个满足条件的函数的.表达式________15.已知抛物线经过点,,,则该抛物线上纵坐标为的另一点的坐标是.________.16.将二次函数解析式配方成的形式为________.17.若抛物线过原点,则该抛物线与轴的另一个交点坐标为________18.若抛物线与轴只有一个交点,且过点,,则.________19.公路上行驶的汽车急刹车时的行驶路程与时间的函数关系式为,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行________才能停下来.20.如图,在平面直角坐标系中,过、两点的抛物线交轴于点,其顶点为点,设的面积为,的面积为.小芳经探究发现:是一个定值.则这个定值为________.三、解答题(共 6 小题,每小题 10 分,共 60 分)21.已知抛物线.求证:无论为任何实数,抛物线与轴总有两个交点;若抛物线对称轴,且反比例函数的图象与抛物线在第一象限内的交点的横坐标为,且满足,求的取值范围.22.我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是元/台.经过市场销售后发现:在一个月内,当售价是元/台时,可售出台,且售价每降低元,就可多售出台.若供货商规定这种空气净化器售价不能低于元/台,代理销售商每月要完成不低于台的销售任务.试确定月销售量(台)与售价(元/台)之间的函数关系式;求售价的范围;当售价(元/台)定为多少时,这种空气净化器所获得的利润能达到元?23.某超市经销一种销售成本为元的商品,据超市调查发现,如果按每件元销售,一周能销售件,若销售单价每涨元,每周销售减少件,设销售价为每件元,一周的销售量为件.求与的函数关系式.设该超市一周的销售利润为元,求的最大值.24.已知,如图,二次函数的图象与轴交于,两点,与轴交于点,且经过点求该抛物线的解析式;求该抛物线的顶点坐标和对称轴.求的面积.25.如图,有长为米的篱笆,一面利用墙(墙的最大可用长度为米),围成一个长方形的花圃.设花圃的宽为米,面积为平方米.求与的函数关系式;写出自变量的取值范围.怎样围才能使长方形花圃的面积最大?最大值为多少?26.如图,在中,,,,点从点出发,以的速度沿运动;同时,点从点出发,以的速度沿运动.当点到达点时,、两点同时停止运动.试写出的面积与动点运动时间之间函数表达式;运动时间为何值时,的面积最大?最大值为多少?答案1.B2.C3.B4.D5.C6.D7.B8.B9.C10.C11.12.,13.14.15.16.17.18.19.20.21.证明:令,则,∴,∴不论为任何实数,都有,即.∴不论为任何实数,抛物线与轴总有两个交点.解:∵抛物线的对称轴为,又∵抛物线对称轴,∴ ,解得:,∴抛物线的解析式为;当时,对于,随着的增大而增大,对于,随着的增大而减小.所以当时,由反比例函数图象在二次函数图象上方,得:,解得:.当时,由二次函数图象在反比例函数图象上方,得:,解得:.所以的取值范围为.22.解:根据题中条件销售价每降低元,月销售量就可多售出台,则月销售量(台)与售价(元/台)之间的函数关系式:,化简得:;根据供货商规定这种空气净化器售价不能低于元/台,代理销售商每月要完成不低于台,则,解得:.所以与之间的函数关系式为:;设这种空气净化器所获得的利润为,,把代入得,解得,∵ 在内,∴当时,这种空气净化器所获得的利润能达到为,即售价定为元/台时,商场每月销售这种空气净化器所获得的利润是元.23.解:根据题意,得:,即;,∵,∴当时,取得最大值,最大值为元.24.解:∵二次函数的图象经过点、,∴ ,解这个方程组,得,∴该二次函数的解析式是;,∴顶点坐标是;对称轴是;∵二次函数的图象与轴交于,两点,∴,解这个方程得:,,即二次函数与轴的两个交点的坐标为,.∴ 的面积.25.解:设花圃的宽为米,则长米.由矩形的面积公式可知:,∴ .∵墙的最大可用长度为米,∴ .解得:.∵ ,,∴ .∵ ,,∴ 随的增大而减小.∵当时,即长为米,宽为米时面积最大,∴长方形花圃的最大面积平方米.26.解:由题意得秒时,,,;,故时,最大.。
苏科版九年级数学下册 第五章 二次函数 单元评估测试卷含答案
苏科版九年级数学下册第五章二次函数单元评估测试卷一、选择题(共 10 小题,每小题 3 分,共 30 分)1.已知二次函数,则其二次项系数,一次项系数,常数项分别是()A.,,B.,,C.,,D.,,2.不在抛物线上的一个点是()A. B. C. D.3.设一元二次方程的两根分别为、,且,则、满足()A. B.C.,D.4.将抛物线向上平移个单位,再向左平移个单位,所得抛物线的表达式为()A. B.C. D.5.抛物线的顶点坐标是()A. B. C. D.6.对于二次函数,下列说法正确的是()A.当时,随的增大而增大B.图象的顶点坐标为C.当时,有最大值D.图象与轴有两个交点7.已知二次函数中,当时,,且的平方等于与的乘积,则函数值有()A.最大值B.最小值C.最大值D.最小值8.二次函数的图象如图所示,下列结论:① ;② ;③ ;④抛物线与轴的另一个交点为.其中正确的结论有()个.A. B. C. D.9.某商品的进价为每件元,现在的售价为每件元,每星期可卖出件.市场调查反映:如果每件售价每涨元(售价每件不能高于元),那么每星期少卖件.设每件售价为元(为非负整数),则若要使每星期的利润最大且每星期的销量较大,应为多少元?()A. B. C. D.10.已知二次函数的图象如图所示,给出以下四个结论:① ;② ;③ ;④ ,其中所有正确结论的序号是()A ②④B ②③④C ①②④D ①④二、填空题(共 10 小题,每小题 3 分,共 30 分)11.将二次函数的图象向右平移个单位,再向下平移个单位后,所得图象的函数表达式是________.12.二次函数,当________时有最________值,这个值为________.13.抛物线顶点为,与轴交于,则抛物线解析式为________.14.若二次函数与轴的两个交点为则的值为________.15.已知以为自变量的二次函数的图象经过原点,则的值是________.16.向空中发射一枚炮弹,经秒后的高度为米,且时间与高度的关系为.若此炮弹在第秒与第秒时的高度相等,当炮弹所在高度最高时是第________秒.17.若将抛物线向左平移个单位长度,再向下平移个单位长度,所得的抛物线为,则________.18.二次函数部分对应值可列表如下:则一元二次方程正根的范围是________.19.如图,是二次函数的图象的一部分,对称轴是直线.① ;② ;③不等式的解集是;④若,是抛物线上的两点,则.上述四个判断中正确的是________(填正确结论的序号).20.如图,抛物线过,,轴于点,四边形为正方形,点在线段上,点在此抛物线上,且在直线的左侧,则正方形的边长为________.三、解答题(共 6 小题,每小题 10 分,共 60 分)21.如图,直线和抛物线都经过,.求的值和抛物线的解析式;写出抛物线的顶点坐标;求不等式的解集.(观察图象,直接写出解集)22.为了改善小区环境,某小区决定要在一块一边靠墙(墙的最大可用长度为米)的空地上修建一个矩形绿化带,绿化带一边靠墙,另三边用总长为米的栅栏围住(如图).若设绿化带的边长为米,绿化带的面积为平方米.求与之间的函数关系式及自变量的的取值范围.栅栏为多少米时,花圃的面积最大?最大面积为多少?23.如图,抛物线与轴交于点,点,与轴交于点,点是该抛物线的顶点,连接,.直接写出点、的坐标;求的面积;点是抛物线上的一动点,若的面积是面积的,求点的坐标.24.某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线表示该产品每千克生产成本(单位:元)与产量(单位:)之间的函数关系;线段表示每千克的销售价(单位:元)与产量(单位:)之间的函数关系.请解释图中点的横坐标、纵坐标的实际意义.求线段所表示的与之间的函数表达式.当时,销售该产品获得的利润与产量的关系式是________;当时,销售该产品获得的利润与产量的关系式是________;总之,当产量为________时,获得的利润最大,最大利润是________.25.如图,已知二次函数的图象与轴交于、两点(点在点的左侧),与轴交于点,且,顶点为.求二次函数的解析式;点为线段上的一个动点,过点作轴的垂线,垂足为,若,四边形的面积为,求关于的函数解析式,并写出的取值范围;探索:线段上是否存在点,使为等腰三角形?如果存在,求出点的坐标;如果不存在,请说明理由.26.为了美化环境,学校准备在如图所示的矩形空地上进行绿化,规划在中间的一块四边形上种花,其余的四块三角形上铺设草坪,要求,已知米,米,设米,种花的面积为平方米,草坪面积平方米.分别求和与之间的函数关系式(不要求写出自变量的取值范围);当的长为多少米时,种花的面积为平方米?若种花每平方米需元,铺设草坪每平方米需元,现设计要求种花的面积不大于平方米,设学校所需费用(元),求与之间的函数关系式,并求出学校所需费用的最大值.答案1.D2.D3.B4.A5.D6.C7.A8.B9.B10.A11.12.大13..14.15.16.17.18.①④20.21.解:将代入得将,代入得∴∴由,知,即,顶点坐标为22.解:由题意得:,自变量的取值范围是:;∵ ,∴当时,有最大值平方米,即栅栏为米时,花圃的面积最大,最大面积为平方米.23.解:当,则,故,,故; ∵点,点,∴ ,∴; ∵ 的面积是面积的,∴ ,∵ ,∴ 点纵坐标为或,当点纵坐标为,则,解得:,,此时点坐标为:或,当点纵坐标为,则,解得:,,此时点坐标为:或,综上所述:点的坐标为:、、、.24.;,,.25.解: ∵ ,∴ ,∴ ,解得分∴二次函数的解析式为;,设直线的解析式为,则有解得∴直线的解析式为∵ 轴,,∴点的坐标为四边形梯形;线段上存在点,,使为等腰三角形,,①当时,,解得,(舍去)此时②当时,,解得,(舍去),此时③当时,解得,此时.26.解:根据题意,,;根据题意,知,即,解得:,,故当的长为米或米时种花的面积为平方米;设总费用为元,则,由知当或时,,在中,当时,随的增大而增大,当时,随的增大而减小,∴当时,取得最大值,最大值,当时,取得最大值,最大值,∴学校所需费用的最大值为元.。
苏科版九年级下册数学第5章 二次函数 含答案
苏科版九年级下册数学第5章二次函数含答案一、单选题(共15题,共计45分)1、如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是()A.①④B.①③C.②④D.①②2、把抛物线y=2x²先向左平移3个单位,再向上平移4个单位,所得到的抛物线的解析式是()A.y=2(x+3)²+4B.y=2(x+3)²-4C.y=2(x-3)²-4D.y=2(x-3)²+43、知二次函数y=ax2﹣2x+2(a>0),那么它的图象一定不经过()A.第一象限B.第二象限C.第三象限D.第四象限4、城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系(a,b,c是常数,且a≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是()A.4.8B.5C.5.2D.5.55、二次函数的图像如图所示,则点Q(,)在()A.第一象限B.第二象限C.第三象限D.第四象限6、苹果熟了,从树上落下所经过的路程s与下落的时间t满足(g 是不为0的常数),则s与t的函数图象大致是( )A. B. C.D.7、若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b,k的值分别()A.0,5B.﹣4,1C.﹣4,5D.﹣4,﹣18、在同一坐标系中,抛物线,,的共同特点是()A.关于y轴对称,开口向上B.关于y轴对称,y随x增大而减小C.关于y轴对称,y随x增大而增大D.关于y轴对称,顶点在原点9、如图,二次函数y=ax2+bx+c的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是()A.y的最小值大于-1B.当x=0时,y的值大于0C.当x=2时,y 的值等于-1D.当x>3时,y的值大于010、下列函数不是二次函数的是()A.y=﹣3(x+1)2+5B.y=6﹣x 2C.y=D.y=(﹣x+2)(x﹣3)11、抛物线y=﹣x2+2kx+2与x轴交点的个数为()A.0个B.1个C.2个D.以上都不对12、二次函数y=ax2+bx+c自变量x与函数值y之间有下列关系:那么(a+b+c)的值为()x …﹣3 ﹣2 0 …y … 3 ﹣1.68 ﹣1.68 …A.6B.﹣6C.D.﹣13、为了备战2012英国伦敦奥运会,中国足球队在某次训练中,一队员在距离球门12米处的挑射,正好从2.4米高(球门横梁底侧高)入网.若足球运行的路线是抛物线y=ax2+bx+c(如图5所示),则下列结论正确的是( )①a<-②-<a<0③a-b+c>0 ④0<b<-12aA.①③B.①④C.②③D.②④14、二次函数的图象如图所示,则下列结论:①,②,③,④,⑤中正确的是()A.②④⑤B.①②④C.①③④D.①③④⑤15、如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一1=mx+n(m≠0)与抛物线交于A,B两点,下列结个交点B(﹣4,0),直线y2论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④<方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2.其中正确的是()y1A.①②③B.①③⑤C.①④⑤D.②③④二、填空题(共10题,共计30分)16、抛物线与x轴有两个交点,且交点位于y轴两侧,则下列关于这个二次函数的说法正确的有________.(填序号)①;②若,则当时,y随x的增大而增大;③;④一元二次方程的两根异号.17、二次函数图象的对称轴是________.18、二次函数的部分图象如图所示,由图象可知,不等式的解集为________.19、已知二次函数自变量x的部分取值和对应函数值y如下表:…-2 -1 0 1 2 3 …… 5 0 -3 -4 -3 0 …则在实数范围内能使成立的x的取值范围是________.20、如图,某涵洞的截面是抛物线形,现测得水面宽AB=1.6m,涵洞顶点O到水面的距离CO为2.4m,在图中直角坐标系内,涵洞截面所在抛物线的解析式是________21、二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是________ (填写序号)22、若二次函数y=4x2﹣6x﹣3的图象与x轴交于点A(x1, 0),B(x1,0)两点,则的值为________.23、铅球行进高度y(m)与水平距离x(m)之间的关系为y=﹣x2+ x+ ,铅球推出后最大高度是________m,铅球落地时的水平距离是________m. 24、二次函数y=ax2+bx+c(a≠0)的部分对应值如下表:x ﹣3 ﹣2 ﹣1 0 1 2y ﹣12 ﹣5 0 3 4 3利用二次函数的图象可知,当函数值y>0时,x的取值范围是________.25、如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B 的左侧),与y轴交于点C.将抛物线沿y轴平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是________.三、解答题(共5题,共计25分)26、已知抛物线的顶点为(2,3),且经过点(3,1),求此抛物线对应的函数解析式。
苏科版九年级下期末复习《第五章二次函数》单元评估试卷有答案
h
②设 BE=x,∵AG=CD=AB=5, ∴EG=AE+AG=5-x+5=10-x, 在 Rt△BCE 中,CE2=BC2-BE2=100-x2 ∵CF=GF(①中已证), ∴CF2= = CG2= (200-20x)=50-5x,
��� ���
,
在 Rt△CEG 中,CG2=EG2+CE2=(10-x)2+100-x2=200-20x,
C2010A2011C2011B2011 都是正方形,则正方形 C2010A2011C2011B2011 的边长为________.
三、解答题(共 7 题;共 57 分)
22.某商店购进一批单价为 20 元的日用品,如果以单价 30 元销售,那么半个月内可以售出 400 件.根据销售经 验,提高销售单价会导致销售量的减少,即销售单价每提高 1 元,销售量相应减少 20 件.问如何提高售价,才能 在半个月内获得最大利润?
C. 大于 0 C. y=(x+2)2﹣3 ) C. 一次项是 100 C.
D. 不能确定 D. y=(x+2)2+3 D. 常数项是 20000 D.
5.若将抛物线 y=x2 向右平移 2 个单位,再向上平移 3 个单位,则得到的抛物线解析式是( ) 6.关于函数 y=(500﹣10x)(40+x),下列说法不正确的是(
的图象先向右平移 2 个单位,再向上平移 3 个单位后,得到的抛物线的解析式是( )
8.二次函数 y=ax2+bx+c 的图象如图所示,若点 A(1,y1)、B(2,y2)是它图象上的两点,则 y1 与 y2 的大小
A. y1<y2 是( ) x 6.17 6.18 6.19
B. y1=y2
C. y1>y2
ܾ
九年级数学下册第五章《二次函数》单元测试题-苏科版(含答案)
九年级数学下册第五章《二次函数》单元测试题-苏科版(含答案)一、单选题1.抛物线y =﹣2(x ﹣3)2﹣4的顶点坐标是( )A .(﹣3,4)B .(﹣3,﹣4)C .(3,﹣4)D .(3,4)2.下列二次函数的图象经过原点的是( )A .y=x 2+1B .y=x 2+xC .y=(x+1)2D .y=x 2-2x+13.用绳子围成周长为10(m )的矩形,记矩形的一边长为x (m ),面积为S (m 2).当x 在一定范围内变化时,S 随x 的变化而变化,则S 与x 满足的函数关系是( ) A .一次函数关系 B .二次函数关系 C .反比例函数关系D .正比例函数关系4.把抛物线y=2x 2向下平移1个单位,则平移后抛物线的解析式为( )A .y=2x 2 + 1B .y=2x 2-1C .y= ()22x 1+D .y= ()22x 1-5.若A (﹣3,y 1), 21B ,y 2⎛⎫⎪⎝⎭,C (2,y 3)在二次函数y =x 2+2x+c 的图象上,则y 1,y 2,y 3的大小关系是( ) A .y 2<y 1<y 3B .y 1<y 3<y 2C .y 1<y 2<y 3D .y 3<y 2<y 16.下列函数:①y=-x ;②y=2x ;③1y x=-;④y=x 2.当x<0时,y 随x 的增大而减小的函数有( ) A .1个B .2个C .3个D .4个7.若将抛物线y=x 2平移,得到新抛物线 2(3)y x =+ ,则下列平移方法中,正确的是( )A .向左平移3个单位B .向右平移3个单位C .向上平移3个单位D .向下平移3个单位8.一次函数y=ax 2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1.下列结论:①abc>0;②若(−3,y 1),(4,y 2)在抛物线上,则y 1<y 2;③当−1<x<3时,y<0时;④8a+c>0.其中正确的有( )A .①②B .①④C .①③④D .②④9.已知:抛物线y 1=x 2+2x-3与x 轴交于A 、B 两点(点A 在点B 的左侧),抛物线y 2=x 2-2ax-1(a>0)与x 轴交于C 、D 两点(点C 在点D 的左侧),在使y 1>0且y 2≤0的x 的取值范围内恰好只有一个整数时,a 的取值范围是( ) A .0<a≤34B .a≥34C .34≤a <43D .34<a≤4310.对于函数y= =ax 2-(a+1)x+1,甲和乙分别得出一个结论:甲:若该函数图象与x 轴只有一个交点,则a=1; 乙:方程ax 2- (a+1)x+1=0至少有一个整数根. 甲和乙所得结论的正确性应是( ) A .只有甲正确 B .只有乙正确 C .甲乙都正确D .甲乙都不正确二、填空题11.校运动会铅球比赛时,小林推出的铅球行进的高度y (米)与水平距离x (米)满足关系式21251233y x x =-++,则小林这次铅球推出的距离是 米. 12.在二次函数y=-x 2+bx+c 中,函数y 与自变量x 的部分对应值如下表.x -3 -2 -1 1 2 3 4 5 y-14-7-22mn-7-14的值为 .13.如图,已知二次函数 21(0)y ax bx c a =++≠ 与一次函数 2(0)y kx m k =+≠ 的图象相交于点A (-2,6)和B (8,3),则能使 y 1 <y2成立的 x 的取值范围 .14.如图,在平面直角坐标系中,抛物线 21:2C y x =-+ 和抛物线 22:2C y x x =+ 相交于点A 、B (点A 在点B 的左侧),P 是抛物线 22:2C y x x =+ 上 AB 段的一点(点P 不与A 、B 重合),过点P 作x 轴的垂线交抛物线 21:2C y x =-+ 于点Q ,以 PQ 为边向右侧作正方形PQMN .设点P 的横坐标为m ,当正方形的四个顶点分别落在四个不同象限时,m 的取值范围是.三、计算题15.已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.16.求二次函数y=x2+4x﹣5的最小值.四、作图题17.在同一平面内画出函数y=2x2与y=2x2+1的图象.五、解答题18.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.19.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.20.已知二次函数y=﹣x2+mx+n与x轴交于A,B两点(点A在点B左侧),其中点A的坐标为(﹣1,0),AB=4.求该二次函数的表达式.21.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.六、综合题22.据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,根据物理知识:梯形OABC在直线l左侧部分的面积表示的实际意义为t(小时)内污染所经过的路程S(千米),其中0≤t≤30.(1)当t=3时,则S的值为;(2)求S与t的函数表达式;(3)若乙城位于甲地的下游,且距甲地171千米,试判断这河流污染是否会侵袭到乙城?若会,求河流污染发生后多长时间它将侵袭到乙城;若不会,请说明理由.23.某商场经营某种品牌童装,进货时的单价是40元,根据市场调查,当销售单价是60元时,每天销售量是200件,销售单价每降低0.5元,就可多售出10件.(1)当销售单价为58元时,每天销售量是件.(2)求销售该品牌童装获得的利润y(元)与销售单价x(元)之间的函数关系式;(3)若商场规定该品牌童装的销售单价不低于57元且不高于60元,则销售该品牌童装获得的最大利润是多少?参考答案1.【答案】C【解析】【解答】解:由抛物线的顶点式y=-2(x-3)2-4可得:该抛物线的顶点坐标为(3,-4),故答案为:C.【分析】二次函数y=a(x-k)2+h(a≠0)的图象的顶点是(k,h),依此解答即可.2.【答案】B【解析】【解答】解:A、当x=0时,y=x2+1=1,则此二次函数的图象不经过原点,A不符合题意;B、当x=0时,y=x2+x=0,则此二次函数的图象经过原点,B符合题意;C、当x=0时,y=(x+1)2=1,则此二次函数的图象不经过原点,C不符合题意;D、当x=0时,y=x2-2x+1=1,则此二次函数的图象不经过原点,D不符合题意.故答案为:B.【分析】二次函数图象过原点,即(0,0)在函数图象上,因此把x=0代入选项四个解析式求出对应的函数值,若y=0,则可判断这个二次函数图象经过原点.3.【答案】B【解析】【解答】解:∵矩形周长为10 m,一边长为x m,∴另一边长为:(10-2x)÷2=5-x (m),∴S=x(5-x)=-x2+5x.故答案为:B.【分析】结合矩形对边相等,将另一边长表示出来,再根据面积=长×宽,建立出S与x的关系式,即可判断.4.【答案】B【解析】【解答】解:∵抛物线y=2x2向下平移1个单位,∴y=2x2-1.故答案为:B.【分析】对于二次函数y=a(x+h)2+k,根据抛物线的平移规律:即左右平移在h后左加右减,上下平移在k后上加下减即可求出结果.5.【答案】A【解析】【解答】解:对称轴为直线x=﹣221=﹣1,∵a=1>0,∴x<﹣1时,y随x的增大而减小,x>﹣1时,y随x的增大而增大,∴y 2<y 1<y 3. 故答案为:A .【分析】求出二次函数的对称轴,再根据二次函数的增减性判断即可.6.【答案】B【解析】【解答】解:一次函数y =-x 中k <0,∴y 随x 的增大而减小,故本选项正确;∵正比例函数y =2x 中,k =2,∴当x <0时,y 随x 的增大而增大,故本选项错误; ∵反比例函数 1y x= 中,k =-1<0,∴当x <0时函数的图象在第二象限,此时y 随x 的增大而增大,故本选项错误;∵二次函数y =x 2,中a =1>0,∴此抛物线开口向上,当x <0时,y 随x 的增大而减小,故本选项正确. 故答案为:B.【分析】一次函数的比例系数k <0的时候,y 随x 的增大而减小,当比例系数k >0的时候,y 随x 的增大而增大,从而即可判断①、②;反比例函数的比例系数k <0的时候,图象的两支分别位于第二、四象限,在每一个象限内,y 随x 的增大而增大,比例系数k >0的时候,图象的两支分别位于第一、三象限,在每一个象限内,y 随x 的增大而减小;函数 y=x 2的二次项系数大于0对称轴是y 轴,图象开口向上,在对称轴左侧,即当x<0时 y 随x 的增大而减小,从而即可一一判断得出答案.7.【答案】A【解析】【解答】解:抛物线y=x 2的顶点坐标为(0,0),抛物线y=(x+3)2的顶点坐标为(-3,0),因为点(0,0)向左平移3个单位长度后得到(-3,0), 所以把抛物线y=x 2向左平移3个单位得到抛物线y=(x+3)2. 故答案为:A.【分析】先确定抛物线y=x 2的顶点坐标为(0,0),抛物线y=(x+3)2的顶点坐标为(-3,0),然后利用顶点的平移情况确定抛物线的平移情况.8.【答案】B【解析】【解答】解:①抛物线开口向上,则a >0,抛物线与y 交于负半轴,则c <0,x=-2ba=1,即b=-2a ,则b <0, ∴abc >0,故①符合题意;②∵(-3,y 1)离对称直线x=1的距离为1-(-3)=4, (4,y 2)离对称直线x=1的距离为4-1=3,∴点(-3,y 1)离对称轴要比点(4,y 2)离对称轴要远,又∵抛物线开口向上,离对称轴越远,函数值越大,4>3, ∴y 1>y 2,故②不符合题意;③观察图象,抛物线与x 轴的一个交点为−1<x<0, ∴当−1<x<3时,y 不一定小于0;故③不符合题意; ④当x=-2时,y >0,则4a-2b+c >0, ∵b=-2a ,∴8a+c >0,所以④符合题意; 综上,正确的有①④, 故答案为:B .【分析】①抛物线开口向上,则a >0,抛物线与y 交于负半轴,则c <0,对称轴为x=-2ba=1,即b=-2a ,则b <0,可得abc >0,故正确;②由抛物线开口向上,离对称轴越远,函数值越大,故②错误;③根据抛物线的对称性及与x 轴的一个交点为−1<x<0,可知当−1<x<3时,y 不一定小于0;④当x=-2时,y=4a-2b+c >0,由b=-2a 可得8a+c >0,故正确.9.【答案】C【解析】【解答】由题意可知()22210y x ax a =-->的对称轴为(0)x a a =>可知对称轴再y 轴的右侧,由2123y x x =+-与x 轴交于A 、B 两点(点A 在点B 的左侧)可知当10y >时可求得31x x -或使1200y y >≤且的x 的取值范围内恰好只有一个整数时∴只要符合将2x =代入()22210y x ax a =-->中,使得20y ≤,且将3x =代入()22210y x ax a =-->中使得20y >即{22−4a −1≤09−6a −1>0 求得解集为:3443x ≤< 故答案为:C【分析】利用抛物线y 2=x 2-2ax-1可求出其对称轴为直线x=a ,利用a 的取值范围可知对称轴再y 轴的右侧;同时可知当x <-3和x >1时y 1>0;再根据y 1>0且y 2≤0的x 的取值范围内恰好只有一个整数,可得到x=2时y 2≤0,当x=3时y 2>0,分别将其代入y 2的函数解析式,可得到关于a 的不等式组,然后求出不等式组的解集.10.【答案】B【解析】【解答】解:甲:当a=0时,y=-x+1,∴当y=0时,x=1,即函数图象与x 轴交于点(1,0),∴甲结论不正确,乙:当a=0时,-x+1=0, ∴x=1;当a≠0时,ax 2-(a+1)x+1=(x-1)(ax-1)=0, 解得x=1或x=1a, ∴方程ax 2-(a+1)x+1=0至少有一个整数根. 故答案为:B.【分析】甲:当a=0时,函数y=-x+1,此时函数图象与x 轴只有一个交点为(1,0),即可判断甲的结论;乙:当a=0时,-x+1=0,解得根为1,当a≠0时,ax 2-(a+1)x+1=(x-1)(ax-1)=0,解得根为1或1a,据此即可判断乙结论. 11.【答案】10【解析】【解答】解:令y=0∴21251233x x -++=0 ∴x 2−8x−20=0解得:x 1=10,x 2=−2(舍去)∴小林这次铅球推出的距离是10米. 故答案为:10.【分析】令y=0,求出x 的值,进而可得小林这次铅球推出的距离.12.【答案】3【解析】【解答】解:由表可得,(-1,-2)和(1,2)在二次函数y=-x 2+bx+c 图象上,∴1212b c b c --+=-⎧⎨-++=⎩, 整理,解得21b c =⎧⎨=⎩,∴二次函数解析式为y=-x 2+2x+1, ∴当x=2时,m=-4+4+1,解得m=1, 当x=3时,n=-9+6+1,解得n=-2, ∴m-n=1-(-2)=3. 故答案为:3.【分析】由表可得,(-1,-2)和(1,2)在函数图象上,先利用待定系数法求出二次函数解析式,再将x=2和x=3分别代入即可计算出m 和n 的值,从而求出m-n 的值.13.【答案】−2<x <8<8< p=""> <8<>【解析】【解答】解:∵二次函数y 1=ax 2+bx +c (a≠0)与一次函数y 2=kx +m (k≠0)的图象相交于点A (−2,6),B (8,3),∴ 结合图象,能使y 1<y 2成立的x 的取值范围是:−2<x <8, 故答案为:−2<x <8,【分析】根据两函数交点坐标得出,能使y 1<y 2成立的x 的取值范围即是图象y 2在图象y 1上面是x 的取值范围,即可得出答案.14.【答案】1170m +<< 【解析】【解答】解:若正方形的四个顶点分别落在四个不同象限,则P 点在第三象限,Q 点在第二象限,M 点在第一象限,N 点在第四象限,∵点P 的横坐标为m ,P 是抛物线 22:2C y x x =+ 上 AB 段的一点∴2(,2)P m m m + , 0m < , 由题意可知Q 点和P 点横坐标相同, ∴2(,2)Q m m -+ ,若Q 在Q 点在第二象限,则 220m -+> , 解得 02m <<,或 02m <<(舍),∴()22222222PQ m m m m m =-+-+=--+ ,即 2222QM PN PQ m m ===--+ , ∴M 、N 的横坐标都为 ()2222222m m m m m +--+=--+ ,∵M 点在第一象限,N 点在第四象限, ∴2220m m --+> ,当 2220m m --+= 时,解得 1117m -= , 2117m +=, 因此 117117m +-<< 时 2220m m --+> , 又∵0m < , ∴1170m +<< , 故答案为: 11704m +-<< . 【分析】若正方形的四个顶点分别落在四个不同象限,则P 点在第三象限,Q 点在第二象限,M 点在第一象限,N 点在第四象限,由点P 的横坐标为m , 通过解析式可表示点P 、Q 的坐标,即可表示PQ 的长,通过正方形的边长相等可表示N 点的横坐标,通过象限内点的坐标特点求解即可.15.【答案】解:令 0y = , 则 ()()2121=0m x m x -+--解关于 x 的方程得 11x =- , 211x m =- 设 ()10A -, , 1(01B m -,) ∵2AB =∴(10B ,) 或 (30B -,) ∴111m =- 或 131m =-- 解得 12m = , 223m = ,经检验 12m = , 223m = 是分式方程的根. ∴m 的值为2或23. 【解析】【分析】令y=0,求关于x 的一元二次方程(m-1)x 2+(m-2)x-1=0的解,即为点A 、B 的横坐标,再根据AB=2求得m 的值即可.16.【答案】解:y=x 2+4x ﹣5=(x+2)2﹣9,则二次函数y=x 2+4x ﹣5的最小值为﹣9【解析】【分析】直接利用配方法得出二次函数顶点式,进而得出二次函数最值. 17.【答案】解:列表得:x ﹣2 -1 0 1 2 y=2x 2 8 2 0 2 8 y=2x 2+193139【解析】【分析】利用二次函数的对称性先列表,再描点,然后用圆滑的曲线连接即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
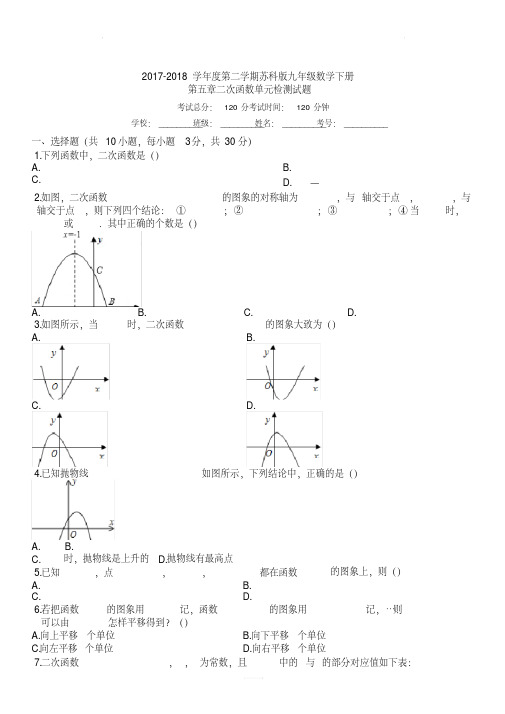
2017-2018学年度第二学期苏科版九年级数学下册
第五章 二次函数 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
1.下列函数中,二次函数是( )
A. B. C. D.
2.如图,二次函数的图象的对称轴为,与轴交于点,,与轴交于点,则下列四个结论:①;②;③;④当时,或.其中正确的个数是( )
A. B. C.
D.
3.如图所示,当时,二次函数的图象大致为( )
A.
B.
C.
D. 4.已知抛物线如图所示,下列结论中,正确的是( )
A. B.
C.时,抛物线是上升的
D.抛物线有最高点
5.已知,点,,都在函数的图象上,则( )
A. B.
C. D.
6.若把函数的图象用记,函数的图象用记,…则可以由怎样平移得到?( )
A.向上平移个单位
B.向下平移个单位
C.向左平移个单位
D.向右平移个单位
7.二次函数,,为常数,且中的与的部分对应值如下表:
;当时,的值随值的增大而减小.是方程的一个根;当时,.
其中正确的个数为()
A.个
B.个
C.个
D.个
8.若二次函数的图象经过原点,则的值必为()
A.或
B.
C.
D.
9.抛物线的图象如图,则下列结论:①;②;③;④.其中正确的结论是()
A.①②
B.②③
C.②④
D.③④
10.如图,在中,,,,动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,
那么经过()秒,四边形的面积最小.
A. B. C. D.
二、填空题(共 10 小题,每小题 3 分,共 30 分)
11.抛物线的顶点是,它与轴交于,两点,它们的横坐标是方程的两根,则
________.
12.设,当取何值时最小,最小是多少?当时,________,当时,的范围是________,当时,的范围是________.
13.如图的一座拱桥,当水面宽为时,桥洞顶部离水面,已知桥洞的拱形是抛物线,以水平方向为轴,建立平面直角坐标系,若选取点为坐标原点时的抛物线
解析式是,则选取点为坐标原点时的抛物线解析式是________.
14.已知二次函数的图象过点,并且,试写出一个满足条件的函数的表达式
________.
15.已知抛物线经过点,,,则该抛物线上纵坐标为的另一点的坐标是________.
16.将二次函数解析式配方成的形式为________.
17.若抛物线过原点,则该抛物线与轴的另一个交点坐标为________.
18.若抛物线与轴只有一个交点,且过点,,则________.
19.公路上行驶的汽车急刹车时的行驶路程与时间的函数关系式为,当遇到紧急
情况时,司机急刹车,但由于惯性汽车要滑行________才能停下来.
20.如图,在平面直角坐标系中,过、两点的抛物线交轴于点,其顶点为点,设
的面积为,的面积为.小芳经探究发现:是一个定值.则这个定值为________.
三、解答题(共 6 小题,每小题 10 分,共 60 分)
21.已知抛物线.
求证:无论为任何实数,抛物线与轴总有两个交点;
若抛物线对称轴,且反比例函数的图象与抛物线在第一象限内的交点的横坐标为,且满足,求的取值范围.
22.我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场
根据民众健康需要,代理销售某种家用空气净化器,其进价是元/台.经过市场
销售后发现:在一个月内,当售价是元/台时,可售出台,且售价每降低元,就
可多售出台.若供货商规定这种空气净化器售价不能低于元/台,代理销售商每
月要完成不低于台的销售任务.
试确定月销售量(台)与售价(元/台)之间的函数关系式;
求售价的范围;
当售价(元/台)定为多少时,这种空气净化器所获得的利润能达到元?
23.某超市经销一种销售成本为元的商品,据超市调查发现,如果按每件元销售,一周能销售件,若销售单价每涨元,每周销售减少件,设销售价为每件元,一
周的销售量为件.
求与的函数关系式.
设该超市一周的销售利润为元,求的最大值.
24.已知,如图,二次函数的图象与轴交于,两点,与轴交于点,且经过点
求该抛物线的解析式;
求该抛物线的顶点坐标和对称轴.
求的面积.
25.如图,有长为米的篱笆,一面利用墙(墙的最大可用长度为米),围成一个长方形的花圃.设花圃的宽为米,面积为平方米.
求与的函数关系式;写出自变量的取值范围.
怎样围才能使长方形花圃的面积最大?最大值为多少?
26.如图,在中,,,,点从点出发,以的速度沿运动;同时,点从点出发,以的速度沿运动.当点到达点时,、两点同时停止运动.
试写出的面积与动点运动时间之间函数表达式;
运动时间为何值时,的面积最大?最大值为多少?
答案
1.B
2.C
3.B
4.D
5.C
6.D
7.B
8.B
9.C
10.C
11.
12.,
13.
14.
15.
16.
17.
18.
19.
20.
21.证明:令,则,∴,
∴不论为任何实数,都有,即.
∴不论为任何实数,抛物线与轴总有两个交点.解:∵抛物线的对称轴为,
又∵抛物线对称轴,∴,解得:,
∴抛物线的解析式为;
当时,
对于,随着的增大而增大,
对于,随着的增大而减小.
所以当时,由反比例函数图象在二次函数图象上方,得:,解得:.
当时,由二次函数图象在反比例函数图象上方,得:,
解得:.
所以的取值范围为.
22.解:根据题中条件销售价每降低元,月销售量就可多售出台,
则月销售量(台)与售价(元/台)之间的函数关系式:,
化简得:;根据供货商规定这种空气净化器售价不能低于元/台,代理销售商每月要完成不低于台,
则,
解得:.
所以与之间的函数关系式为:;设这种空气净化器所获得的利润为,,
把代入得,
解得,
∵在内,
∴当时,这种空气净化器所获得的利润能达到为,
即售价定为元/台时,商场每月销售这种空气净化器所获得的利润是元.
23.解:根据题意,得:
,
即;
,
∵,
∴当时,取得最大值,最大值为元.
24.解:∵二次函数的图象经过点、,
∴,
解这个方程组,得,
∴该二次函数的解析式是;,
∴顶点坐标是;
对称轴是;∵二次函数的图象与轴交于,两点,
∴,
解这个方程得:,,
即二次函数与轴的两个交点的坐标为,.
∴的面积.
25.解:设花圃的宽为米,则长米.
由矩形的面积公式可知:,
∴.
∵墙的最大可用长度为米,
∴.
解得:.∵,,
∴.
∵,,
∴随的增大而减小.
∵当时,即长为米,宽为米时面积最大,∴长方形花圃的最大面积平方米.
26.解:由题意得秒时,,,
;,
故时,.。
