数列求和裂项相消法
高中数学复习-数列求和-裂项相消法

裂项相消法求和把数列的通项拆成两项之差、正负相消剩下首尾若干项。
1、 特别是对于⎭⎬⎫⎩⎨⎧+1n n a a c ,其中{}n a 是各项均不为0的等差数列,通常用裂项相消法,即利用1+n n a a c =⎪⎪⎭⎫⎝⎛-+111n na a d c ,其中()n n a a d -=+1 2、 常见拆项:111)1(1+-=+n n n n)121121(21)12)(12(1+--=+-n n n n])2)(1(1)1(1[21)2)(1(1++-+=++n n n n n n n!)!1(!n n n n -+=⋅)!1(1!1)!1(+-=+n n n n例1 求数列1{}(1)n n +的前n 和n S .例2 求数列1{}(2)n n +的前n 和n S .例3 求数列1{}(1)(2)n n n ++的前n 和n S .例4 求数列⋅⋅⋅++⋅⋅⋅++,11,,321,211n n 的前n 项和.例5:求数列311⨯,421⨯,531⨯,…,)2(1+n n ,…的前n 项和S例6、 求和)12)(12()2(534312222+-++⋅+⋅=n n n S n一、累加法1.适用于:1()n n a a f n +=+ ----------这是广义的等差数列 累加法是最基本的二个方法之一。
2.若1()n n a a f n +-=(2)n ≥,则21321(1)(2) ()n n a a f a a f a a f n +-=-=-=两边分别相加得 111()nn k a a f n +=-=∑例1 已知数列{}n a 满足11211n n a a n a +=++=,,求数列{}n a 的通项公式。
解:由121n n a a n +=++得121n n a a n +-=+则112322112()()()()[2(1)1][2(2)1](221)(211)12[(1)(2)21](1)1(1)2(1)12(1)(1)1n n n n n a a a a a a a a a a n n n n n n nn n n n ---=-+-++-+-+=-++-+++⨯++⨯++=-+-++++-+-=+-+=-++= 所以数列{}n a 的通项公式为2n a n =。
裂项相消法课件(微课堂)

寻找相邻项
在分式中寻找相邻的项,特别是那些 具有相反符号的项,它们是裂项相消 的关键。
裂项相消法的注意事项
验证因式
在应用裂项相消法之前,要确保 分母中的因式是正确的。错误的
因式会导致后续计算出错。
保持代数恒等性
在应用裂项相消法时,要确保等式 的两边在经过变换后仍然保持恒等, 即等式的两边在变换后具有相同的 值。
3
分数裂项相消法的练习题
如求$frac{1}{2} + frac{1}{6} + frac{1}{12} + frac{1}{20} + ldots$的和,可以通过裂项相消法 快速得出结果。
代数表达式的裂项相消法练习
代数表达式裂项相消法的原理
将代数表达式拆分成多个部分,使得在求和或求积的过程中某些项相互抵消,简化计算过 程。
消法快速得出结果。
06Biblioteka 总结与展望裂项相消法的总结
裂项相消法是一种重要的数学方 法,主要用于解决数列求和问题。
它通过将一个数列拆分成若干个 子数列,然后利用相邻子数列的 相消性质,简化了数列求和的过
程。
裂项相消法在数学中有着广泛的 应用,不仅在数列求和中有用, 还可以用于解决一些组合数学问
题。
裂项相消法的应用前景与展望
02
裂项相消法的原理
分数的裂项
01 分数裂项法
将一个分数拆分成两个或多个分数的和或差,以 便于计算。
02 常见裂项形式
如$frac{1}{n(n+1)}$可以拆分为$frac{1}{n}frac{1}{n+1}$。
03 裂项技巧
根据分数的分子和分母特点,选择合适的拆分方 式,简化计算。
数列裂项相消知识点

数列裂项相消是一种常用的数列求和技巧,可以帮助我们简化数列求和的过程。
在本文中,我将为大家介绍数列裂项相消的基本原理和应用方法。
一、数列裂项相消的基本原理在求和过程中,我们经常会遇到连续数列,即数列中的元素相差固定的值。
假设我们有一个连续数列{a, a+d, a+2d, a+3d, …},其中a为首项,d为公差。
如果我们将这个数列从头和从尾开始相加,会发现很多项会相消掉,最后只剩下首项和尾项。
二、数列裂项相消的应用方法假设我们要求解连续数列{1, 3, 5, 7, 9, 11, 13, 15}的和。
我们可以使用数列裂项相消的方法来简化求和过程。
首先,我们可以将这个数列分为两部分:{1, 3, 5, 7}和{9, 11, 13, 15}。
接下来,我们将这两个数列从头和从尾开始相加:1 + 15 = 16 3 + 13 = 16 5 + 11 = 16 7 + 9 = 16可以发现,这四组数的和都是16。
而在原始数列中,这四组数分别位于数列的首项和尾项,所以它们的和也等于数列的和。
所以,我们只需要计算数列的首项和尾项,然后将它们相加,即可得到数列的和。
在这个例子中,首项为1,尾项为15,所以数列的和为1 + 15 = 16。
三、数列裂项相消的推广数列裂项相消不仅适用于连续数列,还可以推广到其他类型的数列。
例如,对于等差数列{a, a+d, a+2d, a+3d, …},我们可以将它裂为两部分:{a, a+d, a+2d, …}和{a+3d, a+4d, a+5d, …}然后将这两个数列从头和从尾开始相加,最后只剩下首项和尾项。
对于等比数列{a, ar, ar^2, ar^3, …},同样可以使用数列裂项相消的方法来简化求和过程。
四、数列裂项相消的优势数列裂项相消的方法在求和过程中可以大大简化计算,特别是对于长数列来说。
通过将数列分为两部分,并从头和从尾开始相加,我们可以消除大部分中间项,只保留首项和尾项,从而大幅度减少计算量。
数列求和——裂项相消法

————裂项相消法
2015全国I卷节选:
若an1
2n
1, 令bn
1 an an 1
, 求{bn}的前n项和Tn。
裂项求和法:
将数列的通项分解成两项或多项的差,使
数列中的项出现有规律的抵消项,只剩下首 尾若干项。
一般有两种类型:
类型一:an
k f (n) f (n c)
A[ 1 f (n)
1[ 1
1
]
n(n 1)(n 2) 2 n(n 1) (n 2)(n 1)
(an
(a 1)an b)(an1
b)
(an
an1 an b)(an1
b)
1 (an b)
1 (an1 b)
类型二:
通过有理化、对数的运算法则、公式的变形、阶乘和组合数
2n Sn
, 求证:T1 T2 L
Tn
3 2
练习:步步高P93例3及跟踪训练3
课堂小结:
1、分解与组合思想在数列求和中的应用。 2、裂项相消常用于方式和根式求和。 可以用通项裂解,也可以利用首项裂解, 甚至可以利用待定系数法去完成裂开通项
(1)应注意抵消后并不一定只剩下第一项和最后一 项,也有可能前面剩多项,后面也剩多项,
(2)再就是将通项公式裂项后,有时候需要调整前 面的系数,使裂开的两项之差和系数之积与原通 项公式相等.
变式:若数列an的前n项和为Sn满足:
Sn
4 3
an
1 3
•
2n1
2 3
(1)求an
(2)设Tn
数列求和裂项相消法公式

数列求和裂项相消法公式
数列裂项相消公式:1/[n(n+1)]=(1/n)-[1/(n+1)]。
裂项是指这是分解与组合思想在数列求和中的具体应用。
是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的。
通项分解(裂项)倍数的关系。
通常用于代数,分数,有时候也用于整数。
公式,在数学、物理学、化学、生物学等自然科学中用数学符号表示几个量之间关系的式子。
具有普遍性,适合于同类关系的所有问题。
在数理逻辑中,公式是表达命题的形式语法对象,除了这个命题可能依赖于这个公式的自由变量的值之外。
数列之裂项相消求和

=1
3
1(1- )
=39
1-
⇒a1=3,所以 an=3n.
(2)由已知得 bn=log332n+1=2n+1,所以 Tn=3+5+…+(2n+1)=n(n+2),
1
=
=
1
=
1 1
( +2) 2
1 1 1
-
2 1 3
-
1
+2
1
1
1
,所以 ∑ = + + +…+
1
=1
1 1 1
1 1 1
1 1
2 2 4
项和
.
解析 (1)因为 , 9 为函数 () = ( − 2)( − 99) 的两个零点且
(−1)
1+
2
= 2, 9 = 99 .又因为 =
= 3 ,所以数列 {
( − 1) = 2 + 1 .
1
(2)因为
所以
1
(
2
=
=
1
(
2
,所以 9
9×8
1+ 2
< 9 ,所以
× 2 = 99 ,解得
(2n+1)
1
1
-
1
1
解析∵an=
= 2n-1 2n+1 ,
(2n-1)
(2n+1) 2
1
1-
1
1
n
1
1
1 1
1
2n+1 =
∴Sn= [(1- )+( - )+…+(
-
)]=
.
2
裂项相消法公式大全

裂项相消法公式大全
裂项相消法是一种数学方法,用于解决等差数列、等比数列以及无理数列的求和问题。
该方法的基本思想是将等差数列、等比数列以及无理数列的每一项分别裂项,然后将裂项相消,从而得到等差数列、等比数列以及无理数列的和。
以下是裂项相消法的一些公式:
1. 等差数列求和公式:
Sn = n * (a1 + an) / 2
其中,n 是数列的长度,a1 是数列的首项,an 是数列的最后一项。
2. 等比数列求和公式:
Sn = (n/2) * (a1 * an) / (an + a1)
其中,n 是数列的长度,a1 是数列的首项,an 是数列的最后一项。
3. 无理数列求和公式:
对于无理数列,可以将每一项裂项,然后相消。
例如,对于无理数列π*(n+1)/n,可以将π*(n+1)/n 裂项为π/n 和 (n+1)*π/n,然后将两项相消。
4. 等差数列裂项公式:
a[n+1] - a[n] = (n+1-n)*a1
其中,a[n+1] 是数列的第 n+1 项,a[n] 是数列的第 n 项,n 是数列的长度。
5. 等比数列裂项公式:
a[n+1]/a[n] = (a[n]/a[n-1])*(a[n-1]/a[n])
其中,a[n+1] 是数列的第 n+1 项,a[n] 是数列的第 n 项,n 是数列的长度。
6. 无理数列裂项公式:
π*(n+1)/n - π/n = (n+1-n)*π
其中,π*(n+1)/n 是数列的第 n+1 项,π/n 是数列的第 n 项,n 是数列的长度。
以上是裂项相消法的一些公式,可以根据实际需要选择合适的公式进行求解。
数列的求和(裂项相消法)
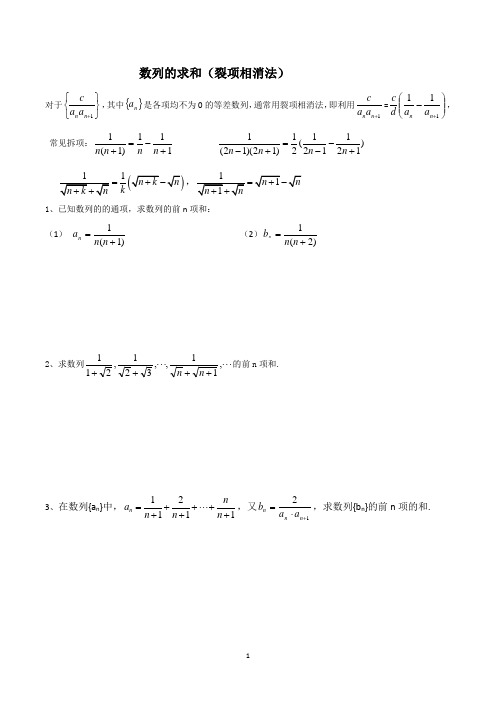
数列的求和(裂项相消法)对于⎭⎬⎫⎩⎨⎧+1n n a a c ,其中{}n a 是各项均不为0的等差数列,通常用裂项相消法,即利用1+n n a a c =⎪⎪⎭⎫⎝⎛-+111n n a a d c , 常见拆项:111)1(1+-=+n n n n)121121(21)12)(12(1+--=+-n n n n1k==1、已知数列的的通项,求数列的前n 项和: (1) )1(1+=n n a n (2))2(1+=n n b n2、求数列⋅⋅⋅++⋅⋅⋅++,11,,321,211n n 的前n 项和.3、在数列{a n }中,11211++⋅⋅⋅++++=n nn n a n ,又12+⋅=n n n a a b ,求数列{b n }的前n 项的和.4、等比数列{a n}的各项均为正数,且2a1+3a2=1,a32=9a2a6,(1)求数列{an}的通项公式;(2)设bn =log3a1+log3a2+…+log3an,求数列{}的前n项和.5、正项数列{an }满足﹣(2n﹣1)an﹣2n=0.(1)求数列{an }的通项公式an;(2)令bn=,求数列{bn}的前n项和Tn.6、已知等差数列{an }满足:a3=7,a5+a7=26.{an}的前n项和为Sn.(1)求an 及Sn;(2)令(n∈N*),求数列{bn}的前n项和Tn.7. 已知数列{}n a 的前n 项和为n S ,点),(n s n n 在直线21121+=x y 上,数列{}n b 满足0212=+-++n n n b b b ,()*N n ∈,113=b,且其前9项和为153.(1)求数列{}n a ,{}n b 的通项公式; (2)设)12)(112(3--=n n n b a c ,求数列{}n c 前n 项的和n T .8、已知等差数列{a n }的前n 项和S n 满足5,053-==S S (1)求{a n }的通项公式; (2)求数列21211n n a a -+⎧⎫⎨⎬⎩⎭的前n 项和.9、S n 为数列{a n }的前n 项和.已知a n >0,(Ⅰ)求{a n }的通项公式: (Ⅱ)设 ,求数列}的前n 项和10、已知公差不为零的等差数列{}n a 中,37a =,且1413,,a a a 成等比数列. (1)求数列{}n a 的通项公式; (2)令211n n b a =-(n N *∈),求数列{}n b 的前n 项和n S .11、已知各项均为正数的等比数列{}n a 的首项12a =,n S 为其前n 项和,且312253S S S =+. (1)求数列{}n a 的通项公式; (2)设2log n n b a =,11n n n c b b +=,记数列{}n c 的前n 项和n T ,求4n Tn +的最大值.12. 已知数列{}n a 的前n 项和为n S ,且22n n S a =-,(1,2,3)n =⋅⋅⋅;数列{}n b 中,11,b = 点1(,)n n P b b +在直线20x y -+=上.(1)求数列{}n a 和{}n b 的通项公式; (2)设数列12n b +⎧⎫⎨⎬⎩⎭的前n 和为n S ,求12111nS S S +++;答案:1(1)1n n +(2)3111-)4212n n +++(21-;3、81n n +;4、(1)13n n a =(2)21n n S n =-+;5、(1)2n a n =(2)21n n T n =+();6、(1)2+1n a n =22n S n n =+(2)1n n T n =+4();7、(1)5;32n n a n b n =+=+(2)21n n T n =+;8、(1)2-n a n =(2)1-2n nT n=;9、(1)2+1n a n =(2)323)n n T n =+(10、(1)2+1n a n =(2)1)n n S n =+4(;11、、(1)2nn a =(2)1n n T n =+,最大值为19;12、(1)2nn a =;21n b n =-(2)21n nT n =+,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
裂项相消法【1 】
典范例题
(以下n均为正整数)
例1:
这是一道较为简略的裂项相消法化简题,1到2,2到3,3到4,……,n到n+1,都相差1,直接裂项即可.(化成1/1-1/2+1/2-1/3...)
例2:
这是例1的升华题,是将分母稍作变更,标题就不一样了.1到3,3到5,5到7,……,2n-1到2n+1,都相差2,裂项后总体要乘以1/2,如许才可以.
例3:
这是例2的拓展题,此时分母每个因数相差3了,做法一样,裂项后总体要乘以1/3,如许才行.
例4:
这是将例1一般化,此时分母每个因数相差1,裂项后直接相消.
例5:
这是将例3的拓展题,此时分母每个因数相差3,做法一样,裂项后总体要乘以1/3,如许才行.
例6:
这道题易错题,易写成,如许就造成错误,本来是正的,如今是负的.正好相反,这一点多留意.
例7:
这道题易错题,如许就造成错误,本来是正的,如今是负的.正好相反,这一点多留意.。
