相似性和相异性的度量
传统相似度量方法

传统相似度量方法嘿,咱今儿来聊聊传统相似度量方法。
你说这东西就像一把神奇的尺子,能衡量各种事物之间的相似程度呢!想象一下,世界上那么多千奇百怪的东西,要怎么知道它们是不是相似呀?这时候传统相似度量方法就派上用场啦!就好比你要找一个和你兴趣相投的朋友,你得从各种方面去比较,看看是不是有共同话题、爱好啥的,这其实就是一种相似度量呀。
比如说,在数学里,我们常用的距离度量就是一种传统相似度量方法。
就像两点之间的距离,简单直观吧!通过计算这个距离,我们就能判断这两个点是不是离得近,是不是有点相似呢。
这就好像在茫茫人海中,通过一些特征去找到和自己比较近的人一样。
还有啊,在图像处理中,也经常用到相似度量方法呢。
比如两张图片,我们怎么判断它们像不像呢?可以从颜色、形状、纹理这些方面去考量呀。
这就像是分辨两个苹果是不是长得差不多,颜色是不是一样红,形状是不是一样圆。
再说说文本处理。
两篇文章,怎么知道它们主题是不是相似呢?那就要看里面的关键词、语句结构啥的啦。
这和我们判断两个人说话风格像不像有点类似呢。
传统相似度量方法可不只是在这些领域有用哦,在很多其他地方都能看到它的身影呢。
它就像一个默默无闻的小助手,在背后悄悄地帮忙。
你想想看,要是没有这些方法,我们怎么能快速准确地找到相似的东西呢?那岂不是像无头苍蝇一样乱撞啦!而且哦,这些方法还在不断发展和完善呢。
就像我们人一样,会不断学习进步,变得越来越好。
它们也在随着科技的发展,变得越来越厉害,能解决更多更复杂的问题。
总之呢,传统相似度量方法可真是个了不起的东西呀!它让我们的世界变得更加有序,让我们能更好地理解和处理各种事物之间的关系。
你说它是不是很神奇呀?咱可得好好感谢那些发明和研究这些方法的人呢,是他们让我们的生活变得更加方便和有趣啦!。
度量数据的相似性和相异性

13
九、余弦相似度
• 文档用数以千计的属性表示,每个属性记录文档中的一个词或短语的频度
• 词频向量通常很长,而且是稀疏的
• 余弦相似性用于度量两个向量间的距离
14
九、余弦相似度
15
• 正定性:
• 对称性:
• 三角不等式:
8
六、数值属性的相异性度量
• 曼哈顿(城市块)距离:( 1 范数)
• 两点之间的街区距离
• 欧几里得(直线)距离:最流行的距离度量方法( 2 范数)
• 上确界( max 范数、 范数)
• 两个向量任意属性间的最大• 通过规格化方法将秩转换到[0,1]区间
• 用区间标度变量的度量方法进行度量
12
八、混合类型属性的相异性
• 一个数据对象可能包含各种类型的属性
• 把所有属性转换到共同区间(如:[0,1]),加权计算它们的综合相异度
• 当 f 为二值或标称属性时:属性值相等距离为0,不相等为1
• 当 f 为数值属性时:使用数值距离度量方法
• 使用平均绝对偏差计算Z分数比使用标准差更加鲁棒
7
六、数值型数据的距离度量
• 闵可夫斯基距离:一种通用的距离度量方法
• = 1 , 2 , … , 和 = 1 , 2 , … , 是两个p维的数据对象,h 是阶(这样定义的距离
又称为 范数)
• 距离的性质
• 性别是对称属性
• 其余属性是不对称属性
• 设Y和P值为1,其余值为0
6
五、数值型数据的标准化
• Z分数(标准分数)
• 是一个数与平均数的差再除以标准差的过程
• 当原始数值大于平均数时 Z分数为负值;大于平均数时Z分数为正值
数据挖掘第一与第二章概述数据收集讲解学习

2022年3月12日星期六
数据挖掘导论
25
数据集的重要特性
• 维度(Dimensionality) – 数据集的维度是数据集中的对象具有的属性数目 – 维灾难(Curse of Dimensionality) – 维归约(dimensionality reduction)
• 稀疏性(Sparsity) – 具有非对称特征的数据集,一个对象的大部分属性上的值都为 0 – 只存储和处理非零值
数据
– 数据中的联系
• 如时间和空间的自相关性、图的连通性、半结构化文本和XML文 档中元素之间的父子联系
2022年3月12日星期六
数据挖掘导论
9
挑战4
• 数据的所有权与分布
– 数据地理上分布在属于多个机构的资源中
• 需要开发分布式数据挖掘技术
– 分布式数据挖掘算法面临的主要挑战包括
• (1) 如何降低执行分布式计算所需的通信量? • (2) 如何有效地统一从多个资源得到的数据挖掘结果? • (3) 如何处理数据安全性问题?
Single 70K
No
Married 120K No
Divorced 95K
Yes
Married 60K
No
Divorced 220K No
Single 85K
Yes
Married 75K
No
Single 90K
Yes
2022年3月12日星期六
数据挖掘导论
28
记录数据: 数据矩阵
• 如果一个数据集族中所有数据对象都具有相同的数 值属性值,则数据对象可以看做多维空间中的点, 每个维代表对象的一个不同属性。
2.1 数据类型
• 数据集的不同表现在很多方面。例如, 某些数据集包含时间序列或者彼此之间具 有明显联系的对象。毫不奇怪,数据的类 型决定我们应使用何种工具和技术来分析 数据。此外,数据挖掘研究常常是为了适 应新的应用领域和新的数据类型的需要而 展开的。
数据属性与其邻近性度量
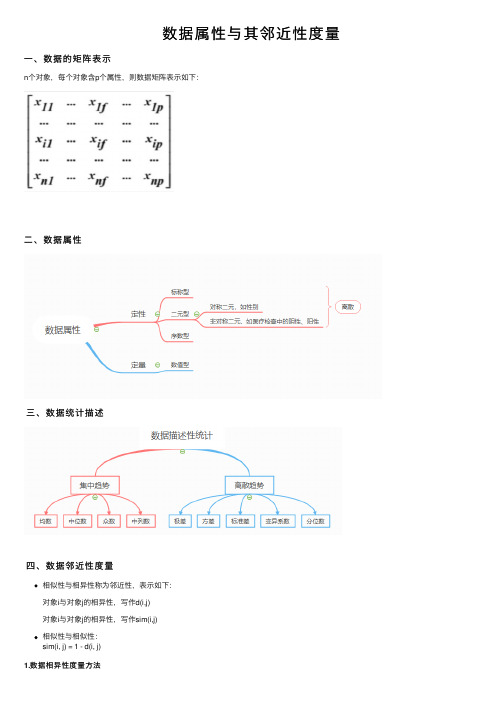
数据属性与其邻近性度量⼀、数据的矩阵表⽰
n个对象,每个对象含p个属性,则数据矩阵表⽰如下:
⼆、数据属性
三、数据统计描述
四、数据邻近性度量
相似性与相异性称为邻近性,表⽰如下:
对象i与对象j的相异性,写作d(i,j)
对象i与对象j的相异性,写作sim(i,j)
相似性与相似性:
sim(i, j) = 1 - d(i, j)
1.数据相异性度量⽅法
标称属性采⽤列联表(类似混淆矩阵)计算度量
q,t 描述了对象i与对象j的相同点;r,s 描述了对象i与对象j的不同点,则相异性计算,
d(i, j) = ( r + s ) / ( q + r + s + t ) ,对于⾮对称的⼆元属性的计算需要去除 t 值。
数值属性根据距离度量两者间的相似性,⽐如采⽤欧⽒距离、曼哈顿距离
序数属性需要⽤排位数代替,标准化处理后采⽤距离度量的⽅法
混合属性则需要获得单个属性的相异性矩阵后指定⼀个权值,乘以各属性的相异性值,然后取计算的平均值作为整体相异性值。
2. 余弦相似性
计算公式:
特性:
余弦相似性,关注两个⽂档共有的属性出现的频率,忽略与0匹配的度量。
sim(x, y)越接近1,则两者间越相似
适⽤情形:
适⽤于稀疏结构(矩阵中有太多0值),⽐如词频统计、⽂本⽂档聚类、信息检索、⽣物学分类等。
数据挖掘知识点归纳

知识点一数据仓库1.数据仓库是一个从多个数据源收集的信息存储库,存放在一致的模式下,并且通常驻留在单个站点上。
2.数据仓库通过数据清理、数据变换、数据集成、数据装入和定期数据刷新来构造。
3.数据仓库围绕主题组织4.数据仓库基于历史数据提供消息,是汇总的。
5.数据仓库用称作数据立方体的多维数据结构建模,每一个维对应于模式中的一个或者一组属性,每一个单元存放某种聚集的度量值6.数据立方体提供数据的多维视图,并允许预计算和快速访问汇总数据7.提供提供多维数据视图和汇总数据的预计算,数据仓库非常适合联机分析处理,允许在不同的抽象层提供数据,这种操作适合不同的用户角度8.OLAP例子包括下钻和上卷,允许用户在不同的汇总级别上观察数据9.多维数据挖掘又叫做探索式多维数据挖掘OLAP风格在多维空间进行数据挖掘,允许在各种粒度进行多维组合探查,因此更有可能代表知识的有趣模式。
知识点二可以挖掘什么数据1.大量的数据挖掘功能,包括特征化和区分、频繁模式、关联和相关性分析挖掘、分类和回归、聚类分析、离群点分析2.数据挖掘功能用于指定数据挖掘任务发现的模式,分为描述性和预测性3.描述性挖掘任务刻画目标数据中数据的一般性质4.预测性挖掘任务在当前数据上进行归纳,以便做出预测5.数据可以与类或概念相关联6.用汇总、简洁、精确的表达描述类和概念,称为类/概念描述7.描述的方法有数据特征化(针对目标类)、数据区分(针对对比类)、数据特征化和区分8.数据特征化用来查询用户指定的数据,上卷操作用来执行用户控制的、沿着指定维的数据汇总。
面向属性的归纳技术可以用来进行数据的泛化和特征化,而不必与用户交互。
形式有饼图、条图、曲线、多维数据立方体和包括交叉表在内的多维表。
结果描述可以用广义关系或者规则(也叫特征规则)提供。
9.用规则表示的区分描述叫做区分规则。
10.数据频繁出现的模式叫做频繁模式,类型包括频繁项集、频繁子项集(又叫频繁序列)、频繁子结构。
09 相异性度量 (1)

因此: d(A,C)<=d(A,B)+d(B,C)
11
第九讲 结束
数据挖掘
12
其中:A和B是集合,A-B是集合差 证明: (1) d(x,y)>=0
if A=B, then A-B=B-A=空集,因此 d(x,y)=0 (2) d(A,B)=size(A-B)+size(B-A)=size(B-A)+size(A-B)=d(B,A) (3) size(A∩B)<=size(B) 并且 size(B∩C)<=size(B)
x
y
p1
0
2
p2
2
0
ቤተ መጻሕፍቲ ባይዱp3
3
1
p4
5
1
p1
p2
p3
p4
p1
0 2.828 3.162 5.099
p2
2.828
0 1.414 3.162
p3
3.162 1.414
0
2
p4
5.099 3.162
2
0
5
数据对象的相异度:闵可夫斯基距离
• 欧式距离可用闵可夫斯基距离推广
d (x, y) n | xk yk |r 1/r
• 邻近度 :相似度和相异度的统称,是两个对象对应属性简单邻近度 的函数
数据挖掘
2
相似性和相异性 --变换
• 相似性和相异性间的转换 • 变换的目的
【数据挖掘】相似性和相异性度量

【数据挖掘】相似性和相异性度量⼀、基础概念1. 相似度(similarity): 两个对象相似程度的数值度量,通常相似度是⾮负的,在[0,1]之间取值相异度(disimilarity): 两个对象差异程度的数值度量,通常也是⾮负的,在[0,1]之间取值,0到∞也很常见我们使⽤邻近度(proximity)表⽰相似度或者相异度: 常见的邻近度有:相关,欧⼏⾥得距离,Jaccard相似性,余弦相似性. 前两者适⽤于时间序列这样的稠密数据,后两者适⽤于⽂本这样的稀疏数据.2. 区间变换: d' = (d-dmin_d)/(max_d - min_d)3. 具有以下三个性质的测度称为度量(metric)(1) ⾮负性(2) 对称性(3) 三⾓不等式⼆、常见相异度和相似性度量函数1. 距离Minkowski distanced(x,y)=(N ∑k=1|x k−y k|r)1/r 1-normal distance/Manhattan distance: ∑n i=1|x i−y i|2-normal distance/Euclidean distance: (∑n i=1|x i−y i|2)1/2p-normal distance: d(x,y)=(∑N k=1|x k−y k|p)1/p∞-nromal distance/Chebyshev distance: lim p→∞(∑N k=1|x k−y k|p)1/p2. 简单匹配系数(Simple Matching Coefficient): SMC = 值匹配属性个数/属性个数 =f11+f00f01+f10+f11+f003. Jaccard系数 J = 匹配个数/属性个数 =f11f01+f10+f114. 余弦相似度cos(x,y)=x⋅y||x||||y||(⽂档相似度中最常⽤的度量)5. ⼴义Jaccard系数/Tanimoto系数6. 相关性Pearson's correlation: corr(x,y)=cov(x,y)std(x)∗std(y)=s x ys x s y7. Bregman散度D(x,y)=ϕ(x)−ϕ(y)<Δϕ(y),(x−y)> Processing math: 100%。
相似的判定方法

相似的判定方法相似的判定方法在各个领域都有着重要的应用,比如在图像识别、文本相似度计算、音乐推荐系统等方面都需要对相似性进行准确的判定。
本文将介绍几种常见的相似性判定方法,以及它们的应用场景和特点。
一、余弦相似度。
余弦相似度是一种常用的相似性度量方法,它可以用来衡量两个向量方向的差异程度。
在文本相似度计算中,可以将每个文档表示为一个向量,然后通过计算这两个向量的余弦值来衡量它们的相似度。
余弦相似度的计算公式如下:cosine_similarity = (A·B) / (||A|| ||B||)。
其中,A和B分别表示两个文档的向量表示,A·B表示这两个向量的点积,||A||和||B||分别表示这两个向量的模。
余弦相似度的取值范围在[-1,1]之间,值越接近1表示相似度越高。
二、Jaccard相似系数。
Jaccard相似系数是一种用来衡量两个集合相似度的方法,它可以用来计算两个集合的交集与并集的比值。
在文本相似度计算中,可以将每个文档表示为一个词的集合,然后通过计算这两个集合的Jaccard相似系数来衡量它们的相似度。
Jaccard相似系数的计算公式如下:J(A,B) = |A∩B| / |A∪B|。
其中,A和B分别表示两个文档的词集合,|A∩B|表示这两个集合的交集的大小,|A∪B|表示这两个集合的并集的大小。
Jaccard相似系数的取值范围在[0,1]之间,值越接近1表示相似度越高。
三、编辑距离。
编辑距离是一种用来衡量两个字符串相似度的方法,它可以用来计算将一个字符串转换成另一个字符串所需要的最少操作次数。
在文本相似度计算中,可以通过计算两个文档之间的编辑距离来衡量它们的相似度。
常见的编辑操作包括插入、删除、替换等。
编辑距离越小表示两个字符串的相似度越高。
四、应用场景。
余弦相似度常用于文本相似度计算、推荐系统中的用户相似度计算等领域。
Jaccard相似系数常用于集合相似度计算、社交网络中的用户相似度计算等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似性和相异性的度量相似性和相异性是重要的概念,因为它们被许多数据挖掘技术所使用,如聚类、最近邻分类和异常检测等。
在许多情况下,一旦计算出相似性或相异性,就不再需要原始数据了。
这种方法可以看作将数据变换到相似性(相异性)空间,然后进行分析。
首先,我们讨论基本要素--相似性和相异性的高层定义,并讨论它们之间的联系。
为方便起见,我们使用术语邻近度(proximity)表示相似性或相异性。
由于两个对象之间的邻近度是两个对象对应属性之间的邻近度的函数,因此我们首先介绍如何度量仅包含一个简单属性的对象之间的邻近度,然后考虑具有多个属性的对象的邻近度度量。
这包括相关和欧几里得距离度量,以及Jaccard和余弦相似性度量。
前二者适用于时间序列这样的稠密数据或二维点,后二者适用于像文档这样的稀疏数据。
接下来,我们考虑与邻近度度量相关的若干重要问题。
本节最后简略讨论如何选择正确的邻近度度量。
1)基础1. 定义两个对象之间的相似度(similarity)的非正式定义是这两个对象相似程度的数值度量。
因而,两个对象越相似,它们的相似度就越高。
通常,相似度是非负的,并常常在0(不相似)和1(完全相似)之间取值。
两个对象之间的相异度(dissimilarity)是这两个对象差异程度的数值度量。
对象越类似,它们的相异度就越低。
通常,术语距离(distance)用作相异度的同义词,正如我们将介绍的,距离常常用来表示特定类型的相异度。
有时,相异度在区间[0, 1]中取值,但是相异度在0和之间取值也很常见。
2. 变换通常使用变换把相似度转换成相异度或相反,或者把邻近度变换到一个特定区间,如[0, 1]。
例如,我们可能有相似度,其值域从1到10,但是我们打算使用的特定算法或软件包只能处理相异度,或只能处理[0, 1]区间的相似度。
之所以在这里讨论这些问题,是因为在稍后讨论邻近度时,我们将使用这种变换。
此外,这些问题相对独立于特定的邻近度度量。
通常,邻近度度量(特别是相似度)被定义为或变换到区间[0, 1]中的值。
这样做的动机是使用一种适当的尺度,由邻近度的值表明两个对象之间的相似(或相异)程度。
这种变换通常是比较直截了当的。
例如,如果对象之间的相似度在1(一点也不相似)和10(完全相似)之间变化,则我们可以使用如下变换将它变换到[0, 1]区间:s' = (s-1)/9,其中s和s'分别是相似度的原值和新值。
一般来说,相似度到[0, 1]区间的变换由如下表达式给出:s'=(s-min_s) / (max_s - min_s),其中max_s和min_s分别是相似度的最大值和最小值。
类似地,具有有限值域的相异度也能用d' = (d - min_d) / (max_d - min_d) 映射到[0, 1]区间。
然而,将邻近度映射到[0, 1]区间可能非常复杂。
例如,如果邻近度度量原来在区间[0 1000]上取值,则需要使用非线性变换,并且在新的尺度上,值之间不再具有相同的联系。
对于从0变化到1000的相异度度量,考虑变换d' = d / (1 + d),相异度0、、2、10、100和1000分别被变换到0、、、、和。
在原来相异性尺度上较大的值被压缩到1附近,但是否希望如此则取决于应用。
另一个问题是邻近度度量的含义可能会被改变。
例如,相关性(稍后讨论)是一种相似性度量,在区间[ -1, 1]上取值,通过取绝对值将这些值映射到[0, 1]区间丢失了符号信息,而对于某些应用,符号信息可能是重要的。
将相似度变换成相异度或相反也是比较直截了当的,尽管我们可能再次面临保持度量的含义问题和将线性尺度改变成非线性尺度的问题。
如果相似度(相异度)落在[0, 1]区间,则相异度(相似度)可以定义为d = 1 - s(或s = 1 - d)。
另一种简单的方法是定义相似度为负的相异度(或相反)。
例如,相异度0,1,10和100可以分别变换成相似度0,- 1,- 10和- 100。
负变换产生的相似度结果不必局限于[0, 1]区间,但是,如果希望的话,则可以使用变换s = 1/(d + 1),。
对于变换s = 1/(d + 1),相异度0, 1, 10, 100分别被变换到1, , , ;对于,它们分别被变换到, , , ;对于s =,它们分别被变换到, , , 。
在这里的讨论中,我们关注将相异度变换到相似度。
一般来说,任何单调减函数都可以用来将相异度转换到相似度(或相反)。
当然,在将相似度变换到相异度(或相反),或者在将邻近度的值变换到新的尺度时,也必须考虑一些其他因素。
我们提到过一些问题,涉及保持意义、扰乱标度和数据分析工具的需要,但是肯定还有其他问题。
2) 简单属性之间的相似度和相异度通常,具有若干属性的对象之间的邻近度用单个属性的邻近度的组合来定义,因此我们首先讨论具有单个属性的对象之间的邻近度。
考虑由一个标称属性描述的对象,对于两个这样的对象,相似意味什么呢由于标称属性只携带了对象的相异性信息,因此我们只能说两个对象有相同的值,或者没有。
因而在这种情况下,如果属性值匹配,则相似度定义为1,否则为0;相异度用相反的方法定义:如果属性值匹配,相异度为0,否则为1。
对于具有单个序数属性的对象,情况更为复杂,因为必须考虑序信息。
考虑一个在标度{poor, fair, OK, good, wonderful}上测量产品(例如,糖块)质量的属性。
一个评定为wonderful的产品P1与一个评定为good的产品P2应当比它与一个评定为OK的产品P3更接近。
为了量化这种观察,序数属性的值常常映射到从0或1开始的相继整数,例如,{poor = 0, fair =1, OK = 2, good = 3, wonderful = 4}。
于是,P1与P2之间的相异度d(P1, P2) = 3-2 = 1,或者,如果我们希望相异度在0和1之间取值,d(P1, P2) = (3-2)/4 = ;序数属性的相似度可以定义为s = 1-d。
序数属性相似度(相异度)的这种定义可能使读者感到有点担心,因为这里我们定义了相等的区间,而事实并非如此。
如果根据实际情况,我们应该计算出区间或比率属性。
值fair与good的差真和OK与wonderful的差相同吗可能不相同,但是在实践中,我们的选择是有限的,并且在缺乏更多信息的情况下,这是定义序数属性之间邻近度的标准方法。
对于区间或比率属性,两个对象之间的相异性的自然度量是它们的值之差的绝对值。
例如,我们可能将现在的体重与一年前的体重相比较,说"我重了10磅。
"在这类情况下,相异度通常在0和x之间,而不是在0和1之间取值。
如前所述,区间或比率属性的相似度通常转换成相异度。
表2-7总结了这些讨论。
在该表中,x和y是两个对象,它们具有一个指明类型的属性,d(x, y)和s(x, y)分别是x和y之间的相异度和相似度(分别用d和s表示)。
其他方法也是可能的,但是表中的这些是最常用的。
下面两节介绍更复杂的涉及多个属性的对象之间的邻近性度量:(1)数据对象之间的相异度;(2)数据对象之间的相似度。
这样分节可以更自然地展示使用各种邻近度度量的基本动机。
然而,我们要强调的是使用上述技术,相似度可以变换成相异度,反之亦然。
3) 数据对象之间的相异度本节,我们讨论各种不同类型的相异度。
我们从讨论距离(距离是具有特定性质的相异度)开始,然后给出一些更一般的相异度类型的例子。
距离我们首先给出一些例子,然后使用距离的常见性质更正式地介绍距离。
一维、二维、三维或高维空间中两个点x和y之间的欧几里得距离(Euclidean distance)d由如下熟悉的公式定义:其中,n是维数,而xk和yk分别是x和y的第k个属性值(分量)。
我们用图2-15、表2-8和表2-9解释该公式,它们展示了这个点集、这些点的x和y 坐标以及包含这些点之间距离的距离矩阵(distance matrix)。
公式(2-1)给出的欧几里得距离可以用公式(2-2)的闵可夫斯基距离(Minkowski distance)来推广:其中r是参数。
下面是闵可夫斯基距离的三个最常见的例子。
r = 1,城市街区(也称曼哈顿、出租车、L1范数)距离。
一个常见的例子是汉明距离(Hamming distance),它是两个具有二元属性的对象(即两个二元向量)之间不同的二进制位个数。
r = 2,欧几里得距离(L2范数)。
r =,上确界(Lmax或L 范数)距离。
这是对象属性之间的最大距离。
更注意不要将参数r与维数(属性数)n混淆。
欧几里得距离、曼哈顿距离和上确界距离是对n的所有值(1, 2, 3,...)定义的,并且指定了将每个维(属性)上的差的组合成总距离的不同方法。
表2-10和表2-11分别给出表2-8数据的L1距离和L 距离的邻近度矩阵。
注意,所有的距离矩阵都是对称的,即第ij个表目与第ji个表目相同,距离(如欧几里得距离)具有一些众所周知的性质。
如果d(x, y)是两个点x和y之间的距离,则如下性质成立。
(1) 非负性。
(a) 对于所有x和y,d(x, y)≥0,(b) 仅当x = y时d(x, y) =0。
(2) 对称性。
对于所有x和y,d(x, y) = d(y, x)。
(3) 三角不等式。
对于所有x,y和z,d(x, z) ≤ d(x, y) + d(y, z)。
满足以上三个性质的测度称为度量(metric)。
有些人只对满足这三个性质的相异性度量使用术语距离,但在实践中常常违反这一约定。
这里介绍的三个性质是有用的,数学上也是令人满意的。
此外,如果三角不等式成立,则该性质可以用来提高依赖于距离的技术(包括聚类)的效率。
尽管如此,许多相异度都不满足一个或多个度量性质。
下面我们给出两个这种测度的例子。
例1非度量的相异度:集合差。
基于集合论中定义的两个集合差的概念举例。
设有两个集合A和B,A-B是不在B中的A中元素的集合。
例如,如果A = {1, 2, 3, 4},而B = {2, 3, 4},则A-B = {1},而B-A = 空集。
我们可以将两个集合A和B之间的距离定义为d(A, B) = size(A-B),其中size是一个函数,它返回集合元素的个数。
该距离测度是大于或等于零的整数值,但不满足非负性的第二部分,也不满足对称性,同时还不满足三角不等式。
然而,如果将相异度修改为d(A, B) = size(A-B) + size(B-A),则这些性质都可以成立。
例2非度量的相异度:时间。
这里给出一个更常见的例子,其中相异性测度并非度量,但依然是有用的。
定义时间之间的距离测度如下:例如,d(1PM, 2PM) = 1小时,而d(2PM, 1PM) = 23小时。
