节约里程计算
配送路线优化里程节约法

配送路线优化里程节约法在现代物流配送中,如何优化配送路线以降低成本、提高效率是企业关注的核心问题之一。
里程节约法作为一种实用且有效的方法,为解决这一难题提供了有力的工具。
首先,让我们来理解一下什么是里程节约法。
简单来说,里程节约法是通过比较不同配送路线的里程差异,找出能够节约里程的组合,从而优化配送路线。
想象一下,有两个客户点 A 和 B,分别距离配送中心为 d1 和 d2,两点之间的距离为 d3。
原本单独配送时,总里程为 2×(d1 + d2)。
但如果将这两个点合并在同一次配送中,总里程就变为了 d1 + d2 + d3。
通过这种方式计算出节约的里程,然后对多个客户点进行组合和比较,就能找到最优的配送路线。
那么,里程节约法的优势在哪里呢?其一,它能够显著降低运输成本。
通过减少不必要的里程,节省了燃油、车辆磨损等费用。
其二,提高了配送效率。
优化后的路线可以减少配送时间,提高客户满意度。
其三,有助于合理规划资源。
企业可以根据节约的里程和时间,更精确地安排车辆和人员。
要成功应用里程节约法,需要做好一系列的准备工作。
第一步是收集准确而详细的基础数据,包括客户的位置、需求量、配送中心的位置等。
这些数据的准确性直接影响到后续路线规划的质量。
第二步是对数据进行整理和分析,明确各个客户点之间的相对位置和距离关系。
在实际应用里程节约法时,需要遵循一定的步骤。
首先,计算出每个客户点之间的距离。
然后,根据距离计算出每两个客户点合并配送所能节约的里程。
接下来,按照节约里程的大小进行排序。
从节约里程最大的组合开始,依次考虑是否能够合并配送,同时要注意满足车辆的载重限制、配送时间限制等约束条件。
比如说,有一家配送企业,要为 10 个客户点进行配送。
通过计算和排序,发现客户点 C 和 D 合并配送的节约里程最大。
但在决定合并时,还需要检查车辆的载重是否能够满足 C 和 D 客户的总需求量。
如果满足,就可以将这两个点合并在同一次配送中。
运输的优化求解、运输问题—节约里程法

1、列运输平衡表
列表时要求表内供销平衡,并将运费标入表内空格。
需
供
B1
B2
B3
A1
x11 90 x12 70 x13 100
供应量 200
A2
x21 80 x22 65 x23 80
250
需求量 100 150
200
250
需求量 100 150
200
450
由于上表中有负检验数,故需继续 进行调整,得新运输方案表。
新运输方案2表
需
供
B1
B2
B3
A1
100 90 100 70
100
A2
80 50 65 200 80
需求量 100
150
200
供应量 200 250 450
对新运输方案表进行检验。
新运输方案2检验表
其需量等于总供量与总需量之差,并设其相应运价为0。这
样,就可以用表上作业法求解产大于销的运输问题。
2、销大于产的运输问题 n m
对于销量大于产量,即 bj ai 的运输问题,必
j 1
i 1
然有一些销地不能得到满足,发生缺货,此时引入虚拟供
应点,并设其相应运价为0。这样,就可以用产销平衡的表
上作业法求解销大于产的运输问题。
450
2、建立初始调运方案
采用最小元素法,即在平衡表中挑取运价最小或
较小的供需点格子尽量优先分配的调运方法。
需
供
B1
A1
0 90
B2
B3
供应量
计算题节约里程法
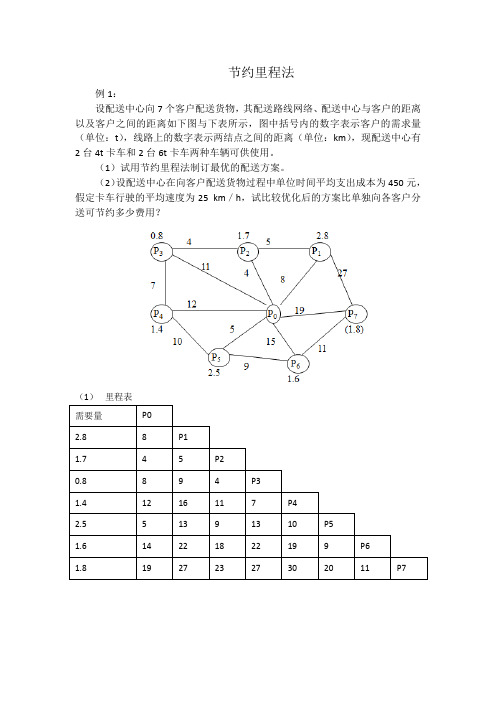
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)里程表需要量P02.8 8 P11.7 4 5 P20.8 8 9 4 P31.4 12 16 11 7 P42.5 5 13 9 13 10 P51.6 14 22 18 22 19 9 P61.8 19 27 23 27 30 20 11 P7(2)节约里程表需要量P02.8 8 P11.7 4 5(7)P20.8 8 9(7)4(8)P31.4 12 16(4)11(5)7(13)P42.5 5 13(0)9(0)13(0)10(7)P51.6 14 22(0)18(0)22(0)19(7)9(10)P61.8 19 27(0)23(0)27(0)30(1)20(4)11(22)P7(3)节约里程数排序序号路线节约里程序号路线节约里程1 P6P722 7 P4P572 P3P413 8 P1P273 P5P610 9 P2P4 54 P2P38 10 P1P4 45 P1P37 11 P5P7 46 P4P67 12 P4P7 1(4)配送路线选择节省的配送时间为节省的费用为:例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
节约里程法

算例:节约里程法以上一个二维码扫描算法算例为例,用节约里程法计算配送线路的安排。
解:① 首先根据上一个二维码扫描算法算例中的距离矩阵表计算出各点间的节约值矩阵表,如表1所示。
表1 节约值矩阵表② 从表1中选出节约值最大值为23,其对应的两个顶点为5、6。
5、6两处的需求量之和为8,未超过一辆车的运输能力14,因此,连接5、6成回路,即0—5—6—0。
再将顶点5与6的节约值赋为0,结果如表2所示。
表2 节约矩阵表计算过程1③ 从表2中再选出节约值最大值为20,其对应的两个顶点为7、8。
7、8两处的需求量之和为7,未超过一辆车的运输能力14,因此,连接7、8成回路,即0—7—8—0。
再将顶点7与8的节约值赋为0,结果如表3所示。
表3 节约矩阵表计算过程2④ 从表3中再选出节约值最大值为16,其对应的两个顶点为5、8或6、8。
如果连接5与8,则上述两条回路合并,其总需求量为15,超过一辆车的运输能力14,因此,5与8不能连接,同样6和8也不能连接,则将顶点5、8和6、8的节约值赋为0,结果如表4所示。
表4 节约矩阵表计算过程3⑤ 从表4中再选出节约值最大值为15,其对应的两个顶点为4、6。
如连接4与6,则形成:0—5—6—4—0回路,其总需求量为11,未超过一辆车的运输能力14,因此,连接4、6成新回路,即0—5—6—4—0。
再将顶点4与6的节约值赋为0,同时,由于顶点6成为回路的中间点,则与顶点6相关的节约值都赋为0。
表示顶点6不可能再与其他点相连,其结果如表5所示。
表5-33 节约矩阵表计算过程4⑥ 按算法步骤迭代运算,直到节约值矩阵表中的值均为0时,迭代结束。
最终的结果为:0—2—3—0,0—5—6—4—0,0—7—8—1—0这三条线路,其运输量分别为9、11、13,总里程数为93。
一般来说,节约里程法可以得到比较好的结果,但此算法也是一种贪婪启发式算法,对于一些特殊的算例,得不到最优解。
上一个二维码中算例的全局最优解是:选择0—1—3—0,0—2—7—8—0,0—5—6—4—0这三条线路,其运输量分别为11、11、11,总里程数为90。
节约里程法应用案例

节约里程法应用案例在当今竞争激烈的商业环境中,物流成本的有效控制对于企业的生存和发展至关重要。
节约里程法作为一种优化配送路线的有效方法,能够显著降低运输成本,提高物流效率。
接下来,让我们通过一个具体的案例来深入了解节约里程法的实际应用。
假设我们有一家位于城市中心的配送中心,需要向位于城市不同区域的五个客户(A、B、C、D、E)配送货物。
每个客户的需求量以及他们之间的距离如下表所示:|客户|需求量(吨)|与配送中心距离(公里)||||||A|5|10||B|8|12||C|3|8||D|6|15||E|4|11||客户|A|B|C|D|E|||||||||A| | 18 | 22 | 25 | 16 ||B| 18 || 10 | 18 | 12 ||C| 22 | 10 || 14 | 9 ||D| 25 | 18 | 14 || 20 ||E| 16 | 12 | 9 | 20 ||首先,我们按照传统的方法,即每个客户单独配送,计算出总运输里程。
配送中心到客户 A 的往返里程为 2×10 = 20 公里。
配送中心到客户 B 的往返里程为 2×12 = 24 公里。
配送中心到客户 C 的往返里程为 2×8 = 16 公里。
配送中心到客户 D 的往返里程为 2×15 = 30 公里。
配送中心到客户 E 的往返里程为 2×11 = 22 公里。
总运输里程为 20 + 24 + 16 + 30 + 22 = 112 公里。
接下来,我们应用节约里程法来优化配送路线。
第一步,计算两两客户之间的节约里程数。
例如,客户 A 和客户 B 之间的节约里程数为:(配送中心到 A 的距离+配送中心到 B 的距离 A 到 B 的距离)× 2 =(10 + 12 18)× 2 = 8 公里。
按照同样的方法,计算出所有两两客户之间的节约里程数,如下表所示:|客户|A|B|C|D|E|||||||||A| | 8 | 6 | 5 | 2 ||B| 8 || 4 | 3 | 4 ||C| 6 | 4 || 2 | 3 ||D| 5 | 3 | 2 || 5 ||E| 2 | 4 | 3 | 5 ||第二步,根据节约里程数的大小对路线进行合并和优化。
【管理资料】节约里程法例题计算汇编

顺序排位
1 2 3 4 4 6 6 6 9 9 11 12
连接线
A- B A- J B- C D- E C- D A- I E- F I- J A- C B- J B- D C- E
节约里程
15 13 11 10 10 9 9 9 8 8 7 6
顺序排位
13 13 13 16 16 16 19 19 21 22 22 22
C
D
B
A 0.32
0.24
路线1 2
E
P 路线2 2
J 0.24
F
G
路线3 2
0.16
0.48
H
0.40
图2 配送路线图
I 0.32
从配送路线图可看出,依次确定的三条配送路线均符合配送中心的约 束条件,需要2t货车3辆,总走行里程为70km,若简单地每个连锁分店 送货,需要2t货车10辆,走行总里程148km。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
连接线
F- G G- H H- I B- I A- D F- H B- E D- F G- I C- J E- G F- I
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
第四步:根据节约里程排序表和配送车辆载重及行驶里程等约束 条件,渐近绘出如图2所示的配送路线图。
0.32
0.40
0.40
第二步:由最短距离表,利用“节约里程”法计算出各连锁分店之 间的节约里程,做出节约里程表(见表3),计算结果有正有负, 节约里程为负数时,无实际意义,在表内写0。
表3 节约里程表
A BC DE F GH I J A B C D E F G H I J
节约里程法

节约里程法计算步骤
4、规划路线(考虑货车载重量和距离限制)
A 1.75 1.1 E 1.15 F G
路线1
1.75 + 1.15+1.1 = 4 全程长度:20+1+6+24=51
路线2
A
B
0.8 C 0.7
1.0 D 1.0+0.7+0.8=2.5 全程长度:9+9+10+12=40
节约法确定配送路径的基本原理
寻求配送方案的常用的方法很 多,这里介绍车辆运行计划法。 车辆运行计划法(VSP, Vehicles Scheduling Program) 又称里程节约法(VSP方法)。 适用于实际工作中为求得较优 解或最优的近似解时采用。它 的基本原理是三角形的一边之 长必定小于另外两边之和。如 图12-7所示。
5、计算总里程 51+40=91千米
案例12- 3:里程节约法确定配送路径
如图12-8所示某配送中心的配送网络图。由配送中心P向A、B、C、 D、E等五个用户配送物品。图中连线上的数字表示公路里程(km)。 图中靠近各用户括号里的数字,表示对货物的需求量(t)。配送中心 备有2t和4t载质量的汽车,且汽车一次巡回行驶里程不能超过30km。 求解该配送中心满意的送货方案。
节约里程法计算步骤
1、计算配送中心A到各配送点,各配送点之间的最短距离。
A A B C D E F G 0
B 9 0
C 12 9 0
D 12 19 10 0
E 20 29 32 25 0
F 24 33 29 19 6 0
G 21 30 33 25 1 6 0
物流线路规划节约里程法案例详解

节约里程法案例详解假如由一家配送中心P向两个用户A、B送货,配送中心到两客户的最短距离分别是L1和L2,A和B间的最短距离为L3,AB的货物需求量分别是Q1和Q2,且Q1+Q2小于车辆装载量Q【如果Q1+Q2大于车辆装载量Q,那一辆车就无法装完两位客户的货物】。
如下图所示:如果配送中心用两辆汽车分别对A、B两个用户各自往返送货时,汽车行驶的总里程L是L=2(L1+ L2)如果用一辆汽车向A、B两个用户巡回送货,则汽车行驶总里程L′为L′= L1+ L2+L3根据三角形的一边之长必定小于另外两边之和的原理,后一种配送方案比前一种方案节约里程△L为△L=2(L1+ L2)-(L1+ L2+L3)= L1+ L2-L3【这就是节约里程法产生的初衷,以最短距离最优配载完成送货作业】案例:位于市内的百家姓配送中心(P0)向它旗下的10家连锁商店p i(i=1,2,…,10)配送商品,其配送网络如下图所示。
图中括号内的数字表示每一家连锁店的需求量(t),线路上的数字表示两节点之间的距离(km)。
配送中心现有2t和4t车辆可供使用(无数量限制),并且每辆车配送距离不得超过30km。
请为百家姓配送中心制定最优的配送方案。
分析:初始方案:如果从P点向各点分别派车送货。
1、从百家姓配送中心出发,需要设计10条配送线路,分别向10家连锁店配送商品;2、需要10辆2t的配送车辆(每家连锁店的需要量都低于2t),总配送距离为148km。
第二种:节约里程法解题思路:相互间的节约里程计算根据△L== L1+ L2-L3 原理,例如以“百家姓配送中心交通图”中的P0(配送中心)到客户d、客户c的节约里程为例:dc△L==P0d(L1)+P0c (L2)-dc(L3 )==8 + 7 - 5=10如此计算出客户d和客户c间的节约里程数为10,以此方法计算出各个节点的节约里程数。
方案修正过程(优化到最终线路)1、方案修正过程实际上是线路规划过程,根据节约里程法原理从节约里程数最大的节点开始选择(这是先要排序的原因);2、所有规划线路的起点和终点都是配送中心,这里是P0;3、最大节约里程是a和b间的节约里程数15,那么路线的走向可以是P0-A或P0-B。
