运筹学C语言实现Dijkstra算法求解图的最短路径
物流管理专业背景下“运筹学”课程思政的教学设计与探索

[收稿日期]2021-10-28[基金项目]全国高校、职业院校物流教改教研课题(JZW2021145);成都文理学院一般项目“应用型本科院校工商管理专业《运筹学》课程教学改革研究”(WLYB2021046)[作者简介]蒲松(1981-),男,四川绵阳人,博士(后),成都工业学院副教授,研究方向:物流管理、运筹优化;夏嫦(1981-),女,成都文理学院副教授,硕士,研究方向:应用数学。
doi:10.3969/j.issn.1005-152X.2022.05.030物流管理专业背景下“运筹学”课程思政的教学设计与探索蒲松1,夏嫦2(1.成都工业学院经济与管理学院,四川成都611730;2.成都文理学院经济与管理学院,四川成都610401)[摘要]以物流管理专业为背景,将知识工具、职业素养与德育价值融通,探索物流管理专业背景下运筹学课程思政的教学设计,不仅使学生掌握专业知识,而且提升其文化自信与民族自豪感,培养其对专业的认同感与使命感,树立正确的人生观、价值观。
[关键词]“运筹学”课程思政;物流管理;知识工具;德育价值;职业素养[中图分类号]G641[文献标识码]A [文章编号]1005-152X(2022)05-0144-04Design and Exploration of Ideological and Political Elements in Operations Research Course forLogistics Management SpecialtyPU Song 1,XIA Chang 2(1.School of Economics &Management,Chengdu Technological University,Chengdu 611730;2.School of Economics &Management,Chengdu College of Arts &Sciences,Chengdu 610401,China)Abstract:In this paper,in the context of the logistics management specialty,and in an attempt to integrate knowledge instrument,professional quality and moral value,we explored the design of the ideological and political elements of the Operations Research course for the logistics management specialty,which aimed not only to enable the students to master professional knowledge,but also enhance their cultural self-confidence and national pride,cultivate their sense of identity and vocational calling,and establish the correct values on life.Keywords:ideological and political element in Operations Research course;logistics management;knowledge instrument;moral value;professional quality0引言随着经济全球化进程的加快和信息社会的来临,网络文化发展迅猛,传统价值观念和话语体系的不断变化,对民族乃至国家精心架构的意识形态樊篱造成巨大冲击[1]。
迪杰斯特拉和弗洛伊德算法示例(详细)

一、简介迪杰斯特拉(Dijkstra)算法和弗洛伊德(Flyod)算法均是用于求解有向图或无向图从一点到另外一个点最短路径。
二、Dijkstra迪杰斯特拉算法也是图论中的明星算法,主要是其采用的动态规划思想,使其在数据结构、算法、离散数学乃至运筹学中都扮演重要的角色。
以下图为例:以A为起点,首先走一步,共有三条边,分别如下:AB(12),AF(16),AG(14)其中最短的是节点B,将AB(12)放入辅助向量。
接着,各节点均继续向下走,此时可以找出4条边。
ABC(22),ABF(19),AF(16),AG(14),同样找出最小值放入向量中。
{AB(12),AG(14)}此后步骤完全相同A B C D A 0426B 50∞12C∞∞3ABC(22),ABF(19),AF(16),AGF(23),AGE(22),选中AF(16)。
同样,接下来的步骤有:ABC(22),AFC(22),AFE(18),AGE(22),选中AFE(18);ABC(22),AFC(22),AFEC(23),AFED(22),这种情况随便选取一个最小值,以ABC(22)为例;ABCD(25),AFED(22)选中后者,至此,已经完全找到A 和所有节点之间的最短路径及最短路径的长度。
最短路径向量为{AB(12),AG(14),AF(16),AFE(18),ABC(22),AFED(22)}三、Floyd弗洛伊德是另外一种求最短路径的方式,与迪杰斯特拉算法不同,弗洛伊德偏重于多源最短路径的求解,即能迪杰斯特拉能够求一个节点到其余所有节点的最短路径,但是弗洛伊德能够求出任意两个节点的最短路径,当然迪杰斯特拉重复N 次也能达到目标。
两种方式的时间复杂度均为O(n^3),但弗洛伊德形式上会更简易一些。
以下面的有向有权图为例:老版visio 不知道为啥这么糊?首先写出图的邻接矩阵AdjA B C DD71∞0若想缩短两点间的距离,仅有一种方式,那就是通过第三节点绕行,如果我们假设仅能通过A点绕行,那么仅需判断是否现有的距离Adj[i][j]小于Adj[i][1]+Adj[1][j]的距离,如果有更短的选择,那么进行更新就好了。
南邮运筹学运输问题实验报告

南邮运筹学运输问题实验报告南邮运筹学运输问题实验报告1.实验目的:本次实验旨在通过针对不同运输问题的建模和解决过程,掌握运筹学在实际运输问题中的应用方法,提高运筹学实践能力。
2.实验内容:本次实验包括两个部分:单源最短路径问题和车辆路径规划问题。
(1)单源最短路径问题:通过建立带权有向图模型,使用Dijkstra算法和Bellman-Ford算法求解从起点到终点的最短路径及其长度。
(2)车辆路径规划问题:通过建立车辆路径规划模型,使用模拟退火算法和遗传算法求解最短路径和最短时间路径。
3.实验结果:(1)单源最短路径问题:使用Dijkstra算法求解起点到终点的最短路径和长度如下图所示:路径:1->3->4->5->7,路径长度为23。
使用Bellman-Ford算法求解起点到终点的最短路径和长度如下图所示:路径:1->3->4->5->7,路径长度为23。
(2)车辆路径规划问题:使用模拟退火算法求解最短路径和最短时间路径如下图所示:最短路径:1->4->5->2->3->1,路径长度为33;最短时间路径:1->3->4->5->2->1,路径时间为15。
使用遗传算法求解最短路径和最短时间路径如下图所示:最短路径:1->4->5->2->3->1,路径长度为33;最短时间路径:1->3->4->5->2->1,路径时间为15。
4.实验结论:本次实验通过求解单源最短路径问题和车辆路径规划问题,掌握了Dijkstra算法、Bellman-Ford算法、模拟退火算法和遗传算法等运筹学方法在实际运输问题中的应用,提高了运筹学实践能力。
5.反思与改进:在实验过程中,我们发现需求和条件的准确描述很重要。
在建模过程中,不光需要理解题目中提供的条件,还需要利用常识和实际情况对模型进行适当的修正和完善。
网络图形最短路径算法分析与研究

网络图形最短路径算法分析与研究湛文红【摘要】着重对求网络图上每一对节点之间最短路径的矩阵算法及Floyed算法进行分析与比较,详述它们的功能、原理及异同点,以求在实际应用中合理选择恰当的算法.【期刊名称】《电脑与电信》【年(卷),期】2010(000)007【总页数】4页(P60-62,73)【关键词】最短路径;算法;Dijkstra;逐次逼近;矩阵;Floyed【作者】湛文红【作者单位】首钢工学院,北京,100144【正文语种】中文1.引言目前,在求网络图形最短路径的问题上主要有四种算法,它们是Dijkstra算法、逐次逼近算法、矩阵算法、Floyed算法,它们分别出现在数据结构、运筹学、图论等课程中。
其中前两种算法都是求图上从某一点至另一点的最短路径,而后两种算法是求出网络图上所有节点之间的最短路径。
由于这些算法分别出现不同的学科课程中,因此人们不易将它们进行统一的归纳总结与分析比较。
Dijkstra算法与逐次逼近算法解决的是从某一个节点到另一节点之间的最短路径问题,算法的时间复杂度是O(n2)。
如果想得到每一对节点之间的最短路径,则需要多次调用算法进行计算。
显然,这种方式对于求网络图中每一对节点之间的最短距离就显得过于麻烦。
矩阵算法与Floyed算法较好地解决了这方面的问题,它可以通过算法的一次调用直接计算出网络中每一对节点之间的最短路径值,因而弥补了前两种算法在这方面的不足。
它们通过一个图的权值矩阵求出每两点间的最短路径矩阵。
从图的带权邻接矩阵A=[a(i,j)]n×n开始,逐渐扩展,最终找到所有节点间的最短路径。
矩阵算法与Floyed算法的时间复杂度是O(n3)。
事实上,许多人混淆了后两种算法,认为它们是同一个算法,原因是它们不但功能相同,而且都是采用矩阵运算的形式进行最短路径的求解。
其实,它们在处理方法上还是有很大区别的,在此基础上分析它们的附加功能也是不同的。
本文将着重对这两种算法进行分析与讨论,以求在实际应用中对读者起到参考借鉴的作用。
运筹学试卷及参考答案

运筹学试卷及参考答案运筹学试卷一、选择题(每小题2分,共20分)1、下列哪个不是线性规划的标准形式?() A. min z = 3x1 + 2x2B. max z = -4x1 - 3x2C. s.t. 2x1 - x2 <= 1D. s.t. x1 + x2 >= 0答案:C2、以下哪个是最小生成树的Prim算法?() A. 按照权值从小到大的顺序选择顶点 B. 按照权值从大到小的顺序选择顶点 C. 按照距离从小到大的顺序选择顶点 D. 按照距离从大到小的顺序选择顶点答案:B3、下列哪个不是网络流模型的典型应用?() A. 道路交通流量优化 B. 人员部署 C. 最短路径问题 D. 生产计划答案:C4、下列哪个是最小化问题中常用的动态规划解法?() A. 自顶向下的递推求解 B. 自底向上的递推求解 C. 分治算法 D. 回溯法答案:A5、下列哪个是最大流问题的 Ford-Fulkerson 算法?() A. 增广路径的寻找采用深度优先搜索 B. 增广路径的寻找采用广度优先搜索 C. 初始流采用最大边的二分法求解 D. 初始流采用最小边的二分法求解答案:B二、简答题(每小题10分,共40分)1、请简述运筹学在现实生活中的应用。
答案:运筹学在现实生活中的应用非常广泛。
例如,线性规划可以用于生产计划、货物运输和资源配置等问题;网络流模型可以用于解决道路交通流量优化、人员部署和生产计划等问题;动态规划可以用于解决最短路径、货物存储和序列安排等问题;图论模型可以用于解决最大流、最短路径和最小生成树等问题。
此外,运筹学还可以用于医疗资源管理、金融风险管理、军事战略规划等领域。
总之,运筹学的理论和方法可以帮助人们更好地解决实际生活中的问题,提高决策的效率和准确性。
2、请简述单纯形法求解线性规划的过程。
答案:单纯形法是一种求解线性规划问题的常用方法。
它通过不断迭代和修改可行解,最终找到最优解。
具体步骤如下: (1) 将线性规划问题转化为标准形式; (2) 根据标准形式构造初始可行基,通常选取一个非基变量,使其取值为零,其余非基变量的取值均为零; (3) 根据目标函数的系数,计算出目标函数值; (4) 通过比较目标函数值和已选取的非基变量的取值,选取最优的非基变量进行迭代; (5) 在迭代过程中,不断修正基变量和非基变量的取值,直到找到最优解或确定无解为止。
Dijkstra算法求解单源最短路径问题
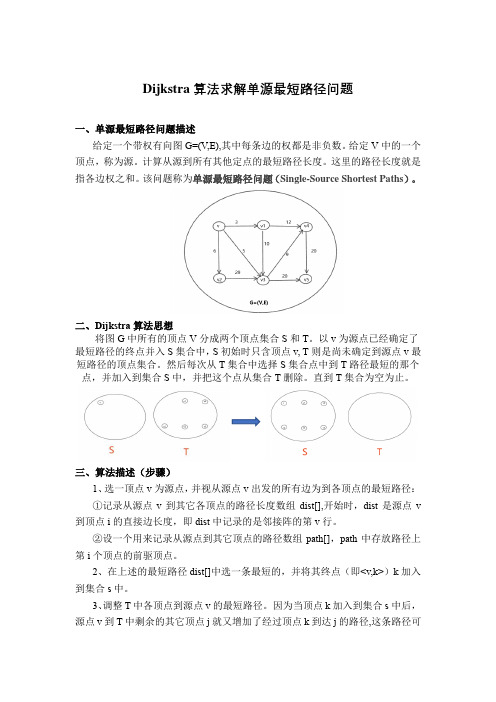
Dijkstra算法求解单源最短路径问题一、单源最短路径问题描述给定一个带权有向图G=(V,E),其中每条边的权都是非负数。
给定V中的一个顶点,称为源。
计算从源到所有其他定点的最短路径长度。
这里的路径长度就是指各边权之和。
该问题称为单源最短路径问题(Single-Source Shortest Paths)。
二、Dijkstra算法思想将图G中所有的顶点V分成两个顶点集合S和T。
以v为源点已经确定了最短路径的终点并入S集合中,S初始时只含顶点v, T则是尚未确定到源点v最短路径的顶点集合。
然后每次从T集合中选择S集合点中到T路径最短的那个点,并加入到集合S中,并把这个点从集合T删除。
直到T集合为空为止。
三、算法描述(步骤)1、选一顶点v为源点,并视从源点v出发的所有边为到各顶点的最短路径:①记录从源点v到其它各顶点的路径长度数组dist[],开始时,dist是源点v到顶点i的直接边长度,即dist中记录的是邻接阵的第v行。
②设一个用来记录从源点到其它顶点的路径数组path[],path中存放路径上第i个顶点的前驱顶点。
2、在上述的最短路径dist[]中选一条最短的,并将其终点(即<v,k>)k加入到集合s中。
3、调整T中各顶点到源点v的最短路径。
因为当顶点k加入到集合s中后,源点v到T中剩余的其它顶点j就又增加了经过顶点k到达j的路径,这条路径可能要比源点v到j原来的最短的还要短。
调整方法是比较dist[k]+g[k,j]与dist[j],取其中的较小者。
4、再选出一个到源点v路径长度最小的顶点k,从T中删去后加入S中,再回去到第三步,如此重复,直到集合S中的包含图G的所有顶点。
四、算法实现(数据结构)1、算法实现输入:一个大于1的整数n.输出:●一个随机生成的有向图G=(V,E),对于每一条边,有一个非负数字c(u,v)与之相关。
●对于每个顶点v∈V,得到从v0到v的最短路径的长度。
matlab dijkstra算法求解最短路径例题

matlab dijkstra算法求解最短路径例题Dijkstra算法是一种用于在带有非负权值的图中找到单源最短路径的算法。
以下是一个用MATLAB实现Dijkstra算法求解最短路径的简单例子:function [shortestDistances, predecessors] = dijkstra(graph, startNode)% 输入参数:% - graph: 表示图的邻接矩阵,graph(i, j) 表示节点i 到节点 j 的权值,如果没有直接连接则为 inf。
% - startNode: 起始节点的索引。
numNodes = size(graph, 1);% 初始化距离数组,表示从起始节点到每个节点的最短距离 shortestDistances = inf(1, numNodes);shortestDistances(startNode) = 0;% 初始化前驱节点数组predecessors = zeros(1, numNodes);% 未访问的节点集合unvisitedNodes = 1:numNodes;while ~isempty(unvisitedNodes)% 选择当前最短距离的节点[~, currentNodeIndex] = min(shortestDistances(unvisitedNodes));currentNode = unvisitedNodes(currentNodeIndex);% 从未访问节点集合中移除当前节点unvisitedNodes(currentNodeIndex) = [];% 更新与当前节点相邻节点的距离for neighbor = unvisitedNodesif graph(currentNode, neighbor) + shortestDistances(currentNode) < shortestDistances(neighbor) shortestDistances(neighbor) = graph(currentNode, neighbor) + shortestDistances(currentNode);predecessors(neighbor) = currentNode;endendendend现在,让我们使用一个简单的例子来测试这个算法:% 创建一个邻接矩阵表示图graph = [0, 2, 0, 4, 0;2, 0, 3, 7, 0;0, 3, 0, 1, 0;4, 7, 1, 0, 5;0, 0, 0, 5, 0];startNode = 1; % 起始节点% 调用Dijkstra算法[shortestDistances, predecessors] = dijkstra(graph, startNode);% 显示结果disp('最短距离:');disp(shortestDistances);disp('前驱节点:');disp(predecessors);这个例子中,graph 表示一个带有权值的图的邻接矩阵,startNode 是起始节点的索引。
最短路径算法―Dijkstra(迪杰斯特拉)算法分析与实现(

Dijkstra( 迪杰斯特拉算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra 算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra 算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。
一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。
设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。
Dijkstra 算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S 中,同时对数组dist作必要的修改。
一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
例如,对下图中的有向图,应用Dijkstra 算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。
Dijkstra 算法的迭代过程:主题好好理解上图!以下是具体的实现(C/C++:A ]***************************************2.* About: 有向图的Dijkstra 算法实现3. * Author: Tanky Woo4. * Blog: 6.7. #i nclude8. using n amespace std;9.9. con st i nt maxnum = 100;10. con st i nt maxi nt = 999999;12.13.11. void Dijkstra(i nt n, int v, int *dist, int *prev, int c[max nu m][max num]12. {13. bool s[maxnum]; // 判断是否已存入该点到 S 集合中14. for(i nt i=1; i<=n; ++i15. {16. dist[i] = c[v][i];17. s[i] = 0; // 初始都未用过该点18. if(dist[i] == maxi nt19. prev[i] = 0;20. else21. prev[i] = v;22. }23. dist[v] = 0;24. s[v] = 1;28.29. // 依次将未放入S 集合的结点中,取 dist[] 最小值的结点,放入结合 S 中5. *************************************30. // 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度31.for(i nt i=2; i<=n; ++i32.{33.i nt tmp = maxi nt;34.i nt u = v;35.// 找出当前未使用的点j的dist[j] 最小值36.for(int j=1; j<=n; ++j37.if((!s[j] && dist[j]38.{39.u = j; // u 保存当前邻接点中距离最小的点的号码40.tmp = dist[j];41.}42.s[u] = 1; // 表示u点已存入S集合中43.43.// 更新dist44.for(i nt j=1; j<=n; ++j45.if((!s[j] && c[u][j]46.{47.int newdist = dist[u] + c[u][j];48.if( newdist < dist[j]49.{50.dist[j] = n ewdist;51.prev[j] = u;52.}53.}54.}55.}58.void searchPath(i nt *prev,i nt v, int u59.{60.int que[max nu m];61.i nt tot = 1;62.que[tot] = u;63.tot++;64.int tmp = prev[u];65.while(tmp != v66.{67.que[tot] = tmp;68.tot++;69.tmp = prev[tmp];70.}71.que[tot] = v;72.for(int i=tot; i>=1; --i73.if(i != 174.cout << que[i] << "-> ";75.else76.cout << que[i] << en dl;77.}78.78.int main(79.{80.freopen("input.txt", "r", stdin;81.II各数组都从下标1开始82.i nt dist[max num]; II 表示当前点到源点的最短路径长度83.i nt prev[max nu m]; II 记录当前点的前一个结点记录图的两点间路径长度84.i nt c[max nu m][max nu m]; II87.88. II输入结点数89. cin >> n;90. II输入路径数91. cin >> line;92. i nt p, q, le n; II 输入p, q93.94. II 初始化c[][] 为maxi nt95. for(i nt i=1; i<=n; ++i96. for(i nt j=1; j<=n; ++j97. c[i][j] = maxi nt;98.99. for(i nt i=1; i<=li ne; ++i100. {101. cin >> p >> q >> len;102. if(len < c[p][q] II 有重边103. {104. c[p][q] = le n; II p 指向q 105. c[q][p] = le n; II q指向p,106. }107. }108.109. for(int i=1; i<=n; ++i110. dist[i] = maxi nt;111. for(i nt i=1; i<=n; ++i112. {113. for(i nt j=1; j<=n; ++j 两点及其路径长度这样表示无向图114.printf("%8d", c[i][j];115.prin tf("\n";116.}117.117.Dijkstra(n, 1, dist, prev, c;119.118.// 最短路径长度119.cout << " 源点到最后一个顶点的最短路径长度:"<< dist[ n] << endl;122.120.// 路径121.cout << " 源点到最后一个顶点的路径为:";122.searchPath(prev, 1, n;123.}复制代码输入数据:571 2 101 4 301 5 1002 3 503 5 104 3 204 5 60输出数据:999999 10 999999 30 10010 999999 50 999999 999999 999999 50 999999 20 1030 999999 20 999999 60100 999999 10 60 999999源点到最后一个顶点的最短路径长度: 60 源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安科技大学
运筹学课程设计报告姓名:***
一、算法思想
运用Dijkstra算法求解图的最短路径。
Dijkstra算法思想为:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S 表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
二、算法流程或步骤
Dijkstr算法具体步骤:
(1)初始时,S只包含源点,即S=,v的距离为0。
U包含除v 外的其他顶点,U中顶点u距离为边上的权(若v与u有边)或)(若u不是v的出边邻接点)。
(2)从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
(3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u(u U)的距离(经过顶点k)比原来距离(不经过顶点
k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
(4)重复步骤(2)和(3)直到所有顶点都包含在S中。
三、算法源程序
#include <iostream.h>
int m;
int n;
float a[100][100];
float dist[100];
int prev[100];
float MAX_V ALUE=10000;
void dijkstra()
{
if(m<0||m>n) //当无顶点的情况
return;
bool *s=new bool[n+1];
for(int i=0;i<n;i++)
{
dist[i]=a[0][i]; //与源点相连的权值
s[i]=false;
if(dist[i]==MAX_V ALUE) //与源点无连接的顶点
prev[i]=0; //设置对应权值为
else
prev[i]=m; //与源点相连接的顶点设置为m }
dist[m]=0;
s[m]=true;
for(int i1=0;i1<n;i1++)
{
float temp=MAX_V ALUE;
int u=m;
for(int j=0;j<n;j++)
if((!s[j])&&(dist[j]<temp))//与源点相连的顶点
{
u=j;
temp=dist[j]; //设置temp成为与源点相连的顶点权值
}
s[u]=true;
for(int j1=0;j1<n;j1++)
if((!s[j1])&&(a[u][j1]<MAX_V ALUE))
{
float newdist=dist[u]+a[u][j1]; //算出与源点不直接相
连的权值和
if(newdist<dist[j1])
{
dist[j1]=newdist;
prev[j1]=u;
}
}
}
}
void path()
{
for(int i=0;i<n;i++)
if(i!=m&&dist[i]<MAX_V ALUE)
{
cout<<"由源到顶点"<<i<<"的最短路径为:(终点位置) "<<i;
int temp=i;
do
{
temp=prev[temp];
cout<<" <-- "<<temp;
}while(temp!=m);
cout<<" (源位置)。
最短路径长度为:"<<dist[i]<<endl;
}
}
void main()
{
cout<<"请输入顶点的个数:";
cin>>n;
cout<<"请分别对两顶点之间赋权值(若无此连接,赋'0'值,请注意两顶点之间的方向):"<<endl;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
if(i==j)
continue;
cout<<"顶点"<<i<<"到顶点"<<j<<"的权值为:";
cin>>a[i][j];
if(a[i][j]==0)
a[i][j]=MAX_V ALUE;
}
cout<<"请输入此带权有向图的源顶点的编号:";
cin>>m;
dijkstra();
path();
}
四、算例和结果
例:设0为源点,求0到其他各顶点(1、2、3)的最短路径。
