利用数学符号的暗示功能解题
数学符号及其含义

数学符号及其寄义之五兆芳芳创作∈属于符号,暗示元素与荟萃之间的一种从属关系∏求积符号∑求和符号∕相当于除号÷√算术平方根,如±2的平方是4,那么4的算术平方根是2 ∝正比于,罕有于物理学,如a∝b说明当a增加,b也增加∞无穷暗示一种趋向,+∞暗示不竭变大的趋势∟直角符号∠角符号∣绝对值符号与除号‖平行刻画两直线的关系∧交符号逻辑根本符号,暗示两个命题同时产生则命题成立∨并符号逻辑根本符号,暗示两个命题有一个产生则命题成立∩交符号荟萃根本符号,暗示两个荟萃同时满足∪并符号荟萃根本符号,暗示至少满足一个荟萃∫不定积分符号微积分根本符号∮积分符号微积分根本符号∴所以∵因为∶比例符号∷比例∽属于符号荟萃根本符号刻画两个荟萃间的从属关系≈约等于符号≌相似符号刻画荟萃图形的根本特征≈约等号刻画两个关系式之间的关系≠不等号两者存在差别的地方≡同余符号数论根本符号,暗示两个整数除以同一个特定的整数余数相等,例如5=2×2+1,7=2×3+1,那么5≡7 (mod 2) ≤不大于关系符号前者小于或等于后者≥不小于关系符号前者大于或等于后者≤远小于等于关系符号前者远小于后者或与后者相等≥远大于等于关系符号前者远大于后者或与后者相等≮非小于同≥≯非大于同≤⊙圆⊙O暗示圆心为O的圆⊥垂直刻画两直线或空间间关系⊿三角形⌒反三角函数sin正弦函数Cos余弦函数tan正切函数cot余切函数sec正割函数csc余割函数log对数ln自然对数lg经常使用对数+加法-减法×乘法÷除法①②③④★☆♀☉ ● ◇ ╬ 〖〗【】〇¥*﹡¤ ? ℃ ← ↑ → ↓ ↖↗↘↙ √ ═ ▇ █ ▓ ◆ ▲ △ ▼▽◎±(加减号) ——外码:jjh-(减号) ——外码:jh×(乘号) ——外码:ch÷(除法) ——外码:cf√(对号) ——外码:dh°(度) ——外码:du⌒(弧) ——外码:hu℃(摄氏度) ——外码:ssd∠(角) ——外码:jiao≡(恒等) ——外码:hd≌(全等) ——外码:qd≈(约等)——外码:yd∽(相似) ——外码:xs≠(不等) ——外码:bd≤(小于等于) ——外码:xydy≥(大于等于) ——外码:dydy ∵因为——外码:yw∴所以——外码:sy⊥垂直——外码:cz‖(平行) ——外码:pxΔ 三角形——外码:sjs⊙圆——外码:yuanπ 圆周率——外码:yzlφ 直径——外码:faiα 阿尔发——外码:aefβ 贝塔——外码:beidΩ 欧姆——外码:om∑ 西格玛——外码:xgm∞(无穷大) ——外码:wqd•符号意义∞ 无穷大PI 圆周率|x| 函数的绝对值∪集归并∩ 荟萃交≥ 大于等于≤ 小于等于≡ 恒等于或同余ln(x) 以e为底的对数lg(x) 以10为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分P为真等于1不然等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至良多情况如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm⊥n m与n互质a ∈ A a属于荟萃A#A 荟萃A中的元素个数。
初一数学易错题带答案

初一代数易错练习1.已知数轴上的A 点到原点的距离为2,那么数轴上到A 点距离是3的点暗示的数为 2.一个数的立方等于它自己,这个数是。
3.用代数式暗示:每间上衣a 元,涨价10%后再降价10%以后的售价( 变低,变高,不变 )4.一艘轮船从A 港到B 港的速度为a,从B 港到A 港的速度为b,则此轮船全程的平均速度为 。
5. 青山镇水泥厂以每年产量增长10%的速度发展,如果第一年的产量为a,则第三年的产量为。
6.已知a b =43,x y =12,则代数式374by ax ay by +-的值为7.若|x|=-x,且x=1x,则x= 8.若||x|-1|+|y+2|=0,则xy=。
9.已知a+b+c=0,abc≠0,则x=||a a +||b b +||c c +||abc abc,根据a,b,c 分歧取值,x 的值为。
10.如果a+b<0,且b>0,那么a,b,-a,-b 的大小关系为。
11.已知m 、x 、y 满足:(1)0)5(2=+-m x , (2)12+-y ab 与34ab 是同类项.求代数式:)93()632(2222y xy x m y xy x +--+-的值.12.化简-{-[-(+2.4)]}= ;-{+[-(-2.4)]}=13.如果|a-3|-3+a=0,则a 的取值范围是 14.已知-2<x<3,化简|x+2|-|x -3|=15.一个数的相反数的绝对值与这个数的绝对值的相反数的关系式 。
在有理数,绝对值最小的数是,在负整数中,绝对值最小的数是 16.由四舍五入得到的近似数17.0,其真值不成能是( ) A 17.02 B 16.99 C 17.0499 D16.4917.一家商店将某种服装按成本价提高40%后标价,又以8折(即按尺度的80%)优惠卖出,结果每作服装仍可获利15元,则这种服装每件的成本是18.已知4个矿泉水空瓶可以换矿泉水一瓶,现有16个矿泉水空瓶,若不交钱,最多可以喝矿泉水19.观察下面的每列数,按某种规律在横线上填上适当的数,并说明你的理由。
用数学表白的情话

用数学表白的情话在浪漫的爱情世界里,表白是一件非常重要的事情。
有的人用花束和巧克力表达自己的感情,而有些人则希望以一种独特而特别的方式向心爱的人表白。
如果你是一个喜欢数学的人,那么用数学表白绝对是一个不错的选择。
下面,我将会用一些数学公式和符号来帮助你用数学的方式表白。
1. 加法是第一步在数学中,加法是最基本的运算之一。
它代表着两个数的相加运算。
那么,我们可以使用一个简单的数学公式来表达你对心爱的人的感情:心爱的人 = 你的心 + 我的心这个公式暗示了你们两个人的心灵可以通过相加来变得更加完整。
2. 用方程解开心扉数学中的方程是一种数学语句,它使用符号和未知数来表示等式。
我们可以利用方程来表达出你对心爱的人的感受:你是我的解方程,让我心心相印。
这句话隐含了需要对心爱的人进行一系列的计算和思考才能找到答案的意思。
3. 用三角函数勾勒爱情轨迹三角函数是数学中的重要概念,它描述了角度和长度之间的关系。
我们可以利用三角函数来勾勒出爱情的轨迹:爱情的轨迹 = cos(时间) + sin(你的拥抱)这个公式告诉了你心爱的人,你的爱情将会随着时间的推移而变得越来越强烈。
4. 用无限数列尽显思念之情无限数列是数学中的重要概念,它表示了一系列无限延伸的数字。
我们可以利用无限数列来表达你对心爱的人的思念:思念的数列 = a + ar + ar^2 + ar^3 + ...其中,a表示你对心爱的人的思念的初始强度,r表示思念的变化率。
这个数列告诉了你心爱的人,你对他/她的思念将会一直延伸下去,永不停息。
5. 用矩阵传递爱的信息矩阵是数学中的重要工具,它由行和列组成。
我们可以利用矩阵来传递爱的信息:爱 = [[我对你的爱],[你对我的爱]]这个矩阵告诉了你心爱的人,爱情是相互的,你们之间的爱是互相传递的。
总结数学是一门充满魅力和美丽的学科,它可以用来表达我们对心爱的人的感情。
通过使用数学公式和符号,我们可以以一种独特而特别的方式向对方表达爱意。
利用数学符号的暗示信息解决数学问题

, ( +. 一/ (一^ 一0故 / () z I 1 ) ) , 为常数 , 从
而 得 出结 论 。
图2
3 数 字 符号 的暗 示信 息
. 一
。
—
—
所 以三 式相 加 即可证 明 。
例 2 若函数 / z 存在, () 且对于一切 ≠
均 有
111
三 一
I + , 一 () () 其中。卢 ’ 、> 。
36 3 1 1 1 1
4 1 24 21
0a , + = 1 试求 厂 )的表达式 。 , ( [ 析] 已知式 子及其 字母 符号 “ 暗示着 分 从 、 它们 的地位 一致 , 换 “ 所 得 的式子 中可推 出 : 互 、
第2 8卷 第 6期 20 0 8年 1 月 1
孝 感 学 院学 报
J OURNAL OF XI AOGAN UNI VERSI TY
V0L 2 NO. .8 6 N0V. 0 8 20
利用数学符号的暗示信息解决数学问题
李金 田 , 李海 涛
( . 感 学院 计 算 机 科 学 系 , 北 孝 感 4 2 0 ;2 孝 感 市 第 一 高 级 中 学 , 北 孝 感 4 2 0) 1孝 湖 30 0 . 湖 3 0 0
数 学 中符 号繁 多 , 目前 为止 , 到 数学 中常 见 的
② 当
C
≤ 0 ̄1 d一 1 方 程无解 。 - 时
,
符号 有两百 多种 , 中学 数 学 中常见 的符 号 也 有一
百多种 , 这些 符号 内涵 深 刻 富 简 明 , 丰 它们 表 达
C
例 2 确定 函数 z l (q - x - y ) = n 2  ̄- 。 +
浅谈暗示教学法在小学数学教学中的运用

浅谈暗示教学法在小学数学教学中的运用作者:张宏来源:《黑河教育》2010年第04期【摘要】暗示教学法是将暗示学原理应用于教学实践中,其特点是用含蓄的间接的暗示方法对人的心理和行为产生影响。
在小学数学教学中巧妙地运用暗示教学法,可以获得良好的课堂学习效果。
【关键词】暗示教学法;小学数学;应用暗示教学法是保加利亚教育家、医学家格奥尔吉?洛扎诺夫(Georgi Lomnov)多年理论和实践研究的成果。
暗示教学法就是对教学环境进行精心设计,用暗示、联想、练习和音乐等各种综合方式使学生建立起无意识的心理倾向,激发学生的学习需要和兴趣,充分发挥学生的潜力,获得良好的课堂学习效果。
一、数学符号的暗示“数学的世界是符号化的世界。
”“符号是意愿的标志,传播一定的意义,因此,符号能暗示信息。
”一般地说,数学符号大致有数字符号、字母符号、运算符号、性质符号、关系符号和图形符号等。
我们在平时的数学教学中,往往只教给学生用符号表达的结果,而常常忽视了对数学符号的“最原始”的暗示功能的挖掘。
笔者认为,搞好数学语言教学的关键是搞好数学符号语言的教学。
因此,在数学教学中要抓住数学符号创设的启发性原则,注意充分挖掘符号的暗示功能。
比如数字符号“0”,在整数、有理数和实数里,它的基本属性是表示唯一的中性数。
在“我有0元钱”里,“0”表示“没有”,在“现在的天气温度是0度”里,“0”表示了这一刻的温度的高低情况,而不是“没有”温度的意思了。
此外,“0”还可以表示零点、零元等。
二、环境暗示暗示教学法认为,暗示是个人和环境之间一个经常性的交流因素,倘若能达到“人——环境”之间的“共振”,人与环境间的不断交流就能达到最为和谐的境界。
我们生活在一个充满暗示的环境中,许多活动从本质上说都是人们无意识地对外界环境的各种暗示所做出的反应。
教学中的环境暗示,就是指通过营造某种场景、氛围来感染学生,使学生在潜意识的作用下自觉地投人学习,主动地参与活动,使学生在无对抗的状态下,乐意、顺利地接受环境的暗示信息,从而达到教育的目的。
把数学讲通俗——提高教学效率的关键

然后走 出了教室 , 还保 号是有必要 、 有好 处 的 , 利 于数学 的研究 、 流 与 的左边一直 画到黑板 的右边 , 有 交
使用. 生认 识到这一点 , 学 就会感到数学符号很实 在 , 持着 画直线 的姿势. 学生惊 讶 : 曾老 师怎么走 出 了教 室?曾老师 回到教室后说 , 哎呀 , 我画了这么久 , 一条 并不枯燥.
把它写完 整是不可能 的. 3 年 , 1 7 欧拉首先倡 导用 希 无限延伸性. 7 湖南省 已故特级教师 曾宪侯老师 曾经是这样教 腊字母 来表示 它 , 既方便又快捷 , 后通用 于世界. 数
他走 进有不少符号都是为了速记. 可见 , 人类创造数学符 直线的 :
三是揭示符号的 暗示功 能.符号是 意愿的标志 ,
因此 , 符号能 暗示信 息. 学符号 数 外 在表现 ,对学生数 学知识 的掌握程度并 没有过多 能传播 一定 的意义 . 所 暗示 的信 息量很 大 , 可信 度高 . 了发展学生 的符 为 的关注. 到底 , 说 就是教 师 的教学效 率并不 高 . 实 , 其 教师必须揭示 符号的暗示功能. 算符号 、 运 数字 对 于数学课 而言 , 热闹不一 定是好 事. 使数学 教学 号感 , 要 效率高 , 关键是要把数 学讲 通俗 , 讲清楚. 具体体现在 规律 、表达式 的结构 特征及 图像 符号均 暗示 了数学 信息, 暗示 着解题思 路. 比如 , 到符号 △, 暗示 我 看 它 以下几个方面. 讲 活数学 符号 . 学的语 言是 由一些 符号 和记 们 , 目要考虑方程 的根 的问题. “ 数 题 讲 清数 学概念 . 概念是数 学 的细胞 , 数学 可见 其 号组成 的语言 ” 数 学的每个分支都有相应 的符号体 .
北京 已故 特级教 师刘 祖植老师 曾经采用描述法
数学符号表 数学符合的意思 数学符号代表的意义 数学符号用法
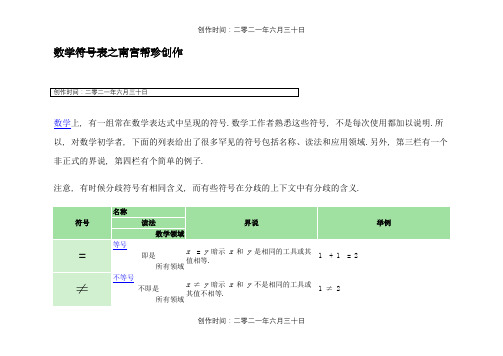
数学符号表之南宫帮珍创作数学上, 有一组常在数学表达式中呈现的符号.数学工作者熟悉这些符号, 不是每次使用都加以说明.所以, 对数学初学者, 下面的列表给出了很多罕见的符号包括名称、读法和应用领域.另外, 第三栏有一个非正式的界说, 第四栏有个简单的例子.注意, 有时候分歧符号有相同含义, 而有些符号在分歧的上下文中有分歧的含义.创作时间:二零二一年六月三十日x< y暗示x小于y. x> y暗示x年夜于y. 3 < 4 5 > 4序理论x≤ y暗示x小于或即是y.x≥ y暗示x年夜于或即是y. 3 ≤4;5 ≤ 5 5 ≥4;5 ≥ 5年夜于即序理论6 + 3 暗示 6 加 3. 6 + 3 = 9算术6 − 3 暗示 6 减 3. 6 − 3 = 3算术−3 暗示 3 的负数. −(−5) = 5 算术A−B暗示包括所有属于A但不属于B的元素的集合. {1,2,4} −{1,3,4} = {2}集合论6 × 3 暗示 6 乘以 3. 6 × 3 = 18算术X× Y暗示所有第一个元素属于X, 第二个元素属于Y的有序对的集合. {1,2} × {3,4} ={(1,3),(1,4),(2,3),(2,4)}创作时间:二零二一年六月三十日集合论向量积u× v暗示向量u和v的向量积. (1,2,5) × (3,4,−1) = (−22, 16, − 2) 向量积向量代数÷/ 除号6 ÷ 3 或 6 / 3 暗示 6 除以 3 或 3除 6.6 ÷ 3 = 212/4 = 3 除以算术根号暗示其平方为x的正数.…的平方根实数复根号若用极坐标暗示复数z = r exp(iφ)(满足 -π < φ ≤ π), 则√z =√r exp(iφ/2).…的平方根复数| | 绝对值|x| 暗示实数轴(或复平面)上x和0的距离.|3| = 3, |-5| = |5||i| = 1, |3+4i| = 5 …的绝对值数! 阶乘n! 暗示连乘积1×2×…×n. 4! = 1 × 2 × 3 × 4 = 24…的阶乘组合论~ 概率分布X ~ D暗示随机变量X概率分布为D. X ~ N(0,1):标准正态分布满足分布统计学创作时间:二零二一年六月三十日A⇒B暗示A真则B也真;A假则B不定.→ 可能和⇒一样, 或者有下面将提到的函数的意思.⊃可能和⇒一样, 或者有下面将提到的父集的意思. x = 2 ⇒x2 = 4 为真, 但x2 = 4 ⇒x = 2 一般情况下为假(因为x可以是−2).A⇔B暗示A真则B真, A假则B假.x+ 5 = y+2 ⇔x+ 3 = y 命题¬A为真当且仅当A为假.将一条斜线穿过一个符号相当于将"¬" 放在该符号前面. ¬(¬A) ⇔Ax≠y⇔¬(x= y)若A为真且B为真, 则命题A∧ B为真;否则为假. n< 4 ∧n>2 ⇔n= 3, 当n是自然数若A或B(或都)为真, 则命题A∨ B 为真;若两者都假则命题为假. n≥ 4∨n≤ 2⇔n≠ 3, 当n是自然数若A和B刚好有一个为真, 则命题A⊕ B为真.A⊻B的意义相同.(¬A) ⊕ A恒为真, A⊕ A恒为假.创作时间:二零二一年六月三十日∀x: P(x) 暗示P(x) 对所有x为真. ∀n∈ N: n2≥ n∃x: P(x) 暗示存在至少一个x使得P(x) 为真.∃n∈ N: n为偶数∃! x: P(x) 暗示有且仅有一个x使得P(x) 为真.∃! n∈ N: n+ 5 = 2nx:= y或x≡ y暗示x界说为y 的一个名字(注意:≡ 也可暗示其它意思, 例如全等).P:⇔Q暗示P界说为Q的逻辑等价. cosh x:= (1/2)(exp x+ exp (−x))A XOR B:⇔(A∨B) ∧¬(A∧B){a,b,c} 暗示a, b,c组成的集合. N= {0,1,2,…}{x: P(x)} 暗示所有满足P(x) 的x{n∈ N: n2< 20} =创作时间:二零二一年六月三十日的集合.{x| P(x)} 和 {x: P(x)} 的意义相同. {0,1,2,3,4}集合论∅暗示没有元素的集合.{} 的意义相同. {n∈ N: 1 < n2< 4} = ∅空集集合论a∈ S暗示a属于集合S;a∉S暗示a不属于S. (1/2)−1∈ N 2−1∉N所有领域A⊆B暗示A的所有元素属于B.A⊂B暗示A⊆B但A≠ B. A∩ B⊆A;Q⊂R…的子集集合论A⊇B暗示B的所有元素属于A.A⊃B暗示A⊇B但A≠ B. A∪ B⊇B;R⊃Q…的父集集合论A∪ B暗示包括所有A和B的元素但不包括任何其他元素的集合. A⊆B⇔A∪ B= B集合论A∩ B暗示包括所有同时属于A和B 的元素的集合. {x∈ R: x2= 1} ∩ N= {1}集合论创作时间:二零二一年六月三十日A\ B暗示所有属于A但不属于B的元素的集合. {1,2,3,4} \ {3,4,5,6} = {1,2}集合论f(x) 暗示f在x的值. f(x) := x2, 则f(3) = 32= 9. (x)集合论先执行括号内的运算. (8/4)/2 = 2/2 = 1;8/(4/2) = 8/2 = 4所有领域ƒ: X→ Y暗示ƒ从集合X映射到集合Y. 设ƒ: Z→ N界说为ƒ(x) = x2.集合论f o g是一个函数, 使得 (f o g)(x) = f(g(x)). 若f(x) = 2x, 且g(x) = x + 3, 则(f o g)(x) = 2(x + 3).集合论N暗示{1,2,3,…}, 另一界说拜会自然数条目. {|a| : a∈ Z} = NN数Z暗示{…,−3,−2,−1,0,1,2,3,…}.{a: |a| ∈ N} = Z Z数创作时间:二零二一年六月三十日ℤQ ℚ有理数Q暗示 {p/q: p,q∈Z,q≠0}.3.14 ∈ Qπ∉Q Q数R ℝ实数R暗示 {limn→∞an: ∀n∈N:an∈ Q, 极限存在}.π∈ R√(−1) ∉R R数C ℂ复数C暗示 {a+ bi: a,b∈R}. i= √(−1) ∈ C C数∞无穷∞ 是扩展的实数轴上年夜于任何实数的数;通常呈现在极限中.limx→01/|x| = ∞无穷数π圆周率π 暗示圆周长和直径之比. A= πr2是半径为r的圆的面积pi几何创作时间:二零二一年六月三十日||x|| 是赋范线性空间元素x的范数. ||x+y|| ≤ ||x|| + ||y|| 线性代数∑k=1n ak暗示a1+ a2+ …+ a n.∑k=14k2= 12+ 22+ 32+ 42=1 + 4 + 9 + 16 = 30算术∏k=1n ak暗示a1a2···a n.∏k=14(k+ 2) = (1 + 2)(2 +2)(3 + 2)(4 + 2) = 3 × 4×5 × 6= 360算术∏i=0n Yi暗示所有(n+1)-元组(y0,…,y n). ∏n=13R = R n集合论f'(x)函数f在x点的倒数, 也就是, 那里的切线斜率. 若f(x) = x2, 则f'(x) = 2x微积分或反导数∫f(x) d x暗示导数为f的函数. ∫x2d x= x3/3 微积分∫a b f(x) d x暗示x-轴和f在x=a和x= b之间的函数图像所夹成的带符号面积. ∫b x2d x= b3/3;微积分∇f (x1, …, x n) 偏导数组成的向量 (df若f (x,y,z) = 3xy + z2则∇创作时间:二零二一年六月三十日1, …, df / dx n). f= (3y, 3x, 2z)f (x1, …, x n), ∂f/∂xi是f的对x i.若f(x,y) = x2y, 则∂f/∂x = 2xy暗示M的鸿沟∂{x : ||x|| ≤ 2} = {x : || x || = 2}暗示f(x)的次数( 也记作y暗示x垂直于y; 更一般的x正y.若l⊥m和m⊥n则l || n.x是最小的元素. ∀x: x∧ ⊥ = ⊥暗示A蕴含B, 在A成立的每个模, B也成立.A⊧A∨ ¬A暗示y由x导出. A→ B⊢¬B→ ¬A创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日 ◅ 正则子群N ◅G 暗示 N 是G 的正则子群.Z (G ) ◅G 是…的正则子群 群论/ 商群G /H 暗示G 模其子群H 的商群.{0, a , 2a , b , b +a , b +2a } / {0, b } = {{0, b }, {a , b +a }, {2a , b +2a }} 模 群论≈ 同构G ≈ H 暗示 G 同构于 HQ / {1, −1} ≈ V , 其中 Q 是四元数群V 是 克莱因四群. 同构于 群论∝ 正比G H 暗示 G 正比于 H若Q V , 则 Q =K V 正比于 所有领域创作时间:二零二一年六月三十日。
三年级数学单元练习_千克与克(重量)

第三单元千克与克之羊若含玉创作一懂得千克和克.1. 明白用途:称一般物品有多重,经常使用千克作单位.称较轻物品有多重,经常使用克作单位.2. 明白写法:千克又叫做“公斤”,也可用符号“kg“暗示.克可用符号“g”暗示.3. 生活中的应用:以生活中的物品为例,1)知道哪些物品通经常使用“千克”做单位,哪些物品经常使用“克”做单位.2)能举例说明 1克重的物品有哪些(一枚两分硬币)1千克重的物品有哪些(一个柚子、大约5个苹果……)3)可以或许看图写出称上暗示的重量.要看清称上标出的单位. 如果称上数字没有全部标出,要看清一大格或一小格暗示若干.二千克与克的进率1. 1千克=1000克(可以从字面“千”入手,引导孩子记忆进率)2. 进率转换时需要注意的问题--0的个数.一定是在千克数量的基本上增加三个0或在克数量的基本上削减三个0.尤其注意90千克=()克10000克=()千克这样的题目.三正确填写单位名称1. 理清学习过的各类暗示单位的词.题目中往往不但仅出现重量单位,还可能搀杂着以前学习过的长度单位.分清用途,才干正确填空.2. 书上列举出的各类物品重量都是以什么作为单位名称的,要清楚.例如:一本数学书大约重300克.3. 具体答题时,不但要懂得物品的通例情况,更要注意题目给出的数量是若干.例如: 1个苹果重200() 5个苹果重2()1颗葡萄大约重3()1串葡萄大约重1()……四重量的大小比较1. 先统一单位,再比较.例如:2千克()15000克单纯看单位,疏忽数字就有可能出错.2. 排序重量的排序,经常都是一些数字差未几的题目.既要注意数字、更要看清单位.少数孩子看题不细致,还会疏忽题目要求的排序顺序,排反的情况时有产生,因此重复读题很重要.在家里可以要求孩子把这样的题目读出声音来.五实际应用1.“合若干千克”.这样的问题往往出现在题目中最后求出的答案为“整千”克数.不克不及直接在答话中写出“合……千克”,而应填补一道算式:……克=……千克,再答话.(不然扣分)2. 油桶问题(难点)一桶油连油带桶共重200千克,倒出一半油以后,连桶重110千克.问:原来油重若干千克?油桶重若干千克?解题思路:1)剖析前后两次重量的不同.相同点:都是连桶带油.不合点:重量轻了.2)为什么会轻?(解题的症结)因为倒出了油(要强调,倒出的是纯油的重量,没有其它的重量包含在内.)3)再看已知条件:倒出若干油?(重复强调只有油的重量)一半油----求出全部油的重量最后求出油桶的重量3. 估量重量问题(难点、积年必考题)1)用直尺画线的办法帮忙估量(注意画线的位置,应从水面椭圆形图的中间开端).2)对于不是一半数量的断定,可以运用到学习过的分数知识,也可以用平均分的思维方法帮忙断定.3)要注意题目标要求:空杯?水?照样“水+杯”的重量?(题目比较灵巧,建议多练.)4. 简略的等量代换第四单元加和减应知应知一.估量得数是几十多.症结1:估量得数是几十多时,可以先把两个数十位上的数相加、减,再依据个位上相加、减后是否进位或退位,最落后行断定.症结2:估量的得数应用“汉字”暗示.例如:35+32(六十多)37+55(九十多)85-63(二十多) 50-37(一十多)二.口算进位加法,掌握口算的办法.症结:将两个加数的十位、个位分离相加,再看个位之和如果要进位,就在十位之和上加1.27+35(先算20+30=50,再算7+5=12,12满10进1所以27+35=62)三.口算退位减法,掌握口算的办法.症结:先盘算个位相减,如果不敷减,向十位借1,最后再盘算十位相减.50-37(先算0-7,不敷减,向十位5借1,再算十位4-3=1,合起来就是13)四.一千几百、整百数加减整百数的口算办法.症结:盘算时可以将末尾的0先放在一边,进行其它数字盘算后,有几个0就在得数的末尾添上几个0.例如:700+400 500+600 900+300五.实际应用(两步盘算).1.选择路线问题:例:估量,熊猫馆到山君馆走哪条路最近?说一说你是怎样估量的.解答:估量的办法有两种:一种是知识估量,也就是“直线距离”最短,应此选择35+44=79(米)别的一种,可以联合加法的估算成果来进行比较.54+42(九十多)、35+44(七十多)、38+52(九十)因此照样选择35+44的路线为最近.注:在实际答题时,作为解决问题,不成以直接写答话,无论采取的是哪一种比较的办法,都应该把暗示旅程的算式列出来,同时在答话中加以说明.症结:1)能准确看清线段图中1份数和几份数之间的关系.2)要注意问题最后要求的到底是什么.3)可以或许用两种办法解决此类型的题目.例:办法1:先求出第二条线段:5×4=20(米)再求出总和:5+20=25(米)办法2:先求出总“份数”:1+4=5再依据一份数是“5”,求出总和:5×5=25(米)例:办法1:先求出长线段:16+7=23(米)再求出总和:16+23=39(米)办法2:假设:两条线段一样长,总长为:16×2=32(米)再加上实际增加的“7米”:32+7=39(米)3.依据题目,画出线段图,再解答.症结:1)线段图的每份数要基底细等2)已知条件必须全部标清:①种类;②数量3)所求问题要标出,即“?”标在哪里.例:鸭有18只,鸡的只数是鸭的2倍,鸡和鸭一共有若干只?请你画出这道题的线段图.例:大汽车有45辆,小汽车比大汽车多17辆,小汽车和大汽车一共有若干辆?请你画出这道题的线段图.1)第一小组有3人,每人要做8朵;第二小组有3人,一共要做26朵,两个小组一共要做若干朵?症结:第一组提供的是人数和平均数,而第二组提供的是总数.2)5只山公一共采了64个桃子,分离装在3个篮子和一个筐里,已知筐里装了28个桃子,平均每个篮子里装了若干个桃子?症结:篮子里的桃子是装完筐里的28个后再平均分的.3)黑天鹅有28只,白日鹅的只数比黑天鹅的3倍多9只,白日鹅有若干只?4)三年级一班借书28本,二班借书33本,三班借书的本数比一班和二班的总和少24本,三班借书若干本?5)妈妈比女儿大27岁,又恰好是女儿年纪的4倍.问:妈妈和女儿各若干岁?(差倍问题,也是书上的思考题,用画线段图的办法帮忙懂得.)第五单元 24时记时法应知应会一.依据时间画出钟面上的指针.症结1:时针→ 粗而短分针→ 细而长症结2:钟面一大格→ 1小时/5分钟1时 12时05分二.普通记时法与24时记时法的区别.一天的24小时,习惯上有两种记时法.1.普通记时法:把24小时分成两段,每段12小时.从子夜0时→ 中午12时是第一段.从中午12时→ 子夜12时是第二段.2.24时记时法:0时→ 24时 .如:下午1时就是 13时夜里12时就是 24时,又叫0时.三.普通记时法与24时记时法转换的办法.1.普通记时法:从0时→12时为止,数字不超出12.必须在时刻前写出“上午、中午、下午、晚上、清晨”这样的时间段.例如:上午8时中午12时30分清晨0时晚上12时2.24时记时法:从0时→24时为止.中午12时以后的时刻,就加上12时.书写时不写出暗示时间段的词语.如果没有超出中午12时或下午1时(13时),写的时候只要把暗示时间段的词语去失落就可以了.例如:20时 12时30分 24时 19时演习:(普通记时法→24时记时法)上午8时________ 中午12︰30________下午2时________ 傍晚6︰25________晚上9时________ 晚上12时________演习( 24时记时法→普通记时法)9时30分___________ 12︰30___________16时___________ 18︰00___________23时___________ 0︰00____________四.小时与时的区别应用.1.小时:又可称为时间.通常,时间暗示有起点,又有终点的一个进程.例如:妈妈上班工作8小时.2.时:又可称为时刻.只暗示时间进程中的一个点.例如:妈妈8时上班.例:某科技馆上午9时开馆,下午4时闭馆,天天开放时间为7小时.暗示时刻的:上午9时下午4时暗示时间的:7小时五.求经由时间的应用题.症结1:注意记时法的统一.(便利盘算)例:商店的营业时间:上午8时–下午5时,盘算商店的营业时间.下午5时=17时 17时-8时=9(小时)5-8=9(小时)错误症结2:盘算的进程中,每一个时间都要把“时、分”这样的单位名称写清楚.例:盘算售票处一天的营业时间 6︰30~11︰30; 13︰30 ~ 20︰30 上午:11时30分-6时30分=5(小时)下午:20时30分-13时30分=7(小时)共:7+5=12(小时)症结3:盘算成果的单位名称要注意.(小时/时/分)例:片子下午2时30离开端,放映2小时,停止时间是?下午2时30分+2小时=下午4时30分例:妈妈上午9时上班,下午5时下班,一天工作多久?下午5时=17时17时-9时=8(小时)症结4:如果遇到不敷减或要进位的情况,应以60为进、退位尺度.(1小时=60分)例:8时35离开端上课,9时15停止,上课时间多长?9时15分=8时75分8时75分-8时35分=40(分钟)例:足球比赛,从下午4点开端,经由130分钟,比赛停止时间是几点?130分=2小时10分下午4时+2小时10分=下午6时10分症结5:盘算时出现跨天到次日,应以24时为尺度,先算出前一天的时间,再加上次日的时间.例:火车晚上8时出发,次日上午9时到达目标地,行驶了几小时?晚上12时-晚上8时=4(小时)……前一天4+9=13(小时)例:盘算娱乐场合营业时间:21时~次日7时24时-21时=3(小时)……前一天3+7=10(小时)特殊的时间问题:1. 列车时刻表到站(出发)时间-开车时间=运行时间2.停电通知星河一村 9︰00~13︰30星河二村 13︰00 ~ 16︰00小林在下午2时回到家,发明家里停电,你知道她家住在哪儿吗?还需要多长时间才会来电?下午2时=14时家住星河二村16时-14时=2(小时)还需要2小时才会来电16时-13时=3(小时)×(因为小林下午2时到家,这里问的“需要多长时间”指的是小林在家里还需要等多长时间才会来电)。
