土力学-土的渗透性及渗流
合集下载
经典土力学课件渗流清华张丙印

水的性质
水的动力粘滞系数: 温度,水粘滞性,k
饱和度(含气量):封闭气 泡对k影响很大,可减少有效 渗透面积,还可以堵塞孔隙 的通道
渗透系数的影响因素
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
天然土层多呈层状
• 确立各层土的ki • 根据渗流方向确定等效渗流系数
等效渗透系数
多个土层用假想单一土层置换, 使得其总体的透水性不变
达西定律
渗透系数的测定
及影响因素
层状地基的等效
渗透系数
仁者乐山 智者乐水
渗流的驱动能量 反映渗流特点的定律 土的渗透性 地基的渗透系数
土的渗透性与渗透规律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
uB w
u0pa
B
静水 A zB
0 基准面
位置水头:到基准面的竖直距离, 代表单位重量的液体从基准面算起 所具有的位置势能
• 井孔抽水试验 • 井孔注水试验
渗透系数的测定方法
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
试验条件: Δh,A,L=const 量测变量: 体积V,t
V=Qt=vAt v=ki
i=Δh/L
h
k VL
土样
L
Aht
A
Q
适用土类:透水性较大的砂性土
V
室内试验方法-常水头试验法
§2.2 土的渗流性与渗透规律
渗透速度v:土体试样全断面的平均渗流速度,也称假想
渗流速度
v
vs
v n
其中,Vs为实际平均流速,孔隙断面的平均流速
达西定律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
适用条件:层流(线性流动) 水 2.0
水的动力粘滞系数: 温度,水粘滞性,k
饱和度(含气量):封闭气 泡对k影响很大,可减少有效 渗透面积,还可以堵塞孔隙 的通道
渗透系数的影响因素
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
天然土层多呈层状
• 确立各层土的ki • 根据渗流方向确定等效渗流系数
等效渗透系数
多个土层用假想单一土层置换, 使得其总体的透水性不变
达西定律
渗透系数的测定
及影响因素
层状地基的等效
渗透系数
仁者乐山 智者乐水
渗流的驱动能量 反映渗流特点的定律 土的渗透性 地基的渗透系数
土的渗透性与渗透规律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
uB w
u0pa
B
静水 A zB
0 基准面
位置水头:到基准面的竖直距离, 代表单位重量的液体从基准面算起 所具有的位置势能
• 井孔抽水试验 • 井孔注水试验
渗透系数的测定方法
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
试验条件: Δh,A,L=const 量测变量: 体积V,t
V=Qt=vAt v=ki
i=Δh/L
h
k VL
土样
L
Aht
A
Q
适用土类:透水性较大的砂性土
V
室内试验方法-常水头试验法
§2.2 土的渗流性与渗透规律
渗透速度v:土体试样全断面的平均渗流速度,也称假想
渗流速度
v
vs
v n
其中,Vs为实际平均流速,孔隙断面的平均流速
达西定律
§2.2 土的渗流性与渗透规律
仁者乐山 智者乐水
适用条件:层流(线性流动) 水 2.0
土力学课件(3土的渗透性与渗流)详解
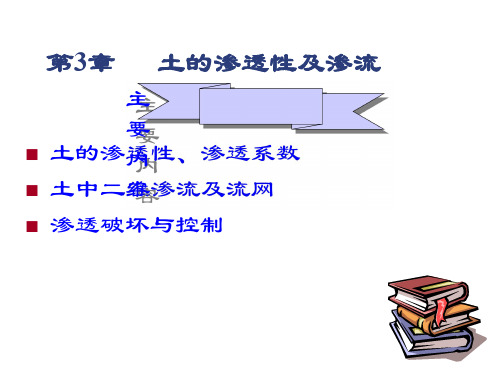
管内减少水量=流经试样水量
-adh=kAh/Ldt 分离变量
积分
k=2.3
aL
At2
t1 lg
h1 h2
k=
aL
A t2
t1 ln
h1 h2
3、影响渗透系数的主要因素 (1)土的粒度成分
v 土粒愈粗、大小愈均匀、形状愈圆滑,渗透系数愈大
v 细粒含量愈多,土的渗透性愈小,
(2)土的密实度 土的密实度增大,孔隙比降低,土的渗透性也减小 土愈密实渗透系数愈小
(3)土的饱和度 土的饱和度愈低,渗透系数愈小
(4)土的结构 扰动土样与击实土样,土的渗透性比同一密度 原状土样的小
(5)水的温度(水的动力粘滞系数) 水温愈高,水的动力粘滞系数愈小 土的渗透系数则愈大
k20 kT T 20
(6)土的构造
T、20分别为T℃和20℃时水的动 力粘滞系数,可查表
水平方向的h>垂直方向v
n
qx q1x q2x qnx qix i1
达西定律
qx kxiH
平均渗透系数
q1x k1 qx q2x k2
q3x k3
H1 H2 H H3
n
qix k1iH 1 k 2iH 2 k n iH n
i 1
整个土层与层面平行的渗透系数
k x
1 H
n
kiH i
i1
(2)垂直渗透系数
H
隧道开挖时,地下 水向隧道内流动
在水位差作用下,水透过土体孔隙的现象称为渗透
渗透
在水位(头)差作用下,水透过土体孔隙的现象
渗透性
土体具有被液体透过的性质
土的渗流 土的变形 土的强度
相互关联 相互影响
土力学 第2章 土的渗透性

n Vv Av 1 Av V A1 A
A > Av
v
vs
v n
Vs=q/Av V=q/A
(3)适用条件
v
层流(线性流):大部分砂土,粉土;
疏松的粘土及砂性较重的粘性土。
o
v=k i
v
v ki (a) 层流 i
(4)两种特例
密实粘性土:近似适用: v=k(i - i0 ) ( i >i0 ) i0:起始水力梯度
选取几组不同的h1和h2及对应的时间t=t2-t1,利用式(2-11)计算出相 应的渗透系数k,然后取其平均值作为该土样的渗透系数。
2. 现场井孔抽水试验
(1)室内试验的优缺点 优点:设备简单、操作方便、费用低廉。 缺点:取样和制样对土扰动、试样不一定是现场的代表性土,导致室内
测定的渗透系数难以反映现场土的实际渗透性。
☆水工建筑物防渗
一般采用“上堵下疏”原则。即上游截渗,延长渗径;下 游通畅渗透水流,减小渗透压力,防止渗透变形。
☆基坑开挖防渗
工程实例:
2003年7月1日,上海市轨道交通4号线发生一起管涌坍 塌事故,防汛墙塌陷、隧道结构损坏、周边地面沉降、造成 三幢建筑物严重倾斜。直接经济损失高达1.5亿人民币。
(2-34)
式中Fs为流土安全系数,通常取1.5~2.0。
பைடு நூலகம்
流土
(2)管涌(潜蚀) 定义:在渗流作用下土体的细土粒在粗土粒形成的孔隙通道中
发生移动并被带出的现象。 长期管涌破坏土的结构,最终导致土体内形成贯通的渗流 管道,造成土体坍陷。
管涌(土体内部细颗粒被带走)
管涌破坏(土体坍塌)
◆判别
①土类条件
第3章 土的渗透性和渗流

板桩墙
基坑
渗流问题 1.渗流量(降水办法) 2.渗透破坏(流砂)
透水层 不透水层
§3.1 概 述
土坝蓄水后水透
土石坝坝基坝身渗流 过坝身流向下游
防渗体
坝体 浸润线
渗流问题: 1.渗流量? 2.渗透破坏?
透水层
3.渗透力?
不透水层
§3.1 概 述 水井渗流
Q 天然水面
透水层
不透水层
渗流问题: 1.渗流量Q? 2.降水深度?
土愈密实,k值得愈小。试
• 土的密实度
验表明,对于砂土,k值对数与孔
• 土的饱和度
隙比及相对密度呈线性关系;对
• 土的结构和构造 粘性土,孔隙比对k值影响更大。
(2)水的性质
§3.2 土的渗透性
4.影响土的渗透系数主要因素
(1)土的性质
• 粒径大小及级配 • 土的密实度
• 土的饱和度 • 土的结构和构造
第3章 土的渗透性和渗流
§3.1 概
述
§3.2 土的渗透性
§3.3 土中二维渗流及流网
§3.4 渗透破坏与控制
§3.1 概 述
土是一种三相组成的多孔介质,其孔隙在空 间互相连通。如果存在水位差的作用,水就会在 土的孔隙中从能量高的点向能量低的点流动。
水等液体在土体孔隙中
流动的现象称为渗流。
土具有被水等液体透过
k1
h1 L1
k2
h2 L2
已知:L1=L2=40cm, k1= 2k2,故2△h1= △h2 ,
代入△h1+△h2 = △h=30cm得:
△h1=10cm,△h2 = 20cm
由此可知,测压管中的水面将升至右端水面以上10cm处。
基坑
渗流问题 1.渗流量(降水办法) 2.渗透破坏(流砂)
透水层 不透水层
§3.1 概 述
土坝蓄水后水透
土石坝坝基坝身渗流 过坝身流向下游
防渗体
坝体 浸润线
渗流问题: 1.渗流量? 2.渗透破坏?
透水层
3.渗透力?
不透水层
§3.1 概 述 水井渗流
Q 天然水面
透水层
不透水层
渗流问题: 1.渗流量Q? 2.降水深度?
土愈密实,k值得愈小。试
• 土的密实度
验表明,对于砂土,k值对数与孔
• 土的饱和度
隙比及相对密度呈线性关系;对
• 土的结构和构造 粘性土,孔隙比对k值影响更大。
(2)水的性质
§3.2 土的渗透性
4.影响土的渗透系数主要因素
(1)土的性质
• 粒径大小及级配 • 土的密实度
• 土的饱和度 • 土的结构和构造
第3章 土的渗透性和渗流
§3.1 概
述
§3.2 土的渗透性
§3.3 土中二维渗流及流网
§3.4 渗透破坏与控制
§3.1 概 述
土是一种三相组成的多孔介质,其孔隙在空 间互相连通。如果存在水位差的作用,水就会在 土的孔隙中从能量高的点向能量低的点流动。
水等液体在土体孔隙中
流动的现象称为渗流。
土具有被水等液体透过
k1
h1 L1
k2
h2 L2
已知:L1=L2=40cm, k1= 2k2,故2△h1= △h2 ,
代入△h1+△h2 = △h=30cm得:
△h1=10cm,△h2 = 20cm
由此可知,测压管中的水面将升至右端水面以上10cm处。
土力学土的渗透性及渗流

8
2、渗流量的计算及渗透变形控制问题
基坑围护结构下的渗流
板桩墙
基坑
透水层
渗流问题:
1. 渗流量? 2. 渗透破坏? 3. 渗水压力?
不透水层
9
基坑开挖降水
井点降水
10
管井降水
11
工程实例 湖南浯溪水电站二期基坑出现管涌
12
2、渗流量的计算及渗透变形控制问题
水井渗流 Q
天然水面
含水层
渗流问题:
38
三、成层土的平均渗透系数
天然土层多呈层状
✓确立各层的k ✓考虑渗流方向
等效渗透系数
39
水平渗流 将土层简化为均质土,便于计算
总流量等于各土层流量之和 (各层的水力梯度相等)
条件:
im
i
h L
Q q j kxiH
q j v j H j k jiH j
等效渗透系数:
m
Q kxiH i k j H j j 1
P1 = γwhw
P2 = γwh2
R + P2 = W + P1
R + γwh2 = L(γ + γw) + γwhw
R = ? R = γ L
0
45
静水中的土体 R = γ L
渗流中的土体
ab
P1
W A=1
P2 R
W = Lγsat=L(γ + γw)
贮水器 hw L 土样
0
Δh
h1 h2
0 滤网
非线性流(紊流) 地下水的渗流速度与 水力梯度成非线性关系
线性稳定流
线性非稳定流
非线性稳定流 非线性非稳定流
我们现在需要掌握和理解的达西定律
2 土力学 第二章 土的渗透性及水的渗流
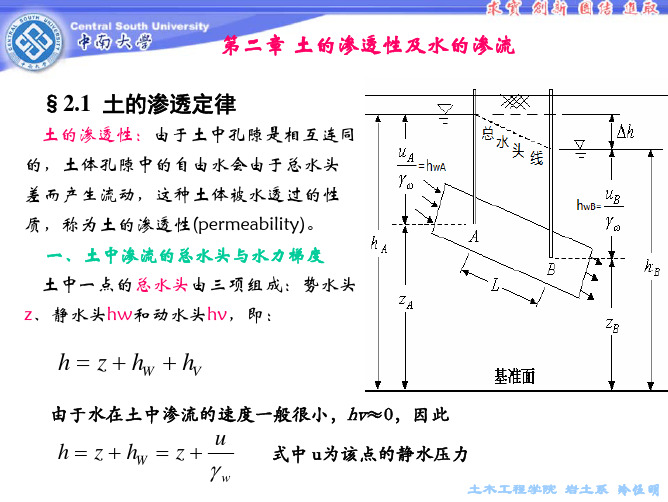
作用方向与渗流方向一致!
二、临界水力梯度及渗透破坏 当土中水向上渗流时,渗透力垂直向上而与土样重力方向相反,若渗透力 等于土样浮度,即
j = iγ w = γ , 得临界水力梯度: i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此,若土中水向上渗流: ⑴若i>icr,会发生流土破坏,即“管涌”; ⑵若i=icr,流土处于临界状态,即“悬浮”; ⑶若i<icr,不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小,hv≈0,因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为:
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差:
作业题:P54: 2-7,2-9 补题1:什么是渗透力、临界水力梯度?
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性:由于土中孔隙是相互连同 的,土体孔隙中的自由水会由于总水头 差而产生流动,这种土体被水透过的性 质,称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成:势水头 z、静水头hw和动水头hv,即:
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得,只能通过试验确定。 测定k值室内方法:定水头法、变水头法。 (1)定水头法 保持总水头差Δh不变,在t时间内,量得透过土样的水量为Q,求k: 根据达西定律
二、临界水力梯度及渗透破坏 当土中水向上渗流时,渗透力垂直向上而与土样重力方向相反,若渗透力 等于土样浮度,即
j = iγ w = γ , 得临界水力梯度: i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此,若土中水向上渗流: ⑴若i>icr,会发生流土破坏,即“管涌”; ⑵若i=icr,流土处于临界状态,即“悬浮”; ⑶若i<icr,不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小,hv≈0,因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为:
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差:
作业题:P54: 2-7,2-9 补题1:什么是渗透力、临界水力梯度?
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性:由于土中孔隙是相互连同 的,土体孔隙中的自由水会由于总水头 差而产生流动,这种土体被水透过的性 质,称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成:势水头 z、静水头hw和动水头hv,即:
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得,只能通过试验确定。 测定k值室内方法:定水头法、变水头法。 (1)定水头法 保持总水头差Δh不变,在t时间内,量得透过土样的水量为Q,求k: 根据达西定律
3清华大学-土力学与地基基础--第02章-土的渗透性和渗流问题

基本要求 绘制方法 主要特点 实际应用
共轭调和,等值线正交
流函数
求解(流网) 边界条件
33
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件
dq e v xdz v zdx
dq o
(vx
v x x
dx )dz
(vz
v z z
平面渗流 稳定渗流
与y、t无关
对单宽dy=1,取一微小单元dx, dz
z
x
Δh
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
32
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
连续性条件 达西定律 流线方程 假定kx=kz
势函数的 基本方程
Laplace方程 (基本方程)
流函数的 基本方程
势函数
dz )dx
dq e dq o
vx vz 0 x z
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
34
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件 v x v z 0
x z
▪ 达西定律
vx
k x
h x
;
vz
k z
观察井
r2 r r1
dr dh
h1 h
h2
缺点: 费用较高,耗时较长
23
§2 土的渗透性和渗流问题 §2.1 土的渗透性与渗流规律
共轭调和,等值线正交
流函数
求解(流网) 边界条件
33
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件
dq e v xdz v zdx
dq o
(vx
v x x
dx )dz
(vz
v z z
平面渗流 稳定渗流
与y、t无关
对单宽dy=1,取一微小单元dx, dz
z
x
Δh
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
32
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
连续性条件 达西定律 流线方程 假定kx=kz
势函数的 基本方程
Laplace方程 (基本方程)
流函数的 基本方程
势函数
dz )dx
dq e dq o
vx vz 0 x z
z
vz
vz z
dz
vx
v
x
v x x
dx
vz
x
34
§2 土的渗透性和渗流问题 §2.2 平面渗流与流网
一. 平面渗流的基本方程及求解 1. 基本方程 水头描述
▪ 连续性条件 v x v z 0
x z
▪ 达西定律
vx
k x
h x
;
vz
k z
观察井
r2 r r1
dr dh
h1 h
h2
缺点: 费用较高,耗时较长
23
§2 土的渗透性和渗流问题 §2.1 土的渗透性与渗流规律
土力学:土的渗透性及渗流

13
3.3.2 流网特征及绘制
等势线表示测压管水头齐平的线,流线表示水质点的运动路线。
1、流网的特征
(1)等势线与流线正交;
(2)流线与等势线构成的各网格长宽比为常数,通常 b / L 1 ;
(3)相邻等势线之间的水头损失相等; (4)各流槽的渗流量相等。
即正交、等比、等水位差、等流量。
2、流网的绘制
土的渗透性及渗流
基本要求:
掌握土的层流渗透定律及渗透性指标;
熟悉渗透性指标的测试方法及影响因素,渗流时渗水量
的计算,渗透破坏与渗流控制问题; 了解二维渗流及流网的概念和应用。
1
本章内容
3.1 概述 3.2 土的渗透性 3.3 土中二维渗流及流网 3.4 渗透破坏与控制
2018/10/22
hi
Hi qy k iy
n
总水头差为: 用等效渗透系数
h hi q y
i 1 i 1
n
Hi k iy
k y表示
H h q y ky
ky H
因此:
k x 由 ki max 控制, k y 由 ki min 控制。
2018/10/22
H
i 1
n
i
/ kiy
12
t
2018/10/22
8
2、现场试验
在现场设置一个抽水井(直径15cm以上)和两个以上的观测井。边抽 水边观察水位情况,当单位时间从抽水井中抽出的水量 q 稳定,并且 抽水井及观测井中的水位稳定之后,测定抽水井和观测井的水位。
qk
dh 2rh dr
q
r2
r1
h2 dr 2k hdh h1 r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dh dr
2)平均流速计算
粗粒土层
h1
h
h2
q v 2 rh
②
不透水层
3)水力梯度计算 4)求渗透系数
dh i dr
r1
③
r r2
将②、 ③代入①,并积分
r2
r1
h2 q dr 2 khdh h1 r
r2 q k ln 2 2 (h2 h1 ) r1
Байду номын сангаас
2. 渗透系数的影响因素
黏土
a×10-7~a×10-10
3. 成层土的平均渗透系数
顺向渗流 垂直渗流
Q Q
⊿h
不透水层
坑底
Q Q Q Q k1 k2 k3
承压水层
⊿h H1 H2 H3
Q1 Q2 Q3
不透水层
k1 k2 k3
H1 H2 H3
H
H
•顺向渗流时
总流量等于各土层流量之和 (各层的水力梯度相等)
m m m
Q v H ki H Q j v j H j k j iH j
cm/s
cm/s i
h L
h
1
(1)v=q/A称为平均流速 discharge velocity,它不是渗流的真实速度。因 为A不是真正的过水面积,而且水在 土中的实际渗流路径是非常复杂的。 (2)Darcy定律是计算分析土的渗 流、渗透固结问题的重要基础。
砂
L
h1
h2
滤 板
2
碎 石
qQ t
'zA=('1 – i1w)L1+('2 – i2w) △ LA =11.34kPa
或
'zA= zA-uzA (1satL1 2sat△ LA) -hwA w =11.34kPa
五、二维稳定渗流steady seepage及流网
渗流状态不随时间而变。
1. 二维稳定渗流的连续方程
(1)连续方程的建立 流入微单元的水量(厚度为1)
z
vx
dz
v z vz dz z vx vx dx x
dqx vx dz 1 vxdz
dqz vz dx dqx dqz vxdz vz dx
流出微单元的水量
vz
dx
x
vx vz (vz dz ) dx (vx dx) dz z x
j 1 j 1 j 1
1 k H
k H
j 1 j
m
j
• 垂直渗流时 总水头损失等于各土层水头损失之和(各层的流量相等)
m m m v v h i H H h j i j H j H j k j 1 k j j 1 j 1
k
k
j 1
H m H j
约1.0×10-6cm/s < 约1.0×10-4cm/s<a×10-2~a×10-3cm/s
(2)孔隙比 决定过水断面面积的大小
孔隙比越大,渗透性越好
e3 , 砂土 k 1 e
黏性土
e2 , e2 1 e
e lg k
(3) 矿物成分 结合水膜使通道减小。 渗透系数:蒙脱石<伊利石<高岭石。 (4)土的结构和构造 黏性土:絮凝结构>分散结构。 层状土:水平和竖向的渗透系数不等。 (5)土的饱和度 不饱和土中的气泡会降低渗透性。 (6)水的动力粘滞度 dynamic coefficient of viscosity 温度越低,粘滞度越大,渗透系数越小。
如图所示,细砂层中的承压水由粉质黏土2(厚度L2=2.5m)、粉质黏土1 (厚度L1=1.5m)向基坑渗入,通过抽水使坑内水位保持在坑底。已知粉质黏土
1的饱和重度为19.5kN/m3,渗透系数为2.5×10-5cm/s;粉质黏土2的饱和重度为
19.8kN/m3,渗透系数为1.0×10-5cm/s;细砂层顶面处的压力水头为6.2m。 (1)计算粉质黏土1、粉质黏土2中的水力梯度。 (2)计算A处( △ LA =0.5m)的静水头。
管 涌
• 发生条件 (1)主要发生在无黏性土。 (2)级配
粒径相差较大(Cu>10);细粒含量较低,不能填满孔隙。
(3)水力梯度
级配连续 时:i = 0.15~0.25; 级配不连续时 :i = 0.10~0.20。
•算 例
坑底 6.2m A 0.5m 粉质黏土2 细 砂 2.5m 粉质黏土1 1.5m
进水
v kTi
h i L
h
温度为T 时的渗透系数
Q 由于 v At
QL 可得渗透系数 kT At h
标准温度下 的渗透系数
土
样
L
滤 板
T k20 kT 20
qQ t
粘滞系数
(2)变水头渗透试验 falling head permeability test 1)由Darcy定律 2)平均流速计算
(1)土颗粒的粒径及级配 决定渗流通道的大小 Hazen(1911)通过对砂的试验发现:土的渗透性由其中的小颗粒控制 渗透系数
2 k c d10
系数 有效粒径 某土的渗透系数
孔隙比e 0.9 >0.25mm粒径 的质量比 70% d10 0.01mm 该土的 渗透系数(重塑) 该土的 用于对比的 渗透系数(原状) 中砂(>0.25mm)
J whA
• 渗透力 seepage force 土中渗流对土粒产生推动、摩擦、拖曳作用力。
j
J wi (kN/m3) V
取土颗粒为隔离体
土粒浮重量
• 有效应力 effective stress 土颗粒之间的作用力。
LA
R LA whA R ( i w ) L A
(2)水力梯度 水头 hydraulic head:单位重量的水所具有的能量。(故量纲为长度)
测压管水头
总水头
h z hw hv z u / w v2 / 2g
势 水 头 位 置 水 头 静 水 头 压 力 水 头 动 水 头 速 度 水 头 孔 隙 水 压 渗 流 速 度
v k (i i0 )
v
vcr
砾及以上的粗粒土 致密黏土
0
i
0 i0
i
三、 渗透系数coefficient of permeability及测定方法
1. 渗透系数测定方法
(1)常水头渗透试验constant head permeability test
由Darcy定律
用于渗透性较好的土
(3)Darcy定律的适用范围 1)砂土及一般黏性土中的渗流通常为层流,故Darcy定律适用。 2)砾及以上的粗粒土在水力梯度较大时形成紊流, Darcy定律 (通常,工程中仍近似采用此关系。) 不适用。 3)黏性很强的致密黏土,水力梯度较小时不发生渗流,且v-i之 间为非线性关系。 v 使用时,可简化为
(2)A处的静水头 总水头 hA= h1 + i1 L1 + i2△ LA=4.781m
6.2m 坑底 粉质黏土1 A 0.5m 粉质黏土2 细 砂 2.5m 1.5m
或者 hA= h2 - i 2( L2 -△ LA)=4.781m 故 hwA= hA - zA= hA - ( L2 -△ LA)= 2.781m (3)A处的有效应力
用于渗透性较差的土
v kTi
①
水头下降
水头 时间
dQ a dh
dt 时间内流过土样的水量
t1
dh
变水头管的截面积
h1
t t+dt
h
v
q dQ 1 a dh ② A dt A A dt
土样截面积 水头差
h2
t2
出 水
L
h 3)水力梯度计算 i L
4)求渗透系数
③
将②、 ③代入①,并积分
j
四、渗透力及临界水力梯度
1. 渗透力
h
hwb
取孔隙水作为隔离体
b-b
b-b截面的孔隙水压
whwb Aw
水的截面积
hwa
渗 流 a-a
L
孔隙水的重量 总渗透力J
w LAw
A
a-a截面的孔隙水压
whwa Aw
whwa Aw
whwb Aw
+ w LAw + J
总渗透力
A Aw
①
② 总的水头损失=流过土1的水头损失+流过土2的水头损失 △ h=△ h1 +△ h2 △ h =i1 L1 + i2 L2 ②
总水头:土1的顶面h1=2.5+1.5=4m,土2的底面h2=6.2m 水头差:△h=h2-h1=6.2-4=2.2m ① 、②联立求解后得到 : i1 =0.2839, i2=0.7097
h 总水 头 x
vz k z
kx kz
第二章 土的渗透性及渗流问题
一、土的渗透性permeability及土中渗流seepage
1. 土的渗透性
土中孔隙相互连通,因此水或其他液体能够在土中流动,形成 渗流,这种性质称为土的渗透性。
2. 土中渗流与工程的关系
(1) 渗透变形及破坏问题 因渗流造成土体变形甚至破坏。 (2) 渗流量的问题 • 土坝坝身、坝基、渠道等的渗漏水量估算; • 基坑开挖渗水量及排水量计算; • 水井供水量估算。
在层流sheet flow状态下,有
v q/ A k i
平 均 流 速 流 量 土 样 的 截 面 积 渗 透 系 数 水 力 梯 度
Henry Philibert Gaspard Darcy (1803-1858) 1803年6月10日出生于法国第戎 (Dijon)。他于1839~1840年设计和 主持建造了第戎镇的供水系统(比巴 黎早20年)。 进水
