2020版高考数学二轮复习专题限时集训7空间几何体的表面积体积及有关量的计算理
高考数学复习考点知识讲解与专项练习17---空间几何体的表面积与体积

因为 VC-ADFE=13× 3+2 4×2 ×2=134,VC-ABE=13× 12×2×2 ×2=43,所以所求几何体的体 积为 VC-ADFE+VC-ABE=134+43=6.
解法三:如图,延长 BC 至点 M,使得 CM=2,延长 EF 至点 N,使得 FN=1,连接
相垂直,且 PA=PB=PC=2,则三棱锥 P-ABC 的外接球与内切球的半径比为________.
3 3+3
答案
2
8 / 23
解析 以 PA,PB,PC 为过同一顶点的三条棱,作长方体,由 PA=PB=PC=2,可知
此长方体即为正方体.设外接球的半径为 R,则 R=
4+4+4 2=
3,设内切球的半径为 r,
A.4 C.36 答案 C
B.16 D.634
解析 设该圆柱的底面半径为 R,则圆柱的高为 2R,则圆柱的表面积 S=S 底+S 侧= 2× R2+2· ·R·2R=54 ,解得 R2=9,即 R=3. 圆柱的体积为 V= R2×2R=54 ,∴该 圆柱的内切球的体积为23×54 =36 .故选 C.
若 O1 的面积为 4 ,AB=BC=AC=OO1,则球 O 的表面积为( )
A.64
B.48
C.36
D.32
10 / 23
答案 A
解析 设 O1 的半径为 r,球的半径为 R,依题意,得 r2=4 ,∴r=2.由正弦定理可
得sinA6B0°=2r,∴AB=2r sin 60°=2 3.∴OO1=AB=2 3.根据球的截面性质,得 OO1⊥平
∴OA= OE2+AE2=
13×
3
2020高考数学总复习空间几何体的表面积和体积PPT课件

1.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱
圆锥
圆台
侧面 展开图
侧面积公式 S 圆柱侧=2πrl S 圆锥侧=πrl
S = 圆台侧 π(r+r′)l
2.多面体的侧面积和表面积 因为多面体的各个面都是平面,所以多面体的侧面积就是侧 面展开图的面积,表面积是侧面积与底面积的和.
A.17 27
B.5 C.10 D.1
9
27
3
(2)若某几何体的三视图(单位:cm)如图所示,则此几何体的 体积等于________cm3.
(3)三棱锥 P-ABC 中,D,E 分别为 PB,PC 的中点,记三棱
锥
D-ABE
的体积为
V 1,P-A B C
的体积为
V
2,则VV
1=________.
2
又∵长方体表面积重叠一部分, ∴几何体的表面积为232+152-2×6×2=360.
1.空间几何体的体积是每年高考的热点,题型为选择题和填 空题.
2.高考对空间几何体的体积的考查常有以下几个命题角度: (1)求简单几何体的体积; (2)求组合体的体积; (3)求以三视图为背景的几何体的体积.
[例 2] (1)如图,网格纸上正方形小格的边长为 1(表示 1 cm), 图中粗线画出的是某零件的三视图,该零件由一个底面半径为 3 cm,高为 6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与 原来毛坯体积的比值为( )
2.直角三角形两直角边 AB=3,AC=4,以 AB 为轴旋转一
周所得的几何体的体积为( )
A.12π
B.16π
C.9π
D.24π
解析:选 B 以 AB 为轴旋转一周所得到的几何体为圆
2020新课标高考总复习数学72空间几何体的表面积与体积
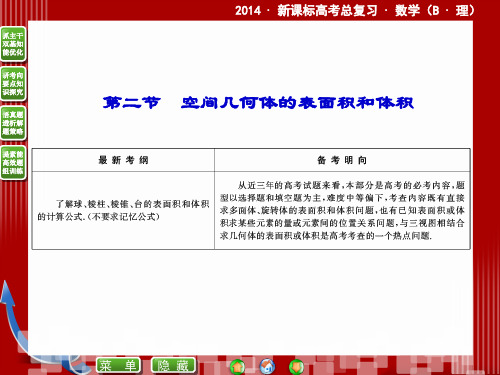
=13×3
2
3×45=2
5
3 .
菜 单 隐藏
抓主干 双基知 能优化
研考向 要点知 识探究
悟真题 透析解 题策略
提素能 高效题 组训练
2014 ·新课标高考总复习 ·数学(B ·理)
菜 单 隐藏
2014 ·新课标高考总复习 ·数学(B ·理)
抓主干 双基知 能优化
研考向
2.(2012年高考上海卷)若一个圆锥的侧面展开图是面积为2π的半
能优化
图和俯视图如图所示,则它的体积的最大值为________,最小值为
研考向
要点知 识探究
________.
悟真题 透析解 题策略
提素能 高效题 组训练
解析:由俯视图及正视图可得,如图所示,由图示可得体积的最 大值为14,体积的最小值为9.
答案:14 9
菜 单 隐藏
2014 ·新课标高考总复习 ·数学(B ·理)
抓主干
双基知
考向三 几何体的展开与折叠
能优化
研考向
[例 3] 如图,在直棱柱 ABC-A′B′C′中,底面是边长为 3 的等
要点知
识探究 边三角形,AA′=4,M 为 AA′的中点,P 是 BC 上一点,且由 P 沿棱
悟真题 透析解
柱侧面经过棱 CC′到 M 的最短路线长为
29,设这条最短路线与 CC′
2014 ·新课标高考总复习 ·数学(B ·理)
抓主干 双基知 能优化
研考向
要点知 识探究
(3)S△PCN=12×CP×CN=12×2×45=45.
悟真题
透析解
题策略
在三棱锥 M-PCN 中,M 到面 PCN 的距离,
提素能 高效题 组训练
2020高考数学二轮微专题空间几何体的表面积和体积考点考向考题点拨(55张)
第3页
考情分析 典型例题 课后作业
微专题八 空间几何体的表面积和体积
(2) 设棱长为 a 的正方体的体积和表面积分别为 V1,S1,底面半径和高均为 r 的圆 锥的体积和侧面积分别为 V2,S2,若VV12=3π,则SS12的值为________.
第4页
考情分析 典型例题 课后作业
4 解析:设圆柱底面的半径为 r,则 V=πr2·6r=3·4π3r3+πr2·8,解得 r=4.
第12页
考情分析 典型例题 课后作业
微专题八 空间几何体的表面积和体积
4. 已知四棱锥的底面是边长为 2的正方形,侧棱长均为 5.若圆柱的一个底面的圆 周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆
2(
等
积
转
换
)
:
V1
=
VB-A1MC
=
1 2
VB-A1AC
=
1 2
VA1-ABC
,
V2
=
2VA1-BC1B1
=
2VB-A1B1C1=2VA1-ABC,所以VV12=14.
第11页
考情分析 典型例题 课后作业专题八 空间几何体的表面积和体积
3. 如图,在一个圆柱形容器内盛有高度为 8 cm 的水,若放入三个相同的球(球的 半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则此圆柱底面的半径是 ________cm.
第6页
考情分析 典型例题 课后作业
微专题八 空间几何体的表面积和体积
(3) 118.8 解析: 长方体 ABCD-A1B1C1D1 的体积为 6×6×4=144(cm3),四边形 EFGH 是菱形,面积为其对角线乘积的一半,S 菱形 EFGH=12×6×4=12(cm2),四棱 锥 O-EFGH 的高为 3 cm,其体积为13×12×3=12(cm3),所以长方体 ABCD-A1B1C1D1 挖去四棱锥 O-EFGH 后所得的几何体的体积为 132 cm3,132×0.9=118.8(g),所以 制作该模型所需原料的质量为 118.8 g.
2020届高考数学(理)二轮复习全程方略课件:专题11 空间几何体的三视图、表面积及体积 Word版含答案

2.(2017·石家庄一模)某几何体的三视图如图所示(网格线中 每个小正方形的边长为 1),则该几何体的表面积为( )
A.48 B.54 C.64 D.60
[解析] 由三视图可知该几何体为棱长分别为 3,4,6 的长方体 所截得,如图所示,其中 M 为棱的中点,S△MCD=12×6×5=15, S△MAD=S△MBC=12×5×3=125,S△MAB=12×6×4=12,S = 矩形 ABCD 6×3=18,所以该几何体的表面积为 15+125×2+12+18=60, 故选 D.
数学
大二轮复习
第一部分
全程方略课件
专题11 空间几何体的三视图、表面 积及体积
知识网络构建
专题11 空间几何体的三视图、表面 积及体积
1 高考考点聚
焦
2 核心知识整
合
3 高考真题体
验
4 命题热点突
破
5 课后强化训练来自高考考点聚焦高考考点
空间几何体的 三视图与直观 图的关系
空间几何体的 表面积与体积 的计算
[答案] 2+π2
6.(2017·江苏卷,6)如图,在圆柱 O1O2 内有一个球 O, 该球与圆柱的上、下底面及母线均相切,记圆柱 O1O2 的体积
为 V1,球 O 的体积为 V2,则VV21的值是32_______.
[解析] 设球 O 的半径为 R, ∵球 O 与圆柱 O1O2 的上、下底面及母线均相切, ∴圆柱 O1O2 的高为 2R,底面半径为 R. ∴VV12=π43Rπ2R·23R=32.
•命题方向1 空间几何体的三视图
(1)(2017·青岛一模)某几何体的三视图如
图所示,且该几何体的体积是 3,则正(主)视图中的 x 的
2020年高考数学专题复习空间几何体的表面积与体积
空间几何体的表面积与体积1.圆柱、圆锥、圆台的侧面展开图及其侧面积公式(1)正方体的棱长为a,外接球的半径为R,内切球的半径为r;①若球为正方体的外接球,则2R=3a;②若球为正方体的内切球,则2r=a;③若球与正方体的各棱相切,则2R′=2a.(2)长方体的共顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a2+b2+c2.(3)正四面体的棱长为a,外接球的半径为R,内切球的半径为r①外接球:球心是正四面体的中心;半径R=64a;②内切球:球心是正四面体的中心;半径r=612a.判断正误(正确的打“√”,错误的打“×”)(1)多面体的表面积等于各个面的面积之和.( )(2)锥体的体积等于底面积与高之积.( )(3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( ) (5)长方体既有外接球又有内切球.( )(6)圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS .( )答案:(1)√ (2)× (3)× (4)√ (5)× (6)×如图,一个空间几何体的正(主)视图、侧(左)视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( )A .1B .12C .13D .16解析:选D.由三视图可知,该几何体为三棱锥,V =13Sh =13×12×1×1×1=16,故选D.一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .2π+4D .3π+4解析:选D.由几何体的三视图可知,该几何体为半圆柱,直观图如图所示. 表面积为2×2+2×12×π×12+π×1×2=4+3π.(教材习题改编)直角三角形三边长分别是3 cm 、4 cm 、5 cm ,绕两直角边旋转一周分别形成两个几何体,则其侧面积分别为________cm 2、________cm 2.答案:20π 15π某几何体的三视图如图所示(单位:cm),则该几何体的表面积是__________ cm 2,体积是__________ cm 3.解析:由三视图可得该几何体是由一个长、宽、高分别为4、4、2的长方体和一个棱长为2的正方体组合而成的,故表面积为S =4×4×2+4×2×4+2×2×4=80(cm 2),体积为V =4×4×2+2×2×2=40(cm 3).答案:80 40空间几何体的表面积(1)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A .17πB .18πC .20πD .28π(2)某几何体的三视图如图所示,则该几何体的表面积等于( )A .8+2 2B .11+2 2C .14+2 2D .15【解析】 (1)由三视图可得此几何体为一个球切割掉18后剩下的几何体,设球的半径为r ,故78×43πr 3=283π,所以r =2,表面积S =78×4πr 2+34πr 2=17π,选A.(2)由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,如图所示.直角梯形斜腰长为12+12=2,所以底面周长为4+2,侧面积为2×(4+2)=8+22,两底面的面积和为2×12×1×(1+2)=3,所以该几何体的表面积为8+22+3=11+2 2.【答案】 (1)A (2)B空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题注意衔接部分的处理. (3)旋转体的表面积问题注意其侧面展开图的应用.1.(2019·嘉兴期中)若圆锥的侧面展开图是圆心角为120°、半径为1的扇形,则这个圆锥的表面积与侧面积的比是( )A .4∶3B .2∶1C .5∶3D .3∶2解析:选A.圆锥的侧面积=π×12×120360=π3,圆锥的底面半径=2π×1×120360÷2π=13, 圆锥的底面积=π·19=π9,圆锥的表面积=侧面积+底面积=4π9,所以这个圆锥的表面积与侧面积的比为4∶3.2.(2019·浙江省名校协作体高三联考)一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的表面积为________.解析:由三视图可知,该几何体为一长方体ABCD A 1B 1C 1D 1中挖去一个四棱锥P ABCD ,如图所示,易得PA =PB =32+(2)2=11,所以S △PAB =12×2×10=10,所以表面积S =22+2×3×4+4×10=28+410. 答案:28+410空间几何体的体积(高频考点)空间几何体的体积是每年高考的热点,多与三视图结合考查,题型多为选择题、填空题,难度较小.主要命题角度有:(1)求简单几何体的体积; (2)求组合体的体积.角度一 求简单几何体的体积(1)如图,将一个长方体用过相邻的三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为________.(2)如图,正方体ABCD A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1EDF 的体积为________.【解析】 (1)设长方体的相邻三条棱长分别为a ,b ,c ,它截出棱锥的体积为V 1=13×12×12a ×12b ×12c =148abc ,剩下的几何体的体积V 2=abc -148abc =4748abc ,所以V 1∶V 2=1∶47. (2)(等积法)三棱锥D 1EDF 的体积即为三棱锥F DD 1E 的体积.因为E ,F 分别为AA 1,B 1C 上的点,所以在正方体ABCD A 1B 1C 1D 1中,△EDD 1的面积为定值12,F 到平面AA 1D 1D 的距离为定值1,所以VD 1EDF =VF DD 1E =13×12×1=16. 【答案】 (1)1∶47 (2)16角度二 求组合体的体积(分割法)(1)(2017·高考浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( )A .π2+1B .π2+3C .3π2+1D .3π2+3(2)(2017·高考山东卷)由一个长方体和两个14圆柱体构成的几何体的三视图如图,则该几何体的体积为________.【解析】 (1)由几何体的三视图可得,该几何体是由半个圆锥和一个三棱锥组成的,故该几何体的体积V =13×12π×3+13×12×2×1×3=π2+1,故选A.(2)由题意知该几何体是由一个长方体和两个14圆柱体构成,其中长方体的体积V 1=2×1×1=2,两个14圆柱体的体积之和V 2=14×π×12×1×2=π2,所以该几何体的体积V =V 1+V 2=2+π2.【答案】 (1)A (2)2+π21.(2018·高考浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( )A .2B .4C .6D .8解析:选C.由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积V =12×(1+2)×2×2=6.故选C.2.(2019·宁波十校联合模拟)如图为某几何体的三视图,则该几何体的体积为________cm 3,表面积为________cm 2.解析:由已知三视图得到几何体是一个底面直角边分别为3,4的直角三角形,高为5的三棱柱,割去一个底面与三棱柱底面相同,高为3的三棱锥,所以该几何体的体积为:12×3×4×5-13×12×3×4×3=24 cm 3;表面积为:12×(2+5)×4+12×(2+5)×3+12×3×4+5×5+34×52=1112+2543 cm 2.答案:241112+2534球与空间几何体的接、切问题(1)(2017·高考全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4C .π2D .π4(2)(2019·温州七校联考)三棱锥P ABC 中,AB =BC =15,AC =6,PC ⊥平面ABC ,PC =2,则该三棱锥的外接球的表面积为( )A .253πB .252πC .833πD .832π【解析】 (1)设圆柱的底面半径为r ,则r 2=12-⎝ ⎛⎭⎪⎫122=34,所以,圆柱的体积V =34π×1=3π4.(2)由题可知,△ABC 中AC 边上的高为15-32=6,球心O 在底面ABC 的投影即为△ABC 的外心D ,设DA =DB =DC =x ,所以x 2=32+(6-x )2,解得x =546,所以R 2=x 2+⎝ ⎛⎭⎪⎫PC 22=758+1=838(其中R 为三棱锥外接球的半径),所以外接球的表面积S =4πR 2=832π,故选D.【答案】 (1)B (2)D若本例(2)中的△ABC 变为边长为3的等边三角形.求三棱锥外接球的表面积. 解:由题意得,此三棱锥外接球即为以△ABC 为底面、以PC 为高的正三棱柱的外接球,因为△ABC 的外接圆半径r =32×3×23=1,外接球球心到△ABC 的外接圆圆心的距离d =1,所以外接球的半径R =r 2+d 2=2,所以三棱锥外接球的表面积S =4πR 2=8π.处理球的“切”“接”问题的求解策略 (1)“切”的处理与球有关的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.(2)“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.1.如图,已知球O 是棱长为1的正方体ABCD A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为( )A .66π B .π3C .π6D .33π解析:选C.平面ACD 1截球O 的截面为△ACD 1的内切圆. 因为正方体的棱长为1, 所以AC =CD 1=AD 1=2, 所以内切圆的半径r =66, 所以S =πr 2=π×636=16π.2.(2019·丽水模拟)三棱锥P ABC 的四个顶点都在体积为500π3的球的表面上,底面ABC 所在的小圆面积为16π,则该三棱锥的高的最大值为( )A .4B .6C .8D .10解析:选C.依题意,设题中球的球心为O 、半径为R ,△ABC 的外接圆半径为r ,则4πR33=500π3,解得R =5,由πr 2=16π,解得r =4,又球心O 到平面ABC 的距离为R 2-r 2=3,因此三棱锥P ABC 的高的最大值为5+3=8.数学文化与立体几何(2019·金华十校联考)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈;上袤二丈,无广;高一丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈,问它的体积是多少?”已知1丈为10尺,现将该楔体的三视图给出,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )A .5 000立方尺B .5 500立方尺C .6 000立方尺D .6 500立方尺【解析】 该楔体的直观图如图中的几何体ABCDEF .取AB 的中点G ,CD 的中点H ,连接FG ,GH ,HF ,则该几何体的体积为四棱锥F GBCH 与三棱柱ADE GHF 的体积之和.又可以将三棱柱ADE GHF 割补成高为EF ,底面积为S =12×3×1=32平方丈的一个直棱柱,故该楔体的体积V =32×2+13×2×3×1=5立方丈=5 000立方尺.【答案】 A求解与数学文化有关的立体几何问题应过的三关我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异”,“幂”是截面积,“势”是几何体的高,意思是两等高立方体,若在每一等高处的截面积都相等,则两立方体体积相等.已知某不规则几何体与如图所对应的几何体满足“幂势同”,则该不规则几何体的体积为( )A .4-π2B .8-4π3C .8-πD .8-2π解析:选C.由祖暅原理可知,该不规则几何体的体积与已知三视图的几何体体积相等.根据题设所给的三视图,可知题图中的几何体是从一个正方体中挖去一个半圆柱,正方体的体积为23=8,半圆柱的体积为12×(π×12)×2=π,因此该不规则几何体的体积为8-π,故选C.处理空间几何体体积问题的思路(1)“转”:指的是转换底面与高,将原来不容易求面积的底面转换为容易求面积的底面,或将原来不容易看出的高转换为容易看出,并容易求解长度的高;(2)“拆”:指的是将一个不规则的几何体拆成几个简单的几何体,便于计算; (3)“拼”:指的是将小几何体嵌入一个大几何体中,如有时将一个三棱锥复原成一个三棱柱,将一个三棱柱复原成一个四棱柱,还台为锥,这些都是拼补的方法.易错防范(1)求组合体的表面积时,要注意各几何体重叠部分的处理.(2)底面是梯形的四棱柱侧放时,容易和四棱台混淆,在识别时要紧扣定义,以防出错.[基础达标]1.(2019·嘉兴期中)某球的体积与表面积的数值相等,则球的半径是( ) A .1 B .2 C .3D .4解析:选C.设球的半径为r ,则球的体积为 43πr 3,球的表面积为4πr 2. 因为球的体积与其表面积的数值相等, 所以43πr 3=4πr 2,解得r =3.2.(2019·义乌模拟)某空间几何体的三视图如图所示,则该几何体的表面积为( )A .12+4 2B .18+8 2C .28D .20+8 2解析:选D.由三视图可知该几何体是底面为等腰直角三角形的直三棱柱,如图.则该几何体的表面积为S =2×12×2×2+4×2×2+22×4=20+82,故选D.3.(2019·浙江高校招生选考试题)如图(1),把棱长为1的正方体沿平面AB 1D 1和平面A 1BC 1截去部分后,得到如图(2)所示几何体,则该几何体的体积为( )A .34B .1724C .23D .12解析:选B.把棱长为1的正方体沿平面AB 1D 1和平面A 1BC 1截去部分后,得到几何体的体积:V =VABCD A 1B 1C 1D 1-VA A 1B 1D 1-VB A 1B 1C 1+VN A 1B 1M=1×1×1-13×⎝ ⎛⎭⎪⎫12×1×1×1-13×⎝ ⎛⎭⎪⎫12×1×1×1+13×⎝ ⎛⎭⎪⎫12×22×22×12=1724. 4.(2019·金华十校联考)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个等腰直角三角形,则该几何体外接球的体积为( )A .32π B .32C .3πD .3解析:选A.由题意得,该几何体为四棱锥,且该四棱锥的外接球即为棱长为1的正方体的外接球,其半径为32,故体积为43π⎝ ⎛⎭⎪⎫323=32π,故选A.5.若某空间几何体的三视图如图所示,则该几何体的表面积是( )A .48+πB .48-πC .48+2πD .48-2π解析:选A.该几何体是正四棱柱挖去了一个半球,正四棱柱的底面是正方形(边长为2),高为5,半球的半径是1,那么该几何体的表面积为S =2×2×2+2×4×5-π×12+2π×12=48+π,故选A.6.(2019·台州四校高三联考)一个多面体的直观图和三视图如图所示,点M 是AB 上的动点,记四面体EFMC 的体积为V 1,多面体ADF BCE 的体积为V 2,则V 1V 2=()A .14B .13C .12D .不是定值,随点M位置的变化而变化解析:选B.由三视图可知多面体ADF BCE 是直三棱柱,其底面是等腰直角三角形(直角边长为a ),且四边形DFEC 与四边形ABCD 都是正方形,它们的边长均为a .因为M 是AB 上的动点,且易知AB ∥平面DFEC ,所以点M 到平面DFEC 的距离等于点B 到平面DFEC 的距离,为a ,所以V 1=V E FMC =V M EFC =13×12a ·a ·a =a 36,又V 2=12a ·a ·a =a32,故V 1V 2=a 36a 32=13,故选B.7. (2019·宁波市余姚中学期中检测)某几何体的三视图如图所示(单位:cm),则该几何体的体积为________ cm 3,表面积为________cm 2.解析:由三视图可知:该几何体是由一个半球去掉14后得到的几何体.所以该几何体的体积=34×12×43×π×13=π2cm 3.表面积=34×12×4π×12+12×π×12+34×π×12=11π4 cm 2.答案:π2 11π48.(2019·瑞安市龙翔高中高三月考)一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为________,正四棱锥的体积为________.解析:由正四棱锥的俯视图,可得到正四棱锥的直观图如图, 则该正四棱锥的正视图为三角形PEF (E ,F 分别为AD ,BC 的中点), 因为正四棱锥的所有棱长均为2, 所以PB =PC =2,EF =AB =2,PF =3, 所以PO =PF 2-OF 2=3-1=2,所以该正四棱锥的正视图的面积为12×2×2=2;正四棱锥的体积为13×2×2×2=423.答案: 24239.(2019·温州市高考模拟)已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为________,表面积为________.解析:根据三视图可知几何体是一个四棱锥,底面是一个边长为2的正方形,PE ⊥平面ABCD ,且PE =2,其中E 、F 分别是BC 、AD 的中点,连接EF 、PA ,所以几何体的体积V =13×2×2×2=83,在△PEB 中,PB =PE 2+BE 2=5,同理可得PC =5,因为PE ⊥平面ABCD ,所以PE ⊥CD ,因为CD ⊥BC ,BC ∩PE =E ,所以CD ⊥平面PBC ,则CD ⊥PC , 在△PCD 中,PD =PC 2+DC 2=5+4=3, 同理可得PA =3,则PF ⊥AD ,在△PDF 中,PF =PD 2-DF 2=9-1=22,所以此几何体的表面积S =2×2+12×2×2+2×12×2×5+12×2×22=6+25+2 2.答案:836+25+2 210.已知球O 的表面积为25π,长方体的八个顶点都在球O 的球面上,则这个长方体的表面积的最大值等于________.解析:设球的半径为R ,则4πR 2=25π,所以R =52,所以球的直径为2R =5,设长方体的长、宽、高分别为a 、b 、c ,则长方体的表面积S =2ab +2ac +2bc ≤a 2+b 2+a 2+c 2+b 2+c 2=2(a 2+b 2+c 2)=50.答案:5011. 如图所示,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,求该多面体的体积.解:如图,分别过点A 、B 作EF 的垂线,垂足分别为G 、H ,连接DG 、CH ,容易求得EG =HF =12,AG =GD =BH =HC =32,所以S △AGD =S △BHC =12×22×1=24,所以该多面体的体积V =V E ADG +V F BHC +V AGD BHC =13×24×12+13×24×12+24×1=23. 12.如图,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).(1)当圆柱底面半径r 取何值时,S 取得最大值?并求出该最大值(结果精确到0.01平方米);(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出用于制作灯笼的三视图(作图时,不需考虑骨架等因素).解:(1)由题意可知矩形的高即圆柱的母线长为 9.6-8×2r8=1.2-2r , 所以塑料片面积S =πr 2+2πr (1.2-2r ) =πr 2+2.4πr -4πr 2=-3πr 2+2.4πr =-3π(r 2-0.8r ).所以当r =0.4米时,S 有最大值,约为1.51平方米. (2)若灯笼底面半径为0.3米,则高为1.2-2×0.3=0.6(米). 制作灯笼的三视图如图[能力提升]1.在封闭的直三棱柱ABC A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4πB .9π2C .6πD .32π3解析:选B.由题意可得若V 最大,则球与直三棱柱的部分面相切,若与三个侧面都相切,可求得球的半径为2,球的直径为4,超过直三棱柱的高,所以这个球放不进去,则球可与上下底面相切,此时球的半径R =32,该球的体积最大,V max =43πR 3=4π3×278=9π2.2.(2019·瑞安市龙翔高中高三月考)如图,已知在四棱锥P ABCD 中,底面ABCD 是菱形,PA ⊥底面ABCD ,AB =1,PA ·AC =1,∠ABC =θ⎝ ⎛⎭⎪⎫0<θ≤π2,则四棱锥P ABCD 的体积V 的取值范围是( )A .⎣⎢⎡⎭⎪⎫26,13 B .⎝ ⎛⎦⎥⎤212,16 C .⎝⎛⎦⎥⎤26,13 D .⎣⎢⎡⎭⎪⎫212,16 解析:选A.由已知,四边形ABCD 的面积S =sin θ, 由余弦定理可求得AC =2-2cos θ, 所以PA =12-2cos θ,所以V =13·sin θ2-2cos θ,所以V =26·sin 2θ1-cos θ=26·1+cos θ.所以,当cos θ=0,即θ=π2时,四棱锥P ABCD 的体积V 的最小值是26;当cos θ=1,即θ=0时,四棱锥P ABCD 的体积V 的最大值是13.因为0<θ≤π2,所以P ABCD 的体积V 的取值范围是⎣⎢⎡⎭⎪⎫26,13. 3.(2019·浙江名校协作体高三联考)某几何体的三视图如图所示,且该几何体的体积是 3 cm 3,则正视图中的x 的值是________cm ,该几何体的表面积是________cm 2.解析:由三视图可知,该几何体是底面为直角梯形的四棱锥,其直观图如图所示,由棱锥的体积公式得,13×12×(1+2)×3x =3⇒x =2,侧面ADS ,CDS ,ABS 为直角三角形,侧面BCS 是以BC 为底的等腰三角形,所以该几何体的表面积为S =12[(1+2)×3+2×2+3×2+1×7+2×7]=53+37+42.答案:253+37+424.如图,在△ABC 中,AB =BC =2,∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD =DA ,PB =BA ,则四面体PBCD 的体积的最大值是________.解析:由AB =BC =2,∠ABC =120°,可得AC =23,要求四面体PBCD 的体积,关键是寻找底面三角形BCD 的面积S △BCD 和点P 到平面BCD 的距离h .易知h ≤2.设AD =x ,则DP =x ,DC =23-x ,S △DBC =12×(23-x )×2×sin 30°=23-x 2,其中x ∈(0,23),且h ≤x ,所以V P BCD =13×S △BCD×h =23-x 6×h ≤23-x 6·x ≤16⎝ ⎛⎭⎪⎫23-x +x 22=12,当且仅当23-x =x ,即x =3时取等号.故四面体PBCD 的体积的最大值是12.答案:125.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置,P 为所在线段中点,Q 为顶点,求在几何体表面上,从P 到Q 点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2, S 圆柱侧=(2πa )·(2a )=4πa 2, S 圆柱底=πa 2,所以S 表=2πa 2+4πa 2+πa 2=(2+5)πa 2. (2)沿P 点与Q 点所在母线剪开圆柱侧面,如图.则PQ =AP 2+AQ 2=a 2+(πa )2=a 1+π2, 所以从P 点到Q 点在侧面上的最短路径的长为a 1+π2.6.已知底面为正三角形的三棱柱内接于半径为1的球,求此三棱柱的体积的最大值. 解:如图,设球心为O ,三棱柱的上、下底面的中心分别为O 1,O 2,底面正三角形的边21 长为a ,则AO 1=23×32a =33a . 由已知得O 1O 2⊥底面,在Rt △OAO 1中,由勾股定理得OO 1=12-⎝ ⎛⎭⎪⎫33a 2=3·3-a 23, 所以V 三棱柱=34a 2×2×3·3-a 23=3a 4-a 62, 令f (a )=3a 4-a 6(0<a <2),则f ′(a )=12a 3-6a 5=-6a 3(a 2-2),令f ′(a )=0,解得a = 2.因为当a ∈(0,2)时,f ′(a )>0;当a ∈(2,2)时,f ′(a )<0,所以函数f (a )在(0,2)上单调递增,在(2,2)上单调递减.所以f (a )在a = 2 处取得极大值.因为函数f (a )在区间(0,2)上有唯一的极值点,所以a = 2 也是最大值点.所以(V 三棱柱)max =3×4-82=1.。
2020届高考数学二轮复习重点模块练:立体几何(3)空间几何体的表面积与体积 Word版含答案【KS5U 高考】
立体几何(3)空间几何体的表面积与体积1、如图,网格纸上小正方形的边长为1,粗线画出的是某个几何体的三视图,则该几何体的表面积为( )A.445π42++() B.445π442+++()C.12π+12D.12π442++2、做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积价格为b元,当造价最低时,锅炉的底面直径与高的比为( )A. abB.2abC.baD.2ba3、几何体甲与几何体乙的三视图如图所示,几何体甲的正视图和侧视图为两个全等的等腰三角形,且等腰三角形的高与几何体乙的三视图中的圆的直径相等,若几何体甲与乙的体积相等,则几何体甲与乙的表面积之比为()3113+31-17+4、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A.7B.6C.5D.35、某几何体的三视图如图所示,图中正方形的边长为2,四条用虚线表示的线段长度均相等,则该几何体的体积为( )A.2π83- B.82π- C.8π83- D.88π-6、将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为( )A.4π3B.2πC.3πD.π67、某几何体的三视图如图所示,其中正视图中的曲线为圆弧,则该几何体的体积为( )A.16π- B.16-4π C.322π- D.644π-8、一正三棱柱的每条棱长都是3,且每个顶点都在球O的表面上,则球O的半径为( )2167 D. 39、如图是某实心机械零件的三视图,则该机械的表面积为()A.662π+B.664π+C.662π-D.664π-10、在三棱锥S ABC -中,SA SB SC ,,两两垂直,且3SA =,4SB =,5SC =,其顶点都在球O 的球面上,则球O 的表面积为 。
11、已知一个圆锥的底面积为π,侧面积为2π,则该圆锥的体积为________12、《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”现有一阳马,其正视图和侧视图是如图所示的直角三角形若该阳马的顶点都在同一个球面上,且该球的表面积为24π,则该“阳马”的体积为______.13、若三个球的表面积之比是1:2:3,则它们的体积之比是 .14、—个直角梯形的两底边长分别为2和5,高为4,绕其较长的底边所在直线旋转一周,所得到的几何体的表面积为__________.15、如图所示,在边长为4的正三角形ABC 中,E,F 依次是AB,AC 的中点,,,AD BC EH BC FG BC ⊥⊥⊥,D,H,G 为垂足,若将ABC △绕AD 旋转180°,求阴影部分形成的几何体的表面积与体积.答案以及解析1答案及解析:答案:A解析:由三视图可知该几何体是一个长、宽、高分别为2,2,1的长方体与一个底面半径为2,高为4的圆锥的组合体,其表面积()221412π2π424445π+422S=⨯⨯+⨯+⨯⨯⨯+=+,故选A.2答案及解析:答案:C解析:如图,设圆柱的底面半径为R,高为h,则2πV R h=,设造价为y,则222222π2π2π2π2ππV bVy R a Rha aR Rb aRR R=+=+⋅=+,∴22'4πbVy aRR=-.令0y'=并将2πV R h=,代人解得2R bh a=.3答案及解析:答案:B解析:由三视图可知甲为圆锥,乙为球,设球的半径为R,设圆锥底面半径为r,则圆锥高2h R=,母线长22l r h+324133R r hππ=,即22222,43R r l r R r==+,221223314S r rl r r rS Rπππ++⋅+===4答案及解析:答案:A解析:设圆台较小底面的半径为,则根据题意有π(3)84πS r r l=+=侧,解得7r=.5答案及解析:答案:A解析:由三视图可知,该几何体是一个棱长为2的正方体挖 去一个底面半径为1,高为2的圆锥而得到的,所以该几何体的体积3212π2π12833V =-⨯⨯⨯=-,故选 A.6答案及解析:答案:A解析:将棱长为2的正方体木块切削成一个体积最大的球时,球的直径等于正方体的棱长2,则球的半径R =1, 则球的体积344ππ33V R =⋅⋅= 故选A.7答案及解析:答案:A 解析:由三视图可得该几何体是正四棱柱挖掉一个14圆柱,底面是正视图中图形(边长为2的正方形截去一个半径为1的14圆),底面积为14π4-,该柱体的高为4,则该柱体的体积为14(4π)16π4⨯-=-.8答案及解析: 答案:A解析:解:正三棱柱的两个底面的中心的连线的中点就是球的球心,球心与顶点的连线长就是半径,所以,2r ==.故选A.9答案及解析:答案:B 解析:将三视图还原为直观图,可得该机械零件是由一个长方体及两个圆柱组合而成,其中圆柱的底面圆心与长方体侧面的中心重合,圆柱的母线与长方体左右侧面垂直,如图. 由三视图可得,长方体的长宽高分别为3,3,4,两个圆柱的底面半径为都为1,高都为1. 所以该机械零件的表面积为长方体的表面积与两个圆柱侧面积之和.因为长方体的表面积为()233343466⨯⨯+⨯+⨯=,两个圆柱的侧面积为22π114π⨯⨯⨯=,所以该机械零件的表面积为664π+.10答案及解析:答案:50π解析:因为SA SB SC ,,两两垂直所以可将三棱锥S ABC -放在长方体中,则长方体的体对角线即为球O 的直径.球O 22222234552SA SB SC ++++,所以球O 的表面积为2524ππ50=⎝⎭⨯.11答案及解析: 3π 解析:设圆锥的底面半径为r ,母线长为l∵圆锥的底面积为π,侧面积为2π∴222rl r ππππ=⎧⎨=⎩解得1,2r l ==∴高22213h =-∴该圆锥的体积为221131333r h πππ=⨯=12答案及解析:答案:163解析:如图所示,设“阳马”的外接球半径为R由球的表面积2424π=πR ,解得6R该“阳马”为四棱锥-P ABCD ,底面ABCD 为矩形, 其中⊥PD 底面ABCD ,2=AB ,4=AD ,则该“阳马”的外接球直径为22226++=PB PD AD AB 解得2=PD ;所以该“阳马”的体积为11642233=⨯⨯⨯=V . 故答案为:163.13答案及解析: 答案:1:2233解析:∵三个球的表面积之比是1:2:3, ∴三个球的半径之比是23∴三个球的体积之比是1:2233故答案为: 1:223314答案及解析:答案:52π解析:直角梯形绕其较长的底边所在直线旋转一周后形成—个高为3、底面半径为4的圆锥和一个高为2、底面半径为4的圆柱的组合体,从而可得其表面积为2221π42π422π43452π2⨯+⨯⨯+⨯⨯+.15答案及解析:答案:所得几何体是一个圆锥挖去一个圆柱后形成的,,221=ππππ4π8π12πS R Rl DC DC AC +=⋅+⋅⨯=+=锥表 ,2S =2π2πRl DG FG =⋅⋅=柱侧∴所求几何体的表面积S 12πS S =+=+锥表柱侧, 由2211=ππ233V BD AD ⋅⋅=⨯⨯=圆锥, 22=ππ1V HD EH ⋅⋅=⨯=圆柱,∴所求几何体的体积为V V -==圆锥圆柱.。
2020新课标高考理科数学二轮复习教师用书:第2部分 专题4 第1讲 空间几何体的表面积、体积及有关量的计算
第1讲 空间几何体的表面积、体积及有关量的计算■做小题·激活思维·1.已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为( )A .1 cmB .2 cmC .3 cm D.32 cm B [S 表=πr 2+πrl =πr 2+πr ·2r =3πr 2=12π,∴r 2=4,∴r =2(cm).]2.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________.92π [设正方体的棱长为a ,则6a 2=18,∴a = 3. 设球的半径为R ,则由题意知2R =a 2+a 2+a 2=3, ∴R =32.故球的体积V =43πR 3=43π×⎝ ⎛⎭⎪⎫323=92π.] 3.(2019·南昌模拟)如图,直角梯形ABCD 中,AD ⊥DC ,AD ∥BC ,BC =2CD =2AD =2,若将该直角梯形绕BC 边旋转一周,则所得的几何体的表面积为________.(2+3)π [由题图中数据可得:S 圆锥侧=12×π×2×2=2π,S 圆柱侧=π×2×1=2π,S 底面=π×12=π.所以几何体的表面积S =S 圆锥侧+S 圆柱侧+S 底面=2π+2π+π=(2+3)π.]4.如图,正三棱柱ABC -A 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 的中点,则三棱锥A -B 1DC 1的体积为________.1 [在正三棱柱ABC -A 1B 1C 1中,∵AD ⊥BC ,AD ⊥BB 1,BB 1∩BC =B ,∴AD ⊥平面B 1DC 1.∴VA -B 1DC 1=13S △B 1DC 1·AD =13×12×2×3×3=1.]5.已知一个圆台的下底面半径为3,高为2,当圆台的上底面半径r ′变化时,圆台体积的变化范围是________.(6π,18π) [V 圆台=13π(r 2+rr ′+r ′2)h,0<r ′<3.当上底面面积为0时,圆台变为圆锥,V 圆锥=13πr 2h =6π;当r ′=3时,圆台变为圆柱,V 圆柱=πr 2h =18π.所以圆台体积的变化范围是()6π,18π.]■扣要点·查缺补漏·1.空间几何体分为多面体和旋转体研究其特性常采用化空间为平面的方法,如截面图、轴截面等,如T1.2.旋转体的表面积和体积公式(1)S 圆柱侧=2πrl ,S 圆锥侧=πrl ,S 圆台侧=π(r 1+r 2)l ,S 球=4πR 2 ,V 柱=sh ,V 锥=13sh ,V 球=43πR 3,如T3.(2)球的截面的性质:用一个平面去截球,截面是圆面;球心和截面圆的距离d 与球的半径R 及截面圆半径r 之间的关系是r =R 2-d 2.3.空间几何体的体积与表面积求法(1)割补法:求不规则几何体的体积或表面积时,通过割补,转化成规则几何体求解.(2)等积变换:涉及三棱锥的体积,注意灵活选择底面和对应的高.如T4.4.多面体与球(1)当球内切于正方体时,球的直径等于正方体的棱长,当球外接于长方体时,长方体的体对角线长等于球的直径;当球与正方体各棱都相切时,球的直径等于正方体底面的对角线长.如T2.(2)若正四面体的棱长为a,则正四面体的外接球半径为64a,内切球半径为612a.考点1空间几何体的展开图、截面图■高考串讲·找规律·1.(2018·全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为()A.334 B.233C.324 D.32切入点:将每条棱所在直线与平面α所成的角相等转化为共顶点的三条棱所在直线与平面α所成角相等.A[记该正方体为ABCD-A′B′C′D′,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱A′A,A′B′,A′D′与平面α所成的角都相等.如图,连接AB′,AD′,B′D′,因为三棱锥A′-AB′D′是正三棱锥,所以A′A,A′B′,A′D′与平面AB′D′所成的角都相等.分别取C′D′,B′C′,BB ′,AB ,AD ,DD ′的中点E ,F ,G ,H ,I ,J ,连接EF ,FG ,GH ,IH ,IJ ,JE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面AB ′D ′平行,且截正方体所得截面的面积最大.又EF =FG =GH =IH =IJ =JE=22,所以该正六边形的面积为6×34×⎝ ⎛⎭⎪⎫222=334,所以α截此正方体所得截面面积的最大值为334,故选A.]2.[一题多解](2019·全国卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.图1 图226 2-1 [先求面数有如下两种方法.法一:由“半正多面体”的结构特征及棱数为48可知,其上部分有9个面,中间部分有8个面,下部分有9个面,共有2×9+8=26(个)面.法二:一般地,对于凸多面体,顶点数(V )+面数(F )-棱数(E )=2.(欧拉公式) 由题图知,棱数为48的半正多面体的顶点数为24.故由V +F -E =2,得面数F =2+E -V =2+48-24=26.再求棱长.作中间部分的横截面,由题意知该截面为各顶点都在边长为1的正方形上的正八边形ABCDEFGH,如图,设其边长为x,则正八边形的边长即为棱长.连接AF,过H,G分别作HM⊥AF,GN⊥AF,垂足分别为M,N,则AM=MH=NG=NF=2 2x.又AM+MN+NF=1,∴22x+x+22x=1.∴x=2-1,即半正多面体的棱长为2-1.]立体几何中的“截、展”(1)“截”,指的是截面,如柱、锥、台的直截面、斜截面以及旋转体的轴截面,它们集中反映了几何体的主要元素的数量关系,能够列出有关量的关系.(2)“展”,指的是侧面展开图,在有关沿表面的最短路径问题中,就是求侧面或某些面展开图上两点间的距离,即将空间问题转化为平面问题.一般多面体常以棱所在的直线为剪开线展开,旋转体以母线为剪开线展开.■考题变迁·提素养·1.(侧面展开图)如图,一立在水平地面上的圆锥形物体的母线长为4 m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处.若该小虫爬行的最短路程为4 3 m,则圆锥底面圆的半径等于________m.43[把圆锥侧面沿过点P的母线展开成如图所示的扇形,由题意OP=4,PP′=43,则cos∠POP′=42+42-(43)22×4×4=-12,所以∠POP′=2π3.设底面圆的半径为r,则2πr=2π3×4,所以r=43.]2.(截面的计算问题)(2019·广州模拟)已知圆锥的底面直径为3,母线长为1,过圆锥的顶点,作圆锥的截面,则截面面积的最大值为________.12[由于圆锥的底面直径为3,母线长为1,设圆锥轴截面的顶角为α,则cos α=1+1-32×1×1=-12.又α∈(0,π),∴α=2π3.因等截面面积的最大值为12×1×1×sinπ2=12.]考点2空间几何体的表面积和体积■高考串讲·找规律·[高考解读·教师授课资源]空间几何体的表面积和体积是每年的必考内容,题型既有选择题也有解答题,以往多与三视图综合考查,由于新课标对三视图不作要求,对表面积和体积的考查也以单一考点的形式出现在高考试题中.角度一:空间几何体的表面积1.(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.122πB.12πC.82πD.10π切入点:过直线O1O2的平面截该圆柱所得的轴截面是面积为8的正方形.关键点:找出圆柱的底面半径及母线的长.B[因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径为22,所以该圆柱的表面积为2×π×(2)2+2π×2×22=12π.]角度二:空间几何体的体积2.(2019·全国卷Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为________g.切入点:E、F、G、H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.关键点:正确求出四棱锥的体积.118.8[由题知挖去的四棱锥的底面是一个菱形,对角线长分别为6 cm和4 cm,故V挖去的四棱锥=13×12×4×6×3=12(cm3).又V长方体=6×6×4=144(cm3),所以模型的体积为V长方体-V挖去的四棱锥=144-12=132(cm3),所以制作该模型所需原料的质量为132×0.9=118.8(g).]3.(2019·全国卷Ⅱ)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.[解](1)证明:由已知得B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,B1C1∩EC1=C1,所以BE⊥平面EB1C1.(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A1EB1=45°,故AE=AB=3,AA1=2AE=6.如图,作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF =AB =3.所以四棱锥E -BB 1C 1C 的体积V =13×3×6×3=18.空间几何体的表面积与体积的求法(1)求三棱锥的体积时,等体积转化是常用的方法,转化原则是其高易求,底面放在已知几何体的某一面上.(2)求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体以易于求解.(3)已知几何体的三视图,可去判断几何体的形状和各个度量,然后求解表面积和体积.■考题变迁·提素养·1.(组合体的表面积)如图1所示,已知正方体面对角线长为a ,沿阴影面将它切割成两块,拼成如图2所示的几何体,那么此几何体的表面积为( )图1 图2A .(1+22)a 2B .(2+2)a 2C .(3+22)a 2D .(4+2)a 2B [拼成的几何体比原正方体的表面增加了两个截面,减少了原来两个正方形面.由于截面为矩形,长为a ,宽为 22a ,所以面积为22a 2,所以拼成的几何体表面积为4×⎝ ⎛⎭⎪⎫22a 2+2×22a 2=(2+2)a 2,故选B.] 2.(等体积法的应用)(2019·潍坊模拟)若正三棱锥A -BCD 中,AB ⊥AC ,且BC =1,则三棱锥A -BCD 的高为( )A.66 B.33C.22 D.63A[设三棱锥A-BCD的高为h.依题意得AB,AC,AD两两垂直,且AB=AC=AD=22BC=22,△BCD的面积为34×12=34.由V A-BCD=V B-ACD得13S△BCD·h=13S△ACD·AB,即13×34×h=13×12×⎝⎛⎭⎪⎫222×22,解得h=66,即三棱锥A-BCD的高h=66.]3.(等体积转化法)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.16[三棱锥D1-EDF的体积即为三棱锥F-DD1E的体积.因为E,F分别为AA1,B1C上的点,所以在正方体ABCD-A1B1C1D1中,△EDD1的面积为定值12,F到平面AA1D1D的距离为定值1,所以VD1-EDF=VF-DD1E=1 3×12×1=16.]考点3球与几何体的切接问题■高考串讲·找规律·[高考解读·教师授课资源]高考对该点的考查要求较高,注重了对空间想象力和化归转化能力的考查,平时训练应强化柱、锥与球切接关系的各种组合训练,进一步提升直观想象及数学运算素养.角度一:球与多面体的切、接问题1.(2017·全国卷Ⅱ)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为________.14π[∵长方体的顶点都在球O的球面上,∴长方体的体对角线的长度就是其外接球的直径.设球的半径为R ,则2R =32+22+12=14.∴球O 的表面积为S =4πR 2=4π×⎝ ⎛⎭⎪⎫1422=14π.] 2.(2016·全国卷Ⅲ)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4π B.9π2 C .6π D.32π3切入点:分析直三棱柱的内切球最大时与哪些面相切.B [由题意得要使球的体积最大,则球与直三棱柱的若干面相切.设球的半径为R .因为△ABC 的内切圆半径为6+8-102=2,所以R ≤2.又2R ≤3,所以R ≤32,所以V max =43π⎝ ⎛⎭⎪⎫323=92π.故选B.] 3.(2019·全国卷Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°, 则球O 的体积为( )A .86πB .46πC .26π D.6πD [因为点E ,F 分别为P A ,AB 的中点,所以EF ∥PB ,因为∠CEF =90°,所以EF ⊥CE ,所以PB ⊥CE .取AC 的中点D ,连接BD ,PD ,易证AC ⊥平面BDP ,所以PB ⊥AC ,又AC ∩CE =C ,AC ,CE ⊂平面P AC ,所以PB ⊥平面P AC , 所以PB ⊥P A ,PB ⊥PC ,因为P A =PB =PC ,△ABC 为正三角形,所以P A ⊥PC ,即P A ,PB ,PC 两两垂直,将三棱锥P -ABC 放在正方体中如图所示.因为AB =2,所以该正方体的棱长为2,所以该正方体的体对角线长为6,所以三棱锥P -ABC 的外接球的半径R =62,所以球O 的体积V =43πR 3=43π⎝ ⎛⎭⎪⎫623=6π,故选D. ]角度二:球与旋转体的切、接问题4.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .π B.3π4 C.π2 D.π4B [设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r =12-⎝ ⎛⎭⎪⎫122=32. ∴圆柱的体积为V =πr 2h =34π×1=3π4.故选B.]解决与球有关的切、接问题的策略,(1)“接”的处理:,①构造正(长)方体,转化为正(长)方体的外接球问题.,②空间问题平面化,把平面问题转化到直角三角形中,作出适当截面(过球心,接点等).,③利用球心与截面圆心的连线垂直于截面定球心所在直线.,(2)“切”的处理:,①体积分割法求内切球半径.,②作出合适的截面(过球心,切点等),在平面上求解,,③多球相切问题,连接各球球心,转化为处理多面体问题.[教师备选题]1.(2017·江苏高考)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________. 32 [设球O 的半径为R ,∵球O 与圆柱O 1O 2的上、下底面及母线均相切,∴圆柱O 1O 2的高为2R ,底面半径为R .∴V 1V 2=πR 2·2R 43πR3=32.] 2.(2018·全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D -ABC 体积的最大值为( )A .12 3B .18 3C .24 3D .54 3B [设等边三角形ABC 的边长为x ,则12x 2sin 60°=93,得x =6.设△ABC的外接圆半径为r ,则2r =6sin 60°,解得r =23,所以球心到△ABC 所在平面的距离d =42-(23)2=2,则点D 到平面ABC 的最大距离d 1=d +4=6,所以三棱锥D -ABC 体积的最大值V max =13S △ABC ×6=13×93×6=18 3.]1.(三棱锥的外接球)三棱锥P -ABC 中,△ABC 为等边三角形,P A =PB =PC =3,P A ⊥PB ,三棱锥P -ABC 的外接球的体积为( )A.272πB.2732π C .273π D .27πB [∵三棱锥P -ABC 中,△ABC 为等边三角形,P A =PB =PC =3,∴△P AB ≌△PBC ≌△P AC .∵P A ⊥PB ,∴P A ⊥PC ,PC ⊥PB .以P A ,PB ,PC 为过同一顶点的三条棱作正方体(如图所示),则正方体的外接球同时也是三棱锥P -ABC 的外接球.∵正方体的体对角线长为32+32+32=33,∴其外接球半径R =332.因此三棱锥P -ABC 的外接球的体积V =4π3×⎝ ⎛⎭⎪⎫3323=2732π,故选B.] 2.(直棱柱的外接球)已知直三棱柱ABC -A 1B 1C 1的各顶点都在以O 为球心的球面上,且∠BAC =3π4,AA 1=BC =2,则球O 的体积为( ) A .43πB .8πC .12πD .20πA [在底面△ABC 中,由正弦定理得底面△ABC 所在的截面圆的半径r =BC 2sin ∠BAC =22sin 3π4= 2.所以直三棱柱ABC -A 1B 1C 1的外接球的半径R =r 2+⎝ ⎛⎭⎪⎫AA 122=(2)2+12= 3.故直三棱柱ABC -A 1B 1C 1的外接球的体积为43πR 3=43π.选A.]3.(动态最值问题)已知点A ,B ,C ,D 在同一个球的球面上,AB =BC =6,∠ABC =90°.若四面体ABCD 体积的最大值为3,则这个球的表面积为( )A .2πB .4πC .8πD .16πD [∵AB =BC =6,∠ABC =90°,∴S △ABC =12×6×6=3,AC =23,△ABC 所在球的小圆的圆心Q 是斜边AC 的中点,∴小圆的半径为 3.∵四面体ABCD 的体积取得最大值,且S △ABC 不变,∴当底面ABC 上的高最大时体积最大.∴当DQ 与平面ABC 垂直时体积最大, 最大值为13·S △ABC ·DQ =3, 即13×3×DQ =3,解得DQ =3,如图所示,设球心为O ,半径为R ,在Rt △AQO 中,OA 2=OQ 2+AQ 2,即R 2=(3-R )2+(3)2,解得R =2.∴这个球的表面积S =4πR 2=16π,故选D.]4.(内切球)已知一个三棱锥的所有棱长均为2,则该三棱锥的内切球的体积为________.354π [由题意可知,该三棱锥为正四面体,如图所示.AE =AB ·sin 60°=62,AO =23AE =63,DO =AD 2-AO 2=233,三棱锥的体积V D -ABC =13S △ABC ·DO =13, 设内切球的半径为r ,则V D -ABC =13r (S △ABC +S △ABD +S △BCD +S △ACD )=13,r =36,V 内切球=43πr 3=354π.]。
全国数学高考二轮复习考点28 空间几何体的表面积与体积-2020年高考数学(文)
专题28 空间几何体的表面积与体积了解球、棱柱、棱锥、台的表面积和体积的计算公式.一、柱体、锥体、台体的表面积1.旋转体的表面积2.多面体的表面积多面体的表面积就是各个面的面积之和,也就是展开图的面积.棱锥、棱台、棱柱的侧面积公式间的联系:二、柱体、锥体、台体的体积 1.柱体、锥体、台体的体积公式2.柱体、锥体、台体体积公式间的关系3.必记结论(1)一个组合体的体积等于它的各部分体积之和或差; (2)等底面面积且等高的两个同类几何体的体积相等. 三、球的表面积和体积 1.球的表面积和体积公式设球的半径为R ,它的体积与表面积都由半径R 唯一确定,是以R 为自变量的函数,其表面积公式为24πR ,即球的表面积等于它的大圆面积的4倍;其体积公式为34π3R . 2.球的切、接问题(常见结论)(1)若正方体的棱长为a ,则正方体的内切球半径是12a ;正方体的外接球半径是2a ;与正方体所有棱相切的球的半径是2a .(2)若长方体的长、宽、高分别为a ,b ,h(3)若正四面体的棱长为a ;与. (4)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径. (5)球与圆台的底面与侧面均相切,则球的直径等于圆台的高.考向一 柱体、锥体、台体的表面积1.已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.2.多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理,以确保不重复、不遗漏. 3.求多面体的侧面积时,应对每一个侧面分别求解后再相加;求旋转体的侧面积时,一般要将旋转体展开为平面图形后再求面积.典例1 某几何体的三视图如图所示,则该几何体的表面积为A .5πB .6πC .6π2+D .5π2+【答案】D【解析】由三视图可知,该几何体为两个半圆柱构成, 其表面积为22π1π12π11215π2⨯⨯+⨯⨯+⨯⨯+⨯=+, 故选D .【名师点睛】本题考查由三视图求表面积,本题的图形结构比较简单,易错点是两个几何体重叠的部分忘记去掉,求表面积时常会设计此种陷阱.典例2 若正四棱柱1111ABCD A B C D -的底边长为2,1AC 与底面ABCD 成45°角,则三棱锥1B ACC -的表面积为A .6+B .4+C .8D .10【答案】A【解析】由1AC 与底面ABCD 成45°角,且正四棱柱1111ABCD A B C D -的底边长为2,可知棱柱的高为故三棱锥1B ACC -的表面积为1111222262222⨯⨯+⨯+⨯⨯=+ 故答案为A.1.某几何体的三视图如图所示,则该几何体的表面积为A .46B .48C .50D .522.榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,凸出部分叫榫,凹进部分叫卯,榫和卯咬合,起到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如图所示是一种榫卯的三视图,其表面积为A.192 B.186C.180 D.198考向二柱体、锥体、台体的体积空间几何体的体积是每年高考的热点之一,题型既有选择题、填空题,也有解答题,难度较小,属容易题. 求柱体、锥体、台体体积的一般方法有:(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用等体积法、割补法等方法进行求解.①等体积法:一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积.②割补法:运用割补法处理不规则的空间几何体或不易求解的空间几何体的体积计算问题,关键是能根据几何体中的线面关系合理选择截面进行切割或者补成规则的几何体.要弄清切割后或补形后的几何体的体积是否与原几何体的体积之间有明显的确定关系,如果是由几个规则的几何体堆积而成的,其体积就等于这几个规则的几何体的体积之和;如果是由一个规则的几何体挖去几个规则的几何体而形成的,其体积就等于这个规则的几何体的体积减去被挖去的几个几何体的体积.因此,从一定意义上说,用割补法求几何体的体积,就是求体积的“加、减”法.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.典例3 如图所示的网格是由边长为1的小正方形构成,粗线画出的是某几何体的三视图,则该几何体的体积为A .40B .103C .163D .803【答案】D【解析】根据三视图可得,该几何体是三棱柱BCE AGF -割去一个三棱锥A BCD -所得的几何体,如图所示:所以其体积为11118044444423223V ⎛⎫=⨯⨯⨯-⨯⨯⨯⨯⨯= ⎪⎝⎭. 故选D.典例4 如图,几何体EF −ABCD 中,DE ⊥平面ABCD ,CDEF 是正方形,ABCD 为直角梯形,AB//CD ,AD ⊥DC ,△ACB 是腰长为2√2的等腰直角三角形.(1)求证:BC ⊥AF ;(2)求几何体EF −ABCD 的体积.【解析】(1)因为△ACB 是腰长为2√2的等腰直角三角形, 所以AC ⊥BC .因为DE ⊥平面ABCD ,所以DE ⊥BC . 又DE//CF ,所以CF ⊥BC , 又AC ∩CF =C ,所以BC ⊥平面ACF . 所以BC ⊥AF .(2)因为△ABC 是腰长为2√2的等腰直角三角形, 所以AC =BC =2√2,AB =√AC 2+BC 2=4,所以AD =BCsin∠ABC =2√2×sin45°=2,CD =AB −BCcos∠ABC =4−2√2×cos45°=2. 所以DE =EF =CF =2,由勾股定理得AE =√AD 2+DE 2=2√2, 因为DE ⊥平面ABCD , 所以DE ⊥AD .又AD ⊥DC,DE ∩DC =D , 所以AD ⊥平面CDEF .所以111333△几何体几何体几何体四边形=ABC EF ABCD A CDEF F ACB CDEF V V V S AD S CF CD DE AD ---=+⋅+⋅⋅⋅=+ 11111162222323323AC BC CF ⨯⋅⋅=⨯⨯⨯+⨯⨯=.3,则a 的值为AB .3C .D 4.如图,在斜三棱柱111ABC A B C -中,底面ABC 是边长为2的正三角形,M 为棱BC 的中点,13BB =,1AB 160CBB ∠=︒.(1)求证:AM ⊥平面11BCC B ; (2)求斜三棱柱111ABC A B C -的体积.考向三 球的表面积和体积1.确定一个球的条件是球心和球的半径,已知球的半径可以利用公式求球的表面积和体积;反之,已知球的体积或表面积也可以求其半径.2.球与几种特殊几何体的关系:(1)长方体内接于球,则球的直径是长方体的体对角线长;(2)正四面体的外接球与内切球的球心重合,且半径之比为3∶1;(3)直棱柱的外接球:找出直棱柱的外接圆柱,圆柱的外接球就是所求直棱柱的外接球.特别地,直三棱柱的外接球的球心是上、下底面三角形外心连线的中点;(4)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径;(5)球与圆台的底面和侧面均相切,则球的直径等于圆台的高.3.与球有关的实际应用题一般涉及水的容积问题,解题的关键是明确球的体积与水的容积之间的关系,正确建立等量关系.4.有关球的截面问题,常画出过球心的截面圆,将空间几何问题转化为平面中圆的有关问题解决.球心到截面的距离d 与球的半径R 及截面圆的半径r 之间满足关系式:d =典例5 《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑, PA ⊥平面ABC ,2PA AB ==,4AC =,三棱锥P ABC -的四个顶点都在球O 的球面上,则球O 的表面积为 A .8π B .12π C .20π D .24π【答案】C【解析】如图,由题可知,底面△ABC 为直角三角形,且则BC ==,则球O则球O 的表面积24π20πS R ==. 故选C.典例6 四棱锥P ABCD -的底面为正方形ABCD ,PA ⊥底面ABCD ,2AB =,若该四棱锥的所有顶点都在体积为9π2的同一球面上,则PA 的长为A .3B .2C .1D .12【答案】C【解析】连接AC 、BD 交于点E ,取PC 的中点O ,连接OE ,可得OE ∥P A ,∵PA ⊥底面ABCD ,∴OE ⊥底面ABCD ,可得O 到四棱锥的所有顶点的距离相等,即O 为球心,设球的半径为R ,可得12R PC ==349ππ32⋅=, 解得P A =1. 故选C .5.一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是A .16πB .14πC .12πD .8π6.已知,,,A B C D 是某球面上不共面的四点,且1AB BC AD ===,BD AC == BC AD ⊥,则此球的体积为A BCD 考向四 空间几何体表面积和体积的最值求解空间几何体表面积和体积的最值问题有两个思路:一是根据几何体的结构特征和体积、表面积的计算公式,将体积或表面积的最值转化为平面图形中的有关最值,根据平面图形的有关结论直接进行判断;二是利用基本不等式或是建立关于表面积和体积的函数关系式,然后利用函数的方法或者利用导数方法解决.典例7 如图,A 1A 是圆柱的母线,AB 是圆柱底面圆的直径,C 是底面圆周上异于A ,B 的任意一点,A 1A =AB =2.(1)求证:BC ⊥平面A 1AC ;(2)求三棱锥A 1-ABC 的体积的最大值.【解析】(1)因为C 是底面圆周上异于A ,B 的任意一点,且AB 是圆柱底面圆的直径, 所以BC ⊥AC .因为AA 1⊥平面ABC ,BC ⊂平面ABC , 所以AA 1⊥BC . 又AA 1∩AC =A , 所以BC ⊥平面AA 1C .(2)方法一:设AC=x(0<x<2),在Rt△ABC中,BC=√AB2−AC2=√4−x2,故V三棱锥A1−ABC =13S△ABC×AA1=13×12×AC×BC×AA1=13x√4−x2=13√x2(4−x2)=13√−(x2−2)2+4.因为0<x<2,0<x2<4,所以当x2=2,即x=√2时,三棱锥A1-ABC的体积取得最大值2 3 .方法二:在Rt△ABC中,AC2+BC2=AB2=4,从而V三棱锥A1−ABC =13S△ABC×AA1=13×12×AC×BC×AA1=13AC×BC≤13×AC2+BC22=23,当且仅当AC=BC=√2时等号成立.所以三棱锥A1-ABC的体积的最大值为2 3 .7.表面积为16π的球内接一个正三棱柱,则此三棱柱体积的最大值为A.4 B.√10C.8 D.√151.3,3,6这个长方体的八个顶点都在同一个球面上,则这个球的表面积是A.12π B.18πC.36π D.6π2.△ABC的斜二侧直观图如图所示,则△ABC的面积为A.22B.1C D.23.某几何体的三视图如图所示,则该几何体的体积为A.1B.2C.3D.64.一个四棱锥的三视图如图所示,其正视图和侧视图为全等的等腰直角三角形,俯视图是边长为2的正方形,则该几何体的表面积为A.B.4C.2+D.4+5.一个与球心距离为2的平面截球所得圆面面积为π,则球的表面积为A.20πB.20√2πC.16πD.16√2π6.我国古代数学名著《孙子算经》中有如下问题:“今有筑城,上广二丈,下广五丈四尺,高三丈八尺,长五千五百五十尺,秋程人功三百尺.问:须工几何?”意思是:“现要筑造底面为等腰梯形的直棱柱的城墙,其中底面等腰梯形的上底为2丈、下底为5.4丈、高为3.8丈,直棱柱的侧棱长为5550尺.如果一个秋天工期的单个人可以筑出300立方尺,问:一个秋天工期需要多少个人才能筑起这个城墙?”(注:一丈等于十尺)A .24642B .26011C .52022D .780337.如图所示,半径为4的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差为A .24πB .28πC .32πD .36π8.已知圆锥的高h 和底面半径r 之比:2:1h r =,且圆锥的体积18πV =,则圆锥的表面积为A .B .9(1π+C .D .9(1π+9.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为A .31π6B .16π3C .17π3D .35π610.中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑.如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,2AD =,1ED =,若鳖臑P ADE -的体积为l ,则阳马P ABCD -的外接球的表面积等于A .17πB .18πC .19πD .20π11.如图,网格纸上小正方形的边长为a ,粗实线画出的是某几何体的三视图,若该几何体的表面积为3+,则a 的值为A .14 B .13C .12D .112.已知三棱锥P ABC -的各顶点都在同一球面上,PC ⊥底面ABC ,若1PC AC ==,2AB =,且60BAC ∠=︒,则此球的表面积等于A .28πB .20πC .7πD .5π13.已知等边三角形的边长为2,将该三角形绕其任一边所在的直线旋转一周而形成的曲面所围成的几何体的体积为__________.14.若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为3,圆心角为2π3的扇形,则该圆锥的体积为__________.15.将若干毫升水倒入底面半径为4cm 的圆柱形器皿中,量得水面高度为8cm,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是__________cm.16.正三棱锥的高为1,底面边长为,正三棱锥内有一个球与其四个面相切,则此球的表面积是 .17.已知三棱锥P ABC -的外接球半径为2,PA ⊥平面ABC ,AB BC ⊥,PA AC =,则该三棱锥体积的最大值为__________.18.已知四面体ABCD 中,5,8AB AD BC DC BD AC ======,则四面体ABCD 的体积为__________.19.如图所示的几何体QPABCD 为一简单组合体,在底面ABCD 中,60DAB ∠=︒,AD DC ⊥,AB BC ⊥,平面QD ABCD ⊥,∥PA QD ,1PA =,2AD AB QD ===.(1)求证:平面平面PAB QBC ⊥; (2)求该组合体QPABCD 的体积.1.(2019年高考浙江卷)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm ),则该柱体的体积(单位:cm 3)是A .158B .162C .182D .3242.(2018新课标I 文科)在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为A .8 B.C.D.3.(2018年浙江卷)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .2B .4俯视图正视图C .6D .84.(2018新课标I 文科)已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A .B .12πC .D .10π5.(2018年高考新课标Ⅲ文科)设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为 A.B .C .D .6.(2017新课标全国Ⅲ文科)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A .90πB .63πC .42πD .36π7.(2017新课标全国Ⅲ文科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .π B .3π4 C .π2D .π48.(2017浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .12π+B .32π+C .312π+ D .332π+ 9.(2019年高考全国Ⅲ卷文科)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.10.(2019年高考北京卷文科)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.11.(2019年高考天津卷文科)底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.12.(2019年高考江苏卷)如图,长方体1111ABCD A B C D 的体积是120,E 为1CC 的中点,则三棱锥E −BCD的体积是 ▲ .13.(2017山东文科)由一个长方体和两个圆柱体构成的几何体的三视图如图,则该几何体的体积为 .14.(2017天津文科)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为___________.1415.(2017江苏)如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 .16.(2018江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.17.(2018天津卷文)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱锥A 1–BB 1D 1D 的体积为__________.18.(2018新课标II 文科)已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30 ,若SAB △的面积为8,则该圆锥的体积为__________.19.(2017新课标全国Ⅰ文科)已知三棱锥S −ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S −ABC 的体积为9,则球O 的表面积为________. 20.(2019年高考全国Ⅱ卷文数)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积.21.(2017新课标全国Ⅰ文科)如图,在四棱锥P −ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o .(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=o ,且四棱锥P −ABCD 的体积为83,求该四棱锥的侧面积.22.(2018新课标I 文科)如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB DA ⊥.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且23BP DQ DA==,求三棱锥Q ABP-的体积.1.【答案】B【解析】该几何体是如图所示的一个四棱锥P ABCD-,棱锥的底面是边长为4的正方形,一条长为3的侧棱与底面垂直,4个侧面都是直角三角形,由所给数据可得该几何体的表面积为34542444822S⨯⨯⎛⎫=⨯++⨯=⎪⎝⎭,故选B.2.【答案】A【解析】由三视图还原几何体,可知该几何体为组合体,上部分是长方体,棱长分别为263,,,下部分为长方体,棱长分别为663,,,其表面积为()4632662623192S=⨯⨯+⨯⨯++⨯⨯=.故选A.【名师点睛】本题考查了求组合体的表面积问题,关键是由三视图还原几何体图形,注意题目中的计算. 3.【答案】A【解析】由三视图可知,几何体的直观图如图:是一个三棱锥和一个三棱柱的组合体,的等腰直角三角形,高为a ,所以体积为2111232a ⨯⨯+⨯2a ⨯⨯=解得a =故选A .【名师点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力.三视图问题是考查学生空间想象能力的最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体的三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状. 4.【解析】(1)如图,连接1B M ,因为底面ABC 是边长为2的正三角形,所以AM BC ⊥,且AM = 因为13BB =,160CBB ∠=o,1BM=,所以222113213cos607B M =+-⨯⨯⨯=o,所以1B M =又因为1AB =所以2221110AM B M AB +==, 所以1AM B M ⊥, 又因为1B M BC M =I , 所以AM ⊥平面11BCC B .(2)设斜三棱柱111ABC A B C -的体积为V ,则111193323sin 60.322A B BC B BC V V S AM -==⨯⋅=⨯⨯⨯=o △ 所以斜三棱柱111ABC A B C -的体积为9.2【名师点睛】本题考查了立体几何中线面垂直的证明,几何体体积的求法,熟练掌握线面关系的证明原理非常重要,属于基础题.(1)根据底面为正三角形,易得AM BC ⊥;由各边长度,结合余弦定理,可求得1B M 的值,再根据勾股定理逆定理可得1AM B M ⊥,从而可证AM ⊥平面11BCC B ;(2)将斜棱柱的体积,转化为棱锥的体积,结合三角形面积公式可求解. 5.【答案】A【解析】由三视图知:几何体是球体切去14后余下的部分,球的半径为2,∴几何体的表面积S =(1﹣14)×4π×22+π×22=16π.故答案为A.【名师点睛】(1)本题主要考查由三视图找到几何体原图,考查几何体的表面积的计算,意在考查学生对这些知识的掌握水平和空间想象推理能力.(2)通过三视图找几何体原图的方法有两种:直接法和模型法. 6.【答案】A【解析】由222AB AD BD +=,得AB AD ⊥,又BC AD ⊥,所以AD ⊥平面ABC ,则AD AC ⊥,又222AB BC AC +=,所以,ABC ACD △△都是直角三角形,由三棱锥的外接球的性质知,球心O 为CD 的中点,且CD =球的半径12R CD ==,所以球的体积A .【名师点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.先确定三角形BCD 外接圆的半径,再解方程得外接球半径,最后根据球的体积公式得结果. 7.【答案】C【解析】由题意,得该球的半径为2,设正三棱柱的侧棱长为2ℎ(0<ℎ<2),底面边长为a ,如图,则O A '=,O ′O =ℎ,ℎ2+(√3a 3)2=4,即a 2=12−3ℎ2,则该正三棱柱的体积为()22124222V a h h h ⎛=⨯⋅=- ⎝⎭,则()2432V h '=-,当0h <<时,V ′>02h <<时,V ′<0,即当h =()24V h =-取到极大值,也是最大值,为8, 故所求三棱柱的体积的最大值为8.故选C .1.【答案】A=,所以该球的表面积是24π12πS ==,故选A.【名师点睛】该题考查的是有关长方体的外接球的表面积问题,在解题的过程中,首先要明确长方体的外接球的球心应在长方体的中心处,即长方体的体对角线是其外接球的直径,从而求得结果. 2.【答案】D【解析】∵1OA =,2OB =,45ACB ∠=︒, ∴原图形中两直角边长分别为2,2, 因此,Rt △ABC 的面积为12222S =⨯⨯=. 故选D . 3.【答案】B【解析】由题意可知该几何体的形状如图:1AC =,2CD =,3BC =,AC CD ⊥,四边形BCDE 是矩形,AC BC ⊥,所以该几何体的体积为:123123⨯⨯⨯=.故选B .【名师点睛】本题考查几何体的体积的求法,画出几何体的图形,利用三视图的数据求解几何体的体积即可.三视图与几何体的对应关系的判断是解题的关键. 4.【答案】D【解析】由三视图可知该几何体为如图所示的正四棱锥:底面为边长为2的正方形,四个侧面为边长为2的等边三角形.故该几何体的表面积为122422422S =⨯+⨯⨯⨯⨯=+ 故选D . 5.【答案】A【解析】用一平面去截球所得截面的面积为π,所以小圆的半径为1.已知球心到该截面的距离为2,所以球的半径为√1+4=√5,所以表面积为4π⋅5=20π.故选A. 6.【答案】B,一个秋天工期所需人数为780330026011300=,故选B.7.【答案】C【解析】由题意知,球的半径4R =,所以球的表面积为24π64πR =.设圆柱的底面半径为r 、高为h ,则22242h r ⎛⎫+= ⎪⎝⎭,得22464r h +=, 即22644h r =-,所以圆柱的侧面积2π224S rh ====4<4 )r =<,所以当28r =,即r =32π. 此时球的表面积与圆柱的侧面积之差是64π32π32π-=. 故选C. 8.【答案】D【解析】圆锥的高h 和底面半径r 之比:2:1h r =,∴2h r =,又圆锥的体积18πV =,即3212ππ18π33r r h ==,解得3r =, ∴6h =,母线长为l ==则圆锥的表面积为22πππ3π39(1πS rl r =+=⨯⨯⨯=+.故选D .9.【答案】A【解析】由题意,根据给定的几何体的三视图可得,该几何体是在一个半球中挖出四分之一圆锥, 其中球的半径为2R =,圆锥的底面半径为1r =,高为2h =, 故所求体积为32141131π2π12π23436V =⨯⋅⋅-⨯⋅⋅⋅=,故选A . 10.【答案】A【解析】由题意,因为PA ⊥平面ABCE ,四边形ABCD 为正方形,2AD =,1ED =, 又鳖臑P ADE -的体积为1,所以111211332△P AED AED V PA S PA -=⨯⨯=⨯⨯⨯⨯=, 解得3PA =,而阳马P ABCD -的外接球的直径是以,,AD AB AP 为宽,长,高的长方体的体对角线,所以2222244917R AD AB AP =++=++=(),即2417R =,则外接球的表面积为24π17πR =. 故选A .【名师点睛】(1)解决关于外接球的问题的关键是抓住外接球的特点,即球心到多面体的顶点的距离都等于球的半径,同时要作一圆面起衬托作用.(2)长方体的外接球的直径即为长方体的体对角线,对于一些比较特殊的棱锥,在研究其外接球的问题时可考虑通过构造长方体,通过长方体的外球球来研究棱锥的外接球的问题. 11.【答案】B【解析】由三视图可知,该几何体为如图所示的直三棱柱ABE DCF -,其中3AB BC BE a ===,AE ==,则292△△ABE CDF S S a ==,2ADFE S =长方形,所以该几何体的表面积为222279(33a a +=+=+,得13a =.故选B .12.【答案】D【解析】在底面三角形ABC 中,由1AC =,2AB =,60BAC ∠=︒,利用余弦定理可得:BC == ∴222AC BC AB +=,即AC BC ⊥,取D 为AB 中点,则D 为△BAC 的外心,可得三角形ABC 外接圆的半径为1,设三棱锥P ABC -的外接球的球心为O ,连接OP ,则OP ==即三棱锥P ABC -的外接球的半径为2R =.∴三棱锥的外接球的表面积等于24π5π⨯=⎝⎭.故选D . 13.【答案】2π【解析】将边长为2的正三角形绕其任一边所在的直线旋转一周而形成的曲面所围成的几何体为一个1,则体积为212π12π3⨯⨯⨯=.故答案为2π.14.【答案】π3【解析】因为展开图是半径为3,圆心角为2π3的扇形,所以圆锥的母线3l =,圆锥的底面的周长为2π32π3⨯=,因此底面的半径1r =,根据勾股定理,可知圆锥的高h =所以圆锥的体积为21π1π33⋅⨯=. 15.【答案】4√183【解析】设倒圆锥形器皿中水面的高为h cm,则水面圆的半径为h tan30°=3h ,则由π×42×8=13×(3h )2× πh ,解得h =4√183.16.【答案】(85π-【解析】如图,球O 是正三棱锥P ABC -的内切球,O 到正三棱锥四个面的距离都是球的半径R .PH 是正三棱锥的高,即1PH =.E 是BC 边中点,H 在AE 上,ABC △的边长为62,所以6HE ==PE =12PAB PAC PBC S S S BC PE ===⋅△△△=,(2ABCS ==△P ABC O PAB O PAC O PBC V V V V ----=++O ABC V -+,所以11113333R R ⨯=⨯⨯+⨯,解得:2R ==,所以此球的表面积是)(24π285πS =⨯=-.【名师点睛】球心是决定球的位置关键点,本题利用球心到正三棱锥四个面的距离相等且为球半径R 来求出R ,以球心的位置特点来抓球的基本量,这是解决球有关问题常用的方法.17.【答案】3【解析】由题意,在长方体中作出满足题意的三棱锥如图所示:则该三棱锥的外接球即是其所在长方体的外接球,故24PC R ==,又PA AC =,所以PA AC ==, 设BC x =,AB y =,由AB BC ⊥可得2228x y AC +==,所以该三棱锥的体积为)22113663△P ABCABC x y VS AP xy -+=⋅=⋅≤=.当且仅当2x y ==时,取最大值..18.【答案】3【解析】如图,取BD 中点O ,AC 中点E ,连结,,AO CO OE , ∵四面体ABCD 中,5,8AB AD BC DC BD AC ======,∴AO BD ⊥,CO BD ⊥,2AO CO ===, ∵AO CO O =I ,∴BD ⊥平面AOC ,又OE AC ⊥,∴182△AOC S =⨯=则1522323A BCDB AOC V V --==⨯⨯⨯=.故答案为3.19.【解析】(1)∵平面QD ABCD ⊥,∥PA QD ,∴平面PA ABCD ⊥, 又∵平面BC ABCD ⊂, ∴PA BC ⊥,又BC AB ⊥,平面PA PAB ⊂,平面AB PAB ⊂,PA AB A =I , ∴平面BC PAB ⊥, 又∵平面BC QBC ⊂, ∴平面平面PAB QBC ⊥.(2)连接BD ,过B 作BO AD ⊥于O , ∵PA ⊥平面ABCD ,平面BO ABCD ⊂, ∴PA BO ⊥,又BO AD ⊥,平面AD PADQ ⊂,平面PA PADQ ⊂,PA AD A =I , ∴平面BO PADQ ⊥,∵2AD AB ==,60DAB ∠=︒,∴△ABD 是等边三角形,∴BO =.∴()111122332梯形B PADQ PADQ V S BO -=⋅=⨯⨯+⨯= ∵90ADC ABC ∠=∠=︒, ∴30CBD CDB ∠=∠=︒, 又2BD AB ==,∴3BC CD ==,∴12sin 30233△BCD S =⨯⨯︒=∵平面QD ABCD ⊥,∴1123339△Q BCD BCD V S QD -=⋅=⨯⨯=.∴该组合体的体积B PADQ Q BCD V V V --=+=.1.【答案】B【解析】由三视图得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯=⎪⎝⎭. 故选B.【名师点睛】本题首先根据三视图,还原得到几何体——棱柱,根据题目给定的数据,计算几何体的体积,常规题目.难度不大,注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心算. 2.【答案】C【解析】在长方体1111ABCD A B C D -中,连接1BC ,。
教辅:高考数学二轮复习考点-空间几何体的表面积与体积
考点十三空间几何体的表面积与体积一、选择题1.(2020·天津高考)若棱长为23的正方体的顶点都在同一球面上,则该球的表面积为()A.12π B.24πC.36π D.144π答案 C解析正方体的外接球半径等于正方体的体对角线长的一半,即外接球半径R=(23)2+(23)2+(23)22=3,所以这个球的表面积为S=4πR2=4π×32=36π.故选C.2.(2020·山东济南6月针对性训练)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切.若O1O2=2,则圆柱O1O2的表面积为()A.4π B.5πC.6π D.π答案 C解析因为该球与圆柱的上、下底面,母线均相切,不妨设圆柱的底面半径为r,故2r=O1O2=2,解得r=1.故该圆柱的表面积为2πr2+2πr×O1O2=2π+4π=6π.故选C.3.(2020·山东聊城三模)最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”“圆罂测雨”“峻积验雪”和“竹器验雪”.其中“天池测雨”法是下雨时用一个圆台形的天池盆收集雨水.已知天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.当盆中积水深九寸(注:1尺=10寸)时,平地降雨量是( )A .9寸B .7寸C .8寸D .3寸答案 D解析 由已知,得天池盆盆口的半径为14寸,盆底的半径为6寸,则盆口的面积为196π平方寸,盆底的面积为36π平方寸.又盆高18寸,积水深9寸,则积水的水面半径为14+62=10(寸),积水的水面面积为100π平方寸,积水的体积为V =13×(36π+36π×100π+100π)×9=588π(立方寸),所以平地降雨量为588π立方寸196π平方寸=3(寸).4.(2020·山东德州高三4月模拟)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SA ⊥平面ABC ,SA =2,AB =1,AC =2,∠BAC =π3,则球O 的体积为( )A.162π3B .82π3C .42πD .42π3 答案 B解析 根据余弦定理,BC 2=AC 2+AB 2-2AB ·AC ·cos ∠BAC =3,故BC = 3.根据正弦定理,2r =BCsin ∠BAC=2,故r =1(r 为△ABC 外接圆半径),设R 为三棱锥S -ABC 外接球的半径,则R 2=r 2+⎝ ⎛⎭⎪⎫SA 22=2,故R =2,故V =43πR 3=82π3.故选B.5.如图,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,EF 是棱AB 上的一条线段,且EF =b <a ,若Q 是A 1D 1上的定点,P 在C 1D 1上滑动,则四面体PQEF 的体积( )A.是变量且有最大值B.是变量且有最小值C.是变量无最大、最小值D.是常量答案 D解析∵EF是定长,Q到EF的距离就是Q到AB的距离,也为定长,即△QEF的底和高都是定值,∴△QEF的面积是定值,∵C1D1∥平面QEF,P在C1D1上滑动,∴P到平面QEF的距离是定值.即三棱锥P-QEF的高也是定值,于是体积固定.∴三棱锥P-QEF的体积是定值,即四面体PQEF的体积是定值.6.(2020·全国卷Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC 的外接圆,若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为() A.64π B.48πC.36π D.32π答案 A解析设圆O1的半径为r,球的半径为R,依题意,得πr2=4π,∴r=2.由=2r,∴AB=2r sin60°=2 3.∴OO1=AB=2 3.根据球中圆截正弦定理可得ABsin60°面的性质得OO1⊥平面ABC,∴OO1⊥O1A,R=OA=OO21+O1A2=OO21+r2=4,∴球O的表面积S=4πR2=64π.故选A.7.(多选)已知正方体的外接球与内切球上各有一个动点M,N,若线段MN的最小值为3-1,则( )A .正方体的外接球的表面积为12πB .正方体的内切球的体积为4π3 C .正方体的棱长为2 D .线段MN 的最大值为2 3 答案 ABC解析 设正方体的棱长为a ,则正方体外接球的半径为体对角线长的一半,即32a ;内切球的半径为棱长的一半,即a2.∵M ,N 分别为外接球和内切球上的动点,∴MN min =32a -a2=3-12a =3-1,解得a =2,即正方体的棱长为2,C 正确;∴正方体的外接球的表面积为4π×(3)2=12π,A 正确;正方体的内切球的体积为4π3,B 正确;线段MN 的最大值为32a +a2=3+1,D 错误.故选ABC.8.(多选)若正三棱柱ABC -A ′B ′C ′的所有棱长都为3,外接球的球心为O ,则下列四个结论正确的是( )A .其外接球的表面积为21πB .直线AB ′与直线BC 所成的角为π3 C .AO ⊥B ′C ′D .三棱锥O -ABC 的体积为938 答案 ACD解析 如图,球心O 到下底面的距离OO ′=32,AO ′=23×32×3=3,所以其外接球的半径R =AO ′2+OO ′2=212,所以其外接球的表面积为4πR 2=21π,A 正确;直线AB ′与直线BC 所成的角即直线AB ′与直线B ′C ′所成的角,设其为θ,在△AB ′C ′中,cos θ=(32)2+32-(32)22×32×3=24,故B 错误;由OO′⊥平面ABC,得OO′⊥BC,O′为△ABC的重心,则AO′⊥BC,故BC ⊥平面AOO′,即BC⊥AO,故AO⊥B′C′,C正确;根据三棱锥的体积公式可得V O-ABC=13×32×⎝⎛⎭⎪⎫12×3×332=938,D正确.二、填空题9.(2020·浙江高考)已知圆锥展开图的侧面积为2π,且为半圆,则底面半径为________.答案 1解析设圆锥底面半径为r,母线长为l,则⎩⎪⎨⎪⎧π×r×l=2π,2×π×r=12×2×π×l,解得r=1,l=2.10.学生到工厂劳动实践,利用3D打印技术制作模型,如图,该模型为圆锥底部挖去一个正方体后的剩余部分(正方体四个顶点在圆锥母线上,四个顶点在圆锥底面上),圆锥底面直径为10 2 cm,高为10 cm,打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为________ g.(π取3.14)答案358.5解析设被挖去的正方体的棱长为x cm,圆锥底面半径为r cm,高为h cm,则22xr=h-xh,即22x52=10-x10,解得x=5,所以制作该模型所需材料质量约为m=Vρ=0.9⎝⎛⎭⎪⎫13πr2·h-x3=0.3π×50×10-0.9×125=358.5 g.11.(2020·山东泰安二轮复习质量检测)已知A,B是球O的球面上两点,∠AOB =90°,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为________.答案 144π解析 如图所示,当点C 位于垂直于面AOB 的直径的端点时,三棱锥的体积最大,设球O 的半径为R ,此时V O -ABC =V C -AOB =13×12R 2×R =16R 3=36,故R =6,则球O 的表面积为S =4πR 2=144π.12.(2020·山东聊城一模)点M ,N 分别为三棱柱ABC -A 1B 1C 1的棱BC ,BB 1的中点,设△A 1MN 的面积为S 1,平面A 1MN 截三棱柱ABC -A 1B 1C 1所得截面的面积为S ,五棱锥A 1-CC 1B 1NM 的体积为V 1,三棱柱ABC -A 1B 1C 1的体积为V ,则V 1V =________,S 1S =________.答案 712 35解析 如图所示,延长NM 交直线C 1C 于点P ,连接P A 1交AC 于点Q ,连接QM .平面A 1MN 截三棱柱ABC -A 1B 1C 1所得截面为四边形A 1NMQ .∵BB 1∥CC 1,M 为BC 的中点,则△PCM ≌△NBM .点M 为PN 的中点.∴△A1MN的面积S1=12S△A1NP,∵QC∥A1C1,PCPC1=13=PQP A1,∴△A1QM的面积=23S△A1PM,∴S1S=35.∵△BMN的面积=18S四边形B1C1CB,∴五棱锥A1-CC1B1NM的体积为V1=78V四棱锥A1-B1C1CB,而四棱锥A1-B1C1CB的体积=23V,∴V1V=78×23VV=712.三、解答题13.如图所示,三棱柱ABC-A1B1C1的侧棱垂直于底面,且底面是边长为2的正三角形,AA1=3,点D,E,F,G分别是所在棱的中点.(1)证明:平面BEF∥平面DA1C1;(2)求三棱柱ABC-A1B1C1夹在平面BEF和平面DA1C1之间部分的体积.解(1)证明:∵E,F分别是A1B1和B1C1的中点,∴EF∥A1C1,∵EF⊄平面DA1C1,A1C1⊂平面DA1C1,∴EF∥平面DA1C1,∵D,E分别是AB和A1B1的中点,∴DB綊A1E,∴四边形BDA1E是平行四边形,∴BE∥A1D,∵BE⊄平面DA1C1,A1D⊂平面DA1C1,∴BE∥平面DA1C1,∵BE∩EF=E,∴平面BEF∥平面DA1C1.(2)由题图可知,三棱柱ABC-A1B1C1夹在平面BEF和平面DA1C1之间的部分,可看作三棱台DBG -A 1B 1C 1减掉三棱锥B -B 1EF 后的剩余部分,∵S △DBG =S △B 1EF =34×12=34,S △A 1B 1C 1=34×22=3, ∴三棱台DBG -A 1B 1C 1的体积为 V 1=13×⎝ ⎛⎭⎪⎫34+34+3×3=734, 三棱锥B -B 1EF 的体积V 2=13×34×3=34,∴三棱柱ABC -A 1B 1C 1夹在平面BEF 和平面DA 1C 1之间部分的体积为V =V 1-V 2=734-34=332.14.如图,已知棱锥S -ABCD 中,底面ABCD 是边长为2的菱形,∠BAD =60°,SA =SD =5,SB =7,点E 是棱AD 的中点,点F 在棱SC 上,且SFSC =λ,SA ∥平面BEF .(1)求实数λ的值;(2)求三棱锥F -EBC 的体积.解 (1)连接AC ,设AC ∩BE =G ,则平面SAC ∩平面EFB =FG ,∵SA ∥平面EFB ,∴SA ∥FG , ∵△GEA ∽△GBC ,∴AG GC =AE BC =12, ∴SF FC =AG GC =12.∴SF =13SC ,∴λ=13.(2)∵SA =SD =5,∴SE ⊥AD ,SE =2, 又AB =AD =2,∠BAD =60°,∴BE =3, ∴SE 2+BE 2=SB 2.∴SE ⊥BE ,∴SE ⊥平面ABCD , ∴V F -EBC =23V S -EBC =13V S -ABCD =13×13×2×2sin60°×2=439.一、选择题1.(2020·山东临沂一模)《九章算术》是我国古代内容极为丰富的数学名著,书中《商功》有如下问题:“今有委粟平地,下周一十二丈,高一丈,问积及为粟几何?”意思是“有粟若干,堆积在平地上,它底圆周长为12丈,高为1丈,问它的体积和粟各为多少?”如图,主人意欲卖掉该堆粟,已知圆周率约为3,一斛粟的体积约为2700立方寸(单位换算:1立方丈=106立方寸),一斛粟米卖270钱,一两银子1000钱,则主人卖后可得银子( )A .200两B .240两C .360两D .400两答案 D解析 该堆粟的底面半径为r =122×3=2,体积V =13×3×22×1=4立方丈=4×106立方寸=4000027斛,故主人卖后可得银子4000027×270÷1000=400两.故选D.2.(2020·海口市高考模拟演练)一个底面边长为3的正三棱锥的体积与表面积为24的正方体的体积相等,则该正三棱锥的高为( )A .12 3B .3233C .3239 D .12答案 C解析因为正方体的表面积为24,所以其棱长为2,体积为23=8.设正三棱锥的高为h,因为正三棱锥的体积与正方体的体积相等,所以13×12×3×3×32h=8,解得h=3239.3.(2020·海南中学高三摸底)已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V=()A.1+26B.1C.26D.1+22答案 A解析根据平面展开图,还原几何体如右图所示,故该几何体是由棱长为1的正方体和底边棱长为1的正四棱锥组合而成.则其体积V=13+13×1×1×2 2=1+26.故选A.4.(2020·海南高考调研测试)张衡是中国东汉时期伟大的天文学家、数学家,他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥A-BCD的每个顶点都在球O的球面上,AB⊥底面BCD,BC⊥CD,且AB=CD=3,BC=2,利用张衡的结论可得球O的表面积为()A.30 B.1010C.33 D.1210答案 B解析 因为BC ⊥CD ,所以BD =7,又AB ⊥底面BCD ,所以球O 的球心为侧棱AD 的中点,从而球O 的直径为10.利用张衡的结论可得π216=58,则π=10,所以球O 的表面积为4π×⎝ ⎛⎭⎪⎫1022=10π=1010.故选B. 5.(2020·山东青岛三模)在三棱柱ABC -A 1B 1C 1中,AB =BC =AC ,侧棱AA 1⊥底面ABC ,若该三棱柱的所有顶点都在同一个球O 的表面上,且球O 的表面积的最小值为4π,则该三棱柱的侧面积为( )A .6 3B .3 3C .3 2D .3答案 B解析 如图,设三棱柱上、下底面中心分别为O 1,O 2,则O 1O 2的中点为O ,设球O 的半径为R ,则OA =R ,设AB =BC =AC =a ,AA 1=h ,则OO 2=12h ,O 2A=23×32AB =33a ,则在Rt △OO 2A 中,R 2=OA 2=OO 22+O 2A 2=14h 2+13a 2≥2×12h ×33a =33ah ,当且仅当h =233a 时,等号成立,所以S 球=4πR 2≥4π×33ah ,所以43π3ah =4π,所以ah =3,所以该三棱柱的侧面积为3ah =3 3.故选B.6.(2020·山东安丘模拟)唐朝的狩猎景象浮雕银杯如图1所示,其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺. 它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示,已知球的半径为R ,酒杯内壁表面积为143πR 2.设酒杯上部分(圆柱)的体积为V 1,下部分(半球)的体积为V 2,则V 1V 2=( )A .2B .32C .1D .34答案 A解析 由球的半径为R ,得半球表面积为2πR 2,又酒杯内壁表面积为143πR 2,∴圆柱的侧面积为83πR 2.设圆柱的高为h ,则2πR ·h =83πR 2,即h =43R .∴V 1=πR 2·43R=43πR 3,V 2=23πR 3.∴V 1V 2=43πR 323πR 3=2.故选A. 7.(多选)沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上、下两个圆锥组成,圆锥的底面直径和高均为8 cm ,细沙全部在上部时,其高度为圆锥高度的23(细管长度忽略不计).假设该沙漏每秒钟漏下0.02 cm 3的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则以下结论正确的是(π≈3.14)( )A .沙漏中细沙的体积为1024π81 cm 3B .沙漏的体积是128π cm 3C .细沙全部漏入下部后此锥形沙堆的高度约为2.4 cmD .该沙漏的一个沙时大约是1985秒答案 ACD解析 对于A ,根据圆锥的截面图可知,细沙在上部时,细沙的底面半径与圆锥的底面半径之比等于细沙的高与圆锥的高之比,所以细沙的底面半径r =23×4=83 cm ,所以沙漏中细沙的体积V 沙=13·πr 2·2h 3=13·64π9·163=1024π81 cm 3,A 正确;对于B ,沙漏的体积V 漏=2×13×π×⎝ ⎛⎭⎪⎫h 22×h =2×13×π×42×8=256π3 cm 3,B 错误;对于C ,设细沙全部漏入下部后的高度为h 1,根据细沙体积不变可知,1024π81=13×π×⎝ ⎛⎭⎪⎫h 22×h 1,所以1024π81=16π3h 1,所以h 1≈2.4 cm ,C 正确;对于D ,因为细沙的体积为1024π81 cm 3,沙漏每秒钟漏下0.02 cm 3的沙,所以一个沙时为1024π810.02=1024×3.1481×50≈1985秒,D 正确.故选ACD. 8.(多选)(2020·山东青岛一模)已知四棱台ABCD -A 1B 1C 1D 1的上、下底面均为正方形,其中AB =22,A 1B 1=2,AA 1=BB 1=CC 1=2,则下述正确的是( )A .该四棱台的高为 3B .AA 1⊥CC 1C .该四棱台的表面积为26D .该四棱台外接球的表面积为16π答案 AD解析 由题意可得该四棱台为正四棱台.由棱台的性质,画出切割前的四棱锥,如图,由AB =22,A 1B 1=2可知△SA 1B 1与△SAB 的相似比为1∶2,所以SA =2AA 1=4,AO =2,所以SO =23,所以OO 1=3,故该四棱台的高为3,A 正确;因为SA =SC =AC =4,所以AA 1与CC 1的夹角为60°,不垂直,B 错误;该四棱台的表面积为S =S 上底+S 下底+S 侧=2+8+4×2+222×142=10+67,C 错误;易知该四棱台外接球的球心在OO 1上,在平面B 1BOO 1中,由于OO 1=3,B 1O 1=1,则OB 1=2=OB ,即点O 到点B 与点B 1的距离相等,则该四棱台外接球的半径r =OB =2,该四棱台外接球的表面积为16π,D 正确,故选AD.二、填空题9.已知圆柱的底面半径为1,母线长为2,则该圆柱的侧面积等于________. 答案 4π解析 ∵圆柱的底面半径为r =1,母线长为l =2,∴其侧面积为S =2πrl =2π×1×2=4π.10.(2020·江苏高考)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半径为0.5 cm ,则此六角螺帽毛坯的体积是________cm 3.答案 123-π2解析 正六棱柱体积为6×34×22×2=12 3 cm 3,挖去的圆柱体积为π×⎝ ⎛⎭⎪⎫122×2=π2 cm 3,故此六角螺帽毛坯的体积为⎝ ⎛⎭⎪⎫123-π2 cm 3. 11.(2020·江苏南京金陵中学、南通海安高级中学、南京外国语学校第四次模拟)设棱长为a 的正方体的体积和表面积分别为V 1,S 1,底面半径和高均为r 的圆锥的体积和侧面积分别为V 2,S 2,若V 1V 2=3π,则S 1S 2的值为________.答案 32π 解析 不妨设V 1=27,V 2=9π,故V 1=a 3=27,所以a =3,所以S 1=6a 2=54.如图所示,因为V 2=13h ×πr 2=13πr 3=9π,所以r =3,又l =2r ,所以S 2=12l ×2πr=2πr 2=92π,所以S 1S 2=5492π=32π.12.(2020·山东潍坊高密二模)在四棱锥P -ABCD 中,P A ⊥平面ABCD ,AP =2,点M 是矩形ABCD 内(含边界)的动点,且AB =1,AD =3,直线PM 与平面ABCD 所成的角为π4.记点M 的轨迹长度为α,则tan α=________;当三棱锥P -ABM 的体积最小时,三棱锥P -ABM 的外接球的表面积为________.答案 3 8π解析 如图,因为P A ⊥平面ABCD ,垂足为A ,则∠PMA 为直线PM 与平面ABCD 所成的角,所以∠PMA =π4.因为AP =2,所以AM =2,所以点M 位于底面矩形ABCD 内的以点A 为圆心,2为半径的圆上,记点M 的轨迹为圆弧.连接AF ,则AF =2.因为AB =1,AD =3,所以∠AFB =∠F AE =π6,则的长度α=π6×2=π3,所以tan α= 3.当点M 位于点F 时,三棱锥P -ABM 的体积最小,又∠P AF=∠PBF =π2,所以三棱锥P -ABM 的外接球的球心为PF 的中点.因为PF =22+22=22,所以三棱锥P -ABM 的外接球的表面积S =4π×(2)2=8π.三、解答题13.如图1,在菱形ABCD中,AB=2,∠DAB=60°,M是AD的中点,以BM为折痕,将△ABM折起,使点A到达点A1的位置,且平面A1BM⊥平面BCDM,如图2.(1)求证:A1M⊥BD;(2)若K为A1C的中点,求四面体M-A1BK的体积.解(1)证明:在图1中,连接BD(如图a),∵四边形ABCD是菱形,∠DAB=60°,M是AD的中点,∴AD⊥BM,故在图2中,BM⊥A1M,∵平面A1BM⊥平面BCDM,平面A1BM∩平面BCDM=BM,∴A1M⊥平面BCDM,又BD⊂平面BCDM,∴A1M⊥BD.(2)在图1中,∵四边形ABCD是菱形,AD⊥BM,AD∥BC,∴BM⊥BC,且BM=3,在图2中,连接CM(如图b),则VA1-BCM=13S△BCM·A1M=13×12×2×3×1=33,∵K为A1C的中点,∴VM-A1BK=VK-MA1B=12VC-MA1B=12VA1-BCM=36.∴四面体M-A1BK的体积为36.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题限时集训(七) 空间几何体的表面积、体积及有关量的计算[专题通关练](建议用时:30分钟)1.在一个密闭透明的圆柱筒内装一定体积的水,将该圆柱筒分别竖直、水平、倾斜放置时,指出圆柱桶内的水平面可以呈现出的几何形状不可能是( )A .圆面B .矩形面C .梯形面D .椭圆面或部分椭圆面C [将圆柱桶竖放,水面为圆面;将圆柱桶斜放,水面为椭圆面或部分椭圆面;将圆柱桶水平放置,水面为矩形面,所以圆柱桶内的水平面可以呈现出的几何形状不可能是梯形面,故选C.]2.[易错题]一个正方体的内切球O 1、外接球O 2、与各棱都相切的球O 3的半径之比为( )A .1∶3∶2B .1∶1∶1C .1∶∶D .1∶2∶332C [设正方体的棱长为1,则其内切球O 1的半径为,外接球O 2的半径为(正方体体1232对角线的一半),与各棱都相切的球O 3的半径为(正方体面对角线的一半),所以它们的半22径之比是1∶∶,故选C.]323.已知三棱锥P ABC 中,PB ⊥平面ABC ,∠ABC =90°,PA =,AB =BC =1,则三棱5锥P ABC 的外接球的表面积为( )A .12πB .6πC .24π D.46π3B [如图,∵PB ⊥平面ABC ,∴PB ⊥AB ,∵AB =1,PA =,∴PB =2,5又AB ⊥BC ,把三棱锥P ABC 补形为长方体,则长方体对角线长为=,22+12+126则三棱锥P ABC 外接球的半径为,62∴三棱锥P ABC 的外接球的表面积为4π×=6π.故选B.](62)24.[重视题]两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为1的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上(如图),该八面体的体积可能值有( )A .1个B .2个C .3个D .无数个D [设ABCD 与正方体的截面四边形为A ′B ′C ′D ′,设AA ′=x (0≤x ≤1),则AB ′=1-x ,|AD |2=x 2+(1-x )2=2+,(x -12)2 12故S 四边形ABCD =|AD |2∈,[12,1]V =S 四边形ABCD ·h ·2=S 四边形ABCD ∈.1313[16,13]∴该八面体的体积可能值有无数个,故选D.]5.已知正三棱柱ABC A 1B 1C 1的底面边长为2,侧棱长为,D 为BC 的中点,则三棱锥3A B 1DC 1的体积为( )A .3B.32C .1 D.32C [∵D 是等边三角形ABC 的边BC 的中点,∴AD ⊥BC .又ABC A 1B 1C 1为正三棱柱,∴AD ⊥平面BB 1C 1C .∵四边形B 为矩形,∴S =S =×2×=.又AD =2× B 1C 1C △DB 1C 112四边形BB 1C 1C 1233=,323∴V =S ·AD =××=1.故选C.]A B 1DC 113△DB 1C 113336.如图所示,图中阴影部分绕AB 旋转一周所形成的几何体的体积为________. [由题知,旋转一周后形成的几何体是一圆台去掉一个半球,其中圆台的体积为140π3V =×(π×22++π×52)×4=52π,半球的体积13π×22×π×52V =××π×23=,则所求体积为52π-=.]124316π316π3140π37.鲁班锁是中国传统的智力玩具,起源与古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为________.(容器壁的厚度忽略不计)41π [由题意,该球形容器的半径的最小值为:=,1222+12+62412 ∴该球形容器的表面积的最小值为4π·=41π.]4148.三棱锥P ABC 的四个顶点均在同一个球面上,其中PA ⊥平面ABC ,△ABC 是正三角形,PA =2BC =4,则该球的表面积为________. [球心应位于过正三角形ABC 的中心且垂直于平面ABC 的直线上,又PA ⊥平面64π3ABC ,PA =4,所以球心O 到平面ABC 的距离为2,所以球的半径r ==,所以球的表433面积为S =4πr 2=.]64π3[能力提升练](建议用时:15分钟)9.(2019·成都七中模拟)《九章算术》中将底面是直角三角形、侧棱垂直于底面的三棱柱称之为“堑堵”,现有一“堑堵”型石材,其底面三边长分别为3,4,5,若此石材恰好可以加工成一个最大的球体,则其高为( )A .4B .3C .2D .1C [如图,是过球心且与底面平行的轴截面,设球的半径为r ,由AC =3,BC =4,可得AB =5,由等面积法可得:×3×4=(3+4+5)r ,解得r =1.∴此石材d 的高为2r =2.故1212选C.]10.(2019·唐山二模)某几何体的三视图如图所示,则该几何体的表面积为( )A .16πB .14πC .10πD .8πC [根据三视图知,该几何体是半球体截去一个圆锥体剩余部分,画出图形如图所示;结合图中数据,计算该几何体的表面积为S =S 半球表面积+S 半球底面圆+S 圆锥侧面积-S 圆锥底面圆=2π·()2+π·()2+π·1·33-π·12=10π.故选C.]3 2+1211.一块边长为6 cm 的正方形铁皮按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,将该容器按如图2放置,若其正视图为等腰直角三角形,则该容器的体积为( )图1 图2A .12 cm 3B .4 cm 366C .27 cm 3D .9 cm 322D [如图2,△PMN 为该四棱锥的正视图,由图1可知,PM +PN =6,且PM =PN ,由△PMN 为等腰直角三角形,可知MN =3,PM =3.设MN 中点为O ,则PO ⊥平面2ABCD ,∴PO =MN =,∴V P ABCD =×2×=×18×=9.选D.1232213(32)322133222]图1 图212.[重视题]正三棱锥S ABC 的底面边长为a ,各侧面的顶角为30°,D 为侧棱SC 的中点,截面△DEF 过D 且平行于AB .当△DEF 的周长最小时,截得的三棱锥S DEF 的侧面积为________.a 2 [将正三棱锥的侧面展开(如图所示),可得三个顶角2+38均为30°的等腰三角形,底面边长为a ,D ′为SC ′的中点,DD ′的连线长即为最短.∵DD ′∥CC ′∥A ′B ′,∴E ′,F ′即为相对应的E ,F .在△SCB ′中,B ′C =a ,∠CSB ′=30°,则SC =SB ′=.2+3 a 2又∵∠CSC ′=90°,∴DD ′=CC ′=·a ·=a ,1222+3123+12即为截面△DEF 的周长的最小值,这时,三棱锥S DEF 的侧面展开图的顶角为90°,∴S △SDD ′==a 2.]14(3+12a )2 2+38题号内容押题依据1数学文化、锥体的体积、柱体的表面积、不等式高考热点之一,通过对几何体的体积计算实现知识间的融合考查了学生的空间想象和数学运算的素养2球的切接体积的最值问题有关球的切接及体积的最值问题一直是高考的热点,考查学生的动态分析问题能力【押题1】 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如“堑堵”指的是底面为直角三角形,且侧棱垂直于底面的三棱柱;“阳马”指的是底面为矩形,一侧棱垂直于底面的四棱锥.如图所示,在堑堵ABC A 1B 1C 1中,AC ⊥BC ,A 1A =AB =2,当堑堵ABC A 1B 1C 1的侧面积取得最大值时,阳马B A 1ACC 1的体积为( )A. B.4383C .4 D.433A [根据题意,设AC =x ,BC =y ,则有x 2+y 2=4,堑堵ABC A 1B 1C 1的侧面积S 侧=(2+x +y )×2=4+2(x +y )≤4+2=4+2,当且仅当x =y =时取等号,2 x 2+y 2 22此时阳马B A 1ACC 1的体积V =×AC ×CC 1×BC =××2×=,故选A.13132243【押题2】 如图,三棱锥A BCD 中,AD ⊥BD ,AC ⊥BC ,∠DAB =,∠BAC =.三棱锥的外接球的表面积π6π4为16π,则该三棱锥的体积的最大值为( )A.B.73433C. D.83143B [设外接球的半径为R .由题意得,4πR 2=16π,解得R =2.由题意知△ADB ,△ABC 都是直角三角形,所以三棱锥A BCD 的外接球的球心为AB 的中点,且AB =4.由∠DAB =,∠BAC =,可求得AD =2,BD =2,AC =BC =2.当三棱锥A BCD 的体积最大π6π432时,平面ADB ⊥平面ABC .所以三棱锥的体积的最大值为V 三棱锥A BCD =V 三棱锥C ABD =××2×21312×2=.故选B.]3433。
