初中数学知识树图
初中数学知识树图(课堂PPT)

螺旋上升的概念思想
如:加强数形,用坐标的方 法处理更多内容(二元一次 方程组.平移.对称.函数等)
如:按照“说点儿理”“说理”“推 理”“符号表示推理”等不同层次,分阶 段培养推理能力,内容注重基础,留有发
展余地
如:方程和函数,按照一次和二次 数量关系使方程和函数交替出现,
螺旋上升。从函数角度认识方程
观 察
思 考
探 究
讨 论
归 纳
贴 示
云 朵
回顾与思考 知识结构图
正文
正文边空
综合性
小结
实践性
数学活动
为加深对相关内容的认识 扩大学生的知识面
运用现代信息技术手段学 习
实阅
观 验 读信
察 与 与息
与 探 思技
猜 究 考术
想
应
用
选学 练习
课上使用
所学 内容 的的 巩固 与延 伸
开放性
节、习题
习题
课内课外作业
统方计数 发法与量展,概关符发率系号展以感空及,间变体观概化会念率规数。律学计的与算列树工现与表状具实、图,
数学知识的图形理与解坐标,认识数
生活的紧密联系,增强应估算用意
平学面知直角识之间的联系。
坐标系
概念表示
一次函数
分类 反比例函数
识,提高运用代数知识与方法
解决问题实的践能活动力。
独立思考 合作交流
一步学习图描形述的数据的方法,
进 能证一计明步算的 体简单会平事概移 件率发的生意的义图概,形与变换 证探究依率明据讨课的。方题一法 ,些具发图有展形与挑应证战用明性数的学研知
识解证明决的问题的意识和能力; 同时含,义 进一步加深对相关
探索基本图形(直线形、圆)
八年级数学上册知识树(共6张PPT)

幂的乘方
平方差公式
(ab)a(b)a2b2(a完b)2全平a方2公2a式 bb2
零指数和负 整数指数幂
积的乘方
乘法公式
单项式乘以 单项式
幂的乘法运算
单项式乘以 多项式
多项式乘以 多项式
同底数幂 的除法
单项式除以 单项式
整式乘法
整式除法
多项式除以 单项式
整式的乘除
和
三角形 的边
三
角
形
第12章知识树
SAS
ASA AAS
全等三角形的 概念
全等三角形
三角形全等的条 SSS 件
角平分线的性质
全等三角形
全
的性质
等
三
角
形
第13章知识树
定义 性质 判定
作图
Hale Waihona Puke 等腰三角形等边三角形 概念
性质
轴对称
轴对称变换
作图
概念
轴
坐标表示
对
称
第14章知识树 整式的乘除知识树
同底数幂 的乘法
八年级数学上册知识树
与三角形有关线段 与三角形有关角
整式 的乘 法
整式
乘法公式
数与式
定义
运算
分式
方程
多边形及其
内角和
三角形
空间与 图形
角平分线性
质与判定
判定
全等三角形
性质
轴对称
定义
八
年
画图
级
数
学
上
册
知
识
树
第11章知识树
内角和1800
外角和3600
角平 分线 中线
高
线段
初中数学知识树图

通分
通分化 成同分
母
分母不变
分子相加 减
注:分子、 分母为多 子积为子 项式时先 母积为母 分解因式
形四状边 方:取形决与于同原圆底相四数除边幂形对角除线法的
相等或垂直
如:加强数形,用坐标的方法处理更多内容(二元一次方程组. 基本性质
对称中心乘是法对公称式点连线的中点
一到单次三项函 顶式数点与与的多反距项比离式例相函等数锐—乘形内法;
示 方
要
对 等
义法 素 角
三 线 合 一
等 角 对 等 边
概念
性质
判定
内角和 定义
多边形 及其 内角和
等腰三角形
内角和 外角的性质
有关的角
三角形
等
边
已知两边
三
求第三边
角
弦图
形
应用
毕达哥拉斯
苏菲尔德
证明
特例
定理
文字.符号
内容 图形
互逆命题
勾股定理
文字.符号
内容 图形
逆定理
直角三角形
锐角三角函数
证明 全等
角的比较与运算
和 相 为 定性 等 1800 义 质
对邻
垂
顶补
直
角角
一“放”二“靠” 三“推”四“画”
画法
同位角相等
定义.表示 度.分.秒互化 进位.计算
角的度量
尺规作角
借助角研究平 面内两条直线 的位置关系
关系
相交线
判定 平行线
直线公理 直线
表示与画法 射线
寻找射线方法
表示与画法 计算与比较
性质
线段
方法
证依探课明据讨题的 ,一些发具展图有应形与挑用证战数明学性的知研识解究 决问证明题的的意识和能力;同时, 进一含步义 加深对相关数学知识
(完整版)初中数学知识点结构图
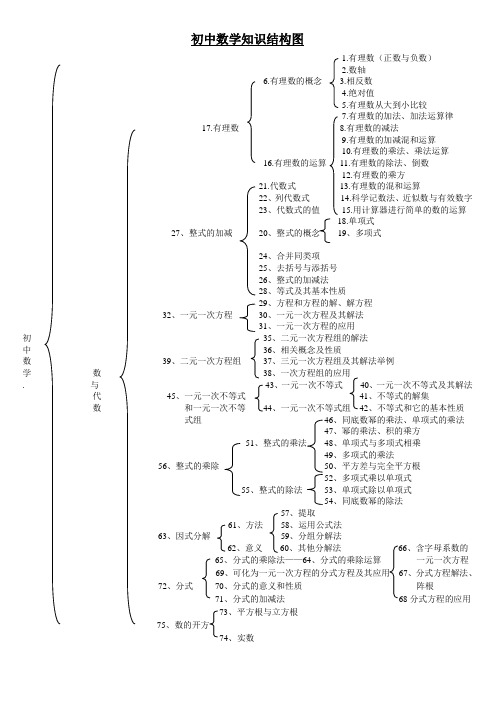
初中数学知识结构图1.有理数(正数与负数)2.数轴6.有理数的概念 3.相反数4.绝对值5.有理数从大到小比较7.有理数的加法、加法运算律17.有理数8.有理数的减法9.有理数的加减混和运算10.有理数的乘法、乘法运算16.有理数的运算11.有理数的除法、倒数12.有理数的乘方21.代数式13.有理数的混和运算22、列代数式14.科学记数法、近似数与有效数字23、代数式的值15.用计算器进行简单的数的运算18.单项式27、整式的加减20、整式的概念19、多项式24、合并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程32、一元一次方程30、一元一次方程及其解法31、一元一次方程的应用初35、二元一次方程组的解法中36、相关概念及性质数39、二元一次方程组37、三元一次方程组及其解法举例学数38、一次方程组的应用. 与43、一元一次不等式40、一元一次不等式及其解法代45、一元一次不等式41、不等式的解集数和一元一次不等44、一元一次不等式组42、不等式和它的基本性质式组46、同底数幂的乘法、单项式的乘法47、幂的乘法、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与完全平方根52、多项式乘以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法57、提取61、方法58、运用公式法63、因式分解59、分组分解法62、意义60、其他分解法66、含字母系数的65、分式的乘除法——64、分式的乘除运算一元一次方程69、可化为一元一次方程的分式方程及其应用67、分式方程解法、72、分式70、分式的意义和性质阵根71、分式的加减法68分式方程的应用73、平方根与立方根75、数的开方74、实数86、二次根式的意义76、最简二次根式79、二次根式的乘除法77、二次根式的除法87、二次根式78、二次根式的加减法82、二次根式的加减法80、二次根式的加减法81、同类二次根式85、二次根式的混合运算83、二次根式的混合运算84、有理化因式93、一元二次方程的解法98、一元二次方程的意义数100、二元二次方程组与102、一元二次方程99、一元二次方程组的根与系数的关系代94、分式方程的解法数97、可化为一元二次方程的分式方程式和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图像的图像和性质105、正比例函数的图像和性质108、二次函数——107二次函数的有关概念113、函数及其图像109、平面直角坐标系110、函数初111、函数的图像中112、反比例函数数114、线段学116、线段、角115、角117、相交线、对顶角、邻角、补角120、相交线118、垂线、点到直线的距离119、同位角、内错角、同旁内角126、相交、平行123、平行线121、平行线概念及性质122、平行线的判定124、空间直线、平面的位置关系空125、命题、公理、定理间129、与三角形有关的边与134、全等三角形图135、等腰三角形形138、三角形133、直角三角形——132、勾股定理131、与三角形有关的角——130、三角形的内角136、轴对称137、基本作图139、平行四边形的概念及其性质140、平行四边形的判定144、平行四边形141、矩形的概念、性质和判定149、多边形142、菱形的概念、性质和判定151、四边形150、中心对称143、正方形的概念、性质和判定145、梯形的相关概念148、梯形146、等腰梯形的概念、性质和判定147、三角形、梯形的中位线156、比例线段158、相似图形157、相似多边形152、相似三角形的相关概念155、相似三角形153、三角形相似的判定154、相似三角形的性质159、解直角三角形161、解直角三角形160、解直角三角形的应163、解直角三角形162、锐角三角形164、圆的有关概念及对称性165、点和圆的位置关系166、过不在同一直线上三点的圆空172、圆的有关性质167、三角形的外接圆间168、垂径定理及其逆定理与169、圆心角、弧、弦、弦心距初图170、圆周角定理中形171、圆内接四边形及其性质数173.直线和圆的位置关系学185、圆174.切线的判定和性质177.直线和圆的位置关系175.三角形的内切圆176. *切线长定理179.正多边形和圆——178.正多边形的有关计算180.圆周长、弧长183.弧长和扇形的面积181.圆、扇形、弓形的面积182.圆柱和圆锥的侧面展开图、侧面积184.圆和圆的位置关系186.几何体、几何图形187.平均数188.众数和中位数191.统计初步189.级差、方差、标准差195.统计与概率190.频数、频率、频率分布直方图192.概率初步——概率计算。
初中数学具体知识点框架图

初中数学整体知识点总结构图第一部分《数与式》知识点2a a π⎧⎪⎧⎪⎨⎪⎩⎪⎪⎧⎨⎨⎪⎩⎪⎪⎧⎪⎪⎨⎪⎪⎩⎩定义:有理数和无理数统称实数.有理数:整数与分数分类无理数:常见类型(开方开不尽的数、与有关的数、无限不循环小数)法则:加、减、乘、除、乘方、开方实数实数运算运算定律:交换律、结合律、分配律数轴(比较大小)、相反数、倒数(负倒数)科学记数法相关概念:有效数字、平方根与算术平方根、立方根、非负式子(,单项式:系数与次数分类多项式整式数与式()01;;(),();();1;m m n m n m n m n m n mn m m m m p m p a a a a a a a a a a ab a b a a b b a +--⎧⎨⎩⎛⎫⋅=÷====== ⎪ ⎪⎝⎭⨯⨯⨯⎛⎫ ⎪÷÷⎝⎭:次数与项数加减法则:加减法、去括号(添括号)法则、合并同类项幂的运算:单项式单项式;单项式多项式;多项式多项式乘法运算:单项式单项式;多项式单项式混合运算:先乘方开方,再乘除,最后算加减;同级运算自左至右顺序计算;括号优先22222()()()2;(a b a b a b a b a ab b a a m a a m b b m b b m ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧+-=-⎪⎨⎪±=±+⎩⎩⎧⎪⎨⎪⎩⨯÷⎛⎫== ⎪⨯÷⎝⎭平方差公式:乘法公式完全平方公式:分式的定义:分母中含可变字母分式分式有意义的条件:分母不为零分式值为零的条件:分子为零,分母不为零分式分式的性质:通分与约分的根据)通分、约分,加、减、乘、除分式的运算先化简再求值(整式与分式化简求值20).0.(0)(0)a a a a a a ⎧⎪⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎪⎧⎨⎨⎪⎪⎩⎩⎩⎡≥⎤⎧=⎨⎢⎥-≤⎩⎣⎦⎧⎪⎨⎪⎩的通分、符号变化)整体代换求值≥叫二次根式二次根式的意义即被开方数大于等于二次根式的性质:最简二次根式(分解质因数法化简)二次根式二次根式的相关概念同类二次根式及合并同类二次根式分母有理化(“单项式与多项式”型)加减法:先化最简,再合并同类二次二次根式的运算222222()()2()()()()a b a b a b a ab b a b x a b x ab x a x b ⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧⎪⎪⎪⎨=⎪⎪⎩⎩⎧⎪⎧-=+-⎪⎪⎨±+=±⎨⎩⎪+++=++⎪⎩根式定义:(与整式乘法过程相反,分解要彻底)提取公因式法:(注意系数与相同字母,要提彻底)平方差公式:分解因式公式法方法完全平方公式:十字相乘法:分组分解法:(对称分组与不对称分组)⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩第二部分《方程与不等式》知识点2⎧⎪⎨⎪⎩⎧⎪⎪⎨⎪⎪⎩⎧⎨⎩定义与解:一元一次方程解法步骤:去分母、去括号、移项、合并同类项、系数化为1.应用:确定类型、找出关键量、数量关系定义与解:解法:代入消元法、加减消元法二元一次方程(组)简单的三元一次方程组:方程简单的二元二次方程组:定义与判别式(△=b -4ac)一元二次方程解法:直接开平方法、配方法、求根公式法、因式分解法.定义与根(增根):分式方程解法:去分母化为整方程与不等式 1.2.3.⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧⎪⎨⎪⎩⎩⎧⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎨⎪⎪⎪⎩⎧⎪⎨⎪⎩式方程,解整式方程,验根.1.行程问题:2.工程(效)问题:3.增长率问题:(增长率与负增长率)4.数字问题:(数位变化)类型5.图形问题:(周长与面积(等积变换))6.销售问题:(利润与利率)方程的应用7.储蓄问题:(利息、本息和、利息税)8.分配与方案问题:线段图示法:常用方法列表法:直观模型法:1.2.3.4.⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎧⎧⎪⎪⎨⎪⎩⎪⎪⎪⎪⎧⎪⎪⎪⎪⎧⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎩⎩⎪⎪⎪⎪⎩一般不等式解法一元一次不等式条件不等式解法解法:(借助数轴)不等式与不等式不等式(组)不等式与方程一元一次不等式组应用不等式与函数最佳方案问题5.最后一个分配问题O x x ⎧⎪⎧⎪⎨⎪⎩⎪⎪⎨⎪⎪⎧⎪⎪⎪⎨⎪⎪⎩⎩①各象限内点的特点:x 轴:纵坐标y=0;②坐标轴上点的特点y 轴:横坐标x=0.③平行于轴,y 轴的线段长度的求法(大坐标减小坐标)直角坐标系④不共线的几点围成的多边形的面积求法(割补法)关于轴对称(x 相同,y 相反)⑤对称点的坐标关于y 轴对称(x 相反,y 相同)关于原点对称(x ,y 都相反)正比例函数:y=kx(k ≠0)(一点求解析式)函数表达式一次函数函数11221212112212.,.1.k k b b k k ⎧⎧⎪⎨⎨⎩⎪⎩==-g 一、三象限角平分线:y=x 二、四象限角平分线:y=-x 一次函数:y=kx+b(k ≠0)(两点求解析式)增减性:y=kx 与y=kx+b 增减性一样,k >0时,x 增大y 增大;k <0,x 增大y 减小平移性:y=kx+b 可由y=kx 上下平移而来;若y=k x+b 与y=k x+b 平行,则≠垂直性: 若y=k x+b 与y=k x+b 垂直,则求交点:00(0)(00y y x x x k y k x k k k ⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩=⎧⎨⎩(联立函数表达式解方程组)正负性:观察图像>与<时,的取值范围(图像在轴上方或下方时,的取值范围)表达式:≠一点求解析式)①区域性:>时,图像在一、三象限;<时,图像在二、四象限.k >0在每个象限内,y 随x 的增大而减小;②增减性反比例函数性质k <0在每个象限内,y 随x 的增大而减小.③恒值性:(图形面积与值有关)④对称性:既是221212,(0),(),(0),()(),(0)y ax bx c a y a x k h a y a x x x x a x x x ⎧⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎩⎧++≠⎪-+≠⎨⎪--≠⎩轴对称图形,又是中心对称图形.求交点:(联立函数表达式解方程组求交点坐标,还可由图像比较函数的大小)①一般式:=其中表达式②顶点式:=其中(k,h)为抛物线顶点坐标;③交点式:=其中,、是函数图象与轴交点的横坐标;性质二次函数2220042444242a a b a a x y x y a x y x y b ac b a a b ac b b ac b a a a ⎧⎨⎩---最小值最大值①开口方向与大小:a >0向上,a <0向下;越大,开口越小;越小,开口越小.②对称性:对称轴直线x=->,在对称轴左侧,增大减小;在对称轴右侧,增大增大;③增减性<,在对称轴左侧,增大增大;在对称轴右侧,增大减小;④顶点坐标:(-,)⑤最值:当a >0时,x=-,y =;a <0时,x=-,y =22.44c a x y a c b b ac a b a b c ⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩-++-+示意图:画示意图五要素(开口方向、顶点、对称轴、与、交点坐标)与:开口方向确定a 的符号,抛物线与y 轴交点纵坐标确定c 的值;的符号:b 的符号由a 与对称轴位置有关:左同右异.符号判断Δ=:Δ>0与x 轴有两个交点;Δ=0与x 轴有两个交点;Δ<0与x 轴无交点:当x=1时,y=a+b+c 的值.:当x=-1时,y=a-b+c 的值..⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎪⎪⎪⎨⎪⎪⎪①求函数表达式:②求交点坐标:函数应用③求围成的图形的面积(巧设坐标):0160160⎧⎪⎨⎪⎩⎧⎪==⎪⎨⎪⎪⎩⎧⎨⎩”’”直线:两点确定一条直线线射线:线段:两点之间线段最短,(点到直线的距离,平行线间的距离)角的分类:锐角、直角、钝角、平角、周角.角的度量与比较:, ;角余角与补角的性质:同角的余角(补角)相等,等角的余角(补角)相等,角的位置关系:同位角、内错角、同旁内角、对顶角、邻补角对顶角:对顶角相等.相交线几何初步垂线:定义,垂直的判定,垂线段最短.平行⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩⎩定义:在同一平面内,不相交的两条直线叫平行线线性质:两直线平行,同位角相等、内错角相等、同旁内角互补;同位角相等或内错角相等或同旁内角互补,两直线平行判定:平行于同一条直线的两条直线平行平面内,垂直于同一条直线的两直线平行000000000R 130cos30223cos454512210cos60,tan3022R .t ααααααα⎧⎪⎪⎪⎧===⎪⎪⎪⎪⎪⎪⎪⎨===⎨⎪⎪⎪⎪⎪===⎪⎪⎪⎩⎪⎪⎩的对边的邻边的对边定义:在tABC 中,sin =,cos =,tan =斜边斜边的邻边sin ,三角函数特殊三角函数值sin45;sin6应用:要构造△,才能使用三角函数1C S 20.⎧⎨⎩⎧⎪⎨⨯⎪⎩⎧⎪⎨⎪⎩按边分类:不等边三角形、等腰三角形、等边三角形分类按角分类:锐角三角形、直角三角形、钝角三角形三边关系:两边之和大于第三边,两边之差小于第三边;边面积与周长:=a+b=c ,=底高.三角形的内角和等于18度,外角和等于360度;角三角形的一个外角等于不相邻的两内角之和;三角形的一个外角大于任何一个不相邻的内角中线:一条中线平分三角形的面积一般三角形角线段三角形.⎧⎪⎨⎪⎩性质:角平分线上的点到角两边的距离相等;平分线判定:到角两边的距离相等的点在角的平分线上内心:三角形三条角平分线的交点,到三边距离相等.高:高的作法及高的位置(可以在三角形的内部、边上、外部)中位线:三角形的中位线平行于第三边且等于第三边的一半.性质:线段垂直平分线上的点到线段两端点的距离相等;中垂线判定:到线段两端点的距离相等的点在线段的垂直平分线上.外心:三角形三边垂直平分线的交点.60.6060⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎩⎩⎧⎨⎩,到三个顶点的距离相等等腰三角形的两腰相等、两底角相等,具有三线合一性质,是轴对称图形性质等边三角形的三边上均有三线合一,三边相等,三角形等都为度有两边相等的三角形是等腰三角形;等腰三角形有两角相等的三角形是等腰三角形;判定有一个角为度的等腰三角形是等边三角形;有两个角是度的三角02220.30C 90.⎧⎪⎪⎪⎪⎧⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎩⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎨⎧⎪⎨⎪=⎩形是等边三角形一个角是直角或两个锐角互余;直角三角形斜边上的中线等于斜边的一半;性质直角三角形中,的锐角所对的直角边等于斜边的一半;勾股定理:两直角边的平方和等于斜边的平方.直角三角形证一个角是直角或两个角互余;判定有一边上的中线等于这边的一半的三角形是直角三角形;勾股定理的逆定理:若a +b =c ,则∠.ASA SAS AAS SSS HL ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎧⎪⎧⎪⎨⎪⎨⎩⎪⎪⎪⎩⎩全等三角形的对应边相等,对应角相等,周长、面积也相等;性质全等三角形全等三角形对应线段(角平分线、中线、高、中位线等)相等判定:,,,,.00.⋅⎧⎪⎧⎪⎪⎪⎧⎪⎪⎪⎨⎪⎧⎨⎪⎪⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩⎩⎩⎩多边形:多边形的内角和为(n-2)180,外角和为360定义:一组对边平行而另一组对边不平行的四边形叫做梯形.直角梯形性质:两腰相等、对角线相等,同一底上的两角相等.梯形特殊梯形两腰相等的梯形是等腰梯形;等腰梯形判定对角线相等的梯形是等腰梯形;同一底上的两角相等的梯形是等腰梯形;两组对边分别平性质:平行四边形的平行四边形四边形...⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎨⎪⎪⎪⎪⎪⇒⎨⎪⎪⎪⎪⎪⎪⎩⎩⎧⎧⎨⎪⎩⎪⎧⎨⎪⎨⎪⎩行且相等两组对角分别相等两条对角线互相平分两组对边分别平行一组对边平行且相等判定:两组对边分别相等的四边形是平行四边形.两组对角分别相等对角线互相平分共性:具有平行四边形的所有性质性质个性:对角线相等,四个角都是直角矩形先证平行四边形,再证有一个直角;判定先证平行四边形,再证对角线相等;三个角是直角的四边形是矩形....1S=2⎪⎪⎪⎪⎩⎧⎧⎨⎪⎩⎪⎪⎧⎨⎪⎪⎨⎪⎪⎪⎩⎩⎧⎪→→⎧⎨⎨⎪→→⎩⎩+共性:具有平行四边形的所有性质性质个性:对角线互相垂直且每条对角线平分一组对角,四条边相等菱形先证平行四边形,再证对角线互相垂直;判定先证平行四边形,再证一组邻边相等;四条边都相等的四边形是菱形性质:具有平行四边形、矩形、菱形的所有性质正方形证平行四边形矩形正方形判定证平行四边形菱形正方形梯形:(上底下底面积求法S=S S S ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⨯⨯⎪⎪⎪⎪⨯⎪⎪⎨=⨯⎪⎪⎪⎪⨯⎪⎪⎪=⨯⎩⎩)高=中位线高平行四边形:底高矩形:长宽菱形:=底高=对角线乘积的一半正方形:边长边长=对角线乘积的一半⎧⎪⎨⎪⎩⎧⎪⎧⎨⎨⎪⎩⎩点在圆外:d >r 点与圆的三种位置关系点在圆上:d =r 点在圆内:d <r 弓形计算:(弦、弦心距、半径、拱高)之间的关系圆的轴对称性定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分线所对的弧在同圆或等圆中,两条弧、两条弦、两个圆心角、两个圆周角、五组量的关系:两条弦心距中有一组量相等,则其余的各组两也分别圆的中心对称性圆009090AB CD P PA PA PC PD..⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪⎪⎨⎨⎪⎪⎩⎪⎪=⎪⎪⎩⎧⎪⎨⎪⎩g g 相等.同弧所对的圆周角是它所对圆心角的一半;圆周角与圆心角半圆(或直径)所对的圆周角是;的圆周角所对的弦是直径,所对的弧是半圆.相交线定理:圆中两弦、相交于点,则圆中两条平行弦所夹的弧相等相离:d >r 直线和圆的三种位置关系相切:d =r(距离法)相交:d <r 性质:圆的切线垂直圆的切线直线和圆的位置关系2PA PB PO APBPA PC PD.⎧⎪⎪⎪⎪⎪⎧⎪⎨⎨⎩⎪⎪⎪⎪=⎪⎪⎩⎧⎪⎨⎪⎩g 于过切点的直径(或半径)判定:经过半径的外端且垂直于这条半径的直线是圆的切线.弦切角:弦切角等于它所夹的弧对的圆周角切线长定理:如图,=,平分∠切割线定理:如图,外心与内心:相离:外离(d >R+r ),内含(d <R-r )圆和圆的位置关系相切:外切(d=R+r ),内切(d=R-r )相交:R-r <d <R+r )圆的有关计算22n n 2360180n 1S 36021S 2(2S l r r r l r r l rl r l r rl πππππππ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪==⎪⎪⎪⎪⎪==⋅⋅⎪⎪⎨⎪⎪⎪=⋅⋅=⎪⎪⎪⎪⎪=+⎪⎩⎩弧长弧长侧全弧长公式:扇形面积公式:圆锥的侧面积:为底面圆的半径,为母线)圆锥的全面积:第五部分《图形的变化》知识点⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎨⎪⎩⎪⎪⎧⎪⎨⎪⎩⎩①轴对称指两个图形之间的关系,它们全等②对应点的连线段被对称轴垂直平分轴对称(折叠)③对应线段所在的直线相交于对称轴上一点(或平行)轴对称④图形折叠后常用勾股定理求线段长①指一个图形轴对称图形②轴对称图形被对称轴分成的两部分全等①平移前后两个图形全等②平移前后对应点的连线段相等且平行(或共线)平 移③平移前后的对应角相等,对应线段相等且平行(或图形的变化⎧⎪⎪⎨⎪⎪⎩⎧⎪⎪⎨⎪⎪⎩⎧⎨⎩共线)④平移的两个要素:平移方向、平移距离①旋转前后的两个图形全等②旋转前后对应点与旋转中心的连线段相等,且它们的夹角等于旋转角旋 转③旋转前后对应角相等,对应线段相等④旋转的三要素:旋转中心、旋转方向、旋转角①大小、比例要适中视图的画法②实线、虚线要画清平行投影:平行光线下的投影,物体平行影子平行或共线视图与投影中心投影:点光源射出的光线下的投影,影子不平投影2.........0)...AB C AC BC AC BC AC BC AB a c ad bc b d a c a b c d b d b d a c m a b m k k b d n b d n b d n ⎧⎪⎪⎪⎪⎧⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎩⎧=⇔=⎪⎪±±⎪=⇒=⎨⎪+++⎪====⇒=+++⎪+++⎩g 行视点、视线、盲区投影的计算:画好图形,相似三角形性质的应用基本性质:比例的性质合比性质:等比性质:,(条件≠黄金分割:线段被点分成、两线段(>),满足=, 相似形C AB ⎧⎨⎩⎧⎪⎨⎪⎩ 则点为的一个黄金分割点性质:相似多边形的对应边成比例、对应角相等相似多边形判定:全部的对应边成比例、对应角相等①对应角相等、对应边成比例性质②对应线段(中线、高、角平分线、周长)的比等于相似比③面积的比等于相似比的平方①有两个角相等的两个三角形相似相似图形②两边对应成比例且夹角相等的两个三角形相似相似三角形判定③三边对应成比例的两个三角形相似④有一条直角边与0222Rt ABC C 90CD AB AC AD AB BC BD AB CD AD BD ⎧⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎨⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪=⋅⎪⎪⎪⎪⋅⋅⎪⎪⎪⎪⎩⎩⎧⎨斜边对应成比例的两个直角三角形相似射影定理:在△中,∠,⊥,则=, =,=(如图)位似图形②位似图形对应点所确定的直线过位似中心③通过位似可以将图形放大或缩小⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩⎩第六部分《统计与概率》知识要点21(x x n →⎧⎨⎩→⎧⎪→⎨⎪→⎩⎧⎧⎪⎪⎨⎪⎪⎪⎪⎩⎨⎪⎪⎪⎪⎩=-普查:总体与个体(研究对象中心词)两查抽样调查:样本与容量(无单位的数量)折线图(发展趋势与波动性横纵轴坐标单位长度要统一)三图条形图(纵坐标起点为零高度之比等于频数或频率之比)扇形图(知道各量的百分比可用加权平均数求平均值)算术平均数平均数参照平均数加权平均数三数众数(可能不止一个)中位数(排序、定位)方差:s 统计与概率三差222122)()()(n x x x x n n n ⎧⎡⎤+-++-⎪⎣⎦⎪⎪⎪⎨⎪⎪⎪⎪⎩⎧⎧⎨⎪⎨⎩⎪⎩L 一组数据整体被扩大倍,平均数扩大倍,方差扩大倍);(一组数据整体被增加m ,平均数增加m ,方差不变)标准差:方差的算术平方根s 极差:最大数与最小数之差(方差与标准差均衡量数据的波动性,方差越小波动越小)必然事件:(概率为1)确定事件事件不可能事件:(概率为0)不确定事件:(概率在0与1之间)频率:(两率⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎧⎪⎪⎨⎪⎪⎨⎪⎪⎪⎪⎪⎩⎩⎩试验值,多次试验后频率会接近理论概率)比例法(数量之比、面积之比等)概率:求法列表法(返回与不返回的两步实验求概率)树状图(返回与不返回的两步或两步以上的试验求概率)。
初中数学有理数知识树图PPT教学课件(推荐)

一个正数。② 由定义可知一个数的绝对 1得到.
第一个不是O的数前面的 方没有关系.如2.10×103与
值是数轴上的点到原点的距离,这说明
所有的 0 个数得到. 2.10的有效数字就相同了.
了有理数的绝对值是非负数,即对任意
有理数总有|a|≥0。③ 绝对值等于0的数
一定是0,绝对值为正数m的数一共有两
即:|a|=|b|,则a=b或a=-b ⑥ 绝对值最小的数是0。
① 通常用a与表示一对相反数。 ② 若a与b互为相反数,则 a+b=0。 ③ 互为相反数的两个数的绝 对值相等,即|-a|=|a|。 ④ 若|a|=|b|,则a=b,或a=- b(a与b互为相反数)。
倒数与相反数都是成对出现 的,单独一个数不能称是倒 数或相反数,互为倒数的两 个数符号相同,互为相反数 的两个数符号相反,0没有倒 数,但是它有相反数。
有理数树形图
温馨提示:① -a不一定表示负数,当
把一个大于10的数表示成 把一个小于1的正数表示 a×10n的形式,(其中a是 成 a×10-n的形式(其中a 整数数位只有一位的正数, 是整数数位只有 一 位的 n是正整数),所用的就是 正数,n是 整数 ).所用 科学记数法.这里的n可 的也是科学记数法,这里
绝对值 相反数
倒数
温馨提示:数轴上的 点与实数是一一对应 的。即数轴上的每一 个点都有唯一的一个 实数与它对应;反之,
数轴
实数
有
0的任何非零 正整数次幂都 是 零.
a0= 1 (a≠0), 1
a-p= a p (a≠0).
实数的运算
加法法则 减 法法则
减去一 这个数 a-b=a 运算转 体现了 想。 规律总 变为加 变成原 ② 按照 计算.
初中数学有理数知识树图 PPT课件 图文

易错警示: 对于一个近似数写成a×10n 后,精确度跟10n有关。例如 2.10×103就精确到十位,而 2.10就精确到百分位;而有效
1.数轴上的两个数 右 边的数总比 左 边 2.正数>0>负数;两个负数比较,绝对值 大 3.a>b 4.差值法比较:
a<0时,-a表示a的相反数,此时-a是 以用原数的整数数位减去 的可以通过查看原数的 数字只看a的部分,与10的乘
一个正数。② 由定义可知一个数的绝对 1得到.
第一个不是O的数前面的 方没有关系.如2.10×103与
值是数轴上的点到原点的距离,这说明
所有的 0 个数得到. 2.10的有效数字就相同了.
了有理数的绝对值是非负数,即对任意
有理数总有|a|≥0。③ 绝对值等于0的数
一定是0,绝对值为正数m的数一共有两
绝对值 相反数
倒数
温馨提示:数轴上的 点与实数是一一对应 的。即数轴上的每一 个点都有唯一的一个 实数与它对应;反之,
数轴
实数
有
0的任何非零 正整数次幂都 是 零.
a0= 1 (a≠0), 1
a-p= a p (a≠0).
实数的运算
加法法则 减 法法则
减去一 这个数 a-b=a 运算转 体现了 想。 规律总 变为加 变成原 ② 按照 计算.
有理数树形图
温馨提示:① -a不一定表示负数,当
把一个大于10的数表示成 把一个小于1的正数表示 a×10n的形式,(其中a是 成 a×10-n的形式(其中a 整数数位只有一位的正数, 是整数数位只有 一 位的 n是正整数),所用的就是 正数,n是 整数 ).所用 科学记数法.这里的n可 的也是科学记数法,这里
运算规律
数学组 初中数学知识树图

④ ②
①
③
垂 径 定 理
外心:是三边垂直平 分线的交点. 到三顶点的距离相等 锐—形内;直—斜边 上;钝—形外 圆 上 圆 外
空间与图形6-3
圆 内
中点 四边形
矩形
菱形
内心:是三角平分 线的交点. 到三边的距离相等 在三角形内
基本性质
点与圆
相交 相切
切线的 性质.判定
判定 性质 对角相等 邻角互补 角 判定 性质 对角线 对角线 互相平分 判定
n
a n
分式
分式方程
应用
去分母 是解
1 n为整数 an
合并 同类项
项
整式方程 解法 解方程
xa
同类项
每个单项式
升降幂排列
多项式
整式
检验 增根
次数
意义
最高 项的 次数
单项式
次数 系数
数 字
字母 指数
代 数 式
二次根 式
定义 性质
(1)
( 2)
运算
乘除
加减
a a 0
a
2
a a 0 双非负
初中数学知识树图
空间与图形
统计与概率
数与代数
沪科版《义务教育教科书》 (数学---初中学段(七~九年 级)
实践与运用
一、新课标对本学段、本学科的基本要求
图形的 体会抽样的必要性以及用 图形的 旋转 图形的 轴对称 样本估计总体的思想,进 相似 一步学习描述数据的方法, 图形的 平移 进一步体会概率的意义, 图形与变换 证明的 能计算简单事件发生的概 方法 率。 探讨一些具有挑战性的研 证明的 图形与证明 依据 究课题,发展应用数学知 证明的 识解决问题的意识和能力; 含义 同时,进一步加深对相关 图形与坐标 数学知识的理解,认识数 平面直角 学知识之间的联系。 一次函数 坐标系 概念表示 函数 分类 反比例函数 常量变量 应用 解法 方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
围绕重点知识.主干知识学习 解决问题注重通性、通法 依托教材中的例题、习题展开
腰 腰 角 平行四边形
线
弧长.扇形
正多边形
有关计算:
中心.中心角.
半径.边心距
弧长l nr 180
扇形s nr 2 360
或 1 lr 2
圆锥的 侧面积、全面积
三、教材内容
基
作对称轴 作等腰三角形 作一点到两点距离相等 作一点到三点距离相等(外心)
翻折后与 另一图形重合
对称点
本对
图称 形轴
旋转角=1800 中心对称图形
旋转1800后与 其自身重合
旋转
中心对称
对称中心是对称 点连线的中点
关于中心对称 两图形全等
图案设计
旋转1800后与 关于原点对称 另一图形重合
用平移.轴对称和旋转 的组合设计图案
用坐标表示 旋转
对称点的坐 标符号相反
三、教材内容
空间与图形6-5
到角两边距 离相等的点
基本性质
分式
代 数 式
化除法为
乘法
运算
乘除 乘方
a b
n
an bn
n为整数
分式方程 应用
an
1 an
n为整数
去分母 整式方程
解法
解方程
是解
xa
检验
二次根 式
运算
增根 加减
定义
性质
乘除
a a 0
(1) a a 0双非负
2
(2) a a(a 0) (3) a2 a
减
小
k<0
K同号时, 有两交点。
K异号时, 有两个、一个
关系 或无交点
数与代数3-2
Y
图象在 一三象限
图象在 二四象限
随
每x
y
y
一的
ox
象增 o x限大
双曲线
内而
增
k>0
k<0
大
图象
性质
最优方案
性质 应用
形如y=kx+b (k.b为常数,k≠0)
一次函 数
解析式
当b=0时, 是
一次 函数 与反 比例 函数
形状:取决于 原四边形对角
线的 相等或垂直
中点 四边形
④ ②
矩形
对边平行 性质
且相等 判定 边
对角相等 性质
邻角互补
角
判定
性质
对角线
对角线
互相平分 判定
性质 判定
等腰 直角
作 高 线
正方形
轴对 称性
旋转 不变性
①③
菱形
垂
等 对
圆 周
径 等角
定 定定
理 理理
空间与图形6-3
外心:是三边垂直平 分线的交点. 到三顶点的距离相等 锐—形内;直—斜边 上;钝—形外
章前图、引言
体
例
导入新课材料 供学生预习
安
排
复习题
复习巩固 综合应用 拓广探索
复习全章使用
二、编者的意图 、体例安排 、内在逻辑关系
内 精简整合
如:代数式“先分散,后集 中”,预备知识与方程问题 有机整合,整式中归纳提高
内
知识横向联系
在
逻
辑
有弹性保基础供发展
关
系
螺旋上升的概念思想
改进学习方式 利于主动学习
如:方程以实际问题为出发 点和归宿,建模型引概念, 讨论解法,用理论探究新问
题,体现实践-理论-实践
三、教材内容
逆用公式
平 方 差、 完 全 平 方
多项式除以 单项式
单项式除以 单项式
同底数幂 除法
相除
公 提式 公法 因
十 字 相 乘
分 组 分 解
式
法法
法
乘法公式
单项式与多项式 幂的乘法
三、教材内容
b>0,图象在
Y
一二三象限
随
x
的
增
b=0,图象在 一三象限
大
而
增 大 b<0,图象在
一三四象限
y
y
ox
o
y
y
o 注意x:过原点o
y
y
ox
o
一条直线
k>0
图象
b>0,图象在 x 一二四象限
Y
随
x
的
b=0,图象在 x 二四象限
增 大
而
减
b<0,图象在 x 二三四象限
小
Y
随
每x 一的 象增 限大 内而
统方计数 发法与量展,概关符发率号系展感以空及,间变体观概化会念率规数。律学计的与算工现列树与表状具实、图,
的理解,认图形识与数坐学标 知识之间
生活的紧密联系,增强应估用算 意
平坐的面标联直系角系。 概念表示
一次函数
分类 反比例函数
识,提高运用代数知识与方法
解决问题实的践能活动力。
独立思考 合作交流
常量变量
函数
二次函数
初
获得体验
应用
中
实践与运用
综合应用
解法
方程
数与代数
数
提炼策略
分类
学
二次根式
代数式
实数
知
分式 整式
识
相关概念 分类 运算
树
课题学习
体会知识 形成过程
发展思维 培养应用
能力
意识
二、编者的意图 、体例安排 、内在逻辑关系
编者的意图
提高能力
培养精神意识 着眼长远发展
学生
更新认识
数学
正确处理 关系
对应点的坐标比 为k或-k
放大或缩小 图形
两图形相似 对应顶点的连线交于一点 对应边平行
适用于 直 角三角形
点到角两边 的距离相等
HL
性质
判定 应用
用坐标表示 位似变换
动 应用
性质 特征
外位似 内位似
对应角相等,
对应边成比例,
周
长的比=相似比 面积
的比=相似比的平方
适合 判定 所有 三角 形全
等
AAS ASA SAS SSS
余角.补角
等角的补角相等
角平分线
叠合法 度量法
角的比较
角的比较与运算
和 相 为 定性 等 1800 义 质
对邻
垂
顶补
直
角角
一“放”二“靠” 三“推”四“画”
画法
同位角相等
定义.表示 度.分.秒互化 进位.计算
角的度量
尺规作角
借助角研究平 面内两条直线 的位置关系
关系
相交线
直线公理 直线
表示与画法 射线
关注需要 适应形势
社会
现代技术 数学课程
改进呈现方式 教材
遵循认知 规律
教师
营造氛围
编
学生
互动提供资源
者
的
提高兴趣
创造空间
意
图
二、编者的意图 、体例安排 、内在逻辑关系
体例安排
各栏目以问题、留白、 填空等形式为学生提供 思维发展、合作交流的 空间
介绍与正 文相关的 背景知识
有助于理 解正文的
问题
小
寻找射线方法
表示与画法 计算与比较
性质
线段
直线.射线.线段
图形认识初 步
多姿多彩的图形
立体图形
平面图形
辨认 确定有标记 展开图 的相对图
点与直线 位置关系
相交线.平行 线
图形 认识 初步 相交 线平 行线
条件 判定
内错角相等 同旁内角互补
平行线
平行公理.推论
性质
同位角相等 内错角相等
同旁内角互补
命题
分类 结构
三、教材内容
空间与图形6-2
条件
定义
镶嵌
外角和
等
表
边
定
示 方
要
对 等
义法 素 角
三 线 合 一
等 角 对 等 边
概念
性质
判定
内角和 定义
多边形 及其 内角和
等腰三角形
内角和 外角的性质
有关的角
三角形
等
边
已知两边
三
求第三边
角
弦图
形
应用
毕达哥拉斯
苏菲尔德
证明
特例
定理
文字.符号
内容 图形
互逆命题
初中数学知识树图
高庙中心校 李怀勤
空间与图形
数与代数
统计与概率
人教版《义务教育课程标准实 验教科书·(五四学制)》(供 天津用)---数学---初中学段 (七~九年级)
实践与运用
一、新课标对本学段、本学科的基本要求
体 本会估抽计样总的体必的图轴要思形对性想的称以,及进图旋形用一转的样步图相形似的 学习描述图数形据的的方法,进一 步 简证体单明会事的 概 件率发平的生移 意的义概,率。能图计形与算变换
勾股定理
文字.符号
内容 图形
逆定理
直角三角 形
锐角三角函数
证明 全等
应用
知三边 定形状
高.中线.角平分线
有关线段
三边关系
定义
三 角 形
解直角三角形 锐角三角函数 特殊值的运算
计算 应用
三边关系 坡度 锐角关系 仰.俯角 边角关系 方位角
定义 正弦 余弦 正切
符号.几何意义. 特殊角的值
三、教材内容
如:加强数形,用坐标的方 法处理更多内容(二元一次 方程组.平移.对称.函数等)
