银行客户平均等待时间
MATLAB模拟银行单服务台排队模型

MATLAB模拟银行单服务台排队模型银行单服务台排队模型是一种常见的排队模型,主要用于描述在银行等排队服务场所中,只有一个服务员的情况下,客户如何排队等待服务的情况。
1.模型假设在进行银行单服务台排队模型的建模过程中,我们需要进行一些假设,以简化问题的复杂性。
这些假设包括:-客户到达时间服从泊松分布:客户到达时间间隔服从泊松分布,即客户到达服从一个固定的时间间隔。
-服务时间服从指数分布:每个客户的服务时间是独立同分布的,服从指数分布。
-服务台只有一个:我们假设只有一个服务台,客户按照到达的顺序排队等待服务。
-客户不能提前离开:我们不考虑客户在等待期间可能会放弃等待而提前离开的情况。
2.模型参数在建立银行单服务台排队模型时,我们需要定义一些模型参数。
这些参数包括:-平均到达率λ:客户的平均到达率,表示单位时间内到达的客户数量的期望值。
-平均服务率μ:服务员的平均服务率,表示单位时间内服务的客户数量的期望值。
-服务台利用率ρ:服务台的利用率,表示服务台的平均使用率。
-平均等待时间W:客户平均等待服务的时间。
-平均队列长度L:客户平均排队等待的队列长度。
3.模拟过程为了模拟银行单服务台排队模型,我们使用MATLAB编程进行模拟。
以下是一个简单的模拟过程:-生成客户到达时间间隔:使用泊松分布生成客户到达时间间隔。
-生成客户服务时间:使用指数分布生成客户的服务时间。
-计算客户到达时间和服务完成时间:根据客户的到达时间间隔和服务时间,计算客户的到达时间和服务完成时间。
-计算客户的等待时间:根据客户的到达时间和服务完成时间,计算客户的等待时间。
-统计模拟结果:统计客户的等待时间、队列长度等模拟结果。
4.结果分析通过对模拟结果的分析,我们可以得到一些关键的结果,包括:-平均等待时间:通过计算客户的平均等待时间,可以评估服务台的效率和客户的等待体验。
-平均队列长度:通过计算客户的平均排队等待的队列长度,可以评估服务台的负载情况。
排队模型——精选推荐
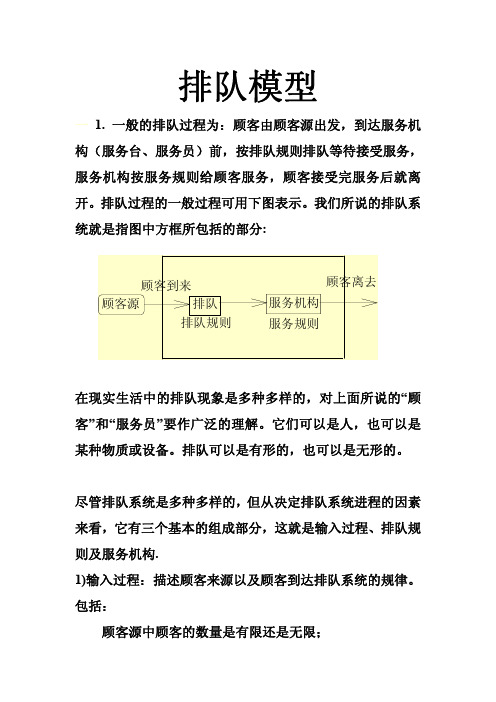
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
排队论习题及答案

排队论习题及答案排队论习题及答案排队论是概率论和数学统计中的一个重要分支,研究的是随机事件的排队问题。
在现实生活中,我们经常会遇到排队的情况,如等候乘坐公交车、购物结账等。
排队论的研究可以帮助我们更好地理解和优化排队过程,提高效率和服务质量。
下面,我们将介绍几个排队论的习题及其解答。
习题一:某银行有两个窗口,顾客到达银行的时间服从平均到达率为λ的泊松分布,每个顾客在窗口办理业务的时间服从平均服务率为μ的指数分布。
求平均等待时间和平均排队长度。
解答:首先,我们可以根据泊松分布和指数分布的性质,得到顾客到达时间和服务时间之间的关系。
假设顾客到达时间服从泊松分布,到达率为λ,那么两个顾客到达时间之间的时间间隔服从参数为λ的指数分布。
同样,假设顾客的服务时间服从指数分布,服务率为μ,那么两个顾客的服务时间之间的时间间隔服从参数为μ的指数分布。
根据排队论的基本原理,平均等待时间等于平均排队长度除以到达率。
平均排队长度可以通过利用排队论的公式计算得到。
在本题中,根据M/M/2模型,可以得到平均排队长度的公式为:Lq = λ^2 / (2μ(μ - λ))其中,Lq表示平均排队长度,λ表示到达率,μ表示服务率。
接下来,我们可以计算平均等待时间。
根据排队论的公式,平均等待时间等于平均排队长度除以到达率。
所以,平均等待时间的公式为:Wq = Lq / λ综上所述,我们可以通过计算得到平均等待时间和平均排队长度。
习题二:某餐厅有4个服务台,每个服务台的服务时间服从平均服务率为μ的指数分布,顾客到达时间服从平均到达率为λ的泊松分布。
求平均等待时间和平均排队长度。
解答:在这个问题中,我们可以使用M/M/4模型来求解。
根据M/M/4模型,平均排队长度的公式为:Lq = (λ/μ)^4 * (1/(4! * (1 - ρ)))其中,Lq表示平均排队长度,λ表示到达率,μ表示服务率,ρ表示系统繁忙度。
平均等待时间的公式为:Wq = Lq / λ通过计算可以得到平均等待时间和平均排队长度。
建行掀起第三次网点转型打造蓝色银行

建行掀起第三次网点转型打造蓝色银行21世纪经济报道丁默2012-11-13 00:11:58 评论(0)条随时随地看新闻核心提示:据建行上述人士透露,近几年该行通过推行前后台分离,已完成网点两次转型,目前正在进行第三次转型,即网点“三综合”建设。
“2012年上半年,全行网点客户平均等待时间为9分37秒,柜员处理每位客户业务的平均时间为7分16秒,均优于上年同期水平。
”2012年11月,建行个人存款与投资部负责人如是告诉记者。
这一简单的数据背后,是一场持续多年的零售银行流程革命,从2007年到2012年,中国建设银行零售网点转型从一代、二代正向三代过渡;而流程再造的显著成效,则是个人客户整体满意度从2007年的57.6%提高到2011年的64.1%。
据建行上述人士透露,近几年该行通过推行前后台分离,已完成网点两次转型,目前正在进行第三次转型,即网点“三综合”建设。
通过内部劳动的组合缩短客户等候时间,提高劳动生产率。
这也是2012年初,建设银行提出清晰的客户发展战略当中的一部分。
今年10月份,建行董事长王洪章撰文表示,未来建行要加强多功能渠道建设,夯实综合化服务渠道基础。
“首先要通过第三次转型,推进网点…三综合‟建设,打造综合性网点、综合制柜员和综合化营销队伍,实施前后台分离,提升网点的综合服务能力。
”在王洪章看来,为进一步深化结构调整和发展方式转变,建设银行将继续大力推进业务发展和经营管理的全面转型,而服务渠道的转型与革命将是未来五年战略转型中的一个重要环节。
“服务渠道从物理网点为主向物理网点和电子渠道并重、多渠道功能互补、协调联动转变;业务流程从部门银行、着眼内部管理需要为主向流程银行、快速响应客户需求转变。
”王洪章表示。
三代网点转型进行时从2007年到2012年,建行零售网点三代转型成效如何?数据显示,截至2011年末,通过开展网点转型和流程优化,客户平均等候时间下降了34%,平均办理业务时间6分42秒,比转型前大为缩短;个人客户整体满意度从2007年的57.6%提高到2011年的64.1%;截止2012年6月底,个人客户经理的客户满意度达到84.9%,连续四年在工、农、中、建、交中排名第一,并连续两年超过招行。
排队论习题答案

排队论习题答案排队论习题答案排队论是运筹学中的一个重要分支,研究的是排队系统中的等待时间、服务时间以及系统的稳定性等问题。
在实际生活中,我们经常会遇到排队的情况,比如超市、银行、医院等地方。
那么,如何有效地解决排队问题,减少等待时间呢?下面我将通过几个习题来探讨排队论的解题方法。
习题一:某银行有两个窗口,分别为A窗口和B窗口,顾客到达的时间间隔服从指数分布,平均每10分钟到达一人。
A窗口的服务时间服从均值为5分钟的指数分布,B窗口的服务时间服从均值为7分钟的指数分布。
求顾客平均等待时间和平均逗留时间。
解答一:首先,我们需要计算平均到达率λ和平均服务率μ。
根据题目给出的信息,平均到达率λ=1/10=0.1人/分钟,平均服务率μA=1/5=0.2人/分钟,平均服务率μB=1/7≈0.1429人/分钟。
根据排队论的基本原理,当λ<μ时,系统稳定,顾客平均等待时间为0。
当λ>μ时,系统不稳定,顾客平均等待时间为ρ/(μ-λ),其中ρ为系统繁忙率。
由于该题目中有两个窗口,所以我们需要计算两个窗口的繁忙率ρA和ρB。
ρA=λ/μA=0.1/0.2=0.5,ρB=λ/μB=0.1/0.1429≈0.7。
由于两个窗口的繁忙率不相等,我们需要使用排队网络的方法来求解。
根据排队网络的基本原理,顾客平均逗留时间等于顾客在每个窗口的平均逗留时间之和。
根据排队网络的公式,顾客在A窗口的平均逗留时间为1/(μA-λ)≈5分钟,顾客在B窗口的平均逗留时间为1/(μB-λ)≈7.5分钟。
所以,顾客平均逗留时间为5+7.5=12.5分钟。
习题二:某医院门诊部有一个窗口,顾客到达的时间间隔服从泊松分布,平均每10分钟到达一人。
窗口的服务时间服从均值为8分钟的指数分布。
求顾客平均等待时间和平均逗留时间。
解答二:同样地,我们需要计算平均到达率λ和平均服务率μ。
根据题目给出的信息,平均到达率λ=1/10=0.1人/分钟,平均服务率μ=1/8=0.125人/分钟。
银行服务改进建议(精简版)

银行服务改进建议银行服务改进建议银行服务改进建议:银行服务改进建议关于改进银行服务的一点建议2根据市场反应和,结合我行自身实际,现将分析与建议呈报如下:一、自身情况我们曾在网银、快易理财、手机银行方面取得较好成果,但现略142字,正式会员可完整阅读)……银行都有自己独特的吸取存款的方式,如果没有总是停留在完成任务上,我们的竞争力会逐步下降,因为相对其他同行我们没有什么有特色的服务,难以形成有力的竞争,银行服务改进建议。
三、客户方面客户是挑剔的,不仅要有优质的服务而且要有高的效率,我们网点办理业务时间相对较长,平均每个客户要等待一个小时,在这快速的社会节奏下,这种速度必然会使我们流失一部分客户,甚至会使原来的客户流向他处。
四、解决方法我们要自己养鱼。
坚持自己的优质服务,改变流水式的批量填单方式,从细节入手留住客户,吸引客户,把客户的利益放至在最高点。
分行任务我们可以在星期天仍然上班,仅为代发工资户批量开功能而工作……本站为您提供“一站通服务”给我行的几点建议X总:您好!来我行工作已x年有余,亲眼目睹了我行的发展、壮大,同时也看到了我行在当前激烈的市场竞争中所面临的种种考验与挑战,现想根据我的个人工作体会给您提几点建议,希望对我行发展能有所帮助,,银行服务改进建议。
当下,国内银行业竞争已日趋激烈,有一个。
可见,我行流水式的批量派单写单,很难以满足客户高效便利的需要,也就影响了我行在客户心目中的形象,即使有钱,也不会转进来。
即便开始在我行开了户,随着以后每次的办理业务等待时间,他们也会选择离开的。
办理业务难、等待时间长,导致有价值客户流失的这一现状,迫切要求我们采取各种措施为客户提供便利,提升业务办理速度。
在这方面,前台金卡拦截是很不错的提速方式,但这也仅是少量拦截,总体效果仍不尽人意。
鱼都是从小养起的,而我感觉,今年我们都放弃了“养鱼”,仅为完成分行任务,个人积分在工作,这种方式是不可取的。
我认为,银行是为存款、为客户存在的,而不应把大量时间都花在已经是我们客户的代发工资户开功能上面。
解决营业厅排队现象的有效方法

解决营业厅排队现象的有效方法关于营业场所排长队的现象从来没有像今天这样受到所有人的关注。
有记者暗访了北京的工商银行营业网点,结果得到的结论让人吃惊。
在他走访的4家国有银行网点中,记者的平均等待时间为85分钟,最短56分钟,最长167分钟;在5家股份制银行网点平均为35分钟,其中招商银行和北京银行分别为48分钟和47分钟。
银行排长队,也不光发生在北京。
盛世指数数据管理有限公司近日调查了北京、上海、广州等10个城市的1680名客户。
结果显示,有78.2%的客户经常遇到排队的情况,仅1%的客户几乎没遇到排队现象,平均等待时间约为14分钟。
当然,排长队也不仅仅发生在银行,移动、电信营业厅也经常出现这样的问题。
排队其实是个很典型的经济学问题,每个排队者都付出了成本(时间),得到收益(服务),尽管每个人的时间价值不同,但排队总体还是体现了公平和效益的原则。
在这里,仍有两种例外,一种是如新闻中所说从票贩子手中买号,另一种是VIP客户可以免排队。
每个人的时间价值不同,能够用金钱买时间,仍然符合经济学的原则。
但是从另一个角度来看,如果每个网点平均等待时间要85分钟之久,尽管客户与客户之间体现了公平原则,但客户和服务机构之间就未必能体现出这种公平原则。
作为客户,在得到的收益不变的前提下,每个人的付出都相应增加(时间价值),即变相地减少了收益。
零点集团公布的一项调查显示,目前,处于26岁~35岁“黄金年龄”、高学历、高收入的优质客户,对中资银行服务不甚满意。
具体到服务细节上,排队时间太长是不满的原因之一。
可见,排队问题对客户服务满意度影响很大。
现代系统工程科学有个分支叫运筹学,运筹学中又细分出“排队论(queueing theory),”或称随机服务系统理论。
该理论在窗口服务经营中运用,就是致力于排队时间与用户等待耐心极限的研究,致力于营业网点设置、人力成本控制与服务质量的平衡研究,并以此作为网点设置和员工配置的科学依据。
过程能力指数案例分析

过程能力指数案例分析过程能力判断过程能力指数的值越大,表明产品的离散程度相对于技术标准的公差范围越小,因而过程能力就越高;过程能力指数的值越小,表明产品的离散程度相对公差范围越大,因而过程能力就越低。
因此,可以从过程能力指数的数值大小来判断能力的高低。
从经济和质量两方面的要求来看,过程能力指数值并非越大越好,而应在一个适当的范围内取值。
过程能力指数案例分析服务是一种无形的产品,对其如何进行质量控制呢?在工业质量管理的方法里,有一种指标叫做过程能力指标C pk,表示生产的部件与设计界限规定的范围的吻合程度,我们发现,把它应用在服务业上,也是一种很好的控制方法。
下面就以某银行为例子,来说明它的应用。
某银行在营业高峰期时,顾客的等待时间最少是4分钟,银行承诺最多11分钟要办理完其全部业务,这是银行对过去的业务经验的总结,同时认为,一般的平均等待时间是8分钟,这反映了其职员处理业务的平均速度和平均熟练程度。
在某个高峰时段银行办理了50位客户业务,每位客户的等待时间如下(为了便于计算0.5表示半分钟):9.5,6.0,8.0,8.5,10.5,8.5,10.0,9.0,6.0,9.5,8.0,8.5,7.59.0,8.5,10.0,7.5,9.0,6.5,9.5,8.0,8.5,10.0,7.0,7.0,9.5,8.5,9.0,8.0,8.0,11.0,7.5,8.5,6.5,10.5,8.0,7.0,9.0,8.59.0,8.0,8.0,6.5,7.5,8.5,8.5,7.0,7.5,9.0,9.0从这些数据可以看出银行实现了对顾客的承诺,每位顾客的等待时间都不超过11分钟,是否可以说该银行的服务质量达到了标准?部门经理应该如何评价本银行的的业务处理能力呢?首先,我们要对这些数据作分析处理,如上图。
从图中我们可以得到,直方图表示数据的频度,数据的分布大体上是服从正态分布的,且曲线中值偏向右侧。
USL和LSL分别表示的是服务要求范围的上限和下限,在本案例中就是11分钟和4分钟,即落在这个界限内的顾客等待时间都是合适的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
clock=arrive;/*时钟推进到下一位客户的到达时间*/
else
clock=finish; /*时钟推进到当前客户办理结束时间*/
}
printf("%.2f\n",wait/m);
}/*main_end*/
typedef float QElemType;
typedef struct QNode{
QElemType arrive;
QElemType treat;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct{
QueuePtr front;
QueuePtr rear;
if(Q.front==Q.rear)
return ERROR;
p=Q.front->next;
arrive=p->arrive;
treat=p->treat;
Q.front->next=p->next;
if(Q.rear==p)
Q.rear=Q.front;
free(p);
return OK;
}
Status EnQueue(LinkQueue &Q,QElemType arrive,QElemType treat)
队列的应用——银行客户平均等待时间
描述
某银行有一个客户办理业务站,在一天内随机地有客户到达,设每位客户的业务办理时间是某个范围内的值。设只有一个窗口,一位业务人员,要求程序模拟统计在一天时间内,所有客户的平均等待时间。模拟数据按客户到达的先后顺序依次由键盘输入,对应每位客户有两个数据,到达时刻和需要办理业务的时间。
Input
第一行:一天内的客户总人数n
第二行:第一个客户的到达时刻和需要办理业务的时间
第三行:第二个客户的到达时刻和需要办理业务的时间
……
第n行:第n - 1个客户的到达时刻和需要办理业务的时间
第n + 1行:第n个客户的到达时刻和需要办理业务的时间
Output
第一行:所有客户的平均等待时间(精确到小数点后2位)
}LinkQueue;
Status InitQueue (LinkQueue &Q)
{
Q.front=(QueuePtr)malloc(sizeof(QNode));
if(!Q.front)
return ERROR;
Q.front->next=NULL;
Q.rear=Q.front;
return OK;
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#define OVERFLOW -2
#define OKK 2
#define OK 1
#define ERROR 0
typedef int Status; // Status是函数的类型,其值是函数结果状态代码,如OK等
}
Status ReQueue(LinkQueue &Q,QElemType &arrive,QElemType &treat)
{
QueuePtr p;
if(Q.front==Q.rear)
return ERROR;
p=Q.front->next;
arrive=p->arrive;
treat=p->treat;
//Q.front->next=p->next;
//if(Q.rear==p)
//Q.rear=Q.front;
//free(p);
return OK;
}
Status DeQueue(LinkQueue &Q,QElemType &arrive,QElemType &treat)
{
QueuePtr p;
for(;n>0;n--)
{
wait+=clock-arrive;/*累计到客户的总等待时间*/
finish=clock+treat;/*设定当前客户业务办理结束时间;*/
DeQueue(Q1,ReQueue(Q1,arrive,treat);/*读入下一位客户信息*/
{
QueuePtr p;
p=(QueuePtr)malloc(sizeof(QNode));
if(!p)
return ERROR;
p->arrive=arrive;
p->treat=treat;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}
Status EmptyQueue(LinkQueue &Q){
//判断队列是否为空
if(Q.front==NULL)
return OK;
else
return OKK;
}
void main()
{
float clock=0,wait=0,count=0,finish;;int n,m,i;float arrive,treat;
LinkQueue Q1;
InitQueue (Q1);
scanf("%d",&n);
m=n;
for(i=1;i<=n;i++)
{
scanf("%f%f",&arrive,&treat);
EnQueue(Q1,arrive,treat);
}
ReQueue(Q1,arrive,treat);/*读入第一位客户信息*/
clock=arrive;/*时钟推进到当前客户的到达时间*/
