第8章力矩分配法
力矩分配法

力矩分配法简介力矩分配法是一种常用的工程分析方法,用于计算和分析物体受到的力的分布情况以及力矩的平衡。
根据力矩分配法,物体处于平衡状态时,所有作用于物体上的力矩和为零。
利用这个原理,可以计算物体上各点的力的大小和分布。
基本原理力矩是一个力在距离某一点的作用线上产生的旋转效果。
当物体受到多个力作用时,在平衡状态下,力的合力和力矩的合力都为零。
根据力矩的定义,可以得到如下的力矩分配方程:其中,表示物体上所有力矩的代数和。
力矩分配法的步骤力矩分配法一般包括以下几个步骤:1.给定各个力的大小和作用点位置。
2.计算每个力的力矩。
力的力矩可以通过力乘以力臂得到,力臂是力的作用点到某一参考点的直线距离。
3.将各个力矩代入力矩分配方程,求解未知力的大小和作用点位置。
可以利用代数方程或者力矩图等方法进行计算。
4.验证计算结果,检查力矩的合力是否为零,以验证平衡状态。
5.如果力矩不为零,则需要重新调整力的大小和作用点位置,再次计算和验证。
力矩分配法的应用力矩分配法在工程中有广泛的应用。
以下是一些常见的应用例子:1.结构平衡:力矩分配法可以用于计算结构上各个部分受力的平衡情况,如梁、桁架等结构的受力分析。
2.机械设计:力矩分配法可以用于计算机械装置中各个零件受力的分布情况,如齿轮传动、支撑结构等。
3.车辆平衡:力矩分配法可以应用于汽车、飞机等交通工具的平衡分析,确保车辆的稳定性和安全性。
4.物体悬挂:力矩分配法可以计算物体悬挂时各个支点的受力情况,如吊车、吊车臂等。
总结力矩分配法是一种常用的力学分析方法,通过计算力矩的平衡来推导出物体上各点的力的分布情况。
它在工程中的应用非常广泛,可以用于结构平衡、机械设计、车辆平衡等领域。
使用力矩分配法可以帮助工程师更好地理解和分析各种力的作用情况,从而设计出更加稳定和安全的结构和设备。
结构力学次课力矩分配法分配系数结点不平衡力矩

梦想不会逃跑,会逃跑的永远都是自己!结构力学第27次课 第8章力矩分配法 分配系数 结点不平衡力矩2012-6-6第1节课 其他约束情况下 超静定单跨梁的转动刚度1 转动刚度:梁端发生单位转角产生的弯矩。
⎪⎪⎩⎪⎪⎨⎧⇒⇒⇒⇒=∆=远端为自由端远端为平行支链杆远端为铰支端远端为固定端0341ik ikik ik ik ik i i i S S M 2 分配系数:与转动刚度成正比()1==∑∑iikiikikik S S μμ3 传递系数:近端发生转角时,远端弯矩与近端弯矩的比值.⎪⎪⎩⎪⎪⎨⎧⇒-⇒⇒==远端为平行支链杆远端为铰支端远端为固定端1021ikkiik M M C ⏹结构力学第26次课(mardi 5-juin -2012)内容回顾( )( )a b1234AllllBCADE=1i =1i =1i =1i第2节课 结点不平衡力矩求解单结点的力矩分配F P q A原结构=F P qAA 状态-MB 状态+A 点附加刚臂阻止转动,承担汇交杆端的不平衡固端弯矩M 。
在结点上加一个反向的力矩。
(相当于刚臂放松)B 状态的内力——分配弯矩用力矩分配法计算A 状态的内力——固端弯矩查表计算例题-M(作用在结点上)结点不平衡力矩3/74/7i iMiiM BM BM B =-MM1. 直接作用结点力偶分配系数:二、结点不平衡力矩例题3/74/7-ql 2/8固端弯矩qiill分配系数:-ql 2/8结点不平衡力矩8ql ⏹结构力学第27次课(merdredi 5-juin -2012)内容回顾2. 杆上作用荷载MB M B8ql单结点的力矩分配例题-F P l 固端弯矩-F P l 0F P l/2F P l 杆端弯矩0F P l /2F P l分配、传递ll2iiF P10F P lF P l/2M 图3. 带悬臂端杆件分配系数:单结点连续梁的力矩分配法小结2.具有一个结点角位移结构的计算步骤:● 加约束:在刚结点i 处加一附加刚臂,求出固端弯矩,再求出附加刚臂给结点的约束力矩f i M 。
龙驭球《结构力学》笔记和课后习题(含真题)详解(渐近法及其他算法简述)

中的计算,进行二次分配传递。 (5)各点循环放松,每次产生的新约束力矩会越来越小,一般进行两三轮计算就能满
3 / 52
圣才电子书
足工程精度。
十万种考研考证电子书、题库视频学习平台
l 转动刚度可由位移法中的杆端弯矩公式导出,以下列出常用转动刚度: 远端固定,S=4i;远端简支,S=3i;远端滑动,S=i;远端自由,S=0。
2.分配系数
任一杆件在某结点的分配系数等于杆件的转动刚度不汇交于该结点的各杆转动刚度之
和的比值。它起到将作用于某结点的弯矩按比例分配到汇交于该结点各杆的近端的作用,用
三、无剪力分配法 1.应用条件 刚架中除杆端无相对线位移的杆件外,其余杆件都是剪力静定杆件。
2.剪力静定杆件的固端弯矩
4 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
先根据静力条件求出杆端剪力,然后将杆端剪力看作杆端荷载。按该端滑动,另端固定 的杆件进行计算。
出附加刚臂给予结点的约束力矩,用 M 表示。约束力矩规定以顺时针转向为正。
(3)放松结点:将丌平衡弯矩(固端弯矩之和)反号后,按分配系数、传递系数进行 分配、传递。
2 / 52
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)结构的实际受力状态:将各杆的固端弯矩、分配弯矩和传递弯矩相加,即得各杆 的最后弯矩。
束力 M C 相反的力矩,由这个 M C 引起的固端弯矩,可利用力矩分配法进行计算。计算后 经过一次传递,B 点处的约束力矩变成了 M B M BC 。
(3)将结点 C 重新固定,放松结点 B,相当于在有一个反向力矩加到 B 点上,即为
力矩分配法ppt课件

Z1 MA'
D
A
Z1
Z1
C Aj
M jA M Aj
B
M BA 2iAB Z1 MCA 0 M DA iADZ1
M BA M AB
CAB
1 2
M CA M AC
C AC
0
M DA M AC
C
AC
1
MAC
MA' A
MAD
在等截面杆件中,弯矩传递系数 C 随远端的MAB支承情况而 不同。三种基本等截面直杆的传递系数如下:
一、单结点连续梁的力矩分配法
⑶放松刚臂,计算刚臂转动
A
Z1时结点的反力矩R11。
3m
M B A 4iZ1 SBAZ1
M B C 3iZ1 SBCZ1 R11 M B A M B C 0
A
基本体系
R11 (M B A M B C ) (SBA SBC )Z1
17
第7章 力 矩 分 配 法
§7.2 力 矩 分 配 法 的 基 本 原 理
⑵计算固端弯矩
20kN/m
100kN
M
F AB
ql 2
12
30 42
12
60.0kN m
A EI=1 B EI=2
92.6
C EI=1 D
M
F BA
60.0kN
m
M
F BC
Fl 8
1008 8
远端固定
C Aj
1 2
远端滑动 C Aj 1
远端铰支 CAj 0
7
第7章
力矩分配法
结构力学——力矩分配法

结构力学——力矩分配法结构力学是研究物体在外力作用下的变形和破坏行为的学科。
其中,力矩分配法是一种求解结构梁的内力和变形的常用方法之一、本文将介绍力矩分配法的基本理论和应用。
首先,对于结构力学的研究,我们需要了解一些基本概念。
力矩是由力的作用点与旋转轴之间的距离和力的大小决定的。
在结构力学中,我们通常考虑作用在梁上的力和力矩。
梁是一种常见的结构元件,可以将其看作是在两个固定点之间作用的力的集合。
在力矩分配法中,我们将梁分割成若干个小段,然后逐段计算每个小段的内力和变形。
假设有一根长度为L,截面形状均匀的梁,并且在两个固定点之间施加了一系列分布力。
我们可以将梁分割成n个小段,每个小段的长度为Δx=L/n。
接下来,我们需要计算每个小段的内力和变形。
首先,我们可以根据材料力学的基本原理得出梁的拉伸、压缩和弯曲的力学方程。
然后,我们可以根据小段的切线方向和切线上的任意一点来推导出该小段的内力和弯曲方程。
最后,我们将内力分量在小段两端的力矩分配系数和位置矩分配系数进行合成,从而得出该小段的内力和弯曲方程。
在力矩分配法中,一个重要的概念是力矩分配系数。
力矩分配系数是一个无量纲的参数,用来表示力和力矩在小段两端分配的比例。
在计算力矩分配系数时,我们可以根据梁的几何形状和分布力的位置,利用力矩的基本原理进行推导。
力矩分配系数是力矩分配法的核心,它可以帮助我们计算出每个小段的内力和变形。
在实际应用中,力矩分配法通常用于求解多跨梁的内力和变形。
我们可以将多跨梁分割成若干个小段,并根据力矩分配法计算出每个小段的内力和变形。
然后,我们可以将各个小段的内力和变形进行叠加,得出整个多跨梁的内力和变形。
需要注意的是,力矩分配法具有一定的局限性。
首先,它只适用于存在弯曲变形的梁,对于其他类型的结构,如框架和板,需要采用其他的分析方法。
其次,力矩分配法仅适用于分布力作用在梁的直线部分上,对于弯曲部分或非均匀分布力的情况,需要采用其他的方法进行分析。
力矩分配法
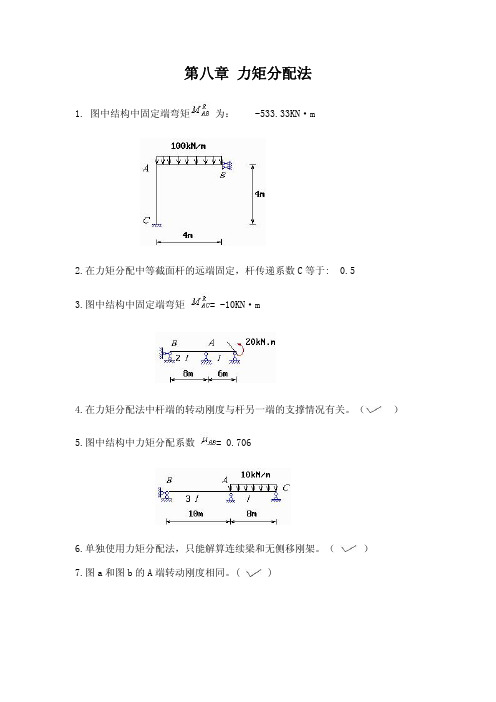
第八章 力矩分配法1. 图中结构中固定端弯矩 为: -533.33KN·m2.在力矩分配中等截面杆的远端固定,杆传递系数C等于: 0.53.图中结构中固定端弯矩 = -10KN·m4.在力矩分配法中杆端的转动刚度与杆另一端的支撑情况有关。
( )5.图中结构中力矩分配系数 = 0.7066.单独使用力矩分配法,只能解算连续梁和无侧移刚架。
( )7.图a和图b的A端转动刚度相同。
( )8.一个刚结点无论连接多少个杆件,这些杆件的力矩分配系数之和总等于( )9.在力矩分配法中已知某杆一端的分配力矩M,若该杆另端为滑动支座,则传递力矩为M。
( )10.力矩分配法中的传递系数等于传递力矩与分配力矩之比,它与荷载作用无关。
( )11.对图示结构,力矩分配系数 和固端弯矩 分别为:( A )A.0.238, -41.67 KN·mB.0.238, 41.67 KN·mC.0.294, -41.67 KN·mD.0.294, 41.67 KN·m12.图示结构中,各杆i等于常数,欲使结点产生顺时针转角,即 =1,要在结点A上施加(顺时针)外力偶为:( A )A.8iB.8iC. 11iD.9i13.用力矩分配法计算图示结构,结点A的不平衡力矩为:( A )A.-16 KN·mB. 16 KN·mC. 0D.-64 KN·m14.图示连续梁,已知 =1/2,则杆端弯矩 为: ( A )A.8 KN·mB.-8 KN·mC.16 KN·mD.-16 KN·m15.用力矩分配法计算图示结构,分配系数 和为4/7和3/7,则杆端弯矩分别为: ( A )A.80 KN·m, 60 KN·mB.-80 KN·m,60 KN·mC.80 KN·m,-60 KN·mD.-80 KN·m,-60 KN·m16.AB杆的弯矩传递系数 与: ( C )A.杆AB的A端支承情况有关B. 杆AB的两端支承情况有关C. 杆AB的B端支承情况有关D. 杆AB的两端支承情况无关17.在力矩分配法中,某杆端分配系数与该杆的转动刚度: ( A )A.成正比B.有时成正比,有时成反比C.无关系D.成反比18.取左半部为如图示对称结构的等代结构,在等代结构中分配系数 等于:( D )A.1/3B.4/11C.2/5D.2/719.用力矩分配法计算图示结构,分配系数 、分别等于: ( D )A.0.5 0.333B.0.25 0.5C.0.25 0.333D.0.50.57120.如图连续梁中,已知 =4/7,则 等于: ( D )A.4/7(-M+Pd/6)B. 4/7(M+Pd/8)C.4/7(-M+Pd/8)D. 4/7(M-Pd/8)。
结构力学 力矩分配法

最后杆端弯矩的计算,是将同一杆 端(表中同一杆端下的列)下的固 端弯矩、分配弯矩及传递弯矩相叠 加得出。
例10-2-2 用力矩分配法计算图示刚架, 并作弯矩图。
q= 20kN /m B C E
A 6m (a)
D 6m
解:1)计算分配系数:设EI/6=1
结点B单元:SBA=4 SBC=8 BA 1 3 BC 2 3
M A3
3 63 21kN m 9
C M 3A 0
3)叠加计算各杆最后弯矩
F M A1 M A1 M A1 28 6 34 kN m
F M A2 M A2 M A2 14 0 14 kN m
M A3 21 9 12 kN m
F M A M Ai i 1 n
(10-1-4)
例10-1-1
q=2kN/m,FP1=10kN,FP2=8kN
试用力矩分配法计算,并作刚架弯矩图。
FP 1 =10kN
FP 2 =8kN 1 A
(a)
6m
6m
FP1 = 10kN
F P2= 8kN 1 A
60kN m 1 14kN m A
例10-2-1
用力矩分配法计算图(a)所示连续梁, 并作弯矩图。
E I
2 2 m m
6 m
4 m
解:1)计算分配系数:令EI=1 B结点分配 单元:
S BA EI 4 1 4
S BC
EI 2 4 6 3
S
Bi
5 3
BA
3 5
BC
2 5
C结点分配单元:
S CB 2 3 8 17
EI 3 S CD 3 4 4 9 CD 17
第八章力矩分配法-精品文档

φK
B
原状态
F A MAK MKA K MKB MBK
MAK
F
固定状态
F FRKF
F F F
放松状态(转动状态)
mK = - FRKF
B
C D D C
K
C
KA 图 示 结 构、、= M M M ? K A K B K C
M KC
φK
l
K结点
M + M + M = m K A K B K C K
EI= C B
r 4 i 3 i i K K K A K B K C
M KB
S S S K A K B K C
l
l
S
KI
如何分配?
KA KK
K
C K
φK
( 3 ) 作 MK及 M 图 F
ห้องสมุดไป่ตู้
2iKA
3
iKB
iKC
(4)求刚度系数和自由项
B
B M
K
基本系
r 4 i 3 i i K K K A K B K C
rK K
4
S S S K A K B K C
iKC
F
RKF
m
F
R K F
K
iKA
K
A K
C
S KI
m
M AK =
2iKA
mK
M
=0
mK
C
IK
B M
F
RKF
传递系数:传递弯矩与分配弯矩之比,记为:C 只与远端约束有关 一般式: M =C M C
C D IK KI KI
K I
K I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 4
传递系数
远端固定,CAB=0.5
远端简支,CAD=0
远端滑动,CAC=-1
D i
分配系数
AB
2 3
AC
1 12
AD
1 4
120kNm
A
2i
i
C
传递系数
CAB=0.5
CAD=0
CAC=-1
B
D
80kNm A 30kNm
B 40kNm
10kNm C
M图
杆端弯矩
M AB
AB M
2 *120
3
固端弯矩
分配和传 递弯矩 杆端弯矩
A -150 -17.2
-167.2
分配系数
4 7
150
3 7
B
-90
-34.3 -25.7
115.7 -115.7
167.2 A
115.7
300
90
B 32.1
158.5
M图(单位kNm)
C 0 0 0 单位kNm
C
单结点力矩分配法计算举例
3)非结点荷载作用刚架
渐近法概述
1、线性代数方程组的解法: 直接法,渐进法
2、结构力学的渐近法:
力学建立方程,数学渐近解 不建立方程式,直接逼近真实受力状态。其 突出的优点是每一步都有明确的物理意义。
3、位移法方程的两个特点:
(1)每个方程一般不超过五项式; (2)主系数大于副系数的总和,即 kii > kij,
适于渐近解法。
80kNm
M AC AC M 10kNm
M AD AD M 30kNm
M BA CAB M AB 40kNm
M CA CAC M AC 10kNm
单结点力矩分配法计算举例
2)非结点荷载作用连续梁
200KN
A 3m
B 3m
20KN/m 6m
解:先固定B结点 固端弯矩:
M
F AB
M
F BA
,
M BA 0.5M AB
转动刚度
S AB
M AB
A
4EI 4i l
B
近端
A MAB
M图
远端
0.5MAB B
传递系数
CAB
0.5M AB M AB
0.5
转动刚度S与传递系数C
MAB EI
远端固定 A A
l
MAB
远端简支 A A
EI
l
MAB
远端滑动 A
EI
A
l
MAB
远端自由 A
EI
A
l
转动刚度 B SAB 4i
B SAB 3i
B
SAB i
B
SAB 0
传递系数 CAB 0.5
CAB 0
CAB 1 CAB 0
例:双跨连续梁的转动刚度
M
A
i
B
2i
C
BA杆 转动刚度 SBA 3i
BC杆
SBC 4* 2i
传递系数 CBA 0
CBC 0.5
杆端弯矩 MBA SBAB
MBC SBCB
平衡条件 MBA MBC M
A
i
8m
D
2i 10kN
B
i
E 10kN
4m
4m
解:
固端弯矩:M
F BC
10kNm
,
M
F CB
10kNm
8m
M
F BE
80kNm
C
转动刚度:SBA 3i , SBC 4i
SBD 2i , SBE 0
8m
BA
分配系数:
(3
3i 4
2)i
1 3
,
BD
2 9
,
BE 0
BC
kij
kik
kii
kir
kis
4、不建立方程组的渐近解法有:
(1)力矩分配法:适于连续梁与无侧移刚架。 (2)无剪力分配法:适于规则的有侧移刚架。 (3)迭代法:适于梁的刚度大于柱刚度的各种刚架。
理论基础:位移法; 计算对象:杆端弯矩; 计算方法:逐渐逼近的方法; 适用范围:连续梁和刚架。
kij
kik
3
M BA
M 11
8
M BC
M 11
分配系数μ :某杆件杆端的转动刚度与杆端所在结点所有的转 动刚度之和的比值。
例:双跨连续梁的分配系数
M
A
i
B
2i
C
转动刚度
BA杆 SBA 3i
分配系数
BA
SBA SBA SBC
杆端弯矩
M BA
BA M
3M 11
BC杆
SBC 8i
BC
SBC SBA SBC
M BC
BC M
8M 11
单结点力矩分配法计算举例
1)结点荷载作用刚架
120kNm
D
B
i
A
2i
i
C
解: 各杆转动刚度
SAB 8i SAC i SAD 3i
分配系数
AB
S AB
S AB SAC
SAD
2 3
AC
S AB
S AC SAC
SAD
1 12
AD
S AB
S AD SAC SAD
两种 情况 相加
150KNm A
200KN
20KN/m
150KNm 90KNm
B
17.2KNm A
-60KNm
25.7KNm B
34.3KNm
C
约束结点B。 约束弯矩为结 C 点B固端弯矩 总和60kNm
放松结点B。 等于施加固端 C 弯矩总和的负 值-60kNm
列表计算
解: 结点B的分配力矩 结点不平衡力矩 15090 60
kii
kir
kis
§8-1 力矩分配法的基本概念
力矩分配:作用在结点的力矩按比例分配给结点处的各杆端 力矩传递:杆件某端分配到的力矩传递到另一端
(分配的力矩为近端弯矩,传递的力矩为远端弯矩)
转动刚度S:杆端对转动的抵抗能力 分配系数μ :某杆件杆端的转动刚度与杆端所在结点所有的转 动刚度之和的比值。 传递系数C:远端弯矩/近端弯矩
第八章 渐近法 Successive approximation method
位移法的计算步骤
1) 拆散,分析各单元杆件,建立各单元的刚度方程 {杆端内力}={跨间无荷载作用下杆端内力}+{固端内力}
2)确定基本未知量 3) 组装,根据力平衡条件建立结构整体的位移法基本方程; 4) 求解基本未知量 5) 代入 1)单元刚度方程计算杆端内力 6) 作内力图
§8-1 力矩分配法的基本概念
力矩分配:?
例:杆端受力矩作用的单跨梁,
M
M
M
M图
M
M图
单跨梁不存在力矩分配的问题
连续梁的力矩分配
M
A
i
B
i
C
1 2
M
A
B
C
1 2
M
M图
由于是对称结构, AB和BC杆的B端所 分配的力矩各一半。
力矩分配:作用在结点的力矩按比例分配给结点处的各杆端
M
A
i
B
2i
C
M图 A
1 * 200*6KNm 8
150KNm
M
F BC
1 * 20*62 KNm 8
90KNm
转动刚度: SBA 4i , SBC 3i
分配系数:
BA
SBA SBA SBC
4 7
BC
SBC SBA SBC
3 7
C
传递系数:
CBA 0.5 CBC 0
计算原理
200KN
A 3m
B 3m
20KN/m 6m
1 3
M
B
C
2 3
M
A
M图 A
M
i
B
2i
3 11
M
B
8 11
M
C
4 11
M
C
力矩传递:杆件某端分配到的力矩传递到另一端 (分配的力矩为近端弯矩,传递的力矩为远端弯矩)
转动刚度S:杆端对转动的抵抗能力,等于杆端力矩/转角 传递系数C:远端弯矩/近端弯矩
MAB
EI
例:A
A
l
用力法进行分析计算可得
A
M ABl 4EI
