第15章 位移法和力矩分配法
建筑力学(力矩分配法)

第十八章力矩分配法力矩分配法理论基础:位移法;计算对象:杆端弯矩;适用范围:连续梁和无侧移刚架。
一、转动刚度转动刚度表示杆端对转动的抵抗能力。
它在数值上等于使杆端产生单位转角时需要施加的力矩,以SAB表示。
A是施力端(近端),B为远端。
1S AB=4i1S AB=3iS AB= i1S AB=0远端固定远端铰支远端滑动远端自由第一节力矩分配法的基本原理1S AB =4i1S AB =3iS AB = i 1S AB =0远端固定远端铰支远端滑动远端自由转动刚度远端固定,S =4i 远端简支,S =3i 远端定向,S =i 远端自由,S =0S AB 与杆的线刚度i 和远端支承情况有关。
i —杆件的线刚度,lEI i二、传递系数M AB = 4i AB ϕAM BA = 2i AB ϕA21==AB BA ABM M C M AB = 3i AB ϕA 0==ABBA ABM M C M AB = i AB ϕAM BA = -i AB ϕA1-==ABBA ABM M C ϕAlAB远端固定ABϕAϕAAB远端铰支远端滑动M BA = 0远端支承转动刚度传递系数固定S=4i C =1/2简支S=3i C =0定向S=i C = -1自由S=0三、力矩分配法的基本原理杆端弯距:取结点A 作隔离体,由∑M =0,得分配系数CA BDi ABi AC i ADAAB A AB AB S i M ϕϕ==4A AC A AC AC S i M ϕϕ==AAD A AD AD S i M ϕϕ==3}M M ABM ACM ADAAD AC AB S S S M ϕ)(++=∑=++=AAD AC AB A SMS S S M ϕMSSM AADAD ∑=M SS M A ABAB ∑=M S S M AACAC ∑=注:1)分配弯矩是杆端转动时产生的近端弯矩。
2)结点集中力偶顺时针为正。
∑=AAkAkSS μMM Ak Ak μ=分配弯矩A ϕM1321=++=∑A A A Ak μμμμ各杆的远端弯矩M kA 可以利用传递系数求出。
结构力学中位移法与力矩分配法的关系分析

文章编号:1009 ̄6825(2020)20 ̄0059 ̄03结构力学中位移法与力矩分配法的关系分析收稿日期:2020 ̄07 ̄13:北部湾大学高等教育本科教学改革工程项目«土木工程系统性教学案例设计研究与实践»(项目编号:17QJGB14)作者简介:姚展环(1998 ̄)ꎬ女ꎬ在读本科生ꎻ㊀杨㊀威(1999 ̄)ꎬ男ꎬ在读本科生ꎻ㊀冯章标(1997 ̄)ꎬ男ꎬ在读本科生ꎻ㊀凌志丹(1998 ̄)ꎬ女ꎬ在读本科生ꎻ㊀农妍妹(1998 ̄)ꎬ女ꎬ在读本科生姚展环㊀杨㊀威㊀冯章标㊀凌志丹㊀农妍妹(北部湾大学建筑工程学院ꎬ广西钦州㊀535011)摘㊀要:超静定结构的求解方法在综合考虑平衡条件㊁几何条件和物理条件的情况下日益增多ꎬ为此需要建立近似状态使其求解方法简化ꎮ通过研究位移法的计算过程ꎬ引入曲率半径㊁转动刚度㊁分配系数和传递系数将位移法求解过程中的方程消除ꎬ从而得到不必解算联立方程的近似解法 力矩分配法ꎮ力矩分配法不必联立方程ꎬ计算步骤简单ꎬ可以直接求得杆端弯矩ꎬ大大降低了求解问题的难度ꎮ关键词:位移法ꎬ力矩分配法ꎬ超静定结构中图分类号:TU311文献标识码:A0㊀引言目前ꎬ计算超静定结构的精确方法主要是位移法ꎬ位移法的思想是法国的纳维于1826年提出的ꎬ其基本未知量包括节点的角位移和独立节点的线位移ꎮ但现实中大多数为多层多跨的结构体系ꎬ有多个未知量ꎬ需要列多个位移法方程来求解ꎮH.克罗斯于1930年在位移法的基础上ꎬ提出了不必解方程组而是逐次逼近的力矩分配法ꎬ大大地减轻了工程的计算工作ꎮ位移法和力矩分配法的共性和特性给我们提供了一个建立二者关系的视角ꎮ两者都需借助不平衡力矩以及查询形常数表和载常数表来获取形常数载常数来计算结构内力ꎮ但两者性质不同ꎬ位移法是精确解法ꎬ是以节点的角位移和独立节点的线位移作为基本未知量ꎮ而力矩分配法是近似解法ꎬ主要是通过对刚节点施加阻止转动的约束得到各固端弯矩ꎬ并分配传递至各刚结点平衡ꎮ通过研究位移法的计算过程ꎬ引入曲率半径㊁转动刚度㊁分配系数和传递系数将位移法求解过程中的方程消除ꎬ从而得到不必解算联立方程的近似解法 力矩分配法ꎮ本文将以例题展开讨论位移法和力矩分配法之间的关系ꎮ1㊀位移法计算过程位移法是以结构的结点位移为基本未知量ꎻ以结点和截面的平衡方程为基本方程ꎬ据以求出结点位移ꎻ最后求出结构的内力ꎮ其最大的特点在于:位移法的思路是先通过加入附加联系固定所有独立结点位移ꎬ此时各附加联系上将产生附加反力(不平衡反力)ꎬ为消除这些附加反力ꎬ同时放松各结点(即同时取消所有附加联系)ꎬ从而同时消除各附加联系上的附加反力ꎮ若附加联系不止一个ꎬ则必须求解联立的位移法典型方程[3]ꎮ例题:用位移法计算如图1所示连续梁的弯矩ꎮ1)基本体系(见图2):2)位移法方程:k11Δ1+F1P=0(1)其中ꎬΔ1为连续梁结点B角位移ꎻk11为基本结构在单位转角Δ1=1作用下在附加约束中的约束力矩ꎻF1P为基本结构在荷载作用下在附加约束中的约束力矩ꎮ图1原结构AqCBll图2位移法基本体系ABCq3)计算k11ꎬF1P(见图3~图6):图3Δ1=1作用的M 1图AC3i3i图4计算k 11k 113i3iB由结点B的力矩平衡可得:ðMB=0ꎬk11=3i+3i=6i(2)由结点B的力矩平衡可得:ðMB=0ꎬF1P=ql2/8(3)95 ㊀㊀㊀㊀第46卷第20期2020年10月㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀山西建筑SHANXI㊀ARCHITECTURE㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.46No.20Oct.㊀2020图5荷载作用的M PA Cql 2/8ql 2/16图6计算F 1PF 1PBql 2/84)计算Δ1:Δ1=-F1P/k11=-ql2/48i(4)5)作M图(如图7所示):由弯矩的叠加原理:M=M1Δ1+MP(5)其中ꎬM1为基本结构在单位转角Δ=1中任一截面上所产生的弯矩ꎻ由形常数表可查得ꎮMP为荷载在基本结构中相应截面上所产生的弯矩ꎮMBA=3iˑ(-ql2/48i)+ql2/8=ql2/16(6)MBC=3iˑ(-ql2/48i)=-ql2/16(7)其中ꎬMBA为AB杆的B端弯矩ꎻMBC为BC杆的B端弯矩ꎮ图7弯矩图ACBql 2/163ql 2/322㊀力矩分配法计算过程力矩分配法的求解思路则有所不同ꎬ第一步先约束所有独立结点角位移ꎬ得到基本结构ꎬ显然各结点将产生不平衡力矩ꎮ为了使基本结构转化为原结构ꎬ必须消除各结点不平衡力矩(因为原结构中不存在这些不平衡力矩)[3]ꎮ由例题ꎬ1)先在B结点加上阻止转动的约束(见图8):图8力矩分配法基本体系ACBqMFBA=ql2/8(8)其中ꎬMFBA为在结点B加上阻止转动的约束时ꎬ由荷载产生的固端弯矩ꎮ2)松开结点B:相当于结点B施加一个力偶荷载-ql2/8ꎮ转动刚度:SBA=3iBA=3i(9)BBC=3iBC=3i(10)其中ꎬSBA为AB杆B端的转动刚度ꎻSBC为BC杆B端的转动刚度ꎮ分配系数:μBA=SBA/(SBA+SBC)=3i/(3i+3i)=0.5(11)μBC=SBC/(SBA+SBC)=3i/(3i+3i)=0.5(12)其中ꎬμBA为AB杆在B端的分配系数ꎻμBC为BC杆在B端的分配系数ꎮðμ=μBA+μBC=1(13)分配弯矩:MᶄBA=0.5ˑ(-ql2/8)=-ql2/16(14)MᶄBC=0.5ˑ(-ql2/8)=-ql2/16(15)其中ꎬMᶄBA为AB杆B端的分配弯矩ꎻMᶄBC为BC杆B端的分配弯矩ꎮ传递弯矩均为0ꎮ即:MᶄCB=0(16)MᶄAB=0(17)其中ꎬMᶄCB为BC杆C端的传递弯矩ꎻMᶄAB为AB杆A端的传递弯矩ꎮ计算过程见图9ꎮ图9力矩分配的计算格式AC0.50.5B000000ql 2/8-ql 2/16-ql 2/16ql 2/16-ql 2/16ðMB=ql2/16-ql2/16=0(18)3㊀位移法与力矩分配法关系分析位移法与力矩分配法均运用了不平衡力矩ꎬ都借助不平衡力矩来计算结构内力ꎮ两者都需要查询形常数和载常数表来获取形常数载常数以便计算ꎮ由式(2)ꎬ图4可知:k11=ði(19)由式(3)ꎬ图6可知:F1P=-M(20)由式(4)ꎬ式(19)ꎬ式(20)得:Δ1=-F1P/K11=M/ði(21)由式(5)ꎬM1由形常数表可查得ꎬ因此设:M1=ii(22)由式(21)ꎬ式(22)可得:M1Δ1=iiΔ1=iiM/ði(23)由曲率K表示单位弧段上切线转过角度的大小作如下定义:K=Δα/Δs(24)06 第46卷第20期2020年10月㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀山西建筑㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀其中ꎬK为杆件中性层的曲率ꎻΔα为转角增量ꎻΔs为弧长增量ꎮ由曲率与曲率半径的互为倒数的关系有:K=1/ρ(25)其中ꎬρ为杆件中性层的曲率半径ꎮ由式(24)ꎬ式(25)得:1/ρ=Δα/Δs(26)或:Δα=Δs/ρ(27)由转动刚度S为单位转角所需的力矩作如下定义:S=M/Δα(28)由杆件的弯矩:M=EI/ρ(29)其中ꎬE为材料的弹性模量ꎻI为杆件截面的惯性矩ꎮ由式(27)~式(29)得:S=M/Δα=(EI/ρ)/(Δs/ρ)=EI/Δs(30)由可变形固体的小变形假设由Δsʈ1ꎬ因此得:S=EI/ΔsʈEI/l=i(31)由力矩分配系数μ为同一刚结点上的某一根杆的转动刚度与所有杆的转动刚度和的比值ꎬ作如下定义:μ=Si/ðSi=ii/ði(32)由式(23)得分配弯矩:M1Δ1=μMꎮ令Mᶄ远=μM即:Mᶄ远=M1Δ1(33)其中ꎬMᶄ远为所求杆端的远端分配弯矩ꎮ对于等截面杆件ꎬ由于均匀性假设与影响线ꎬ可知同一杆件弯矩变化为线性变化ꎬ由相似原理ꎬ与传递系数C表示当杆件近端产生转角时ꎬ杆件远端弯矩与近端弯矩的比值作如下定义ꎬ即:C=i远/i近=Mᶄ远/Mᶄ近ꎮ得:M远=CˑMᶄ近(34)其中ꎬMᶄ近为节点近端的分配弯矩ꎮ因为位移法中荷载在基本结构中相应截面上所产生的弯矩MP与力矩分配法中在节点加上阻止转动的约束后由荷载产生的固端弯矩MF均由等截面直杆的载常数可查得ꎬ即:MP=MF(35)由式(33)ꎬ式(35):MP+M1Δ1=MF+Mᶄ(36)其中ꎬMᶄ为远端或近端的分配弯矩ꎮ故位移法与力矩分配法的计算结果相同ꎮ对于多结点的体系ꎬ由于其处于平衡状态ꎬ即每个结点的内力与外力合力为0ꎬ所以当结点合力不近似于0时ꎬ不为0的合力矩继续传递直至结点合外力近似等于0ꎮ最终累加各杆端所得的分配弯矩可得各杆端弯矩ꎮ4㊀结语位移法是通过平衡条件建立位移法方程ꎬ取隔离体来计算不平衡力矩ꎮ而力矩分配法是在位移法的基础上引入曲率半径㊁转动刚度㊁分配系数与传递系数将位移法求解过程中的方程消除ꎬ所以力矩分配法不需要列方程ꎬ只需按照分配系数来分配不平衡力矩ꎬ但计算过程相对繁杂ꎬ需要很强的细心及耐心ꎮ致谢:本文是在蒋琼明博士的指导下完成的ꎬ在此表示深深的感谢ꎮ参考文献:[1]㊀包世华ꎬ熊㊀峰ꎬ范小春.结构力学教程[M].武汉:武汉理工大学出版社ꎬ2017.[2]㊀陈玉骥.力矩分配法教学中体现其数学意义的方法[J].长沙铁道学院学报(社会科学版)ꎬ2003ꎬ4(4):98 ̄99.[3]㊀同济大学数学系.高等数学第七版上册[M].北京:高等教育出版社ꎬ2014.[4]㊀孙训方ꎬ方孝淑ꎬ关来泰.材料力学(Ⅰ)[M].第5版.北京:高等教育出版社ꎬ2009.ModifiediterativeinitialvaluesforthereliabilitycalculatingofmarineconcretestructuresYaoZhanhuan㊀YangWei㊀FengZhangbiao㊀LingZhidan㊀NongYanmei(CollegeofCivilEngineeringandArchitectureꎬBeibuGulfUniversityꎬQinzhou535011ꎬChina)Abstract:Thesolutionmethodsofstaticallyindeterminatestructuresareincreasingundertheconditionofcomprehensiveconsider ̄ationofequilibriumconditionsꎬgeometricconditionsandphysicalconditions.Bystudyingthecalculationprocessofdisplacementmethodꎬthecurvatureradiusꎬrotationstiffnessꎬdistributioncoefficientandtransfercoefficientareintroducedtoeliminatethee ̄quationintheprocessofdisplacementmethodꎬsothattheapproximatesolutionofsimultaneousequationwithoutsolvingmomentdistributionmethodisobtained.Themomentdistributionmethoddoesnotneedsimultaneousequationsꎬthecalculationprocedureissimpleꎬandthemomentattheendoftherodcanbecalculateddirectlyꎬwhichgreatlyreducesthedifficultyofsolvingtheprob ̄lem.Keywords:displacementmethodꎬmomentdistributionmethodꎬstaticallyindeterminatestructure16 ㊀㊀㊀第46卷第20期2020年10月㊀㊀㊀㊀㊀㊀㊀㊀姚展环等:结构力学中位移法与力矩分配法的关系分析。
结构力学教案位移法和力矩分配法
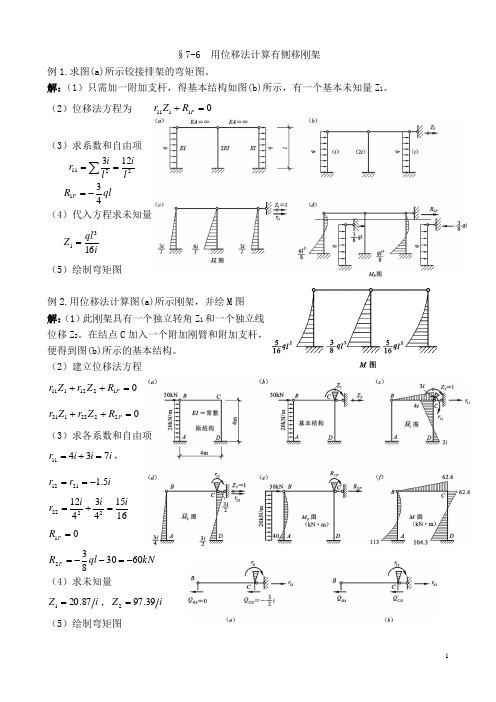
§7-6 用位移法计算有侧移刚架例1.求图(a)所示铰接排架的弯矩图。
解:(1)只需加一附加支杆,得基本结构如图(b)所示,有一个基本未知量Z 1。
(2)位移法方程为 01111=+P R Z r(3)求系数和自由项2211123l il i r ==∑ql R P 431-=(4)代入方程求未知量iql Z 1631=(5)绘制弯矩图例2.用位移法计算图(a)所示刚架,并绘M 图 解:(1)此刚架具有一个独立转角Z 1和一个独立线位移Z 2。
在结点C 加入一个附加刚臂和附加支杆,便得到图(b)所示的基本结构。
(2)建立位移法方程01212111=++P R Z r Z r 02222121=++P R Z r Z r (3)求各系数和自由项i i i r 73411=+=, i r r 5.12112-==1615434122222ii i r =+=01=P RkN ql RP 6030832-=--=(4)求未知量i Z 87.201=,i Z 39.972= (5)绘制弯矩图例3.用直接平衡法求刚架的弯矩图。
解:(1)图示刚架有刚结点C 的转角Z 1和结点C 、D 的水平线位移Z 2两个基本未知量。
设Z 1顺时针方向转动,Z 2向右移动。
(2)求各杆杆端弯矩的表达式3421+-=Z Z M CA 3221--=Z Z M AC 13Z M CD = 25.0Z M BD -= (3)建立位移法方程有侧移刚架的位移法方程,有下述两种:Ⅰ.与结点转角Z 1对应的基本方程为结点C 的力矩平衡方程。
∑=0CM , 037021=+-⇒=+Z Z M M CD CAⅡ.与结点线位移Z 2对应的基本方程为横梁CD 的截面平衡方程。
∑=0xF, 0=+D C CA Q Q取立柱CA 为隔离体(图(d)),∑=0A M , 331216262121-+-=---=Z Z ql Z Z Q CA 同样,取立柱DB 为隔离体((e)),∑=0B M , 2212165.0Z Z Q DB =--= 代入截面平衡方程得 03125012133121221=-+-⇒=+-+-Z Z Z Z Z(4)联立方程求未知量 Z 1=0.91 Z 2=9.37(5)求杆端弯矩绘制弯矩图将Z 1、Z 2的值回代杆端弯矩表达式求杆端弯矩作弯矩图。
结构力学——6位移法和力矩分配法

△ △
4、5、6 三个固定端都是不动的点,结点1 、2、3均无竖向位移。又因两根横梁其长 度不变,故三个结点均有相同的水平位移 FP △ 。
1
2
3
4
5
6
(a)
事实上,图(a)所示结构的独立线位移数 将结构的刚结点(包括固定支座)都变成 目,与图(b)所示铰结体系的线位移数目 铰结点(成为铰结体系),则使其成为几何 是相同的。因此,实用上为了能简捷地确 不变添加的最少链杆数,即为原结构的独 定出结构的独立线位移数目,可以 立线位移数目(见图b)。
4
5
6
(a)
共有四个刚结点,结点线位移数目为二 ,基本未知量为六个。基本结构如图所 示。
7
10 返回
5
6
(b)
例:确定图a所示连续梁的基本结构。 D B A C D B A C
(图a)
A A
B B
基本结构 基本结构
C C
D (图b) D
在确定基本结构的同时,也就确定了基本未知量及其数目。
EI
第六章
位移法和力矩分配法
§6—1 位移法的基本概念 §6—2 位移法基本未知量的确定 §6—3 位移法典型方程计算步骤和示例 §6—4 力矩分配法的基本概念 §6—5 用力矩分配法计算连续梁 §6—6 用力矩分配法计算无接点线位移刚架
1
§6—1
位移法的基本概念
一、位移法的提出(Displacement Method)
M
A
B
0
2i
r11 4i 4i 0
8EI r11 8i l
2i
M1
得
15
求自由项R1P,作出基本结构在荷载作用时的弯矩 图(MP图)。 取结点B为隔离体
力矩分配法

1渐近法2用力法、位移法分析超静定结构,都需要求解多元联立方程组,求出基本未知量。
当未知量较多时,计算颇为繁重。
渐近法—采用逐步地逼近真实解的方法。
渐近法主要有:一、渐近法概述(1)力矩分配法:适于连续梁与无侧移刚架。
(2)无剪力分配法:适于规则的有侧移刚架。
(3)迭代法:适于梁的刚度大于柱刚度的各种刚架。
3力矩分配法理论基础:位移法;计算对象:杆端弯矩;计算方法:逐渐逼近的方法;适用范围:连续梁和无侧移刚架。
4只有结点角位移而无结点线位移的梁和刚架。
?力矩分配法的适用范围:力矩分配法的适用范围:5只有结点角位移而无结点线位移的梁和刚架。
√6力矩分配法以杆端弯矩为计算对象,采用:固定放松分配、传递逐次逼近杆端弯矩的精确解。
计算原理及符号规则均与位移法相同,只是计算过程不相同。
7计算过程:1.固定结点求出固定状态的杆端弯矩FijM 附加刚臂处的不平衡弯矩iM依次将结点上的不平衡弯矩反号分配于各杆近端,并传向远端。
2.逐次放松各结点8若干次循环计算= 也即逐次恢复转角的过程直接表达为各杆端弯矩逐次修正的过程放松结束,也即变形(转角)、内力趋于实际状态。
9——基本运算A BCM ABM BAM BC A BCM FAB M FBAM FBCM BM BM F BAM F BCM B =M F BA +M F BCABC-M BBAM ′BCM ′AB M ′0-M BBAM ′BCM ′)(B BA BAM M −⋅=′μ)(B BC BCM M −⋅=′μ+=最后杆端弯矩:M BA =M F BA +BAM ′M BC =M F BC +BCM ′M AB =M F AB +AB M ′然后各跨分别叠加简支梁的弯矩图,即得最后弯矩图。
固端弯矩带本身符号单结点的力矩分配分配系数分配弯矩10例1. 用力矩分配法作图示连续梁的弯矩图。
3m 3m 6m EI EI 200kN 20kN/m (1)固定B 结点A BC 200kN 20kN/m M F AB =M F BA =M F BC=mkN ⋅−=×−15086200m kN ⋅150m kN ⋅−=×−9086202M B =M F BA + M F BC =m kN ⋅60-150150-90(2)放松结点B,即加-60进行分配60A B C-60设i =EI/l 计算转动刚度:S BA =4iS BC =3i分配系数:571.0344=+=i i iBAμ429.073==iiBCμ0.5710.429分配力矩:3.34)60(571.0−=−×=′BAM 7.25)60(429.0−=−×=′BCM -34.3-25.7-17.2+(3) 最后结果。
力法位移法。力矩分配法常见问题

建筑力学常见问题解答6 超静定结构內力计算1.什么是超静定结构?它和静定结构有何区别?答:单靠静力平衡条件不能确定全部反力和內力的结构为超静定结构。
从几何组成的角度看,静定结构是没有多余约束的几何不变体系。
若去掉其中任何一个约束,静定结构即成为几何可变体系。
也就是说,静定结构的任何一个约束,对维持其几何不变性都是必要的,称为必要约束。
对于超静定结构,若去掉其中一个甚至多个约束后,结构仍可能是几何不变的。
2.什么是超静定结构的超静定次数?答:超静定结构多余约束的数目,或者多余约束力的数目,称为结构的超静定次数。
3.超静定结构的基本结构是否必须是静定结构?答:超静定结构的基本结构必须是静定结构。
4.如何确定超静定结构的超静定次数?答:确定结构超静定次数的方法是:去掉超静定结构的多余约束,使之变为静定结构,则去掉多余约束的个数,即为结构的超静定次数。
5.撤除多余约束的方法有哪几种?答:撤除多余约束常用方法如下:(1)去掉一根支座链杆或切断一根链杆,等于去掉一个约束。
(2)去掉一个固定铰支座或拆去一个单铰,等于去掉两个约束。
(3)去掉一个固定端支座或把刚性连接切开,等于去掉三个约束。
6.用力法计算超静定结构的基本思路是什么?答:用力法计算超静定结构的基本思路是:去掉超静定结构的多于约束,代之以多余未知力,形成静定的基本结构;取多余未知力作为基本未知量,通过基本结构的位移谐调条件建立力法方程,利用这一变形条件求解多余约束力;将已知外荷载和多余约束力所引起的基本结构的内力叠加,即为原超静定结构在荷载作用下产生的内力。
7.什么是力法的基本结构和基本未知量?答:力法的基本结构是:超静定结构去掉多余约束后得到的静定结构。
力法的基本未知量是对应于多余约束的约束反力。
8.简述n次超静定结构的力法方程,及求原结构的全部反力和內力的方法。
答:(1)n次超静定结构的力法方程对于n次超静定结构,撤去n个多余约束后可得到静定的基本结构,在去掉的n个多余约束处代以相应的多余未知力。
建筑力学18位移法和力矩分配法

4
18.1
18.1.1
位移法
位移法基本变形假设
位移法的计算对象是由等截面直杆组成的杆系结 构,例如刚架、连续梁。在计算中认为结构仍然符合 小变形假定,同时位移法假设:
第 三 篇 结 构 力 学
(1)各杆端之间的轴向长度在变形后保持不变;
(2)刚性结点所连各杆端的截面转角是相同的。
5
18.1
18.1.2
12
18.1
位移法
第 三 篇 结 构 力 学
图18.3 附加链杆法
13
18.1
18.1.3
位移法
位移法的杆端内力
第 三 篇 结 构 力 学
(1)运用位移法计算超静定结构时,需要将结 构拆成单杆,单杆的杆端约束视结点而定,刚结点视 为固定支座,铰结点视为固定铰支座。当讨论杆件的 弯矩与剪力时,由于铰支座在杆轴线方向上的约束力 只产生轴力,因此可不予考虑,从而铰支座可进一步 简化为垂直于杆轴线的可动铰支座。结合边界支座的 形式,位移法的单杆超静定梁有三种形式,如图18.4 所示。
14
18.1
位移法
第 三 篇 结 构 力 学
图18.4 单杆超静定梁的约束形式
15
18.1
位移法
第 三 篇 结 构 力 学
(2)位移法规定杆端弯矩顺时针转向为正,逆 时针转向为负(对于结点就变成逆时针转向为正), 如图18.5所示。以后运用位移法进行结构内力分析时, 弯矩的正负号都遵从这个规定。要注意的是,这和前 面梁的内力计算中规定梁弯矩下侧受拉为正是不一样 的,因为对于整体结构来说,杆件不仅仅有水平杆件, 还有竖向、斜向杆件。对于剪力、轴力的正负规定, 则和前面的规定保持一致。
第 三 篇 结 构 力 学
结构力学6位移法和力矩分配法
△
4、5、6 三个固定端都是不动的点,结点 1
2△
3△
1、2、3均无竖向位移。又因两根横梁其
长度不变,故三个结点均有相同的水平位 移△ 。Biblioteka FP456
(a)
事将实结上构,的图刚(a结)所点示(包结括构固的定独支立座线)都位变移成数
铰目结,点与(图成(为b)铰所结示体铰系结)体,则系使的其线成位为移几数何目不 变是添相加同的的最。少因链此杆,数实,用即上为为原了结能构简的捷独地立确
线定位出移结数构目的(独见立图线b)位。移数目,可以
7
(b)
返回
ZZ1 1
Z 1Z 1
FF11
CC
DD
CC
DD
FF22
BB
BB ZZ2 2
EE Z2Z2
EE
AA
FF
AA
FF
结构有四个刚结点——四个结点角位移。
需增加两根链杆, 2个独立的线位移。
位移法的基本未知量的数目为6个。
需注意:对于曲杆及需考虑轴向变形的杆件, 变形后两端之间的距离不能看作是不变的。
D l
l
1
FC
B
B
F
C
B B
l/ 2 l/2
A
l/ 2 l/ 2
三次超静定图示刚架
力 法:三个未知约束力。 位移法:一个未知位移(θB)。
l
力法与位移法必须满足的条件:
1.力的平衡; 2. 位移的协调; 3. 力与位移的物理关系。
位移法的基本假定:
(1)对于受弯杆件,只考虑弯曲变形,忽略轴向变形和剪切变形的影响。
例如 ( 见图a) 基本未知量三个。
2
3
5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.计算各杆固端弯矩
3.计算分配弯矩和传递弯矩 4.叠加求得最终杆端弯矩
35
例:用力矩分配法作弯矩图。
1.各杆转动刚度、分配系数和传递系数 AB: S BA 4
EI 2 EI 6 3 EI 1 3 EI 6 2
BA 0.571
CBA 0.5 CBC 0
BC: S BC
S
远端铰支:S 3i
远端自由: S 0
31
m
A D
分配系数:
C
Dj
S Dj
S
j A, B, C
M Dj Dj m
B
Dj 1
SiDA 3 DA M DA m S DC 3i 4 S SiDB S DA DB iDC DA 4 SiDB M DB m S DC 3iDA 4 S Si S DA DB iDC DB SiDC M DC m 3 4 iDC S SiDA Si DA DB S DC DB
转动刚度
30
3iDA ii D i i D m m iDA 4 4 3 D DB D DB DCDC
D
m 3iDA 4iDB iDC
转动刚度
表示杆端对转动的抵抗能力 在数值上等于使杆端发生单位转角时 需要施加的力矩。 远端固定:S 4i 远端定向: S i
CDC
33
M AD 0 M DA M BD 1 M DB 2
远端铰支 远端固定
M DB 4iDB D
M DC iDC D
M BD 2iDB D
M CD iDC D
M CD 1 远端定向 M DC
二、力矩分配法的基本运算
A B
C
限制转动
A B
MB
C
M B
32
分配系数 : 传递系数μ C:
m
A D
C
S Dj Dj j A, B, C 表示当近端有转角时,远端弯 S 矩与近端弯矩的比值。 M Dj Dj m
对于等截面杆件,传递系数 Dj 1 与远端的支承情况有关
B
M DA 3iDA D
M AD 0
CDA CDB
16
结点B的转角1
结点C的水平位移2
基本步骤
第一步:控制附加约束,使得结点位移均为零。 ——即荷载单独作用。 第二步:控制附加约束,使结构依次发生单位结点位移
1和2 。此时,结点内的附加约束力也相应
改变。 基本体系转化为原超静定结构的条件是: 基本结构在给定荷载及结点位移1和2的共同作用 下,附加约束中产生的总约束力F1和F2应等于零。 F1 k11 1 k12 2 F1P 0 F1 0
2.承受反对称荷载
FP
C
FP
C1 C 2
FP
I 2
FP FP
I 2
I D
D1 D2 C1
对称轴柱上没有轴力和轴向变形,但有弯矩 和弯曲变形
26
D1 D1
例题
q
q
a
a
a
27
2a
2a
力法与位移法的对比
力法 位移法
基本未知量 基本体系
基本方程
多余约束力
结点位移
去除多余约束 增加约束后的 后的静定结构 体系
M CD iDC D
4.回代,求杆端弯矩
3iDA M DA m 3iDA 4iDB iDC 4iDB M DB m 3iDA 4iDB iDC iDC M DC m 3iDA 4iDB iDC
3.基本方程
M D 0 M DA M DB M DC m
a
2a
x
y
B
B
FP
FN 1
FN 5
B
F
Y
0
FP
EA/l是使杆端产生单位位移时所施加的杆端力,称为杆 件的刚度系数,表明杆端力与杆端位移之间的关系,称 为杆件的刚度方程。
3
3、位移法的基本思路
C
C
拆
A
B
E
A A A
B A A A
A
E
D
搭
杆端力: 结点位移引起的: 荷载所引起的:
4
AC M A
1 0.737 / i 2 7.58 / i
M M1 1 M2 2 MP
21
对于n个基本未知量问题,位移法方程为
k11 1 k12 2 k21 1 k22 2 kn1 1 kn 2 2
k1n n F1P 0 k2 n n F2 P 0 knn n Fn P 0
k12
B
0
2 1 k22
k12 1.5i
C
k22
A D
15 i 16
20
解方程,回代,绘弯矩图
k11 1 k12 2 F1P 0 k21 1 k22 2 F2P 0
10i 1 1.5 2 4 0 1.5i 1 15 i 2 6 0 16
C
在对称轴截面上,没有转角和水平位移,可有竖向位移。
23
一.奇数跨对称结构
2.承受反对称荷载
FP
C
FP
FP
在对称轴截面上,没有竖向位移,可有转角和水平位移。
24
二.偶数跨对称结构
1.承受对称荷载
C
D
在对称轴截面上,没有转角和水平位移,由于不计轴向变形 ,也没有竖向位移。
25
二.偶数跨对称结构
EI EA
9
§15-4 直接平衡法—无侧移刚架的计算
6 4. 求出最终各杆端弯矩 M 2i 15 16.72kN m 7 i 无侧移刚架 :结点上只有角位移没有线位移
AB
5.例 作内力图 1:如图所示连续梁结构,各杆i =常数,作弯矩图。
1. 位移法基本未知量 B 2. 各杆杆端弯矩 3. 位移法的基本方程
q
ql 2
C
l
l
D
13
§15-5 直接平衡法有侧移刚架的计算
有侧移刚架 ——结点处不仅有角位移,还有结点线位移
A
基本未知量:结点角位移和线位移
在杆件分析中,需考虑线位移的影响
建立基本方程时,需增加与线位移相对应的平 衡方程
14
2. 基本方程的建立
B= 0.737/ i (1) 基本未知量 B = 7.58/i
M AB
DM AD
M AE
4. 位移法的基本要点 I. 位移法的基本未知量是结构的结点位移
II. 位移法的基本方程是平衡方程
III. 建立基本方程的步骤: 第一步,拆——把结构拆成杆件,得出杆件的刚 度方程; 第二步,拼——把杆件综合成结构,整体分析, 得出基本方程。 IV. 杆件分析是位移法的基础。杆件的刚度方程是位 移法基本方程的基础。——刚度法。
5
§15-3 形常数和载常数
6
§15-2 位移法的基本未知量
1.基本未知量的选取
结点角位移=刚结点的个数 结点线位移
不考虑轴向变形
7
不考虑轴向变形
8
EI EI
EI
EI为无限大的杆件有内力,但没有弯曲变形,因此,与 EI为无穷大的杆件相连的刚节点均不作为位移法的基本 未知量。
(2) 杆端弯矩
1 AB:M AB 2i B 6i 3 42 4 12 1 M BA 4iB 6i 3 42 4 12
(4) 解方程
BC:M BC 3 2i B CD:M DC 3i 4 小结:位移法的基本方程都是根据平衡方程得出的。 (3) 基本方程 基本未知量中每一个转角有一个相应的结点力矩平衡方程, M 0, M BA M4 0 0 10 i 1.5 i BB BC 1 每一个独立结点线位移有一个相应的截面平衡方程。平衡 M A 0, FQBA (M AB M BA ) 6 4 1.5 i 0.9375 i 6 0 0 0, FQBA FQ 方程的个数与基本未知量的个数彼此相等,正好解出全部 F 1 xB CD M D 0, FQBA M DC 基本未知量。 4
11
小结
无侧移刚架的位移法计算要点: 基本未知量:结点的转角位移
转角位移的个数=刚结点的个数 基本方程:结点的合力矩平衡方程
方程个数=刚结点的个数
12
练习:利用直接平衡法作图示结构弯矩图(各杆EI为常数)
ql
B A
q
D B
q
A
ql D
l
C C
l l l
0.5l 0.5l
l
ql
A B
0.5l 0.5l
k11 k12 k21 k22 kn1 kn 2
k1n k2 n knn
位移法典型方程
结构的刚度矩阵
kii——主系数,恒大于零; kij=kji——副系数,可正、可负、可为零;
22
§15–7
对称性的应用
——半边结构法
一.奇数跨对称结构
1ห้องสมุดไป่ตู้承受对称荷载
F2 0
F2 k21 1 k22 2 F2P 0
17
1.荷载单独作用
q≠ 0, Δ1 =0, Δ2 =0
F1P
B
M BA
F2 P
C
1 3 42 4kN .m 12 3 4 FQBA kN 6kN 2
F1P 4kN .m
A D
F2 P 6kN
变形协调方程 力的平衡方程
