结构力学_杨海霞_位移法和力矩分配法汇总
结构力学教案位移法和力矩分配法
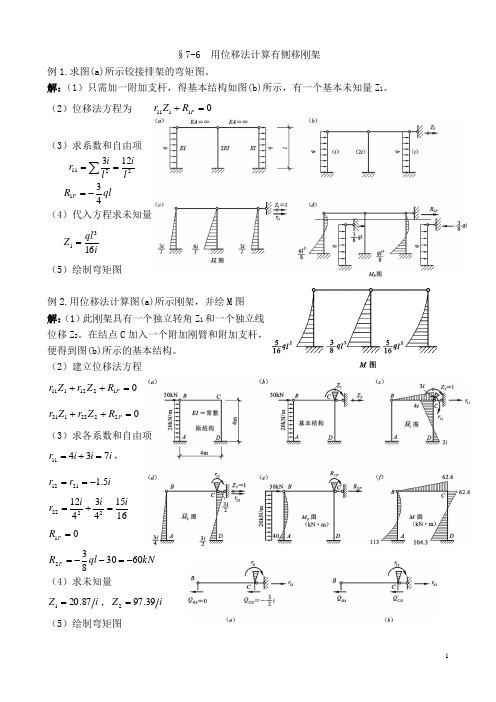
§7-6 用位移法计算有侧移刚架例1.求图(a)所示铰接排架的弯矩图。
解：（1）只需加一附加支杆，得基本结构如图(b)所示，有一个基本未知量Z 1。
（2）位移法方程为 01111=+P R Z r（3）求系数和自由项2211123l il i r ==∑ql R P 431-=（4）代入方程求未知量iql Z 1631=（5）绘制弯矩图例2.用位移法计算图(a)所示刚架，并绘M 图 解：（1）此刚架具有一个独立转角Z 1和一个独立线位移Z 2。
在结点C 加入一个附加刚臂和附加支杆，便得到图(b)所示的基本结构。
（2）建立位移法方程01212111=++P R Z r Z r 02222121=++P R Z r Z r （3）求各系数和自由项i i i r 73411=+=， i r r 5.12112-==1615434122222ii i r =+=01=P RkN ql RP 6030832-=--=（4）求未知量i Z 87.201=，i Z 39.972= （5）绘制弯矩图例3.用直接平衡法求刚架的弯矩图。
解：（1）图示刚架有刚结点C 的转角Z 1和结点C 、D 的水平线位移Z 2两个基本未知量。
设Z 1顺时针方向转动，Z 2向右移动。
（2）求各杆杆端弯矩的表达式3421+-=Z Z M CA 3221--=Z Z M AC 13Z M CD = 25.0Z M BD -= （3）建立位移法方程有侧移刚架的位移法方程，有下述两种：Ⅰ.与结点转角Z 1对应的基本方程为结点C 的力矩平衡方程。
∑=0CM ， 037021=+-⇒=+Z Z M M CD CAⅡ.与结点线位移Z 2对应的基本方程为横梁CD 的截面平衡方程。
∑=0xF， 0=+D C CA Q Q取立柱CA 为隔离体(图(d))，∑=0A M ， 331216262121-+-=---=Z Z ql Z Z Q CA 同样，取立柱DB 为隔离体（(e))，∑=0B M ， 2212165.0Z Z Q DB =--= 代入截面平衡方程得 03125012133121221=-+-⇒=+-+-Z Z Z Z Z（4）联立方程求未知量 Z 1=0.91 Z 2=9.37（5）求杆端弯矩绘制弯矩图将Z 1、Z 2的值回代杆端弯矩表达式求杆端弯矩作弯矩图。
结构力学(I)力矩分配法
M1B M1FB
M1C M1FC
S1 B ( R ) M1FB 1B ( R1P ) S 1P
1
1
S1C ( R ) M 1FC 1C ( R1P ) S 1P
1
力矩分配法采用了与位移法相同的基本结 构，即固定刚结点，在固定状态下刚臂上产生 约束力矩，为恢复到原状态，将刚臂放松（加 反方向约束力矩），求出放松状态产生的杆端 力矩，将固定状态与放松状态的杆端力矩叠加 即得结构的实际杆端力矩.
一. 基本概念
远端支撑 固定 铰支 滑动 转动刚度S 4i 3i i 传递系数C 1/2 0 -1
1
1
1
可避免解联立方程 不需要求出角位移 计算程式简单机械
哈工大 土木工程学院
4i
1 / 31
2i
3i
哈工大 土木工程学院
i
2 / 31
讨论 1 点在M作用下各杆端的弯矩 1M m1 0
列表法
练习：用力矩分配法求图示结构弯矩图
B
EI
A
EI
C
40 kN
10m
10m
q 10 kN/m
M F 100
分 配 传 递
0.571 0.429 100 0 57.1 42.9 42.9 42 .9
0 0
A
4m
EI
BБайду номын сангаас
4m
EI
C
6m
28.6
M 128.6
128 .6
0
42.9
M
哈工大 土木工程学院
ql 2 /12
A
F F M BC M CB 0
结构力学6位移法和力矩分配法
△
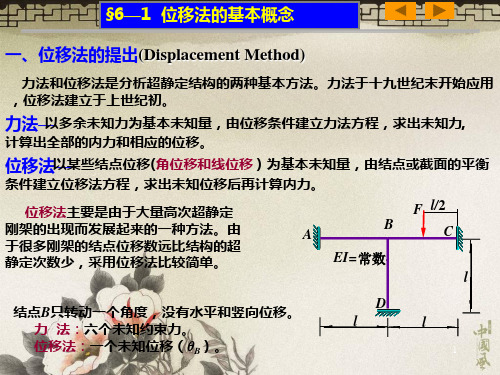
4、5、6 三个固定端都是不动的点，结点 1
2△
3△
1、2、3均无竖向位移。又因两根横梁其
长度不变，故三个结点均有相同的水平位 移△ 。Biblioteka FP456
(a)
事将实结上构，的图刚(a结)所点示(包结括构固的定独支立座线)都位变移成数
铰目结，点与(图成(为b)铰所结示体铰系结)体,则系使的其线成位为移几数何目不 变是添相加同的的最。少因链此杆，数实，用即上为为原了结能构简的捷独地立确
线定位出移结数构目的(独见立图线b)位。移数目，可以
7
(b)
返回
ZZ1 1
Z 1Z 1
FF11
CC
DD
CC
DD
FF22
BB
BB ZZ2 2
EE Z2Z2
EE
AA
FF
AA
FF
结构有四个刚结点——四个结点角位移。
需增加两根链杆， 2个独立的线位移。
位移法的基本未知量的数目为6个。
需注意：对于曲杆及需考虑轴向变形的杆件， 变形后两端之间的距离不能看作是不变的。
D l
l
1
FC
B
B
F
C
B B
l/ 2 l/2
A
l/ 2 l/ 2
三次超静定图示刚架
力 法：三个未知约束力。 位移法：一个未知位移（θB）。
l
力法与位移法必须满足的条件：
1.力的平衡; 2. 位移的协调; 3. 力与位移的物理关系。
位移法的基本假定：
（1）对于受弯杆件，只考虑弯曲变形，忽略轴向变形和剪切变形的影响。
例如 ( 见图a) 基本未知量三个。
2
3
5
工程力学-结构力学课件-8力矩分配法
40kN .m
求不平衡力矩
40kN.m
A EI
6m
C B EI
4m
MBu
20kN / m
40kN .m
60
60
M
u B
60
40
100kN .m
A
60 B
C
40
8 /17 9 /17
M F 60
60
分 配
23.5
传
递
47 53
M 83.5 13 53
§8-2多结点的力矩分配A q 12kN / m
对于同层柱等高，剪力分配系数可简化为按各柱的线刚度进行
分配，即
i
ii ii
顶层：
1
i1 ii
1 3
2
3
底层：
5
i5
2
0.4
ii 1.5 2 1.5
4
i4 ii
1.5 1.5 2 1.5
0.3
6
(2)计算各柱剪力
第8章 渐近法及其他算法简介
§8-1 力矩分配法的基本概念
力法、位移法：精确，求解方程。 力矩分配法是基于位移法，逐步逼近精确解 的近似方法。 单独使用时只能用于无侧移（无线位移）的 结构。
1.名词解释
B
q 1
C
M1B 3i ql2 / 8
M1A 4i ql 2 / 4
M1C i
1.8 3.5 2.6
… … ...
M1FA ql 2 / 8 150
M1F2 ql 2 / 12 100
S21 4i
S2B 3i
结构力学第八章位移法
二、等截面直杆的刚度方程
D
EI 1. 两端固定梁 i l
MAB 4iA M BA 2i A
由上图可得： i
A
M AB 4i A 2i B
M BA
B( ) 3．杆件两端相对侧移 杆件两端相对侧移
C ( )
A A
EI
B
A
B 可写成：
6i l 6i 2i A 4i B l
F M BA 0 F M BC
B
EI
C
上图示连续梁，取结点B的转角θB作为基本未 知量，这保证了AB杆与BC杆在B截面的位移协 这保 与 在 截 位移协 调。
2
2）令 ）令B结点产生转角 结点产生转角 B ( ) 。此时 。此时AB、BC杆 杆 类似于B端为固端且产生转角 B 时的单跨梁。
l
MAB
B
MBA
MAB 2iB M BA 4i B
杆件两端相对侧移△，其与弦转角β 的正负 号一致。而β以顺时针方向为正，逆时针方向 为负。 为负 l B A A B
l
13
A
i
MAB
B
B
A
A
EI
B
l
B
A
i
MBA
M AB 4i 2i 6i A l B M 2i 4i 6i BA l
F M AB
A
i EI l
A
B
A
i EI l
A
B
1．结点转角未知量θ 结构有几个刚结点就有几个结点转角未知量。 A B C D
MBA 4iA
MBA 2iA
结构力学——力矩分配法分解课件
THANK YOU
复杂结构的力矩分配法分析
总结词
需要对复杂结构进行精细的力矩分配
详细描述
对于复杂结构，如桥梁、高层建筑等，力矩分配法需要更加精细的分析。这需要对结构的各种参数进 行详细的计算和调整，包括转动刚度、分配系数、传递系数等。通过合理的简化模型和精细的计算， 可以获得结构的整体性能和局部细节，满足工程设计的需要。
应用范围
适用于具有刚性转动 部分的连续梁和框架
适用于具有弹性支撑 的连续梁和框架
适用于具有弹性转动 部分的连续梁和框架
适用条件
结构体系为连续梁或框架 结构具有刚性转动部分，且转动部分在分配力矩后不会出现弹性变形
结构具有弹性支撑，且弹性支撑在分配力矩后不会出现弹性变形
计算复杂度与精度要求
力矩分配法的计算复杂度取决于梁和框 架的自由度数量，自由度越多，计算越
。
误差传递
由于传递系数和分配系数的近似 计算，可能会引入一定的误差，
影响分析结果的准确性。
计算复杂度
对于大型复杂结构，力矩分配法 的计算量可能会变得很大，需要
借助计算机辅助分析。
改进与发展方向
01
02
03
04
数值优化
通过改进算法和优化计算方法 ，提高力矩分配法的计算效率
和精度。
考虑非线性因素
将非线性因素纳入力矩分配法 中，以适应更广泛的结构类型
在力矩分配法中，将结构中的结点分为两类：基本结点和附属结点。基本结点是承 受力矩的结点，附属结点则是传递力矩的结点。
力矩分配法的原理是将所有结点的力矩自由度进行分配，通过调整传递系数来使各 结点的力矩平衡，从而求解出各个结点的位移。
刚度系数与传递系数
刚度系数是指单位力矩作用下结 点的位移，它反映了结点的刚度
结构力学 课件 力矩分配法
SAB
1
2 传递系数C
传递系数： 一单跨超静定梁的一端（A端）单位转角时，发生于远 端（B端）的弯矩与近端（A端）的弯矩之比。
如： 当远端（B端）固定，C AB
M
BA
SAB
1 2 S AB
MBA
A B
图(a)
1
C 当远端（B端）铰支 ， AB
M
SAB
A
B
BA
0
SAB
A
1
图(b)
S AB
(1)设想在结点B增加一个附加刚臂，得到位 移法基本结构。阻止其转动如图(g)所示。 查表容易得到各单跨超静定梁的杆 端弯矩。则附加刚臂的约束力矩由 结点B的平衡条件得
M
B
Fp
A
q
B C
图(f)
MB
A
Fp
B
q
C
图(g)
M
F BA
M
F BC
MB MBAF -MB
A B C
附加刚臂的约束力矩MB 是原结构 上所没有的，它反映了基本结构汇 交于B结点的各杆B端弯矩所不能平 衡的差额。我们称之为B结点的不 平衡力矩。
MBCF
图(h)
(2)原结构在结点B本来没有转动约束，即不存在不平衡力矩MB ，因 此，为了与实际情况相符，必须消除人为引入的附加刚臂，即使MB 0，这就相当于在 MB的基础上再施加上一个（- MB ）如图(h)所示。
此时梁将产生新的杆端弯矩M´BA 、 M´BC （分配弯矩），在远端将产生新 的杆端弯矩M´AB 、 M´CB 、（传递弯 矩）。 (3)原结构在荷载的作用下的实际杆端弯 矩应为图(g) 和图(h)两种情况的叠加。 下面举例说明力矩分配法的解题过 程。
结构力学-力矩分配法
5.8 5097.1 －62.342－.3109.3
1,3
16 15.2 1537.6 20.9
2
－5.2 －10.3－18.2
0.762 0.238 33.3 －288
129141.1.7 60.6 －51.4
41.7 13
－9.1 288
1解,3 :
2
1,3
1) 求分配2.系7 2数.5: 2)M求1 固 7端8弯.1－矩100:.92
SBA=4×3i=12i SBC=3×4i=12i
AA －15
BB
CC
－30
M－图30（kN.m)
μBA=12i/24i=1/2 μBC=12i/24i=1/2
3）叠加1）、2）得到最后杆端弯矩。 计算过程可列表进行
返回
例题 2
单结点力矩分配法
用力矩分配法计算,画M图。
解：1）求μ
μAB= 4/9 μAC= 2/9
AA1155kkNN↓↓↓↓44↓↓i00↓↓=kk↓↓1NN↓↓↓↓//mm↓↓↓↓ DD
MA 10
80
mAB
M=15 i=2
mAD mAC CC
MM图图（（kkNN..mm))
22mm
22mm
44mm
A
C
D
AD
AC
CA
DA
3/9
2/9
－ 80
15
10
－10 返回
－ 65
10
－ 10
三、多结点力矩分配法
3iij
由此可见，在同一结点上各杆杆端转角相等的前提下，两杆i端的
DM ' ik
DM ik
1 2
DM
6第六章 位移法和力矩分配法PPT课件
FF QBA
15
第2节 位移法的基本原理
力法：是以结构的多余约束力作为未知量，
按照位移条件将多余约束力求出，然后再根 据平衡条件求解其他的约束力、内力 以及求 位移等等。
力法是将超静定结构化为静定结构来计算的。
位移法：是以结构的某些位移作为未知量， 利用变形协调条件，通过对超静定梁系的计 算建立平衡条件，求出结点位移，再根据内 力与位移之间的关系，确定结构的内力。
11F/16 -5F/16
B －ql2/8 0
5ql/8 -3ql/8
11
14、
A 1
A
EI
l
杆端弯矩
杆端剪力
B MAB
MBA FQAB
FQBA
i
-i
0
0
12
15、
a
A
F
b
EI
l
16、
q
A
EI
l
杆端弯矩
杆端剪力
B MAB
MBA FQAB
FQBA
-Fa(l+b)/2l -Fa2/2l F
0
a=0
-Fl/2
X1
B
X2 X1 =1
X2 =1
11
l EI
22
l3 3EI
12
l2 2EI
M2 Fa
1F
Fa2 EI
2F
Fa2 6EI
(3b2a)
F MF
4
F
A
aC
b
B
l
F
A
C
X1
B
X2
F ab 2
l2
F a 2b
l2
M
解得：
X1
结构力学第8章 力矩分配法(31-33)
4/7 A
2 1/2
3/7
C 3 4 0 0
SBA = 4i SBC = 3i
B
4
4. 传递力矩
2 A
B 3
C M图（kN· m）
2.3 结点力矩下单结点力矩分配的解题步骤
例2：若梁线刚度 i 相同，用力矩分配法求梁各杆端弯矩。
M=7kN· m
A 1. 结点力矩 2. 分配系数 3. 分配力矩 B C
■ 约束力矩等于固端弯矩之和。
（2）在结点B加上一个力偶-MB。
（3）两种情况叠加，得到实际杆端弯矩。
总结 ■ 先在刚结点B上加阻止转动的约束，把连续梁 分为单跨梁，求出杆端弯矩。结点B各杆固端弯矩之 和即为约束力矩MB。 ■ 去掉约束，求出各杆B端新产生的分配力矩和 远端新产生的传递弯矩。 ■ 叠加各杆端的力矩就得到实际的杆端弯矩。
θB
MAB A 2iB
θB
C 0 MCB
B MBA MBC B 4iB 3iB
1）B点产生转角 SBA=4i SBC=3i
例1：若梁线刚度 i 相同，求梁各杆端弯矩。 M
A
B
θB
C
SBA=4i
SBC=3i
（2）分配系数μ
Bj
S
B
S Bj
是指杆件转动刚度与结点连接所有杆件转动刚度和的比值。
BA
M BA
S BA 4i 4 S BA S BC 4i 3i 7
4 MB 7 M BC 3 MB 7
BC
3 7
例1：若梁线刚度 i 相同，求梁各杆端弯矩。 M
A
B
θB
C
4 3 M BA M B M BC M B 7 7 （3）传递系数C
结构力学_杨海霞_位移法和力矩分配法汇总
第五章位移法和力矩分配法一、判断题（“对”打√，“错”打）1.位移法和力矩分配法只能用于求超静定结构的内力，不能用于求静定结构的内力。
（）2.用位移法求解图示结构基本未知量个数最少为5。
（）3.对于图（a）所示结构，利用位移法求解时，采用图（b）所示的基本系是可以的。
（）（a）(b)4.图示两刚架仅在D点的约束不同，当用位移法求解时，若不计轴向变形则最少未知量数目不等，若计轴向变形则最少求知量数目相等。
（）（a）(b)5.图（a）所示结构的M图如图(b)所示。
（）（a）(b)6．某刚架用位移法求解时其基本系如图所示，则其MF图中各杆弯矩为0，所以有附加连杆约束力FR1F=0。
( )7.图a结构用位移法计算的基本系如图b，则其2图如图c所示。
（）(a) (b)(c)8.图示连续梁在荷载作用下各结点转角的数值大小排序为A>B>C> D. ( )9.图示两结构（EI均相同）中MA相等。
（）（a）(b)10.下列两结构中MA相等。
（）（a）(b)11.图示结构结点无水平位移且柱子无弯矩。
（）12.图示结构下列结论都是正确的：. ( )13.用位移法计算图示结构，取结点B的转角为未知量，则. ( )14.图a对称结构（各杆刚度均为EI）可以简化为图b结构（各杆刚度均为EI）计算。
（）（a）(b)15.图a对称结构可以简化为图b结构计算（各杆刚度不变）。
（）（a）(b)16.图a对称结构可以简化为图b结构计算。
（）（a） (b)17.图（a）所示对称结构，利用对称性简化可得计算简图，如图(b)所示。
（）(a） (b) 18.图示结构中有c点水平位移和BE杆B点弯矩（）19.图示结构的弯矩图与是否有AB杆和BC杆无关。
（）20.用力矩分配法计算图示结构，则分配系数μCD=，传递系数。
（）21.根据力矩分配法，图示结构最后弯矩有关系：（）22.图a所示连续梁当线刚度i2?i1时，可简化为图b结构按力矩分配法计算。
结构力学位移法
（2）远端为固定铰支座
MAB
A
EI l
因MBA = 0，代入(1)式可得
（3）远端为定向支座
QAB
MAB
3i l 6i 6i 12i QBA 0 (2) A BQ 2 0 , Q 因 B AB BA l l l M AB 3i A
A
l
3i
l2
A
θ=1
B
i
－i
0
q
q B
A
EI
EI
ql 2 2
l
X1 （ a） 力法基本体系 X1 1、力法基本未知量－ 2、力法基本体系－悬臂梁
MP
3、力法基本方程－ 11 X 1 1P 0
l
பைடு நூலகம்
X1 1
M1
ql 2 8
ql2 8
4、系数与自由项 1 P , 11
M 1M 1 l 11 dx EI 3 EI M 1M P 1 1 ql 2 3 ql 4 1P dx ( l l) EI EI 3 2 4 8EI
位移法：以结构的某些位移作基本未知量，按受力 平衡条件求出后，据此求出位移内力及位移。 共同点：利用基本结构的变形和受力情况与原结构 相同的条件解题。
§6-2 P
θA
位移法的基本概念 C 荷载效应包括：
A
θA
内力效应：M、Q、N；
位移效应：θA B
附加 刚臂
P A
C
θA 附加刚臂限制结
A
θA
C
施加力偶使结点产 生的角位移，以实
1/ l
QAB QBA
6i 6i 12i A B 2 (2) l l l
结构力学课件11位移法1共20页文档
位移法的特点： 基本未知量—— 独立结点位移
基本体系——一组？单跨超静定梁
基本方程—— 平衡条件
09.10.2019
13
二、基本未知量的选取
1、结点角位移数： 结构上可动刚结点数即为位移法计算的结点角位移数。
2、结构独立线位移： 每个结点有两个线位移，为了减少未知量，引入与实际相符的两个假设：
（2）由于相对线位移引起的A和B
A
B
l
以上两过程的叠加
A3 1iMAB 6 1iMBA l
B6 1iMAB 3 1iM BA l
MAB4iA MBA2iA
2iB 4iB
6i 6i
l (1) l
Q A BQ B A 6 li A 6 li B 1 l2 i 2 7 (2 )
设 EI i
l
A31iMAB61iMBA
09.10.2019
1
同理可得
B61iMAB31i6MBA
MAB
A
MAB
A
EI
l
B
MBA
B
MBA
A B
我们的任务是要由杆端位移求 杆端力，变换上面的式子可得：
09.10.2019
A31iMAB61iMBA
B61iMAB31iMBA
（4）由杆件的刚度方程求出杆件内力，画弯矩图。
关于刚架的结点未知量
A
P C
A
q
B
A
M AB
P A
A
M AB A
C
B
09.10.2019
5
§11-2 等截面杆件的刚度方程
一、由杆端位移求杆端弯矩
结构力学 力矩分配法
同时：各杆远端产生传递弯矩：
M A B
1 2
M
B A
MCB 0
（三）(b)图+(c)图=(a)图，即：
M BA
M
g BA
M B A
M AB
M
g AB
M A B
M BC M B C
MCB 0
归纳：
②①② ①放固放 固松 定松定节 节节节点 点点点， ，，，分 各分各配 杆配杆弯 端弯端矩 有矩有， 固，固传 端传端弯递弯递弯 矩弯矩矩 ，矩，。 有。有节节点点不不平平衡衡力力矩矩。。
第8章 力矩分配法
8.1 力矩分配法的基本概念
属于位移法类型的渐近解法。 一、力矩分配法依据
1. 理论基础：位移法 2. 解题方法：渐进法 3. 适用范围：连续梁、无结点线位移的刚架 4. 计算对象：杆端弯矩，正负号规定与位移法相同 二、力矩分配法的三个基本概念
（一）转动刚度 转动刚度表示杆端对转动的抵抗能力。数值上
M
M AB
S AB S
M
D
A θA
B
A
M AC
S AC S
M
分配弯矩
A
C
θA
M
S
A
M AD
S AD S
M
A
令
μAj
S Aj S
(
j
B,C, D)
A
(a)
M AB SAB θA 4 iAB θA
M AC S AC θA iAC θA
M AD S AD θA 3iAD θA
例: 试绘制连续梁的弯矩图。
力矩分配法与位移法的联合应用
F1P
F11 k11Z1
B C
B
C
B
C
B
C
k11
Z1 1
A
D
A
D
A
D
A
D
基本体系
不能侧移
实际侧移Z1
在右侧第1图中，只有节点角位移，无节点线位移，采用力矩 分配法绘其弯矩图即为MP图，并取如图脱离体求出F1P。
C B C B C
F1p
A
D
A
D
第1步,锁住节点 求固端弯矩
第2步,将不平衡弯矩 反号分配，传递
首先，先用位移法求解，不考虑节点角位移，只考虑节点线位
移，即只取节点线位移为基本未知量，建立方程。
k11Z1 F1P 0
B C B C
F1P
B C
B
F11 k11Z1 C
Z1 1
k11
A
D
A
D
A
D
A
D
基本体系 不能侧移 实际侧移Z1 其次，在右侧 两图中均只有节点角位移，可用力矩分配法绘图
总结：解题思路 求解一般有结点线位移的刚架; 用力矩分配法考虑角位移的影响; 用位移法考虑线位移的影响（只取线位移为基本未知量）。 1）位移法方程
基本结构
k 1 1 1 F1 p 0
侧移 引起 荷载 引起
荷载作用
侧移作用
2）用力矩分配法
作
M
1
图，求 k 1 1
3）代入位移法方程求解 4）求内力
1
p
作 M P 图，求 F1 P
M M 1 1 M
本节结束
•
•
谢谢观赏
第2步,将不平衡弯矩 反号分配，传递
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章位移法和力矩分配法一、判断题（“对”打√，“错”打）1.位移法和力矩分配法只能用于求超静定结构的内力，不能用于求静定结构的内力。
（）2.用位移法求解图示结构基本未知量个数最少为5。
（）3.对于图（a）所示结构，利用位移法求解时，采用图（b）所示的基本系是可以的。
（）（a）(b)4.图示两刚架仅在D点的约束不同，当用位移法求解时，若不计轴向变形则最少未知量数目不等，若计轴向变形则最少求知量数目相等。
（）（a）(b)5.图（a）所示结构的M图如图(b)所示。
（）（a）(b)6．某刚架用位移法求解时其基本系如图所示，则其MF图中各杆弯矩为0，所以有附加连杆约束力FR1F=0。
( )7.图a结构用位移法计算的基本系如图b，则其2图如图c所示。
（）(a) (b)(c)8.图示连续梁在荷载作用下各结点转角的数值大小排序为A>B>C> D. ( )9.图示两结构（EI均相同）中MA相等。
（）（a）(b)10.下列两结构中MA相等。
（）（a）(b)11.图示结构结点无水平位移且柱子无弯矩。
（）12.图示结构下列结论都是正确的：. ( )13.用位移法计算图示结构，取结点B的转角为未知量，则. ( )14.图a对称结构（各杆刚度均为EI）可以简化为图b结构（各杆刚度均为EI）计算。
（）（a）(b)15.图a对称结构可以简化为图b结构计算（各杆刚度不变）。
（）（a）(b)16.图a对称结构可以简化为图b结构计算。
（）（a） (b)17.图（a）所示对称结构，利用对称性简化可得计算简图，如图(b)所示。
（）(a） (b)18.图示结构中有c点水平位移和BE杆B点弯矩（）19.图示结构的弯矩图与是否有AB杆和BC杆无关。
（）20.用力矩分配法计算图示结构，则分配系数μCD=，传递系数。
（）21.根据力矩分配法，图示结构最后弯矩有关系：（）22.图a所示连续梁当线刚度i2»i1时，可简化为图b结构按力矩分配法计算。
（）(a）(b)(b)23.图示连续梁发生支座移动如图所示，用力矩分配法计算时结点C的不平衡力矩为零。
（）24.图a所示结构可简化为图b结构，用力矩分配法计算。
（）（a）(b)三、填空题1．用位移法求图示桁架受对称荷载时，基本未知量个数最少为个。
2．图示结构用位移法求解时，基本未知量个数最少为个。
3.图示单跨梁当A支座有垂直向下单位位移时，MAB= 。
当支座A有垂直于AB的向右下方的单位位移时，MAB= 。
当支座A在水平方向有单位位移时，MAB= 。
4.根据互等定理知道位移法典型方程中的副系数kij=kji,该互等定理可由互等定理导出。
5.若如图示刚架在mB的作用下，B结点产生单位转角。
则mB= 。
（各杆杆长l，刚度为EI）6.对图示结构用位移法求解时，其典型方程一般形式为，其中系数项k11= ，自由项FR1F= 。
7.某结构用位移法求解时，基本系如图所示，则典型方程中的系数k11= ，k12= ，k21= ，k22= ，自由项FR1F= ，FR2F= 。
8．图示结构，EI=常数，已知结点C的水平线位移为，则结点B的角位移B= ，转向为。
（填顺时针或逆时针）9.图示结构，EI=常数，已知结点D的转角，则MDB= ，且侧受拉。
MCD= ，侧受拉。
10.欲使图a和图b中的MB=MB′，则。
11.图示结构A点的弯矩MA= 。
12.利用位移法判断结点A的转角A的转向为。
13.已如图示结构中，则C点水平位移△c=。
14.利用位移法概念求图示结构支座反力FRD= 。
15.图示结构用位移法计算，取结点B的水平位移△1为未知量，则系数k11= 。
16.图示为一连续梁的位移法基本系，则系数k12= ， k22= 。
17.图示对称刚架受对称荷载，由位移法可知，MCB= kN·m ,MAB=kN·m.18.图示结构，FQCB= ，FQBE= 。
19.图示结构，MCB= ，侧受拉，MBC= 。
20.图示结构，根据结构和荷载特点分析得FNCB= ，FQCB= 。
21.力矩分配法中，传递系数表示当杆件近端有转角时，与的比值，它与杆件远端的有关。
22.图示结构用力矩分配法计算时，A点的不平衡力矩m= 。
23.用力矩分配法计算图示结构，则分配系数μAB= ,传递系数CAC= 。
24．图示结构用力矩分配法求解时，其结点不平衡力矩mk= .25.图示结构的弯矩MBA= ,MBC= 。
（顺时针为正）26.用力矩分配法计算图示刚架，则分配系数μBA= ，传递系数CBA= 。
（各杆l，EI相同）27.力矩分配法与位移法在消去附加刚臂作用的做法上的不同是：位移法通过满足典型方程使各刚架上反力矩为零，而力矩分配法则是。
一、是非题1、×.位移法取结点位移为基本未知量、附加约束的结构为基本结构,所以也可以用于求静定结构内力,力矩分配法亦类似，但它只可求解无结点线位移的静定结构。
力法须解除多余约束，故不可用于求静定结构内力。
2、×.铰上方的刚结点转角可不取未知量,该题基本未知量数最少为3个(一个线位移、两个角位移)。
3、√.是可以的，但未知量数不是最少的。
矩阵位移法电算中就是这样处理的。
4、√.不计轴向变形基本未知量为(a)4个、(b)3个,计轴向变形均为6个。
5、√.中间的铰无线位移并将结构分为三个部分,它们之间无力矩的传递,可独立画出各自的弯矩图。
6、×.根据截面剪力平衡条件可知。
7、√.注意此时斜杆只有刚体位移无弯矩。
8、√.可根据下列步骤作定性分析:(1)草绘弯矩图和挠曲线图,(2)按超静定结构求位移的方法,取三跨简支梁为静定基本系,(3)分别建立虚力状态计算各跨简支梁两端转角,根据图乘法分析可比较出各支座处转角的大小。
9、√.按力矩分配法计算,两结构的分配系数、传递系数和固端弯矩均相同,故可得出结论。
用位移法分析也可以得出该结论。
10、√. 两结构相对线刚度相同, 分配系数、传递系数和结点不平衡力矩均相同。
11、√. 此结构因水平杆,故刚结点无转角,又若有结点水平线位移,则横梁在水平方向无法平衡,故也无结点水平位移,所以柱子无弯矩。
12、√. 因BC杆,故;若,则ABC杆水平方向无法平衡,故;由于以上两点,BD杆无弯矩;AB 杆相当于B端固定A端铰支,故有。
13、√. 该结构无结点线位移.位移法固定状态下,两杆B端抗弯劲度为,故得。
14、×.因荷载反对称,故在半结构中,原来位于对称轴上的杆的刚度应取为。
15、√.对称结构受对称荷载作用,位于对称轴上两刚结点只能上下移动,但受两斜杆支撑又不能上下移动,故相当于固定。
16、√.对无支座的平衡体,可假设某点相对不动(即固定),对该结构设最下面结点相对固定,其半结构即图(b).17、√.因对称,两刚结点处无转角和水平位移，不仅如此，竖杆任一点也无转角、无水平位移和无弯矩。
简化后的半结构在两刚结处位移条件与原结构相同,故两横梁弯矩不变。
18、×.根据ABCD水平方向平衡可知，E点处无水平约束力，故，但是FEG部分不对称，E点有水平位移要引起C点水平位移。
19、√.因结构对称受对称荷载，B结点无转角和无位移,只有水平杆有弯矩，去掉两斜杆后，以上状态不变。
20、√.结构中D点无转动和移动，可视CD杆为两端固定梁来考虑(当C结点转动时)。
21、×. A端向B端的传递系数，只有当B端固定无转动时才等于，而现在B端为弹性的，故不成立。
22、√.根据条件,第一跨相当于两端固定梁，可求出右端弯矩为，其他部分可简化为图(b)计算。
23、√.力矩分配法固定状态下，BC杆为两端固定梁,求出支座位移作用下的固端弯矩即可叠加出不平衡力矩。
24、√.左边F简化为结点外力偶，右边F简化为杆端外力偶，简化去掉的杆的弯矩按静定法求出。
二、选择题1、B. 左边铰上刚结点转角可不取为未知量，右边铰连接的刚结点转角要取为未知量。
2、C. 其他三图结构均有结点线位移。
3、D. 图A结点无转角，若有水平线位移，则横梁在水平方向无法平衡；图B由对称性，可知无水平线位移；图D结构中间的两刚结点有线位移,独立线位移1个。
4、C. 组合结点铰端转角不是基本未知量。
5、A. 结点A无线位移，又假设A点不能转动，则B、C点也不能转动和位移,故只有一个基本未知量。
6、C. 因为必须。
7、A. BA杆B端抗弯劲度为0。
8、C. A点向右，B点向上，AB杆转的角度为；AB杆两端垂直杆轴的相对位移为杆长乘转角，即；杆件按两端固定梁计算得杆端弯矩。
9、B. 根据位移法，要，必须自由项，即可求得。
10、C. 左边四个竖杆对的贡献均为；右边四杆中除右下角的杆子外,对的贡献均为。
11、D. 结点上集中力F要考虑。
12、D. 应等于各杆A端抗弯劲度之和，右横梁抗弯劲度为0。
13、A. 应等于各杆刚结点处的固端弯矩之和，右边的集中力可简化成结点集中力偶6kNm。
14、A. 图b结构A结点无线位移，受结点集中力作用时结构无弯矩。
图a结构则非。
15、B. 由ABCE部分水平方向平衡条件知E点无水平约束力，故此部分为对称受力状态，故有。
其他三个均不为0。
16、C. 不引起；F可视为反对称荷载,由此求出底部两水平反力为,则可求出。
17、C. 由对称知，则可求.B点无线位移，则A点的弯矩为B点的一半.故有。
18、D. 因为图D结构有侧移。
19、A. 注意杆AD的抗弯劲度为0，AB杆与两端固定梁一样。
20、C. 注意分配系数的计算式并非它的定义。
21、B. 分配系数、传递系数是结构固有的，与荷载无关。
22、A. 水平杆无弯矩，又刚结点无线位移故按传到固定端。
23、C. 用力矩分配法分析，图b结构两杆分配系数和传递系数均相同，故有和截面弯矩相等；其他等式均不成立。
24、A. 按力矩分配法概念，作用结点C的外力偶矩全部分配给CD杆C端(分配系数)。
三、填空题1、6. 由于结构约束不对称，虽然受力对称但位移不对称，有四个水平位移和3个竖向位移未知量，考虑到结构最终保持对称的变形状态。
A ,C两点竖向位移相同，故基本未知量为6个。
2、1. 若将下面一个刚结点加刚臂约束住，则上面一个刚结点就不能转动和移动。
3、 0,,. A支座向下移动，AB杆向下平移；A支座垂直于杆轴移动时，可按一端固定，另一端铰支处理；A支座向右水平移动，B点向上,AB杆转过的角度为 ,引起两端相对位移为,进而再按一端固定一端铰支计算固端弯矩。
4、反力, 虚功。
5、. 应等于各杆B端抗弯劲度之和。
6、, , 0. 该结构只有一个水平线位移未知量。
7、, , , , 0, . 注意在作用下,斜杆为刚体平移，无弯矩。
8、, 顺时针. 建立一个位移法方程:即可求出(即)9、, 右, , 下. 可按计算,简单地也可按单跨梁分别计算:,也可按两端固定梁AD,受及F作用的结果相叠加得到。