电力系统分析(铁路方向) 第八章 电力系统不对称短路分析与计算-续
合集下载
第8章 电力系统不对称故障的分析和计算_2014
第8章 电力系统不对称故障的分析和计算
简单不对称短路的分析
序网方程
单相(a相)接地短路
序分量边界条件
联立方程求解
复合序网
故障点各相电流电压
相量图
特例分析(I&II)
特例分析(III)
特例分析(IV)
两相(b相和c相)短路 序分量边界条件
不对称故障电压电流分布计算---基本步骤
由序网方程和序分量边界条件求解故障口电流电压各序 分量(复合序网、方程求解等)； 由各序网络计算电流电压各序分量的分布情况； 对某一节点各序电压分量或者支路各序电流分量进行综 合即可得到相应的电压和电流相量； 必须注意对称分量经过变压器后的相位变换问题。
非全相断线的故障口电压电流各序分量
非全相断线的分析计算---举例
应用节点阻抗矩阵计算不对称故障
各序网络的电压方程式
各序网络的电压方程式---小结
各种故障边界条件
各种故障序分量边界条件
正序等效定则
本章小结
各种故障序分量边界条件； 复合序网的概念和正序等效定则； ™ 电压电流对称分量经过变压器后的相位变换； ™ 利用阻抗矩阵计算不对称故障的原理和方法。
序分量边界条件 关于故障特殊相和参考相---使序分量边界条件表达式简单
复合序网
正序等效定则
非金属性短路 单相(a相)非金属性接地短路 序分量边界条件
复合序网
两相(b相和c相)非金属性短路
序分量边界条件
复合序网
两相(b相和c相)非金属性短路接地
联立方程求解
复合序网
故障点各相电流电压
相量图
简单不对称短路的分析
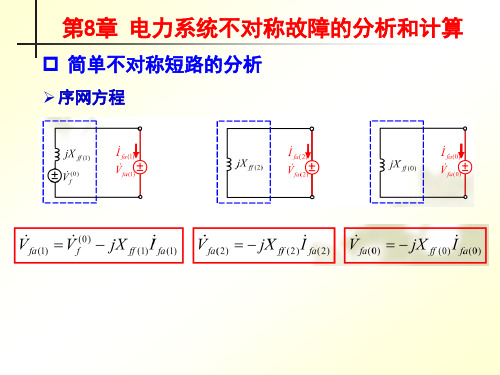
序网方程
单相(a相)接地短路
序分量边界条件
联立方程求解
复合序网
故障点各相电流电压
相量图
特例分析(I&II)
特例分析(III)
特例分析(IV)
两相(b相和c相)短路 序分量边界条件
不对称故障电压电流分布计算---基本步骤
由序网方程和序分量边界条件求解故障口电流电压各序 分量(复合序网、方程求解等)； 由各序网络计算电流电压各序分量的分布情况； 对某一节点各序电压分量或者支路各序电流分量进行综 合即可得到相应的电压和电流相量； 必须注意对称分量经过变压器后的相位变换问题。
非全相断线的故障口电压电流各序分量
非全相断线的分析计算---举例
应用节点阻抗矩阵计算不对称故障
各序网络的电压方程式
各序网络的电压方程式---小结
各种故障边界条件
各种故障序分量边界条件
正序等效定则
本章小结
各种故障序分量边界条件； 复合序网的概念和正序等效定则； ™ 电压电流对称分量经过变压器后的相位变换； ™ 利用阻抗矩阵计算不对称故障的原理和方法。
序分量边界条件 关于故障特殊相和参考相---使序分量边界条件表达式简单
复合序网
正序等效定则
非金属性短路 单相(a相)非金属性接地短路 序分量边界条件
复合序网
两相(b相和c相)非金属性短路
序分量边界条件
复合序网
两相(b相和c相)非金属性短路接地
联立方程求解
复合序网
故障点各相电流电压
相量图
电力系统不对称故障的分析计算
第八章 电力系统不对称故障的分析计算主要内容提示：电力系统中发生的故障分为两类：短路和断路故障。
短路故障包括：单相接地短路、两相短路、三相短路和两相接地短路；断路故障包括：一相断线和两相断线。
除三相短路外，均属于不对称故障，系统中发生不对称故障时，网络中将出现三相不对称的电压和电流，三相电路变成不对称电路。
直接解这种不对称电路相当复杂，这里引用120对称分量法，把不对称的三相电路转换成对称的电路，使解决电力系统中各种不对称故障的计算问题较为方便。
本章主要内容包括：对称分量法，电力系统中主要元件的各序参数及各种不对称故障的分析与计算。
§8—1 对称分量法及其应用利用120对称分量法可将一组不对称的三相量分解为三组对称的三序分量（正序分量、负序分量、零序分量）之和。
设c b a F F F •••为三相系统中任意一组不对称的三相量、可分解为三组对称的三序分量如下：()()()()()()()()()021021021c c c c b b b b a a a a F F F F F F F F F F F F ••••••••••••++=++=++= 三组序分量如图8-1所示。
··F·120° 120°120°F·ω120°120°120° F·F·ω正序分量： ()1a F •、()1b F •、()1c F •三相的正序分量大小相等，彼此相位互差120°，与系统正常对称运行方式下的相序相同，达到最大值的顺序a →b →c ，在电机内部产生正转磁场，这就是正序分量。
此正序分量为一平衡的三相系统，因此有：()()()111c b a F F F •••++=0。
负序分量：()2a F •、()2b F •、()2c F •三相的负序分量大小相等，彼此相位互差120°，与系统正常对称运行方式下的相序相反，达到最大值的顺序a →c →b ，在电机内部产生反转磁场，这就是负序分量。
电力系统分析第8章 电力系统不对称故障的分析和计算
V fa(1) V fa(2) jX ff (2) I fa(2) jX ff (2) I fa(1)
第八章 电力系统不对称故障的分析和计算
8-1 简单不对称短路的分析
➢短路点故障相的电流为
•
•
•
•
•
I fb 2 I fa(1) I fa(2) I fa(0) ( 2 ) I fa(1) j
•
I
fa ( 0)
( 2
X
ff (2)
X
ff (0)
•
)I
fa (1)
X ff (2) X ) ff (0)
•
I
fc
•
I
2
fa (1)
•
I
•
fa(2) I
fa ( 0)
(
X ff (2)
2
X
ff
(0)
)
•
I
fa (1)
X ff (2) X ff (0) )
➢短路电流为
I (1,1) f
， ，
图8-1 单相接地短路
单相（a相）接地短路的边界条件为
•
V fa 0
•
I fb 0
•
I fc 0
第八章 电力系统不对称故障的分析和计算
8-1 简单不对称短路的分析
用对称分量表示为
I I I I 0 ， •
•
•
V fa(1) V fa(2) V fa(0) 0
• 2
第八章 电力系统不对称故障的分析和计算
8-1 简单不对称短路的分析
•
I fa(1)
•
V f (0)
j( X ff (1) X ff (2) X ) ff (0)
电力系统不对称短路的分析与计算
f
Ufb Ufa
Ufc c
b a
Ifa
Ifb
Ifc
Za
Zb
Zc
K
即：不同类型的短路，相当于在短路点接一各相阻 抗值不同，中心点接地方式不同的三相负载！
1.2 不对称短路的特征
在任意某系统某点f发生不对称短路时
特征：短路点元件参数不对称 （三相阻抗不等） 运行参量不对称
（各相电压电流不对称）
？ 如何处理这种不对称特征？
2 IB 三相正序电流向量
电力系统正常运行时的正序相序的确定
d轴
若：XX’绕组为A相，则
X
Z'
显然YY’绕组为B相，ZZ ’ 绕组为C相。
Y'
若： ZZ’绕组为A相，则
Y
q轴
显然XX’绕组为B相，YY 绕组为C相。
’
Z
X'
即：先设定其中一相，
则其他两相即可确定
正序三相向量的数学描述：
定义： a e j120 cos120 j sin120
经消弧线圈接地（属于不接地方式）
C
B
U&c
N
U&b
U&a
L I&L A
I&d
I&bd
I&cd
B
C
U&bd
U&b N U&c
U&cd
U&N U&a
I&d
A U&ad 0
I&L
IL Id 全补偿——不允许（系统会产生谐振过电压） IL Id 过补偿——经常采用 IL Id 欠补偿——一般不采用
本章内容
第8章-电力系统不对称故障的分析计算
F F F F a a1 a2 a0 2 F F F F F a F aF b b1 b2 b0 a1 a2 a0 F F aF a2F F F F c c 1 c 2 c 0 a 1 a 2 a0
Xq Xd
X 2 1.22 X d
， 无阻尼绕组 X2 1.45Xd
二、电力系统元件序参数和各序等值电路
1、同步发电机—零序电抗
三相零序电流在气隙中产生的合成磁势为零，因此其零序电抗仅 由定子线圈的漏磁通确定。 同步发电机零序电抗在数值上相差很大（绕组结构形式不同）：
将 V120 Z sc I120 展开可得
ZI V 1 a1 a1 Va 2 Z 2 I a2 V Z I 0 a0 a0
Z1 0 0 Z s 2Z m 0
结论：在三相参数对称的线性电路中，各序对称分量具有独 立性。即，当电路通以某序电流时，只产生同一序对称分量 的电压降。因此，可以对正序、负序、零序分量分别进行计 算。
一、对称分量法在不对称短路计算中的应用
3、对称分量法在不对称短路计算中的应用
根据以上各序电压方程式，可以绘 出各序的一相等值电路。 I (Z Z ) V E
a a1 G1 L1
a1
(Z Z ) V 0 I a2 G2 12 a2 ( Z Z 3Z ) V 0 I
或写成 V abc
Z ab Z bb Z bc
Z ac I a Z bc I b Z cc I c
ZI abc
图8-2 静止三相电路元件
电力系统不对称故障的分析和计算.ppt
2)
I
fa(1)
(8
9)
Vfa(0) jX I ff (0) fa(0) 0
2019/10/11
8-1 简单不对称短路的分析 2. 两相(b相和c相)短路—复合序网
I fa(1)
jX ff (1) V (0)
f
V fa(1) I fa(2)
jX ff (2)
V fa(2)
8-1 简单不对称短路的分析 1. 单相(a相)接地短路—序分量边界条件
(1)相量表示的边界条件：Vfa 0, I fb 0, I fc 0
(2)对称分量表示的边界条件 Vfa V fa(1) V fa(2) V fa(0) 0 I fb I fb(1) I fb(2) I fb(0) 0 I fc I fc(1) I fc(2) I fc(0) 0
a b c Vfa 0
I fa V fb
I fb 0
I fc 0 V fc
(3)以a相为参考相 V fa V fa(1) V fa(2) V fa(0) 0
I fb 2 I fa(1) I fa(2) I fa(0) 0 I fc I fa(1) 2 I fa(2) I fa(0) 0
I fc(2)
I fa(0) I fb(0) I fc(0)
V fc
2019/10/11
V fa (1)
Vfa 0 V fa ( 2) V fa(0)
V fa (1)
V fc ( 2 )
V fb(2)
V fc (1) V fb
V fa(2) V fa ( 0 )
V fb (1)
第8章 电力系统不对称故障的分析与计算
(3) YNyn(Y0/Y0)联结变压器
图8-12 三相三柱式变压器 a)铁心和零序磁通路径 b)油箱壁中感应电流
(3) YNyn(Y0/Y0)联结变压器
图8-13 中性点经阻抗接地的YNd联结变压器及其等效电路 a)中性点经阻抗接地的YNd联结变压器 b)等效电路
2. 三绕组变压器
图8-14 三绕组变压器零序等效电路 a) YNdy联结 b) YNdyn联结 c) YNdd联结
8.1.2 对称分量法在不对称故障分析中的应用
图8-5 三序序网图
8.1.2 对称分量法在不对称故障分析中的应用
图8-6 a相接地的复合序网等效电路
8.2 电力系统元件的序参数和等效电路
8.2.1 8.2.2 8.2.3 8.2.4 8.2.5 8.2.6 同步发电机的各序参数 异步电动机的各序电抗 变压器的各序电抗和等效电路 输电线路的序阻抗和等效电路 电缆线路的零序阻抗 电力系统的零序等效电路
3. 自耦变压器
(1)中性点直接接地的YNa(Y0/Y0)和YNad(Y0/Y0/△)联结自耦变压器 (2)中性点经电抗接地的YNa和YNad联结自耦变压器
(1)中性点直接接地的YNa(Y0/Y0)和YNad(Y0/Y0/△)联 结自耦变压器
图8-15 中性点直接接地的自耦变压器的零序等效电路 a) YNa联结 b) YNad联结
2.两相短路
f点发生两相(b、c相)短路，如图8-31所示，该点 三相对地电压及流出该点的相电流(短路电流)具 有下列边界条件： Ifa=0，Ifb=－Ifc，Ufb=Ufc(8-56) 将它们转换为用对称分量表示，先转换电流 If(1)If(2)If(0)=131aa21a2a1110Ifb－Ifb=jIfb31－10 即为 If(0)=0If(1)=－If(2)(8-57)
《电力系统分析》第8章习题答案
−
j
900
⎥ ⎥
=
⎢ ⎢0.494e
j 2550
⎥ ⎥
1 ⎥⎦⎢⎣2e j1350 ⎥⎦
⎢⎣0.195e
j1350
⎥ ⎦
8-13 试画出图 8-62 所示电力系统 k 点发生接地短路时的正序、负序和零序等值网络。
图 8-62 习题 8-13 附图
解：正序、负序、零序等值网络见下图 a)、b)、c)。
（3）k 点发生 a、c 两相接地短路时
Ib1
=
j( X 1∑
E1Σ
=
+ X 2∑ // X 0∑ )
j1 j(0.202 + 0.214 // 0.104)
= 3.677
Ib2
=
−
X 0∑ X2∑ + X0∑
Ib1
=
−
0.104 0.214 + 0.104
× 3.677
=
−1.203
Ib0
=
−
X 2∑ X2∑ + X0∑
Ib1
=
− 0.214 × 3.677 0.214 + 0.104
=
−2.474
U b1 = U b2 = U b0 = − jX 2∑ Ib2 = − j0.214 × (−1.203) = j0.257
Ib = 0
Ic = a 2 Ib1 + aIb2 + Ib0 = e j240° × 3.677 − e j120° ×1.203 − 2.474 = 5.624e− j131.29° Ia = aIb1 + a2 Ib2 + Ib0 = e j120° × 3.677 − e j240° ×1.203 − 2.474 = 5.624e j131.29° Ub = 3Ub1 = 3× j0.257 = j0.771 U a = U c = 0
第八章电力系统不对称故障的分析
•
U
fc (1)
•
U
fc ( 2 )
•
U
fc ( 0 )
1
•
U
fc
3
同一类型短路故障发生在不同相上时，基准相的序分量 故障边界条件的形式不会改变，于是复合序网的形式不 会改变，计算公式、结论均不会改变，只是表达式中下 脚符号改变而已。
j a2 a X ff (2) a2 1 X ff (0) I&fa(1)
U&fc aU&fa(1) a2U&fa(2) U&fa(0)
j a a2 X ff (2) a 1 X ff (0) I&fa(1)
（四）向量图：
Ifc(2) Ifb(1)
Ifc(1) Ifb(2)
•
I fa(2)
X ff (0)
•
I fa(1)
X ff (2) X ff (0)
•
I fa(2)
X ff (2)
•
I fa(1)
X ff (2) X ff (0)
U&fa(1) U&fa(1) U&fa(1)
j
X X ff (2) ff (0)
•
I fa(1)
X ff (2) X ff (0)
（2）两故障相中的短路电流的绝对值相等，方向相反， 数值上为正序电流的 3 倍；
（3）当在远离发电机的地方发生两相短路时，可通过对序网 进行三相短路计算来近似求两相短路的电流；
（4）两相短路时的正序电流在数值上与在短路点加一个附加阻
抗
Z (2)
构成一个增广正序网而发生三相短路时的电流相等。即
•
•
•
第八章 电力系统不对称故障的分析
如果a相金属性接地短路，即Xk＝0，则有
U a U a0 U a1 U a2 0
a1 I I a2 Ia0 E1/j(X1 X2 X0)
a1 j(X0 X2)Ia1 U Ia U 2 j X2 a1 jX U a0 0Ia1
18
非故障相电压
例8－1
①数值总是相等的，其相角差的大小与X0Σ/X2Σ有 关； ②X0Σ=0，Ub与Uc反相； ③X0Σ=∞，单相接地短路电流为零，非故障相电 压的数值升高为线电压。
19
二、两相短路
U a U b
a b c
U c
I b I a
jXk
a 0 I bI I c 0
. a 1
. 1a
I
2
(
)k j X 1 E I .
1 1
X
X
)k j X X
I a0 0
. . .
.
.
.
1
. 1 . .
1
. . 11
)
a
I
.
jX1 2
. 1
11
2
Ua0 jX0 Ia0 0
23
短路点的各相电流和电压的计算
第8章
电力系统不对称 故障的分析
1
不对称故障的类型
单相接地短路 横向故障 两相短路 两相接地短路
不对称故障
单相断线
纵向故障
两相断线
2
不对称短路计算的基本思路
①计算短路点各序电流、电压分量； ②计算各序电流、电压在网络中的分布，遇有变压 器支路，还需注意相位变化； ③将各序分量合成得出网络各支路中的各相电流以 及各节点各相电压。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 2 0.1167 U G 1 0.175
4 0.1588
D
6 0.175
IG1
5 2
Il 1 U l 1
I D1 UD1
6 3
Ul 1 U D1 jx4 I l 1 0.46074.03 j 0.1588 (0.0729 j1.0349) 0.2952 j0.0208
x0 3 x1
负荷： 1: 54+j26.15MVA, L 2 : 38+j12.5MVA, x1 1.2, x2 0.35 L
已知正常运行时发电机输出功率 92 j47.3MVA
双回线路始端输送功率为 38 j18.1MVA
节点1、2、3电压标幺值分别为
U 1(0) 1.045311.11 U 2(0) 1.01197.50 U 3(0) 0.98524.03
4. 支路各序电流和节点各序电压 利用叠加原理，故障前正常运行时，各支路（正序）电流、 节点（正序）电压为
U G (0) U1(0) 1.045311.11 U l (0) U 2(0) 1.01197.50
U D(0) 0.98524.03
1 0.1167
D1
U D(0) UD1 UD1 UD(0)
I D1
D1 I
k
D1
UD1 UD1 UD(0)
总结
越靠近电源点，正序电压分量越高；越靠近短路点，正 序电压分量越低，电源点的正序电压最高。在电源与短 路点之间正序电压逐渐降低，短路点处正序电压最低， 就等于故障点正序电压分量。
UC 1
a
b
U B1
c
U e j 30，I I e j 30 Ua1 A1 a1 A1 U e－j 30 I I e－j 30 U
A1 a1 A1 a1
原副边接线图
A B
负序电压相量图
Ua2 a
A
C
Ub2
b
U A2
30
UD1 UD1 UD(0) 0.52454.03 0.98524.03 0.46074.03
正序故障ቤተ መጻሕፍቲ ባይዱ量分布
U D1 0.46074.03 I l 1 I D1 1.1826-85.97 j( x3 x6 ) j(0.1750 3) 0.0729 j1.0349
j (0.3056 0.1379) 1.1826-85.97
X 0 0.1375
0.52454.03
U D 2 jX 2 I D1
U D0
I D0
j 0.3056 1.1826-85.97 0.36144.03
U D 0 jX 0 I D1 j 0.1379 1.1826-85.97 0.16314.03
基本上是“电路”知识的应用，从各个序网中
推算各支路电流和各节点电压各相序分量的计 算值； 2、任意处各相电流、电压由其实际正、负、零 三个序分量合成。
短路前网络中的正常电流电压 已知时，可利用叠加原理求正 序电流电压分布
Ei
i
正序 网络
（当然，也可以直接求 解正序网络）
短路点的正序电压 U D1 用两个理想电压源代替
§8 电力系统不对称短路分析 （续）
2. 对称分量经变压器后的相位变换
只有Y/Y-12，△/△-12接线变压器，变压器两
侧的各序电压、电流相位不发生变化。
Y/△-11接线变压器
A B
正序电压相量图
U A1 A aU a1
30
C
原 副 边 接 线 图
b
U b1
a
b
c
c
U c1
2 0.175
4 0.4764
3 0.175
零序 网
U D0
U D0 0.16314.03 Il 0 0.2504-85.97 j( x2 x4 ) j(0.1750 0.4764)
Ul 0 jx2 Il 0 j0.1750 0.2504-85.97 0.0438-175.97
a
b
c
Uc2 c
UB2
a
b
UC 2
c
j 30
U a 2 U A2e
U e j 30 U A2 a 2
，I a 2 I A2e
j 30
I e j 30 I A2 a 2
总结：
Y/△-11接线变压器 ① Y→△ :正序分量逆时针转过30º； 负序分量顺时针转过30º；
2. 构建各序网络 正序网络
1 0.1167
2 0.175
4 0.1588
D
3 0.175
EG(0)
5 2
U D1
6 3
G
2
T1
115kV
4
D
T2 6
7
5
1
L2
3
L1
负序网络
3 0.175
1 0.1167
2 0.175
4 0.1588
D
5 0.5833
UD2
6 0.875
G
2
IG 0 0
UG 0 0
6. 求故障电流、电压分布 设D点发生a相接地短路。线路各相的电流
G
2 T1
115kV
4
D
T2 6
7
5
1
L2
3
L1
1 I la Il1 Il 2 Il 0 2 1 1.2541 68.06 0.8384 -85.97 0.2504 -85.97 2 1.1573 76.38 1 a 2 I aI I 0.3303143.25 I lb l1 l2 l0 2 1 aI a 2 I I 0.552788.08 I lc l1 l2 l0 2
U l 2 U D 2 jx4 I l 2 0.36144.03 j 0.1588 0.8384-85.97 0.2283-175.97
5. 求负序、零序电流电压分布 负序 网
1 0.1167
2 0.175
4 0.1588
D
3 0.175
5 0.5833
5. 求负序、零序电流电压分布 负序 网
1 0.1167
2 0.175
4 0.1588
D
3 0.175
5 0.5833
UD2
6 0.875
U D2 0.36144.03 Il 2 I D2 1.1826 -85.97 j ( x6 x7 ) j (0.175 0.875) 0.8384-85.97
正常时的电压 短路点正序电压故 障分量
Ek
k
D1 I
D1
U D(0) UD1 UD1 UD(0)
Ei
i
正序 网络
短路前
Ek
k
正常运 行状态
Ei
i
正序 网络
D1 I D(0) 0
U D(0)
叠加原理
Ek
k i
正序 网络
正序故 障分量
D1 I
UD2
6 0.875
UG 2 U l 2 jx2 I l 2 0.2283-175.97 j 0.1750 0.8384-85.97 0.0815-175.97
IG 2 UG 2 0.0815-175.97 0.6987-85.97 jx1 j 0.1167
j 30
I Y1 I 1e
j 30
U e j 30 UY2 2
I e j 30 I Y2 2
不对称短路时网络中电流电压的分布计算
1. 计算各序网中任意处各序电流、电压
任意处各序电流、电压的计算是网络化简的逆
过程。由故障点开始，根据正、负、零三个序 网逐段推算；
T1
115kV
4
D
T2 6
7
5
1
L2
3
L1
零序网络
2 0.175
4 0.4764
3 0.175
U D0
X1 0.3896
I D1
U D(0) 0.98524.03
U D1
X 2 0.3056
ID2
UD2
复 合 序 网
X 0 0.1375
I D0
单相短路接地时正序电压值降低最少； 两相短路接地时正序电压降低的情况仅次于三相短路；
三相短路时，短路点的正序电压为零，系统中其他各点的 正序电压降低最严重。
负序和零序网络中没有电源，短路点的负序和零序电压 分量相当于电源，因此短路点的负序和零序电压值最大， 最大等于故障点的负序、零序电压分量。越远离短路点 负序和零序电压值越小。
2 0.175
4 0.1588
D
3 0.175
EG(0)
5 2
U D1
6 3
4. 支路各序电流和节点各序电压 利用叠加原理，故障前正常运行时，各支路（正序）电流、 节点（正序）电压为 SG (0) 0.92 j0.473 I G (0) 0.9508 j0.2744 U 1.045311.11 G (0) 0.38 j0.181 Sl (0) I l (0) 0.3957 j0.1283 U 1.01197.50 l (0)