电工学第6讲 相量法
合集下载
【第8章】 相量法
实轴 +1
复数在复平面上可 以用向量表示。
0
a1
2. 复数的四种表示形式
⑴ 表达式 ① 代数形式 A= a1+ ja2 +j a2 A
② 极坐标形式
③ 三角函数式 ④ 指数形式
0 模 幅角 A a cos j + j a sin j
A aj
a φ
a1 +1
A ae jj
（由欧拉公式e jφ = cos φ + jsin φ得到） ⑵ 四种表达式关系
I e jy i I y I m m m i
复振幅与正弦量的一一对应关系： 复振幅的模是正弦量的最大值 复振幅的幅角为正弦量的初相位
jy i I Ie Iy i 复有效值
复有效值与正弦量的一一对应关系： 复有效值的模是正弦量的有效值 复有效值的幅角为正弦量的初相位
同样可以建立正弦电压与相量的对应关系：
φ =0，同相； i i1
0 i2
φ = (180o) ，反相； i i1 i2
wt
0 i i1
wt
φ = /2，正交；
i2
wt 因为规定了： |φ| (180°)。 0 所以，我们说i1 领先 i2 /2, 而不说i2落后i1 3 /2
注：我们此处比较的是两个电流的相位差，那么，我们是 否可以比较一个电压和一个电流的相位差？在今后的分析 中可以利用电压和电流的相位差来判断电路的性质。
线圈从中性面开始转过了ωt 时，导线切割磁 力线的速度是ωr SIN ωt
可见：交流电是电流的大小和方向都随时间做周期 性变化的电流。
交流电有许多优点: •交流电可以用变压器升高或降低电压， •交流电可以驱动结构简单，运行可靠的交流 感应电动机，交流电是廉价的动力或能量来源。
复数在复平面上可 以用向量表示。
0
a1
2. 复数的四种表示形式
⑴ 表达式 ① 代数形式 A= a1+ ja2 +j a2 A
② 极坐标形式
③ 三角函数式 ④ 指数形式
0 模 幅角 A a cos j + j a sin j
A aj
a φ
a1 +1
A ae jj
（由欧拉公式e jφ = cos φ + jsin φ得到） ⑵ 四种表达式关系
I e jy i I y I m m m i
复振幅与正弦量的一一对应关系： 复振幅的模是正弦量的最大值 复振幅的幅角为正弦量的初相位
jy i I Ie Iy i 复有效值
复有效值与正弦量的一一对应关系： 复有效值的模是正弦量的有效值 复有效值的幅角为正弦量的初相位
同样可以建立正弦电压与相量的对应关系：
φ =0，同相； i i1
0 i2
φ = (180o) ，反相； i i1 i2
wt
0 i i1
wt
φ = /2，正交；
i2
wt 因为规定了： |φ| (180°)。 0 所以，我们说i1 领先 i2 /2, 而不说i2落后i1 3 /2
注：我们此处比较的是两个电流的相位差，那么，我们是 否可以比较一个电压和一个电流的相位差？在今后的分析 中可以利用电压和电流的相位差来判断电路的性质。
线圈从中性面开始转过了ωt 时，导线切割磁 力线的速度是ωr SIN ωt
可见：交流电是电流的大小和方向都随时间做周期 性变化的电流。
交流电有许多优点: •交流电可以用变压器升高或降低电压， •交流电可以驱动结构简单，运行可靠的交流 感应电动机，交流电是廉价的动力或能量来源。
分析正弦交流电路的相量法
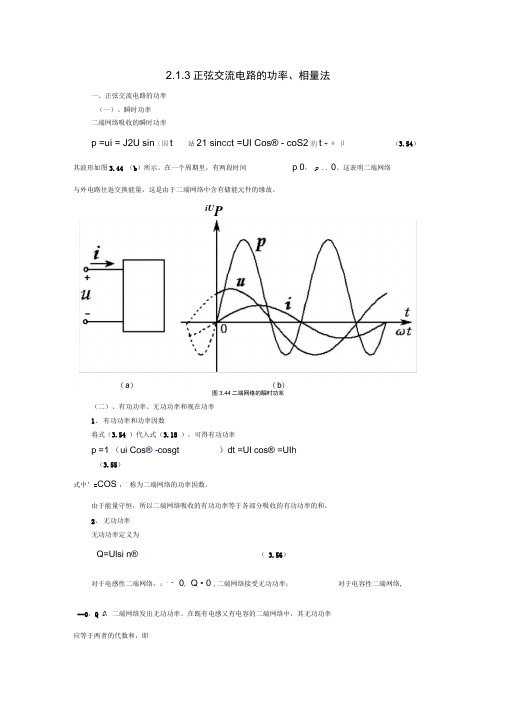
2.1.3正弦交流电路的功率、相量法一、正弦交流电路的功率（一）、瞬时功率二端网络吸收的瞬时功率p =ui = J2U sin（国t 站21 sin cc t =UI Cos® - coS2豹t + ® 卩（3.54）其波形如图3.44 （b）所示。
在一个周期里，有两段时间p 0，p .. 0。
这表明二端网络与外电路往返交换能量，这是由于二端网络中含有储能元件的缘故。
iU P图3.44二端网络的瞬时功率（二）、有功功率、无功功率和视在功率1、有功功率和功率因数将式（3.54 ）代入式（3.18 ），可得有功功率p =1 （ui Cos® -cosgt ）dt =UI cos® =UI h（3.55）式中’=COS ：：称为二端网络的功率因数。
由于能量守恒，所以二端网络吸收的有功功率等于各部分吸收的有功功率的和。
2、无功功率无功功率定义为Q=Ulsi n® （3.56）对于电感性二端网络，：：・0, Q • 0 ,二端网络接受无功功率；对于电容性二端网络,--0，Q 0，二端网络发出无功功率。
在既有电感又有电容的二端网络中，其无功功率应等于两者的代数和，即图3.45功率三角形S p ；p 2 Q 2 tan■ = cos=p(3.58)(3.59)(3.60)正好构成一个直角三角形（如图 3.45所示），称为功率三角形。
例3.25试求图3.46所示电路的有功功率、无功功率和视在功率，其中 尺=2OJR 2 =1OJC =2mF,L =0.1H ,u =50 2sin100tV 。
22Mt图 3.46 例 3.25解:Q = Q L Q C一般来说，二端网络吸收的无功功率等于各部分吸收的无功功率的代数和。
3、视在功率 视在功率定义为S =UI（ 3.57）其SI 主单位为伏安（VA ），工程上也常用千伏安（KVA ）。
由于电机和变压器的容 量是由它们的额定电压和额定电流来决定的，因此可以用视在功率来表示它们的容量。
电路PPT-相量法
I IΨi UL w LI Ψi π 2
jw L
相量關係：
U L
jwL I jXLI
相量模型
有效值關係： U=w L I 相位關係： u=i +90°
返回 上頁 下頁
感抗和感納
XL=wL=2fL，稱為感抗，單位為 (歐姆) BL=-1/w L =-1/2fL， 稱為感納，單位為 S
返回 上頁 下頁
I 0
u的所有正弦電流用相量表示
時仍滿足KCL；而任一回路所有支路正弦電壓用
相量表示時仍滿足KVL。
返回 上頁 下頁
例2 已知電流錶讀數： A1 ＝8A A2 ＝6A
週期性電流、電壓的暫態值隨時間而變，為 了衡量其平均效果工程上採用有效值來表示。
週期電流、電壓有效值定義
物 直流I R 理 意
義 W RI2T
交流 i R
W
T
0
Ri2 (t )dt
返回 上頁 下頁
均方根值
def
I
定義電壓有效值：
1 T
T
0
i2
(t )dt
def
U
1 T u2 (t)dt
T0
正弦電流、電壓的有效值
試用相量表示i, u .
•
•
解 I 10030o A, U 220 60o V
•
例2 已知 I 5015 A, f 50Hz .
試寫出電流的暫態值運算式。
解 i 50 2cos(314t 15) A
返回 上頁 下頁
相量圖
相量是一個複數，它在複平面上的
圖形稱為相量的圖。
i(t) 2Icos(ω t Ψ ) I IΨ
•
i(t) 2I cos(w t Ψ ) I IΨ
相量法
）
u1
i2
2
Icos（t
）
i2
12 （t u1）（t i2） u1 i2
①12>0 ②12<0 ③12=0 ④|12|=π /2
－－u1超前i2； －－u1滞后i2； －－u1和i2同相； －－u1和i2正交；
主值12 〔 ，〕， 若12 〔 ，〕，则用 12 2 来规范它。
jt〕
C
d（Re〔U dt
C
e
jt〕）
Re〔jCU C e
jt〕
②相量形式：IC jCU C
U C
IC
jC
j 1
C
IC
IC LUC ，UC IC / C
u
i
2
iC(t)
O 90o
I C
t(rad)
U C
uC(t)
电容元件 VCR 的波形示意及相量图
2
F1
O
1
+1
复数的乘法
3．除法运算：
①代数形式：
F1 F2
a1 a2
jb1 jb2
（（aa21
jb1）（a2 jb2）（a2
jb2） jb2）
（aa12）a22ຫໍສະໝຸດ b1b2 （b2）2
j（aa22）b21
a1b2 （b2）2
②指数形式：
④图解法：
F1 F2
5．极坐标形式： F F
负数几种形式的转换
例1：将 F1 9.573 化为直角坐标形式。
解： F1 9.5cos73 j9.5sin73 2.78 j9.08
相量法
15
1.正弦量的相量表示 设正弦电流 i 2 I cos(wt y i ) 复常数 构造复指数函数： F (t ) 2 Ie j(wt y i ) 2 Ie jy i e jwt +j 2Icos(wt y i ) j 2Isin( wt y i ) w
wt
Im
yi
O
+1
( 2) i1 ( t ) 10 cos(100 t 300 ) i2 ( t ) 10 sin(100 t 150 )
i2 (t ) 10 cos(100t 1050 )
j 300 (105 0 ) 135 0
i2 (t ) 3 cos( 100 t 150 0 )
e jwt ) Re( 2U e jwt ) u u1 u2 Re( 2U 1 2 e jwt 2U e jwt ) Re( 2 (U U )e jwt ) Re( 2U 1 2 1 2
U U U 1 2
相量加减运算：用代数式计算。
F1 F2 1 2
F1 F2 F1 e j1 F2 e j 2 F1 F2 e j(1 2 )
模相乘 角相加
F1 | F1 | θ1 | F1 | e jθ1 | F1 | j( θ1θ2 ) e jθ 2 F2 | F2 | θ2 | F2 | e | F2 | |F1| θ1 θ2 |F2|
Im I ，I m 2 I 2
13
同理，正弦电压有效值与最大值的关系：
Um U ，U m 2U 2
正弦电流、电压也可以表示为：
i 2I cos(wt y i )，u 2U cos(wt y u )
1.正弦量的相量表示 设正弦电流 i 2 I cos(wt y i ) 复常数 构造复指数函数： F (t ) 2 Ie j(wt y i ) 2 Ie jy i e jwt +j 2Icos(wt y i ) j 2Isin( wt y i ) w
wt
Im
yi
O
+1
( 2) i1 ( t ) 10 cos(100 t 300 ) i2 ( t ) 10 sin(100 t 150 )
i2 (t ) 10 cos(100t 1050 )
j 300 (105 0 ) 135 0
i2 (t ) 3 cos( 100 t 150 0 )
e jwt ) Re( 2U e jwt ) u u1 u2 Re( 2U 1 2 e jwt 2U e jwt ) Re( 2 (U U )e jwt ) Re( 2U 1 2 1 2
U U U 1 2
相量加减运算：用代数式计算。
F1 F2 1 2
F1 F2 F1 e j1 F2 e j 2 F1 F2 e j(1 2 )
模相乘 角相加
F1 | F1 | θ1 | F1 | e jθ1 | F1 | j( θ1θ2 ) e jθ 2 F2 | F2 | θ2 | F2 | e | F2 | |F1| θ1 θ2 |F2|
Im I ，I m 2 I 2
13
同理，正弦电压有效值与最大值的关系：
Um U ，U m 2U 2
正弦电流、电压也可以表示为：
i 2I cos(wt y i )，u 2U cos(wt y u )
电路分析相量法
量的相量乘以 jω ，即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ，辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ，其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i )，则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 ， F2 a2 jb2 ，则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则：
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1－F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明：
复指数函数实部的导数等于复指数函数导数的实部；
相量法.PPT
§16-2 二端口网络的方程与参数
一、Y方程和 Y参数
Y方程是一组以二端口网络的电压 U1和 U 2表征电流 I1 和 I 的方程 。二端口网络以电压 U 和 U 作为独立变量，
2 1 2
电流 I1 和 I 2 为待求量。
1
.
.
根据替换定理，将二端
口网络的端口电压U1和U 2 用
可得：
Y11 Y 21
Z22 Z 12 Y12 z z Z11 Y 22 Z21 z z
其中 z
结论：二端口网络的Y参数矩阵与Z参数矩阵互为逆阵：
Z Y 1
Y Z 1
例3：求图示二端口网络的Z
参数矩阵。
解：先令二端口网络的输出 端开路(İ2=0)，由图可得：
例1 确定角频率时的Y 参数
. .
解：由KCL：
1 1 I1 I L I1' U1 (U1 U1) j L R 1 1 n ( )U1 U 2 j L R R
' 2
1 +
.
I1
R I’1 +
.
.
.
I’2 n:1 *
.
I2 2 +
I2(S) I1(S)
+
U1(S) N0
+
Z U2(S)
U 2 (S ) I1 ( S ) 转移阻抗函数 H (S )
Transform impedance
I 2 (S ) H (S ) I1 ( S )
I1(S) U1(S) N0 I2(S)
Current gain
电路原理相量法
1. 正弦量
i
T
波形
瞬时值表达式 0
i(t)=Imcos( t+y) 正弦量为周期函数 f(t)=f ( t+kT )
周期T 和频率f
t
f 1 T
周期T ：重复变化一次所需的时间。单位：秒s 频率f ：每秒重复变化的次数。单位：赫(兹)Hz
15
正弦电流电路 激励和响应均为同频率的正弦量的线性电路
（正弦稳态电路）称为正弦电路或交流电路。
研究正弦电路的意义 1.正弦稳态电路在电力系统和电子技术领域 占有十分重要的地位。
优 ①正弦函数是周期函数，其加、减、求导、 点 积分运算后仍是同频率的正弦函数；
②正弦信号容易产生、传送和使用。
16
2.正弦信号是一种基本信号，任何非正弦周期信 号可以分解为按正弦规律变化的分量。
i1t 50 2 cos 2ft 15 70.7 cos 314 t 15
i2t 220 2 cos 2ft 60 311cos 314t 60 180
311cos 314t 120
35
四 . 用相量表示正弦量运算
I
u(t) 2U cos (t θ) U U θ
不同频率的相量不能画在一张向量图上。
相量图是把相量在复平面上表示出来的图形。
三、正弦量和相量关系
一个振幅相量乘以旋转因子ejt后得到的复指数函数
的实部即为该相量对应的正弦量。
2U e jt 2Ue j e jwt 2Ue jt +j
2
U1
311.1cos(314t
60
180 )
电路分析基础课件第6章 相量法
+j
设相量
相量 乘以 ，
将逆时针旋转 90， 得到
A
0ψ +1
相量 乘以
，
- A
将顺时针旋转 90，得到
应用举例
例： 6-5 在图示相量图中， 己知I1=10A， I2=5A, U=110V， f=50Hz，试分别写出 它们的 相量表达式和瞬时值表达式，并说明它们之间的相位关系。
解： 相量表达式为 I1 10 30 A I2 5 45 A
F2
(1) 加法运算：
F1 F2 (a1 a2 ) j(b1 b2 )
F1 +1
F1 F2 F2
(2) 减法运算：
作图方法：首尾相连
F1 F2 (a1 a2 ) j(b1 b2 )
平行四边形
(3) 乘法运算：
F1 F2 F1 F2 (1 2 )
试分别画出它们的波形图，求出它们的有效值、频率及相位差。
解：u 10 2sin(314t 30)
i、u
10 2cos(314t 120)
ui
i、u波形图如图所示。其有效值为
I 20 14.142Α 2
0 π 2π ωt
U 10V
i、u 的频率为 f ω 314 50Hz
2π 2 3.14
u、i 的相位差为：
ψu ψi 120 60 180
应用举例
例： 6-3已知正弦电压 u 311cos(314t 60)V，试求：(1)角频率ω、频率f、周期T、
最大值Um和初相位Ψu ；(2)在t=0和t=0.001s时，电压的瞬时值；(3)用交流电压 表去测量电压时，电压表的读数应为多少？
电路(第八章)相量法
复数运算
或
a | A | cosθ b | A | sinθ
Im A2
图解法
(1)加减运算——采用代数形式 若 则
A1=a1+jb1， A2=a2+jb2 A1±A2=(a1±a2)+j(b1±b2)
A1
0 Re
(2) 乘除运算——采用指数形式或极坐标形式
若 则:
A1=|A1| 1 ，A2=|A2| 2
Im 2I
i ( t ) I m cos(w t Ψ ) 2 I cos(w t Ψ )
同理，可得正弦电压有效值与最大值的关系：
U
1 2
Um
或
U m 2U
若一交流电压有效值为U=220V，则其最大值为Um311V； U=380V， Um537V。
注 （1）工程上说的正弦电压、电流一般指有效值，如设
j >0， u超前ij 角，或i 落后u j 角(u 比i先到达最大值)； u, i u i
yu yi j j <0， i 超前 uj 角，或u 滞后 i j 角,i 比 u 先到达最大值。
O
wt
特殊相位关系：
j = (180o ) ，反相：
u, i u u i 0 iw t
j ＝ 0， 同相：
直流I
物 理 意 义
R
交流i
R
W RI T
2
W Ri ( t )dt
T 2 0
电流有效 值定义为
1 T 2 I 0 i (t )dt T
def
有效值也称均方根值 (root-meen-square)
同样，可定义电压有效值：
正弦电流、电压的有效值 设 i(t)=Imcos(w t+ )
或
a | A | cosθ b | A | sinθ
Im A2
图解法
(1)加减运算——采用代数形式 若 则
A1=a1+jb1， A2=a2+jb2 A1±A2=(a1±a2)+j(b1±b2)
A1
0 Re
(2) 乘除运算——采用指数形式或极坐标形式
若 则:
A1=|A1| 1 ，A2=|A2| 2
Im 2I
i ( t ) I m cos(w t Ψ ) 2 I cos(w t Ψ )
同理，可得正弦电压有效值与最大值的关系：
U
1 2
Um
或
U m 2U
若一交流电压有效值为U=220V，则其最大值为Um311V； U=380V， Um537V。
注 （1）工程上说的正弦电压、电流一般指有效值，如设
j >0， u超前ij 角，或i 落后u j 角(u 比i先到达最大值)； u, i u i
yu yi j j <0， i 超前 uj 角，或u 滞后 i j 角,i 比 u 先到达最大值。
O
wt
特殊相位关系：
j = (180o ) ，反相：
u, i u u i 0 iw t
j ＝ 0， 同相：
直流I
物 理 意 义
R
交流i
R
W RI T
2
W Ri ( t )dt
T 2 0
电流有效 值定义为
1 T 2 I 0 i (t )dt T
def
有效值也称均方根值 (root-meen-square)
同样，可定义电压有效值：
正弦电流、电压的有效值 设 i(t)=Imcos(w t+ )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Im
(1)加减运算——采用代数形式
A2
若 A1=a1+jb1， A2=a2+jb2
0
则 A1±A2=(a1±a2)+j(b1±b2)
A1 Re
(2) 乘除运算——采用极坐标形式
若 A1=|A1| 1 ，A2=|A2| 2
则:
A1 A2
A1 e j1
A2 e j2
A1
A e j(1 2 ) 2
复数 ej =cos +jsin =1∠
A
0
Re
A• ej 相当于A逆时针旋转一个角度 ，而模不变。
故把 ej 称为旋转因子。
几种不同值时的旋转因子
,
2
j
e2
cos
j sin
j
2
2
Im
jI
I
0
Re
I jI
,
j
e2
是无有一物物个理理正意意弦义义量
2Icos(wt ) j 2Isin(wt Ψ )
对A(t)取实部：Re[ A(t)] 2I cos(w t Ψ )
对于任意一个正弦时间函数都有唯一与其对应的复数函数
i 2Icos(w t Ψ) A(t)
A(t)还可以写成
A(t ) 2Ie jψ ejωt
i , Im , I
６.2 正弦量的相量表示
1. 复数及运算
复数A的表示形式 A=a+jb (j 1 为虚数单位)
Im
b
A
Im
b
A
|A|
jb
A | A | e j
A | A | e j | A | (cos j sin ) a jb
cos(
)
j sin(
)
j
2
2
2
, e j cos() j sin() 1
故 +j, –j, -1 都可以看成旋转因子。
2. 正弦量的相量表示
两个正弦量的相加
i1 2 I1 cos(w t y 1 ) i2 2 I2 cos(w t y 2 )
第６讲 相量法
重点： 1. 正弦量的表示、相位差； 2. 正弦量的相量表示 3. 电路定理的相量形式；
６.1 正弦量的基本概念
正弦电流电路
激励和响应均为正弦量的电路称 为正弦电路或交流电路。
1. 正弦量
i
T
波形：
瞬时值表达式：
i(t)=Imcos(w t+y)
y/w O
周期T (period)和频率f (frequency) :
U2 460o V
U U1 U2 630 460 5.19 j3 2 j3.46 7.19 j6.46 9.6441.9o V
u(t) u1(t) u2(t) 9.64 2cos(314t 41.9o ) V
也可借助相量图计算
角频率：
ui1, i
w
i1
i2
w
i2
有效值： I1 0 I2
初相位： 1
2
i1+ii23wi3
wI3t 3
因同频的正弦量相加仍得到同频的正弦量，所以，只 要确定初相位和有效值(或最大值)就行了。因此，
正弦量
复数
实际是变 换的思想
正弦量的相量表示
造一个复函数 A(t ) 2Iej(wt)
)
Re(
2
•
(U
1
•
U
2
)e
jwt
)
可得其相量关系为： U U1 U2
U
故同频正弦量相加减运算变 成对应相量的相加减运算。
i1 i2 = i3
I1 I2 I3
例 u1(t) 6 2cos(314t 30) V
U1 630o V
u2(t) 4 2cos(314t 60o ) V
A1 A2 1 2 乘法：模相乘，角相加。
A1 A2
| A1 |θ 1 | A2 |θ 2
| A1 | ejθ1 | A2 | ejθ 2
| A1 | ej(θ1θ 2 ) | A2 |
| A1 | | A2 |
θ1 θ2
除法：模相除，角相减。
例1. 547 10 25 ?
(2) i1(t) 10cos(100 t 300 ) i2(t) 10sin(100 t 150 )
(3) u1(t) 10cos(100 t 300 ) u2(t) 10cos(200 t 450 )
(4) i1(t) 5cos(100 t 300 ) i2(t) 3cos(100 t 300 )
w
t
Ψ
)
dt
T cos2( w t Ψ ) dt
T 1 cos 2(w t Ψ ) 1
dt t
T
1 T
0
0
2
20 2
I
1 T
I
2 m
T 2
Im 2
0.707Im
Im 2I
i(t) Im cos(w t Ψ ) 2I cos(w t Ψ )
同理，可得正弦电压有效值与最大值的关系：
1 U 2 Um
或 Um 2U
若一交流电压有效值为U=220V，则其最大值为Um311V；
U=380V，
Um537V。
注 （1）工程上说的正弦电压、电流一般指有效值，如设
备铭牌额定值、电网的电压等级等。但绝缘水平、耐压值指
的是最大值。因此，在考虑电器设备的耐压水平时应按最大
值考虑。
（2）测量中，电磁式交流电压、电流表读数均为有效值。 （3）区分电压、电流的瞬时值、最大值、有效值的符号。
试写出电流的瞬时值表达式。
解 i 50 2cos(314t 15) A
相量图
•
U
在复平面上用向量表示相量的图
i(t) 2Icos(ω t ) I I
u(t) 2Ucos(w t θ ) U Uθ
•
I
3. 相量法的应用
(1) 同频率正弦量的加减
u1(t)
2 U1 cos(w t Ψ 1) Re(
2
•
U
1
e
jw
t
)
u2(t)
2 U2 cos(w t Ψ 2) Re(
2
•
U
2
e
jw
t
)
u(t) u1(t) u2(t) Re(
2
•
U
1
e
jwt
)
Re(
2
•
U
2
e
jwt
)
Re(
•
2U1
e jwt
2
•
U
2
e jwt
j ＝ 0， 同相：
u, i
u
u, i
u
0
i
0
wt
u, i
u
j= /2：
u 领先 i /2, 不说 u 落后 i 3/2；
i 落后 u /2, 不说 i 领先 u 3/2。
i 0
iw t wt
同样可比较两个电压或两个电流的相位差。
例 计算下列两正弦量的相位差。 解
(1) i1(t) 10cos(100 t 3 4) i2(t) 10cos(100 t 2)
解 547 10 25 (3.41 j3.657) (9.063 j4.226)
12.47 j0.569 12.48 2.61
例2. 220 35 (17 j9) (4 j6) ?
20 j5
解
原式
180.2
j126.2
两个正弦量进行相位比较时应满足同频率、同函数、同符 号，且在主值范围比较。
4. 周期性电流、电压的有效值
周期性电流、电压的瞬时值随时间而变，为了衡量其大 小工程上采用有效值来表示。
周期电流、电压有效值(effective value)定义
直流I R
物
交流i R
理
意
义 W RI 2T
W T Ri2(t)dt 0
y =
例
i
100
50
0 t1
已知正弦电流波形如图，w＝103rad/s，（1） 写出i(t)表达式； （2）求最大值发生的时间t1
t 解 i(t) 100cos(103 t )
t 0 50 100cos
由于最大值发生在计时起点之后
i(t) 100cos(103 t )
A | A | e j | A |
两种表示法的关系：
A=a+jb
A=|A|ej =|A|
直角坐标表示 极坐标表示
Im
b
A
|A|
0
a Re
| A |
a2 b2
θ arctg b
a
或
a | A | cosθ
b | A | sinθ
图解法
复数运算
相位变化的速度， 反映正弦量变化快慢。
w 2 f 2 T
单位： rad/s ，弧度 / 秒
(3) 初相位(initial phase angle) y
i
T
反映正弦量的计时起点。