理论力学 Fx1-h
理论力学第7版第一章

物质层次 线度(m) 运动形式
学科
宇观
>108 天体运动 宇宙学,天体物理
宏观
10-3~103 机械运动 理论力学 ,经典力学
亚宏观 10-6~10-3 热运动 热学,统计物理
原子
10-10~10-9 电磁运动 电磁学,原子物理
核
10-14~10-13 核运动 核物理,高能物理
夸克
<10-8 基本粒子运动 粒子物理,色动物理
平衡时F3 必与 F12 共线则三力必汇交O 点,且共面.
公理4 作用和反作用定律 作用力和反作用力总是同时存在,同时消失,等值、
反向、共线,作用在相互作用的两个物体上.
在画物体受力图时要注意此公理的应用.
公理5 刚化原理
变形体在某一力系作用下处于平衡,如将此变形体刚 化为刚体,其平衡状态保持不变。
• 理论力学(广义):在公理基础上通过数学 推导建立运动与力的关系。
牛顿定律、Lagrange原理、Hamilton原理
• 理论力学(狭义):研究质点、质点系和刚 体系的平衡、移动、转动及振动等运动 规律。不研究连续介质。
矢量力学(几何力学):以伽利略、牛 顿定律为基础。
分析力学:以变分原理为基础。
机械原理、机械设计、结构力学、弹塑性力学、飞 行力学等。 o 学会一种研究方法。
送给大家的话
勤于观察 善于思考 富于联想 勇于创新
学会学习 学会关心 学会反省 学会感激
静力学引言
静力学 (Statics):
研究物体的受力分析、力系的等效替换(或简化)、建 立各种力系的平衡条件的科学.
1、物体的受力分析:分析物体(包括物体系)受 哪些力,每个力的作用位置和方向,并画出物体的 受力图.
【最新试题库含答案】清华理论力学课后答案4

清华理论力学课后答案4篇一:理论力学课后习题答案第4章运动分析基础第4章运动分析基础4-1 小环A套在光滑的钢丝圈上运动,钢丝圈半径为R(如图所示)。
已知小环的初速度为v0,并且在运动过程中小环的速度和加速度成定角θ,且 0 <θ<?,试确定小环2A的运动规律。
22解:asin??a?v,a?v nRsin?R2vdvt1a?dv?acos??v,?dt t2??v00vdtRtan?Rtan?v?ds?v0Rtan?dtRtan??v0tstv0Rtan?ds??0?0Rtan??v0tdtAs?Rtan?lnRtan?Rtan??v0t习题4-1图2??x?3sint?x?4t?2t1.?, 2.?2y?2cos2t?y?3t?1.5t??4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的解:1.由已知得 3x = 4y ? v?5?5t?y?3?3t? ?a??5 ??y??3????4x????4?4t?x(1)为匀减速直线运动,轨迹如图(a),其v、a图像从略。
2.由已知,得arcsinx3?12arccosy242(b)习题4-2图化简得轨迹方程:y?2?x9(2)轨迹如图(b),其v、a图像从略。
4-3 点作圆周运动,孤坐标的原点在O点,顺钟向为孤坐标的正方向,运动方程为s?12?Rt2,式中s以厘米计,t以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y坐标值最大的位置时,求点的加速度在x和y轴上的投影。
解:v?s???Rt,at?v???R,an?v??2Rt2y坐标值最大的位置时:?s? ax?at??R,ay???R22R12?Rt2??22R,?t?1习题4-3图4-4 滑块A,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮以匀角速度ω转动,如图所示。
试求滑块的速度随距离x 的变化规律。
解:设t = 0时AB长度为l0,则t时刻有:r (?t?arcta?arctan)r?l?x2?r2l0x2?r2对时间求导:?r??r2x22xx?r?rx ???xx2?r2???xxx?r224-5 凸轮顶板机构中,偏心凸轮的半径为R,偏心距OC = e,绕轴O以等角速转动,从而带动顶板A作平移。
理论力学[1](第七版)课后题答案哈工大.高等教育出版社
课后题答案哈工大.高等教育出版社](https://img.taocdn.com/s3/m/4468d4b7c77da26925c5b0bd.png)
如图 2-4a 所示。 火箭的推力 2-4 火箭沿与水平面成 β = 25° 角的方向作匀速直线运动,
F1=100 kN,与运动方向成 θ = 5° 角。如火箭重 P=200 kN,求空气动力 F2 和它与飞行方向 的交角 γ 。
y
F2
ϕ
γ β
F1
(a) 图 2-4
θ
x
P
(b)
解
坐标及受力如图 2-4b 所示,由平衡理论得
∠( FR , F1 ) = arccos( F1 + F2 × 4 / 5 ) FR 100 N + 50 N × 4 / 5 = arccos( ) = 29.74 o = 29 o 44′ 161 N
(2)解析法 建立如图 2-1c 所示的直角坐标系 Axy。
∑ Fx = F1 + F2 × 3 / 5 == 50 N + 50 N × 3 / 5 = 80 N ∑ Fy = F1 + F2 × 4 / 5 = 100 N + 50 N × 4 / 5 = 140 N
B ′ FB
D
q
FN 2 FN 3
(n2)
F
B
D
F
FA
A
(o)
B
FC
C
(o1)
F
FE
E
FG
G
FB
A FA
(o2)
B ′ FB
D
D
F
F C C (o3)
图 1-2
FD
′ FD
FE FF E (o4)
8
理论力学(第七版)课后题答案 哈工大.高等教育出版社
第2章 平面汇交力系与平面力偶系
2-1 铆接薄板在孔心 A,B 和 C 处受 3 个力作用,如图 2-1a 所示。 F1 = 100 N ,沿铅 直方向; F3 = 50 N ,沿水平方向,并通过点 A; F2 = 50 N ,力的作用线也通过点 A,尺 寸如图。求此力系的合力。
理论力学02习题课

M F d 1 2 F d 2ABC 2
平面内两个力偶,如果力偶矩相等,则两个力偶等效
8
主要内容和方法
平面力偶系的合成和平衡条件
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩的 代数和。
M FR d F1d F2 d M1 M 2
例题7:在刚体的A、B、C、D四点作用 有四个大小相等的力,此四力沿四个边 恰好组成封闭的力多边形,如图所示.此 刚体是否平衡?选择其中一对平行力, 同时改变方向,此刚体是否平衡? 答:图示情况下刚体不平衡,依然存在顺时针方向力矩,选择其 中一对平行力,同时改变方向,此时刚体平衡。
14
典型题目
例题8:在下面各图中,力或力偶对点A的矩都相等,它们引起的支座 约束力是否相同?
解:
F 0 F F 0 M 0 F l M 0
x A B A B
M M FA ; FB l l
23
作业题
2-12已知梁上作用有力偶,重量不计,在下面三种情况下,计算 之作的约束力
解:
F 0 F cos F cos 0 M 0 F l cos M 0
Fx 0 F FA
2 5 0 FA F 2 5
Fy 0 FD FA
19
1 1 0 FD F 2 5
支座A点的约束力与假设的方向相反
作业题
2-6如图所示,输电线重量沿AB均匀分布,求电线中点和两 端拉力 f 1m, AB 40m, P 400 N
0 M 2 F cos r2 0 M1 r cos r2 M 1 2 cos r1 r1
《理论力学》(范钦珊)习题解答第1篇第1-3章
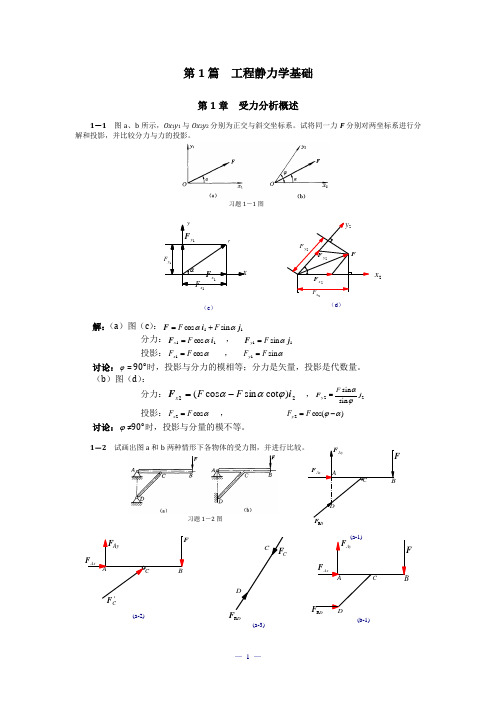
C(a-2)D R F(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c ) 22x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)B(a-1)(b-1)F Ay(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D,则A 端受力改变,因为HG 与ABC 为不同的刚体。
(f-1) 'A(f-2)1O(f-3)F F'F 1(d-2)F yB 21(c-1)F A B1B FDx y(b-2)1F'(b-3)F yB 2 A A B1B F习题1-5图AxF(b-3)E D(a-3)B(b-2)(b-1)F 'CBC(c)'AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
理论力学-达朗贝尔原理及其应用
t aC
FIR =-m a C
a
n C
C
n FR
t n 2、定轴转动 FIR =-m aC =-m( aC aC )
FR
3、平面运动 FIR =-m a C
C
O
FR
Ft R
aC
12.3 刚体惯性力系的简化
惯性力系的主矩与刚体的运动形式有关!
理论力学 第三篇 动力学
第三篇 动力学
第12章 达朗贝尔原理
第12章 达朗贝尔原理
12.1 质点惯性力与达朗贝尔原理 12.2 质点系的达朗贝尔原理 12.3 刚体惯性力系的简化
第12章 达朗贝尔原理
12.1 质点惯性力与达朗贝尔原理
12.1 质点惯性力与达朗贝尔原理
z m A
FI2 a1
m C FIi m2 a2
mi
FR FIi mi ai maC
主矢
ai
FIR maC
主矢与刚体的运动形式无关。
主矩
12.3 刚体惯性力系的简化
刚体平移时,惯性力系向质心简化 ● 主矢
1.刚体作平移
m1
FIR maC
FI2
m2 FI1
a2 maC FIR an m FIn n
12.2 质点系的达朗贝尔原理
例题3
FnIi FtIi F at an
Ny
r
a
FI1
A
mg
解: 对象:系统 受力:如图 运动:略 方程: FNx 惯性力 F I1 n FI 2 a F dm a
B m2g
理论力学第一章
第一章 静力学基本概念与物体的受力分析
第一部分
静力学
第一章 静力学基本概念与物体的受力分析
主要研究以下三个问题:
1.受力分析——分析作用在物体上的各种力,弄清研究对象 的受力情况。
2.平衡条件——建立物体处于平衡状态时,作用在物体上的 力系应满足的条件。
A
z
F
Az
F Ax
A
y
x
(2)滚动轴承
第一章 静力学基本概念与物体的受力分析
止推轴承约束
z
A
F
A F
Ay
Ax
x
F
y
z
Az
F
B
F By
Bz
y
x
F Bx
5、光滑球铰链 人造髋关节
第一章 静力学基本概念与物体的受力分析
A
FAz
A
FAx
FAy
6、固定端约束
P
A
B
(平面)
F
A
(空间)
第一章 静力学基本概念与物体的受力分析
圆柱O
【解】
FNA
FT
P
O
F NB
第一章 静力学基本概念与物体的受力分析
例1-3 作受力图。(不计摩擦)
B E
Do P
F C
【解】
B
A
F
F
NE
C FND
FA
FAx FAy
FNE
折杆ABC、圆柱体O
FND
O
P
F NF
第一章 静力学基本概念与物体的受力分析
上海杨浦大桥
汕头海湾大桥
理论力学第七版答案、高等教育出版社出版
仅供个人学习参考哈工大理论力学(I )第7版部分习题答案1-2两个老师都有布置的题目2-3?2-6?2-14?2-?20?2-30?6-2?6-4?7-9??7-10?7-17?7-21?8-5?8-8?8-16?8-24?10-4?10-6?11-5?11-15?10-3以下题为老师布置必做题目1-1(i,j ),1-2(e,k)2-3,2-6,2-14,2-20,2-306-2,6-47-9,7-10,7-17,7-21,7-268-5,8-8(瞬心后留),8-16,8-2410-3,10-410-611-5,11-1512-10,12-15,综4,15,16,1813-11,13-15,13-166-2图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5m 在铅垂面内转动,杆AB=0.8m ,A 端为铰链,B 端有放置工件的框架。
在机构运动时,工件的速度恒为0.05m/s ,杆AB 始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B 的轨迹方程。
10-3如图所示水平面上放1均质三棱柱A ,在其斜面上又放1均质三棱柱B 。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA 三棱柱B 质量mB 的3倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A 、B 两三棱柱组成1质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统 质心位置在水平方向守恒。
设A 、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c 所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4如图所示,均质杆AB ,长l ,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A 相对图b 所示坐标系的轨迹。
理论力学Fx1hppt课件
擦系数f=0.5。重物的重量为m。 问:⑴轮子能否保持平衡?
⑵轮子与斜面间的静滑动摩擦力大小。
⑶AB段绳子的张力。
Fx 0 ,
y
F
Fy 0 ,
x MC(F) 0 ,
Rr
C
2mg mg
FS mg ,
FS
FN
当FS f FN 时,轮子平衡
求平衡时最大角度 ,已知两杆长相等、重量相同。
13
FAy FAx
FN FS FBy
解:[整体]
M A(F ) 0,
2FN
l sin
2
2P
l cos
22
0
- - - - - - - (1)
[BC杆]
M B (F ) 0,
FN
l
sin
2
FS
l cos
2
P
l cos
22
0
- - - (2)
FAy 1
A FAx FBy D
B FBx
FBy D
B FBx
P
1
1
1
解:[整体]
C
E
M A(F ) 0,
1
FBx 1 P 4 0
F
FBx 4P 8(kN)
FDC
FFE
[BF杆]
Fx 0 ,
F
FBx FDC cos45 0
FDC
FBx cos45
8
2(kN2)5
[练习6] 已知:P=10kN,轮子半径 r =0.3m,
FDN OD Q BC 0 FDN Q 100 N
[轮子]
Fy 0 , 得 FEN 150 N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B F1
P 2
A
FAx
FAy
M A ( F ) 0 , 得 : FB
[CB杆]
MC (F ) 0 , 得 : F1 2 P
25
[练习] 已知:P=2kN,杆自重不计,长度单位为m,求CD 杆受力大小,是受拉还是受压?
FAy 1 FAx D F FDC D B FBx F FFE 1 C 1
Q
F 1m
C
45°
MG (F ) 0 , FCy 1 Q 1 0
FCy 5(kN)
G
FCx
FFG
Fx 0 , FCx FFG cos 45 0
FCx 10(kN)
9
FCy
A 1m
1m
1m
B
E
D F
取AB杆为研究对象,受力如图
M A ( F ) 0 , FDE sin 45 1 Q 2 0
FAy A FAx
M
B
解:[整体]
Fx 0 ,
C
Fy 0 ,
M A (F ) 0 ,
FD D
P
29
[ACB杆]
MC (F ) 0,
FAy A FAx FAy P
FAx C
FBD
B
P
30
[练习5]
正立方体,边长为a,F力对 x,y,z 轴的矩分别为: Mx(F)= z , My(F)= , Mz(F)= 。
FDx
M A ( F ) 0,
得 : M A 13 kN m
MA
21
[例5] 已知力G在CD杆的中点,G=8kN,q=4kN/m,
a=1m,各杆自重不计,求支座A的约束力。 q B C
a
2a
FAy A FAx
2a
45° G FDy
D FDx
MA
22
FBy
q
B
FBx
FB'x
B
2a
38
E
FES
FEN
设D点不滑,E点处在临界状态
C
Q
B
[OBC杆]
MO (F ) 0 ,
FOx O FOy FDS
D
FDN OD Q BC 0 FDN Q 100 N
Mx(F)= z
F
Fy 1 kN
Fz 1 kN
A(1,0,1) y
M x (F ) yFz zFy
M y (F ) zFx xFz
x
M z (F ) xFy yFx
32
[练习8] F=100N,力F在x轴上的投影Fx= 的矩为:Mx(F)= z B(0,4,4) 。 (长度单位为m)
为 f2=0.2 , BC=BD=OD=a=5cm ,轮 A 半径 R=2cm ,求
使轮A保持平衡所能施加的最大水平力P。
C
O D
Q
B
P
解: 设E点不滑,D点处在 临界状态
A E
37
解: 设E点不滑,D点处在临界状态
C
Q
B
[OBC杆]
MO (F ) 0 ,
FOx Q BC 0
14
FAy FAx
解:[整体]
M A ( F ) 0,
2FN l sin 2P l cos 0 - - - - - - - (1) 2 2 2 [ BC 杆 ]
FN FS
M B ( F ) 0,
FBy
FN l sin FS l cos P l cos 0 - - - (2) 2 2 2 2
a=1m。求固定端A的约束反力。 q A P FC 45° a a P
45° a a
17
M
B
C
MA
FAx a
a
[BC杆] 解:
M B (F ) 0,
FBy B
FC
C
[ABC杆] Fx 0 , FBx Fy 0 ,
M A ( F ) 0,
解: [BC杆] M B ( F ) 0,
, 对 x轴
Fx
3 F 5
F y x A(3,4,0)
33
[例 ]
在图示边长为a、b、c的长方体的角点A沿对角线AB作 用一力F, 则该力在z轴上的投影及对x轴之矩为:
FZ = z
Mx(F) = A
c
b
F a
B
y
x
34
[练习6] 已知P=300N,M=60N· m,a=25cm,b=20cm,求支
FAy (Q P)
M A ( F ) 0, M A FC 2a tan (P Q) a 0
M A ( 2Q P ) a
13
[例7] 匀质杆AB和BC在B端铰接,A端铰接在墙上,C 端
则由墙阻挡,墙与C 端接触处的摩擦系数f=0.5,试 求平衡时最大角度 ,已知两杆长相等、重量相同。
MO xO 11.67 cm FRy
8
[例2] 已知: Q=5kN,杆重不计。求C点的反力和DE杆、FG杆 的内力。
A 1m 1m
解:研究整体,受力如图
B
1m
D
E
MC (F ) 0, FFG sin 45 1 Q 2 0
FFG 14.14(kN)
h=20cm,b=10cm,求力系向原点O简化的结果: FRx = ;FRy =
FRz=
My (F)=
;Mx (F)=
;Mz (F)=
z b
F4
F3
y x
F2
h
O
F1
36
[练习7] 轮A重W=50N,其上放置一可绕O轴转动的无重直角 曲杆OBC,点C作用水平力Q=100N,若物A与曲杆之 间的摩擦系数为 f1=0.35 ,物 A 与地面之间的摩擦系数
1
静力学的任务 静力学主要研究受力物体平衡时作用力
所应满足的条件;物体受力的分析方法;力
系的简化方法。
2
(一) 基本定理(常用的) ①三力平衡必汇交,必共面(用于确定未知力的方向)
②合力投影定理:FRx=Fx , FRy=Fy ③合力矩定理: 投影式: ④力的平移定理
M O ( FR ) M O ( Fi )
1 E
P
解:[整体]
A
M A ( F ) 0,
1
FBy
FBx 1 P 4 0
FBx 4 P 8(kN)
B
FBx FBy
[BF杆]
Fx 0 , FBx FDC cos45 0
FBx 26 FDC 8 2(kN ) cos45
[练习6] 已知:P=10kN,轮子半径 r =0.3m, AB=AC=CD=l=1m ,不计摩擦和杆重,求支 座A和B的反力。 解:[整体] FAy
[BC杆] [CD杆]
M B ( F ) 0,
得 : FCy 2 kN
Fy 0 ,
得 : FDy 2 kN
q FDx
D
FDy
20
[整体] 5m B
Fx 0,
得 : FAx 6 kN
M
C
Fy 0,
得 : FAy 2 kN
3m
FAy
A FAx D
FDyq
y
500 N
F3
a
a a
x
y Fyi F2 cos 45 F1 FR
FR x FR y FR
2 2
150 N
F2
a
F1
5002 1502 522 N
MO MO (F ) F1 a F3 a
1750 N cm
Fz 0
4
解题步骤,解题技巧,解题注意问题
(一)解题步骤:①选研究对象 ②作受力图(有用的和没有用的力均画上 ) ③选坐标系、列方程 ④解方程,求出未知数
5
(二) 解题技巧: ①先找二力杆。 ②选坐标轴未知力。 ③选取矩点(轴)与未知力相交或平行。 ④从已知力下手,物体系问题由整体→局部和局部→整体。 (三) 注意问题: ①力偶在坐标轴投影不出现。 ②力偶对任意一点的矩都等于力偶矩。 ③摩擦力的方向一般不能假设。 ④附加方程中的≥或≤号最后别忘记。
C
FCx
a
2a FAy A FAx
FB'y FCy
C
FCy
FCx
MA
45°
FDy G
D
23
FDx
q B FB'x FB'y C
2a
45° G FDy
2a
D FDx
24
[练习1]求DE杆的内力,不计各杆自重。
P
C 30° D 4a E
F´ 1 FB
B
F2 ´ FCx C [整体]
FCy
FB
2a
a
a
FDN Q 100 N
FDN FDN D
C
FDS PP
Q
FDS f1 FDN 35 N
D A A
B
[轮子] M A ( F ) 0 ,得 FES FDS 35 N
W E
Fx 0 , 得 P 70 N Fy 0 , 得 FEN 150 N
因为 FES f 2 FEN , 假设不成立
F y a
2 M x (F ) F a 2 M y (F ) 2 F a 2
M z (F ) 2 F a 2
a
