机械模态分析作业例题
复杂工况机械密封动环的振动模态分析

A: ・
J — L _ .
T G 4 2:
. J
j
3 )
。
- L ^
.
0 — ! 扣・ 0
山
^ J - 乱 A (
.
!
0L
b
乙
, 。
.
上 J 卜 ^ 二
・
一 5乱_ 匕 一 1 L , k 一2 0 1 7 Jb L
6 j
。
’
v
l
呋
L 。 山
J .
I
. - 》
多 t 蛐
I
4 - o
: 8 3 0 0 4 7・ ( 8 3 0 0 4 7・
j c . ,
— L 。0
. ' 卜 - I l
一 月 一 多
二 —0. 1 ) 崮L - _. 2
型 以及 各阶对 应 的最 大变 形量 和振 动应 力 ,得 到 了各 阶主 振型 图及振 动 应力和 变 形 曲线 的 变化 图,分 析 了机 械 密封摩 擦 副动环 在 工作过 程 中 的振 动 模态特 性 ,为机 械密 封动 环结构
参数 的优 化 设计提 供 了科 学依 据 。 关键 词 :机械 密封 ;动 环 ;振 动模 态 ;数值 分析
j L . _ - . 二 - jL - .I
j —
—
. L 却 I L 盘 L L 。 工 山 , o 童 L 。 — ^ j 一 L _ . J . L ^ . ’
oL ^J t 童 L J— ・ — 。 j
.
L o
: _ JL I 江- I : L 0 L
: L o - _ j
机械原理例题机构分析模板
A
2
4
C
B
6
1
5
7
D
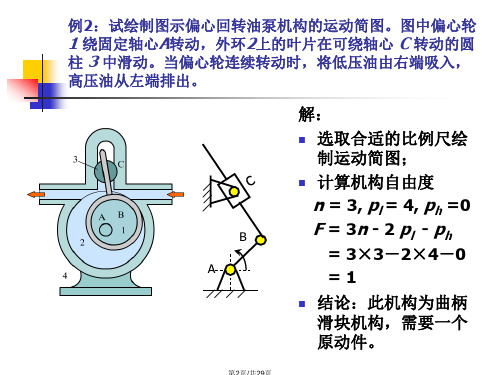
解:
齿轮3-5啮合中心距保持不 变,故算一个高副。
齿轮5-齿条7啮合中心距变 化,齿的两侧面保持接触, 故为两个高副。
n = 6, pl = 7, ph =3 F = 3n - 2pl - ph
= 3×6-2×7-3
=1
2-23:图示一内燃机的机构运动简图,试计算其自由 度。当分别以构件AB和EG为原动件时,试对该机构 进行结构分析。
= 3×4-2×5-1
=1
2-17:计算图示机构的自由度: (b)图示凸轮—连杆组合机构。在D处为铰接 在一起的两个滑块。
F E
A
虚约束 D
局部自由度
B C
F=3×5+2×6-2=1
2-17:计算图示机构的自由度: (c)凸轮——连杆组合机构:精压机构
解: 该机构中存在结构对称部分,从
运动传递的独立性来看,有机构
ABCDE 就可以了,其余部分对
机构的运动传递没有影响,故引 入了虚约束。 将机构中的虚约束部分去掉不计,
C处为复合铰链, n = 5, pl = 7, ph =0 F = 3n - 2pl - ph
= 3×5-2×7-0 =1
2-17:计算图示机构的自由度: (d)齿轮——连杆组合机构:
3
Ⅰ级杆组
G
HH
Ⅱ级杆组
(2)EG为原动件: 该机构为Ⅲ级机构。
2-24(a):计算图示机构的自由度,并在高副低代后分析组 成该机构的基本杆组。
D n
C B n
A
F E
F
D
F
E C
解:
滚子局部自由度1个,虚约束1个 n = 4, pl = 5, ph = 1
液力机械的模态分析考核试卷

6.为了减少计算量,可以采用______方法对液力机械模型进行简化。(答案:子结构/超单元)
7.液力机械模态分析中,______是评价结构动态性能的关键指标之一。(答案:频率响应函数)
8.在模态分析中,______方法可以用来识别结构的模态参数。(答案:系统识别/参数识别)
A.子结构方法
B.超单元方法
C.简化模型
D.提高计算精度
9.液力机械模态分析中,以下哪些参数与模态振型相关?()
A.模态频率
B.模态位移
C.模态参与因子
D.模态阻尼比
10.以下哪些软件工具可以用于液力机械的模态分析?()
A. ANSYS
B. MATLAB
C. ABAQUS
D. AutoCAD
11.液力机械模态试验中,以下哪些因素会影响测试结果的准确性?()
B.每一阶模态对结构响应的贡献可以通过模态参与因子来表示
C.只有低阶模态对结构响应起主要作用
D.高阶模态的贡献可以忽略不计
7.在进行液力机械的模态分析时,以下哪些因素可能导致模态遗漏?()
A.测点数量不足
B.激励力频率范围不够
C.传感器灵敏度不足
D.数据采集时间过短
8.以下哪些方法可以用来减少液力机械模态分析的计算量?()
B.流体动力学特性
C.温度场分布
D.控制系统性能
2.在进行液力机械模态分析时,以下哪个参数不是基本的动力参数?()
A.质量
B.阻尼
述是错误的?()
A.模态分析可以确定结构的自然频率
B.模态分析可以识别结构的薄弱环节
C.模态分析无需考虑外部激励
模态分析算法原理与实例

5.模态计算中接触设置
Training Manual
Advanced Contact & Fasteners
模态计算中可以定义不同结构之间的接触,但是因为模态计 算是一个纯线性分析,因此模态计算中接触定义与其他非线性 问题中定义中的接触不同,模态计算中接触的具体设置如下:
6.预应力模态分析
• 具有预应力结构的模态分析; • 同样的结构在不同的应力状态下表现出不同的动力特性。
Advanced Contact & Fasteners
i 2
其中: fi的单位为Hz,即转/秒。 如果模型的约束不足导致产生刚体运动,则总体刚度矩阵[K]为半正 定型,则会出现固有频率为0的情况。
3.模态计算的方法
在大多数情况下,建议用户选用 Program Controlled选项,程序会自 动优化进行选择算法。
Training Manual
Advanced Contact & Fasteners
用户也可以设置输出应力和应变;
注意:模态计算中的应力和应变只是一个相对值,不是真实的应 力值;应力值并没有实际意义,但如果振型是相对于单位矩阵归 一的,则可以在给定的振型中比较不同点的应力,从而发现可能 存在的应力集中。
Training Manual
Advanced Contact & Fasteners
(1)Direct-Block Lanczos
-能够处理对称矩阵; -是一种功能强大的方法,当提取中型到大型模型(50000 ~ 100000 个 自由度)的大量振型时(40+),这种方法很有效; -经常应用在具有实体单元或壳单元的模型中; -可以很好地处理刚体振型; -需要较高的内存。
《模态分析例题》PPT幻灯片PPT

构造模态分析ansys例题
2021-10-25 星期一
构造模态分析根本步骤
模态分析的求解主要分为四个步骤: 建模 加载及求解 扩展模态 观察结果 模型的建立: 建模过程和其他类型的分析类型类似,但应注意以下两点: 在模态分析中只有线性行为是有效的。如果指定了非线性单元,将作为现行的来
分析中用到的单元模型
在摸一个自由度上指定了一个非零的位移约束,程序将以零唯一约束取代。可 以施加除唯一约束以外的其它载荷,但在模态提取时将被忽略。 模态扩展: 模态扩展指将阵型写入结果文件,如果要在后处理器中查看振型,就必须进展扩 展。 观察结果: 模态分析的结果被写入结果文件Jobname.RST中,包括:固有频率、振型、相对应 力分布。
对待。 材料性质可以是线性的和非线性的、各向同性的或正交各向异性的、恒定或与温
度相关。在模态分析中必须定义弹性模量EX和密度DENS〔或某种形式的质量〕。 加载并求解:
构造模态分析根本步骤
加载并求解: 首先定义分析类型、定义载荷和边界的模态分析(预应力效用除外)中,唯一有效的‘载荷’是零唯一约束,如果
齿轮模型几何信息
齿轮构造的工作状态时变化的, 即动态的,由于构造的振动特 性决定构造对于各种动力载荷 的响应情况,所以在准备进展 其它动力分析之前首先要进展 模态分析,如图 标准齿轮 齿顶直径:24 齿底直径:20 齿数:10 厚度:8 中间厚度:3 弹性模量:2.06e11 密度:7.8e3kg/m3
印刷设备模态分析与应用考核试卷

12. 在印刷设备模态分析中,以下哪些因素会影响系统的阻尼特性?( )
A. 材料特性
B. 结构设计
C. 环境温度
D. 激励频率
13. 以下哪些方法可以用于验证印刷设备模态分析的结果?( )
A. 实验测试
B. 理论计算
C. 数值模拟
D. 专家评估
14. 印刷设备模态分析中,以下哪些情况可能导致设备振动异常?( )
A. 建立数学模型
B. 测试设备振动
C. 数据处理与分析
D. 优化设备外观
5. 在印刷设备模态分析中,以下哪个参数表示系统的固有频率( )。
A. 阻尼比
B. 振幅
C. 相位角
D. 固有频率
6. 印刷设备模态分析中,以下哪种现象可能导致设备失效( )。
A. 频率耦合
B. 振幅过大
C. 阻尼比过小
D. A、B、C都是
A. 振动幅度增大
B. 振动幅度减小
C. 振动频率降低
D. 振动频率升高
18. 以下哪个不是印刷设备模态分析中常用的数据处理方法( )。
A. 快速傅里叶变换
B. 传递函数分析
C. 主成分分析
D. 频谱分析
19. 在印刷设备模态分析中,以下哪个因素可能导致系统振动加剧( )。
A. 阻尼比增大
B. 阻尼比减小
7. 以下哪种方法通常用于印刷设备的模态测试( )。
A. 激光测振仪
B. 声级计
C. 温度传感器
D. 照相机
8. 在印刷设备模态分析中,以下哪个因素不会影响固有频率( )。
A. 结构材料
B. 结构几何
C. 外部负载
D. 激励力
9. 以下哪个不是模态分析中常用的激励方式( )。
小型甘蔗联合收获机械车架的模态分析
台 构 建 机 械 振 动 测 试 分 析 系 统 来 测 量 响 虚 与 被 测 输 入 力 之 间 的 比值 , 出 频 率 响应 函数 ( R 。为此 , 得 F F) 通 过 在 车 架 的指 定 点 ( 称 预 定 点 )上 所 做 的 一 组 也
频 率 响 应 函 数 测 量 ,来 绘 制 一 幅 车 架 的 响 应 图 , 从
维普资讯
20 08年 3月
农 机 化 研 究
第 3期
小 型 甘 蔗 联 合 收 获 机 械 车 架 的 模 态 分 析
唐 治宏 ,黄 炳 琼 ,欧 阳石 坤 ,卢 福 宁 ,高风 伟
( . 西 大 学 a 机 械 工 程 学 院 ; b 实 验 设 备 处 , 南 宁 5 0 0 ; 2 玉 柴 机 器 股 份 有 限 公 司 , 广 西 玉 林 1广 . . 304 .
术 和 计 算 机 技 术 等 学 科 的 基 础 上 发 展 起 来 的 。模 态
分 析 可 在 时 域 或 频 域 中 进 行 ,最 终 获 得 结 构 的 模 态
参 数 ,其 分 析 路 线 如 图 l所 示 。
时 域 F T F 信
号
频 传 递 函 数 域 信
号
传 参 数 递 识 别 函
1 车 架 模 态 分 析 原 理
模 态 分 析 即模 态 参 数 识 别 ,是 在 振 动 理 论 、信 号 分 析 、数 据 处 理 、概 率 统 计 、 自动 控 制 、测 试 技
收 稿 日期 : 2 0 — 5 2 0 70 ~5
基 金 项 目 : 国 家 自 然 科 学 基 金 资 助 项 目 ( 0 6 O l】 5 35 0 作 者 简 介 : 唐 治 宏 (1 6 一), ( 族 ) 广 西 德 人 。 l程 师 94 男 壮 , 苴
机械故障分析练习题(含答案)
机械故障分析练习题(含答案)
一、故障情况描述
一台机器在正常运行过程中出现了故障,现在请您根据以下描
述进行故障分析。
故障描述:当机器运行到一定时间后,出现了明显的异响,同
时机器转速明显下降,无法正常工作。
二、问题分析与解答
1. 请问可能是什么原因导致机器出现明显的异响和转速下降?
答案:这可能是由于机器的轴承磨损所引起的。
机器运转一段
时间后,轴承的润滑油会逐渐消耗,导致轴承磨损加剧,从而引起
了异响和转速下降。
2. 除了轴承磨损,还有哪些可能导致机器出现类似故障的原因?
答案:除了轴承磨损外,还可能是由于传动带松弛、机器内部
零部件松动、齿轮磨损等原因导致的。
这些问题都可能会引起异响
和转速下降。
3. 对于这种故障,应该如何解决?
答案:首先,需要对机器进行彻底的检查,确定具体的故障原因。
然后,针对不同的原因采取相应的措施进行修复。
对于轴承磨
损而引起的故障,需要更换磨损的轴承,并重新润滑。
对于其他原
因导致的故障,需要进行相应的调整和修复。
三、总结
通过对机器故障的分析,我们可以了解到机器故障的原因可能
是多方面的,需要进行仔细的检查和分析。
及时发现和解决机器故障,可以保证机器的正常运行,提高工作效率。
同时,合理使用和
维护机器,也能延长机器的使用寿命。
以上是关于机械故障分析的练习题及答案,希望对您有所帮助。
如有任何疑问,请随时联系。
谢谢!。
机械结构实验模态分析实验报告书
开课实验室:汽车结构实验室2010年月日
学院
姓名
成绩
课程
名称
机械结构实验模态分析
实验项目
名称
机械结构实验模态分析
指导教师
教师评语
教师签名:
年月日
机械结构实验模态分析实验报告
一、实验目的和意义
模态分析技术是近年来在国内外得到迅速发展的一门新兴科学技术,广泛应用于航空、航天、机械制造、建筑、汽车等许多领域,在识别系统的动力学参数、动态优化设计、设备故障诊断等许多方面发挥了日益重要的作用。
5、求取系统多测点加权传递函数幅频特性并产生频率阻尼识别文件。
6、识别系统的频率阻尼产生频率阻尼数据文件。
7、识别系统振型,产生振型数据文件。
8、可以显示打印系统的频率阻尼表及振型表。
9、模态的动画显示观察各阶振型的特点,复模态和实模态的区别。
10、灵敏度分析
在进行框架模态分析中应注意以下问题:
1、结构测量点的选择及布置:模态分析布点的基本原则是结构的重要部分密布,次要部分稀疏,为了使活动振型的显示更直观,整个测点的连线构成的图形要保持测试系统的基本几何特点。
三、实验模态分析的基本原理
对于一个机构系统,其动态特性可用系统的固有频率、阻尼和振型来描述,与模态质量和模态刚度一起通称为机械系统的模态参数。模态参数既可以用有限元的方法对结构进行简化得到,也可以通过激振实验对采集的振动数据进行处理识别得到。通过实验数据求取模态参数的方法就是实验模态分析。只要保证测试仪器的精度、实验条件和数据分析处理的精度就能获得高质量的模态参数。
2、SSDAS-1系统由各测点识别出系统的模态参数的步骤。
3、动画显示。
4、灵敏度分析及含义。
叶轮的模态分析技术实例
转子的 『 占 1 有振 动频率 是转速的 函数 ,转子本 身属 于连续弹性体 , 因此根据转速的不 同, 有多 阶围有 振动
频率。在某阶频 率振动时各点位移做 出的图形 即为振 型。 根据 1 作参数 ( 如 叶轮旋转频率 ) , 选定 叶轮固有频 率允许范围 ,可以为初 步确定叶轮结构和避免振 动提
2 . , 模型 的建 立
本文使用 了 i 维 参 数 化 建 模
后导入 , 再进 行 网
卜 _
格 划分 冈 1 为气 浮 机 叶 轮 的 模 型
视网 , 叶 轮有 8片
图 1 三 维 几何 模 型
叶片, 有 一个 中心
孔与 轴相 连 , 在 叶 片 设 有通 气腔
图 2 网格 生 成 2 . 2 模 态 振 型
f r a ( - ' t t uP l T 1 r ‘ ‘ h l l 1 j ‘ ‘ } l H P S S I I I (  ̄ I l t me t h ( ) d o h ) g y{ l l ’ o f f s h o  ̄ P s l l t l ( ’ t u t ‘ a l
需要解决 ” J :
■i
方 法 建寸 模型 , 并对结构修改进行 预测 , 其 最 大 的 优 - 鳅 越 — ■ ■ 凰 藤 鞣 _ _ — 飘 麟 嘲 删 _ 一 一 : I
.
。
1
’
一
( 1 ) 模态信息在频域 是被截断的, 因此需 要考虑撼断
对精 度 所带 来 的影 响 。 ( 2 ) 模 态 模 型心 考 虑扭 转 自由度 的影 响 , 然 I { 1 于扭 转 模 态 测 试技 l 术发 展 尚不 充 分 ,使得 模 型 中 往往 还 不能
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目:完成一个综合作业(What I hear, I forgot. What I see, I remember. What I do, I understand.)作业:如图所示的两自由振动系统,已知m 1=100kg ,m 2=5kg ,k 1=10000N/m ,k 2=500N/m ,c 2=1N ·m-1·s ,F 1(t)=F 1e j ωt。
求:1. 物理坐标下的振动微分方程;2. 频响函数矩阵;3. 频响函数的模态展式矩阵; 4. 脉冲相应函数;5. 画出H 11(ω)的幅频特性曲线,相频特性曲线,实频特性曲线,虚频特性曲线,Nyquist 图,Bode 图; 6. 固有频率,阻尼固有频率; 7. 画出振型图;8. 模态坐标系下的振动微分方程;9. 模态参数:复模态质量,复模态刚度,复模态阻尼。
解:1.振动微分方程对质量m 1、m 2绘分离体图(如图1-1),用牛二定律列分离体在铅垂方向的力平衡方程得1221221111122122122()()()()F c x x k x x k x m x c x x k x x m x ∙∙∙∙∙∙∙∙+-+--=----= (1.1)将(1.1)整理可得:112211221122222222000m x cc x k k k x F m c c k k x x x ∙∙∙∙∙∙⎡⎤⎡⎤-+-⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦(1.2) 且m 1=100、m 2=5、k 1=10000、k 2=500、c 2=1,代入(1.2)得:111122************50005115005000x x x F x x x ∙∙∙∙∙∙⎡⎤⎡⎤--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦(1.3) 可以得出此二自由度系统振动微分方程为:()M x C x K x f t ∙∙∙++=其中100005M ⎡⎤=⎢⎥⎣⎦;1111C -⎡⎤=⎢⎥-⎣⎦;10500500500500K -⎡⎤=⎢⎥-⎣⎦;1()0F f x ⎡⎤=⎢⎥⎣⎦图1-1、系统的分离体图2.频响函数矩阵由书P25(1.4-58)公式可知,此二自由度系统频响函数矩阵为一2×2方阵,其表达式为:21()()H K M j C ωωω-=-+,其中100005M ⎡⎤=⎢⎥⎣⎦;1111C -⎡⎤=⎢⎥-⎣⎦;10500500500500K -⎡⎤=⎢⎥-⎣⎦(2.1) 写成矩阵形式:12111222122()()10500100500()()()5005005H H j j H H H j j ωωωωωωωωωωω-⎡⎤-+--⎡⎤==⎢⎥⎢⎥---+⎣⎦⎣⎦(2.2)3.频响函数的模态展式矩阵1)求解瑞利阻尼矩阵由于粘性阻尼矩阵C 无法进行正交性对角化,故不能直接应用坐标变换将(1.3)解耦。
由于在该题中,粘性阻尼相对很小,对于小阻尼振动系统,可以利用瑞利比例阻尼来代替粘性阻尼,以获得可对角化的阻尼矩阵。
(1)瑞利比例阻尼系数的确定瑞利比例阻尼:C M K αβ=+,其中100005M ⎡⎤=⎢⎥⎣⎦;10500500500500K -⎡⎤=⎢⎥-⎣⎦;α、β 为瑞利比例阻尼系数瑞利比例阻尼系数存在以下关系:1112222222βωαξωβωαξω⎧+=⎪⎪⎨⎪+=⎪⎩,其中i ω为圆频率2i i f ωπ=(i f 为系统固有频率,书中表示为0i ω);i ξ为阻尼比0i i iσξω=将上式写为矩阵形式:111222122122ωωξαξωβω⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦可得:1111222122122ωωξαξβωω-⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦,其中2i i f ωπ=、0i i iσξω=(3.1)由此可知,只要我们确定了一个系统任意两阶的固有频率及其阻尼比,就可以确定出瑞利比例阻尼系数,从而得到瑞利比例阻尼矩阵。
(2)求该二阶系统的一、二阶固有频率及其阻尼比利用求解该系统振动微分方程()M x C x K x f t ∙∙∙++=的特征值i λ来确定固有频率及其阻尼比。
由书P23(1.4-43)-(1.4-46)公式为求解步骤,下面利用Matlab 来计算固有频率0i ω和阻尼比i ξ:编写Matlab 程序polynomial.m 求特征方程,程序如下:syms x;m 1=100; m2=5; k1=10000; k2=500; c2=1; M=[m1 0;0 m2];C=[c2 -c2;-c2 c2];K=[k1+k2 -k2; -k2 k2];y=det(M*x^2+C*x+K)解以上求得的多项式:>> p=[500 105 102500 100005000000];>> x 0=roots(p)由特征值可得:20118.94528.9453ωλ==≈、11010.03560.00408.9453σξω===02211.1791ωλ==≈、22020.06940.006211.1791σξω===(3)求瑞利比例阻尼系数及瑞利比例阻尼矩阵 根据公式(3.1)编写Matlab 程序rayleigh.m 求解特征方程,程序如下:function Cr=rayleigh() %--计算瑞利阻尼系数alpha 和beta--xi1=0.0040; xi2=0.0062;f1=8.9453; f2=11.1791;omega1=2*pi*f1; omega2=2*pi*f2;A=[1/(2*omega1) omega1/2;1/(2*omega2) omega2/2]; xi=[xi1;xi2];x=inv(A)*xi;alpha=x(1,1)beta=x(2,1)%--计算瑞利阻尼矩阵Cr(2*2)-- m1=100; m2=5; k1=10000; k2=500; M=[m1 0;0 m2];K=[k1+k2 -k2;-k2 k2];Cr=alpha*M+beta*K;可知:瑞利比例阻尼系数-0.3004α=、4=2.374110β-⨯瑞利比例阻尼矩阵-27.5422-0.1187-0.1187-1.3830C ⎡⎤=⎢⎥⎣⎦2)求解模态矩阵(及特征矢量矩阵)书P23已说明根据粘性比例阻尼振动系统的微分方程所求得的特征矢量与该系统无阻尼振动下求得的特征矢量相等。
因此,我们可以利用求此二阶系统在无阻尼振动下的微分方程的特征矢量更简单的得出模态矩阵改写Matlab 程序polynomial.m 求解此二阶系统在无阻尼振动下的微分方程的特征方程,程序如下:syms x;m1=100; m2=5; k1=10000; k2=500; M=[m1 0;0 m2];K=[k1+k2 -k2;-k2 k2];y=det(K-x^2*M) 解以上求得的多项式:>> p=[500 -102500 5000000]; >> x0=roots(p)可知:20180ω=、202125ω=。
将其分别代入回2()0K M ωϕ-=,可得:112125005000500100ϕϕ-⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦ 、122220005000500125ϕϕ--⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦(3.2)求得模态矩阵[]11121221221154ϕϕϕϕϕϕϕ⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦ 3)求解频响函数的模态展式矩阵(1)求模态质量矩阵、模态刚度矩阵和模态阻尼矩阵151000112250[]1405540180Ti diag m M ϕϕ⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦ 151********1180000[]1450050054022500Ti diag k K ϕϕ-⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦15-27.5422-0.11871163.30420.000963.3042[]14-0.1187-1.3830540.000948.7206048.7206Ti diag c C ϕϕ---⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤===≈⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦(2)由此可得频响函数的模态展式为:221()Ti ii i i iH k m j c ϕϕωωω==-+∑(3.3)写成矩阵形式为:22111221112212222211122211122211122221222111221221222222111222111222()()()()()k m j c k m j c k m j c k m j c H H H H H k m j c k m j c k m j c k m j c ϕϕϕϕϕϕωωωωωωωωωωωωωϕϕϕϕϕϕωωωωωωωω⎡⎤++⎢⎥-+-+-+-+⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦++⎢⎥-+-+-+-+⎣⎦将所求ϕ、[]i diag m 、[]i diag k 、[]i diag c 代入:111221212122()()1514()(1800022563.3042)(2250018048.7206)()()525416H H H j j H H ωωωωωωωωω---⎡⎤⎡⎤⎡⎤==--⨯+--⨯⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦4.脉冲响应函数对(3.3)作傅立叶逆变换,得到脉冲响应函数矩阵:21()sin i Tti idi i i dih t et m σϕϕωω-==∑(4.1)5.11()H ω的幅频、相频、实频、虚频特性曲线以及导纳图和博德图 1)11()H ω的幅频特性曲线:11()H ω与ω的关系11()H ω=,其中01ωωΩ=,i ξ为阻尼比。
代入可得:1111()H ω=+(5.1)编写Matlab 程序figure1.m 画图,程序如下:omega=5:.01:15;o1=omega/sqrt(80); o2=omega/sqrt(125); k1=18000; k2=22500; xi1=0.0040; xi2=0.0062;y11=1./(k1.*sqrt((1-o1.^2).^2+(2.*xi1.*o1).^2))+1./(k2.*sqrt((1-o2.^2).^2+(2.*xi2.*o2).^2));plot(omega,y11,'LineWidth',2); grid onxlabel('频率 Hz') ylabel('幅值 mm') title('m1的一阶幅频特性')输出图形:2)11()H ω的相频特性曲线:11ϕ与ω的关系112211221222arctan arctan 11ξξϕ⎛⎫⎛⎫-Ω-Ω=+⎪ ⎪-Ω-Ω⎝⎭⎝⎭。
