方差分析讲义
合集下载
第11章-方差分析讲课讲稿
第11章-方差分析第一节 方差分析的概述一、方差分析的由来t 检验法（z 检验法也是如此）适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验，但在公共管理的研究中经常会遇到比较多个处理优劣的问题，即需进行多个平均数间的差异显著性检验。
这时，若仍采用t 检验法就不适宜了。
这是因为：①检验过程烦琐。
例如，一实验包含5个处理，采用t 检验法要进行25C =10次两两平均数的差异显著性检验；若有k 个处理，则要作k (k-1)/2次类似的检验。
②无统一的实验误差，误差估计的精确性和检验的灵敏性低。
对同一实验的多个处理进行比较时，应该有一个统一的实验误差的估计值。
若用t 检验法作两两比较，由于每次比较需计算一个21x x S ，故使得各次比较误差的估计不统一，同时没有充分利用资料所提供的信息而使误差估计的精确性降低，从而降低检验的灵敏性。
例如，实验有5个处理，每个处理重复6次，共有30个观测值。
进行t 检验时，每次只能利用两个处理共12个观测值估计实验误差，误差自由度为2(6-1)=10；若利用整个实验的30个观测值估计实验误差，显然估计的精确性高，且误差自由度为5(6-1)=25。
可见，在用t 检法进行检验时，由于估计误差的精确性低，误差自由度小，使检验的灵敏性降低，容易掩盖差异的显著性。
③推断的可靠性低，检验的I 型错误率大。
即使利用资料所提供的全部信息估计了实验误差，若用t 检验法进行多个处理平均数间的差异显著性检验，由于没有考虑相互比较的两个平均数的秩次问题，因而会增大犯I 型错误的概率，降低推断的可靠性。
由于上述原因，多个平均数的差异显著性检验不宜用t 检验，须采用方差分析法。
方差分析(analysis of variance)是由英国统计学家R.A.Fisher 于1923年提出的。
这种方法是将k个处理的观测值作为一个整体看待，把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度，进而获得不同变异来源总体方差估计值；通过计算这些总体方差的估计值的适当比值，就能检验各样本所属总体平均数是否相等。
第二章 方差分析课件
误差
DFAB a 1b 1 6
SSe SST SSt 1170
当 p 3 时，
0.05 水平上不显著 0.05 水平上不显著 0.05 水平上不显著
yC yA 8 0.05 水平上显著 yD yB 6 0.05 水平上不显著 当 p 4 时， yD yA 9 0.05 水平上显著
3、新复极差法（SSR法） 同 q 法，其中：LSR SSR;df , p SE 例2.4 接例2.1数据
地块A
B1 化学控制
田间管理B
B2 集成虫害管理
合计TA
B3 改良集成虫害管理
平均yi
A1 A2 A3 A4 A5 A6
合计TB 平均y j
71 90 59 75 65 82
442 73.67
73 90 70 80 60 86
459 76.50
77 92 80 82 67 85
483 80.50
T
2 j
.
C
a
MS B
a 1 b 1 SSe SST SSA SSB MSe
ab 1
SST y2 C
F F
MS A MS e MS B MS e
多重比较：
A因素
SE MSe b
B因素
SE MSe a
例2.5 为了研究不同的田间管理方法对草莓产 量的影响，选择了6个不同的地块，每个地块分 成3个小区，随机安排3种田间管理方法，数据 入下表。进行方差分析。
221
73.67
272
90.67
209
69.67
237
79.00
192
64.00
253 84.33
T 1384
解：由题可知 a 6,b 3
DFAB a 1b 1 6
SSe SST SSt 1170
当 p 3 时，
0.05 水平上不显著 0.05 水平上不显著 0.05 水平上不显著
yC yA 8 0.05 水平上显著 yD yB 6 0.05 水平上不显著 当 p 4 时， yD yA 9 0.05 水平上显著
3、新复极差法（SSR法） 同 q 法，其中：LSR SSR;df , p SE 例2.4 接例2.1数据
地块A
B1 化学控制
田间管理B
B2 集成虫害管理
合计TA
B3 改良集成虫害管理
平均yi
A1 A2 A3 A4 A5 A6
合计TB 平均y j
71 90 59 75 65 82
442 73.67
73 90 70 80 60 86
459 76.50
77 92 80 82 67 85
483 80.50
T
2 j
.
C
a
MS B
a 1 b 1 SSe SST SSA SSB MSe
ab 1
SST y2 C
F F
MS A MS e MS B MS e
多重比较：
A因素
SE MSe b
B因素
SE MSe a
例2.5 为了研究不同的田间管理方法对草莓产 量的影响，选择了6个不同的地块，每个地块分 成3个小区，随机安排3种田间管理方法，数据 入下表。进行方差分析。
221
73.67
272
90.67
209
69.67
237
79.00
192
64.00
253 84.33
T 1384
解：由题可知 a 6,b 3
第九章 方差分析ppt课件
SSW/dW f MW S 14.71/5 1 9410 .4111
（3）计算F值。
精选PPT课件
18
（4） 确定显著性水平和F临界值 取α=0.05，查F分布表得 F0.05(3,14) 3.34。由于计
算的F=3.52> F0.05(3,14) 3.34，P<0.05，所以拒绝原假
设，接受备择假设，认为各组平均数中至少有一对不
精选PPT课件
25
计算自由度： dBfk 14 13；
dW fk n k4 5 4 1；6
df T df B df W =16+3=19
求均方：
MS B
SS B df B
370122.3 3
，
MSW
SSW dfW
35622.25 16
（3）计算F值：
FMBS12.325.50 MW S 22.25
1、提出假设 2、计算平方和与自由度 3、计算F值 4、确定显著性水平并查F临界值表 5、列方差分析总表
精选PPT课件
3
一、方差分析的逻辑思想
1、方差分析是一种综合的检验方法
方差分析是对引起方差变化的各种因 素进行统计分析，检验引起各样本差异 的主要原因（或因素），并与理论值比 较，以判断其显著性。
首先将总体变异分解成样本组间变异 和由抽样误差等其它原因产生的组内变 异，然后分析变异各组成部分的关系。
如果样本组间变异比抽样误差等其它 原因产生的变异显著地大，则认为样本 组间有本质性的差异，否则，认为样本 组间无本质差异。
精选PPT课件
6
在方差分析中，观测值之间的差异情 况用离差平方和表示，符号为SS。方差分析首先 是把总体平方和分解为组间平方和和组内平方和， 即：
（3）计算F值。
精选PPT课件
18
（4） 确定显著性水平和F临界值 取α=0.05，查F分布表得 F0.05(3,14) 3.34。由于计
算的F=3.52> F0.05(3,14) 3.34，P<0.05，所以拒绝原假
设，接受备择假设，认为各组平均数中至少有一对不
精选PPT课件
25
计算自由度： dBfk 14 13；
dW fk n k4 5 4 1；6
df T df B df W =16+3=19
求均方：
MS B
SS B df B
370122.3 3
，
MSW
SSW dfW
35622.25 16
（3）计算F值：
FMBS12.325.50 MW S 22.25
1、提出假设 2、计算平方和与自由度 3、计算F值 4、确定显著性水平并查F临界值表 5、列方差分析总表
精选PPT课件
3
一、方差分析的逻辑思想
1、方差分析是一种综合的检验方法
方差分析是对引起方差变化的各种因 素进行统计分析，检验引起各样本差异 的主要原因（或因素），并与理论值比 较，以判断其显著性。
首先将总体变异分解成样本组间变异 和由抽样误差等其它原因产生的组内变 异，然后分析变异各组成部分的关系。
如果样本组间变异比抽样误差等其它 原因产生的变异显著地大，则认为样本 组间有本质性的差异，否则，认为样本 组间无本质差异。
精选PPT课件
6
在方差分析中，观测值之间的差异情 况用离差平方和表示，符号为SS。方差分析首先 是把总体平方和分解为组间平方和和组内平方和， 即：
《方差分析讲义》课件
双因素方差分析
介绍双因素方差分析，该方 法用于比较两个因素对一个 变量的影响，以及它们之间 的交互作用。
单因素方差分析
1 单因素方差分析的基本原理
解释单因素方差分析的基本原理，包括组内变异和组间变异的比较。
2 单因素方差分析中的F检验
介绍单因素方差分析中的F检验，用于判断组间差异是否显著。
3 单因素方差分析的应用举例
提供一些实际应用中的单因素方差分析案例，展示其在不同领域的应用。
双因素方差分析
双因素方差分析的基本原理
解释双因素方差分析的基本原理， 包括主效应和交互作用效应。
双因素方差分析中的交互 作用效应
讨论双因素方差分析中的交互作 用效应，即两个因素共同影响一 个变量。
双因素方差分析的应用举例
给出一些实际应用中的双因素方 差分析案例，展示其在研究中的 重要性。
方差分析在实际应用中的研究方向
展望方差分析在实际应用中的研究方向，如新的数据分析方法和技术。
方差分析的未来发展趋势
讨论方差分析的未来发展趋势，如与其他统计方法的整合和自动化分析工具的应用。
《方差分析讲义》PPT课 件
方差分析讲义是一份用于PPT演示的课件，主要介绍了方差分析的基本概念、 原理、应用以及局限性。
什么是方差分析
方差分析的基本概念
解释方差分析是一种统计方 法，用于比较两个或多个样 本间的差异。
单因素方差分析
介绍单因素方差分析，该方 法用于比较一个因素（组别） 对一个变量的影响。
方差分析的局限性
1
方差分析的局限性与注意事项
2
介绍方差分析的局限性和注意事项，帮
助用户正确解读结果。
3
方差分析的前提条件
方差分析()专题知识讲座
FB
MSB MSE
~
F (n
1, rnm
rn)
FAB
MSAB MSE
~
F[(r
1)(n
1), rnm
rn]
29
SST ( X ijl X )2
SSA nm ( X i X )2
SSB rm ( X . j. X )2
SSAB m ( X ij. X i.. X . j. X )2
SSE ( X ijl X ij. ) 2
26
离差平方和SST、SSA、SSB、SSAB和SSE 旳自由度分别是rnm-1、r-1、n-1、(r1)(n-1)和rn(m-1)。
SSE ( X ij X i. X . j X )2
20
SSA表达旳是原因A旳组间方差总和，SSB是 原因B旳组间方差总和，都是各原因在不同水 平下各自均值差别引起旳；SSE仍是组内方 差部分，由随机误差产生。各个方差旳自由 度是：SST旳自由度为nr-1，SSA旳自由度 为r-1，SSB旳自由度为n-1，SSE旳自由度 为nr-r-n-1=（r-1）(n-1)。
10
检验因子影响是否明显旳统计量是一种F统计 量：
组间均方差 F 组内均方差
F统计量越大，越阐明组间方差是主要方差起 源，因子影响越明显；F越小，越阐明随机方 差是主要旳方差起源，因子旳影响越不明显。
11
第二节 单原因方差分析
一、单原因条件下离差平方和旳分解 数据构造如下：
12
总离差平方和 SST=SSE+SSA
7
三、方差分析旳原理 （一）方差旳分解。样本数据波动就有二个
起源：一种是随机波动，一种是因子影响。 样本数据旳波动，可经过离差平方和来反应， 这个离差平方和可分解为组间方差与组内方 差两部分。组间方差反应出不同旳因子对样 本波动旳影响；组内方差则是不考虑组间方 差旳纯随机影响。
地学数理方法方差分析课件
➢ 计算各因素离差平方和S S ，各平方和的自由度 f ；
➢ 计算各因素均方差S ；
➢ 构造并计算统计量 F ；
➢ 查检验临界值F 。 ➢ 判断某因素作用是否显著，据此拒绝或接受原假设。
地学数理方法方差分析课件
§4.1 基本概念与原理
❖ 方差分析原理与程序
❖ 方差分析表
方差来源
偏差平方和
因素 A（组间） SSA
§3 方差分析
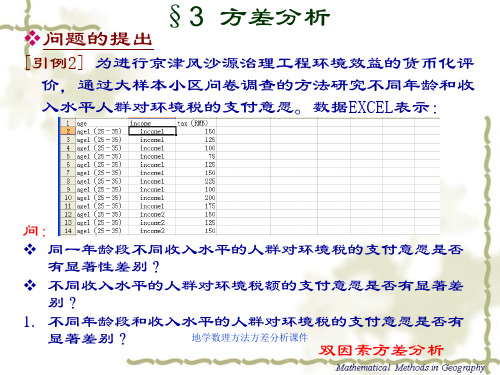
❖问题的提出
[引例2] 为进行京津风沙源治理工程环境效益的货币化评 价，通过大样本小区问卷调查的方法研究不同年龄和收 入水平人群对环境税的支付意愿。数据EXCEL表示：
问：
❖ 同一年龄段不同收入水平的人群对环境税的支付意愿是否 有显著性差别？
❖ 不同收入水平的人群对环境税额的支付意愿是否有显著差
设有a个独立子样
Y1 : y 11, ,y 1r
基本概念与原理
Ya : y a1, ,y ar
分别来自具有相同方差的独立总体，即
N1 (1,2) Na(a,2) 如果，检验原假设H0:1= 2 a成立，
那么，这 个正态总体方差和均值都相等。
因此，从这 个完全相同的正态总体中各抽取一个
样本为r 的子样，相当于从一个正态总体N (, 2中) 分别
误差 e（组内） SSe
自由度
fA
fe
均方差
S A = SSA/ fA Se = SSe / fe
F
F= S A / Se
临界值 显著性
Fα
总和
SST
fT
ST =SST / fT
Sum of squares
df
Mean Square
F
Sig.
心理统计学课件第九章 方差分析
ij
Xj
X
2 k n j 1 i 1
Xt
2
SST SSW SSB
总平方和，表示实验中产生的总变异，即 把所有被试的数值作为一个整体考虑，是 用所有被试的因变量的值计算得到的 组间平方和，表示由于不同的实验处理而 造成的变异，可以用两个平均数之间的离 差表示。 组内平方和，表示有实验误差或个体差异 造成的变异。
n2Fra bibliotekX n
2
组内平方
和
SSW X 2
2 X
n
总平方和
SST X
2
X
n
2
6、列方差分析表
变异来源 平方和 自由度 方差 F 值 概率
组间变异
组内变异
SSB
SSw
dfB
dfw
MSB
MSw
F
MS B MSW
P
总变异
SST
dfT
SSB
2 X
第九章 方差分析
第一节 方差分析的基本原理及步骤 第二节 完全随机设计的方差分析
方差分析
方差分析又称为变异分析（analysis of variance，ANOVA），是由斯内德克 （George Waddel Snedecor）提出的一种 方法。 探讨一个因变量和一个或多个自变量之间 关系的一种检验方法。 主要功能：分析实验数据中不同来源的变 异对总变异的贡献大小，从而确定实验中 的自变量是否对因变量有重要影响。
第二节 完全随机设计的方差分析
各实验处理组样本容量相同 各实验处理组样本容量不同 利用样本统计量进行方差分析
一、各实验处理组样本容量相同
第一节方差分析课件
地块
品种
B1
B2
B3
B4
B5
A1
32.3
34.0
34.7
36.0
35.5
A2
33.2
33.6
36.8
34.3
36.1
A3
30.8
34.4
32.3
35.8
32.8
A4
29.5
26.2
28.1
28.5
29.4
方差来源
平方和
自由度
均方
F值
显著性
品种(A)
SA=134.65
3
44.88
20.49
**
地块(B)
下页
结束
kt
总离差平方和: ST
(xij x)2
i1 j 1
它反映了观测数据 总的变异程度
组间平方和:
k
SA t(xi. x)2 i 1
kt
组内(误差)平方和: Se
(xij xi. )2
i1 j1
反映因子A的不同水 平效应间的差异。
反映了随机误差εij 对响应值影响的总和
这是由于 yi• ai i• y
首页
上页
返回
下页
结束
来源 A B e
总和
平方和
S A
r i 1
xi2 s
2
nx
SB
s j 1
x2j r
2
nx
Se ST SA SB
r
ST
s
xi2j
2
nx
i1 j1
自由度
方差分析表 均方和
r-1 s-1 (r-1)(s-1)
SA r 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
S A与SE独立,
H
为真时
0
,
S A / 2～ 2 (s 1)
下面检验假设 H0 : 1 2 s , H1 : 1, 2, , s不全相等.
构造F SA (s 1) SE (n s)
H 0不真时, 分子取值有偏大的趋势.
拒绝域形如 F SA (s 1) k SE (n s)
H0为真时, SA / 2～ 2 (s 1), SE 2 ～ 2 (n s)
1)(s
1))
取显著性水平为 ,得假设H02的拒绝域为
FB
SB SE
F (s
1,(r
1)(s 1))
双因素无重复试验方差分析表spss：
二、双因素等重复试验的方差分析（理
论）
因素A : A1 , A2 , , Ar . 因素B : B1 , B2 , , Bs .
S A与SE独立,
H
为真时
0
,
S A / 2～ 2 (s 1)
下面检验假设 H0 : 1 2 s , H1 : 1, 2, , s不全相等.
构造F SA (s 1) SE (n s)
H 0不真时, 分子取值有偏大的趋势.
拒绝域形如 F SA (s 1) k SE (n s)
H0为真时, SA / 2～ 2 (s 1), SE 2 ～ 2 (n s)
j1 i1
1 nj
X•j
nj
X ij
i 1
— 水平Aj下的样本平均值
s nj
ST
( X ij X )2
j1 i1
s nj
s nj
ST
( X ij X• j )2
(X•j X )2
j1 i1
j1 i1
SE SA
s nj
SE
( X ij X• j )2 —误差平方和（随机误差）
SA
SA s1
SE
SE ns
F比 F SA SE
解 s 3, n1 n2 n3 5, n 15, ST 0.00124533, S A 0.00105333, SE 0.000192.
方差分析表 方差来源 平方和 自由度 均 方 F 比 因 素A 0.00105333 2 0.00052667 32.92
H 0为真时,
SA SE
(s 1) (n s)
SA 2
(s 1)
拒绝域为
SE 2 ～F (s 1, n s)
(n s)
F
SA SE
(s 1) (n s)
F (s 1,n
s)
数学模型
设因素A有s个水平A1 , A2 , , As ,在水平Aj ( j
1,2, , s)下,进行nj (nj 2)次独立试验,得到如下表
j1 i1
s nj
s
SA
(X•j X )2 nj (X•j X随机误差、系统误差）
• 总变异＝组间变异＋组内变异
其中：组间变异由各因素所引起； 组内变异由个体差异或者说由误差 引起的。
s
可以证明：SE 2 ～2 (n s), 其中n n j . j 1
i1 j1
ST S E S A SB S AB
误差 平方和 因素 A 的 因素 B 的 因素A,B的交
效应平方和 效应平方和 互效应平方和
要解决的问题：检验假设
H 01 H11
:1 : 1,
2
2 ,
r 0, ,r 不全为零.
H 02 H12
: :
1 1,
2
2 ,
,s
s 0,
误 差 0.000192 12 0.000016
总 和 0.00124533 14
F 32.92 F0.05(2,12) 3.89.在水平0.05下拒绝H0 . 各机器生产的薄板厚度有显著差异.
单因素方差分析表spss：
方 差 相 等 检 验
可以检验不同因素对观察变量产生了显著影响。
判断哪个组和其他组 有显著的均值差别， 方法是两两作比。
s nj
s
SA
(X•j X )2 nj (X•j X )2
j1 i1
j 1
—效应平方和（随机误差、系统误差）
ST SE SA
• 总变异＝组内变异＋组间变异
其中：组内变异由个体差异或者
说由误差引起的;组间变异由各因素 所引起；
H0 : 1 2 3 , H1 : 1 , 2 , 3不全相等.
问 题——检验同方差的多个正态总体均 值是否相等.
解决方法——方差分析法,一种统计方法.
X
1 n
s j 1
nj i 1
X ij
1 nj
X • j n j i1 X ij
s nj
ST
( X ij X )2
j1 i1
s nj
SE
( X ij X• j )2
—误差平方和（随机误差）
j1 i1
方差分析
• 单因子方差分析 • 双因子方差分析
(等重复和无重复)或（有交互和无交互）
引入 t 统计量作为检验统计量:
t X Y ,
Sw
11 n1 n2
其中
Sw2
( n1
1)S12 (n2 n1 n2 2
1)S22
.
其拒绝域的形式为
xy
t
t / 2(n1 n2 2).
sw
11 n1 n2
F
(r
1, rs(t
1))
类似地
,
取显著性水平为
,
得假设H
的拒绝域为
02
FB
SB (s 1) SE (rs(t 1))
F (s
1,rs(t
1))
取显著性水平为
,
得假设H
的拒绝域为
03
FAB
S AB ((r 1)(s 1)) SE (rs(t 1))
F ((r 1)(s 1), rs(t 1))
不同组的方差不同时选择.
方差齐性的检验.
认为三个组总体方差相等。 至少一个组和其他组有显著差别.
两两作比.
二、双因素等重复试验的方差分析
表9.3 火箭的射程
推进器(B)
B1
B2
B3
A1
58.2 52.6
56.2 41.2
65.3 60.8
燃料(A) A2 A3
49.1 42.8 60.1 58.3
X i••
st
X ijk
j1 k1
X• j•
1 rt
rt
X ijk
i1 k1
432
SE
( X ijk X )2
i1 j1 k 1
4
SA st ( X i•• X )2 i 1
3
SB rt ( X • j• X )2
j 1
43
SAB t
( X ij• X i•• X • j• X )2
x 0.242, y 0.256,t 5.26,t0.025(8) 2.3060
例2 不同的教学方法对考试平均分的影响是否显著？
试验指标:考试平均分
因素:教学方法
水平:不同的三种方法是因素的三个不同的水平
H0 : 1 2 3 , H1 : 1 , 2 , 3不全相等.
例3 一火箭用四种燃料,三种推进器作射程试验. 每种燃料与每种推进器的组合各发射火箭两次,得 射程如下（以海里计）.问不同燃料、不同推进器对射程
的影响是否显著？交互作用是否显著？ 表9.3 火箭的射程
推进器(B)
B1
B2
B3
A1
58.2 52.6
56.2 41.2
65.3 60.8
燃料(A) A2 A3
49.1 42.8 60.1 58.3
54.1 50.5 70.9 73.2
51.6 48.4 39.2 40.7
A4
75.8 71.5
58.2 51.0
(2)不同水平Aj下的样本之间相互独立.
X ij～N ( j , 2 ), X ij j～N (0, 2 ).
记X ij j ij ,表示随机误差,那么X ij可写成
X ij j ij ,
ij～N (0, 2 ),各 ij 独立,
i
1,2,
,nj
,
j
1,2,
, s,
j与 2均未知
例1
x1
问题分析在每一个水平下进行独立试验,结果是一 个随机变量.将数据看成是来自三个总体的样本值.
设总体均值分别为1 , 2 , 3 . 检验假设 H0 : 1 2 3 ,
H1 : 1 , 2 , 3不全相等.
检验假设 H0 : 1 2 3 , H1 : 1 , 2 , 3不全相等.
进一步假设各总体均为正态变量,且各总体的 方差相等,但参数均未知.
表 9.8
因素B 因素A
B1
B2
Bs
A1
X111, X112 , X121, X122 ,
, X 11t
, X 12t
X 1s1 , X 1s2 , , X 1st
A2
X 211, X 212 , X 221, X 222 ,
, X 21t
, X 22t
X 2s1 , X 2s2 , , X 2st
方差 平方 来源 和 因素A S A
因素B SB
误 差 SE
自由度
均方
F比
r 1
SA
SA r 1
FA
SA SE
s1
SB
SB s1
FB
SB SE
(r 1) (s 1)
SE
SE (r 1)(s 1)
总 和 ST rs 1
H
为真时
0
,
S A / 2～ 2 (s 1)
下面检验假设 H0 : 1 2 s , H1 : 1, 2, , s不全相等.
构造F SA (s 1) SE (n s)
H 0不真时, 分子取值有偏大的趋势.
拒绝域形如 F SA (s 1) k SE (n s)
H0为真时, SA / 2～ 2 (s 1), SE 2 ～ 2 (n s)
1)(s
1))
取显著性水平为 ,得假设H02的拒绝域为
FB
SB SE
F (s
1,(r
1)(s 1))
双因素无重复试验方差分析表spss：
二、双因素等重复试验的方差分析（理
论）
因素A : A1 , A2 , , Ar . 因素B : B1 , B2 , , Bs .
S A与SE独立,
H
为真时
0
,
S A / 2～ 2 (s 1)
下面检验假设 H0 : 1 2 s , H1 : 1, 2, , s不全相等.
构造F SA (s 1) SE (n s)
H 0不真时, 分子取值有偏大的趋势.
拒绝域形如 F SA (s 1) k SE (n s)
H0为真时, SA / 2～ 2 (s 1), SE 2 ～ 2 (n s)
j1 i1
1 nj
X•j
nj
X ij
i 1
— 水平Aj下的样本平均值
s nj
ST
( X ij X )2
j1 i1
s nj
s nj
ST
( X ij X• j )2
(X•j X )2
j1 i1
j1 i1
SE SA
s nj
SE
( X ij X• j )2 —误差平方和（随机误差）
SA
SA s1
SE
SE ns
F比 F SA SE
解 s 3, n1 n2 n3 5, n 15, ST 0.00124533, S A 0.00105333, SE 0.000192.
方差分析表 方差来源 平方和 自由度 均 方 F 比 因 素A 0.00105333 2 0.00052667 32.92
H 0为真时,
SA SE
(s 1) (n s)
SA 2
(s 1)
拒绝域为
SE 2 ～F (s 1, n s)
(n s)
F
SA SE
(s 1) (n s)
F (s 1,n
s)
数学模型
设因素A有s个水平A1 , A2 , , As ,在水平Aj ( j
1,2, , s)下,进行nj (nj 2)次独立试验,得到如下表
j1 i1
s nj
s
SA
(X•j X )2 nj (X•j X随机误差、系统误差）
• 总变异＝组间变异＋组内变异
其中：组间变异由各因素所引起； 组内变异由个体差异或者说由误差 引起的。
s
可以证明：SE 2 ～2 (n s), 其中n n j . j 1
i1 j1
ST S E S A SB S AB
误差 平方和 因素 A 的 因素 B 的 因素A,B的交
效应平方和 效应平方和 互效应平方和
要解决的问题：检验假设
H 01 H11
:1 : 1,
2
2 ,
r 0, ,r 不全为零.
H 02 H12
: :
1 1,
2
2 ,
,s
s 0,
误 差 0.000192 12 0.000016
总 和 0.00124533 14
F 32.92 F0.05(2,12) 3.89.在水平0.05下拒绝H0 . 各机器生产的薄板厚度有显著差异.
单因素方差分析表spss：
方 差 相 等 检 验
可以检验不同因素对观察变量产生了显著影响。
判断哪个组和其他组 有显著的均值差别， 方法是两两作比。
s nj
s
SA
(X•j X )2 nj (X•j X )2
j1 i1
j 1
—效应平方和（随机误差、系统误差）
ST SE SA
• 总变异＝组内变异＋组间变异
其中：组内变异由个体差异或者
说由误差引起的;组间变异由各因素 所引起；
H0 : 1 2 3 , H1 : 1 , 2 , 3不全相等.
问 题——检验同方差的多个正态总体均 值是否相等.
解决方法——方差分析法,一种统计方法.
X
1 n
s j 1
nj i 1
X ij
1 nj
X • j n j i1 X ij
s nj
ST
( X ij X )2
j1 i1
s nj
SE
( X ij X• j )2
—误差平方和（随机误差）
j1 i1
方差分析
• 单因子方差分析 • 双因子方差分析
(等重复和无重复)或（有交互和无交互）
引入 t 统计量作为检验统计量:
t X Y ,
Sw
11 n1 n2
其中
Sw2
( n1
1)S12 (n2 n1 n2 2
1)S22
.
其拒绝域的形式为
xy
t
t / 2(n1 n2 2).
sw
11 n1 n2
F
(r
1, rs(t
1))
类似地
,
取显著性水平为
,
得假设H
的拒绝域为
02
FB
SB (s 1) SE (rs(t 1))
F (s
1,rs(t
1))
取显著性水平为
,
得假设H
的拒绝域为
03
FAB
S AB ((r 1)(s 1)) SE (rs(t 1))
F ((r 1)(s 1), rs(t 1))
不同组的方差不同时选择.
方差齐性的检验.
认为三个组总体方差相等。 至少一个组和其他组有显著差别.
两两作比.
二、双因素等重复试验的方差分析
表9.3 火箭的射程
推进器(B)
B1
B2
B3
A1
58.2 52.6
56.2 41.2
65.3 60.8
燃料(A) A2 A3
49.1 42.8 60.1 58.3
X i••
st
X ijk
j1 k1
X• j•
1 rt
rt
X ijk
i1 k1
432
SE
( X ijk X )2
i1 j1 k 1
4
SA st ( X i•• X )2 i 1
3
SB rt ( X • j• X )2
j 1
43
SAB t
( X ij• X i•• X • j• X )2
x 0.242, y 0.256,t 5.26,t0.025(8) 2.3060
例2 不同的教学方法对考试平均分的影响是否显著？
试验指标:考试平均分
因素:教学方法
水平:不同的三种方法是因素的三个不同的水平
H0 : 1 2 3 , H1 : 1 , 2 , 3不全相等.
例3 一火箭用四种燃料,三种推进器作射程试验. 每种燃料与每种推进器的组合各发射火箭两次,得 射程如下（以海里计）.问不同燃料、不同推进器对射程
的影响是否显著？交互作用是否显著？ 表9.3 火箭的射程
推进器(B)
B1
B2
B3
A1
58.2 52.6
56.2 41.2
65.3 60.8
燃料(A) A2 A3
49.1 42.8 60.1 58.3
54.1 50.5 70.9 73.2
51.6 48.4 39.2 40.7
A4
75.8 71.5
58.2 51.0
(2)不同水平Aj下的样本之间相互独立.
X ij～N ( j , 2 ), X ij j～N (0, 2 ).
记X ij j ij ,表示随机误差,那么X ij可写成
X ij j ij ,
ij～N (0, 2 ),各 ij 独立,
i
1,2,
,nj
,
j
1,2,
, s,
j与 2均未知
例1
x1
问题分析在每一个水平下进行独立试验,结果是一 个随机变量.将数据看成是来自三个总体的样本值.
设总体均值分别为1 , 2 , 3 . 检验假设 H0 : 1 2 3 ,
H1 : 1 , 2 , 3不全相等.
检验假设 H0 : 1 2 3 , H1 : 1 , 2 , 3不全相等.
进一步假设各总体均为正态变量,且各总体的 方差相等,但参数均未知.
表 9.8
因素B 因素A
B1
B2
Bs
A1
X111, X112 , X121, X122 ,
, X 11t
, X 12t
X 1s1 , X 1s2 , , X 1st
A2
X 211, X 212 , X 221, X 222 ,
, X 21t
, X 22t
X 2s1 , X 2s2 , , X 2st
方差 平方 来源 和 因素A S A
因素B SB
误 差 SE
自由度
均方
F比
r 1
SA
SA r 1
FA
SA SE
s1
SB
SB s1
FB
SB SE
(r 1) (s 1)
SE
SE (r 1)(s 1)
总 和 ST rs 1