计量经济学4.
计量经济学简答题四

计量经济学简答题四第一章绪论(一)基本知识类题型1-1.什么是计量经济学?1—2.简述当代计量经济学发展的动向.1-3.计量经济学方法与一般经济数学方法有什么区别?1-4.为什么说计量经济学是经济理论、数学和经济统计学的结合?试述三者之关系。
1—5.为什么说计量经济学是一门经济学科?它在经济学科体系中的作用和地位是什么?1-6.计量经济学的研究的对象和内容是什么?计量经济学模型研究的经济关系有哪两个基本特征?1-7.试结合一个具体经济问题说明建立与应用计量经济学模型的主要步骤。
1-8.建立计量经济学模型的基本思想是什么?1-9.计量经济学模型主要有哪些应用领域?各自的原理是什么?1—10.试分别举出五个时间序列数据和横截面数据并说明时间序列数据和横截面数据有和异同?1-11.试解释单方程模型和联立方程模型的概念并举例说明两者之间的联系与区别。
1-12.模型的检验包括几个方面?其具体含义是什么?1—13.常用的样本数据有哪些?1-14.计量经济模型中为何要包括随机误差项?简述随机误差项形成的原因。
1—15.估计量和估计值有何区别?哪些类型的关系式不存在估计问题?1—16.经济数据在计量经济分析中的作用是什么?1—20.模型参数对模型有什么意义?习题参考第一章绪论1-1.答:计量经济学是经济学的一个分支学科是以揭示经济活动中客观存在的数量关系为内容的分支学科是由经济学、统计学和数学三者结合而成的交叉学科。
1-2.答:计量经济学自20年代末、30年代初形成以来无论在技术方法还是在应用方面发展都十分迅速尤其是经过50年代的发展阶段和60年代的扩张阶段使其在经济学科占据重要的地位主要表现在:①在西方大多数大学和学院中计量经济学的讲授已成为经济学课程表中有权威的一部分;②从1969~2003年诺贝尔经济学奖的XX位获奖者中有XX位是与研究和应用计量经济学有关;著名经济学家、诺贝尔经济学奖获得者萨缪尔森甚至说:“第二次世界大战后的经济学是计量经济学的时代”.③计量经济学方法与其他经济数学方法结合应用得到发展;④计量经济学方法从主要用于经济预测转向经济理论假设和政策假设的检验;⑤计量经济学模型的应用从传统的领域转向新的领域如货币、工资、就业、福利、国际贸易等;⑥计量经济学模型的规模不再是水平高低的衡量标准人们更喜欢建立一些简单的模型从总量上、趋势上说明经济现象.1—3.答:计量经济学方法揭示经济活动中各个因素之间的定量关系用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各个因素之间的理论关系用确定性的数学方程加以描述。
计量经济学课程第4章(多元回归分析)

§4.1 多元线性回归模型的两个例子
一、例题1:CD生产函数
Qt AKt 1 Lt 2 et
这是一个非线性函数,但取对数可以转变为一个 对参数线性的模型
ln Qt 0 1 ln Kt 2 ln Lt t
t ~ iid(0, 2 )
注意:“线性”的含义是指方程对参数而言是线 性的
R 2 1 RSS /(N K 1) TSS /(N 1)
调整思想: 对 R2 进行自由度调整。
Page 20
基本统计量TSS、RSS、ESS的自由度:
1.
TSS的自由度为N-1。基于样本容量N,TSS
N i1
(Yi
Y
)2
因为线性约束 Y 1 N
Y N
i1 i
而损失一个自由度。
分布的多个独立统计量平方加总,所得到的新统计量就服从
2 分布。
《计量经济学》,高教出版社2011年6月,王少平、杨继生、欧阳志刚等编著
Page 23
双侧检验
概 率 密 度
概率1-
0
2 1 / 2
2 /2
图4.3.1
2
(N-K-1)的双侧临界值
双侧检验:统计值如果落入两尾中的任何一个则拒绝原假设
《计量经济学》,高教出版社2011年6月,王少平、杨继生、欧阳志刚等编著
Page 24
单侧检验
概 率 密 度
概率 概率
0
2 1
2
图4.3.2 (2 N-K-1)的单侧临界值
H0:
2
2,
0
HA :
2
2 0
计量经济学第四章

Ⅰ、联立方程模型的提出
联立方程计量经济学模型是相对于单方程 计量经济学模型而言的,它以经济系统为 研究对象;以揭示经济系统中各部分、各 因素间的数量关系和系统的数量特征为目 标;用于经济系统的预测、分析和评价。 使计量经济学模型的重要组成部分。
3
计量经济学
一、联立方程计量经济学模型问题
单方程计量经济学模型,只能描述经济变 量间的单向因果关系。但经济现象是错综 复杂的,许多经济变量间存在着交错的双 向或多项因果关系,因此需要建立多个单 方程组成的多方程模型,即联立方程模型。 其中每个方程都描述变量间的一个因果关 系。
0 Ct - b1Yt It - b0 - b2Yt-1 - 0 Gt u2t
- Ct Yt - It - 0- 0 Yt-1 - Gt 0
16
计量经济学
C t - a 1 Y t 0 I t - a 0 - 0 Y t -1 - 0 G t u 1t 0 C t - b 1 Y t I t - b 0 - b 2 Y t -1 - 0 G t u 2t - C t Y t - I t - 0 - 0 Y t-1 - G t 0 矩阵形式: BY X N
Ⅲ、联立方程计量经济学模型的识别
联立方程模型的识别性,主要指联立方程模型 中包含的各种影响和关系,是否可以明确辨别 或惟一确定。联立方程模型的识别性,实际上 与结构参数和简化参数之间存在明确的一一对 应关系有关,因此对联立方程模型的分析有重 要影响。
27
计量经济学
同上
联立方程模型的识别问题的本质:由于联立 方程模型中有许多个方程,内生变量的水平 是由多个方程的共同作用所决定的,因此能 否根据观测到的变量数据推测出生成它们的 各方面经济关系,很值得疑问。
计量经济学(庞浩主编)第四章练习题参考解答
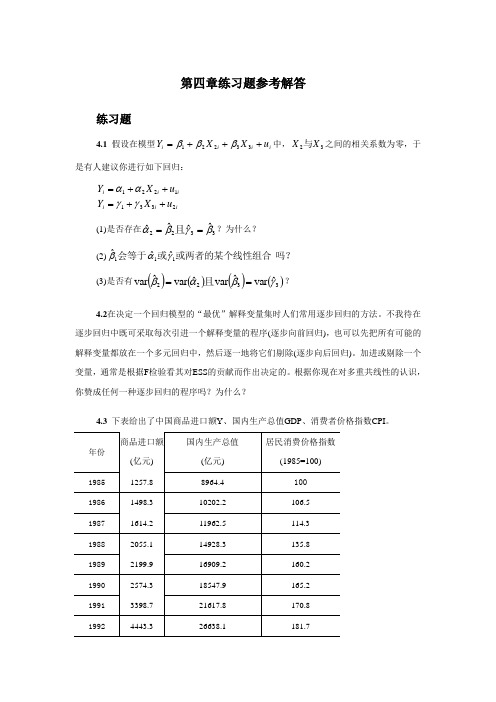
第四章练习题参考解答练习题4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,于是有人建议你进行如下回归:ii i i i i u X Y u X Y 23311221++=++=γγαα(1)是否存在3322ˆˆˆˆβγβα==且?为什么? (2)吗?或两者的某个线性组合或会等于111ˆˆˆγαβ (3)是否有()()()()3322ˆvar ˆvar ˆvar ˆvar γβαβ==且? 4.2在决定一个回归模型的“最优”解释变量集时人们常用逐步回归的方法。
不我待在逐步回归中既可采取每次引进一个解释变量的程序(逐步向前回归),也可以先把所有可能的解释变量都放在一个多元回归中,然后逐一地将它们剔除(逐步向后回归)。
加进或剔除一个变量,通常是根据F 检验看其对ESS 的贡献而作出决定的。
根据你现在对多重共线性的认识,你赞成任何一种逐步回归的程序吗?为什么?4.3 下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
资料来源:《中国统计年鉴》,中国统计出版社2000年、20XX 年。
请考虑下列模型:i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗? (3)进行以下回归:it t i t t i t t v CPI C C GDP v CPI B B Y v GDP A A Y 321221121ln ln ln ln ln ln ++=+=+=++根据这些回归你能对数据中多重共线性的性质说些什么?(4)假设数据有多重共线性,但32ˆˆββ和在5%水平上个别地显著,并且总的F 检验也是显著的。
对这样的情形,我们是否应考虑共线性的问题?4.4 自己找一个经济问题来建立多元线性回归模型,怎样选择变量和构造解释变量数据矩阵X 才可能避免多重共线性的出现?4.5 克莱因与戈德伯格曾用1921-1950年(1942-1944年战争期间略去)美国国内消费Y 和工资收入X1、非工资—非农业收入X2、农业收入X3的时间序列资料,利用OLSE 估计得出了下列回归方程:37.107 95.0 (1.09) (0.66) (0.17) (8.92) 3121.02452.01059.1133.8ˆ2==+++=F R X X X Y (括号中的数据为相应参数估计量的标准误)。
(完整word版)计量经济学第四章习题详解

第四章习题4.1 没有进行t检验,并且调整的可决系数也没有写出来,也就是没有考虑自由度的影响,会使结果存在误差.4.3200224430.3120332。
7 330.6200334195。
6135822.8 334。
6200446435.8159878.3 l347.7200554273.7183084.8 353.9200663376.9211923。
5 359。
2200773284。
6249529。
9 376.5200879526.5314045.4 398.7200968618。
4340902。
8 395。
9201094699.3401512.8 408。
92011113161.4472881.6 431.0一研究的目的和要求我们知道,商品进口额与很多因素有关,了解其变化对进出口产品有很大帮助。
为了探究和预测商品进口额的变化,需要定量地分析影响商品进口额变化的主要因素。
二、模型的设定及其估计经分析,商品进口额可能与国内生产总值、居民消费价格指数有关。
为此,考虑国内生产总值GDP、居民消费价格指数CPI为主要因素。
各影响变量与商品进口额呈正相关。
为此,设定如下形式的计量经济模型:=+ln+lnCP式中,亿元);lnGDP为国内生产总值(亿元);lnCPI为居民消费价格指数(以1985年为100)。
各解释变量前的回归系数预期都大于零。
为估计模型,根据上表的数据,利用EViews软件,生成Y、lnGDP、lnCPI等数据,采用OLS方法估计模型参数,得到的回归结果如下图所示:模型方程为:lnY=-3。
111486+1。
338533lnGDP-0.421791lnCPI(0。
463010)(0。
088610)(0。
233295)t= (—6。
720126) (15。
10582)(—1。
807975)=0.988051 =0.987055 F=992。
2582该模型=0.988051,=0。
987055,可决系数很高,F检验值为992.2582,明显显著。
计量经济学-第4章

问题本质
OLS的估计思想:
(1)寻找参数估计量 ˆ0,ˆ1,,ˆK,使得样本回归
函数与所有样本观测点的偏离最小,即残差平方 和最小。
为什么不选择离差之和最小化或者离差绝对 值之和最小化呢?
因为离差之和会使正负误差抵消,而离差绝对 值不便于数学上做优化处理,所以选择了离差平 方和最小化作为优化目标,这也就是为什么这种 估计方法被称为最小二乘法的原因。
《计量经济学》,高教出版社2019年6月,王少平、杨继生、欧阳志刚1等3 编著
2. 回归系数的OLS估计:以二元回归模型为例
Y i01 X 1 i2 X 2 ii
基于残差平方和的最小化,得到正规方程组:
ˆ N i1 i
0
X N i1 1i
ˆi
0
X N i1 2i
以原假设的参数值作为检验统计量中的参数真值。如果原 假设为“真”,则检验统计量就服从相应的理论分布。反 之,检验统计量就不服从该分布。
基于所选择的显著性水平,将检验统计量的理论分布区间 划分为小概率的“拒绝域”和大概率的“不拒绝域”。
根据参数的估计值计算检验统计量的值。如果检验统计值 出现在拒绝域,根据“小概率事件原理”,原假设很可能 是“假”的,则拒绝原假设。反之,就没有充分的理由拒 绝原假设。
二、 多元线性回归模型的一般形式
一般形式可以表述为如下的形式:
Y i0 1 X 1 i K X K ii
i1,2,,N
均值方程
E ( Y iX 1 i, ,X K ) i 0 1 X 1 i K X Ki
线性回归方程与均值方程的联系
Y i E (Y i X 1i, ,XK)ii
《计量经济学》,高教出版社2019年6月,王少平、杨继生、欧阳志刚等5 编著
计量经济学(第四章多重共线性)

06
总结与展望
研究结论总结
多重共线性现象普遍存在于经济数据中,对计量 经济学模型的估计和解释产生了重要影响。
通过使用多种诊断方法,如相关系数矩阵、方差膨 胀因子(VIF)和条件指数(CI),可以有效地识别 多重共线性问题。
在存在多重共线性的情况下,普通最小二乘法 (OLS)估计量虽然仍然是无偏的,但其方差可能 变得很大,导致估计结果不稳定。
主成分分析法的优点
可以消除多重共线性的影响,同 时降低自变量的维度,简化模型。
岭回归法
岭回归法的基本思想
通过在损失函数中加入L2正则化项(即所有自变量的平方和),使得回归系数的估计更加稳定, 从而消除多重共线性的影响。
岭回归法的步骤
首先确定正则化参数λ的值,然后求解包含L2正则化项的损失函数最小化问题,得到岭回归系数的估 计值。
逐步回归法的优点
可以自动选择重要的自变量,同时消除多重共线性的影响。
主成分分析法
主成分分析法的基本思想
通过正交变换将原始自变量转换 为互不相关的主成分,然后选择 少数几个主成分进行回归分析。
主成分分析法的步骤
首先对原始自变量进行标准化处理, 然后计算相关系数矩阵并进行特征值 分解,得到主成分及其对应的特征向 量。最后,选择少数几个主成分作为 新的自变量进行回归分析。
岭回归法的优点
可以有效地处理多重共线性问题,同时避免过拟合现象的发生。此外,岭回归法还可以提供对所 有自变量的系数进行压缩估计的功能,使得模型更加简洁易懂。
05
实证研究与结果分
析
数据来源及预处理
数据来源
本研究采用的数据集来自于公开的统 计数据库,涵盖了多个经济指标和影 响因素的观测值。
数据预处理
计量经济学-第4章

TSS ESS RSS
4
4.1.1 总离差平方和旳分解
已知由一组样本观察值(Xi,Yi),i=1,2…,n 得到如下样本回归直线
Yˆi ˆ0 ˆ1 X i
yi Yi Y (Yi Yˆi ) (Yˆi Y ) ei yˆi
2
即
P(i
t s t s ) P(t 2
i i
si
t ) 1
2
2
i
i
i
2
i
1
21
于是得到:(1-)旳置信度下, i旳置信区间是
(i
t
2
si , i
t
2
si )
在上述收入-消费支出例中,假如给定 =0.01,
查表得:
因为
t (n 2) t0.005 (8) 3.355 2
▪判断成果合理是否,是基于“小概率事件不易 发生”旳原理
➢ 一次抽样中,尽然不能支持原假设,也就是举反 例否决。
13
4.2.2 变量旳明显性检验
ˆ1 ~ N (1,
2
) xi2
t ˆ1 1 ˆ1 1 ~ t(n 2)
ˆ 2 xi2
S ˆ1
14
检验环节:
(1)对总体参数提出假设
H0: 1=0,
18
4.3 参ห้องสมุดไป่ตู้旳置信区间检验法
假设检验能够经过一次抽样旳成果检验总体参数 假设值旳范围(如是否为零),但它并没有指出 在一次抽样中样本参数值究竟离总体参数旳真值 有多“近”。
要判断样本参数旳估计值在多大程度上能够“近 似”地替代总体参数旳真值,往往需要经过构造 一种以样本参数旳估计值为中心旳“区间”,来 考察它以多大旳可能性(概率)包括着真实旳参 数值。这种措施就是参数检验旳置信区间估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. Properties of the normal distribution
1) The normal distribution curve is symmetrical around its mean value μ. 2) The PDF of the distribution is the highest at its mean value but tails off at its extremities. 3) μ±σ 68% μ±2σ 95% μ±3σ 99.7% 4) A normal distribution is fully described by its two parameters: μandσ2
W W
W (a X bY )
2 2 2 W (a 2 X b 2 Y )
6) For a normal distriband kurtosis (K) is 3.
2. The Standard Normal Distribution
5) A linear combination (function) of two (or more) normally distributed random variables is itself normally distributed. X and Y are independent, X ~ N ( , 2 ) X X Y ~ N ( , 2) Y Y W=aX+bY, then W ~ N[ , 2 ]
· each X included in the sample must have the same PDF; · each X included in the sample is drawn independently of the others.
②Random sampling: a sample of iid random variables, a iid sample.
X ~ N (, 2 / n)
A standard normal variable:
Z
X
n
2. The Central Limit Theorem
The central limit theorem (CLT)—if X1,X2, ..., Xn is a random sample from any population (i.e., probability distribution) with mean μ and variance σ2 , the sample mean tends to be normally distributed with mean μ and varianceσ2/n as the sample size increases indefinitely (technically, infinitely.) The sample mean of a sample drawn from a normal population follows the normal distribution regardless of the sample size. Uniform distribution: the PDF of a continuous r.v. X on the interval from a to b.
Z
X X
Z~N(0,1)
X
Note: Any normally distributed r.v.with a given mean and variance can be converted to a standard normal variable, then you can know its probability from the standard normal table.
Chapter 4
SOME IMPORTANT PROBABILITY DISTRIBUTIONS
4.1 The Normal Distribution
X~N(μ,σ2)
The Normal distribution: a continuous r.v.whose value depends on a number of factors, yet no single factor dominates the others.
4.2 THE SAMPLING , OR PROBABILITY,
DISTRIBUTION OF THE SAMPLE MEAN
1. The sample mean and its distribution
X
(1)The sample mean The sample mean can be treated as an r.v., and it has its own PDF.
①Random sample and random variables: ——X1, X2,..., Xn are called a random sample of size n if all these Xs are drawn independently from the same probability distribution (i.e., each, Xi has the same PDF). The Xs are independently and identically distributed, random variables,i.e. i.i.d. random variables.
(2)Sampling, or prob., distribution of an estimator If X1, X2,..., Xn is a random sample from a normal distribution with meanμand varianceσ2, then the sample mean, also follows a normal distribution with the same meanμbut with a varianceσ2/n.
