山东省华侨中学2014-2015学年高二数学6月月考试题 理
【历史】山东省华侨中学2014-2015学年高一6月月考

山东省华侨中学2014—2015第二学期月考(6月)高一历史试题第I卷(选择题共60分)一、选择题(本大题共40小题,每小题1.5分,共60分, 在每小题列出的四个选项中,只有一项最符合题目要求。
)1、“二月二,龙抬头,大仓满,小仓流。
”这一天是民间传说“龙抬头”的日子,也称为“春龙节”,人们用许多美食祭拜龙王,希望它能够行云布雨,广洒甘霖。
从节日的起源看,形成这一风俗的主要因素是()A.宗教习俗B.祭祀祖先C.纪念庆典D.农业生产2、古代中国都城经历了从黄河时代到运河时代的变迁。
从下图中可以看出,唐朝以后都城( )①交通运输比较便捷②政治中心与经济重心保持一致③逐渐东移近海④明成祖迁都的北京缺点是“远饷近虏”A.①②③④ B.①③④ C.①②③ D.②③④3、历史老师要求同学们开展一堂题为“大唐长安商业”的探究课,以下是同学们收集的部分史料,其中不符合探究课主题的是 ( )A.“凡市,以日中击鼓三百响,而众以会”B.“皆云西市有贾胡及波斯邸,能辨识珠宝”C.“夜三更,东市失火,烧东市曹门以西十二行四千余家”D.“草市多樵客,渔家足水禽”4、乾隆《震泽县志》载:(农村)“无产者赴逐雇倩(请),抑心殚力,计岁而受值者曰长工,计时而受值者日短工……少隙则又计日受值为人佣作日忙工。
”这说明当时震泽县农村( )A.存在农业雇佣关系 B.自给自足的自然经济占统治地位C.商品经济发展迅速 D.农业经营方式发生根本变化5、“在中国的近代化进程中,1860年是个很重要的时间点”。
以下史实最能支持这一观点的是( )A.第二次鸦片战争的结束 B.《资政新篇》的颁布C.洋务运动的兴起 D.“西学东渐”的开始6、发昌机器厂最初只是由铁匠方举赞和孙英德合伙设立的一家打铁作坊,资本200元左右,工人有四五人,专门为外商船坞打造修配船用零件。
约到1869年,开始使用车床。
1876年制造第一艘小火轮,1877年兼造车床,到1890年已发展成为拥有车床10多台,可以容纳200人工作的工厂。
山东省华侨中学高二数学6月月考试题 文

高二月考数学(6月)第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设P 、Q 为两个非空实数集合,定义集合P +Q ={a +b |a ∈P ,b ∈Q },若P ={0,2,5},Q ={1,2,6},则P +Q 中元素的个数为( )A .9B .8C .7D .62.设函数21,1()2,1x x f x x x⎧+≤⎪=⎨>⎪⎩则f (f (4))=( )A.12B .2 C.32D.543.已知四个条件,①b >0>a ,②0>a >b ,③a >0>b ,④a >b >0,不能推出1a <1b成立的是( )A .①B .③C .③D .④4.已知直线l的参数方程为122t x y ⎧=+⎪⎪⎨⎪=+⎪⎩ (t 为参数),则其直角坐标方程为( )A.3x +y +2-3=0B.3x -y +2-3=0 C .x -3y +2-3=0 D .x +3y +2-3=05.设函数f (x )=g (x )+x 2,曲线y =g (x )在点(1,g (1))处的切线方程为y =2x +1,则曲线y =f (x )在点(1,f (1))处切线的斜率为( )A .-14B .2C .4D .-126..函数y =13x -2+lg(2x -1)的定义域是( ) A.⎣⎢⎡⎭⎪⎫23,+∞ B.⎝ ⎛⎭⎪⎫12,+∞ C.⎝ ⎛⎭⎪⎫23,+∞D.⎝ ⎛⎭⎪⎫12,237.在极坐标系中,点(2,π3)到圆ρ=2cos θ的圆心的距离为( )A .2B .4+π29C.1+π29D . 38.在同一平面直角坐标系中,经过伸缩变换⎩⎪⎨⎪⎧x ′=5x ,y ′=3y 后,曲线C 变为曲线'2'2()()1x y +=,则曲线C 的方程为( )A .25x 2+9y 2=1 B .9x 2+25y 2=1 C .25x +9y =1 D .x 225+y 29=19.若2-m 与|m |-3异号,则m 的取值范围是( ) A .m >3 B .-3<m <3 C .2<m <3D .-3<m <2或m >310.函数f (x )=x +eln x 的单调递增区间为( ) A .(0,+∞) B .(-∞,0) C .(-∞,0)和(0,+∞)D .R11.具有性质:f ⎝ ⎛⎭⎪⎫1x=-f (x )的函数,我们称为满足“倒负”变换的函数,下列函数:①y =x -1x ;②y =x +1x ;③y =⎩⎪⎨⎪⎧x ,0<x <1,0,x =1,-1x ,x >1.其中满足“倒负”变换的函数是( )A .①②B .①③C .②③D .①12.甲、乙两人同时从寝室到教室,甲一半路程步行,一半路程跑步,乙一半时间步行,一半时间跑步,如果两人步行速度、跑步速度均相同,则 ( )A .甲先到教室B .乙先到教室C .两人同时到教室D .谁先到教室不确定第Ⅱ卷(共90分)二、填空题:(本大题共4小题,每题5分,共20分,把最简答案写在答题卡的横线上)13. 已知f (x )=x (2 014+ln x ),f ′(x 0)=2 015,则x 0=________.14.已知函数f (x )=⎩⎪⎨⎪⎧2,x ≥0,-x +2,x <0,则满足不等式f (3-x 2)<f (2x )的x 的取值范围为________________.15.函数y =xx 2+x +1(x >0)的值域是________.16.极坐标系中,圆ρ2+2ρcos θ-3=0上的动点到直线ρcos θ+ρsin θ-7=0的距离的最大值是________.三.解答题(本大题共6小题,共70分. 解答应写出必要的文字说明、证明过程或演算步骤).17.(本题满分10分) 已知函数f (x )=b ·a x(其中a ,b 为常量,且a >0,a ≠1)的图像经过点A (1,6),B (3,24).(1)求f (x );(2)若不等式(1a )x +(1b)x-m ≥0在x ∈(-∞,1]时恒成立,求实数m 的取值范围.18.(本题满分12分) 在极坐标系中,圆C 的方程为ρ=22sin ⎝⎛⎭⎪⎫θ+π4,以极点为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系,直线l 的参数方程为⎩⎪⎨⎪⎧x =t ,y =1+2t(t为参数),判断直线l 和圆C 的位置关系.19.(本题满分12分) .已知函数f (x )=|x +1|,g (x )=2|x |+a . (1)当a =0时,解不等式f (x )≥g (x );(2)若存在x ∈R ,使得f (x )≥g (x )成立,求实数a 的取值范围.20.(本题满分12分) .已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x 轴的正半轴重合,且两个坐标系的单位长度相同,已知直线l 的参数方程为⎩⎪⎨⎪⎧x =-1+t cos α,y =1+t sin α(t 为参数),曲线C 的极坐标方程为ρ=4cos θ.(1)若直线l 的斜率为-1,求直线l 与曲线C 交点的直角坐标; (2)若直线l 与曲线C 的相交弦长为23,求直线l 的参数方程.21.(本题满分12分) 已知函数f (x )=|x -8|-|x -4|.(1)作出函数y =f (x )的图象; (2)解不等式|x -8|-|x -4|>2.22.已知函数f (x )=x 3+ax 2-a 2x +m (a >0).(1)若a =1时函数f (x )有三个互不相同的零点,求实数m 的取值范围; (2)若对任意的a ∈,不等式f (x )≤1在上恒成立,求实数m 的取值范围.数学答案(文1.解析:选B ∵P +Q ={a +b |a ∈P ,b ∈Q },P ={0,2,5},Q ={1,2,6},∴当a =0时,a +b 的值为1,2,6;当a =2时,a +b 的值为3,4,8;当a =5时,a +b 的值为6,7,11,∴P +Q ={1,2,3,4,6,7,8,11},∴P +Q 中有8个元素.2.解析:选D f (4)=12, 2115((4))()()1224f f f ==+=. 3.解析:选C 由a >b ,ab >0,可得1a <1b,即②、④能推出1a <1b.又因为正数大于负数,①能推出1a <1b ,③不能推出1a <1b.4.解析:选B ∵⎩⎪⎨⎪⎧x -1=t 2,y -2=32t , ∴y -2=3(x -1),即3x -y +2-3=0.5.解析:选C ∵曲线y =g (x )在点(1,g (1))处的切线方程为y =2x +1,∴g ′(1)=k =2.又f ′(x )=g ′(x )+2x ,∴f ′(1)=g ′(1)+2=4,故切线的斜率为4.6.解析:选C 由⎩⎪⎨⎪⎧3x -2>0,2x -1>0得x >23.7.解析:选D 由⎩⎪⎨⎪⎧x =ρcos θ=2cos π3=1,y =ρsin θ=2sin π3=3可知,点(2,π3)的直角坐标为(1,3),圆ρ=2cos θ的方程为x 2+y 2=2x ,即(x -1)2+y 2=1,则圆心到点(1,3)的距离为 3.8.答案 A9.解析:选D 法一:2-m 与|m |-3异号,所以(2-m )·(|m |-3)<0,所以(m -2)(|m |-3)>0,所以0(2)(3)0m m m ≥⎧⎨-->⎩或0(2)(3)0m m m <⎧⎨--->⎩解得m >3或0≤m <2或-3<m <0.方法二:由选项知,令m =4符合题意,排除B 、C 两项,令m =0可排除A 项.10.解析:选A 函数定义域为(0,+∞),f ′(x )=1+ex>0,故单调增区间是(0,+∞).11.解析:选B 对于①,f (x )=x -1x,f ⎝ ⎛⎭⎪⎫1x =1x -x =-f (x ),满足;对于②,f ⎝ ⎛⎭⎪⎫1x =1x+x =f (x ),不满足;对于③,f ⎝ ⎛⎭⎪⎫1x =⎩⎪⎨⎪⎧1x ,0<1x <1,0,1x =1,-x ,1x >1,即f ⎝ ⎛⎭⎪⎫1x =⎩⎪⎨⎪⎧1x ,x >1,0,x =1,-x ,0<x <1,故f ⎝ ⎛⎭⎪⎫1x =-f (x ),满足.综上可知,满足“倒负”变换的函数是①③.12.解析:选B 设甲用时间为T ,乙用时间为2t ,步行速度为a ,跑步速度为b ,距离为s ,则T =s 2a +s2b =s 2a +s 2b =s a +b 2ab ,ta +tb =s ⇒2t =2sa +b,T -2t =s a +b 2ab -2s a +b =s ×a +b 2-4ab 2ab a +b =s a -b 22ab a +b>0,即乙先到教室.13. 答案: 1 解析 由题意可知f ′(x )=2 014+ln x +x ·1x=2 015+ln x .由f ′(x 0)=2 015,∴ln x 0=0,解得x 0=1.14.答案:(-3,0) 解析 作出f (x )图像如图.∵f (3-x 2)<f (2x ),∴⎩⎪⎨⎪⎧3-x 2>2x ,2x <0.解得-3<x <0.15.答案 (0,13] 解析 由y =x x 2+x +1(x >0),得0<y =xx 2+x +1=1x +1x+1≤12x ·1x+1=13,因此该函数的值域是(0,13]. 16.答案:42+2 解析:圆ρ2+2ρcos θ-3=0的直角坐标方程为x 2+y 2+2x -3=0,即(x +1)2+y 2=4.直线ρcos θ+ρsin θ-7=0的直角坐标方程为x +y -7=0.圆心(-1,0)到直线的距离为|-1-7|2=42,所以圆上的动点到直线的距离的最大值为42+2. 17.解:(1)∵f (x )=b ·a x图像过点A (1,6),B (3,24), ∴⎩⎪⎨⎪⎧b ·a =6,b ·a 3=24,又a >0且a ≠1,∴a =2,b =3,∴f (x )=3·2x. ………………5分 (2)由(1)知不等式(1a )x +(1b )x -m ≥0即为(12)x +(13)x-m ≥0.∴问题转化成当x ∈(-∞,1]时m ≤(12)x +(13)x恒成立.…………8分令g (x )=(12)x +(13)x,易知g (x )在(-∞,1]上为减函数.∴g (x )≥g (1)=12+13=56.∴m ≤56. …………10分18.解:消去参数t ,得直线l 的直角坐标方程为y =2x +1,………2分 ρ=22sin ⎝ ⎛⎭⎪⎫θ+π4,即ρ=2(sin θ+cos θ),……4分 两边同乘以ρ得ρ2=2(ρsin θ+ρcos θ),………5分 得圆C 的直角坐标方程为(x -1)2+(y -1)2=2,………8分 圆心C 到直线l 的距离d =|2-1+1|22+12=255<2,………11分 所以直线l 和圆C 相交.………12分 19.解: (1)由题意,得|x +1|≥2|x |. 故x 2+2x +1≥4x 2,∴-13≤x ≤1.∴不等式f (x )≥g (x )的解集为. ………5分(2)若存在x ∈R ,使得|x +1|≥2|x |+a 成立,即存在x ∈R ,使得|x +1|-2|x |≥a 成立. ………6分令φ(x )=|x +1|-2|x |,则a ≤φ(x )max . ………8分 又φ(x )=⎩⎪⎨⎪⎧1-x ,x ≥0,3x +1,-1≤x <0,x -1,x <-1,………9分当x ≥0时,φ(x )≤1;当-1≤x <0时,-2≤φ(x )<1; 当x <-1时,φ(x )<-2. ………11分综上可得:φ(x )≤1,∴a ≤1,即实数a 的取值范围为(-∞,1].………12分20.解:(1)直线l 的普通方程为y -1=-(x +1),即y =-x .① ………2分 曲线C 的直角坐标方程为x 2+y 2-4x =0.② ……4分 ①代入②,得2x 2-4x =0,解得x =0或x =2. ……5分 ∴A (0,0),B (2,-2).…… 6分(2)由题意可得圆心C (2,0)到相交弦的距离为22-32=1. ……7分设直线l 的斜率为k ,则l 的方程为y -1=k (x +1),即y =kx +k +1. ∴|2k +k +1|k 2+1=1,∴k =0或k =-34. ……10分∴l :⎩⎪⎨⎪⎧x =-1+t ,y =1 (t 为参数)或⎩⎪⎨⎪⎧x =-1-45t ,y =1+35t (t 为参数).…12分21.解:(1)f (x )=⎩⎪⎨⎪⎧4, x ≤4,-2x +12, 4<x ≤8,-4, x >8,………………4分图象如下:………………6分(2)不等式|x -8|-|x -4|>2,即f (x )>2. 由-2x +12=2,得x =5. ……10分由函数f (x )图象可知,原不等式的解集为(-∞,5).……12分 22.解: (1)当a =1时f (x )=x 3+x 2-x +m . ∵函数f (x )有三个互不相同的零点,∴x 3+x 2-x +m =0即m =-x 3-x 2+x 有三个互不相等的实数根. 令g (x )=-x 3-x 2+x ,则g ′(x )=-3x 2-2x +1=-(3x -1)·(x +1),∴g (x )在(-∞,-1)和⎝ ⎛⎭⎪⎫13,+∞上均为减函数,在⎝⎛⎭⎪⎫-1,13上为增函数,∴极小值=g (-1)=-1,极大值=g ⎝ ⎛⎭⎪⎫13=527, ∴m 的取值范围是⎝ ⎛⎭⎪⎫-1,527.…………………………6分 (2)∵f ′(x )=3x 2+2ax -a 2=3⎝ ⎛⎭⎪⎫x -a 3(x +a ),且a >0,∴当x <-a 或x >a3时,f ′(x )>0;当-a <x <a3时,f ′(x )<0.∴函数f (x )的单调递增区间为(-∞,-a )和⎝ ⎛⎭⎪⎫a 3,+∞,单调递减区间为⎝⎛⎭⎪⎫-a ,a3.当a ∈时,a3∈,-a ≤-3.又x ∈,∴max =max{f (-2),f (2)}, 又f (2)-f (-2)=16-4a 2<0, ∴max =f (-2)=-8+4a +2a 2+m . 又∵f (x )≤1在上恒成立, ∴max ≤1即-8+4a +2a 2+m ≤1, 即当a ∈时,m ≤9-4a -2a 2恒成立. ∵9-4a -2a 2在上的最小值为-87,∴m 的取值范围是(-∞,-87].…………………………12分。
山东省华侨中学高二4月月考数学(理)试题
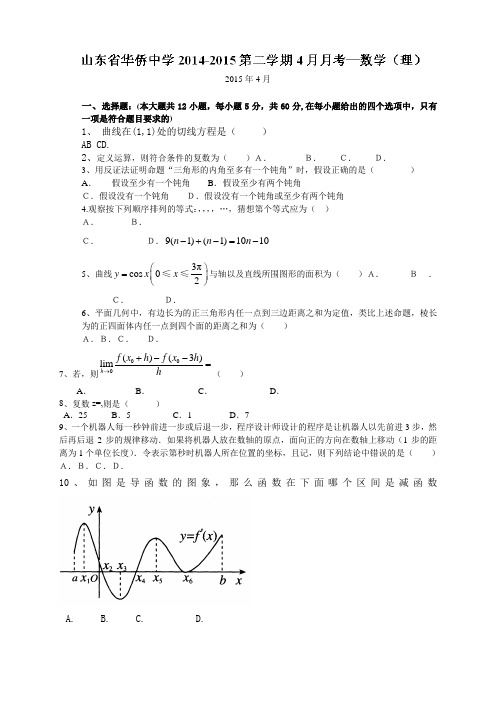
2015年4月一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、 曲线在(1,1)处的切线方程是( ) AB CD.2、定义运算,则符合条件的复数为( )A. B. C. D.3、用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( ) A . 假设至少有一个钝角 B .假设至少有两个钝角C.假设没有一个钝角 D.假设没有一个钝角或至少有两个钝角 4.观察按下列顺序排列的等式:,,,,…,猜想第个等式应为( ) A. B. C.D.9(1)(1)1010n n n -+-=-5、曲线3πcos 02y x x ⎛⎫= ⎪⎝⎭≤≤与轴以及直线所围图形的面积为( )A. B.C. D.6、平面几何中,有边长为的正三角形内任一点到三边距离之和为定值,类比上述命题,棱长为的正四面体内任一点到四个面的距离之和为( ) A.B.C. D.7、若,则000()(3)limh f x h f x h h →+--=( )A .B .C .D .8、复数z=,则是( ) A .25 B .5 C .1 D .79、一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令表示第秒时机器人所在位置的坐标,且记,则下列结论中错误的是( ) A.B.C.D.10、如图是导函数的图象,那么函数在下面哪个区间是减函数A. B. C. D.11、设*211111()()123S n n n n n n n=+++++∈+++N ,当时,( )A.B.C. D. 12、如果10N 的力能使弹簧压缩10cm ,为在弹性限度内将弹簧从平衡位置拉到离平衡位置6cm 处,则克服弹力所做的功为( )(A)0.28J (B)0.12J (C)0.26J (D)0.18J13. 曲线在点处的切线与轴、直线所围成的三角形的面积为( )(A ) (B ) (C ) (D ) 14. 已知直线是的切线,则的值为( )(A ) (B ) (C ) (D ) 15. 有一段“三段论”推理是这样的:对于可导函数,如果,那么是函数的极值点,因为函数在处的导数值,所以,是函数的极值点.以上推理中( )A .大前提错误B . 小前提错误C .推理形式错误D .结论正确 16. 在复平面内, 复数1 + i 与i 分别对应向量和, 其中为坐标原点,则=( ) A. B. C. D.17. 某个命题与正整数有关,若当时该命题成立,那么可推得当时该命题也成立,现已知当时该命题不成立,那么可推得( )(A)当时,该命题不成立 (B)当时,该命题成立 (C)当时,该命题成立 (D)当时,该命题不成立18. 若点P 在曲线y =x 3-3x 2+(3-3)x +34上移动,经过点P 的切线的倾斜角为α,则角α的取值范围是( )A .[0,π2)B .[0,π2)∪[2π3,π)C .[2π3,π)D .[0,π2)∪(π2,2π3]二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. 19、=---⎰dx x x )2)1(1(1220、设= i 4+ i 5+ i 6+…+ i12, = i 4 · i 5·i 6·…·i 12,则Z 1 ,关系为21.已知(为常数),在上有最小值,那么在上的最大值是22.函数g (x )=ax 3+2(1-a )x 2-3ax 在区间⎝⎛⎭⎪⎫-∞,a 3内单调递减,则a 的取值范围是________.三、解答题:本大题共4小题,共40分.解答应写出文字说明,证明过程或演算步骤. 23、(本小题10分) 20()(28)(0)xF x t t dt x =+->⎰.(1)求的单调区间;(2)求函数在上的最值. 24.(本小题10分)设是二次函数,方程有两个相等的实根,且. (1)求的表达式;(2)若直线把的图象与两坐标轴所围成图形的面积二等分,求的值. 25、(本小题10分)某宾馆有50个房间供游客居住,当每个房间定价为每天180元时,房间会全部住满;房间单价增加10元,就会有一个房间空闲,如果游客居住房间,宾馆每间每天需花费20元的各种维护费用。
山东省华侨中学高二上学期开学考试数学试题

山东省华侨中学2015-2016学年新高二开学检测数学第I 卷(选择题 共60分)一.选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求.1.设,且,则下列不等式正确的是( )A . B. C . D .2.已知数列为等差数列,若,则( )A .24B .12C .6D . 3.在△ABC 中,,,,则=( )A. B. C. D .4.在等比数列中,若,是方程x 2-4x+1=0的两个根,则=( )A .2B . C. D . 5.在△ABC 中,,则A 的值是( )A. B. C. D.6.设满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,x +y -1≥0,x ≤3,则的最小值是( )A .-1B .11C .2D .17.据科学计算,运载“神七”的“长征”二号系列火箭在点火后第一秒钟通过的路程为 2 km ,以后每秒钟通过的路程增加2 km ,经过15秒火箭与飞船分离,则这15秒火箭共飞行了( )A .480 kmB .65534 kmC .120 kmD .240 km 8.不等式对任意实数恒成立,则实数的取值范围为( )A .B .C .D .9.《莱因德纸草书》(Rhind papyrus )是世界上最古老的数学著作之一.该书中有一道这样的题目:100个面包分给5个人,每人一份,若按照每个人分得的面包个数从少到多排列,可得到一个等差数列,其中较多的三份和的等于较少的两份和,则最多的一份面包个数为( ) A .35 B. 32 C .30 D. 27 10.在中,,若有两解,则的取值范围是( )A . B. C . D.11.不等式和22(21)0x a x a a -+++>的解集分别为和,且,则实数取值范围是( )A .B .C .D . 12.如下图所示,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角∠MAN=60°,C 点的仰角∠CAB=30°以及∠MAC=105°;从C 点测得∠MCA=45°.已知山高BC =150米,则所求山高MN 为( )米.A . B. C . D.第II 卷(非选择题,共90分)二.填空题:本大题共4小题,每小题4分,共16分. 13.在△ABC 中,,,,则内角=_________. 14.已知正数满足,则的最大值为________. 15.已知数列满足*11(1,),1n n a n n N a -=>∈-,则数列的前6项和=____.16.已知(2,3),(1,5)OA OB =-=,若将满足条件0OA OM OB OM ⎧⋅≥⎪⎨⋅≥⎪⎩的动点所表示的平面区域记为D.则单位圆落在区域D 内的部分的弧长为_________.三.解答题:本大题共6小题,共74分。
【新课标】2014-2015上学期高二月考(2)数学(理) Word版含答案

2014-2015学年度上学期第二次月考高二数学(理)试题【新课标】一、选择题(本大题共10小题,每小题5分,共50分) 1. “执果索因”是下列哪种证明方法的特点( ) A .数学归纳法 B .反证法 C .分析法D .综合法2.若直线1:260l ax y ++=与直线2:(1)60l x a y +-+=平行,则实数a =( ) A .23B . 2C . 1-D . 1-或23.在下列结论中,正确的结论为( )①“p 且q”为真是“p 或q”为真的充分不必要条件 ②“p 且q”为假是“p 或q”为真的充分不必要条件 ③“p 或q”为真是“p Ø”为假的必要不充分条件 ④“p Ø”为真是“p 且q”为假的必要不充分条件 A .①②B .①③C .②④D .③④4.焦点为()6,0,且与双曲线2212x y -=有相同的渐近线的双曲线方程为( )A .1241222=-x y B .1241222=-y x C .1122422=-x yD .1122422=-y x 5.在极坐标系中,点(2,)6π到直线sin )2ρθθ+=的距离为( )A .34B .2C1D .16.若关于x的方程x b +=有两个不同的实数解,则实数b 的取值范围是( )A .(-B . (1,1)-C .D .7.对任意实数x ,不等式|2|||x x a -+>恒成立的一个充分不必要条件是( ) A . 2a <B . 1a <C .2a >D .1a >8.过椭圆)0(12222>>=+b a by a x的左焦点F 1作x 轴的垂线交椭圆于点P ,F 2为右焦点,若321π=∠F F P ,则椭圆的离心率为( ).A. 33B. 22C. 21D. 319.如图,过抛物线x y 42=焦点的直线依次交抛物线与圆1)1(22=+-y x 于A 、B 、C 、D 四点,则AB CD?uu u r uu u r( )A .4B .2C .1D .21 10.如图,液体从圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经3分钟漏完.已知圆柱中液面上升的速度是一个常量,H 是圆锥形漏斗中液面下落的距离,则H 与下落时间t (分)的函数关系表示的图象只可能是( )二、填空题:(本大题共5小题,每小题5分,共25分)11.对于命题R x p ∈∃:,使得012<++x x ,则p ⌝:________________;12.如果椭圆221369x y +=的弦被点(2,2)平分,则这条弦所在的直线方程是______________;13.直线l的参数方程为3x t y ì=-+ïïíï=ïî(t 为参数).圆C 的参数方程为3cos 3sin x y θθì=ïïíï=ïî(θ为参数),则直线l 被圆C 截得的弦长为 ;14.把正整数排列成如图甲的三角形数阵,然后擦去第偶数行的奇数和第奇数行中的偶数,得到如图乙的三角数阵,再把图乙中的数按从小到大的顺序排成一列,得到数列{}n a ,若2013n a =,则n =____.1 1234 2 45678 95 7 910 11 12 13 14 15 16 10 12 14 1617 18 19 20 21 22 23 24 25 17 19 21 23 2526 27 28 29 30 31 32 33 34 35 36 26 28 30 32 34 36………………………………………………图甲图乙15.以下命题中:①.“直线l 与曲线C 相切”是“直线l 与曲线C 只有一个公共点”的充要条件; ②.“若两直线12l l ^,则它们的斜率之积等于1-”的逆命题;③.“在平面内,到定点)1,2(的距离与到定直线01043=-+y x 的距离相等的点的轨迹是抛物线”的逆否命题;④.“曲线C 上的点的坐标都是方程(,)0f x y =的解”是“(,)0f x y =是曲线C 的方程”的必要不充分条件。
山东省华侨中学2014-2015学年高二4月月考 数学理 Word版及答案

山东省华侨中学2014-2015学年高二4月月考数学(理)试题2015年4月一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、 曲线2x y =在(1,1)处的切线方程是( ) A 230x y ++=B 032=--y x C 210x y ++= D. 012=--y x2、定义运算a b ad bc c d=- ,则符合条件1142i iz z -=+ 的复数z 为( )A.3i - B.13i + C.3i + D.13i -3、用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( ) A . 假设至少有一个钝角 B .假设至少有两个钝角C.假设没有一个钝角 D.假设没有一个钝角或至少有两个钝角4.观察按下列顺序排列的等式:9011⨯+=,91211⨯+=,92321⨯+=,93431⨯+=,…,猜想第*()n n ∈N 个等式应为( )A.9(1)109n n n ++=+ B.9(1)109n n n -+=- C.9(1)101n n n +-=-D.9(1)(1)1010n n n -+-=-5、曲线3πcos 02y x x ⎛⎫= ⎪⎝⎭≤≤与x 轴以及直线3π2x =所围图形的面积为( )A.4B.2C.52D.36、平面几何中,有边长为a,类比上述命题,棱长为a 的正四面体内任一点到四个面的距离之和为( )7、若'0()3f x =-,则000()(3)limh f x h f x h h →+--=( )A .3-B . 12-C .9-D .6- 8、复数z=534+i,则z 是( ) A .25 B .5 C .1 D .79、一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令()P n 表示第n 秒时机器人所在位置的坐标,且记(0)0P =,则下列结论中错误的是( )A.(3)3P =B.(5)1P =C.(2007)(2006)P P >D.(2003)(2006)P P <10、如图是导函数/()y f x =的图象,那么函数()y f x =在下面哪个区间是减函数A. 13(,)x xB. 24(,)x xC.46(,)x xD.56(,)x x11、设*211111()()123S n n n n n n n =+++++∈+++N ,当2n =时,(2)S =( )A.12B.1123+C.111234++ D.11112345+++12、如果10N 的力能使弹簧压缩10cm ,为在弹性限度内将弹簧从平衡位置拉到离平衡位置6cm 处,则克服弹力所做的功为( )(A)0.28J (B)0.12J (C)0.26J (D)0.18J13. 曲线3x y =在点)1,1(处的切线与x 轴、直线2=x 所围成的三角形的面积为( )(A )38 (B )37 (C )35 (D )34 14. 已知直线kx y =是x y ln =的切线,则k 的值为( )(A )e 1 (B )e 1- (C )e 2 (D )e2- 15. 有一段“三段论”推理是这样的:对于可导函数()f x ,如果0()0f x '=,那么0x x =是函数()f x 的极值点,因为函数3()f x x =在0x =处的导数值(0)0f '=,所以,0x =是函数3()f x x =的极值点.以上推理中( )A .大前提错误B . 小前提错误C .推理形式错误D .结论正确16. 在复平面内, 复数1 + i 与31+i 分别对应向量OA 和OB , 其中O 为坐标原点,( )A.2B.2C.10 D. 417. 某个命题与正整数有关,若当)(*N k k n ∈=时该命题成立,那么可推得当=n 1+k 时该命题也成立,现已知当5=n 时该命题不成立,那么可推得( ) (A)当6=n 时,该命题不成立 (B)当6=n 时,该命题成立 (C)当4=n 时,该命题成立 (D)当4=n 时,该命题不成立18. 若点P 在曲线y =x 3-3x 2+(3-3)x +34上移动,经过点P 的切线的倾斜角为α,则角α的取值范围是( )A .[0,π2)B .[0,π2)∪[2π3,π)C .[2π3,π)D .[0,π2)∪(π2,2π3]二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. 19、=---⎰dx x x )2)1(1(1220、设1Z = i 4+ i 5+ i 6+…+ i12,2Z = i 4 · i 5·i 6·…·i 12,则Z 1 ,2Z 关系为21.已知32()3f x x x a =++(a 为常数),在[33]-,上有最小值3,那么在[33]-,上()f x 的最大值是22.函数g (x )=ax 3+2(1-a )x 2-3ax 在区间⎝⎛⎭⎪⎫-∞,a 3内单调递减,则a 的取值范围是________.三、解答题:本大题共4小题,共40分.解答应写出文字说明,证明过程或演算步骤. 23、(本小题10分) 20()(28)(0)xF x t t dt x =+->⎰.(1)求()F x 的单调区间;(2)求函数()F x 在[13],上的最值.24.(本小题10分)设()y f x =是二次函数,方程()0f x =有两个相等的实根,且()22f x x '=+.(1)求()y f x =的表达式;(2)若直线(01)x t t =-<<把()y f x =的图象与两坐标轴所围成图形的面积二等分,求t 的值. 25、(本小题10分)某宾馆有50个房间供游客居住,当每个房间定价为每天180元时,房间会全部住满;房间单价增加10元,就会有一个房间空闲,如果游客居住房间,宾馆每间每天需花费20元的各种维护费用。
山东省华侨中学1415学年度高一6月月考——物理物理
山东省华侨中学2014—2015学年度下学期6月月考高一物理试题第Ⅰ卷(选择题,共40分)一、选择题(本题共12个小题,1-10为单选题,11-12为多选题,每题4分,共48分,选对的得4分,选不全得2分,有错选或不选得0分)1.关于功的概念,下列说法中正确的是( )A.力对物体做功多,说明物体的位移一定大B.力对物体做功少,说明物体的受力一定小C.力对物体不做功,说明物体一定无位移D.功的多少是由力的大小和物体在力的方向上位移的大小确定的2.关于功率,以下说法中正确的是( )A.据P=W/t可知,机器做功越多,其功率就越大B.据P=Fv可知,汽车牵引力一定与速度成反比C.据P=W/t可知,只要知道时间t内机器所做的功,就可以求得这段时间内任一时刻机器做功的功率D.根据P=Fv可知,发动机功率一定时,交通工具的牵引力与运动速度成反比3.下列关于运动物体所受的合外力、合外力做功和动能变化的关系,正确的是( )A.如果物体所受的合外力为零,那么,合外力对物体做的功一定为零B.如果合外力对物体所做的功为零,则合外力一定为零C.物体在合外力作用下做变速运动,动能一定变化D.物体的动能不变,所受的合外力必定为零4.关于重力势能与重力做功的下列说法中正确的是( )A.物体克服重力做的功等于重力势能的减少量B.在同一高度,将物体以相同的初速度沿不同方向从抛出到落地过程中,重力做的功相等,物体所减少的重力势能一定相等C.重力势能等于零的物体,不可能对别的物体做功D.用手托住一个物体匀速上举时,手的支持力做的功等于克服重力做的功与物体所增加的重力势能之和5.一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻F的功率是( )A. B. t12 C. t1 D. t126.自然界中有很多物体做曲线运动,在所有的曲线运动中,物体的运动速度()A. 大小一定改变B.方向一定改变C. 方向一定不变D.大小一定不变7.一艘炮艇沿长江由西向东快速行驶,在炮艇上发射炮弹射击正北岸的目标。
试题
2014-2015学年度第二学期半期考试高二理科数学试题(时间120分钟 满分150分)命题人:李应宗一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、函数3x y =在区间]2,1[上的平均变化率为( )A. 4B. 5 B. 6 D . 72.如图所示,阴影部分的面积是( )A .323B .2- 3C. 353D. 2 33.下面几种推理是合情推理的是( )①由直角三角形、等腰三角形、等边三角形的内角和是180°,归纳出所有三角形的内角和都是180°;②圆的性质类比出球的有关性质;③由ABC ∆∽111C B A ∆⇒1A A ∠=∠;④三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得出凸多边形的内角和是(n -2)·180°A .①②③B .①③④C .①②④D .②③④4.已知2)(23-+=x ax x f 且4)1(=-'f ,则实数a 的值等于( )A .–2B .32C .2D .38 5.在复平面内,复数Z 满足i i i Z -=+123,则Z 对应的点位于( ) A.第一象限 B.第二象限 C.第三象限D.第四象限 6.设()f x '是函数()f x 的导函数,()y f x '=的图象如图2所示,则()y f x =的图象最有可能的是( )图27.已知1>x ,则函数122)(-+=x x x f 的最小值为( ) A 、4 B 、5 C 、6 D 、78.不等式|x-1|+|x+2|m ≤的解集不是空集,则实数m 的取范围是( )A ()3,∞-B [)+∞,3C ()+∞,3D (]3,∞-9.函数3123223+--=x x x y 在[0,3]上的最大值与最小值分别是( )A.3 , -17B.3 , 2C.-2 , -17D.3,-1810.函数y=x x -+-5314的最大值为( )A 、10B 、27C 、36D 、8 11. 设)(21312111)(*∈+++++++=N n nn n n n f ,则=-+)()1(n f n f ( ) A .121+n B .221+n C .221121+++n n D .221121+-+n n 12.已知函数()()()2log 030x x x f x x >⎧⎪=⎨⎪⎩≤,且关于x 的方程()0f x x a +-=有且只有一个实根,则实数a 的范围是( )A. (),0-∞B. ()1,+∞C. ()0,1D. ()1,2二、填空题(共4小题,每小题4分,共16分)13. 已知集合},4|6|1|{N x x x A ∈<-<=,求A= ;14. 已知复数=Z 21i+,则=Z ,=Z ; 15. 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:则第n 个图案中有白色地面砖 块.16.16.已知下列函数,①|1|x x y += ; ②1)x ,0(log ln ≠>+=且x e x y x ; ③24-+=x x y ;④2322++=x x y ;⑤x x e e y -+= ; ⑥),0(,2sin 4sin π∈-+=x x x y ; 其中最小值为2的函数是 (填入所有正确命题的序号)三、解答题(共6小题,共70分. 解答应写出文字说明、演算步骤或推证过程)17.(本题10分) (1)计算31i i +-+ii +-122 (2)设a, b 为实数,若复数11+2i i a bi=++,求a , b 的值18、(本题12分)(1)证明:83105->-(2)上移动,在直线已知点43),(=+y x n m 求n m 82+的最小值。
山东省华侨中学2014-2015学年高二上学期第二学段(1月)学情检测
山东省华侨中学2014-2015学年高二上学期第二学段(1月)学情检测山东省华侨中学2014-2015学年高二上学期第二学段(1月)学情检测2015.01 本试卷分第卷和第卷两部分,共8页,满分150分。
考试时间150分钟。
第卷(共60分)一、(48分,每小题3分)1.下列词语中,加点字的注音全都正确的一项是A.摭(zh)拾哄(hng)笑擎(qn)天柱钻(zun)木取火B.屏(bng)息包扎(zh)夹(ji)克衫言之凿凿(zo)C.孱(cn)弱牌坊(fng)干(gn)细胞铩(sh)羽而归D.吟哦()皲(jn)裂胳(g)肢窝蜚(fi)声中外2.下列各句中,没有错别字的一项是A.这个节目融合了京剧、粤剧、秦腔等中国戏曲的精萃,舞者多变的动作和戏剧化的表情,淋漓尽致地表达了喜怒哀乐的情绪。
B.城郊的这座园林,亭台楼阁错落有致,溪流小径曲折萦纡,到了春天,杂花生树,草长莺飞,真是一处世外桃源。
C.在全球一体化进程中,有些备受国人青睐的外国名品,其实是用中国的原料,在中国的流水线上生产出来的,已不是地道的泊来品。
D.该公司在把握市场脉搏的基础上,另辟蹊径,依靠独树一帜的管理理念以及出奇不意的营销策略赢得了商机,获得了发展。
3.下列各句中,加点词语使用正确的一句是A.阳春三月,一位老人在杭州西湖岸边展示他高超的拳脚功夫,引来许多行人侧目观赏。
B.大学毕业已经十年了,其间,他换过几种不同性质的工作,但始终没有放弃专业学习。
C.老王一直热衷于收藏,每当得到心仪的藏品,喜悦的心情总让他如坐春风,夜不成寐。
D.此前中国航空西南分公司一直与四川航空公司鼎足而立,所占市场份额相差无几。
4.下列各句中,标点符号使用正确的一句是A.最近两天,京津地区、华北中南部、黄淮、江淮、汉水流域、贵州等地的日平均气温达到了入夏以来的最高值。
B.《新民丛报》虽然名为“报”,其实却实期刊,是梁启超等人于1902年在日本横滨创办的,曾产生过较大影响。
高二2014-2015学年度第二学期月考数学试卷
高二2014-2015学年度第二学期月考数学试卷1.函数()12ln 2+=x y 的导数是( A ) A.1242+x x B.1212+x C.()10ln 1242+x x D.()e x x 22log 124+ 2.若关于x 的函数2m n y mx -=的导数为4y x '=,则m n +=( ) A.3- B.4 C.1 D.33.设f(x)=x 2(2-x),则f(x)的单调增区间是( A ) A.(0,)34 B.(,34+∞) C.(-∞,0)D.(-∞,0)∪(34,+∞)4.若()122x k dx k +=-⎰,则定值k 为( )A . 1B .12C . 12- D .05.设函数f(x)在0x 处可导,则xx f x x f x ∆-∆-→∆)()(lim000等于 ( C )A .)('0x fB .)('0x f -C .-)('0x fD .-)('0x f - 6.已知32()(6)1f x x ax a x =++++有极大值和极小值,则a 的取值范围为( ). A .-1<a <2 B .-3<a <6 C .a <-1或a >2D .a <-3或a >67.若()f x 的导函数()f x '图象如右图所示,那么()f x 的图象最有可能是( )8.方程0109623=-+-x x x 的实根个数是( A )A .3B .2C .1D .09.设函数322()3(1)1f x kx k x k =+--+在区间(0,4)上是减函数,则k 的取值范围是( D )A.13k <B.103k <≤C.103k ≤≤D.13k ≤10.曲线12e x y =在点2(4e ),处的切线与坐标轴所围三角形的面积为( D )A .29e 2B .24eC .22eD .2e11.已知函数f(x)的导函数为)(x f ',且满足f(x)=3x 2+2x )2('f ,则)5('f =( )A.8B.7C. 6D.5 12.函数)(x f 的定义域为R ,(1)3f -=-,对任意R x ∈,()1f x '<,则()2f x x >-的解集为( )A.)1,1(-B.),1(+∞-C.)1,(--∞D.),(+∞-∞ 二、填空题13.dx x ⎰--3329= 92π ,14.已知函数c ax x f +=2)(,且(1)f '=2,则a 的值为15.曲线S :y=3x-x 3的过点A (2,-2)的切线的方程是y=-9x+16或y=-2 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二月考理科数学(6月)(考试时间: 120分钟 分值:150分 )一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数4312i z i+=+的虚部为( ) A .i B .i - C .1- D .12.设,x m 均为复数,若2,x m = 则称复数x 是复数m 的平方根,那么复数34i -(i 是虚数单位)的平方根为( )A.2i - 或2i -+B.2i + 或2i --C.2i - 或2i + D .2i -- 或2i -+3.满足条件|z -i|=|3-4i|的复数z 在复平面上对应点的轨迹是( )A .一条直线B .两条直线C .圆D .椭圆4.设⊕是R 上的一个运算,A 是R 的非空子集,若对任意a ,b ∈A ,有a ⊕b ∈A ,则称A 对运算⊕封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是 ( )A .自然数集B .整数集C .有理数集D .无理数集5.曲线的参数方程为⎩⎨⎧-=+=12322t y t x (t 是参数),则曲线是( ) A.线段 B.双曲线的一支 C.圆 D.射线6.已知函数()y f x =上任一点()0,0()x f x 处的切线斜率()()20021k x x =-+ ,则该函数的单调递减区间为( )A.[)1,-+∞B.(],2-∞ B.()(),1,1,2-∞- D.[)2,+∞7.由曲线y =2y x =- 及y 轴所围成的图形的面积为( ) A.103 B.4 C.163D.6 8.曲线y =e-2x +1在点(0,2)处的切线与直线y =0和y =x 围成的三角形的面积为( ). A .13B.12C.23 D .1 9.设x ,y ,z ∈(0,+∞),a =x+1y ,1b y z =+ ,1c z x =+ ,则,,a b c 三数( ) A .至少有一个不大于2 B .都小于2 C .至少有一个不小于2 D .都大于210.设'()f x 是函数()f x 的导函数,将y ='()f x 和()y f x =的图象画在同一个直角坐标系中,不可能正确的是11.函数sin cos y x x x =+,(),x ππ∈- 的单调递增区间是( )A.,,0,22πππ⎛⎫⎛⎫--⎪ ⎪⎝⎭⎝⎭ B.,0,0,22ππ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭C.,,,22ππππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭D. ,0,,22πππ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭ 12.设函数()f x 的导函数为'()f x , 对任意x∈R 都有()f x > '()f x 成立, 则A. 3f (ln2)<2f (ln3)B. 3f (ln2)=2f (ln3)C. 3f (ln2)>2f (ln3)D. 3f (ln2)与2f (ln3) 的大小不确定二、填空题(每空5分,共20分)。
13.在极坐标系中,过点A (4,2π-)引圆4sin ρθ=的一条切线,则切线长 .14.若数列{a n }(n ∈N*)是等差数列,则有数列12n n a a a b n +++=(n ∈N*) 也是等差数列;类比上述性质,相应地:若数列{c n }是等比数列,且c n >0,则有数列 d n = ()*n N ∈ 也是等比数列。
15.已知函数3()f x x ax =+在R 上有两个极值点,则实数a 的取值范围是 .16.已知函数32()f x x ax bx c =-+++ 在(),0-∞上是减函数,在()0,1是增函数,函数()f x 在R 上有三个零点,且1是其中一个零点,则(2)f 的取值范围是 .三、解答题:(共70分)解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)已知函数f (x )=aln x x +1+b x,曲线y =f (x )在点(1,f (1))处的切线方程为x +2y -3=0,求a 、b 的值.18.(本小题满分12分)在极坐标中,已知圆C 经过点()4P π,,圆心为直线sin 3ρθπ⎛⎫-= ⎪⎝⎭与极轴的交点,求圆C 的极坐标方程. 19.(本小题满分12分)如图,一矩形铁皮的长为8cm ,宽为5cm ,在四个角上截去 四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大?20.(本小题满分12分)已知a ∈R ,函数()f x =(-x 2+ax )xe (x ∈R ,e 为自然对数的底数).(1)当a =2时,求函数()f x 的单调递增区间;(2)若函数()f x 在(-1,1)上单调递增,求a 的取值范围;21.(本小题满分12分)在平面直角坐标系xoy 中,已知曲线C 1 122=+y x ,以平面直角坐标系xoy 的原点O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l :6)sin cos 2(=-θθρ(1)将曲线C 1上的所有点的横坐标,纵坐标分别伸长为原来的3、2倍后得到曲线C 2,试写出直线l 的直角坐标方程和曲线C 2的参数方程.(2)在曲线C 2上求一点P ,使点P 到直线l 的距离最大,并求出此最大值.22.(本小题满12分)己知函数32()1(1)f x n ax x x ax =++--. (1) 若 x =23为()f x 的极值点,求实数a 的值; (2) 若a =-1时,方程 3(1)(1)b f x x x ---=有实根,求实数b 的取值范围.数学答案(理)一、CACCD BCACD AC二、13. (,0)-∞ 16. 5,2⎛⎫-+∞ ⎪⎝⎭三、17.解 f ′(x )=a ⎝⎛⎭⎪⎫x +1x -ln x x +2-bx 2,-------------4分 由于直线x +2y -3=0的斜率为-12,且过点(1,1),-------------6分 故⎩⎪⎨⎪⎧ f =1,f =-12即⎩⎪⎨⎪⎧ b =1,a 2-b =-12.------------9分解得a =1,b =1. -------------10分18.解:圆C 的圆心为直线sin 3ρθπ⎛⎫-= ⎪⎝⎭与极轴的交点,∴在sin(3πρθ- )=,中令θ=0,得ρ=1. -------------3分 ∴圆C 的圆心坐标为(1,0). ----------5分∵圆C 经过点4πρ⎫⎪⎭, -------------8分∴圆C 的半径为PC 1. ---------------10分∴圆C 经过极点.∴圆C 的极坐标方程为ρ=2cos θ. -------------12分19.解:设小正方形的边长为x 厘米,则盒子底面长为82x -,宽为52x -(502x << )----------3分 32(82)(52)42640V x x x x x x =--=-+ --------------6分 '2'10125240,0,1,3V x x V x x =-+===令得或,103x =(舍去) ---------------9分(1)18V V ==极大值,在定义域内仅有一个极大值,18V ∴=最大值--------------12分20.解:(1)当a =2时,f (x )=(-x 2+2x )e x,∴f ′(x )=(-2x +2)e x +(-x 2+2x )e x =(-x 2+2)e x . -------------2分令f ′(x )>0,即(-x 2+2)e x >0,--------------3分∵e x >0,∴-x 2+2>0, 解得-2<x < 2.--------------5分∴函数f (x )的单调递增区间是(-2,2).-------------6分(2)∵函数f (x )在(-1,1)上单调递增,∴f ′(x )≥0对x ∈(-1,1)都成立.--------------8分∵f ′(x )=e x ,∴e x ≥0对x ∈(-1,1)都成立.∵e x >0,∴-x 2+(a -2)x +a ≥0对x ∈(-1,1)都成立,即x 2-(a -2)x -a ≤0对x ∈(-1,1)恒成立.------------9分设h (x )=x 2-(a -2)x -a , 只需满足(1)0(1)0h h -≤⎧⎨≤⎩,解得a ≥32.------------12分 21.解:(1)由题意知,直线l 的直角坐标方程为: 2x-y-6=0 -----------2分∵曲线C 2的直角坐标方程为2212y ⎛⎫+= ⎪⎝⎭--------------4分∴曲线C 2的参数方程为(θ为参数)。
--------------6分(2)设点P 的坐标则点P 到直线l 的距离为:d ︒== --------------10分∴当sin (60θ︒-)=-1时,点P 3,12⎛⎫- ⎪⎝⎭--------------11分此时max d ==。
--------------12分--------2分23x =为f(x)的极值点, 2()03f '∴= 22223+3-2)(2)033a a a ∴-+=()(且21003a a +≠∴=------------4分 又当a =0时,()(32)f x x x '=-, -----------5分从而23x =为f(x)的极值点成立. -------------6分 (2)若1a =-时,方程3(1)(1)b f x x x ---=可得2ln (1)(1)b x x x x --+-= 即223ln (1)(1)ln b x x x x x x x x x x =--+-=+-在0x >上有解----------8分 即求函数23()ln g x x x x x =+-的值域.2(ln )b x x x x =+- ,令2()ln h x x x x =+-,由1(21)(1)()12x x h x x x x+-'=+-=------------10分 0x >∴当01x <<时, h '(x)>0,从而h(x)在(0,1)上为增函数;当1x >时, ()0h x '<,从而h(x)在(1,)+∞上为减函数.()(1)0h x h ∴≤=,而h(x)可以无穷小, b ∴的取值范围为(,0]-∞.------------12分。
