等腰三角形判定方法
合集下载
等腰三角形的判定
lpt48hkn
为“藏传佛教的八大神山之首。”我们到达梅里雪山的时候是在早晨，结束了几天的地下生活，到了梅里雪山脚下，阳光刺的我睁不 开眼睛，过了一会终于适应了。阳光明媚，山上的雪被阳光照得熠熠生辉，极蓝与极白相交辉映，看着这样的风景好像心也被洗干净 了，空气里都满是雪的味道。我现在终于体会到什么是壮观，在大自然的面前人类是多么的渺小。巍峨的雪山直插云霄，真是雾笼云 遮缥缈中，浑然浩气贯苍穹。山神说拉着我的手，我啊了一声，有点不好意思，脸红的发烫，感觉都红到耳根了。山神看着我说： “想什么呢，拉着我，我们飞上去，这样会节省不少时间。”这是要是有一条地缝，不管多小，我都要挤进去。可等了半天，山神也 没什么动静，他的手依旧如此冰凉。我以为他还在酝酿，只见他眉头紧皱，我说怎么了，我们怎么还在这里。山神说：“在这里，我 居然不能使用法术，我的法术好像被什么禁锢了一样，没法使出来。”我心想这座山这么厉害，居然连山神的法力都被禁锢了，看来， 我们凶多吉少了，真是壮士一去兮不复返啊。我说：“这样啊，那我们还是走吧，万一在这里挂掉了，我还好，你可怎么办啊，多不 划算啊。”我边说边往回走。山神说：“来都来了，再说了，怕什么，这是神山，不会有什么妖怪的。看来，我们只有爬上去了”。 这里有十三座峰，主峰卡瓦格博峰海拔高达6740米，看着主峰，我咽了口唾沫，心想这次不死也要退层皮了。我们修整了一会开始爬 山，我们就一直走，也无心欣赏身边的风景了，山很陡峭，有几次险些摔倒下去，我们一直提心吊胆地走了一天，到傍晚的时候终于 到达了雪线，我们又继续往前走，天也渐渐暗下来了，想想开始露出来，星星离我们很近，温度逐渐降低，风越来越大，尽管穿着很 厚很厚地冬衣，依然感觉很冷，只要一张口，风吹着雪就直往喉咙里灌，山神怕我摔倒后爬不起来，就一直拉着我走，满眼的白色， 一直看着白色突然头一阵眩晕，一不小心就跌了个狗**。山神连忙把我扶起来。山神还是一身玄色衣服，他无论在什么样的恶劣条件 都是这样，丝毫不受影响。走到后来就是他拖着我走了，他怕我失去意识，就一直不停的跟我说话。我们又走了一夜，到第二天中午， 我们来到了一个山洼里，这的山洼很奇怪，它很宽很大，周围长满了野花和野草，还能看到很多蝴蝶，一条清澈的小溪从旁边流过， 这里这的是一处世外桃源啊，想不到大山之中还能有这样的地方不受风雪的侵扰。山神的眼睛很尖，一下就看到了被草掩埋的相机， 拿起来一看，这是尼康FM3A上面的金属机身已经长锈了，相机更新速度很快，现在已经停产了，我们也不能评这个就判断时间，万一 他是胶卷相机的忠实用户呢，这也说不定，随后我们又找到
等腰三角形的判定
O
A
B
O 已知：如图，在ΔOAB中， ∠A=∠B，求证:OA=OB. A C 证明：过O点作OC⊥AB，垂足为C. 在ΔOAC和ΔOBC中， ∠A=∠B ∠OCA= ∠OCB=90° OC=OC ∴ ΔOAC ≌ΔOBC ∴ OA=OB
B
等腰三角形的判定：
如果一个三角形中有两个角 相等,那么这两个角所对的边也相 等.(等角对等边)
A 有两边 相等的 三角形 是等腰 三角形。 C
1.两边相等。
2.等边对等角, 3. 三线合一。 4.是轴对称图形.
2.等角对等边,
思考题1 如图,线段AB的端点B在直线 l 上(AB与直线 l 不 垂直)，请在直线 l 上另找一点C,使ΔABC为等腰 三角形，这样的点能找几个？你能说出它们的画 法吗？ A
理由．
B
30
O
60
O
A D
C
心动
不如行动
A
如图:△ABC中AB=AC,∠B=∠C， BD=CE，说明∠1=∠2的理由，
B D
1
2
E ∠1=∠2
C
方法一:
BD=CE ∠B=∠C AB=AC
△ABD≌ △ACE
AD=AE
方法二: △ABD≌ △ACE
方法三:
BE=CD ∠B=∠C AB=AC
∠ADB＝∠AEC
A C
如图，标杆AB高5m， 为了将它固定，需要由 它的中点C向地面上与点 B距离相等的D，E两点 拉两条绳子，使得点D， B，E在一条直线上。量 得DE=4m，绳子CD和 CE要多长？
E
D
B
例1：一次数学实践活动的内容是测量河宽，如图，即 测量A,B之间的距离.同学们想出了许多方法,其中小聪 的方法是：从点Ａ出发,沿着与直线AB成60°角的AC方 向前进至C，在C处测得∠C＝30°.量出AC的长，它就是 河宽（即A,B之间的距离）．这个方法正确吗？请说明
A
B
O 已知：如图，在ΔOAB中， ∠A=∠B，求证:OA=OB. A C 证明：过O点作OC⊥AB，垂足为C. 在ΔOAC和ΔOBC中， ∠A=∠B ∠OCA= ∠OCB=90° OC=OC ∴ ΔOAC ≌ΔOBC ∴ OA=OB
B
等腰三角形的判定：
如果一个三角形中有两个角 相等,那么这两个角所对的边也相 等.(等角对等边)
A 有两边 相等的 三角形 是等腰 三角形。 C
1.两边相等。
2.等边对等角, 3. 三线合一。 4.是轴对称图形.
2.等角对等边,
思考题1 如图,线段AB的端点B在直线 l 上(AB与直线 l 不 垂直)，请在直线 l 上另找一点C,使ΔABC为等腰 三角形，这样的点能找几个？你能说出它们的画 法吗？ A
理由．
B
30
O
60
O
A D
C
心动
不如行动
A
如图:△ABC中AB=AC,∠B=∠C， BD=CE，说明∠1=∠2的理由，
B D
1
2
E ∠1=∠2
C
方法一:
BD=CE ∠B=∠C AB=AC
△ABD≌ △ACE
AD=AE
方法二: △ABD≌ △ACE
方法三:
BE=CD ∠B=∠C AB=AC
∠ADB＝∠AEC
A C
如图，标杆AB高5m， 为了将它固定，需要由 它的中点C向地面上与点 B距离相等的D，E两点 拉两条绳子，使得点D， B，E在一条直线上。量 得DE=4m，绳子CD和 CE要多长？
E
D
B
例1：一次数学实践活动的内容是测量河宽，如图，即 测量A,B之间的距离.同学们想出了许多方法,其中小聪 的方法是：从点Ａ出发,沿着与直线AB成60°角的AC方 向前进至C，在C处测得∠C＝30°.量出AC的长，它就是 河宽（即A,B之间的距离）．这个方法正确吗？请说明
等腰三角形的判定
求证： AB=AC
A
B
D
C
方法一：作BC边上的高AD 方法二：作∠A的角平分线AD
方法三：“作BC边上的中线AD”可行吗？ 不行!
归纳总结
在△ABC中， ∵ ∠B=∠C ( 已知 ) ∴ AC= AB ( 等角对等边 ) B
A
C
如果一个三角形有两个角相等，
那么 那么这个三角形是等腰三角形 这两个角所对的边也相等。 简写成 “等角对等边”
∴ ∠1= ∠2=90° 在⊿ABD和⊿ACD中， B ∠B=∠C， ∠1=∠2 AD=AD ∴ ⊿ABD≌ ⊿ACD（ AAS ） ∴AB=AC（ 全等三角形的对应边相等 ）
即：⊿ABC是等腰三角形
1 2 D
C
已知：⊿ABC中，∠B=∠C 求证：AB=AC： 证明：作∠BAC的平分线AD ∴ ∠1=∠2 在⊿ABD和⊿ACD中， ∠B=∠C ∠1=∠2 AD=AD B
D
C
考考大家：
• 例：已知等腰三角形的底边为a，底边上的 高的长为b，求作这个等腰三角形.
M
a
b
A
B 作法：（1）作线段BC，使BC=a； D （2）作BC的垂直平分线MN，交BC于D N ； （3）在MN上截取DA=h,得A点； （4）连结AB、AC，则△ABC即为所求等 腰三角形。
C
练习：如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，E、F是垂足，DE＝DF，求证：AB＝AC.
1 2
C B
∵∠1=∠2 （已知） ∴ DC=BC （等角对等边）
错，因为∠1和∠2 不是同一个三角形的内角。
例1：求证：如果三角形一个外角的平分线平行于 外角 平分线 平行于
三角形的一边，那么这个三角形是等腰三角形。 三角形的一边 ∥
A
B
D
C
方法一：作BC边上的高AD 方法二：作∠A的角平分线AD
方法三：“作BC边上的中线AD”可行吗？ 不行!
归纳总结
在△ABC中， ∵ ∠B=∠C ( 已知 ) ∴ AC= AB ( 等角对等边 ) B
A
C
如果一个三角形有两个角相等，
那么 那么这个三角形是等腰三角形 这两个角所对的边也相等。 简写成 “等角对等边”
∴ ∠1= ∠2=90° 在⊿ABD和⊿ACD中， B ∠B=∠C， ∠1=∠2 AD=AD ∴ ⊿ABD≌ ⊿ACD（ AAS ） ∴AB=AC（ 全等三角形的对应边相等 ）
即：⊿ABC是等腰三角形
1 2 D
C
已知：⊿ABC中，∠B=∠C 求证：AB=AC： 证明：作∠BAC的平分线AD ∴ ∠1=∠2 在⊿ABD和⊿ACD中， ∠B=∠C ∠1=∠2 AD=AD B
D
C
考考大家：
• 例：已知等腰三角形的底边为a，底边上的 高的长为b，求作这个等腰三角形.
M
a
b
A
B 作法：（1）作线段BC，使BC=a； D （2）作BC的垂直平分线MN，交BC于D N ； （3）在MN上截取DA=h,得A点； （4）连结AB、AC，则△ABC即为所求等 腰三角形。
C
练习：如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，E、F是垂足，DE＝DF，求证：AB＝AC.
1 2
C B
∵∠1=∠2 （已知） ∴ DC=BC （等角对等边）
错，因为∠1和∠2 不是同一个三角形的内角。
例1：求证：如果三角形一个外角的平分线平行于 外角 平分线 平行于
三角形的一边，那么这个三角形是等腰三角形。 三角形的一边 ∥
等腰三角形性质
性质1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合（简写成“等腰三角形三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.一般的等腰三角形是轴对称图形,只有一条对称轴，顶角平分线所在的直线是它的对称轴。
但等边三角形（特殊的等腰三角形）有三条对称轴。
每个角的角平分线所在的直线，三条中线所在的直线，和高所在的直线就是等边三角形的对称轴。
8.等腰三角形中腰长的平方等于底边上高的平方加底的一半的平方（勾股定理）。
9.等腰三角形的腰与它的高的关系：腰大于高；腰的平方等于高的平方加底的一半的平方。
判定的方式定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
判定定理：在同一三角形中，如果两个角相等，那么这两个角所对的边也相等（简称：等角对等边）。
除了以上两种基本方法以外，还有如下判定的方式：在一个三角形中，如果一个角的平分线与该角对边上的中线重合，那么这个三角形是等腰三角形，且该角为顶角。
在一个三角形中，如果一个角的平分线与该角对边上的高重合，那么这个三角形是等腰三角形，且该角为顶角。
在一个三角形中，如果一条边上的中线与该边上的高重合，那么这个三角形是等腰三角形，且该边为底边。
显然，以上三条定理是“三线合一”的逆定理。
有两条角平分线（或中线，或高）相等的三角形是等腰三角形。
2.4等腰三角形的判定定理
36°
D
2 1
36 72° °
答： ∠1= 72°, ∠2= 36°
△ABC、 △ABD、 △BDC是等腰三角形。 、 B
（2）
C
例：一次数学实践活动的内容是测量河宽，如图，即测 量A,B之间的距离.同学们想出了许多方法,其中小聪的 方法是：从点Ａ出发,沿着与直线AB成60°角的AC方向
前进至C，在C处测得∠C＝30°.量出AC的长，它就是河
2. 已知:如图,DE∥BC,∠1=∠2.
求证:BD=CE.
证明: ∵∠1=∠2（已知）
∴AD=AE（在同一个三角形中，等 角对等边） ∵DE∥BC（已知） ∴∠1=∠B，∠2=∠C ∴∠B=∠C B D 1
A
2 E
C
∴AB=AC（在同一个三角形中，等角对等边） ∴AB－AD=AE－AC
即 BD=CE
D
B
H
C F E
3:如图，AD平分△ABC的外角∠EAC，AD//BC，则 △ ABC是等腰三角形吗？说明你的理由。
证明：∵AD∥BC， ∴∠1=∠B（两直线平行，同位角相等） ∠2=∠C（两直线平行，内错角相等）
E
∵ ∠1=∠2， ∴∠B=∠C ∴AB=AC（等角对等边）
B
1 A 2 D
C
△ODE的周长=BC=16
O D E C
B
名 图 形 称 等 腰 三 角 形
A
概念
性
质
判 定 两边相等
有两边 两腰相等
相等的
三角形
B C
等边对等角 等角对等边 三线合一
是等腰
三角形
说能出你这节课的收获和体验让大家 与你分享吗？
2.已知：△ABC中，AB=AC，D是AB上一点， 延长AC至点E，使CE=BD，连结DE交BC于F。 A 求证：DF=EF
D
2 1
36 72° °
答： ∠1= 72°, ∠2= 36°
△ABC、 △ABD、 △BDC是等腰三角形。 、 B
（2）
C
例：一次数学实践活动的内容是测量河宽，如图，即测 量A,B之间的距离.同学们想出了许多方法,其中小聪的 方法是：从点Ａ出发,沿着与直线AB成60°角的AC方向
前进至C，在C处测得∠C＝30°.量出AC的长，它就是河
2. 已知:如图,DE∥BC,∠1=∠2.
求证:BD=CE.
证明: ∵∠1=∠2（已知）
∴AD=AE（在同一个三角形中，等 角对等边） ∵DE∥BC（已知） ∴∠1=∠B，∠2=∠C ∴∠B=∠C B D 1
A
2 E
C
∴AB=AC（在同一个三角形中，等角对等边） ∴AB－AD=AE－AC
即 BD=CE
D
B
H
C F E
3:如图，AD平分△ABC的外角∠EAC，AD//BC，则 △ ABC是等腰三角形吗？说明你的理由。
证明：∵AD∥BC， ∴∠1=∠B（两直线平行，同位角相等） ∠2=∠C（两直线平行，内错角相等）
E
∵ ∠1=∠2， ∴∠B=∠C ∴AB=AC（等角对等边）
B
1 A 2 D
C
△ODE的周长=BC=16
O D E C
B
名 图 形 称 等 腰 三 角 形
A
概念
性
质
判 定 两边相等
有两边 两腰相等
相等的
三角形
B C
等边对等角 等角对等边 三线合一
是等腰
三角形
说能出你这节课的收获和体验让大家 与你分享吗？
2.已知：△ABC中，AB=AC，D是AB上一点， 延长AC至点E，使CE=BD，连结DE交BC于F。 A 求证：DF=EF
等腰三角形的判定课件(共21张PPT)
复习回顾
等腰三角形的性质定理
1、从边看：等腰三角形的两腰相等。 （定义）
2、从角看：等腰三角形的两底角相等。 （性质定理1）
3、从重要线段看：等腰三角形的顶角平分线、 底边上的中线和底边上的高三线合一。 （性质定理2）
如何判定一个三角形是等腰三角形？
定义：有两边相等的三角形是等腰三角形。
还有其他方法吗？
A
B
D C
例2：已知：AD交BC于点O，AB∥CD，OA=OB
求证：OC=OD
问题：
1、若已知AB∥ CD，OC=OD，能
A
否证明OA=OB？
2、若已知OA=OB，OC=OD，能否
证明AB ∥ CD？
C
B O
D
规律：
AB ∥ CD，OA=OB，OC=OD中已知任两 个可推出第三个。
例3、如图，在Rt△ABC和Rt△A’B’C’中,
已知：△ABC中，∠B=∠CBAC的平分线AD
A
在△ BAD和△ CAD中， 1 2
∠B=∠C，
∠1=∠2，
B
AD=AD
C
D
∴ △ BAD≌ △ CAD（AAS）
∴AB=AC（全等三角形的对应边相等）
思考:作底边上的高可以吗?作底边中线呢?
等腰三角形的判定定理：
如果一个三角形有两个角相等,那么这两个 角所对的边也相等(简写成“等角对等边”)
∠ABC= ∠A’B’C’=90°，
AB=A’B’,AC=A’C’，
区别:条件和结论互换。
3、已知：ED ∥ OB，EO=ED
求证：Rt△ABC≌Rt△A’B’C’ 求证：OD平分 AOB。
例1 :已知：如图，∠CAE是△ABC的外角∠1=∠2，
等腰三角形的性质定理
1、从边看：等腰三角形的两腰相等。 （定义）
2、从角看：等腰三角形的两底角相等。 （性质定理1）
3、从重要线段看：等腰三角形的顶角平分线、 底边上的中线和底边上的高三线合一。 （性质定理2）
如何判定一个三角形是等腰三角形？
定义：有两边相等的三角形是等腰三角形。
还有其他方法吗？
A
B
D C
例2：已知：AD交BC于点O，AB∥CD，OA=OB
求证：OC=OD
问题：
1、若已知AB∥ CD，OC=OD，能
A
否证明OA=OB？
2、若已知OA=OB，OC=OD，能否
证明AB ∥ CD？
C
B O
D
规律：
AB ∥ CD，OA=OB，OC=OD中已知任两 个可推出第三个。
例3、如图，在Rt△ABC和Rt△A’B’C’中,
已知：△ABC中，∠B=∠CBAC的平分线AD
A
在△ BAD和△ CAD中， 1 2
∠B=∠C，
∠1=∠2，
B
AD=AD
C
D
∴ △ BAD≌ △ CAD（AAS）
∴AB=AC（全等三角形的对应边相等）
思考:作底边上的高可以吗?作底边中线呢?
等腰三角形的判定定理：
如果一个三角形有两个角相等,那么这两个 角所对的边也相等(简写成“等角对等边”)
∠ABC= ∠A’B’C’=90°，
AB=A’B’,AC=A’C’，
区别:条件和结论互换。
3、已知：ED ∥ OB，EO=ED
求证：Rt△ABC≌Rt△A’B’C’ 求证：OD平分 AOB。
例1 :已知：如图，∠CAE是△ABC的外角∠1=∠2，
等腰三角形的判定
M N D E
C
中考链接
如图，已知三角形ABC中，AD垂直于 ∠C 的平分线于D，DE∥BC交AB于E. A 求证：EA=EB
分析：等腰三角形具有“顶角 B 平分线垂直平分底边”的性质 若“三线合一”，则三角形必 为等腰三角形。因此，可延长 AD构造出等腰三角形。
E D C F
(2004泉州)我们来探究“雪花曲线”的有 关问题，图中是边长为1的正三角形，将此正 三角形的每条边三等分，以居中的线段为底再 作正三角形，然后以其两腰代替底边，得到第 二个图形，重复上述的作法得到第三个图形， 则得到第五个图形的周长应等于（ ）
分析：本题的条件只有两类， C 角平分线和平行线，因此容 K 易找出它的基本图形是等腰 三角形，从而证明，AP=PL， 同理可证：AP=KP ∴KP=PL M
B P
)1 )2
3(
L N
D
A
证明：∵AD是BAN的平分线 ∴ 1=2 又∵ KL∥MN ∴2=3 ∴1=3 ∴AP=PL 同理可证；AP=KP ∴KP=PL
一、概念回顾
1.什么叫等腰三角形？
答：有两边相等的三角形叫做等腰三角形.
2.等腰三角形有哪些性质？ （1）等腰三角形的两个底角相等。 （2）等腰三角形顶角平分线，底边上中线和高线互相重合。 （3）等腰三角形是轴对称图形，对称轴是底边的中垂线。
等腰三角形的判定： 等角对等边； 有两边相等； “三线合一”的逆定理.
rtz85qts
都是我的娃儿啊，怎么会知道你家里的事情呢！后来，李长善也就不再问了。时间就这样一天天地过去，耿老爹在山镇 上李长善的家里已经待了快三年了。在此期间，他在对李家的三个孩子百般呵护的同时，也严格地管教他们，并且督促 他们多多干活儿，以报答李家的收留庇护之恩。而他自己更是手脚不闲，家里地里的大小活计，逮着什么干什么。对于 李家的街坊邻居们来说，他们就这样的事情也都慢慢地见怪不怪了。每当看到耿老爹高高兴兴地呼唤着尚文兄妹三人上 街逛游，或是下地干活儿时，大家都会报以友善的微笑，并不指指点点说些什么。大家相互传说着，都已经知道了事情 的原委，内心里边很为这个不幸的耿老爹由内而外迸发出来的伟大父爱而深深地感动了，并且也非常赞赏李长善一家人 的感恩之心和博大胸怀，背地里都在竖起大拇指言赞他们呢！想到鄱阳湖周围有些名气的郎中都已经请遍了，但这位耿 大哥仍然还是这个样子，李家开始有些失望了。加之近日来李长善的腰腿疼旧疾复发，行动非常不便。更重要的是，愿 意接手医治耿老爹这个病症的郎中越来越少了。李长善夫妇俩终于无奈地决定，放弃继续为这位好心人的，就让他高高 兴兴得和自己心目中的儿女们，一直像现在这样愉快地生活下去吧！艰难地做出了这个决定之后，李家夫妻俩一直想找 机会和自己的三个孩子说一些话，但无奈三个孩子和耿老爹在一起的时间，总是比和自己的父母在一起的时间多得多， 大家凑在一起就更不容易了。且说耿老爹看到李长善腰腿疼旧疾复发行动不便已经多日了，但还不见他请人医治，就对 他说：“我没有病，李大哥你还老是请郎中给我治病。你现在真得有病了，怎么就不请个郎中来看看啊？”李长善说： “我这是老毛病了，以前也看过的，没有用啊！耿大哥你放心，这个老毛病啊，过些日子自己就会全好了的！”耿老爹 只好说：“那你就放心歇着吧，家里地里的活计，有我和正儿他们干就行了！”李长善感激地说：“那就有劳耿大哥了 啊！放心，我会安心养病的！”那日一早起来，耿老爹见行动更加不便的李大哥随手拿了一根核桃粗细的木头棍儿拄着 走路，就对他说：“李大哥，这木头棍儿拄着多不应手，不如让我给你做个好使的拐杖用吧！”李长善一听这耿大哥竟 然还会做拐杖，倒觉得蛮有趣儿，就高兴地说：“好啊！耿大哥你还会做这个，那就给我做一个吧！我这老毛病啊，还 真不知道什么时候会好，什么时候又给犯了呢！我就备他一个拐杖得了！”耿老爹说：“我做得不一定有多好，但总归 会比这根木头棍儿多少好使一点儿的！”说干就干。当日午饭后，耿老爹果真就放弃了打盹儿午休一小会儿的习惯，在 院子里认真地做起拐杖来了，李长善夫妇赶快趁此机会把儿女们聚在一起。这一家
《等腰三角形的判定》课件
A O
B DE C
A
FG
D
B
C
E
开启 智慧
By 杜小二
已知:如图,在△ABC中，BF、CF分别平∠DBC、 ∠ECB并交于点F,过F作 DE∥BC求证:DE=BD+CE
A
B
C
D
F
E
试一试
By 杜小二
已知:如图,在△ABC中，BO、CO分 别平分∠ABC、∠ACB并交于点O, 过点O作 OD∥AB, OE∥AC,BC=16, 求: △ODE的周长
Ａ
By 杜小二
1.如图:ΔABC中,已知AB=AC,
Ｂ
Ｃ
∠B=∠C．在三角形中等边对等角．
２、反过来：在ΔABC中，∠B=∠C， AB=AC成立吗？
By 杜小二
归纳总结
如果一个三角形有两个角相等，
By 杜小二
那么这个三角形是等腰三角形。
用符号语言表示为：
A
在△ABC中，
∵∠B=∠C (已知 )
By 杜小二
等腰三角形的判定
By 杜小二
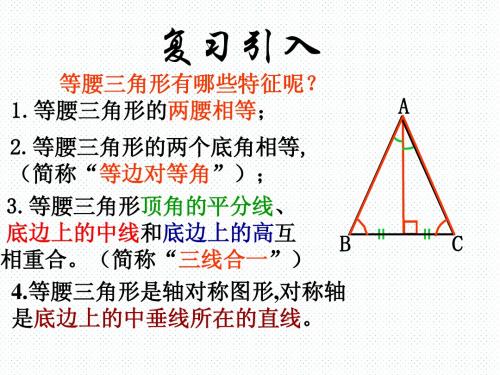
温故而知新
等腰三角形有哪些特征呢？ 1.等腰三角形的两腰相等；
By 杜小二
A
2.等腰三角形的两个底角相等, （简称“等边对等角”）；
3.等腰三角形顶角的平分线、
底边上的中线和底边上的高互 B
C
相重合。（简称“三线合一”）
4.等腰三角形是轴对称图形,对称轴 是顶角的平分线所在的直线。
∴ AC=AB.
(在一个三角形中，等角对等边)
B
C
这又是一个判定两条线段相等根据之一.
已知：在△ABC中，∠B＝∠C。 By 杜小二
求证：AB＝AC A A
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
等腰三角形判定方法
等腰三角形是指至少两边长度相等的三角形。
判定一个三角形是否为等腰三角形可以使用以下方法：
1. 比较边长：测量三条边的长度，如果有两条边的长度相等，则三角形为等腰三角形。
2. 角度判断：如果一个三角形有两个角相等，则它是一个等腰三角形。
3. 等腰线段：在三角形中找出两个等长的边，通过比较三角形的边长，寻找等腰线段。
4. 高度比较：通过三角形的高度也可以判断是否为等腰三角形，如果有两个等长的边，则它的高度也相等。
使用上述方法中的任意一种都可以判定一个三角形是否为等腰三角形。