R语言arima模型时间序列分析报告(附代码数据)
R语言arima模型时间序列分析报告(附代码数据)
#偏自相关值选5阶。#故我们的ARMIA模<-arima(timeseries,order=c(5,2,5))
servearima
#偏自相关值选5阶。
##
## Call:
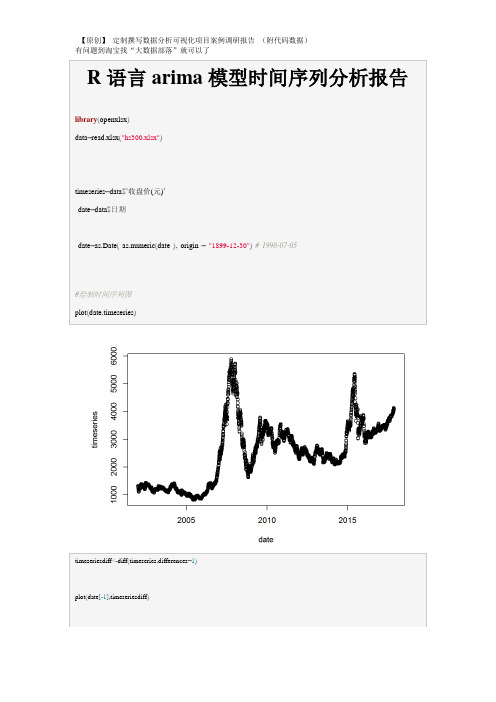
#绘制时间序列图
plot(date,timeseries)
timeseriesdiff<-diff(timeseries,differences=1)
plot(date[-1],timeseriesdiff)
#时间序列分析之ARIMA模型预测#我们可以通过键入下面的代码来得到时间序列(数据存于“timeseries”)的一阶差分,并画出差分序列的图:
## s.e. NaN NaN NaN NaN NaN NaN 0.1400 NaN
## ma4 ma5
## -0.5481 -0.0482
## s.e. 0.1311 NaN
##
## sigma^2 estimated as 2672: log likelihood = -20640.51, aic = 41303.02
library("forecast")
#对沪深300指数在2017年12月4日至2017年12月31日之间的每日收盘价进行预测
#时间序列分析之ARIMA模型预测#上图预测中的时间曲线图显示出对着时间增加,方差大致为常数(大致不变)(尽管上半部分的时间序#列方差看起来稍微高一些)。时间序列的直方图显示预测误大致是正态分布的且平均值接近于0(服从零均值的正态分布的)。因此,把预测误差看作平均值为0方差为常数正态分布(服从零均值、方差不变的正态分布)是合理的。
【原创】R语言时间序列arima和随机森林模型预测分析报告(附代码数据)
##
## Model df: 4. Total lags used: 8
checkresiduals(lm_mod)
##
## Breusch-Godfrey test for serial correlation of order up to 10
## Q* = 2.2891, df = 5, p-value = 0.8079
##
## Model df: 3. Total lags used: 8
checkresiduals(arireg)
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(2,2,1) errors
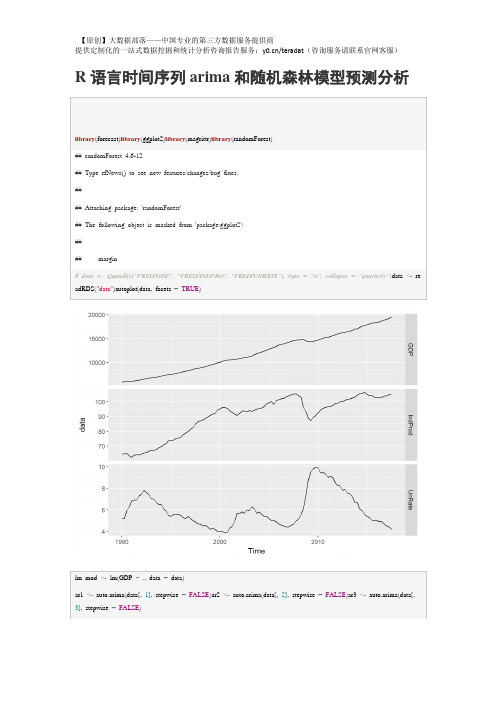
lm_mod<-lm(GDP~.,data=data)
ar1<-auto.arima(data[,1],stepwise=FALSE)ar2<-auto.arima(data[,2],stepwise=FALSE)ar3<-auto.arima(data[,3],stepwise=FALSE)
GDP<-forecast(ar1)$meanIndProd<-forecast(ar2)$meanUnRate<-forecast(ar3)$meanf3<-cbind(IndProd,UnRate)arireg<-auto.arima(data[,1],stepwise=FALSE,xreg=data[,-1])
summary(lm_mod)
##
## Call:
## lm(formula = GDபைடு நூலகம் ~ ., data = data)
r语言时间序列预测代码

r语言时间序列预测代码一、引言R语言是一种广泛使用的统计软件,在做时间序列预测中有着非常重要的作用。
本文将介绍其在时间序列预测中的基本原理和应用例子,并提供R语言时间序列预测代码。
二、R语言时间序列预测原理时间序列预测就是根据历史数据预测未来数据发展的趋势。
它有三种主要的类型:趋势分析、季节性分析和平稳性分析。
趋势分析就是预测从过去到将来的趋势变化。
季节性分析就是预测一些带有明显季节性变动的变量,例如气温变化,季节性分析可以用来减少预测中的不确定性并预测出可能出现的短期变化。
平稳性分析就是预测在某一时间点之后,变量会围绕某一水平进行摆动的变化,这就是ARIMA模型。
R语言有三种常用的时间序列预测模型:ARIMA模型、自回归模型和移动平均模型。
三、R语言时间序列预测示例下面的示例使用R语言的ARIMA模型来预测一个出行指数的变化: # 导入模块library(forecast)# 读取数据data <- read.csv('travel_index.csv')# 将数据转换成时间序列data_ts <- ts(data, frequency =12,start=c(2015,1),end=c(2020,10))# 训练模型arima_model <- auto.arima(data_ts)# 预测forecast <- forecast(arima_model, h = 24)# 结果可视化plot(forecast)四、结论本文介绍了R语言在时间序列预测中的基本原理和应用,并提供了一个实例的R语言时间序列预测代码。
R语言在时间序列预测中有着广泛的应用,使用起来很方便,可以快速得到准确结果。
ARIMA模型---时间序列分析---温度预测
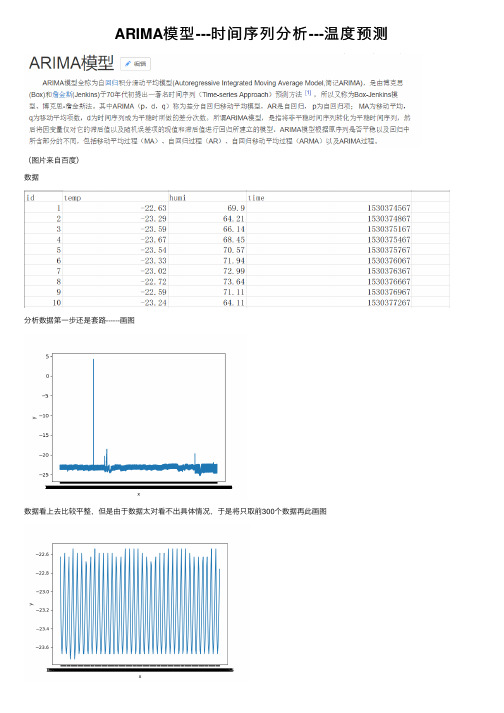
ARIMA模型---时间序列分析---温度预测(图⽚来⾃百度)数据分析数据第⼀步还是套路------画图数据看上去⽐较平整,但是由于数据太对看不出具体情况,于是将只取前300个数据再此画图这数据看上去很不错,感觉有隐藏周期的意思代码#coding:utf-8import csvimport matplotlib.pyplot as pltdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1]))aim_list_2.append(data[3])returndef plot_picture(x, y):plt.xlabel('x')plt.ylabel('y')plt.plot(x, y)plt.show()returnif__name__ == '__main__':temp = []tim = []file_name = 'C:/Users/lichaoxing/Desktop/testdata.csv'read_csv_data(temp, tim, file_name)plot_picture(tim[:300], temp[:300])使⽤ARIMA模型(ARMA)第⼀步观察数据是否是平稳序列,通过上图可以看出是平稳的如果不平稳,则需要进⾏预处理,⽅法有对数变换差分对于平稳的时间序列可以直接使⽤ARMA(p, q)模型进⾏拟合ARMA (p, q) : AR(p) + MA(q)此时参数p和q的确定可以通过观察ACF和PACF图来确定通过观察PACF图可以看出,阶数为9也就是p=9,这⾥ACF图看出⾃相关呈现震荡下降收敛,但是怎么决定出q,我没太明⽩,这⾥姑且拍脑袋才⼀个吧就q=3但是这⾥我遇到了⼀个问题,没有搞懂,就是平稳的序列,如果我进⾏⼀阶差分后应该仍然是平稳的序列,但是这个时候我⼜画了⼀个ACF 与PACF图,竟然是下图这样,lag的范围是-0.04到0.04(不懂)lag的范围是-0.04到0.04的问题原因(修改于再次使⽤此模型)原因:当时,我使⽤的是⼀阶差分,也就是让数据的后⼀个值减去前⼀个值得到新的值,这样就会导致第⼀个值变为缺失值(下⾯的数据是再此使⽤此模型时的数据,与原博客数据⽆关)就是因为此处的值为缺失值,导致绘制ACF与PACF时数据有问题⽽⽆法成功显⽰解决办法,在绘制上述图形前,将第⼀个数据去除:dta= dta.diff(1)dta = dta.truncate(before= ym[1])#删除第⼀个缺失值其实还有就是使⽤ADF检验,得到的结果如图,这个p值很⼩===》平稳画图代码def acf_pacf(temp, tim):x = timy = tempdta = pd.Series(y, index = pd.to_datetime(x))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=50,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=50,ax=ax2)show()ADF检验代码def test_stationarity(timeseries):dftest = adfuller(timeseries, autolag='AIC')return dftest[1]这⾥先使⽤ARMA(9,3)来实验测试⼀下效果,取前300个数据中的前250个作为train,后⾯的作为test 效果可以说这个模型是真的强⼤,预测的还是⼗分准确的代码def test_300(temp, tim):x = tim[0:300]y = temp[0:300]dta = pd.Series(y[0:249], index = pd.to_datetime(x[0:249]))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=30,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=30,ax=ax2)arma_mod = sm.tsa.ARMA(dta, (9, 3)).fit(disp = 0)predict_sunspots = arma_mod.predict(x[200], x[299], dynamic=True)fig, ax = plt.subplots(figsize=(9, 6))ax = dta.ix[x[0]:].plot(ax=ax)predict_sunspots.plot(ax=ax)show()其实,可以通过代码来⾃动的选择p和q的值,依据BIC准则,⽬标就是bic越⼩越好代码def proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModel遇到的问题,预测时predict函数没怎么使⽤明⽩当写于某些预测区间的时候,会报 “start”或“end”的相关错误,还有⼀个函数forcast,这个函数使⽤就是forcast(N):预测后⾯N个值返回的是预测值(array型)标准误差(array型)置信区间(array型)还有:对于构造时间序列,时间可以是时间格式:如 “2018-01-01” 或者就是个时间戳,在⽤时间戳的时候,其实在序列⾥它会⾃动识别时间戳,并加上起始时间1970-01-01 00:00:01形式附录(代码)预测⼀序列中某⼀点的值#coding:utf-8import csvimport timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport argparseimport warningswarnings.filterwarnings('ignore')def timestamp_datatime(value):value = time.localtime(value)dt = time.strftime('%Y-%m-%d %H:%M',value)return dtdef time_timestamp(my_date):my_date_array = time.strptime(my_date,'%Y-%m-%d %H:%M')my_date_stamp = time.mktime(my_date_array)return my_date_stampdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1])) #1:温度 2:湿度dt = int(data[3])aim_list_2.append(dt)returndef proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q)) #bugtry:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModeldef test_300(temp, tim, time_in):x = []y = []end_index = len(tim)for i in range(0, len(tim)):if (time_in - (tim[i]) < 300):end_index = ibreakif (end_index < 100):x = tim[0: end_index]y = temp[0: end_index]else:x = tim[end_index - 100: end_index]y = temp[end_index - 100: end_index]tidx = pd.DatetimeIndex(x, freq='infer')dta = pd.Series(y, index = tidx)print(dta)arma_mod = proper_model(dta, 9)predict_sunspots = arma_mod.forecast(1)return predict_sunspots[0]def predict_temperature(file_name, time_in):temp = []tim = []read_csv_data(temp, tim, file_name)result_temp = test_300(temp, tim, time_in)return result_tempif__name__ == '__main__':parser = argparse.ArgumentParser()parser.add_argument('-f', action='store', dest='file_name')parser.add_argument('-t', action='store', type = int, dest='time_')args = parser.parse_args()file_name = args.file_nametime_in = args.time_result_temp = predict_temperature(file_name, time_in)print ('the temperature is %f ' % result_temp)在上⾯的代码中,预测某⼀点的值我采⽤序列中此点的前100个点作为训练集如果给出待预测的多个点,由于每次都要计算模型的p和q以及拟合模型,时间会很慢,于是考虑将给定的待预测时间点序列切割成⼩段,使每⼀段中最⼤与最⼩的时间间隔在某⼀范围内在使⽤forcast(n)函数⼀次预测多点,然后在预测值中找到与待预测的时间值相近的值,速度⼤⼤提升,思路如图代码#coding:utf-8import csv#import timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport warningswarnings.filterwarnings('ignore')def proper_model(timeseries, maxLag):init_bic = 1000000000init_p = 1init_q = 1for p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_p = pinit_q = qinit_bic = bicreturn init_p, init_qdef read_csv_data(file_name, clss = 1):i = 0aim_list_1 = [] #temperature(1) or humidity(2)aim_list_2 = [] #timecsv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[clss]))dt = int(data[3])aim_list_2.append(dt)tidx = pd.DatetimeIndex(aim_list_2, freq = None)dta = pd.Series(aim_list_1, index = tidx)init_p, init_q = proper_model(dta[:aim_list_2[100]], 9)return init_p, init_q, aim_list_2, dtadef for_kernel(p, q, tim, dta, tmp_time_list, result_dict):interval = 20end_index = len(tim) - 1for i in range(0, len(tim)):if (tmp_time_list[0]["time"] - tim[i] < tim[1] - tim[0]):end_index = ibreakif (end_index < 100):dta = dta.truncate(after = tim[end_index])else:dta = dta.truncate(before= tim[end_index - 101], after = tim[end_index])arma_mod = ARMA(dta, order=(p, q)).fit(disp = 0, method='css')#为未来interval天进⾏预测,返回预测结果,标准误差,和置信区间predict_sunspots = arma_mod.forecast(interval)####################################for tim_i in tmp_time_list:for tim_ in tim:if tim_i["time"] - tim_ >= 0 and tim_i["time"] - tim_ < tim[1] - tim[0]:result_dict[tim_i["time"]] = predict_sunspots[0][tim.index(tim_) - end_index] returndef kernel(p, q, tim, dta, time_in_list):interval = 20time_first = time_in_list[0]det_time = tim[1] - tim[0]result_dict = {}tmp_time_list = []for time_ in time_in_list:if time_first["time"] + det_time * interval > time_["time"]:tmp_time_list.append(time_)continuetime_first = time_for_kernel(p, q, tim, dta, tmp_time_list, result_dict)tmp_time_list = []tmp_time_list.append(time_first)for_kernel(p, q, tim, dta, tmp_time_list, result_dict)return result_dictdef predict_temperature(file_name, time_in_list, clss = 1):p, q, tim, dta = read_csv_data(file_name, clss)result_temp_dict = kernel(p, q, tim, dta, time_in_list)return result_temp_dictdef predict_humidity(file_name, time_in_list, clss = 2):p, q, tim, dta = read_csv_data(file_name, clss)result_humi_dict = kernel(p, q, tim, dta, time_in_list)return result_humi_dictif__name__ == '__main__':file_name = "testdata.csv"time_in = [{"time":1530419271,"temp":"","humi":""},{"time":1530600187,"temp":"","humi":""},{"time":1530825809,"temp":"","humi":""}] #time_in = [{"time":1530600187,"temp":"","humi":""},]result_temp = predict_temperature(file_name, time_in)print(result_temp)由于后续⼜改动了需求,需要预测温度以及湿度,完成了项⽬在github。
R 语言环境下用ARIMA模型做时间序列预测
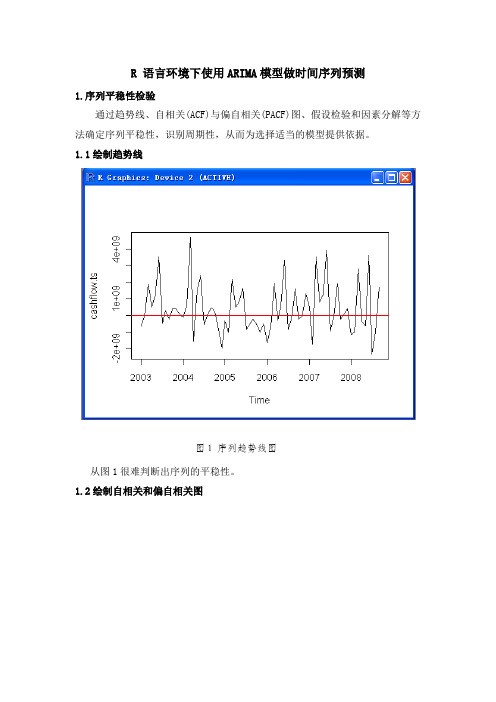
R 语言环境下使用ARIMA模型做时间序列预测1.序列平稳性检验通过趋势线、自相关(ACF)与偏自相关(PACF)图、假设检验和因素分解等方法确定序列平稳性,识别周期性,从而为选择适当的模型提供依据。
1.1绘制趋势线图1 序列趋势线图从图1很难判断出序列的平稳性。
1.2绘制自相关和偏自相关图图2 序列的自相关和偏自相关图从图2可以看出,ACF拖尾,PACF1步截尾(p=1),说明该现金流时间序列可能是平稳性时间序列。
1.3 ADF、PP和KPSS 检验平稳性图3 ADF、PP和KPSS检验结果通过ADF检验,说明该现金流时间序列是平稳性时间序列(p-value for ADF test <0.02,拒绝零假设).pp test和kpss test 结果中的警告信息说明这两种检验在这里不可用。
但是这些检验没有充分考虑趋势、周期和季节性等因素。
下面对该序列进行趋势、季节性和不确定性因素分解来进一步确认序列的平稳性。
1.4 趋势、季节性和不确定性因素分解R 提供了两种方法来分解时间序列中的趋势、季节性和不确定性因素。
第一种是使用简单的对称过滤法,把相应时期内经趋势调整后的观察值进行平均,通过decompose()函数实现,如图4。
第二种方法更为精确,它通过平滑增大规模后的观察值来寻找趋势、季节和不确定因素,利用stl()函数实现。
如图5。
图4 decompose()函数分解法图5 stl()函数分解法两种方法得到的结果非常相似。
从上图可以看出,该现金流时间序列没有很明显的长期趋势。
但是有明显的季节性或周期性趋势,经分解后的不确定因素明显减少。
综上平稳性分析检验,我们选用包含季节性因素的S-ARIMA模型来预测现金流时间序列。
2.S-ARIMA模型2.1 建立SARIMA模型在R 软件包中包含auto.arima()、expand.grid() 等函数,针对p,d,q 众多的可能取值,可以通过expand.grid()建立所有的可能参数组合,用for()条件函数代入相应的arima()模型,把结果储存在BIC当中。
时间序列分析R语言代码

时间序列分析R语言代码时间序列分解分析的R语言操作如下:选取R语言自带的数据包UKgas,即1960-1986每月英国天然气消耗的数据,并将其赋值于n:n<-UKgassummary()函数提供了最小值、最大值、四分位数和数值型变量的均值: summary(n)画出UKgas的时序图:plot(n)时间序列分解分析方法一:基础包stats的decompose函数调用基础包stats:library("stats")利用基础包stats的decompose函数对时间序列进行分解分析,命名为fit1。
该函数基于移动平均方法,multiplicative表示使用乘法模型:fit1=decompose(n, type = c("multiplicative"))展示decompose函数的分解结果:fit1绘制方法一,即利用decompose函数分解的分解图:plot(fit1)`时间序列分解分析方法二:基础包stats的stl函数stl函数stl(x,s.window,s.degree=0,t.window = NULL, t.degree = 1, robust = FALSE,na.action = na.fail)x----待分解的变量s.window----提取季节性时的loess算法时间窗口宽度,可设为periodic,或者设为奇数并不能低于7s.degree -----提取季节性时局部拟合多项式的阶数,须为0或1 t.window----提取长期趋势性时的loess算法时间窗口宽度,缺省为NULL,或者奇数t.degree-----提取长期趋势性时的局部拟合多项式的阶数,须为0或1robust -----在loess过程中是否使用鲁棒拟合利用基础包stats的stl函数对时间序列进行分解分析,命名为fit2:fit2<-stl(n,s.window="periodic",s.degree = 0, t.window = NULL, t.degree = 1,robust= FALSE,na.action = na.fail)展示stl函数的分解结果:fit2绘制方法二的分解图: plot(fit2)。
【原创】r语言外汇数据进行arima指数平滑时间序列分析

对外汇数据进行时间序列分析时间序列存在于社会的经济、医学等很多领域,其中时间序列的趋势分析是一个具有重要现实意义的研究领域,因为人们掌握事物的发展趋势(内在规律),就能利用这些规律制定相应的决策。
传统对时间序列的分析多从系统的角度出发,而本文对时间序列的分析是从数据挖掘的角度出发。
外汇汇率时间序列,往往含有较多的干扰因素,因此必须对原始数据进行平滑处理,尽可能的除去附加的干扰因素。
为了能够对时间序列进行数据挖掘,必须从时间序列数据中抽取决定时间序列行为发展趋势的静态属性。
数据选取首先我们从网站http://fx.sauder.ubc.ca/data.html下载CAD和USD需货币对的两年汇率,并将数据读入RDownload the exchange rate of your desired currency pairs for at least two years from the website: http://fx.sauder.ubc.ca/data.html, and read the data into R. (5 points)浏览数据dataJul.Day YYYY.MM.DD Wdy D1 2457025 2015/01/02 Fri 0.651012 2457028 2015/01/05 Mon 0.656443 2457029 2015/01/06 Tue 0.658964 2457030 2015/01/07 Wed 0.663445 2457031 2015/01/08 Thu 0.66151...576 2457864 2017/04/20 Thu 0.77942577 2457865 2017/04/21 Fri 0.78233578 2457868 2017/04/24 Mon 0.78227579 2457869 2017/04/25 Tue 0.77907580 2457870 2017/04/26 Wed 0.77896581 2457871 2017/04/27 Thu 0.77587582 2457872 2017/04/28 Fri 0.77299583 2457875 2017/05/01 Mon 0.77420584 2457876 2017/05/02 Tue 0.77392585 2457877 2017/05/03 Wed 0.77476586 2457878 2017/05/04 Thu 0.77456587 2457879 2017/05/05 Fri 0.77177588 2457882 2017/05/08 Mon 0.77263589 2457883 2017/05/09 Tue 0.77337590 2457884 2017/05/10 Wed 0.77278591 2457885 2017/05/11 Thu 0.77656592 2457886 2017/05/12 Fri 0.77651593 2457889 2017/05/15 Mon 0.77479594 2457890 2017/05/16 Tue 0.77466595 2457891 2017/05/17 Wed 0.77186596 2457892 2017/05/18 Thu 0.76994597 2457893 2017/05/19 Fri 0.76776598 2457897 2017/05/23 Tue 0.77037599 2457898 2017/05/24 Wed 0.77232600 2457899 2017/05/25 Thu 0.77218601 2457900 2017/05/26 Fri 0.78092绘制时间序列图收集历史资料,加以整理,编成时间序列,并根据时间序列绘成统计图。
用R语言做时间序列分析

用R语言做时间序列分析时间序列(time series )是一系列有序的数据。
通常是等时间间隔的采样数据。
如果不是等间隔,则一般会标注每个数据点的时间刻度。
下面以time series 普遍使用的数据airline passenger 为例。
这是^一年的每月乘客数量,单位是千人次。
Time如果想尝试其他的数据集,可以访问这里:https:///data/list/?q=provider:tsdl可以很明显的看出,airli ne passe nger 的数据是很有规律的。
time series data mining 主要包括decompose (分析数据的各个成分,例如趋势,周期性),prediction (预测未来的值),classificatio n (对有序数据序列的feature 提取与分类),clusteri ng (相似数列聚类)等。
这篇文章主要讨论prediction (forecast,预测)问题。
即已知历史的数据,如何准确预测未来的数据。
先从简单的方法说起。
给定一个时间序列,要预测下一个的值是多少,最简单的思路是什么呢?(1)m ean (平均值):未来值是历史值的平均。
(2)exponential smoothing (指数衰减):当去平均值得时候,每个历史点的权值可以不一样。
最自然的就是越近的点赋予越大的权重。
= aX± + ct^X2 + a3X3+ …或者,更方便的写法,用变量头上加个尖角表示估计值X t+1 = aX t+ (1 - a)X t(3) sn aive :假设已知数据的周期,那么就用前一个周期对应的时刻作为下一个周期对应时刻的预测值(4)d rift :飘移,即用最后一个点的值加上数据的平均趋势tX t+h|t =禺+占2心-斗-丄= x t +占(罠-如Tt = •介绍完最简单的算法,下面开始介绍两个time series 里面最火的两个强大的算法:Holt-Winters 和ARIMA 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#时间序列分析之ARIMA模型预测#二次差分(上面)后的时间序列在均值和方差上确实看起来像是平稳的,随着时间推移,时间序列的水平和方差大致保持不变。因此,看起来我们需要对data进行两次差分以得到平稳序列。#第二步,找到合适的ARIMA模型#如果你的时间序列是平稳的,或者你通过做n次差分转化为一个平稳时间序列,接下来就是要选择合适的ARIMA模型,这意味着需要寻找ARIMA(p,d,q)中合适的p值和q值。为了得到这些,通常需要检查[平稳时间序列的(自)相关图和偏相关图。#我们使用R中的“acf()”和“pacf”函数来分别(自)相关图和偏相关图。“acf()”和“pacf设定“plot=FALSE”来得到自相关和偏相关的真实值。
## arima(x = timeseries, order = c(5, 2, 5))
##
## Coefficients:
## Warning in sqrt(diag(x$var.coef)):产生了NaNs
## ar1 ar2 ar3 ar4 ar5 ma1 ma2 ma3
## -0.8663 -0.6281 -0.5714 0.0499 0.0582 -0.0862 -0.2969 -0.0206
#绘制时间序列图
plot(date,timeseries)
timeseriesdiff<-diff(timeseries,differences=1)
plot(date[-1],timeseriesdiff)
#时间序列分析之ARIMA模型预测#我们可以通过键入下面的代码来得到时间序列(数据存于“timeseries”)的一阶差分,并画出差分序列的图:
## s.e. NaN NaN NaN NaN NaN NaN 0.1400 NaN
## ma4 ma5
## -0.5481 -0.0482
## s.e. 0.1311 NaN
##
## sigma^2 estimated as 2672: log likelihood = -20640.51, aic = 41303.02
library("forecast")
#对沪深300指数在2017年12月4日至2017年12月31日之间的每日收盘价进行预测
#时间序列分析之ARIMA模型预测#上图预测中的时间曲线图显示出对着时间增加,方差大致为常数(大致不变)(尽管上半部分的时间序#列方差看起来稍微高一些)。时间序列的直方图显示预测误大致是正态分布的且平均值接近于0(服从零均值的正态分布的)。因此,把预测误差看作平均值为0方差为常数正态分布(服从零均值、方差不变的正态分布)是合理的。
pacf(na.omit(timeseriesdiff2),lag.max=20)
#偏自相关值选5阶。#故我们的ARMIA模型为armia(1,2,5)
servearima<-arima(timeseries,order=c(5,2,5))
servearima
#偏自相关值选5阶。
##
## Call:
acf(na.omit(timeseriesdiff2),lag.max=20)
#时间序列分析之ARIMA模型预测
#自相关图显示滞后1阶自相关值基本没有超过边界值,虽然6阶自相关值超出边界,那么很可能属于偶然出现的,而自相关值在其他上都没有超出显著边界,而且我们可以期望1到20之间的会偶尔超出95%的置信边界。
R语言arima模型时间序列分析报告
library(openxlsx)
data=read.xlsx("hs300.xlsx")
timeseries=data$`收盘价(元)`
date=data$日期
date=as.Date(as.numeric(date),origin="1899-12-30")# 1998-07-05
