实验三：ARIMA模型建模与预测实验报告
【原创】R语言时间序列arima和随机森林模型预测分析报告(附代码数据)
##
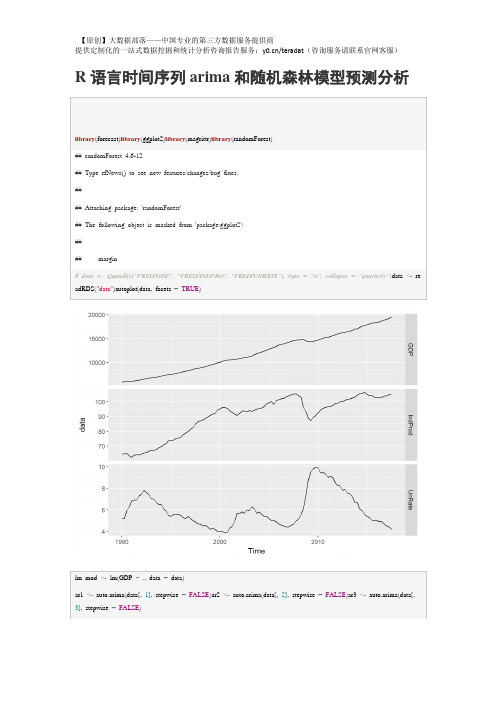
## Model df: 4. Total lags used: 8
checkresiduals(lm_mod)
##
## Breusch-Godfrey test for serial correlation of order up to 10
## Q* = 2.2891, df = 5, p-value = 0.8079
##
## Model df: 3. Total lags used: 8
checkresiduals(arireg)
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(2,2,1) errors
lm_mod<-lm(GDP~.,data=data)
ar1<-auto.arima(data[,1],stepwise=FALSE)ar2<-auto.arima(data[,2],stepwise=FALSE)ar3<-auto.arima(data[,3],stepwise=FALSE)
GDP<-forecast(ar1)$meanIndProd<-forecast(ar2)$meanUnRate<-forecast(ar3)$meanf3<-cbind(IndProd,UnRate)arireg<-auto.arima(data[,1],stepwise=FALSE,xreg=data[,-1])
summary(lm_mod)
##
## Call:
## lm(formula = GDபைடு நூலகம் ~ ., data = data)
ARIMA模型---时间序列分析---温度预测
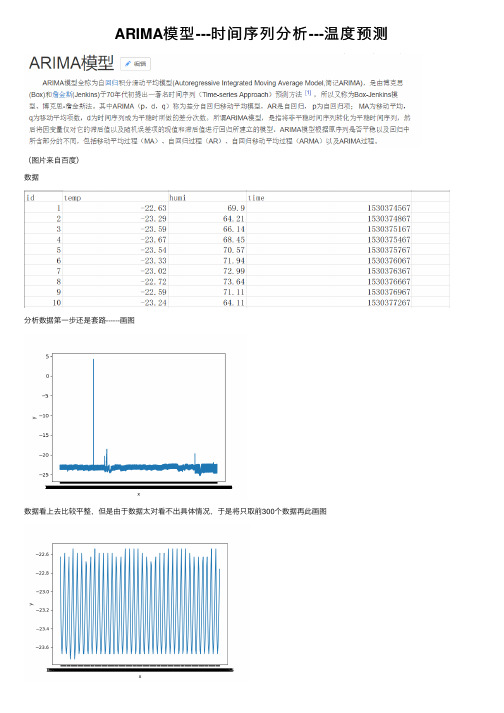
ARIMA模型---时间序列分析---温度预测（图⽚来⾃百度）数据分析数据第⼀步还是套路------画图数据看上去⽐较平整，但是由于数据太对看不出具体情况，于是将只取前300个数据再此画图这数据看上去很不错，感觉有隐藏周期的意思代码#coding:utf-8import csvimport matplotlib.pyplot as pltdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1]))aim_list_2.append(data[3])returndef plot_picture(x, y):plt.xlabel('x')plt.ylabel('y')plt.plot(x, y)plt.show()returnif__name__ == '__main__':temp = []tim = []file_name = 'C:/Users/lichaoxing/Desktop/testdata.csv'read_csv_data(temp, tim, file_name)plot_picture(tim[:300], temp[:300])使⽤ARIMA模型（ARMA）第⼀步观察数据是否是平稳序列，通过上图可以看出是平稳的如果不平稳，则需要进⾏预处理，⽅法有对数变换差分对于平稳的时间序列可以直接使⽤ARMA(p, q)模型进⾏拟合ARMA (p, q) : AR(p) + MA(q)此时参数p和q的确定可以通过观察ACF和PACF图来确定通过观察PACF图可以看出，阶数为9也就是p=9，这⾥ACF图看出⾃相关呈现震荡下降收敛，但是怎么决定出q，我没太明⽩，这⾥姑且拍脑袋才⼀个吧就q=3但是这⾥我遇到了⼀个问题，没有搞懂，就是平稳的序列，如果我进⾏⼀阶差分后应该仍然是平稳的序列，但是这个时候我⼜画了⼀个ACF 与PACF图，竟然是下图这样，lag的范围是-0.04到0.04（不懂）lag的范围是-0.04到0.04的问题原因（修改于再次使⽤此模型）原因：当时，我使⽤的是⼀阶差分，也就是让数据的后⼀个值减去前⼀个值得到新的值，这样就会导致第⼀个值变为缺失值（下⾯的数据是再此使⽤此模型时的数据，与原博客数据⽆关）就是因为此处的值为缺失值，导致绘制ACF与PACF时数据有问题⽽⽆法成功显⽰解决办法，在绘制上述图形前，将第⼀个数据去除：dta= dta.diff(1)dta = dta.truncate(before= ym[1])#删除第⼀个缺失值其实还有就是使⽤ADF检验，得到的结果如图，这个p值很⼩===》平稳画图代码def acf_pacf(temp, tim):x = timy = tempdta = pd.Series(y, index = pd.to_datetime(x))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=50,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=50,ax=ax2)show()ADF检验代码def test_stationarity(timeseries):dftest = adfuller(timeseries, autolag='AIC')return dftest[1]这⾥先使⽤ARMA(9,3)来实验测试⼀下效果，取前300个数据中的前250个作为train，后⾯的作为test 效果可以说这个模型是真的强⼤，预测的还是⼗分准确的代码def test_300(temp, tim):x = tim[0:300]y = temp[0:300]dta = pd.Series(y[0:249], index = pd.to_datetime(x[0:249]))fig = plt.figure(figsize=(9,6))ax1 = fig.add_subplot(211)fig = sm.graphics.tsa.plot_acf(dta,lags=30,ax=ax1)ax2 = fig.add_subplot(212)fig = sm.graphics.tsa.plot_pacf(dta,lags=30,ax=ax2)arma_mod = sm.tsa.ARMA(dta, (9, 3)).fit(disp = 0)predict_sunspots = arma_mod.predict(x[200], x[299], dynamic=True)fig, ax = plt.subplots(figsize=(9, 6))ax = dta.ix[x[0]:].plot(ax=ax)predict_sunspots.plot(ax=ax)show()其实，可以通过代码来⾃动的选择p和q的值，依据BIC准则，⽬标就是bic越⼩越好代码def proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModel遇到的问题，预测时predict函数没怎么使⽤明⽩当写于某些预测区间的时候，会报 “start”或“end”的相关错误，还有⼀个函数forcast，这个函数使⽤就是forcast(N)：预测后⾯N个值返回的是预测值（array型）标准误差（array型）置信区间（array型）还有：对于构造时间序列，时间可以是时间格式：如 “2018-01-01” 或者就是个时间戳，在⽤时间戳的时候，其实在序列⾥它会⾃动识别时间戳，并加上起始时间1970-01-01 00:00:01形式附录（代码）预测⼀序列中某⼀点的值#coding:utf-8import csvimport timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport argparseimport warningswarnings.filterwarnings('ignore')def timestamp_datatime(value):value = time.localtime(value)dt = time.strftime('%Y-%m-%d %H:%M',value)return dtdef time_timestamp(my_date):my_date_array = time.strptime(my_date,'%Y-%m-%d %H:%M')my_date_stamp = time.mktime(my_date_array)return my_date_stampdef read_csv_data(aim_list_1, aim_list_2, file_name):i = 0csv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[1])) #1：温度 2：湿度dt = int(data[3])aim_list_2.append(dt)returndef proper_model(timeseries, maxLag):init_bic = 100000000init_properModel = Nonefor p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q)) #bugtry:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_properModel = results_ARMAinit_bic = bicreturn init_properModeldef test_300(temp, tim, time_in):x = []y = []end_index = len(tim)for i in range(0, len(tim)):if (time_in - (tim[i]) < 300):end_index = ibreakif (end_index < 100):x = tim[0: end_index]y = temp[0: end_index]else:x = tim[end_index - 100: end_index]y = temp[end_index - 100: end_index]tidx = pd.DatetimeIndex(x, freq='infer')dta = pd.Series(y, index = tidx)print(dta)arma_mod = proper_model(dta, 9)predict_sunspots = arma_mod.forecast(1)return predict_sunspots[0]def predict_temperature(file_name, time_in):temp = []tim = []read_csv_data(temp, tim, file_name)result_temp = test_300(temp, tim, time_in)return result_tempif__name__ == '__main__':parser = argparse.ArgumentParser()parser.add_argument('-f', action='store', dest='file_name')parser.add_argument('-t', action='store', type = int, dest='time_')args = parser.parse_args()file_name = args.file_nametime_in = args.time_result_temp = predict_temperature(file_name, time_in)print ('the temperature is %f ' % result_temp)在上⾯的代码中，预测某⼀点的值我采⽤序列中此点的前100个点作为训练集如果给出待预测的多个点，由于每次都要计算模型的p和q以及拟合模型，时间会很慢，于是考虑将给定的待预测时间点序列切割成⼩段，使每⼀段中最⼤与最⼩的时间间隔在某⼀范围内在使⽤forcast(n)函数⼀次预测多点，然后在预测值中找到与待预测的时间值相近的值，速度⼤⼤提升，思路如图代码#coding:utf-8import csv#import timeimport pandas as pdimport numpy as npfrom statsmodels.tsa.arima_model import ARMAimport warningswarnings.filterwarnings('ignore')def proper_model(timeseries, maxLag):init_bic = 1000000000init_p = 1init_q = 1for p in np.arange(maxLag):for q in np.arange(maxLag):model = ARMA(timeseries, order=(p, q))try:results_ARMA = model.fit(disp = 0, method='css')except:continuebic = results_ARMA.bicif bic < init_bic:init_p = pinit_q = qinit_bic = bicreturn init_p, init_qdef read_csv_data(file_name, clss = 1):i = 0aim_list_1 = [] #temperature(1) or humidity(2)aim_list_2 = [] #timecsv_file = csv.reader(open(file_name,'r'))for data in csv_file:if (i == 0):i += 1continueaim_list_1.append(float(data[clss]))dt = int(data[3])aim_list_2.append(dt)tidx = pd.DatetimeIndex(aim_list_2, freq = None)dta = pd.Series(aim_list_1, index = tidx)init_p, init_q = proper_model(dta[:aim_list_2[100]], 9)return init_p, init_q, aim_list_2, dtadef for_kernel(p, q, tim, dta, tmp_time_list, result_dict):interval = 20end_index = len(tim) - 1for i in range(0, len(tim)):if (tmp_time_list[0]["time"] - tim[i] < tim[1] - tim[0]):end_index = ibreakif (end_index < 100):dta = dta.truncate(after = tim[end_index])else:dta = dta.truncate(before= tim[end_index - 101], after = tim[end_index])arma_mod = ARMA(dta, order=(p, q)).fit(disp = 0, method='css')#为未来interval天进⾏预测，返回预测结果，标准误差，和置信区间predict_sunspots = arma_mod.forecast(interval)####################################for tim_i in tmp_time_list:for tim_ in tim:if tim_i["time"] - tim_ >= 0 and tim_i["time"] - tim_ < tim[1] - tim[0]:result_dict[tim_i["time"]] = predict_sunspots[0][tim.index(tim_) - end_index] returndef kernel(p, q, tim, dta, time_in_list):interval = 20time_first = time_in_list[0]det_time = tim[1] - tim[0]result_dict = {}tmp_time_list = []for time_ in time_in_list:if time_first["time"] + det_time * interval > time_["time"]:tmp_time_list.append(time_)continuetime_first = time_for_kernel(p, q, tim, dta, tmp_time_list, result_dict)tmp_time_list = []tmp_time_list.append(time_first)for_kernel(p, q, tim, dta, tmp_time_list, result_dict)return result_dictdef predict_temperature(file_name, time_in_list, clss = 1):p, q, tim, dta = read_csv_data(file_name, clss)result_temp_dict = kernel(p, q, tim, dta, time_in_list)return result_temp_dictdef predict_humidity(file_name, time_in_list, clss = 2):p, q, tim, dta = read_csv_data(file_name, clss)result_humi_dict = kernel(p, q, tim, dta, time_in_list)return result_humi_dictif__name__ == '__main__':file_name = "testdata.csv"time_in = [{"time":1530419271,"temp":"","humi":""},{"time":1530600187,"temp":"","humi":""},{"time":1530825809,"temp":"","humi":""}] #time_in = [{"time":1530600187,"temp":"","humi":""},]result_temp = predict_temperature(file_name, time_in)print(result_temp)由于后续⼜改动了需求，需要预测温度以及湿度，完成了项⽬在github。
ARMA模型建模与预测指导
实验三 ARMA 模型建模与预测指导一、实验目的学会通过各种手段检验序列的平稳性；学会根据自相关系数和偏自相关系数来初步判断ARMA 模型的阶数p 和q ，学会利用最小二乘法等方法对ARMA 模型进行估计，学会利用信息准则对估计的ARMA 模型进行诊断，以及掌握利用ARMA 模型进行预测。
掌握在实证研究中如何运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念宽平稳：序列的统计性质不随时间发生改变，只与时间间隔有关。
AR 模型：AR 模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测， 自回归模型的数学公式为:1122t t t p t p t y y y y φφφε---=++++式中: p 为自回归模型的阶数i φ（i=1，2， ，p ）为模型的待定系数，t ε为误差， t y 为一个平稳时间序列。
MA 模型：MA 模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
滑动平均模型的数学公式为:1122t t t t q t q y εθεθεθε---=----式中: q 为模型的阶数； j θ（j=1，2， ，q ）为模型的待定系数；t ε为误差； t y 为平稳时间序列。
ARMA 模型：自回归模型和滑动平均模型的组合， 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA ， 数学公式为:11221122t t t p t p t t t q t q y y y y φφφεθεθεθε------=++++----三、实验内容及要求1、实验内容：（1）根据时序图判断序列的平稳性；（2）观察相关图，初步确定移动平均阶数q 和自回归阶数p ；（3）对某企业201个连续生产数据建立合适的ARMA （,p q ）模型，并能够利用此模型进行短期预测。
2、实验要求：（1）深刻理解平稳性的要求以及ARMA 模型的建模思想；（2）如何通过观察自相关，偏自相关系数及其图形，利用最小二乘法，以及信息准则建立合适的ARMA 模型；如何利用ARMA 模型进行预测；（3）熟练掌握相关Eviews 操作，读懂模型参数估计结果。
arima模型
ARIMA模型（英文：自回归综合移动平均模型），差分综合移动平均自回归模型（也称为综合移动平均自回归模型（移动也称为滑动））是时间序列预测和分析的方法之一。
在ARIMA（P，D，q）中，AR 是“自回归”，P是自回归项的数量；Ma是“移动平均值”，q是移动平均值项的数量，D是使其成为固定序列的差异度（阶数）。
尽管ARIMA的英文名称中没有出现“ difference”一词，但这是关键的一步。
建立ARIMA模型的方法和步骤采集时间序列时间序列可以通过相关部门的实验分析或统计数据获得。
对于获得的数据，首先应检查是否存在突变点，并分析由于人为疏忽等原因而存在的突变点。
确保获得的数据的准确性是建立合适的模型，是确保正确分析的第一步。
时间序列的预处理时间序列的预处理包括测试的两个方面：静态测试和白噪声测试。
ARMA模型可以分析和预测的时间序列必须满足平稳非白噪声序列的条件。
测试数据的平稳性是时间序列分析中的重要一步。
通常，时间序列的稳定性通过时间序列图和相关图进行测试。
时序图的特点是直观，简单，但误差很大。
自相关图，即自相关和部分自相关函数图，相对较复杂，但结果更为准确。
本文使用时序图进行直观判断，然后使用相关图进行进一步测试。
对于非平稳时间序列，如果存在上升或下降趋势，则需要进行差分处理，然后进行平稳性测试，直到稳定为止。
从理论上讲，差异数是模型ARIMA（P，D，q），差异数越多，时间序列信息的非平稳确定性信息的提取就越充分。
但是从理论上讲，差异的数量并不是更好。
每次差异操作都会导致信息丢失。
因此，应避免差异太大。
通常，在应用中，差异的顺序不超过2。
模型识别模型识别是从已知模型中选择与给定时间序列过程一致的模型。
有多种模型识别方法，例如box Jenkins模型识别。
型号订单确定确定模型的类型后，我们需要知道模型的顺序，可以通过BIC准则方法确定。
参数估计模型参数的估计方法通常包括相关矩估计，最小二乘估计和最大似然估计。
ARMA模型建模与预测指导
实验三 ARMA 模型建模与预测指导一、实验目的学会通过各种手段检验序列的平稳性；学会根据自相关系数和偏自相关系数来初步判断ARMA 模型的阶数p 和q ，学会利用最小二乘法等方法对ARMA 模型进行估计，学会利用信息准则对估计的ARMA 模型进行诊断，以及掌握利用ARMA 模型进行预测。
掌握在实证研究中如何运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念宽平稳：序列的统计性质不随时间发生改变，只与时间间隔有关。
AR 模型：AR 模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测， 自回归模型的数学公式为:1122t t t p t p t y y y y φφφε---=++++式中: p 为自回归模型的阶数i φ（i=1，2， ，p ）为模型的待定系数，t ε为误差， t y 为一个平稳时间序列。
MA 模型：MA 模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
滑动平均模型的数学公式为:1122t t t t q t q y εθεθεθε---=----式中: q 为模型的阶数； j θ（j=1，2， ，q ）为模型的待定系数；t ε为误差； t y 为平稳时间序列。
ARMA 模型：自回归模型和滑动平均模型的组合， 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA ， 数学公式为:11221122t t t p t p t t t q t q y y y y φφφεθεθεθε------=++++----三、实验内容及要求1、实验内容：（1）根据时序图判断序列的平稳性；（2）观察相关图，初步确定移动平均阶数q 和自回归阶数p ；（3）对某企业201个连续生产数据建立合适的ARMA （,p q ）模型，并能够利用此模型进行短期预测。
2、实验要求：（1）深刻理解平稳性的要求以及ARMA 模型的建模思想；（2）如何通过观察自相关，偏自相关系数及其图形，利用最小二乘法，以及信息准则建立合适的ARMA 模型；如何利用ARMA 模型进行预测；（3）熟练掌握相关Eviews 操作，读懂模型参数估计结果。
ARIMA模型预测案例
ARIMA模型预测案例假设我们要预测公司未来一年的销售额，已经收集到了该公司过去几年的销售额数据，我们希望通过ARIMA模型对未来的销售额进行预测。
首先，我们需要对销售额数据进行初步的可视化和分析。
通过绘制时间序列图，可以观察到销售额的趋势、季节性和随机性。
这些特征将有助于我们选择ARIMA模型的参数。
接下来，我们需要对数据进行平稳性检验。
ARIMA模型要求时间序列具有平稳性，即序列的均值和方差不随时间变化。
可以通过ADF检验或单位根检验来判断序列是否平稳。
如果序列不平稳，我们需要对其进行差分处理，直到达到平稳性。
接下来，我们需要确定ARIMA模型的参数。
ARIMA模型由AR（自回归）、I（差分）和MA（移动平均）三个部分组成。
AR部分反映了序列的自相关性，MA部分反映了序列的滞后误差，I部分反映了序列的差分情况。
我们可以使用自相关函数（ACF）和部分自相关函数（PACF）的图像来帮助确定ARIMA模型的参数。
根据ACF和PACF图像的分析，我们可以选择初始的ARIMA模型参数，并使用最大似然估计方法来进行模型参数的估计和推断。
然后，我们可以拟合ARIMA模型，并检查拟合优度。
接着，我们需要进行模型诊断，检查模型的残差是否满足白噪声假设。
可以通过Ljung-Box检验来判断残差的相关性。
如果残差不满足白噪声假设，我们需要重新调整模型的参数，并进行重新拟合。
最后，我们可以利用已经训练好的ARIMA模型对未来的销售额进行预测。
通过调整模型的参数，我们可以得到不同时间范围内的销售额预测结果。
需要注意的是，ARIMA模型的预测结果仅仅是一种可能的情况，并不代表未来的真实情况。
因此，在实际应用中，我们需要结合其他因素和信息来进行决策。
综上所述，ARIMA模型是一种经典的时间序列预测方法，在实际应用中具有广泛的应用价值。
通过对时间序列数据的分析和模型的建立，我们可以对未来的趋势进行预测，并为决策提供参考。
然而，ARIMA模型也有一些限制，如对数据的平稳性要求较高，无法考虑其他因素的影响等。
时间序列：ARIMA模型
实验：建立ARIMA模型（综合性实验）实验题目：某城市连续14年的月度婴儿出生率数据如下表所示：26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.90123.175 23.227 21.672 21.870 21.439 21.089 23.709 21.66921.752 20.761 23.479 23.824 23.105 23.110 21.759 22.07321.937 20.035 23.590 21.672 22.222 22.123 23.950 23.50422.238 23.142 21.059 21.573 21.548 20.000 22.424 20.61521.761 22.874 24.104 23.748 23.262 22.907 21.519 22.02522.604 20.894 24.677 23.673 25.320 23.583 24.671 24.45424.122 24.252 22.084 22.991 23.287 23.049 25.076 24.03724.430 24.667 26.451 25.618 25.014 25.110 22.964 23.98123.798 22.270 24.775 22.646 23.988 24.737 26.276 25.81625.210 25.199 23.162 24.707 24.364 22.644 25.565 24.06225.431 24.635 27.009 26.606 26.268 26.462 25.246 25.18024.657 23.304 26.982 26.199 27.210 26.122 26.706 26.87826.152 26.379 24.712 25.688 24.990 24.239 26.721 23.47524.767 26.219 28.361 28.599 27.914 27.784 25.693 26.88126.217 24.218 27.914 26.975 28.527 27.139 28.982 28.16928.056 29.136 26.291 26.987 26.589 24.848 27.543 26.89628.878 27.390 28.065 28.141 29.048 28.484 26.634 27.73527.132 24.924 28.963 26.589 27.931 28.009 29.229 28.75928.405 27.945 25.912 26.619 26.076 25.286 27.660 25.95126.398 25.565 28.865 30.000 29.261 29.012 26.992 27.897（1）选择适当模型拟和该序列的发展（2）使用拟合模型预测下一年度该城市月度婴儿出生率实验内容：给出实际问题的非平稳时间序列，要求学生利用R统计软件，对该序列进行分析，通过平稳性检验、差分运算、白噪声检验、拟合ARMA模型，建立ARIMA模型，在此基础上进行预测。
《2024年基于ARIMA-LSTM混合模型的云平台软件老化预测方法研究》范文
《基于ARIMA-LSTM混合模型的云平台软件老化预测方法研究》篇一一、引言随着云计算技术的飞速发展，云平台已经成为各种企业和组织的主要数据处理和应用支撑环境。
然而，随着使用年限的增长，云平台软件老化问题日益凸显，严重影响着其运行性能和可靠性。
因此，准确预测云平台软件的老化趋势，对提高其性能、保证其可靠性具有重要的实际意义。
本文将针对这一问题，研究基于ARIMA-LSTM混合模型的云平台软件老化预测方法。
二、研究背景与相关技术1. 云平台软件老化现象及影响云平台软件在长时间运行过程中，由于软硬件的相互影响和系统环境的变化，可能会出现性能下降、错误率增加等老化现象，这些问题直接影响着云平台服务的稳定性和可靠性。
2. 时间序列预测模型时间序列预测模型是一种常用的预测方法，其中ARIMA （自回归积分滑动平均）模型和LSTM（长短期记忆）模型是两种重要的模型。
ARIMA模型适用于具有稳定统计特性的时间序列预测，而LSTM模型则能够处理具有复杂非线性特征的时间序列数据。
三、基于ARIMA-LSTM混合模型的云平台软件老化预测方法1. 数据收集与预处理首先，我们需要收集云平台软件的相关运行数据，包括CPU 使用率、内存使用率、磁盘I/O等。
然后，对这些数据进行清洗和预处理，以适应后续的模型训练。
2. ARIMA模型的应用将预处理后的数据分为训练集和测试集，使用ARIMA模型对训练集进行建模。
通过分析时间序列数据的自相关性和偏自相关性，确定模型的阶数和差分次数，从而构建出适用于云平台软件老化预测的ARIMA模型。
3. LSTM模型的应用将ARIMA模型的预测结果作为LSTM模型的输入，利用LSTM模型对云平台软件的老化趋势进行更精确的预测。
LSTM 模型能够捕捉时间序列数据中的长期依赖关系，从而对云平台软件的老化趋势进行更准确的预测。
4. ARIMA-LSTM混合模型的应用将ARIMA模型和LSTM模型进行结合，形成ARIMA-LSTM 混合模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课 程 论 文
（2016 / 2017学年 第 1 学期）
课程名称 应用时间序列分析
指导单位
经济学院
指导教师
易莹莹
学生姓名 班级学号
学院(系) 经济学院 专 业
经济统计学
实验三ARIMA模型建模与预测实验指导
一、实验目的：
了解ARIMA模型的特点和建模过程，了解AR，MA和ARIMA模型三者之间的区别
与联系，掌握如何利用自相关系数和偏自相关系数对ARIMA模型进行识别，利用最小二乘
法等方法对ARIMA模型进行估计，利用信息准则对估计的ARIMA模型进行诊断，以及如
何利用ARIMA模型进行预测。掌握在实证研究如何运用Eviews软件进行ARIMA模型的
识别、诊断、估计和预测。
二、基本概念：
所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将平稳的时间序
列建立ARMA模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括
移动平均过程（MA）、自回归过程（AR）、自回归移动平均过程（ARMA）以及ARIMA过
程。
在ARIMA模型的识别过程中，我们主要用到两个工具：自相关函数ACF，偏自相关函
数PACF以及它们各自的相关图。对于一个序列tX而言，它的第j阶自相关系数j为它
的j阶自协方差除以方差，即j＝j0，它是关于滞后期j的函数，因此我们也称之为
自相关函数，通常记ACF(j)。偏自相关函数PACF(j)度量了消除中间滞后项影响后两滞后
变量之间的相关关系。
三、实验任务：
1、实验内容：
（1）根据时序图的形状，采用相应的方法把非平稳序列平稳化；
（2）对经过平稳化后的1950年到2005年中国进出口贸易总额数据建立合适的
(,,)ARIMApdq
模型，并能够利用此模型进行进出口贸易总额的预测。
2、实验要求：
（1）深刻理解非平稳时间序列的概念和ARIMA模型的建模思想；
（2）如何通过观察自相关，偏自相关系数及其图形，利用最小二乘法，以及信息准则建立
合适的ARIMA模型；如何利用ARIMA模型进行预测；
（3）熟练掌握相关Eviews操作，读懂模型参数估计结果。
四、实验要求：
实验过程描述（包括变量定义、分析过程、分析结果及其解释、实验过程遇到的问题及体会）。
实验题：对经过平稳化后的1950年到2005年中国进出口贸易总额数
据建立合适的(,,)ARIMApdq模型，并能够利用此模型进行进出口贸易
总额的预测。