定积分的几何应用PPT课件
合集下载
定积分的应用平面曲线弧长课件

参数方程中的x(t)和y(t)表示曲线上某一点在x和y方向上的坐标,t表示该点在曲 线上的位置。
参数方程的转换
参数方程转换为普通方程
将参数方程中的参数t消除,将参数方程转换为普通方程。
参数方程的微分形式
将参数方程转换为微分形式,以便于计算曲线的切线斜率和 弧长。
03 定积分在平面曲线弧长中 的应用
理论完善
随着定积分在平面曲线弧长中的应用越来越广泛,其理论体系也可能会得到进一步完善。例如,可能会发现新的定理 和公式,以更好地描述和解决定积分问题。
应用领域的拓展
随着科技的不断发展,定积分的应用领域也可能会进一步拓展。例如,在人工智能、机器学习等领域中, 定积分可能会被用来解决一些新的问题。
定积分在平面曲线弧长中的实际价值
弧长公式的应用
计算特定曲线的弧长
利用弧长公式,可以计算出给定参数 方程的曲线上任意一段弧的长度。这 迹的长度 等。
比较不同曲线的长度
通过比较不同曲线的弧长,可以得出 它们之间的形状差异。例如,可以利 用弧长公式比较不同函数的图像长度。
弧长公式的拓展
弧长公式的推导
弧长公式的基本概念
弧长公式是定积分的一个重要应用,它用于计算平面曲线上某段弧的长度。在推 导弧长公式之前,需要了解曲线的基本参数方程和弧长的定义。
弧长公式的推导过程
通过将曲线分割成许多小段,并利用定积分计算每小段线段的长度,然后将这些 长度相加,最终得到整个弧的长度。这个过程涉及到极限和定积分的概念。
建立方程
首先需要确定曲线的起点和终点,以 及曲线在起点和终点处的切线方向。
根据起点、终点和参数,建立曲线的 参数方程。
选择参数
选择一个合适的参数,例如时间或角 度,来表示曲线上每一点的位置。
参数方程的转换
参数方程转换为普通方程
将参数方程中的参数t消除,将参数方程转换为普通方程。
参数方程的微分形式
将参数方程转换为微分形式,以便于计算曲线的切线斜率和 弧长。
03 定积分在平面曲线弧长中 的应用
理论完善
随着定积分在平面曲线弧长中的应用越来越广泛,其理论体系也可能会得到进一步完善。例如,可能会发现新的定理 和公式,以更好地描述和解决定积分问题。
应用领域的拓展
随着科技的不断发展,定积分的应用领域也可能会进一步拓展。例如,在人工智能、机器学习等领域中, 定积分可能会被用来解决一些新的问题。
定积分在平面曲线弧长中的实际价值
弧长公式的应用
计算特定曲线的弧长
利用弧长公式,可以计算出给定参数 方程的曲线上任意一段弧的长度。这 迹的长度 等。
比较不同曲线的长度
通过比较不同曲线的弧长,可以得出 它们之间的形状差异。例如,可以利 用弧长公式比较不同函数的图像长度。
弧长公式的拓展
弧长公式的推导
弧长公式的基本概念
弧长公式是定积分的一个重要应用,它用于计算平面曲线上某段弧的长度。在推 导弧长公式之前,需要了解曲线的基本参数方程和弧长的定义。
弧长公式的推导过程
通过将曲线分割成许多小段,并利用定积分计算每小段线段的长度,然后将这些 长度相加,最终得到整个弧的长度。这个过程涉及到极限和定积分的概念。
建立方程
首先需要确定曲线的起点和终点,以 及曲线在起点和终点处的切线方向。
根据起点、终点和参数,建立曲线的 参数方程。
选择参数
选择一个合适的参数,例如时间或角 度,来表示曲线上每一点的位置。
高中数学-定积分在几何中的应用-课件

求由一条曲线 y=f(x)和直线 x=a,x=b(a<b)及 y=0 所围成平面图形的面积 S.
①如图 1 所示,f(x)>0, bf(x)dx>0. a
∴S= bf(x)dx. a
②如图 2 所示,f(x)<0, bf(x)dx<0, a
∴S=| bf(x)dx|=- bf(x)dx.
a
a
2×23x32
|
2 0
=136,
8
S2=2 [4-x-(- 2x)]dx
=4x-12x2+2
3
2x32|
8 2
=338,
于是 S=136+338=18.
方法二:选y作为积分变量,
将曲线方程写为x=y22及x=4-y.
则S=2-44-y-y22dy
=4y-y22-y63|
2 -4
=18.
变式训练 1:由曲线 y= x,直线 y=x-2 及 y 轴所围成
解.
由方程组
y2=2x y=4-x
解出抛物线和直线的交
点为(2,2)及(8,-4).
方法一:选 x 作为积分变量,由图可看出 S=S1+S2,
由于抛物线在 x 轴上方的方程为 y= 2x,
在 x 轴下方的方程为 y=- 2x,
2
所以 S1=0 [ 2x-(- 2x)]dx
=2
2 1
20x2 dx=2
❖1.7 定积分的简单应用
❖1.7.1 定积分在几何中的应用
自主学习 新知突破
❖ 1.理解定积分的几何意义.
❖ 2.会通过定积分求由两条或多条曲线 围成的平面图形的面积.
复习回顾
[问题 1]定积分的几何意义.
由三条直线 x=a,x=b(a<b),x 轴及 一条曲线 y=f(x)(f(x)≥0)围成的曲边 梯形的面积 S=________.
高数课件第六章定积分的应用:第二节定积分的几何应用

y
c
b O
x
bx
x
x x 1 sh dx ch dx c c b x xb s 2 ch dx 2c sh 0 c c 0 x b 1 x 2c sh ( c ch ) c sh c c c c
2
e e ch x 2 x x e e sh x 2 (ch x) sh x
Hale Waihona Puke 2 (t ) 2 (t ) d t
因此所求弧长
s
2 (t ) 2 (t ) d t
(3) 曲线弧由极坐标方程给出:
令 x r ( ) cos , y r ( ) sin , 则得
dx [r ( ) cos r ( ) sin ]d dy [r ( ) sin r ( ) cos ]d
2
选 x 为积分变量 (1) x [2, 0], dA1 ( x 3 6 x x 2 )dx 于是所求面积 A A1 A2
特别注意:
各积分区间 A ( x 3 6 x x 2 )dx 0 (x x 6 x)dx 上被积函数的 2 253 形式不同. . 12
0
3
2
3
x2 1 练习:1.求曲线 y , y 与直线 x 3 2 1 x 2
x 3 所围成的图形的面积。
2.求曲线 xy 1 与直线
x y 0 y 2
x y 2
P1
2
所围成的图形的面积。 2014考研题
提示:1
P2
y
1
32 1 0 2 1 1 3 x 1 x 1 1 s 2[ ( )d x ( ( 3 3 2) ) d x ] 2 0 1 x 1 3 2 2 1 x2
高等数学(第三版)课件:定积分的应用

线 y f ( x,) 直线 x a, x b (a b) 与
• x 轴围成的面积是在x 轴上方和下方曲边梯形
面积的差.
• • 同样可由微元法分析
•⒉ 一般地,根据微元法由曲线 y f ( x), y g( x),
• ( f ( x) g( x)) 及直线x a, x b 所围的图形
• 面积.(右图所示)
• 解: 取 为积分变量,
•
面积微元为
d
A
1 2
(a )2
d
• 于是
A 2 1 (a )2d a 2 2
02
23
2 4 a 2 3
03
• 例5 计算双纽线 r 2 a2 cos2 (a 0)
•
所围成的平面图形的面积(下图所示)
• 解 因 r 2 0,故 的变化范围是 [ 3 , 5 ,]
• ⑴分割区间[a,b],将所求量(曲边梯形面积 A )
分为部分量(小曲边梯形面积 Ai)之和;
• ⑵确定各部分量的近似值(小矩形面积);
Ai f (i )xi
• ⑶求和得所求量的近似值(各小矩形面积之和);
n
A f (i )xi
i 1
• ⑷对和式取极限得所求量的精确值(曲边梯形面积).
n
A lim 0
• 它表示高为f ( x) 、底为 dx 的一个矩形面积.
• ⑵由定积分几何意义可知,当 f (x) 0 时,由曲
线 y f (x),直线 x a, x b (a b) 与 x 轴所围成
的曲边梯形的面积A为
A
b
f (x)dx
.
a
• ⑶当 f ( x)在区间 [a, b]上的值有正有负时,则曲
•
定积分在几何中的应用 课件

y=x2-3围成平面图形的面积是
S [3 2x (x2 3)]dx 3 (3 2x x2 )dx
1
1
(3x
x2
1 3
x3
31
(3 3 32 1 33) [1 3 (1)2 1 (1)3]
3
3
9 2 1 32 . 33
【拓展提升】求函数图象围成平面图形面积的方法 (1)画出两个函数的图象,先将两个函数方程联立方程组求 解,得到函数图象的交点的横坐标a,b(a<b),确定积分区间 [a,b]. (2)在公共的积分区间上,由上界函数减去下界函数作为被积 函数,定积分的值就等于两个函数图象围成平面图形的面
积,即 S a[b f1(x) (f其2 (中x)]fd1x(x)>f2(x)).
类型 二 计算复杂平面图形的面积 【典型例题】 1.由两条曲线y=x2, y 1 x2与直线y=1围成平面区域的面积
4
是_______.
2.求曲线 y x 与直线y=2-x,y 1 x 围成图形的面积.
3
【解题探究】1.题1中怎样确定积分变量的区间? 2.如何将图形的面积转化为定积分计算? 探究提示: 1.由直线y=1分别与曲线y=x2y, 1 x联2 立,求出交点坐标,
(2x
1 2
x2
1 6
x2)
13
=2 3
1 6
(2x
1 3
x2
)
13
=5 6 1 9 21 1 1=2 1 .
63
36
【互动探究】若将题2中条件变为如图由直线y=x-2,曲线 y2=x所围成图形,试求其面积S.
【解析】由
y2
x得, x=1或x=4,
y x 2,
故A(1,-1),B(4,2),如图所示:
高等数学第六章第二节定积分在几何学上的应用课件.ppt
解:
cos x 0,
2
x
2
s
2
2
2 2 0
1 y2 dx 1 ( cos x)2 dx
2 2
2 cos x dx
0
2
2
2
2
sin
x 2
2
0
4
的弧长.
例11. 计算摆线
一拱
的弧长 .
y
解: ds
(dd
x t
)2
(
d d
y t
)
2
d
t
o
a2 (1 cos t)2 a2 sin2 t d t
1 y2 dx
因此所求弧长
s b 1 y2 dx a
b
a
1 f 2(x) dx
y
y f (x)
ds
o a xxdxb x
(2) 曲线弧由参数方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
(3) 曲线弧由极坐标方程给出:
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a
《定积分课件》课件

03 定积分的应用
CHAPTER
面积与体积的计算
总结词
定积分在计算平面图形的面积和三维物体的体积方面具有广 泛应用。
详细描述
利用定积分,可以计算出由曲线围成的平面图形的面积,例 如由y=sinx和y=cosx围成的图形面积。此外,定积分还可以 用于计算三维物体的体积,例如球体、圆柱体和旋转体的体 积。
详细描述
在静水压力问题中,压力分布是深度的函数。通过定积分,我们可以计算任意 深度的压力分布,从而了解水下物体的受力情况。
引力场的强度
总结词
通过定积分计算引力场的强度,理解引 力场的分布规律。
VS
详细描述
在引力场中,场强是位置的函数。通过定 积分,我们可以计算任意位置的场强,从 而了解物体在引力场中的运动规律。
符号表示
02
定积分的符号为∫,读作“拉姆达”。
计算方法
03
定积分的计算方法是通过微积分基本定理,将定积分转化为求
原函数在某点的值。
定积分的几何意义
平面区域面积
定积分可以用来计算平面图形的面积,特别是 当面积元素与坐标轴平行时。
体积
定积分还可以用来计算三维物体的体积,例如 旋转体的体积。
曲线下面积
定积分可以用来计算曲线下在某一区间内的面积。
定积分的计算方法
要点一
总结词
定积分的计算方法包括直接法、换元法和分部积分法等。
要点二
详细描述
定积分的计算可以通过多种方法进行。直接法是根据微积 分基本定理,通过求原函数并计算其差值来得到定积分的 结果。换元法是在积分变量进行换元,使得积分简化。分 部积分法则是通过将两个函数的乘积进行积分,将一个积 分转化为另一个积分,从而简化计算。这些方法在计算定 积分时常常需要结合使用。
高中数学选修2-2定积分在几何中的应用课件

的交点为 (0, 0)
取x为积分变量, 则 x [0, 3].
所求的几何图形的面积表示为
A 3 ( x2 3x)dx 0
A 3 ( x2 3x)dx 9.
0
2
= 2
2
3
x2
3
4 0
+
2
2 3
3
x2
8 4
-
1 2
x-4 2
8 4
= 40 3
新知探究
例3
计算由曲线 y = x3 6x 和 y = x2 所围成的图形的面积.
首先画出草图,并设法把所求图形的面积问题转化为求两部分的面积问题.其次,确定被积函数 和积分的上、下限.
新知探究
由图可知,我们需要把所求图形的面积分成两部分 S1和S2 .需要求出曲线 y = x3 - 6x 、曲 线 y = x2 两个交点.
n
i =1 b
F = lim f λ →0 i=1
ξi Δxi =
f
a
x dx
新知探究
平面图形的面积 直角坐标系 设平面图形由上下两条曲线y=f上(x)与y=f下(x)及左右两 条直线x=a与x=b所围成.
新知探究
在点x处面积增量的近似值为 [f上(x)-f下(x)]dx, 它也就是面积元素. 因此平面图形的面积为
极坐标方程的情形
设由曲线 r = φθ 及射线 θ = α、θ = β 围成一曲边扇形, 求其面积.这里 φθ 在 α,β 上连续,且 φθ≥0 .
曲边扇形面积元素 dA = 1 [φ(θ)]2 dθ 2
d
r ( )
d
曲边扇形的面积公式 A = β 1[j(θ)]2 dθ. α2
o x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)确定左右曲线:
左 ( y)
1 2
y2,
右 ( y)
y4
(4)计算积分
S
4
2
(
y
4
1 2
y2)dy
[
1 2
y2
4y
1 6
y3]42
18
例例33 求椭圆 x2 y2 1 所围成的图形的面积 a2 b2
解 椭圆的面积是椭圆在第一象限部分的四倍.
椭圆在第一象限部分的面积元素为 ydx,
于是
S 40a ydx
当所求量U 符合下列条件:
(1)U 是与一个变量x 的变化区间a, b 有关
的量;
(2)U 对于区间a, b具有可加性,就是说, 如果把区间a, b分成许多部分区间,则U 相
应地分成许多部分量,而U 等于所有部分量之
和;
(3)部分量Ui 的近似值可表示为 f (i )xi ;
就可以考虑用定积分来表达这个量U
微元法的一般步骤:
1)根据问题的具体情况,选取一个变量例如x 为积分变量,并确定它的变化区间[a, b] ;
2)设想把区间[a, b]分成n 个小区间,取其中任 一小区间并记为[ x, x dx],求出相应于这小区 间的部分量U 的近似值.如果U 能近似地表示 为[a, b]上的一个连续函数在x 处的值 f ( x) 与 dx 的乘积,就把 f ( x)dx 称为量U 的元素且记 作 dU ,即dU f ( x)dx ;
形的面积如何表示为定积分?
提示:
面积元素为[j右(y)j左(y)]dy,
面积为
S
d
c
[右 ( y) 左 ( y)]dy
S ab[ f上(x) f下(x)]dx
S
d
c
[右
(
y)
左(
y)]dy
例1 计算抛物线y2x与yx2所围成的图形的面积.
解 (1)画图;
(2)确定在x轴上的投影区间: [0, 1];
例7
计算由椭圆
x2 a2
y2 b2
1所成的图形绕x轴旋转而成的
旋转体(旋转椭球体)的体积
解 旋转椭球体可以看作是由半个椭圆 y b a2 x2 及 x a
围成的图形的面积.
解解
S
20
1 2
[a(1
c
os
]2
d
a2
0
(
1 2
2c
os
1 2
c
os2
)d
a2[23
2sin
1 4
sin
2
]0
3 2
a2
三、体积
1.旋转体的体积
旋转体就是由一个平面图形绕这平面内一条直线旋转一 周而成的立体. 这直线叫做旋转轴.
1.旋转体的体积 旋转体都可以看作是由连续曲线yf(x)、直线xa、ab及
因为椭圆的参数方程为
xacost, ybsint,
所以
SS440a0ayyddxx 4400bbssininttdd((aaccoosstt)) 22
4ab0sin2 tdt
2ab02 (1cos2t)dt
2
2ab2 ab
2.极坐标情形
•曲边扇形
曲边扇形是由曲线()及射线, 所围成的图形.
3)以所求量U 的元素 f ( x)dx 为被积表达式,在
区间[a, b]上作定积分,得U
b
a
f
( x)dx ,
即为所求量U 的积分表达式.
这个方法通常叫做元素法.
应用方向:
平面图形的面积;体积;平面曲线的弧长; 功;水压力;引力和平均值等.
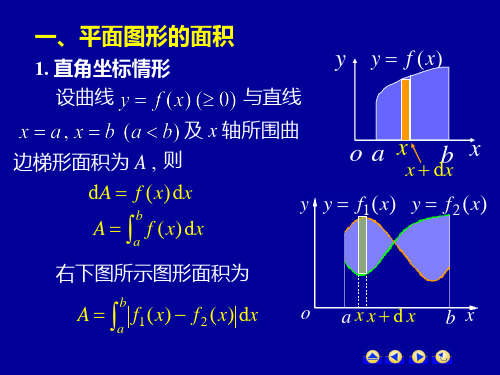
二、平面图形的面积
1.直角坐标情形
设平面图形由上下两条曲线
(1)把区间[a, b]分成n 个长度为xi 的小区间,相应的曲
边梯形被分为n个小窄曲边梯形,第i 个小窄曲边梯形
n
的面积为Ai ,则 A Ai .
i 1
(2)计算Ai 的近似值
Ai f (i )xi i xi
n
(3) 求和,得A的近似值 A f (i )xi . i 1
(4) 求极限,得A的精确值
(3)确定上下曲线 f上(x) x, f下(x) x2 (4)计算积分
S 01( x x2)dx
[
2 3
x
3 2
1 3
x3]10
1 3
S ab[ f上(x) f下(x)]dx
S
d
c
[右
(
y)
左(
y)]dy
例2 计算抛物线y22x与直线yx4所围成的图形的面积.
解 (1)画图;
(2)确定在y轴上的投影区间: [-2, 4].
例6 连接坐标原点O及点P(h, r)的直线、直线xh及x轴围
成一个直角三角形. 将它绕x轴旋转构成一个底半径为r、高为
h的圆锥体. 计算这圆锥体的体积.
解 直角三角形斜边的直线方程为 y r x
V
0h
(
r h
x)2
dx
h
r 2
h2
[1 3
x3]0h
1hr2
3
旋转体的体积:V ab[ f (x)]2dx
§6.2 定积分在几何学上的应用
一、元素法 二、平面图形的面积 三、体积 四、平面曲线的弧长
一、元素法
回顾 曲边梯形求面积的问题
曲边梯形由连续曲线 y
y f ( x)( f ( x) 0) 、
x 轴与两条直线x a 、
x b所围成。
oa
A
b
a
f
(
x)dx
y f (x)
bx
面积表示为定积分的步骤如下
•曲边扇形的面积元素
dS
1 2
[
(
)]2d
•曲边扇形的面积
S
1 2
[(
)]2
d
曲边扇形的面积:S
1 2
[
(
)]2
d
( ( ), )
例4 计算阿基米德螺线a (a>0)上相应于从0变到2
的一段弧与极轴所围成的图形的面积.
解解
S02
1(a)2d
2
1 2
a2[13
3]02
4 3
a2
3
例5 计算心形线a(1cos)(a>0)所
yf上(x)与yf下(x)及左右两条直线 xa与xb所围成.
在点x处面积增量的近似值为 [f上(x) f下(x)]dx,
它也就是面积元素. 因此平面图形的面积为
S ab[ f上(x) f下(x)]dx
S ab[ f上(x) f下(x)]dx
S
d
c
[右
(
y)
左(
y)]dy
讨论:
由左右两条曲线xj左(y)与xj右(y)及 上下两条直线yd与yc所围成的平面图
x轴所围成的曲边梯形绕x轴旋转一周而成的立体.
•旋转体的体积元素
考虑旋转体内点x处垂直于x轴的厚度为dx的切片, 用圆柱体的体积[f(x)]2dx作为切片体积的近似值, 于是体积元素为 dV[f(x)]2dx.
•旋转体的体积
V ab[ f (x)]2dx
旋转体的体积:V ab[ f (x)]2dx
n
A
lim
0
i 1
f
(i )xiΒιβλιοθήκη bf ( x)dx
a
提示 若用A 表示任一小区间 [ x, x x]上的窄曲边梯形的面积,y
则 A A,并取A f ( x)dx,
面 积 元 素
dA
y f (x)
于是 A f ( x)dx
b
o a x x dxb x
A lim f ( x)dx a f ( x)dx.
