六杆机构加速度分析
6连杆机构优化设计
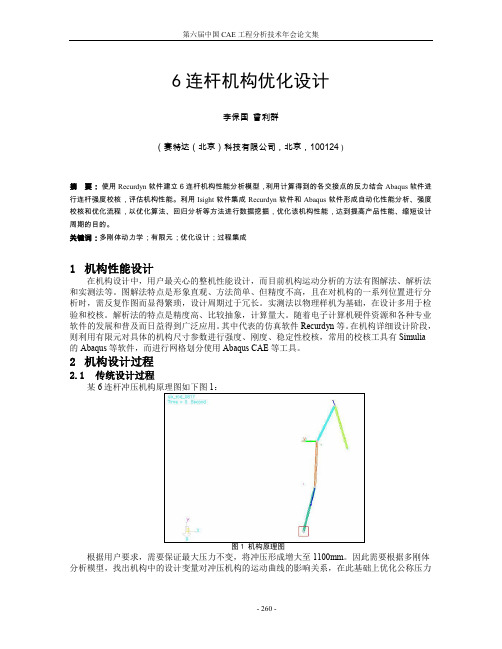
2000t,行程 1100mm 的多连杆机构。为满足用户使用要求和最小化生产厂家变更引起费用,此机 构必须满足下列条件: 驱动臂 R=250~280mm;支撑点变化范围 X=1100~1300,Y=150~350mm; 曲柄中心到下死点距离 2800~3150;公称压力 2400T,公称压力行程 30mm; 滑块拉伸行程为 400mm,拉伸行程内速度小于 21m/s,最大小于 23m/s,为保证冲压质量, 在拉伸行程内拉伸曲线要接近直线,如图 3 示; 连杆压力角小于 45 度; 摆杆与摇杆之间传动角大于 55 度; 连杆最大应力小于 60MPa。 对应的冲头的位移、速度、加速度曲线如图示:
1 机构性能设计
在机构设计中,用户最关心的整机性能设计,而目前机构运动分析的方法有图解法、解析法 和实测法等。图解法特点是形象直观、方法简单、但精度不高,且在对机构的一系列位置进行分 析时,需反复作图而显得繁琐,设计周期过于冗长。实测法以物理样机为基础,在设计多用于检 验和校核。解析法的特点是精度高、比较抽象,计算量大。随着电子计算机硬件资源和各种专业 软件的发展和普及而日益得到广泛应用。 其中代表的仿真软件 Recurdyn 等。 在机构详细设计阶段, 则利用有限元对具体的机构尺寸参数进行强度、刚度、稳定性校核,常用的校核工具有 Simulia 的 Abaqus 等软件,而进行网格划分使用 Abaqus CAE 等工具。
- 262 -
第六届中国 CAE 工程分析技术年会论文集
图 6:Isight 集成 Recurdyn、Abaqus 试验设计流程
粒子群算法(particle swarm optimization,PSO)由 Kennedy 和 Eberhart 在 1995 年提出,该算法 模拟鸟集群飞行觅食的行为,鸟之间通过集体的协作使群体达到最优目的,是一种基于 Swarm Intelligence 的优化方法。同遗传算法类似,也是一种基于群体叠代的,但并没有遗传算法用的交 叉以及变异,而是粒子在解空间追随最优的粒子进行搜索。PSO 的优势在于简单容易实现同时又 有深刻的智能背景,既适合科学研究,又特别适合工程应用,并且没有许多参数需要调整。目前, 已有的群智能理论和应用研究证明群智能方法是一种能够有效解决大多数优化问题的新方法,更 重要是,群智能潜在的并行性和分布式特点为处理大量的以数据库形式存在的数据提供了技术保 证。无论是从理论研究还是应用研究的角度分析,群智能理论及应用研究都是具有重要学术意义和 现实价值的。 粒子群算法(particle swarm optimization,PSO)搜索方向按照下式更新。
机械原理-机构运动分析的解析法

l
1
φ θ
2
l
x
a2 x 2l cos al sin a2 y 2l sin al cos
已知:构件的长度L及运动参数角位置θ 、角速度ω 、 角加速度ε ,1点的运动参量。
求: 3点的运动参量。
解: P 3x P 1 x l cos( ) v3 x v1 x l sin( ) P v3 y v1 y l cos( ) 3y P 1 y l sin( )
运 动 副 点 号
要求赋值
构 件 号
构 件 长 度
角位置角速度角加速 度,位置 速度 加速 度 n1
r1
m>0——实线 M<=0——虚线
不赋值
已知: 外运动副N1的位置P、速度v、加速度a,导路上任意参考点 N2的位置P、 速度v、加速度a,构件1的长度及导路的角位置、角速度、角加速度。 求:内运动副N3的运动参量、构件①的运动参量、 r2、vr2、ar2
P 3x P 1x l1 cos 1 P 3y P 1 y l1 sin 1
P 3y P 2y 2 arctan P P 2x 3x
rrrk(m,n1,n2,n3,k1,k2,r1,r2,t,w,e,p,vp,ap)
装 配 模 式
n3 k1 k2 r2 n2 N3’
}
y
3
l
1
φ
l
2
θ
x
bark(n1,n2,n3,k,r1,r2,gam,t,w,e,p,vp,ap)
关 键 点 号 构 n n 件 1 1 号 n n ∠ n3 n1 2 3 间 间 n2 距 距 离 离 角位置角速度 角加速度,位 置 速度 加速度
机械原理牛头刨床的VB

一·机构简介·1.1牛头刨床的组成牛头刨床主要由床身、滑枕、刀架、工作台、横梁、进给机构和变速机构等组成。
(1)床身床身内部有变速机构和曲柄摇杆机构。
床身的顶面有水平导轨,滑枕沿水平导轨作往复直线运动。
在床身前面有垂宜导轨,横梁带动工作台沿垂直导轨升降。
2)滑枕滑枕的前端有环状T形槽,用来安装刀架和调节刀架的偏转角度:滑枕的内部装有调整滑枕行程位置的机构,它是由一对锥齿轮和丝杠组成。
滑枕的下部有两条燕尾型导轨,它与床身上部的水平导轨配合。
在曲柄摇杆机构的带动下,滑枕在床身水平导轨上作往复直线运动。
(3)横梁与工作台校梁安装在床身前部垂直导轨上。
横梁的底部装有升降丝杠,使校梁能沿着床身前部的垂直导轨作上下移动。
工作台和滑板连接在一起,安装在横梁水平导轨上,转动安装在校梁凹框内的横向进给丝杠,工作台就沿着横梁的水平导轨作横向移动。
工作台的前部底下装有支架,以防止工作台在刨削过程中产生向下倾斜和振动现象。
工作台的上平面和两侧面均制有T形槽、v 形槽和圆孔,用来固定不同形状的工件或夹具。
(4)刀架刀架用于装夹刨刀,并使刨刀沿着垂直方向和倾斜方向移动。
刀架由手柄、丝杠、刻度转盘、夹刀座、拍板、拍板座、滑板等组成。
刻度转盘6用T形职栓5紧固在滑枕前端的“环”状T形槽内。
可按加工的需要作160’的回转。
刻度转盘6与滑板13通过导轨相配合,只要摇动丝杠3上端的手柄1,就可使滑板13沿着刻度转盘6上的导轨移动,通过刻度环2来控制背吃刀量的大小。
拍板10与拍板座11的凹槽相配合,用铰链销7连接。
在拍板10的孔内装有夹刀座8刨刀就装在它的槽孔内,拍板10可以绕铰链销7向前上方拾起,这样可避免滑枕回程时刨刀与工件已加工。
(5)进给机构进给机构主要用来控制工作台横向进给运动的大小。
(6)变速机构操纵变速机构的手柄,可以把各种不同的转速传递到曲柄摆杆机构而改变格杆在相同时间间隔内的摆动次数。
(7)曲柄摇杆机构主要作用是把电动机的旋转运动转换为滑枕的往复直线运动。
平面机构的运动分析习题和答案

71.在图示的四杆机构中, mm, mm, mm, 。当构件1以等角速度 rad/s逆时针方向转动时,用瞬心法求C点的速度。
72.图示机构运动简图取比例尺 m/mm。已知 rad/s,试用速度瞬心法求杆3的角速度 。
51.图示为按比例尺绘制的牛头刨床机构运动简图和速度矢量多边形。试由图中的比例尺计算导杆3的角速度 和滑块2的角速度 ,并指出其方向。(提示: 为构件3上特殊点,据 、 求得,作题时不必去研究 如何求得。)
(取 m/mm, (m/s)/mm。)
52.试求图示机构的速度瞬心数目、各瞬心位置、各构件角速度的大小和方向、杆2上点M的速度大小和方向。(机构尺寸如图: mm, mm, mm, mm, , mm, m/mm。)已知 rad/s。
9.当两构件组成转动副时,其速度瞬心在处;组成移动副时,其速度瞬心在处;组成兼有相对滚动和滑动的平面高副时,其速度瞬心在上。
10..速度瞬心是两刚体上为零的重合点。
11.铰链四杆机构共有个速度瞬心,其中个是绝对瞬心,个是相对瞬心。
12.速度影像的相似原理只能应用于的各点,而不能应用于机构的的各点。
13.作相对运动的3个构件的3个瞬心必。
86.图示机构的运动简图取长度比例尺 m/mm,其中 m, m, m,构件1以 rad/s等角速度顺时针方向转动,试用相对运动图解法求图示位置:
(1) 、 、 和 的大小和方向;
(2) 、3、4和5的大小和方向;
(3)在机构运动简图上标注出构件2上速度为零的点 ,在加速度多边形图上标注出构件2上点 的加速度矢量 ,并算出点 的加速度 的大小。在画速度图及加速度图时的比例尺分别为: =0.02 (m/s)/mm, (m/s2)/mm。
基于UGCAE的平面六杆机构的运动分析

基于UG/CAE的平面六杆机构的运动分析1、题目说明如上图所示平面六杆机构,试用计算机完成其运动分析。
已知其尺寸参数如下表所示:题目要求:两人一组计算出原动件从0到360时(计算点数37)所要求的各运动变量的大小,并绘出运动曲线图及轨迹曲线。
注:为了使计算的结果更好的拟合运动的实际情况,同时考虑到UG在运动仿真分析计算方面的快速性,我们决定在绘制曲线时将计算点由37点增加到600点。
数据输出到Excel表格时计算点取100点。
建模及其分析方法附后!2、建模及其运动分析软件介绍:UG NX是集CAD\CAE\CAM于一体的三维参数化软件,也是当今世界最先进的设计软件,它广泛应用于航空航天、汽车制造、机械电子等工程领域。
还有在系统创新、工业设计造型、无约束设计、装配设计、钣金设计、工程图设计等方面的功能。
运动仿真是UG/CAE(Computer Aided Engineering)模块中的主要部分,它能对任何二维或三维机构进行复杂的运动学分析、动力分析和设计仿真。
通过UG/Modeling的功能建立一个三维实体模型,利用UG/Motion的功能给三维实体模型的各个部件赋予一定的运动学特性,再在各个部件之间设立一定的连接关系既可建立一个运动仿真模型。
UG/Motion的功能可以对运动机构进行大量的装配分析工作、运动合理性分析工作,诸如干涉检查、轨迹包络等,得到大量运动机构的运动参数。
通过对这个运动仿真模型进行运动学或动力学运动分析就可以验证该运动机构设计的合理性,并且可以利用图形输出各个部件的位移、坐标、加速度、速度和力的变化情况,对运动机构进行优化。
我们通过学习UG,通过建立平面六杆机构模型,通过UG/CAE模块对平面连杆的运动进行分析。
3.六连杆机构的三维造型连杆L1连杆L2连杆L3连杆L5连杆L6六杆机构装配示意图机构装配后运动演示见附件—平面六杆运动演示.avi (本报告相同目录下)3. 运动分析数据计算结果在附件的Excel表格中。
六连杆铰链机构的运动仿真分析

六连杆铰链机构的运动仿真分析运用CATIA DMU运动仿真模块对六连杆铰链机构进行运动仿真,分析六连杆铰链机构的运动特性。
根据分析结论,对六连杆铰链机构进行改善设计。
标签:CATIA DMU;六连杆铰链;运动仿真六连杆铰链因其结构强度高,占用空间小、开启角度大等优点被广泛应用于大型客车的侧围行李舱门上。
如图1所示为六连杆铰链的基本结构:支座AB(可视为杆AB),杆AC,杆CD,杆EF,杆BE,支座DF(可视为杆DF)通过7个转动副(A、B、C、D、E、F、O)组合成一个统一的整体。
其中杆CD通过转动副O与杆BE连结,孔G为气弹簧固定点。
支座AB固定在车身上,侧围行李舱门锁付于支座DF上。
由于六连杆铰链输出的是六根连杆的组合运动,其运动特性比较复杂,单靠二维CAD绘图很难绘制出其完整的运动轨迹,从而无法对侧舱门的运动过程进行完整的校核。
而CATIA DMU运动机构模块[1]提供了一个非常直观的分析工具。
应用该模块,我们能对运动机构进行运动仿真,能绘制指定机构的运动轨迹,还能测量指定位置的速度、加速度等运动参数。
通过模拟运动过程,我们可以更加直观、准确的对侧舱门进行运动校核,防止干涉的产生。
1 运动仿真分析1.1 建立仿真模型切换到CATIA DMU运动机构模块,对六连杆机构的7个转动销轴添加转动副[2]。
由于支座AB与车身相连接,因此对支座AB添加一个固定副,由此来观察其余杆的运动特性。
正常情况下,六连杆机构运动的驱动外力是由锁付于G 点的气弹簧提供。
模拟时,可把杆AC当成驱动构件,因此对杆AC施加一个转动命令。
至此,仿真模型建立完成。
因为仓门锁付于支座DF上,与其相对静止,运动状况一致,因此仿真时对支座DF的运动状况进行分析并进行轨迹绘制。
通常仓门的开启角度达到120度[3]时(与铅垂面夹角)即可满足存取货物的需求,因此,对支座DF在0到120时的运动状况进行仿真分析,如图3所示。
1.2 运动分析2 结论验证及运用初步分析完六连杆铰链机构的运动特性,还需将铰链装配到整车环境下进行验证结论是否正确。
牛头刨床的连杆机构运动分析

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
RRR-RRP平面六杆Ⅱ级机构的运动学仿真

机构 的运动 分 析 , 要是 获 得 机 构 中某 些 构件 的动态 仿真 。采用 MA L B对 机构 进 行仿 真 , 乎 主 TA 几
的位 移 、 角速 度 和 加速 度 , 以及 某 些 点 的轨 迹 , 速度 所 有 的构件 运 动 参 数 都 在 仿 真 模 型 的数 据 线 上 传 和加 速度 。它是机 械设计 及评 价机 械运 动和动 力性 输 , 只要将该 数 据 线 上 的 信 息 引入 Sm u 模 块 , iot 就
柄 、R R RⅡ级 杆组 、 R R PⅡ级 杆 组 三 个 基 本 模 组 的 运 动 学 数 学 模 型 , 用 其 组 成 机 构 杆 组 并 搭 建 平 面 连 杆 机 构 的 运 动 学 仿 真 利
模型 , 充分利用 MA L B的 Sm l k TA i ui 仿真模型数据可视化的特点, n 观察和分析其运动参数的变化 。 [ 中图分类号 ]T 3 19 P 9 . [ 文献标志码 ]A [ 文章编号]10 4 2 (00)4— 0 6— 5 0 1— 9 6 2 1 0 04 0
能 的基础 , 是 分析 现 有 机械 优 化 综合 新 机 械 的基 可 以观察 到该 运 动 参 数 是 如 何 变 化 的及 相 应 的数 也
本手段 。
一
据, 并可 以 图形 的形 式直 观地 表现 出来 。 为 了利用 Ma a t b仿 真 软 件 包 的数 值 积 分 算 法 l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福州大学课程名称机械原理及系统仿真姓名张景铜班级 12机械2班学号 261280458院系工程技术学院专业机械设计制造及其自动化平面六杆机构运动分析一、问题描述如图所示,机构是由原动件(曲柄1)和1个RRR杆组、RRP干组组成的RRR-RRP六杆机构,各构件的尺寸为r1=70mm,r2=150mm,r3=100mm,r4=150mm,r5=120mm。
复数向量坐标如图所示,构件1以等角速度10rad/s逆时针方向回转,试求C点的加速度、构3的角加速度、构件6的速度、加速度及构件5的角速度和角加速度。
二、杆组分析将机构进行拆杆组分解,分为曲柄1+第一个RRR杆组(BCD)+第二个RRP杆组(CDE)。
对此分别建立三个3个M函数模块,分别为crank.m,RRRki.m和RRPki.m。
Crank.m函数模块的输入参数为曲柄1的角位移、角速度和角加速度,输出的参数曲柄端部(B)的加速度和水平分量和垂直分量。
RRRki.m函数模块的输入参数为构件2和构件3的角位移、角速度、B处的加速度,输出的参数是构件2和3的角加速度和C处的位移。
RRPki.m函数模块的输入参数为构件5的角位移、角速度和构件转动副C的加速度,输出的参数是构件5的角加速度和构件6的加速度。
三、确定输入初值(1)当主动件(曲柄)初始角度设置为45°时,可通过如下程序求出和的精确值;输入参数运行如下:>> x=[45*pi/180 16*pi/180 64*pi/180 0.070 0.150 0.100 0.150] ;>> y=rrrposi(x)y =0.2721 1.1154程序:function y=rrrposi(x)%Script used to implement Newton -Raphson method for solving nonlinear%Input parameters%x(1)=theta-1;%x(2) =theta-2 guess value ;%x(3) =theta-3 guess value%x(4) =r1;%x(5) =r2;%x(6) =r3;%x(7) =r4%Output parameters%y(1) =theta-2;%y(2) =theta-3theta2=x(2);theta3=x(3);epsilon=1.0E-6;f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)-x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)-x(6)*sin(theta3)];while norm(f)>epsilonJ=[-x(5)*sin(theta2) x(6)*sin(theta3);x(5)*cos(theta2) -x(6)*cos(theta3)];dth=inv(J)*(-1.0*f);theta2=theta2+dth(1);theta3=theta3+dth(2);f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)-x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)-x(6)*sin(theta3)];norm(f);end;y(1)=theta2;y(2)=theta3;(2.)、根据已知量可确定出连杆(r2)和从动件(r3)的角速度,>> x=[45*pi/180 0.2721 1.1154 10 0.070 0.150 0.100 0.150] ;>> y=rrrvel(x)y =-2.02484.6025程序:function y=rrrvel(x)%%Script for solving velosity of RRR bar group %%%Input parameters%x(1)=theta-1%x(2) =theta-2%x(3) =theta-3%x(4) =dtheta-1%x(5) =r1%x(6) =r2%x(7) =r3%Output parameters%y(1) =dtheta-2%y(2) =dtheta-3% %A=[-x(6)*sin(x(2)) x(7)*sin(x(3));x(6)*cos(x(2)) -x(7)*cos(x(3))];B=[x(5)*sin(x(1)); -x(5)*cos(x(1))]*x(4);y=inv(A)*B;(3)、根据前面求出的参数及已知条件可按以下程序求出构件5的角速度和构件6的速度。
>> u=[4.6025 1.1154 -0.8378];>> [x]=compvel(u)x =-2.5211-0.6382程序:function [x]=compvel(u)%% function to compute the unknown velocities for a slider crank with% constant crank input% u(1)=omega-3% u(2)=theta-3% u(3)=theta-5%% Define the geometry%r3=0.7;r5=1.2;%a=[r5*sin(u(3)) 1; -r5*cos(u(3)) 0];b=[-r3*u(1)*sin(u(2)); r3*u(1)*cos(u(2))];%x=inv(a)*b;四、编辑创建杆组M文件(1)、编写crank.m文件function y=crank(x)%%Function to compute the accleration of crank%Input parameters%x(1)=rj%x(2)=thetaj%x(3)=dthetaj%x(4)=ddthetaj%0utput parameters%y(1)=Re[ddB]%y(2)=Im[ddB]ddB=[x(1)*x(4)*cos(x(2)+pi/2)+x(1)*x(3)^2*cos(x(2)+pi); x(1)* x(4)*sin(x(2)+pi/2)+x(1)*x(3)^2*sin(x(2)+pi)];y=ddB;(2)、编写RRRki.m文件function y=RRRki(x)%function to compute the acceleration for RRR bar group%Input parameters%x(1)=ri%x(2)=rj%x(3)=theta-i%x(4)=theta-j%x(5)=dtheta-i%x(6)=dtheta-j%x(7)=Re[ddB]%x(8)=Im[ddB]%x(9)=Re[ddD]%x(10)=Im[ddD]%Output parameters%y(1)=ddtheta-i%y(2)=ddtheta-j%y(3)=Re[ddC]%y(4)=Im[ddC]a=[x(1)*cos(x(3)+pi/2) -x(2)*cos(x(4)+pi/2);x(1)*sin(x(3)+pi/2) -x(2)*sin(x(4)+pi/2)];b=[-x(1)*cos(x(3)+pi) x(2)*cos(x(4)+pi);-x(1)*sin(x(3)+pi) x(2)*sin(x(4)+pi)]*[x(5)^2;x(6)^2]+[x(9)-x(7);x(10)-x(8)];ddth=inv(a)*b;y(1)=ddth(1);y(2)=ddth(2);y(3)=x(7)+x(1)*ddth(1)*cos(x(3)+pi/2)+x(1)*x(5)^2*cos(x(3)+pi);y(4)=x(8)+x(1)*ddth(1)*sin(x(3)+pi/2)+x(1)*x(5)^2*sin(x(3)+pi);(3)、编写RRPki.m文件function y=RRPki(x)%function to compute the acceleration for RRP bar group%Input parameters%x(1)=ri%x(2)=theta-i%x(3)=theta-j%x(4)=dtheta-i%x(5)=Re[ddB]%x(6)=Im[ddB]%x(7)=Re[ddK]%x(8)=Im[ddK]%x(9)=ds%Output parameters%y(1)=ddtheta-i%y(2)=dds%a=[x(1)*cos(x(2)+pi/2) -cos(x(3));x(1)*sin(x(2)+pi/2) -sin(x(3))];b=[-x(1)*cos(x(2)+pi) 0; -x(1)*sin(x(2)+pi)0]*[x(4)^2;x(9)]+[x(7)-x(5);x(8)-x(6)];y=inv(a)*b;五、创建模型在Simulink中创建输入输出模型,如下所示:各初值为:th1=45*pi/180; dth1=10; th2=0.2721; th3=1.1154; dth2=-2.0248;dth3=4.6025; th5=-0.8378; dth5=-1.7648; s-6=0.27357; ds6=-4.4673;六、程序运行及结果输出过程。
