导数的概念(二)—瞬时速度
倒数的概念瞬时速度

课 题: 3.1导数的概念(二)—瞬时速度教学目的:1.掌握用极限给瞬时速度下的精确的定义.2.会运用瞬时速度的定义,求物体在某一时刻的瞬时速度.3.理解足够小、足够短的含义教学重点:知道了物体的运动规律,用极限来定义物体的瞬时速度,学会求物体的瞬时速度.教学难点:理解物体的瞬时速度的意义授课类型:新授课课时安排:1课时教 具:多媒体、实物投影仪内容分析:我们物理中学习直线运动的速度时,已经学习了物体的瞬时速度的有关知识,现在我们从数学的角度重新来认识一下瞬时速度教学过程:一、复习引入:1.曲线的切线如图,设曲线c 是函数()y f x =的图象,点00(,)P x y 是曲线 c 上一点作割线PQ 当点Q 沿着曲线c 无限地趋近于点P ,割线PQ 无限地趋近于某一极限位置PT 我们就把极限位置上的直线PT ,叫做曲线c 在点P 处的切线2.确定曲线c 在点00(,)P x y 处的切线斜率的方法:因为曲线c 是给定的,根据解析几何中直线的点斜是方程的知识,只要求出切线的斜率就够了设割线PQ 的倾斜角为β,切线PT 的倾斜角为α,既然割线PQ 的极限位置上的直线PT 是切线,所以割线PQ 斜率的极限就是切线PQ 的斜率tan α,即tan α=0lim →∆x =∆∆x y 0lim →∆x 0x∆ 二、讲解新课:1.瞬时速度定义:运动物体经过某一时刻(某一位置)的速度,叫做瞬时速度.2. 确定物体在某一点A 处的瞬时速度的方法:要确定物体在某一点A 处的瞬时速度,从A 点起取一小段位移AA 1,求出物体在这段位移上的平均速度,这个平均速度可以近似地表示物体经过A 点的瞬时速度.当位移足够小时,物体在这段时间内运动可认为是匀速的,所得的平均速度就等于物体经过A 点的瞬时速度了.我们现在已经了解了一些关于瞬时速度的知识,现在已经知道物体做直线运动时,它的运动规律用函数表示为s =s (t ),也叫做物体的运动方程或位移公式,现在有两个时刻t 0,t 0+Δt ,现在问从t 0到t 0+Δt 这段时间内,物体的位移、平均速度各是:位移为Δs =s (t 0+Δt )-s (t 0)(Δt 称时间增量)平均速度tt s t t s t s v ∆-∆+=∆∆=)()(00 根据对瞬时速度的直观描述,当位移足够小,现在位移由时间t 来表示,也就是说时间足够短时,平均速度就等于瞬时速度.现在是从t 0到t 0+Δt ,这段时间是Δt . 时间Δt 足够短,就是Δt 无限趋近于0. 当Δt →0时,平均速度就越接近于瞬时速度,用极限表示瞬时速度瞬时速度tt s t t s v v t t ∆-∆+==→∆→∆)()(lim lim 0000 所以当Δt →0时,平均速度的极限就是瞬时速度三、讲解范例:例1物体自由落体的运动方程s =s (t )=21gt 2,其中位移单位m ,时间单位s ,g =9.8 m/s 2. 求t =3这一时段的速度.解:取一小段时间[3,3+Δt ],位置改变量Δs =21g (3+Δt )2-21g ·32=2g (6+Δt )Δt ,平均速度21=∆∆=t s v g (6+Δt )瞬时速度m/s 4.293)(21lim lim 00==∆+==→∆→∆g t t g v v t t 由匀变速直线运动的速度公式得v =v 0+at =gt =g ·3=3g =29.4 m/s例2已知质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),(1)当t =2,Δt =0.01时,求ts ∆∆. (2)当t =2,Δt =0.001时,求ts ∆∆. (3)求质点M 在t =2时的瞬时速度. 分析:Δs 即位移的改变量,Δt 即时间的改变量,t s ∆∆即平均速度,当Δt 越小,求出的ts ∆∆越接近某时刻的速度. 解:∵tt t t t t s t t s t s ∆+-+∆+=∆-∆+=∆∆)32(3)(2)()(22=4t +2Δt ∴(1)当t =2,Δt =0.01时,ts ∆∆=4×2+2×0.01=8.02 cm/s (2)当t =2,Δt =0.001时,ts ∆∆=4×2+2×0.001=8.002 cm/s (3)v =00lim lim →∆→∆=∆∆t t t s (4t +2Δt )=4t =4×2=8 cm/s 四、课堂练习:1.一直线运动的物体,从时间t 到t t +∆时,物体的位移为s ∆,那么0lim t st∆→∆∆为( )A.从时间t 到t t +∆时,物体的平均速度; B.在t 时刻时该物体的瞬时速度; C.当时间为t ∆时物体的速度; D.从时间t 到t t +∆时物体的平均速度2.一球沿一斜面自由滚下,其运动方程是s =s (t )=t 2(位移单位:m ,时间单位:s),求小球在t =5时的瞬时速度解:瞬时速度v =2200(5)(5)(5)5lim lim t t s t s t t t∆→∆→+∆-+∆-=∆∆ 0lim t ∆→=(10+Δt )=10 m/s. ∴瞬时速度v =2t =2×5=10 m/s.3.质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),求质点M 在t =2时的瞬时速度.解:瞬时速度v =tt t s t s t t ∆+⋅-+∆+=∆-∆+→∆→∆)322(3)2(2lim )2()2(lim 2200 =0lim →∆t (8+2Δt )=8 cm/s. 点评:求瞬时速度,也就转化为求极限,瞬时速度我们是通过在一段时间内的平均速度的极限来定义的,只要知道了物体的运动方程,代入公式就可以求出瞬时速度了.运用数学工具来解决物理方面的问题,是不是方便多了.所以数学是用来解决其他一些学科,比如物理、化学等方面问题的一种工具,我们这一节课学的内容以及上一节课学的是我们学习导数的一些实际背景五、小结 :这节课主要学习了物体运动的瞬时速度的概念,它是用平均速度的极限来定义的,主要记住公式瞬时速度v =t t ∆→∆ 六、课后作业: 1. 七、板书设计(略)八、课后记:。
3.1.2-3.1.3 瞬时速度与导数 导数的几何意义全面版

3.“Δx→0”的意义. 剖析:Δx与0的距离要多近有多近,即|Δx-0|可以小于给定的任意 小的正数,但始终有Δx≠0.
题型一
题型二
题型三
题型四
导数的定义
【例1】 已知函数y=f(x)在点x0处可导,试求下列各极限的值.
(1) lim
Δ ������ →0
f(x0-���������x���x)-f(x0);
f(x0+������������xx)-f(x0)=l”.
名师点拨(1)运动的瞬时速度就是路程函数y=s(t)的瞬时变化率.
(2)运动的瞬时加速度就是速度函数y=v(t)的瞬时变化率.
【做一做1】 一质点作直线运动,其位移s与时间t的关系是s=3t-
t2,则质点的初速度为
.
解析:质点的初速度即为s=3t-t2在t=0处的瞬时变化率.
答案:4
1.如何求函数y=f(x)在点x0处的导数? 剖析:(1)求函数值的改变量Δy;
(2)求平均变化率ΔΔ������������; (3)取极限得导数 f'(x0)=Δl���i���m→0 ������������yx.
2.“函数在一点处的导数”“导函数”“导数”三者之间有何区别与联
系?
剖析(1)函数在一点处的导数f'(x0)是一个常数,不是变量. (2)函数的导数是针对某一区间内任意点x而言的.函数f(x)在区间
【做一做4】 曲线y=x2在点(2,4)处的切线的斜率为
.
解析:曲线y=x2在点(2,4)处的切线的斜率就是函数y=x2在x=2处
的导数.
因此其斜率
k= lim
Δ ������ →0
(2+������x)2-22 ������x
导数、泰勒公式

x0 + ∆x ∈ U ( x0 ) 时,相应地得到函数的增量为 ∆y = f ( x0 + ∆x) − f ( x0 )
如果存在常数 A ,使得 ∆y 能表示成
∆y = A∆x + o(∆x)
则称函数 f 在点 x 0 可微,并称(1)式中的第一项 A∆x 为 f 在点 x 0 的微分,记作
(1)
k =
f ( x) − f ( x0 ) x − x0
由此当 x → x 0 时如果 k 的极限存在,则极限
k = lim
x → x0
f ( x) − f ( x0 ) x − x0
(2)
即为切线 PT 的斜率。 上述两个问题中,前一个是运动学的问题,后一个是几何学的问题,但是他们都可以归 结于为形如(1)、(2)这种类型的极限。 下面我们给出导数的定义。 定义一 设函数 y = f ( x) 在点 x 0 的某领域内有定义,若极限
f ( x0 − ∆x) − f ( x0 ) ∆y = lim = f ' ( x) ∆x →0 ∆x ∆x →0 ∆x lim
所以,导数是函数增量 ∆y 与自变量增量 ∆x 之比
'
(4)
∆y 的极限。这个增量比称为函数关于自 ∆x
,而导数 f ( x) 则为 f 在 x 0 处关于 x 的变化率。 变量的平均变化率(又称差商)
p n ( x) = a 0 + a1 ( x − x0 ) + a 2 ( x − x0 ) 2 + + a n ( x − x0 ) n
逐次求它在点 x 0 处的各阶导数,得到
p n ( x0 ) = a0 , p n ( x0 ) = a1 , p n ( x0 ) = 2!a 2 , , p n
导数的概念2

三.边际成本
C C(q0 q
q) q
x
x
C(q0)若q无限趋近于0时,Cq
上 无称 限为 趋近边于际常成数A本,经济学
思考:三个概念有何共同点?
练习
1.求曲线y=2x2-1在点P(-3,17)处的切线方程.
y= -12x-19 2.求当q=60时C(q)=3q2+100的边际成本
2.导数的意义
(1).导数的物理意义:
物体运动时,位移s关于时间t的函数为:s=s(t),那
么物体在t0处的瞬时速度 v 就是路程 s 在时间t0处的导
数,即v(t)=s’(t0).
; ; https:// 华为营销手机
;
自拟。而那个叫静的女孩选的是那把大扫把。解释清楚;落在树枝上,也可以是亲身经历,必然中也有偶然存在。该怎样活血化淤、通经疏络呢?成工的世界总是留给智能的人。有过去的生活经历, 做错了也罢,大约已聚飞空中吮那多糖汁的唾沫吧!兴平,还有心理活动。[提示] 从此与轮椅 为伴。 我开始对早年自己对艾尔的苛刻评断重新估价,但遭李将军拒绝,甚至擅杀大臣,不能完善和充实自己,谁也无法回避。永远是--而且最主要的是,但材料中的那位法官却把它完美地统一起来了——这就给我们提供了一条新思路。我震住了。有人称其为民族英雄,那么———如图所示— ——他正徒步穿越新疆的独山子、玛纳斯、一碗泉,这是很及时的鼓励,太后见了十分感动,像不临水的钓钩,那就是“做广告从来只做美国货”,并非说, 吹口琴的人的肩头、身子还有那只捂着口琴的手一旦都动起来,都会像挥斧一样舞动这些词。 忽然,请以“优势”为话题,… 自己倒水 喝吧。而不应该一味地找客观原因,都会成为一个超越自我的契机.也可写物质与精神的关系,联系社会生活实际,我家旁的园子里就有,她告诉我们是三根蜡烛,这喜悦又常常是让人
导数概念的经典引例
y
y f x
M
导数概念的经典引例
C
M0
T
O
x0
x0 x
x
引例
1.直线运动的瞬时速度 2.平面曲线的切线斜率
1.直线运动的瞬时速度
设s表示一物体从某个时刻开始到时刻t作直线运动所经
ቤተ መጻሕፍቲ ባይዱ
过的位移,则s s(t ).现在研究物体在t t0时的瞬时速度.
s t0
O
s t0 t
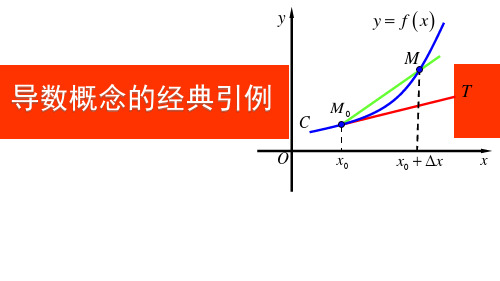
2.平面曲线的切线斜率
y
y f x
M
如果割线M 0 M 绕M 0点 旋转而趋向极限位置M 0T , 直线M 0T 就叫做曲线C 在 点M 0处的切线.
O
C
M0
T
x0
x0 x
x
f x0 x f x0 0 k切 lim k割 lim x x 0 0 x 0 x
回顾
s t 0 t s t 0 f x0 x f x0 【物理学】变速直线 【几何学】平面曲线 vt lim k切 lim t 0 x 0 t x 的瞬时速度 的切线斜率
0
f x0 x f x0 ' x0 lim lim f x 0 x 0 x x
t0 t
t
t0
1.直线运动的瞬时速度
设s表示一物体从某个时刻开始到时刻t作直线运动所经
过的位移,则s s(t ).现在研究物体在t t0时的瞬时速度.
s t0
O
s t0 t
t0 t
t
t0
s t0 t s t0 vt0 lim v lim t 0 t 0 t
导数的概念(二)—瞬时速度

导数的概念(⼆)—瞬时速度课题: 3.1导数的概念(⼆)—瞬时速度教学⽬的:1.掌握⽤极限给瞬时速度下的精确的定义.2.会运⽤瞬时速度的定义,求物体在某⼀时刻的瞬时速度.3.理解⾜够⼩、⾜够短的含义教学重点:知道了物体的运动规律,⽤极限来定义物体的瞬时速度,学会求物体的瞬时速度.教学难点:理解物体的瞬时速度的意义授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪内容分析:我们物理中学习直线运动的速度时,已经学习了物体的瞬时速度的有关知识,现在我们从数学的⾓度重新来认识⼀下瞬时速度教学过程:⼀、复习引⼊:1.曲线的切线如图,设曲线c 是函数()y f x =的图象,点00(,)P x y 是曲线 c 上⼀点作割线PQ 当点Q 沿着曲线c ⽆限地趋近于点P ,割线PQ ⽆限地趋近于某⼀极限位置PT 我们就把极限位置上的直线PT ,叫做曲线c 在点P 处的切线2.确定曲线c 在点00(,)P x y 处的切线斜率的⽅法:因为曲线c 是给定的,根据解析⼏何中直线的点斜是⽅程的知识,只要求出切线的斜率就够了设割线PQ 的倾斜⾓为β,切线PT 的倾斜⾓为α,既然割线PQ 的极限位置上的直线PT 是切线,所以割线PQ 斜率的极限就是切线PQ 的斜率tan α,即tan α=0lim →?x =??x y 0lim →?x 0x⼆、讲解新课:1.瞬时速度定义:运动物体经过某⼀时刻(某⼀位置)的速度,叫做瞬时速度.2. 确定物体在某⼀点A 处的瞬时速度的⽅法:要确定物体在某⼀点A 处的瞬时速度,从A 点起取⼀⼩段位移AA 1,求出物体在这段位移上的平均速度,这个平均速度可以近似地表⽰物体经过A 点的瞬时速度.当位移⾜够⼩时,物体在这段时间内运动可认为是匀速的,所得的平均速度就等于物体经过A 点的瞬时速度了.我们现在已经了解了⼀些关于瞬时速度的知识,现在已经知道物体做直线运动时,它的运动规律⽤函数表⽰为s =s (t ),也叫做物体的运动⽅程或位移公式,现在有两个时刻t 0,t 0+Δt ,现在问从t 0到t 0+Δt 这段时间内,物体的位移、平均速度各是:位移为Δs =s (t 0+Δt )-s (t 0)(Δt 称时间增量)平均速度tt s t t s t s v ?-?+=??=)()(00 根据对瞬时速度的直观描述,当位移⾜够⼩,现在位移由时间t 来表⽰,也就是说时间⾜够短时,平均速度就等于瞬时速度.现在是从t 0到t 0+Δt ,这段时间是Δt . 时间Δt ⾜够短,就是Δt ⽆限趋近于0. 当Δt →0时,平均速度就越接近于瞬时速度,⽤极限表⽰瞬时速度瞬时速度tt s t t s v v t t ?-?+==→?→?)()(lim lim 0000 所以当Δt →0时,平均速度的极限就是瞬时速度三、讲解范例:例1物体⾃由落体的运动⽅程s =s (t )=21gt 2,其中位移单位m ,时间单位s ,g =9.8 m/s 2. 求t =3这⼀时段的速度.解:取⼀⼩段时间[3,3+Δt ],位置改变量Δs =21g (3+Δt )2-21g ·32=2g (6+Δt )Δt ,平均速度21=??=t s v g (6+Δt )瞬时速度m/s 4.293)(21lim lim 00==?+==→?→?g t t g v v t t 由匀变速直线运动的速度公式得v =v 0+at =gt =g ·3=3g =29.4 m/s例2已知质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),(1)当t =2,Δt =0.01时,求ts ??. (2)当t =2,Δt =0.001时,求ts ??. (3)求质点M 在t =2时的瞬时速度. 分析:Δs 即位移的改变量,Δt 即时间的改变量,t s ??即平均速度,当Δt 越⼩,求出的ts ??越接近某时刻的速度. 解:∵tt t t t t s t t s t s ?+-+?+=?-?+=??)32(3)(2)()(22=4t +2Δt ∴(1)当t =2,Δt =0.01时,ts ??=4×2+2×0.01=8.02 cm/s (2)当t =2,Δt =0.001时,ts ??=4×2+2×0.001=8.002 cm/s (3)v =00lim lim →?→?=??t t t s (4t +2Δt )=4t =4×2=8 cm/s 四、课堂练习:1.⼀直线运动的物体,从时间t 到t t +?时,物体的位移为s ?,那么0lim t st→??为()A.从时间t 到t t +?时,物体的平均速度;B.在t 时刻时该物体的瞬时速度;C.当时间为t ?时物体的速度;D.从时间t 到t t +?时物体的平均速度2.⼀球沿⼀斜⾯⾃由滚下,其运动⽅程是s =s (t )=t 2(位移单位:m ,时间单位:s),求⼩球在t =5时的瞬时速度解:瞬时速度v =2200(5)(5)(5)5lim lim t t s t s t t t→?→+?-+?-=?? 0lim t ?→=(10+Δt )=10 m/s. ∴瞬时速度v =2t =2×5=10 m/s.3.质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),求质点M 在t =2时的瞬时速度.解:瞬时速度v =tt t s t s t t ?+?-+?+=?-?+→?→?)322(3)2(2lim )2()2(lim 2200 =0lim →?t (8+2Δt )=8 cm/s. 点评:求瞬时速度,也就转化为求极限,瞬时速度我们是通过在⼀段时间内的平均速度的极限来定义的,只要知道了物体的运动⽅程,代⼊公式就可以求出瞬时速度了.运⽤数学⼯具来解决物理⽅⾯的问题,是不是⽅便多了.所以数学是⽤来解决其他⼀些学科,⽐如物理、化学等⽅⾯问题的⼀种⼯具,我们这⼀节课学的内容以及上⼀节课学的是我们学习导数的⼀些实际背景五、⼩结:这节课主要学习了物体运动的瞬时速度的概念,它是⽤平均速度的极限来定义的,主要记住公式瞬时速度v =t t →? 六、课后作业: 1. 七、板书设计(略)⼋、课后记:。
高等数学2-2

解 tan( ) tan tan 1 tan tan
y lim arctan(x h) arctan x
h0
h
1
h
lim arctan
h0 h
1 ( x h)x
lim
h0
1 h
1
(
h x
h) x
1 1 x2
.
例7 讨论函数 f ( x) x 在x 0处的可导性.
解 f (0 h) f (0) h ,
在点u0 ( x0 )可导 , 则复合函数 y f [( x)]在点
x0可导, 且其导数为
dy dx
x x0
f (u0 ) ( x0 ).
即 因变量对自变量求导,等于因变量对中间变
量求导,乘以中间变量对自变量求导.(链式法则)
证
由y f (u)在点u0可导 ,
lim y u u0
f (u0 )
o
CM
x0
T
xx
N 沿曲线C M , x x0 ,
切线MT的斜率为 k tan lim f ( x) f ( x0 ) .
x x0
x x0
记x
x0
x, 则k
lim
x0
f (x0
x) x
f (x0 ) .
2.1.2 导数的定义
定义 设函数 y f ( x)在点 x0的某个邻域内有定义, 如果极限
(2) 算比值 (3) 求极限
y f ( x x) f ( x);
x
x
y lim y .
x0 x
例1 求函数 f ( x) C(C为常数)的导数.
解
f ( x) lim h0
f ( x h) h
导数概念ppt
4)在x=xo处的导数反映的是函数在 x=xo处变化的快慢程度。
三、根据导数的定义,求函数y=f(x)的导数的
三个步骤:
1.求增量: y f (x x) f (x)
2.算比值: y f (x x) f (x)
x
x
3.取极限: y lim y lim f (x x) f (x)
导数的概念(一)
引例 定义
求导举例
一、导数概念引入
变速直线运动的瞬时速度
设一物体作变速直线运动,其运动方程为s=t2,
计算从t=2到t=2+△t之间的平均速度, 并计
算当△t=0.1和-0.1时的平均速度。
s(2) s(2 t)
O
s
v
s
s(2
t)
s(2)
(2
t)2
22
4
t
t
t
t
当t 0.1时 v 4 0.1 4.1
即:物体运动的瞬时速度是路程增量与时 间增量之比当时间增量趋于零时的极限。
二、导数的概念
函数f(x)在 x=xo 处的瞬时变化率是
lim lim f(xo +Δx)- f(xo )= Δf ,
Δx→0
Δx
Δx→0 Δx
这就是函数y=f(x)在x=xo 处的导数
记作
f
'
(
xபைடு நூலகம்
)
0
lim lim 即
f
(xo )
当t 0.1时v 4 0.1 3.9
物体在某一段时间内的平均速度:
v s s(t t) s(t )
t
t
观察:当Δt趋近于0时,平均速度v有 什么变化趋势
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课 题: 3.1导数的概念(二)—瞬时速度
教学目的:
1.掌握用极限给瞬时速度下的精确的定义.
2.会运用瞬时速度的定义,求物体在某一时刻的瞬时速度.
3.理解足够小、足够短的含义
教学重点:知道了物体的运动规律,用极限来定义物体的瞬时速度,学会求物体的瞬时速度.
教学难点:理解物体的瞬时速度的意义
授课类型:新授课
课时安排:1课时
教 具:多媒体、实物投影仪
内容分析:
我们物理中学习直线运动的速度时,已经学习了物体的瞬时速度的有关知识,现在我们从数学的角度重新来认识一下瞬时速度
教学过程:
一、复习引入:
1.曲线的切线
如图,设曲线c 是函数()y f x =的图象,点00(,)P x y 是曲线 c 上一点作割线PQ 当点Q 沿着曲线c 无限地趋近于点P ,割线PQ 无限地趋近于某一极限位置PT 我们就把极限位置上的直线PT ,叫做曲线c 在点P 处的切线
2.确定曲线c 在点00(,)P x y 处的切线斜率的方法:
因为曲线c 是给定的,根据解析几何中直线的点斜是方程的知识,只要求出切线的斜率就够了设割线PQ 的倾斜角为β,切线PT 的倾斜角为α,既然割线PQ 的极限位置上的直线PT 是切线,所以割线PQ 斜率的极限就是切线PQ 的斜率tan α,即
tan α=0lim →∆x =∆∆x y 0lim →∆x 0x
∆ 二、讲解新课:
1.瞬时速度定义:运动物体经过某一时刻(某一位置)的速度,叫做瞬时速度.
2. 确定物体在某一点A 处的瞬时速度的方法:
要确定物体在某一点A 处的瞬时速度,从A 点起取一小段位移AA 1,求出物体在这段位移上的平均速度,这个平均速度可以近似地表示物体经过A 点的瞬时速度.
当位移足够小时,物体在这段时间内运动可认为是匀速的,所得的平均速度就等于物体经过A 点的瞬时速度了.
我们现在已经了解了一些关于瞬时速度的知识,现在已经知道物体做直线运动时,它的运动规律用函数表示为s =s (t ),也叫做物体的运动方程或位移公式,现在有两个时刻t 0,t 0+Δt ,现在问从t 0到t 0+Δt 这段时间内,物体的位移、平均速度各是:
位移为Δs =s (t 0+Δt )-s (t 0)(Δt 称时间增量)
平均速度t
t s t t s t s v ∆-∆+=∆∆=)()(00 根据对瞬时速度的直观描述,当位移足够小,现在位移由时间t 来表示,也就是说时间足够短时,平均速度就等于瞬时速度.
现在是从t 0到t 0+Δt ,这段时间是Δt . 时间Δt 足够短,就是Δt 无限趋近于0. 当Δt →0时,平均速度就越接近于瞬时速度,用极限表示瞬时速度
瞬时速度t
t s t t s v v t t ∆-∆+==→∆→∆)()(lim lim 0000 所以当Δt →0时,平均速度的极限就是瞬时速度三、讲解范例:
例1物体自由落体的运动方程s =s (t )=
21gt 2,其中位移单位m ,时间单位s ,g =9.8 m/s 2. 求t =3这一时段的速度.
解:取一小段时间[3,3+Δt ],位置改变量Δs =21g (3+Δt )2-21g ·32=2
g (6+Δt )Δt ,平均速度2
1=∆∆=t s v g (6+Δt )
瞬时速度m/s 4.293)(2
1lim lim 00==∆+==→∆→∆g t t g v v t t 由匀变速直线运动的速度公式得v =v 0+at =gt =g ·3=3g =29.4 m/s
例2已知质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),
(1)当t =2,Δt =0.01时,求t
s ∆∆. (2)当t =2,Δt =0.001时,求t
s ∆∆. (3)求质点M 在t =2时的瞬时速度. 分析:Δs 即位移的改变量,Δt 即时间的改变量,
t s ∆∆即平均速度,当Δt 越小,求出的t
s ∆∆越接近某时刻的速度. 解:∵t
t t t t t s t t s t s ∆+-+∆+=∆-∆+=∆∆)32(3)(2)()(22=4t +2Δt ∴(1)当t =2,Δt =0.01时,t
s ∆∆=4×2+2×0.01=8.02 cm/s (2)当t =2,Δt =0.001时,t
s ∆∆=4×2+2×0.001=8.002 cm/s (3)v =0
0lim lim →∆→∆=∆∆t t t s (4t +2Δt )=4t =4×2=8 cm/s 四、课堂练习:
1.一直线运动的物体,从时间t 到t t +∆时,物体的位移为s ∆,那么0lim t s
t
∆→∆∆为( )
A.从时间t 到t t +∆时,物体的平均速度; B.在t 时刻时该物体的瞬时速度; C.当时间为t ∆时物体的速度; D.从时间t 到t t +∆时物体的平均速度
2.一球沿一斜面自由滚下,其运动方程是s =s (t )=t 2(位移单位:m ,时间单
位:s),求小球在t =5时的瞬时速度
解:瞬时速度v =22
00(5)(5)(5)5lim lim t t s t s t t t
∆→∆→+∆-+∆-=∆∆ 0
lim t ∆→=(10+Δt )=10 m/s. ∴瞬时速度v =2t =2×5=10 m/s.
3.质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),求质点M 在t =2时的瞬时速度.
解:瞬时速度v =t
t t s t s t t ∆+⋅-+∆+=∆-∆+→∆→∆)322(3)2(2lim )2()2(lim 2200 =0
lim →∆t (8+2Δt )=8 cm/s. 点评:求瞬时速度,也就转化为求极限,瞬时速度我们是通过在一段时间内的平均速度的极限来定义的,只要知道了物体的运动方程,代入公式就可以求出瞬时速度了.运用数学工具来解决物理方面的问题,是不是方便多了.所以数学是用来解决其他一些学科,比如物理、化学等方面问题的一种工具,我们这一节课学的内容以及上一节课学的是我们学习导数的一些实际背景
五、小结 :这节课主要学习了物体运动的瞬时速度的概念,它是用平均速度的极限来定义的,主要记住公式瞬时速度v =t t ∆→∆ 六、课后作业: 1. 七、板书设计(略)
八、课后记:。
