第一节定积分的概念
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界, 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动:
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
(2)近似代替
y Ai f (i )xi
(i 1,2,, n)
(3)求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
第一节 定积分的概念和性质 定积分问题举例1

Ai f ( i )xi
曲边梯形面积的近似值为
A f ( i )xi
i 1 n
当分割无限加细,即小区间的最大长度
max{ x1 , x2 , xn }
趋近于零 ( 0) 时,
曲边梯形面积为 A lim f ( i )xi
0
i 1
n
实例2 (求变速直线运动的路程)
(1)分割
T1 t 0 t1 t 2 t n1 t n T2 t i t i t i 1 si v ( i )t i
部分路程值
某时刻的ቤተ መጻሕፍቲ ባይዱ度
(2)求和
s v ( i )t i
i 1
n
(3)取极限 max{t1 , t 2 ,, t n } 路程的精确值 s lim v ( i )t i
设某物体作直线运动,已知速度v v (t ) 是 时 间 间 隔 [T1 , T2 ] 上t 的 一 个 连 续 函 数 , 且
v ( t ) 0 ,求物体在这段时间内所经过的路程.
思路:把整段时间分割成若干小段,每小段上 速度看作不变,求出各小段的路程再相加,便 得到路程的近似值,最后通过对时间的无限细 分过程求得路程的精确值.
把区间 [a , b] 分成 n 个小区间 [ xi 1 , xi ], 长度为 xi xi xi 1 ;
y
在每个小区间 [ xi 1 , xi ] 上任取一点 i,
o a
x1
x i 1 x i
i
x n1 b
x
以 [ xi 1 , xi ]为底, ( i ) 为高的小矩形面积为 f
o
a
b
x
用矩形面积近似取代曲边梯形面积
定积分的概念与性质

x
区间长度为: xi xi xi 1 , i 1,2,
,n
将曲边 梯形AabB 分成 n 个小曲边梯形,
si 表示第 i 个小曲边梯形的面积, 用s 表示曲边梯形 AabB 的面积, 则有: n s s1 s2 sn si
i 1
(2)近似求和 在每个小区间[ xi 1 , xi ] 上任取一点 i ( xi 1 i xi ),
n
当 0 时,和 总有共同的极限 I ,则称 I 为函数 b f ( x ) 在 [a , b] 上的定积分, 记为 f ( x )dx , 即
b
a
f ( x )dx I lim f ( i )xi
0
i 1
n
a
积分上限
[a , b] 称为积分区间
a
积分下限
s
i 1
n
i
si v ( i )t i
并作和:
( i 1,2, , n)
i
sn
v( )t
i 1 i n
n
则有 s sn v ( i )t i
i 1
n
(3)求极限 记 max{t i }, 当 0 时, 1 i n 有: s lim v ( i )t i
匀速直线运动: s v t 变速直线运动:
O
v(t )
T1
.
T2
.
t
用类似的方法解决如下: (1)分割
OT
1
t0
t1 t 2
ti
t i 1 tn T2
t
用 si 表示第 i 个小时间段行驶的距离, 则 s (2)近似求和 在每个时间段 [t i 1 , t i ] 上任取一时刻 i ,
第一节定积分的概念与性质

第五章定积分5.1 定积分的概念与性质数学与统计学院武忠祥12定积分问题举例1主要内容34定积分的定义定积分的性质12定积分问题举例1主要内容34定积分的定义定积分的性质1 定积分问题举例例1曲边梯形的面积问题abxyo)(x f y =abxyo)(x f y =面积,)(k x f ≡,)(k x f ≡/)(a b k A -=(设f 是[a ,b ]上的非负连续函数)1 定积分问题举例例1曲边梯形的面积问题abxyo)(x f y =面积,)(k x f ≡,)(k x f ≡/)(a b k A -=(设f 是[a ,b ]上的非负连续函数)1 定积分问题举例例1曲边梯形的面积问题abxyo)(x f y =面积,)(k x f ≡,)(k x f ≡/)(a b k A -=(设f 是[a ,b ]上的非负连续函数)1) 分bx x x x x x x a n n k k =<<<<<<<<=--11210 a bxyo1x 1-k x k x 1-n x1 定积分问题举例例1曲边梯形的面积问题abxyo)(x f y =面积,)(k x f ≡,)(k x f ≡/)(a b k A -=(设f 是[a ,b ]上的非负连续函数)1) 分b x x x x x x x a n n k k =<<<<<<<<=--11210 a bxyo1x 1-k x k x 1-n x kξ2) 匀任取)()(1--=∆∆≈∆k k k k k k x x x x f A ξ],[1k k k x x -∈ξ1 定积分问题举例例1曲边梯形的面积问题abxyo)(x f y =面积,)(k x f ≡,)(k x f ≡/)(a b k A -=(设f 是[a ,b ]上的非负连续函数)1) 分b x x x x x x x a n n k k =<<<<<<<<=--11210 a bxyo1x 1-k x k x 1-n x kξ2) 匀任取)()(1--=∆∆≈∆k k k k k k x x x x f A ξ],[1k k k x x -∈ξ3) 合knk kx f ∆∑=1)(ξ≈A1 定积分问题举例例1曲边梯形的面积问题abxyo)(x f y =面积,)(k x f ≡,)(k x f ≡/)(a b k A -=(设f 是[a ,b ]上的非负连续函数)1) 分b x x x x x x x a n n k k =<<<<<<<<=--11210 a bxyo1x 1-k x k x 1-n x kξ2) 匀任取)()(1--=∆∆≈∆k k k k k k x x x x f A ξ],[1k k k x x -∈ξ3) 合knk kx f ∆∑=1)(ξ≈A 4) 精},,max{21n x x x d ∆∆∆= knk kd x f ∆∑=→1)(lim ξ=A两个问题的共性:1) 求解具有同样特征的量2) 解决问题的思想方法和步骤相同3) 都归结为同样数学结构的和式极限的计算体现在两个方面:(1)都是分布在区间上的量,且对区间具有可加性;(2)量是非均匀分布在区间上的.思想方法都是四步:分、匀、和、精,核心都是匀、精,在均匀分布时都采用积运算.都是乘积的和式的极限,只是函数的表示不同罢了.12定积分问题举例1主要内容34定积分的定义定积分的性质1)定义(定积分)],,[b a 任意划分bx x x x x a n n =<<<<<=-1210 1)分],,[1k k k x x -∈ξ任取.)(k k x f ∆ξ做乘积2)匀3)合knk kx f ∆∑=1)(ξ时怎样选取怎样划分如果无论0,,],[→d b a k ξk nk kx f ∆∑=1)(ξ4)精趋于同一常数,⎰b adx x f )(knk k d x f ∆=∑=→)(lim 1ξ2 定积分的定义,],[)(上的有界函数是定义在设b a x f .],[)(上可积在则称b a x f=⎰b ax x f d )(k nk k d x f ∆∑=→1)(lim ξ;代替所以不能用不等价与)0,01→∞→+∞→→d n n d 注:2)两个任意性;.],[)()(3有关和仅与)b a x f dx x f ba⎰.],[称为积分区间b a 积分是处理均匀量的积运算在处理相应非均匀量中的发展⎰=baxx f A d )(⎰=batt v s d )(积分上限积分下限被积函数积分变量被积式积分和时,b a >⎰b a dx x f )(时,b a =0)(=⎰badx x f ②补充规定:①⎰-=abdxx f )(曲边梯形面积曲边梯形面积的负值1A2A 3A 2)定积分的几何意义abxyo)(x f y =,)(变号x f ⎰>ba dx x f x f )(,0)(A =⎰<b a dx x f x f )(,0)(A-=312)(A A A dx x f b a--=⎰x120.x d x ⎰例4 计算定积分3)定积分存在的条件可积的充分条件可积有界可积性计算上连续;在],[)()1b a x f .],[)()2断点上只有有限个第一类间在b a x f knk k bad x f dx x f ∆=∑⎰=→1)(lim )(ξ个子区间的右端点,则有12定积分问题举例1主要内容34定积分的定义定积分的性质],[b a R 3.定积分的性质Riemann积分R b a R g f ∈∈βα,],,[,],[b a R g f ∈+βα⎰⎰⎰+=+ba b ab a dx x g dx x f dx x g x f )()()]()([βαβα1)线性性质:设,则且I Ic b a ∈,,2)对区间的可加性:设是有限闭区间,)(I R f ∈⎰⎰⎰+=b a ca b c dx x f dx x f dx x f )()()(且,则k b c k k k c a x f x f ∆+∆=∑∑)()(],[],[ξξk b a k x f ∆∑)(],[ξ证设,b c a <<。
定积分的概念

f ( i ) xi ,
i 1
记 max{ x1 , x2 ,, xn },如果不论对[a, b]
怎样的分法, 也不论在小区间[ xi1 , xi ]上
点i 怎样的取法,只要当 0时,和式总趋于 确定的极限I ,我们称这个极限 I 为函数 f ( x)
在区间[a, b]上的定积分, 记为
积分上限
b a
f ( x)dx
I
lim 0
n i 1
f
(i )xi
积分和
积分下限
被 积 函 数
被
积
[a,b] 积分区间
积
分
表 达 式
变 量
定积分的本质是一种特殊结构的和式的极限
曲边梯形面积A:
n
A lim 0 i1
f (i )xi
记为 b f x dx a
隔[T1 ,T2 ]内,v 的变化不大,可近似看作是
匀速运动问题。按照求曲边梯形面积的思 想。
思路:把整段时间分割成若干个小段,每小段上 速度看作不变。求出各小段的路程再相加,便得到 路程的近似值。最后通过对时间的无限细分过程求 得路程的精确值。
(1)分割 T1 t0 t1 t2 tn1 tn T2 ti ti ti1
sin xdx
1
A2
4
sin
xdx
所以
5
A sin xdx 4 sin xdx
1
内容小结
1. 定积分的定义 — 乘积和式的极限
b
n
a
f ( x)dx lim 0 i1
f (i )xi
2. 定积分的几何意义
高教社2024高等数学第五版教学课件-5.1 定积分的概念与性质

第一节 定积分的概念与性质
一、问题的提出
实例1 (求曲边梯形的面积)
由连续曲线 = ()(() ≥ 0)、
轴、直线 = 、 = 所围成的图形
称为曲边梯形。
用矩形面积近似取代曲边梯形面积
y
o
y
a
b
(四个小矩形)
x
o
a
b
x
(九个小矩形)
显然,小矩形越多,矩形总面积越接近曲边梯形面积.
→0
= max ∆
1≤≤
= σ=1 ± σ=1
=
→0
±
→0
性质1可以推广到有限个可积函数作和或者作差的情况.
性质2 被积函数的常数因子可提到积分号的外面,即
)(
总有下式成立:
)( = )( + )( .
例如,若 < < ,则
=
+
,
故 )( = )( − )(
= )( + )( .
证
因为 ≤ () ≤ ,由性质4得
≤ ≤ )( ,
又 = − ,
故( − ) ≤ ( ≤ )( − ).
性质6(积分中值定理)
∈
[, ],使)(
设函数()在[, ]上连续,则至少存在一点
5.1 定积分的概念与性质

lim ( )Δ =
→0
=1
则称这个极限为函数()在区间[, ]上的定积分,记为
න ()d
第一节 定积分的概念与性质
定积分
第五章
即
积分上限
定积分
积分和
න ()d = = lim ( )Δ
积分下限
→0
=1
被积被
积分积
[, ]积分区间 函 变 表
[, ]
[, ]
( − )≤ න ()d ≤( − ) ( < )
证
∵ ≤()≤,
∴ න d≤ න ()d≤ න d ,
( − )≤ න () d≤( − ).
第一节 定积分的概念与性质
此性质可用于
估计积分值的
第五章
8. 定积分中值定理
如果 () 在区间[, ]上连续, 则至少存在一点 ∈ [, ], 使
න ()d = ( )( − )
证
设()在[, ]上的最小值与最大值分别为 , ,
1
න ()d≤
则由性质7可得 ≤
−
根据闭区间上连续函数介值定理, ∃ ∈ [, ], 使
= lim ( )
=
lim ( ) ⋅
→∞
− →∞
故它是有限个数的平均值概念的推广.
第一节 定积分的概念与性质
把区间[, ]分成个小区间,
[0 , 1 ], [1 , 2 ], ⋯ , [−1 , ], ⋯ , [−1 , ]
各个小区间的长度依次为
高等数学第五章第一节定积分的概念及性质课件.ppt

二、定积分定义
a x0 x1 x2 xn b ,
任一种分法 任取
总趋于确定的极限 I ,则称此极限 I 为函数
上的定积分,
记作
b
a
f
( x) dx
即
b a
f
(
x)
dx
lim
0
n
i1
f
(
i
)
xi
o
a x1
此时称 f ( x ) 在 [ a , b ] 上可积 .
在区间
i
x xi1xi b
证: f (i ) xi 0
i1
b
n
a
f
( x) d
x
lim
0 i1
f
(i ) xi
0
推论1. 若在 [a , b] 上
则
推论2.
(a b)
证: f (x) f (x) f (x)
b
b
b
a f (x) dx a f (x) dx a f (x) dx
即
b
b
a f (x) dx a f (x) dx
使
因此定理成立.
说明:
• 积分中值定理对
• 可把
b
a f (x) dx f ( )
ba
因
y f (x) y
oa bx
故它是有限个数的平均值概念的推广.
例4. 计算从 0 秒到 T 秒这段时间内自由落体的平均 速度.
解: 已知自由落体速度为
v gt
故所求平均速度
1 1 g T 2 gT
第一节
第五章
定积分的概念及性质
一、定积分问题举例 二、 定积分的定义 三、 定积分的性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算步骤 (1)分割
以上两问题虽然不同,但解决问题的方法却相同,即归结为求同一结构的总 和的极限.由此引入定积分的概念.
二、定积分的概念
定义
定积分(简称积分)
其中f(x)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b 叫做积分上限,[a,b]叫做积分区间.
根据定积分的定义,前面所讨论的两个引例就可 以用定积分概念来描述:
一、引入定积分概念的实例
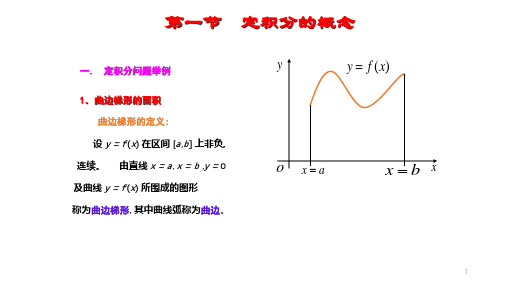
引例1 曲边梯形的面积 曲边梯形 设函数f(x)在区间[a,b](a<b)上非负且连续,由曲线y=f(x),直线x=a,x=b
及x轴围成的图形称为曲边梯形,其中曲线弧y=f(x)称为曲边,线段ab称为底边.
问题 求由x=a, x=b, y=0与y=f(x) 所围成的曲边梯形的面积.
求曲边梯形的面积A的具体做法: (1)分割 在(a,b)内插入n–1个分点
把区间[a,b]分成n个小区间
记每一个小区间
的长度为
过每个分点xi(i=1,2,…,n)作y轴的平行线,将曲 边梯形分割成n个小曲边梯形.
我们同样可以用这种“分割,近似、求和,取极限”的方法解决变力作功的问 题.
引例2 变力做功
三、定积分的存在定理
定理6.1
定理6.2
在几何上表示由曲线y=f(x),直线x=a,
如果在[a,b]上
,此时由曲线y=f(x),直线x=a,x=b及x轴所围成的曲边
梯形位于x轴的下方,则定积分
在几何上表示上述曲边梯形的面积A的相反
数.
如果在[a,b]上f(x)既可取正值又可取负值,则定积分
在几何上表示介
于曲线y=f(x),直线x=a,x=b及x轴之间的各部分面积的代数和.
曲线
、x轴及两条直线x=a,x=b所围成的曲边梯形面积A等于函数
f(x)在区间[a线运动,由起始位置a移动到b,变力对质点所做之 功等于函数F(s)在[a,b]上的定积分,即
如果函数f(x)在区间[a,b]上的定积分存在,则称函数f(x)在区间[a,b]上可积.
关于定积分的概念,还应注意两点:
(1)定积分
是积分和式的极限,是一个数值,定积分值只与被积函数f(x)
及积分区间[a,b]有关,而与积分变量的记法无关.即有
(2)在定积分 的定义中,总假设 ,为了
今后的使用方便,对于
时作如下规定:
定积分的几何意义:
如果在[a,b]上
,则
x=b及x轴所围成的曲边梯形的面积.
