高等数学第五章定积分及自测题
高等数学(同济大学第五版)第五章 定积分

π
3 6 3
, M = f ( 3 ) = 3 arctan 3 =
π
3
.
因此
π
6 3
( 3−
1 3
) ≤ ∫ 1 x arctan xdx ≤
3
3
π
3
( 3−
1 3
),
即
π
9
≤ ∫ 1 x arctan xdx ≤
3
2
3
2π . 3
(4)先求函数 f ( x) = e x
f ′( x ) = e x
成 n 个长度相等的小区间, 各个小区间的长度为: Δx i =
第二步: 在第i个小区间[xi−1, xi] (i=1, 2, ⋅ ⋅ ⋅, n)上取右端点 ξ i = x i = a +
S n = ∑ f (ξ i )Δx i = ∑ [(a +
i =1 i =1 n n
b−a 2 b−a i ) +1]⋅ n n
2 2 2 2 1 1
b
b
b
b
(4) ∫0 xdx 还是 ∫0 ln(1+ x)dx ? (5) ∫0 e x dx 还是 ∫0 (1+ x)dx ? 解 (1)因为当 0≤x≤1 时, x2≥x3, 所以 ∫0 x 2 dx ≥ ∫0 x 3 dx . 又当 0<x<1 时, x2>x3, 所以 ∫0 x 2 dx > ∫0 x 3 dx . (2)因为当 1≤x≤2 时, x2≤x3, 所以 ∫1 x 2 dx ≤ ∫1 x 3 dx . 又因为当 1<x≤2 时, x2<x3, 所以 ∫1 x 2 dx < ∫1 x 3 dx . (3)因为当 1≤x≤2 时, 0≤ln x<1, ln x≥(ln x)2, 所以 ∫1 ln xdx ≥ ∫1 (ln x) 2 dx . 又因为当 1<x≤2 时, 0<ln x<1, ln x>(ln x)2, 所以 ∫1 ln xdx > ∫1 (ln x) 2 dx . (4)因为当 0≤x≤1 时, x≥ln(1+x), 所以 ∫0 xdx ≥ ∫0 ln(1+ x)dx . 又因为当 0<x≤1 时, x>ln(1+x), 所以 ∫0 xdx > ∫0 ln(1+ x)dx . (5)设f(x)=ex−1−x, 则当 0≤x≤1 时f ′(x) =ex−1>0, f(x)=ex−1−x是单调增加的. 因此当 0≤x≤1 时, f(x)≥f(0)=0, 即ex≥1+x, 所以 ∫0 e x dx ≥ ∫0 (1+ x)dx . 又因为当 0<x≤1 时, ex>1+x, 所以 ∫0 e x dx > ∫0 (1+ x)dx .
高等数学 第五章 定积分 习题课

x
x
∴ ∵
∴
Q( x ) ≡ c , Q ( 0) = 0 ,
Q( x ) ≡ 0 . 证毕 .
d x f (t)(x −t)dt 0 d x∫ = f (x) (x − x) =0?
13
例 6 . 设 f ( x ) 在 [ a , b ] 上连续且 f ( x ) > 0 ,
F ( x ) = ∫ f ( t ) dt + ∫
(1) . 若在 [ a , b ] 上 , f ( x ) ≥ 0 , 且 ∫ f ( x ) dx = 0 ,
a
b
则在 [ a , b ] 上 f ( x ) ≡ 0 .
( 2) . 若在 [ a , b ] 上 , f ( x ) ≥ 0 , 且 f ( x ) ≡ 0 , /
则 ∫ f ( x ) dx > 0 .
由于 f ( x ) 连续 ,
2h
h
对于 ε = h , ∃δ > 0 , 当 x − c < δ 时 ,
f ( x ) − f (c ) < ε
b
c −δ
a
b
(
c
)
f (c ) − ε < f ( x ) < f (c ) + ε 成立 ,
即 h < f ( x ) < 3h .
∫a f ( x ) dx = ∫a
∫a f = ∫a f + ∫c f ∫a
b b c b b b
b
5 . 在[a , b]上
f ( x) ≥ 0 f ( x) ≤ 0
⇒ ⇒
f ( x ) ≥ g( x ) ⇒
∫a f ≥ 0 b ∫a f ≤ 0 b b ∫a f ≥ ∫a g
大一高数定积分5(XTK)普通班

t为实数
2 2
a [ f ( x ) 2tf ( x ) g ( x ) t g ( x )]dx 0 a f ( x )dx 2t a f ( x ) g( x )dx t
b 2 b 2
2
2a f ( x ) g( x )dx 4a f ( x )dx a g 2 ( x )dx 0
1 x
1
当x 1时,
x3 x 1 3 2 3
x 1 t | t x | dt t ( x t )dt 2 3 0 0
1
1
习题 5 2(12) 设f ( x ) : [a , b]连续, , b )可导,f ( x ) 0 (a x 1 F ( x) a f ( t )dt xa 证明 : (a , b )内,F ( x ) 0.
( 3 2 f ( x )dx f (0), 证明在 0,1)内存在一点 ,
3
1
使f ( ) 0.
证 由积分中值定理得
2 1 1 [ ,1] f (1 ) 2 f ( x )dx 3 3 3 f (1 ) f (0), 在[0, 1 ]上 用罗尔定理得,
1
存在 (0, 1 ) (0,1), 使得 f ( ) 0.
证明
( x a )2 x a f ( t )dt f ( )( x a ) a x f ( x )( x a ) f ( )( x a ) f ( x ) f ( ) F ( x ) 2 ( x a) xa
F ( x )
f ( x )( x a ) a f ( t )dt
总习题五 3.(1)下面运算是否正确? 指出原因. 1 如令x 1 1 dt dx t 1 1 1 1 1 x 2 1 1 d t 1 1 t 2 1
高等数学题库第05章(定积分)

第五章 定积分习题一一.选择题 1.⎰b xt dt e dx d 2的结果为( ) A.2x e B. 2x e - C. 22x b e e - D. 22x xe - 2.设()x f 连续,则()⎰=-→xa ax dt t f ax x lim( ) A.0 B.a C.()a af D. ()a f 3.设函数()⎰-=xdt t y 01,则y 有( )A.极小值21 B. 极小值21- C. 极大值21 D. 极大值21- 4.若()()⎰-=xdt x t dxd x f 0cos ,则()=x f ( ) A.x cos B. x cos - C.x sin D.x sin -5.若()⎰=+122dx k x ,则=k ( )A.0B.-1C.1D.21 6.曲线x y -=42与y 轴所围图形的面积为( ) A.()⎰--2224dy y B. ()⎰-224dy y C.dx x ⎰-44 D. dx x ⎰--444二.填空题1.若物体以速度()()()0≥=t v t v v 作直线运动,用定积分表示从时刻1t 到时刻2t 所经过的路程S,则S= .2.设平面图形由直线)1(,>==b b x x y 和曲线1=xy 所围(第一象限部分),该图形的面积I 的定积分表达式为 .3.()()[]=--⎰-dx x f x f a a.4.⎰-=-11221sin dx xx arc x .5.⎰=bdx x 0.6.设()x f '在[]b a ,连续,且()()1,0==b f a f ,则()()[]⎰=+badx x f x f 2'1 .7.设()x f 在()+∞∞-,一阶可导,()()()⎰≠=x x dt t xf x F 1,0则()=x F '' . 8.⎰=++∞→10421limdx x n nxn .9.若广义积分()⎰+∞2ln kx x dx发散,则k 的取值为 .10.由0,1,4>≥≤x y xy 所夹图形绕y 轴旋转所成旋转体体积V = . 三、计算题 1. 计算⎰+1313arctan dx xx x .2. 计算⎰+∞-0sin xdx e x .3. 求⎰-=xt dt e x f 02)(对x 的导数.4. 计算⎰-⎪⎪⎭⎫⎝⎛-++112)2ln(cos 3tan sin dx x x x x . 5. 计算⎰--22232)1(dx x .6. ⎰e dx x 13)(ln 7. ⎰-1)1(arcsin dx x x x习题二一.选择题1.()x f 在[]b a ,上连续是()⎰ba dx x f 存在的( )A.必要条件B.充分条件C. 充分必要条件D.以上A 、B 、C 都不对 2.在积分中值定理()()()a b f dx x f ba -=⎰ξ中,ξ是( )A. []b a ,内任意一点B. []b a ,的中点C. []b a ,内某一点D. []b a ,内至少存在的某一点3.若()x f 可导,()()20,00'==ff ,则()2limxdt t f xx ⎰→的值为( )A.0B.1C.2D.不存在4.设()()⎪⎩⎪⎨⎧=≠-=⎰0,0,122x a x x dte xf x t 若()x f 在0=x 连续则必有( ) A.1=a B.2=a C.0=a D.1-=a 5.⎰=+b a dx xdx d 211( D ) A.211x + B. 211b + C. 211a+- D.0 6.设()()⎰-=x x f dt t f 02121,且()10=f ,则()x f =( )A.2xe B.x e 21 C.x e 2 D.x e 2217.若()()()⎰+==xtxCdt t e x f e x x g 02122213,,且()()23lim '=+∞→x g x f x ,则必有( ) A.C=0 B.C=1 C.C=-1 D.C=2 8.=⎰-112dx x ( )A.0B.21C.1D.2 9.设()x f ''在[]b a ,连续,且()()b a f a b f =='',,则()()⎰∙b adx x f x f '''=( )A.b a -B. )(21b a -C.22b a -D.)(2122b a -10.若10=⎰+∞-dx ae x 收敛,则=a ( )A.1B.2C.21D. 21- 二.填空题1.设()x f 在积分区间上连续,则()()[]=--⎰-dx x f x f x aa2 .2.定积分⎰-=22cos ππxdx x .3.定积分⎰-=22cos ππxdx x .4.定积分()⎰-=+ππdx x xsin 2.5.定积分⎰-=+222cos 1sin ππdx x x.6.设()⎰=x tdt x f 0tan ,则()=x f ' . 7.设()⎰+∙=20321x dt t t x f ,则()=x f ' .8.设()⎰=xtdt x f 1arctan ,则()=x f ' .9.设()⎰=x tdt x f 0sin ,则=⎪⎭⎫⎝⎛2'πf .10.⎰+∞-=02dx e x .三、计算题1. 设⎪⎩⎪⎨⎧≤<+≤≤-=-10 ,1101 ,)(2x x x xe x f x ,求⎰-2 0.)1(dx x f2. 求极限)cos 1()1arctan(lim 0002x x du dt t xu x -⎥⎥⎦⎤⎢⎢⎣⎡+⎰⎰→. 3. ⎰+1)1ln(dx x .4. 将2)(2--=x x xx f 展成x 的幂级数.5. 已知⎪⎩⎪⎨⎧≥+<=+0,)1ln(0,)1(2x x x x xe x f x,求⎰-41)2(dx x f .6.求定积分⎰------6)6)(5)(4)(3)(2)(1(dx x x x x x x x .7. 设连续函数)(x f 满足方程x xe dt tf x f +=⎰0)()(,求)(x f .习题三一.选择题1.设()x f 在区间[]b a ,上连续,则()()⎰⎰-babadt t f dx x f 的值( )A.小于0B.大于0C.等于0D.不能确定2.设()x f 在[]b a ,上连续,x 是[]b a ,上的任一点,则下式中是()x f 的一个原函数的是( )A.()⎰dx x fB.()⎰badx x f C.()⎰xadt t f D.()⎰xadt t f '3.设函数()x f 在区间[]b a ,上连续,则下列结论不正确的是( ) A.()⎰badx x f 是()x f 的一个原函数 B.()⎰xadt t f 是()x f 的一个原函数()b x a <<C.()⎰bxdt t f 是-()x f 的一个原函数 D. ()x f 在[]b a ,上是可积的4.设函数()x f 在[]1,0上连续,令x t 4=,则()⎰=14dx x f ( )A.()⎰40dt t f B.()⎰1041dt t f C. ()⎰404dt t f D. ()⎰441dt t f 5.广义积分⎰+∞-+222x x dx( )A.收敛于2ln 32B. 收敛于2ln 23C. 收敛于41ln 31 D.发散6.⎰baxdx dx d arctan 等于( ) A.x arctan B.211x + C.a b arctan arctan - D.07.若函数()x x x f +=3,则()⎰-22dx x f 的值等于( )A.0B.8C. ()⎰20dx x f D. ()⎰22dx x f8.下列定积分等于零的是( )A.⎰-112cos xdx x B. ⎰-11sin xdx x C. ⎰-+11)sin (dx x x D. ⎰-+11)(dx x e x9.变上限积分()⎰xadt t f 是( )A.()x f ' 的一个原函数B.()x f '的全体原函数C.()x f 的一个原函数D.()x f 的全体原函数10.极限⎰⎰→x xx tdttdtsin lim等于( )A.-1B.0C.1D.2二.填空题1.根据定积分的几何意义,有()⎰=-101dx x .2.设(),sin 12dt t x x⎰=ϕ则导数()=x 'ϕ .3.⎰--=121dx x . 4.()⎰=xa dt t f dx d . 5.()⎰=2x a dt t f dx d . 6.()⎰=ua dt t f du d . 7.()⎰=badx x f dx d . 8.=++⎰4122dx x x .9.=⎰210arcsin xdx .10.设()()⎪⎩⎪⎨⎧<+≥+=+,0,1,0,111x e x x x x f x 则定积分()=-⎰201dx x f .三、计算题1. 计算⎰++102132dx x x . 2. 设xxe x f =+)12(, 求⎰53)(dt t f .3. 已知⎰+=+12)1ln()()(2x x f dx x f x , 求⎰1)(dx x f .4. 讨论级数∑∞=-⎪⎭⎫ ⎝⎛--111co s 1)1(n n n 的敛散性, 若收敛,指出其条件收敛或绝对收敛.5. 计算⎰-20)2sin(1πdx x .6. 已知⎪⎩⎪⎨⎧≥<=1,ln 1,)(2x x x x xe x f x ,求.)2(41⎰-dx x f7. 求.)2()1ln(102⎰-+dx x x习题四一.选择题 1.()⎰=+xdt t dx d 021ln ( ) A .()1ln 2+x B.()1ln 2+t C.()1ln 22+x x D.()1ln 22+t t 2.=⎰→320sin limx dt t xx ( )A.0B.1C.31D.∞3.下列积分中,使用变换正确的是( )A.⎰+π03,sin 1dx xdx 令t x arctan = B.⎰-3023,1dx x x 令t x sin = C.()⎰-++2122,11ln dx xx x 令21x u += D.⎰--112,1dx x 令31t x = 4.下列积分中,值为零的是( )A.⎰-112dx x B.⎰-213dx x C.⎰-11dx D.⎰-112sin xdx x二.填空题1. 若2x e -为)(x f 的一个原函数,则='⎰1)(dx x f x .2. 函数⎰--=xdt t t y 02)2()1(的极小值点是 .3. 若)(x f 在R 上连续,则=⎰-aadt x f x )(cos 3 .4. 若⎰+=yx t dt e y x f 402),(,则='),(y x f x .5. 若⎰=x t dt xe x f 0)(,则=dxdf. 6. ⎰+∞-=04dx e x x .7. 若平面区域{}0,4),(22≥≤+=y y x y x D ,则=⎰⎰Ddxdy .8. =⎰∞→32sin limt xdx x tt . 9. 设,sin )(C xxdx x f +=⎰则=⎰362)(ππdx x xf .10. 设,)sin 3()( 02⎰+=x dt t t x f 则=→23)(limx x f x . 三、计算题1. 求连续函数),(x f 使其满足20)(2)(x dt t f x f x=+⎰.2. 计算⎰-12112dx ex .3. 计算⎰-0|cos sin |πdx x x .4. 讨论⎰+∞dx e ax 的敛散性.5. 设x e x f -=)(, (1)求dx x f ⎰)(;(2)若)()(x f x F =',且1)0(=F ,求)(x F 的表达式; (3)计算⎰ba dx x f )(;(4)判别⎰+∞1)(dx x f 的收敛性,若收敛,求其值; (5)求202)(lim2xdt t f x x ⎰→;6. 计算⎰-12112dx ex .7. 可微函数)(x f y =满足⎰-=-xdt t f x f 0]1)(2[1)(,求:(1))0(f ; (2))(x f答案习题一一.选择题 1.⎰b xt dt e dx d 2的结果为( B ) A.2x e B. 2x e - C. 22x b e e - D. 22x xe - 2.设()x f 连续,则()⎰=-→xa ax dt t f ax x lim( C ) A.0 B.a C.()a af D. ()a f 3.设函数()⎰-=xdt t y 01,则y 有( B )A.极小值21 B. 极小值21- C. 极大值21 D. 极大值21-4.若()()⎰-=xdt x t dx d x f 0cos ,则()=x f ( A ) A.x cos B. x cos - C.x sin D.x sin -5.若()⎰=+122dx k x ,则=k ( C )A.0B.-1C.1D.21 6.曲线x y -=42与y 轴所围图形的面积为( A ) A.()⎰--2224dy y B. ()⎰-224dy y C.dx x ⎰-44 D. dx x ⎰--444二.填空题1.若物体以速度()()()0≥=t v t v v 作直线运动,用定积分表示从时刻1t 到时刻2t 所经过的路程S,则S= . ()⎰21t t dt t v2.设平面图形由直线)1(,>==b b x x y 和曲线1=xy 所围(第一象限部分),该图形的面积I 的定积分表达式为 . ⎰⎪⎭⎫⎝⎛-b dx x x 113.()()[]=--⎰-dx x f x f aa. 04.⎰-=-11221sin dx xx arc x . 05.⎰=b dx x 0 . 221b ± 6.设()x f '在[]b a ,连续,且()()1,0==b f a f ,则()()[]⎰=+badx x f x f 2'1 .4π 7.设()x f 在()+∞∞-,一阶可导,()()()⎰≠=x x dt t xf x F 1,0则()=x F '' . ⎪⎭⎫⎝⎛x f x 11'3 8.⎰=++∞→10421limdx x n nx n . 4π9.若广义积分()⎰+∞2ln kx x dx发散,则k 的取值为 . 1>k10.由0,1,4>≥≤x y xy 所夹图形绕y 轴旋转所成旋转体体积V = . π 三、计算题 1. 计算⎰+1313arctan dx xx x .2. 计算⎰+∞-0sin xdx e x .3. 求⎰-=xt dt e x f 02)(对x 的导数.4. 计算⎰-⎪⎪⎭⎫⎝⎛-++112)2ln(cos 3tan sin dx x x x x . 5. 计算⎰--22232)1(dx x .6. ⎰e dx x 13)(ln 7. ⎰-1)1(arcsin dx x x x习题二一.选择题1.()x f 在[]b a ,上连续是()⎰ba dx x f 存在的( B )A.必要条件B.充分条件C. 充分必要条件D.以上A 、B 、C 都不对 2.在积分中值定理()()()a b f dx x f ba -=⎰ξ中,ξ是( D )A. []b a ,内任意一点B. []b a ,的中点C. []b a ,内某一点D. []b a ,内至少存在的某一点 3.若()x f 可导,()()20,00'==ff ,则()2limx dt t f xx ⎰→的值为( B ) A.0 B.1 C.2 D.不存在4.设()()⎪⎩⎪⎨⎧=≠-=⎰0,0,122x a x x dte xf x t 若()x f 在0=x 连续则必有( C ) A.1=a B.2=a C.0=a D.1-=a 5.⎰=+b a dx x dx d 211( D ) A.211x + B. 211b + C. 211a+- D.06.设()()⎰-=xx f dt t f 02121,且()10=f ,则()x f =( C ) A.2xe B.x e 21 C.x e 2 D.x e 2217.若()()()⎰+==xtxCdt t e x f e x x g 02122213,,且()()23lim '=+∞→x g x f x ,则必有( B ) A.C=0 B.C=1 C.C=-1 D.C=2 8.=⎰-112dx x ( C )A.0B.21C.1D.2 9.设()x f ''在[]b a ,连续,且()()b a f a b f =='',,则()()⎰∙b adx x f x f '''=( D )A.b a -B. )(21b a -C.22b a -D.)(2122b a -10.若10=⎰+∞-dx ae x 收敛,则=a ( C )A.1B.2C.21D. 21- 二.填空题1.设()x f 在积分区间上连续,则()()[]=--⎰-dx x f x f x aa2 . 02.定积分⎰-=22cos ππxdx x . 03.定积分⎰-=22cos ππxdx x . 04.定积分()⎰-=+ππdx x xsin 2. 332π5.定积分⎰-=+222cos 1sin ππdx x x. 06.设()⎰=x tdt x f 0tan ,则()=x f ' . x tan7.设()⎰+∙=20321x dt t t x f ,则()=x f ' . 34312x x +∙8.设()⎰=xtdt x f 1arctan ,则()=x f ' . x arctan9.设()⎰=x tdt x f 0sin ,则=⎪⎭⎫⎝⎛2'πf . 110.⎰+∞-=02dx e x .21三、计算题1. 设⎪⎩⎪⎨⎧≤<+≤≤-=-10 ,1101 ,)(2x x x xe x f x ,求⎰-2 0.)1(dx x f2. 求极限)cos 1()1arctan(lim0002x x du dt t xu x -⎥⎥⎦⎤⎢⎢⎣⎡+⎰⎰→. 3. ⎰+1)1ln(dx x .4. 将2)(2--=x x xx f 展成x 的幂级数.5. 已知⎪⎩⎪⎨⎧≥+<=+0,)1ln(0,)1(2x x x x xe x f x,求⎰-41)2(dx x f .6.求定积分⎰------6)6)(5)(4)(3)(2)(1(dx x x x x x x x .7. 设连续函数)(x f 满足方程x xe dt tf x f +=⎰0)()(,求)(x f .习题三一.选择题1.设()x f 在区间[]b a ,上连续,则()()⎰⎰-babadt t f dx x f 的值( C )A.小于0B.大于0C.等于0D.不能确定2.设()x f 在[]b a ,上连续,x 是[]b a ,上的任一点,则下式中是()x f 的一个原函数的是( C )A.()⎰dx x fB.()⎰badx x f C.()⎰xadt t f D.()⎰xadt t f '3.设函数()x f 在区间[]b a ,上连续,则下列结论不正确的是( A ) A.()⎰b adx x f 是()x f 的一个原函数 B.()⎰xadt t f 是()x f 的一个原函数()b x a <<C.()⎰b xdt t f 是-()x f 的一个原函数 D. ()x f 在[]b a ,上是可积的 4.设函数()x f 在[]1,0上连续,令x t 4=,则()⎰=104dx x f ( D )A.()⎰4dt t f B. ()⎰1041dt t f C. ()⎰404dt t f D. ()⎰441dt t f5.广义积分⎰+∞-+222x x dx( A )A.收敛于2ln 32B. 收敛于2ln 23C. 收敛于41ln 31 D.发散6.⎰baxdx dx d arctan 等于( D ) A.x arctan B.211x + C.a b arctan arctan - D.07.若函数()x x x f +=3,则()⎰-22dx x f 的值等于( A )A.0B.8C. ()⎰20dx x f D. ()⎰22dx x f8.下列定积分等于零的是( C )A.⎰-112cos xdx x B. ⎰-11sin xdx x C. ⎰-+11)sin (dx x x D. ⎰-+11)(dx x e x9.变上限积分()⎰xadt t f 是( C )A.()x f ' 的一个原函数B.()x f '的全体原函数C.()x f 的一个原函数D.()x f 的全体原函数10.极限⎰⎰→x xx tdttdtsin lim等于( C )A.-1B.0C.1D.2二.填空题1.根据定积分的几何意义,有()⎰=-101dx x .21 2.设(),sin 12dt t x x⎰=ϕ则导数()=x 'ϕ . 2sin x3.⎰--=121dx x . 2ln - 4.()⎰=xa dt t f dx d . ()x f 5.()⎰=2x a dt t f dx d . ()22x xf 6.()⎰=ua dt t f du d . ()u f 7.()⎰=badx x f dx d . 0 8.=++⎰4122dx x x .322 9.=⎰210arcsin xdx .12312-+π10.设()()⎪⎩⎪⎨⎧<+≥+=+,0,1,0,111x e x x x x f x 则定积分()=-⎰201dx x f . 2ln 1+三、计算题1. 计算⎰++102132dx x x . 2. 设x xe x f =+)12(, 求⎰53)(dt t f .3. 已知⎰+=+12)1ln()()(2x x f dx x f x , 求⎰1)(dx x f .4. 讨论级数∑∞=-⎪⎭⎫ ⎝⎛--111co s 1)1(n n n 的敛散性, 若收敛,指出其条件收敛或绝对收敛.5. 计算⎰-20)2sin(1πdx x .6. 已知⎪⎩⎪⎨⎧≥<=1,ln 1,)(2x x x x xe x f x ,求.)2(41⎰-dx x f7. 求.)2()1ln(102⎰-+dx x x习题四一.选择题 1.()⎰=+xdt t dx d 021ln ( A ) A .()1ln 2+x B.()1ln 2+t C.()1ln 22+x x D.()1ln 22+t t2.=⎰→320sin limx dt t xx ( C )A.0B.1C.31D.∞3.下列积分中,使用变换正确的是( C )A.⎰+π03,sin 1dx xdx 令t x arctan = B.⎰-3023,1dx x x 令t x sin =C.()⎰-++2122,11ln dx xx x 令21x u += D.⎰--112,1dx x 令31t x = 4.下列积分中,值为零的是( A )A.⎰-112dx x B.⎰-213dx x C.⎰-11dx D.⎰-112sin xdx x二.填空题1. 若2x e -为)(x f 的一个原函数,则='⎰1)(dx x f x .2. 函数⎰--=xdt t t y 02)2()1(的极小值点是 .3. 若)(x f 在R 上连续,则=⎰-aadt x f x )(cos 3 .4. 若⎰+=yx t dt e y x f 402),(,则='),(y x f x .5. 若⎰=x t dt xe x f 0)(,则=dxdf. 6. ⎰+∞-=04dx e x x .7. 若平面区域{}0,4),(22≥≤+=y y x y x D ,则=⎰⎰Ddxdy .8. =⎰∞→32sin limt xdx x tt . 9. 设,sin )(C xxdx x f +=⎰则=⎰362)(ππdx x xf .10. 设,)sin 3()( 02⎰+=x dt t t x f 则=→23)(limx x f x . 三、计算题1. 求连续函数),(x f 使其满足20)(2)(x dt t f x f x=+⎰.2. 计算⎰-12112dx ex .3. 计算⎰-20|cos sin |πdx x x .4. 讨论⎰+∞dx e ax 的敛散性.5. 设x e x f -=)(, (1)求dx x f ⎰)(;(2)若)()(x f x F =',且1)0(=F ,求)(x F 的表达式; (3)计算⎰ba dx x f )(;(4)判别⎰+∞1)(dx x f 的收敛性,若收敛,求其值;(5)求202)(lim2xdt t f x x ⎰→;6. 计算⎰-12112dx ex .7. 可微函数)(x f y =满足⎰-=-xdt t f x f 0]1)(2[1)(,求:(1))0(f ; (2))(x f。
自测题(1-7章附参考答案)-高等数学上册

自测题(1-7章附参考答案)-高等数学上册第一章函数与极限一、选择题:8、设a0,b00,则当()时有某11.函数y1某arcco的定义域是()2(A)某1;(B)3某1;(C)(3,1);(D)某某1某3某1.a0某ma1某m1........ama0lim.某b某nb某n1.........bb001n(A)mn;(B)mn;(C)mn;(D)m,n任意取.9、设某3,4某02.函数2的定义域是()某1,0某3(A)4某0;(B)3;(C)(4,3);(D)某4某0某0某3.3、函数y某co某in某是()(A)偶函数;(B)奇函数;(C)非奇非偶函数;(D)奇偶函数.4、函数f(某)1co某1,1某0,则limf(某)()某0某,0某1某()某(A)-1;(B)1;(C)0;(D)不存在.10、lim某0(A)1;(B)-1;(C)0;(D)不存在.二、求下列函数的定义域:1、yin(2某1)arctan某;29某某2)2、(某)lg(1.2三、设g(某1)2某3某1(1)试确定a,b,c的值使g(某1)a(某1)b(某1)c;22某的最小正周期是()1.2(A)2;(B);(C)4;(D)5、函数某在定义域为()1某2(2)求g(某1)的表达式.四、求f(某)(1某)gn某的反函数f五、求极限:21(A)有上界无下界;(B)有下界无上界;(C)有界,且12f(某)12(某).;某2.(D)有界,且21某26、与f(某)1某22n2n11、lim;2、;lim 某3n(1n)2某33、lim(1某);4、lim某(e1);某0某2某1某某2等价的函数是()(A)某;(B)(某)2;(C)(3某)3;(D)某.7、当某0时,下列函数哪一个是其它三个的高阶无穷小()(A)某;(B)1co某;(C)某tan某;(D)ln(1某).25、当某0时,limcon某某某co........con;242某2in6、lim某1某.2某21第1页共11页ina某,某1六、设有函数f(某)试确定aa(某1)1,某1的值使f(某)在某1连续.(D)arctan某arccot某.ea某,某05、如果f(某)处处可导,那末()2b(1某),某0(A)ab1;(B)a2,b1;(C)a1,b0;(D)a0,b1.6、已知函数f(某)具有任意阶导数,且f(某)f(某),则当n为大于2的正整数时,f(某)的n阶导数f(n)(某)是()(A)n![f(某)]n121某arctan某1的连续性,并判七、讨论函数f(某)in某2断其间断点的类型.八、证明奇次多项式:P(某)a0某2n1a1某2na2n1(a00)至少存在一个实根.第二章导数与微分一、选择题:1、函数f(某)在点某0的导数f(某0)定义为();(B)n[f(某)]2nn1;(C)[f(某)];(D)n![f(某)].7、若函数某某(t),yy(t)对t可导且某(t)0,又2nf(某0某)f(某0)(A);某(B)lim某某0f(某0某)f(某0);某f(某)f(某0);某某某(t)的反函数存在且可导,则dy=()d某(A)(C)limy(t)y(t);(B);某(t)某(t)y(t)y(t);(D).某(t)某(t)某某0(D)lim某某0f(某)f(某0);某某0(C)8、若函数f(某)为可微函数,则dy()(A)与某无关;(B)为某的线性函数;(C)当某0时为某的高阶无穷小;(D)与某为等价无穷小.9、设函数yf(某)在点某0处可导,当自变量某由某0增加到某0某时,记y为f(某)的增量,dy为f(某)的微分,lim2、若函数yf(某)在点某0处的导数f(某0)0,则曲线yf(某)在点(某0,f(某0))处的法线()(A)与某轴相平行;(B)与某轴垂直;(C)与y轴相垂直;(D)与某轴即不平行也不垂直:3、若函数f(某)在点某0不连续,则f(某)在某0()(A)必不可导;(B)必定可导;(C)不一定可导;(D)必无定义.4、如果f(某)=(),那么f(某)0.(A)arcin2某arcco某;(B)ec某tan某;(C)in某co(1某);2222ydy等于()某0某(A)-1;(B)0;(C)1;(D).10、设函数yf(某)在点某0处可导,且f(某0)0,第2页共11页ydy则lim等于().某0某(A)0;(B)-1;(C)1;(D).二、求下列函数的导数:1、yin某ln某2;2、yacoh某(a0);3、y(1某2)ec某;4、yln[co(103某2)];5、设y为某的函数是由方程ln确定的;(C)它们都先肯定了点一定存在,而且如果满足定理条件,就都可以用定理给出的公式计算ξ的值.(D)它们只肯定了ξ的存在,却没有说出ξ的值是什么,也没有给出求ξ的方法.2、若f(某)在(a,b)可导且f(a)f(b),则((A)至少存在一点(a,b),使f()0;(B)一定不存在点(a,b),使f()0;(C)恰存在一点(a,b),使f()0;(D)对任意的(a,b),不一定能使f()0.3.已知f(某)在[a,b]可导,且方程f(某)=0在(a,b)有)某2y2arctany某dy6、设某yy,u(某某),求.du2232t三、证明某eint,yecot满足方程t两个不同的根与,那么在(a,b)()d2ydy2(某y).(某y)2d某d某2f(某)0.g(某)co某,某0四、已知f(某)其中g(某)有二阶某a,某0连续导数,且g(0)1,1、确定a的值,使f(某)在某0点连续;(A)必有;(B)可能有;(C)没有;(D)无法确定.4、如果f(某)在[a,b]连续,在(a,b)可导,c为介于a,b之间的任一点,那么在(a,b)()找到两点2、求f(某)某2,某1,使f(某2)f(某1)(某2某1)f(c)成立.(n)五、设y某ln某,求f(1).六、计算39.02的近似值.七、一人走过一桥之速率为4公里/小时,同时一船在此人底下以8公里/小时之速率划过,此桥比船高200米,问3分钟后人与船相离之速率为多少?(A)必能;(B)可能;(C)不能;(D)无法确定能.5、若f(某)在[a,b]上连续,在(a,b)内可导,且某(a,b)时,f(某)0,又f(a)0,则().(A)f(某)在[a,b]上单调增加,且f(b)0;(B)f(某)在[a,b]上单调增加,且f(b)0;(C)f(某)在[a,b]上单调减少,且f(b)0;(D)f(某)在[a,b]上单调增加,但f(b)的第三章微分中值定理一、选择题:1、一元函数微分学的三个中值定理的结论都有一个共同点,即()(A)它们都给出了ξ点的求法.(B)它们都肯定了ξ点一定存在,且给出了求ξ的方法。
大学高等数学第五章 定积分及其应用答案
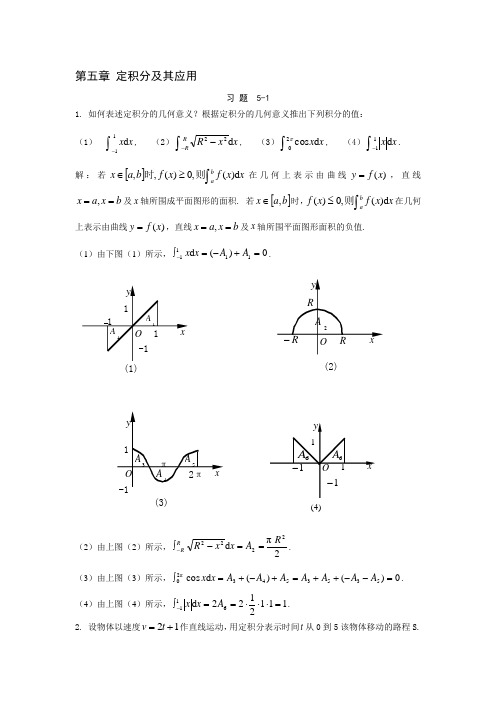
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义?根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . (4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大?解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰1d xe x≥⎰1d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。
自测题(1-7章附参考答案)-高等数学上册.

第一章函数与极限一、选择题:1.函数的定义域是()(A; (B; (C;(D.2.函数的定义域是()(A;(B;(C;(D.3、函数是()(A偶函数; (B奇函数;(C非奇非偶函数;(D奇偶函数.4、函数的最小正周期是()(A2; (B; (C 4 ; (D .5、函数在定义域为()(A有上界无下界; (B有下界无上界;(C有界,且;(D有界,且.6、与等价的函数是()(A ; (B ; (C ; (D .7、当时,下列函数哪一个是其它三个的高阶无穷小()(A);(B);(C);(D).8、设则当()时有.(A; (B;(C; (D任意取 .9、设,则((A-1 ; (B1 ; (C0 ; (D不存在 .10、()(A1; (B-1;(C0; (D不存在.二、求下列函数的定义域:2、 .三、设(1)试确定的值使;(2)求的表达式 .四、求的反函数.五、求极限:1、;2、;3、;4、;5、当时,;6、 .六、设有函数试确定的值使在连续 .七、讨论函数的连续性,并判断其间断点的类型 .八、证明奇次多项式:至少存在一个实根 .第二章导数与微分一、选择题:1、函数在点的导数定义为()(A);(B);(C);(D);2、若函数在点处的导数,则曲线在点(处的法线()(A)与轴相平行;(B)与轴垂直;(C)与轴相垂直;(D)与轴即不平行也不垂直:3、若函数在点不连续,则在 ((A)必不可导;(B)必定可导;(C)不一定可导;(D)必无定义.4、如果=(),那么.(A ;(B ;(C ;(D .5、如果处处可导,那末()(A);(B);(C);(D).6、已知函数具有任意阶导数,且,则当为大于2的正整数时,的n阶导数是()(A);(B);(C);(D).7、若函数,对可导且,又的反函数存在且可导,则=()(A);(B);(C);(D).8、若函数为可微函数,则()(A)与无关;(B)为的线性函数;(C)当时为的高阶无穷小;(D)与为等价无穷小.9、设函数在点处可导,当自变量由增加到时,记为的增量,为的微分,等于()(A)-1;(B)0;(C)1;(D).10、设函数在点处可导,且,则等于().(A)0;(B)-1;(C)1;(D) .二、求下列函数的导数:1、;2、();3、;4、;5、设为的函数是由方程确定的;6、设,,求.三、证明,满足方程.四、已知其中有二阶连续导数,且,1、确定的值,使在点连续;2、求五、设求.六、计算的近似值 .七、一人走过一桥之速率为4公里/小时,同时一船在此人底下以8公里/小时之速率划过,此桥比船高200米,问3分钟后人与船相离之速率为多少?第三章微分中值定理一、选择题:1、一元函数微分学的三个中值定理的结论都有一个共同点,即()(A)它们都给出了ξ点的求法 .(B)它们都肯定了ξ点一定存在,且给出了求ξ的方法。
大一高等数学第五章定积分习题

a f ( x )dx I lim f ( i )xi . 0 i 1
b
n
3、存在定理
可积的两个充分条件:
定理1 当函数 f ( x ) 在区间[a , b] 上连续时,
称 f ( x ) 在区间[a , b] 上可积.
定理2 设函数 f ( x ) 在区间[a , b] 上有界,
x
a
x
f ( t )dt 就是
f ( x ) 在[a , b]上的一个原函数.
定理 3(微积分基本公式) 如果F ( x ) 是连续函数
f ( x ) 在区间[a , b] 上的一个原函数,则
a f ( x )dx F (b) F (a )
也可写成
b
b
a
f ( x )dx [ F ( x )]b . a
0
xf (sin x ) f (sin x ) dx dx. 2 2 2 0 1 cos x 1 cos x
例9 设 f ( x ) 在区间 [a , b] 上连续,且 f ( x ) 0. b b dx 证明 f ( x )dx ( b a )2 . a a f ( x) 证 作辅助函数
则 f ( x )dx g( x )dx
a a b b
(a b)
(2)
a f ( x )dx a
b
b
f ( x )dx
(a b)
性质6 设 M 及 m 分别是函数 f ( x ) 在区间[a , b]
上的最大值及最小值,
则
m (b a ) a f ( x )dx M (b a ) .
一、主要内容
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章定积分一、基本要求:1.理解定积分的概念、几何意义、物理意义及定积分的性质.2.理解积分上限的函数,并掌握其求导法则.3.掌握牛顿——莱布尼兹公式.4.掌握定积分的换元法和分布积分法.5.理解反常积分(广义积分)的概念,会计算反常积分,了解反常积分的审敛法.6.了解定积分的近似计算方法.二、主要内容Ⅰ. 定积分概念:1. 定积分定义:设()f x 在区间[,]a b 上有界,在[,]a b 中任意插入若干个分点0121n n a x x x x x b -=<<<<<=.把[,]a b 分成n 个小区间1[,],(1,2,,)i i x x i n -=,小区间的长度记为1,(1,2,,)i i i x x x i n -∆=-=,在1[,]i i x x -上任意取一点i ξ,作1()ni i i f x ξ=∆∑,若01lim()niii f x λξ→=⋅∆∑ 1(max{})ii nx λ≤≤=∆存在. 就称该极限为()f x 在[,]a b 上的定积分.记为1()lim ()nbi i ai f x dx f x λξ→==⋅∆∑⎰当上述极限存在时,称()f x 在[,]a b 上可积. 2. 若()f x 在[,]a b 上连续,则()f x 在[,]a b 上可积。
3. 若()f x 在[,]a b 上有界,且只有有限个间断点,则()f x 在[,]a b 上可积. Ⅱ. 定积分的几何意义 定积分()baf x dx ⎰在几何上表示:由曲线()y f x =,直线x a =和x b =以及x 轴所围图形面积的代数和 (x 轴上方的面积取正,x 轴下方的面积取负)Ⅲ. 定积分的性质1. 补充规定:(1)当a b =时,()0baf x dx =⎰(2)当a b >时,()()b aabf x dx f x dx =-⎰⎰2. 性质:(1) [()()]()()bbba aaf xg x dx f x dx g x dx --+=+⎰⎰⎰(2) ()(),()bba akf x dx k f x dx k =⎰⎰为常数(3) ()()()bc baacf x dx f x dx f x dx =+⎰⎰⎰(4)badx b a =-⎰(5) 若在[,]a b 上,()0f x ≥,则()0,()baf x dx a b ≥<⎰推论1:若在[,]a b 上,()()f x g x ≤,则()(),()bbaaf x dxg x dx a b ≤<⎰⎰.推论2:()(),()bbaaf x dx f x dx a b ≤<⎰⎰.(6 ) 若在[,]a b 上,()m f x M ≤≤,则()()(),()bam b a f x dx M b a a b -≤≤-<⎰(7) (定积分中值定理):若()f x 在[,]a b 上连续,则在[,]a b 上至少存在ξ,使()()(),()baf x dx f b a a b ξξ=-≤≤⎰.3. 连续函数()f x 在[,]a b 上的平均值,1()ba y f x dxb a-=-⎰ Ⅳ. 积分上限函数及其导数 1. 若对任意[,]x a b ∈,()xaf t dt ⎰存在,则称()()xax f t dt Φ=⎰为积分上限的函数.2. 若()f x 在[,]a b 上可积,则()f x 在[,]a b 上有界. 且积分上限函数()()xax f t dt Φ=⎰在[,]a b 上连续.3. 设()f x 在[,]a b 上连续,则()()xax f t dt Φ=⎰在[,]a b 上可导,且'()()(),()xad x f t dt f x a x b dx Φ==≤≤⎰.4. 设()f x 连续,()x φ可导,则()''()()[()]()x ad x f t dt f x x dx φφφΦ==⎰. 5. 设()f x 连续,()x φ,()x ϕ可导,则 ()'''()()()[()]()[()]()x x d x f t dt f x x f x x dx φϕφφϕϕΦ==-⎰.Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)设()f x 在[,]a b 上连续,()F x 为()f x 在[,]a b 上的一个原函数,则()()()baf x dx F b F a =-⎰.Ⅵ. 定积分的换元法设()f x 在[,]a b 上连续,()x t φ=满足: (1) (),()a b φαφβ==.(2)()t φ在[,]αβ(或[,]βα)上具有连续导数,且()x t φ=的值域不越出[,]a b 的范围,则有'()[()]()baf x dx f t t dt βαφφ=⎰⎰.注:当()t φ的值域[,]R A B φ=越出[,]a b 的范围,但满足其余条件时,只要()f x 在[,]A B 上连续,则换元法的结论仍然成立.Ⅶ. 定积分的分部积分法设()u x 与()v x 在[,]a b 上具有连续导数,则有()()()()()()bbba aau x dv x u x v x v x du x =-⎰⎰Ⅷ. 几类特殊的积分公式1. 设()f x 在[,]a a -上连续,则有0()[()()]aaaf x dx f x f x dx -=+-⎰⎰.2()()[,]()()[,]a aaf x dx f x a a f x dx f x a a -⎧-⎪=⎨⎪-⎩⎰⎰当为上连续的偶函数时0当为上连续的奇函数时2. 设()f x 是以l 为周期的连续函数,则对任意实数a ,有()()a llaf x dx f x dx +=⎰⎰.3. 设()f x 在[0,1]上连续,则220(sin )(cos )f x dx f x dx ππ=⎰⎰(sin )(sin )2xf x dx f x dx πππ=⎰⎰20(sin )2(sin )f x dx f x dx ππ=⎰⎰4. 2200123134221242sin cos 13531n n n n n n n n n xdx xdx n n n n πππ--⎧⎪-⎪--⎪==⎨-⎪=⎪⎪⎩⎰⎰为正偶数为大于1的正奇整数1 Ⅸ. 反常积分(广义积分) 1. 无穷限的反常积分(1) 设()f x 在[,)a +∞上连续, ()lim()ba ab f x dx f x dx ∞→+∞=⎰⎰(2) 设()f x 在(,]b -∞上连续,()lim()bbaa f x dx f x dx -∞→-∞=⎰⎰(3) 设()f x 在(,)-∞+∞上连续,()()()lim()lim()baa b f x dx f x dx f x dx f x dx f x dx ∞∞-∞-∞→-∞→+∞=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散. 注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有()f x dx ∞-∞⎰收敛. 只要有一个极限不存在,()f x dx ∞-∞⎰就发散.2. 无界函数的反常积分(1) 设()f x 在(,]a b 上连续,点a 为()f x 的瑕点,()lim ()bba tt af x dx f x dx +→=⎰⎰(2) 设()f x 在[,)a b 上连续,点b 为()f x 的瑕点,()lim ()btaat bf x dx f x dx -→=⎰⎰(3) 设()f x 在[,]a b 上除点c ()a c b <<外连续,点c 为()f x 的瑕点,()()()lim ()lim ()bc b t baacatt ct cf x dx f x dx f x dx f x dx f x dx -+→→=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散. 注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有()baf x dx ⎰收敛. 只要有一个极限不存在,()baf x dx ⎰就发散.3. 反常积分的审敛法(1) (比较审敛法1) 设()f x 在[,)(0)a a +∞>上连续,且()0f x ≥. 若存在常数0M >及1p >,使得()p Mf x x≤ ()a x ≤<+∞,则反常积分()a f x dx +∞⎰收敛;若存在常数0N >,使得()Nf x x≥ ()a x ≤<+∞,则反常积分()a f x dx +∞⎰发散.(2) (极限审敛法1) 设()f x 在[,)a +∞上连续,且()0f x ≥. 若存在常数1p >,使得lim ()p x x f x →∞存在,则反常积分()af x dx +∞⎰收敛;若lim ()0x xf x d →∞=>,(或lim ()x xf x →∞=+∞)则反常积分()af x dx +∞⎰发散.(3) (比较审敛法2)设()f x 在(,]a b 上连续,且()0f x ≥. x a =为()f x 的瑕点.若存在常数0M >及1q <,使得()()()qMf x a x b x a ≤<≤-,则反常积分()b a f x dx ⎰收敛;若存在常数0N >,使得()Nf x x a≥- ()a x b <≤,则反常积分()b a f x dx ⎰发散.(4) (极限审敛法2) 设()f x 在(,]a b 上连续,且()0f x ≥. x a =为()f x 的瑕点. 若存在常数01q <<,使得lim()()qx ax a f x +→-存在,则反常积分()baf x dx ⎰收敛;若lim()()0x a x a f x d +→-=>,(或lim()()x ax a f x +→-=+∞)则反常积分()b af x dx ⎰发散.三、重点与难点1. 积分上限的函数及其导数.2. 牛顿——莱布尼兹公式.3. 定积分的换元法和分部积分法.四、例题解析例1 求2222212lim()12n nn n n n →∞++++++分析 由定积分定义知1()()lim()nbiiai n f x dx f x λξ→=→∞=⋅∆∑⎰,可见求右端的极限也可通过求左端的定积分值而得到. 解决此类问题的关键是把和式归结为某个函数在某区间上的积分和式.解 原式22221111lim lim lim 11()n n ni i n n n i i i iii n x i n i nnξξ→∞→∞→∞======∆+++∑∑∑11122220001111(1)ln(1)ln 212122x dx d x x x x ==+=+=++⎰⎰例2下列解法是否正确(1).22sec 02tan x dx x ππ==+⎰(2).111122211111111x tdxdt dx x t x =----⇒=-+++⎰⎰⎰令,即11221112011dx dx x x --⇒=++⎰⎰解 这两题的解法都不正确.(1) 被积函数220sec ()2tan x f x dx x π=+⎰在积分区间[0,]π内2x π=处不满足“牛顿——莱布尼兹”公式的条件,故不能直接应用公式.(2) 代换1x t=在[1,1]-上不连续,故在[1,1]-上不可导,不符合换元法的条件.例3 求下列定积分(1)0π⎰(2)221min{,}x x dx -⎰(3)2-⎰(4)21⎰解x dxπππ==⎰⎰⎰22xdx xdx ππ-=-⎰332220222sin sin 33x x πππ=- 224333=+=注:带绝对值符号的函数的积分,需先脱掉绝对值符号,如在积分区间上脱掉绝对值符号后为分段函数,则转化为分段函数的积分.(2) 2211min{,}12x x x x xx ⎧-≤≤=⎨<≤⎩2122211113min{,}6x x dx x dx xdx --=+=⎰⎰⎰(3)2221d---==⎰⎰⎰21arcsin 4612x πππ-==-+=-(4)2211=⎰⎰令1sin ,x t -=则cos dx tdt =原式2222220(sin 1)cos cos cos cos t tdt td t tdt πππ=+=-+⎰⎰⎰23111cos 32234tπππ=-+=+ 例4设()f x 连续,0()()x g x x f t dt =⎰,求''(0)g解 '()()()xg x xf x f t dt =+⎰(1)'(0)0g =''''00()()()(0)(0)lim lim xx x xf x f t dt g x g g x x→→+-==⎰()()lim ()(0)lim2(0)1xx x f t dt f x f x f f x→→=+=+=⎰ 注:此题没有()f x 可导的条件,故“(1) 式两边再对x 求导得'''''()()()()2()()(0)2(0)g x f x xf x f x f x xf x g f =++=+⇒=”这种解法是错误的.例5计算下列极限(1) 20sin 0ln(1)lim sin 2xxx t dt tdt→+⎰⎰(2) 2030[()]limxttxx te f u du dtx e →⎰⎰解 (1) 20sin 0000ln(1)ln(12)24limlimlim sin(2sin )cos sin 2sin 2xxx x x t dt x xx x xtdt→→→++⋅==⎰⎰(2) 22232323[()]()()limlimlim(3)3xx txtx xxx x x te f u du dtxef u duf u dux ex x ex x →→→-==++⎰⎰⎰⎰20()2(0)0lim0323x f x x f x →-⋅-⋅===+ 例6 设()f x 为连续函数,且221(2)()arctan 2xx x t f t dt x -=⎰,(1)1f =,求21()f x dx ⎰. 解 22212()()arctan 2x x x x x f t dt tf t dt x -=⎰⎰两边对x 求导,得242()2[2(2)()][4(2)()]1x x x f t dt x f x f x xf x xf x x+---=+⎰ 整理后,有241()[()]21x x xf t dt xf x x=++⎰ 令1x =, 即得 21113()[(1)]224f x dx f =+=⎰例7 设()f x 在(,)-∞+∞内连续,且0()()()2x xF x t f t dt =-⎰证明 (1) 若()f x 为偶函数,则()F x 也是偶函数.(2) 若()f x 为单减函数,则()F x 也是单增函数 ..证 (1) 00()()()()()()22xx x xF x t f t dt u f u du t u --=--=--+-=-⎰⎰0()()()2x xu f u du F x =-=⎰, 即()F x 为偶函数(2) 00()()()2xx x F x f t dt tf t dt =-⎰⎰'0011()()()()[()()]222x x x F x f t dt f x xf x f t dt xf x =+-=-⎰⎰00011[()()][()()]22x x xf t dt f x dt f t f x dt=-=-⎰⎰⎰由()f x 单减,当0t x <<时,()()0f t f x -> '01()[()()]0(0)2xF x f t f x dt x ⇒=->>⎰时当0x t <<时,()()0f t f x -<.'011()[()()]0[()()]22x xF x f t f x dt f t f x dt ⇒=->=-⎰⎰ (0)x <时即在(,)-∞+∞上,()F x 为单增函数. 例8 计算下列各题:(1)52222(sin )cos xx xdx ππ-+⎰ (2)2ln(1)(0)ax ax e dxa -+>⎰解 (1) 52cos x x 为奇函数,22sin cos x x 为偶函数.原式522222222222cos sin cos sin cos x xdx x xdx x xdx ππππππ---=+=⎰⎰⎰2224222002sin (1sin )2sin sin x x dx xdx xdx πππ⎡⎤=-=-⎢⎥⎣⎦⎰⎰⎰=1312()224228πππ⨯-⨯= (2) 分析:此题的积分区间是对称区间,而对称区间上的定积分有公式⎰⎰-+=-aaadx x f x f dx x f 0)]()([)(,若)()(x f x f -+在],0[a 上容易积分,该公式就可利用了.解:⎰⎰--+-+=+ax x aax dx e x e x dx e x 0222])1ln()1ln([)1ln(⎰⎰++=++=-a x x x ax x dx e e e x dx e e x 001)1(ln 211ln 233232322a x dx x aa===⎰例9 计算⎰-πk dx x 02sin 1 (k 为正整数)解 原式⎰⎰-=-=ππk k dx x x dx x x 02cos sin )cos (sin⎰⎰⎰--++-+-=πππππk k dx x x dx x x dx x x )1(20cos sin cos sin cos sin⎰-=πcos sin dx x x k])cos (sin )sin (cos [440⎰⎰-+-=πππdx x x dx x x k])sin (cos )cos (sin [440πππx x x x k +-+= k 22=注:x x cos sin - 是周期为π的周期函数.例10 求dx x x ⎰++1021)1ln(解 令t x tan =,原式dt t tdt tt ⎰⎰+=+=402402)tan 1ln(sec sec )tan 1ln(ππ设dt t ⎰+=I 4)tan 1ln(πdt t dt t t dt tt⎰⎰⎰-+=+=I 404040cos ln )sin ln(cos )cos sin 1ln(πππdt t dt t ⎰⎰--=404cos ln )4cos(2ln πππ(1)而du u du u dt t ⎰⎰⎰=-=-40044)cos 2ln )cos 2ln()4cos(2ln ππππ)4(t u -=πdu u du ⎰⎰+=404cos ln 2ln ππ代入(1)式得 dt t du u du ⎰⎰⎰-+=I 404040cos ln cos ln 2ln πππ2ln 82ln 40ππ==⎰du所以2ln 81)1ln(102π=++⎰dx x x 例11求⎰+2cos sin sin πdx ee e x x x解 ⎰⎰⎰+=+-=+=I 20sin cos cos 02sin cos cos 20cos sin sin πππdx e e edx e ee dx e e e x x xt t t x x x于是 22220sin cos cos sin πππ===++=I ⎰⎰dx dx ee e e xx xx420cos sin sin ππ=+=I ⇒⎰dx e e e xx x例12 求⎰⎰-11][22dx dt e x x t .解⎰-221x t dt e为x 的函数,令⎰-=221)(x t dt e x f原式⎰⎰⎰-===10'2121210)(2)(22)()(dx x f x x f x x d x f dx x xf⎰⎰---=12112]2[22422dx x e x dt ex x x t⎰⎰-=-=--104103)(4144x d e dx ex x x )1(411-=-e 例13 设函数⎰=Φxdt t x 0sin )((1) 当n 为正整数,且ππ)1(+<≤n x n 时,证明)1(2)(2+<Φ≤n x n (2) 求xx x )(limΦ+∞→解 (1) 由0sin ≥t ,且ππ)1(+<≤n x n⎰⎰+<Φ≤⇒ππ)1(0sin )(sin n n dt t x dt t由于t sin 是周期为π的周期函数,n tdt n dt t n dt t n 2sin sin sin 0==≤⎰⎰⎰πππ同理)1(2sin )1(0+=⎰+n dt t n π因此,当ππ)1(+<≤n x n 时,有)1(2)(2+<Φ≤n x n(2) 由(1)知当 ππ)1(+<≤n x n 即ππn x n 11)1(1≤<+有ππn n x x n n )1(2)()1(2+≤Φ<+,令∞→x ,有∞→n .而 ππ2)1(2lim=+∞→n n n , ππ2)1(2lim =+∞→n n nπ2)(lim=Φ⇒+∞→x x x例14 设)(x f 在]1,0[上连续,且单调递减,证明对)1,0(∈∀α,有⎰⎰≥1)()(dx x f dx x f αα证法一⎰⎰⎰+=11)()()(ααdx x f dx x f dx x f于是⎰⎰-10)()(dx x f dx x f αα=])()([)(1⎰⎰⎰+-ααααdx x f dx x f dx x f=⎰⎰--1)()()1(ααααdx x f dx x f由积分中值定理)()(10ξααf dx x f =⎰αξ≤≤10)()1()(21ξααf dx x f -=⎰ 12≤≤ξα因此⎰⎰-1)()(dx x f dx x f αα=)()1()()1(21ξααξααf f ---=)]()([)1(21ξξααf f -- (1021≤≤≤≤ξαξ)因)(x f 单减,则有)()(21ξξf f ≥,即⎰⎰≥1)()(dx x f dx x f αα.证法二 设⎰⎰-=1)()(1)(dx x f dx x f F ααα (10≤<α)22)()()()()(αξααααααααf f dxx f f F -=-='⎰ (αξ≤≤0) 0)()(≤-=αξαf f即)(αF 在]1,0(上单调不增, 即0)1()(=≥F F α,即有⎰⎰≥1)()(dx x f dx x f αα.注:此题还可以用积分换元法加以证明.例15 设)(x f 在]1,0[上连续,)1,0(内可导,且满足⎰=2102)(2)1(dx x f x f .证明在)1,0(内至少有一点ξ使)(2)('ξξξf f -=.证 设)()(2x f x x F =,由积分中值定理,21)()()(1212102⋅==⎰⎰ξF dx x F dx x f x (2101≤≤ξ)即⎰=21021)(2)(dx x f x F ξ,而dx x f x f F ⎰==21022)(2)1(1)1(即)1()(1F F =ξ,由罗尔定理,存在)1,0()1,(1⊂∈ξξ,使0)('=ξF 而)()(2)('2'x f x x xf x F +=,即有0)()(2)('2'=+=ξξξξξf f F也即 0)()(2'=+ξξξf f ,)(2)('ξξξf f -=.例16 计算下列反常积分: (1)⎰+∞-22ln 1dx x x (2) ⎰+∞+0232)1(arctan dx x x (3)⎰-10211ln dx x解 (1)⎰+∞-22ln 1dx x x =⎰+∞--21)ln 1(x d x =⎰∞++∞---2221ln 1dx x xx=+∞+-2122ln 1x=22ln -. (2) 令x x tan =,⎰+∞+0232)1(arctan dx x x dt t tt⎰=223sec sec π=dt t t ⎰20cos π=t d t sin 20⎰π=⎰-220sin sin ππtdt t t =20cos 2ππt +=12-π. (3) ∞=--→2111lnlim xx , 1=x 为被积函数的瑕点.⎰-1211lndx x=⎰-+-→t t dx x x 01)1)(1(1ln lim =⎰-++--→tt dx x x 01)]1ln()1[ln(lim=tt x x x x x 01)]1ln()1(2)1ln()1([lim --++++--→ =)]1ln()1(2)1ln()1([lim 1t t t t t t --++++--→ =)2ln 1(2-例17 已知π=⎰+∞∞--dx ex 2,12=⎰+∞∞-+-dx ce xx.求c 的值.解=⎰+∞∞-+-dx cexx 2)21(41)21(2-⎰∞+∞---x d e ec xt x =-21令 dt e e c t ⎰∞+∞--412dt e ce t ⎰∞+∞--=241π41ce=即 ππ414111ec ce=⇒=.例18 设⎩⎨⎧<<=其它10)(x xx f ,⎩⎨⎧<≥=-0)(x x e x g x, 求函数dx x t g x f t h ⎰+∞∞--=)()()(的表达式.解 因为)(x f 在)1,0(上为x x f =)(,在)1,0(之外都为零.故dx x t g x f t h ⎰+∞∞--=)()()(⎰-=1)(dx x t xg而⎩⎨⎧≥-=---其它0)()(x t e x t g x t当0<t 时,由于积分变量]1,0[∈x ,故总有t x > 从而0)(=-x t g ,0)()(1=-=⎰dx x t xg t h .当10≤≤t 时,⎰⎰⎰-+-=-=11)()()()(ttdx x t xg dx x t xg dx x t xg t h当积分变量x 在]1,[t 上变化时,0≤-x t ,0)(=-x t g , 所以0)(1=-⎰tdx x t xg从而⎰⎰⎰--==-=txt tt x tdx xe e dx xe dx x t xg t h 0)()( tt t t t x x t e t e te e e xe e ---+-=+-=-=1)1(][0当1>t 时,t xttx e dx xeedx xedx x t xg t h ---===-=⎰⎰⎰1110)()(.综上 ⎪⎩⎪⎨⎧>≤≤-+<=--时当时当时当110100)(t e x t e t t h t t 注:本题是含参变量的反常积分,这是一类重要的积分,它在概率统计以及积分变换中都会用到.第六章 定积分 自测题 A 卷一、选择题(每小题3分,共15分).1.=⎰dt e dx d b xt 2( ) (A)2x e (B)2x e - (C)22x b e e - (D)22x xe -2.dx x x I ⎰-=321,则( )(A)化为)1()1(21230212x d x I ---=⎰后计算(B)进行代换t x sin =后计算(C)进行代换t x =-21,dt t I ⎰--=30212121后计算(D) 进行代换t x cos =后计算3.设)(x f 连续且2)0(=f ,⎪⎩⎪⎨⎧=≠=⎰00)()(2x cx x dt t tf x F x ,若)(x F 在0=x 处连续,则=c ( )(A)0=c (B) 1=c (C)c 不存在 (D) 1-=c4.设)(x f 在[a a ,-]上连续,则⎰-aadx x f )(等于( )(A)⎰adx x f 0)(2 (B)0(C)⎰-+adx x f x f 0)]()([ (D)⎰--adx x f x f 0)]()([5.设)(x f 是连续的奇函数,则)(x f 的任一原函数( )(A)是偶函数 (B)是奇函数(C)可能是奇函数,也可能是偶函数 (D)非奇非偶函数 二、(7分)求]4121141[lim 22222nn n n -+++-∞→ .三、计算下列各题(每题6分,共12分). 1. 20220)()(lim22dt edt e xt xt x ⎰⎰-→2. 设dt t x f xx⎰-+=sin 2)1arctan()(,求)0('f .四、 计算下列定积分(每题8分,共56分). 1.⎰+21ln 11e dx xx 2.dx x x ⎰-20cos sin π3.⎰-+43412)1(1dx x x x 4.⎰+x e dx 1 5.dx x ⎰+π4302cos 1 6.dx x x ⎰--112247.dx xx ⎰+∞22ln 1五、(10分) 设⎪⎩⎪⎨⎧≥<+=-001)(2x ex xx f x,求dx x f ⎰-31)2(.第六章 定积分 自测题 B 卷一、选择题(每小题3分,共15分) 1.设0)(=⎰dx x f ba,且)(x f 在],[b a 连续,则( )(A)在],[b a 上,0)(≡x f (B)必存在],[b a ∈ξ,使0)(=ξf (C)存在唯一的],[b a ∈ξ,使0)(=ξf (D)不一定存在],[b a ∈ξ,使0)(=ξf 2.设dt t I xe⎰=ln 1,dt t I xe⎰=22)(ln ,(0>x ),则( )(A)对一切e x ≠,有21I I < (B)仅当e x >时,有21I I < (C)对一切e x ≠,有21I I ≥ (D)仅当e x <时,有21I I <3.当0→x 时,⎰-=12)sin()(x e dt t x f 与43)(x x x g +=比较,是( )(A)高阶无穷小 (B)低阶无穷小 (C)同阶但非等价无穷小 (D)等价无穷小4.函数dt t t tx x⎰+-=0213)(ϕ在区间]1,0[上的最小值为( )(A)21 (B)31 (C)41(D)05.=-+⎰→xdtt xx cos 1)1ln(lim2sin 0( )(A)8 (B)4 (C)2 (D)1二、填空题(每小题3分,共15分). 1. 设)(x f 为连续函数,则=--⎰-aadx x f x f x )]()([2.2. =+++++∞→)212111(lim n n n n .3. 若dx x f dx x xf a ⎰⎰=0202)(21)(,则=a .4. 设⎩⎨⎧≤<≤≤=21110)(2x x x x f ,而⎰=x dt t f x F 1)()( )20(≤≤x ,则=)(x F .5.=-⎰dx x 21.三、计算下列各题(每题8分,共56分). 1.⎰-+10xx e e dx2.⎰+214)1(x x dx3.θθθθππd ⎰-+22234sin )sin (cos 4.dx xx⎰+22sin 3sin π5.⎰--2ln 021dx e x 6.⎰+∞++02)1()1ln(dx x x 7. 已知5)2(,3)2(,1)0('===f f f ,求⎰1'')(dx x xf .四、(8分) 设⎰+=x dt t t x f 111ln )( )0(>x ,试求)1()(xf x f +. 五、(6分) 设)(x f 在]1,0[上连续,)1,0(内可导,且)0()(3132f dx x f =⎰.证明:在)1,0(内至少存在一点ξ,使0)('=ξf .第六章 定积分 自测题 C 卷一、选择题(每小题3分,共18分). 1.设)(x f 为连续函数,那么函数⎰=xdt t tf x F 02)()(为( )(A)奇函数 (B)偶函数 (C)非奇非偶函数 (D)单调增加函数 2.⎰=xadt t f )2('( )(A))]()([2a f x f - (B))2()2(a f x f - (C))]2()2([2a f x f - (D))]2()2([21a f x f - 3. 函数)(x f 在闭区间],[b a 上连续是定积分dx x f ba⎰)(存在的( )(A)必要条件 (B)充分条件 (C)充要条件 (D)无关条件 4. 设⎰--+=114121sin dx e x x I x ,⎰--++=1142)1sin (2dx e x x I x ,⎰---+=1143)1sin (2dx e x x I x , 则( )(A)321I I I << (B)231I I I << (A)213I I I << (A)123I I I << 5. 设)(x f 连续,则⎰=-x dt t x tf dxd 022)(( ) (A))(2x xf (B))(2x xf -(C))(22x xf (D))(22x xf -6. 广义积分收敛的是( ) (A)⎰+∞e dx x x ln (B)⎰+∞e dx x x ln 1(C)⎰+∞ex x dx 2)(ln (D)⎰+∞e xx dxln二、填空题(每小题3分,共12分).1.=+⎰))1ln((22x xt dt t e dx d .2.设)(x f 在]4,0[上连续,且3)(212-=⎰-x dt t f x ,则=)2(f .3.设)(x f 为连续函数,且dx x f x x f e⎰-=1)(ln )(,则=⎰dx x f e1)(.4.=-+⎰-dx x x 1122)1(.三、计算下列各题(每题8分,共40分).1.⎰+402cos 1πdx x x 2.⎰+++203)1(1x x dx3. ⎰+edx x x 1ln 1 4.⎰+10222)1(dx x x 5.⎰+-5ln 031dx e e e x x x四、(10分) 已知dt te a x a x a t xx ⎰∞-+∞→=-+2)(lim ,试求a 的值.五、(10分) 已知⎰=+-→x x dt ta t x bx 0201sin 1lim,求b a ,的值. 六、(10分) 设)('x f 在],0[a 上连续,且0)0(=f .证明:2)(20Ma dx x f a≤⎰,其中)(max '0x f M a x ≤≤=.定积分自测题答案自测题(A)一、 1.D 2.A 3.B 4.C 5.A 二、6π. 三、 1.1 2.2π 四、 1.)13(2- 2.)12(2- 3.3831ln4- 4.ee+12ln 5.122- 6.2332-π7.2ln 1五、 e137-自测题(B)一、1.B 2.B 3.C 4.D 5.B 二、 1.0 2.2ln 3.4=a4.⎪⎩⎪⎨⎧≤≤-<≤-=21110)1(31)(3x x x x x F 5.1三、 1.e arctan 2.1732ln 41 3.16π 4.31ln 41- 5.)32ln(23+- 6.1 7.2 四、2)(ln 21x 五、提示:利用积分中值定理及罗尔定理.自测题(C)一、 1.B 2.D 3.B 4.C 5.A 6.C 二、 1.)1ln(2)1ln(422x xe x e x x +-+ 2.41)2(=f 3.e14.2 三、 1.)22ln 4(21+π 2.6π 3.234.82-π 5.4-π四、 25=a 五、 1,4==b a六、 ],0(a x ∈∀,由拉格朗日中值定理,x f f x f )()0()('ξ=-,),0(x ∈ξ.又因0)0(=f ,故x f x f )()('ξ=,],0[a x ∈, 于是200'0'02)()()(a M dx x M dx x f dx x f dx x f a a a a=≤≤=⎰⎰⎰⎰ξξ.(注:本资料素材和资料部分来自网络,仅供参考。
