4.2.1线段、直线、射线
《4.2.1直线、射线、线段》练习题1
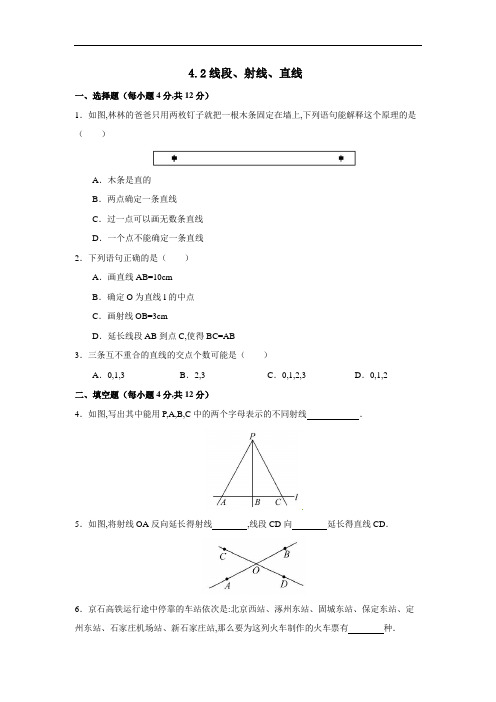
4.2线段、射线、直线一、选择题(每小题4分,共12分)1.如图,林林的爸爸只用两枚钉子就把一根木条固定在墙上,下列语句能解释这个原理的是()A.木条是直的B.两点确定一条直线C.过一点可以画无数条直线D.一个点不能确定一条直线2.下列语句正确的是()A.画直线AB=10cmB.确定O为直线l的中点C.画射线OB=3cmD.延长线段AB到点C,使得BC=AB3.三条互不重合的直线的交点个数可能是()A.0,1,3 B.2,3 C.0,1,2,3 D.0,1,2二、填空题(每小题4分,共12分)4.如图,写出其中能用P,A,B,C中的两个字母表示的不同射线.5.如图,将射线OA反向延长得射线,线段CD向延长得直线CD.6.京石高铁运行途中停靠的车站依次是:北京西站、涿州东站、固城东站、保定东站、定州东站、石家庄机场站、新石家庄站,那么要为这列火车制作的火车票有种.三、解答题(共26分)7.(8分)数一数,图中共有多少条线段?并分别写出这些线段.8.(8分)A,B,C,D四点如图所示,读下列语句,按要求作出图形(不写画法): (1)连接AD,并延长线段DA.(2)连接BC,并反向延长线段BC.(3)连接AC,BD,它们相交于点O.(4)DA延长线与BC反向延长线交于点P.【拓展延伸】9.(10分)动手画一画,再数一数.(1)过一点A能画几条直线?(2)过两点A,B能画几条直线?(3)已知平面上共有三个点A,B,C,过其中任意两点画直线,可画几条?(4)已知平面上共有n个点(n为不小于3的整数),其中任意三个点都不在同一直线上,那么连接任意两点,可画多少条直线?答案解析1.【解析】选B.根据两点确定一条直线,故选B.2.【解析】选D.A,直线无限长;B,直线不能度量,没有中点;C,射线可向一方无限延长;D,延长线段AB到点C,使得BC=AB,正确.3.【解析】选C.分四种情况:1.三条直线平行,有0个交点;2.三条直线相交于同一点,有1个交点;3.一条直线截两条平行线有2个交点;4.三条直线两两相交有3个交点.4.【解析】图形中能用P,A,B,C中的两个字母表示的不同射线有:射线PA 、射线PB 、射线PC 、射线AB 、射线BC 、射线BA 、射线CB .答案:射线PA 、射线PB 、射线PC 、射线AB 、射线BC 、射线BA 、射线CB5.【解析】将射线OA 反向延长得射线OB,线段CD 向两方延长得直线CD .答案:OB 两方6.【解析】画一条直线,在直线上依次取A,B,C,D,E,F,G 七个点,它们依次表示北京西站、涿州东站、固城东站、保定东站、定州东站、石家庄机场站、新石家庄站.点A 分别与B,C,D,E,F,G 形成6条线段;点B 分别与C,D,E,F,G 形成5条线段;点C 分别与D,E,F,G 形成4条线段;点D 分别与E,F,G 形成3条线段;点E 分别与F,G 形成2条线段;点F 与G 形成1条线段,所以直线上共有线段的条数是6+5+4+3+2+1=21,考虑往返情况,所以应制作火车票21×2=42(种).答案:42【知识拓展】若一条直线上有n 个点,那么以这n 个点中的任意两点为端点的线段共有(n-1)+(n-2)+…+2+1=21n (n-1)(条). 7.【解析】由图形得:共有10条线段,分别为:线段AB 、线段BC 、线段CD 、线段DA 、线段AC 、线段AO 、线段CO 、线段BD 、线段BO 、线段DO .8.【解析】如图所示.9.【解析】(1)过一点A 能画无数条直线.(2)过两点A,B 只能画一条直线.(3)①若三点共线则可画一条,②若三点不共线则可画三条.故可画1条或3条.(4)根据过两点的直线有1条,过不在同一直线上的三点的直线有3条,过任意三点都不在一条直线上的四点的直线有6条,按此规律由特殊到一般可得过任意三个点都不在同一直线上的n 个点共能画21n (n-1)条直线.。
2024年秋新湘教版七年级上册数学课件 第4章 图形的认识 4.2 第1课时 线段、射线、直线

关怀的温暖;自觉接受学生的评价,努力做学生喜欢的老师。 教师要学会宽容,宽容学生的错误和过失,宽容学生一时没有取得很大的进步。苏霍姆林斯基说过:有时宽容引起的道德
生活中有哪些事物可以作为直线、射线、线 段的原型?试举例说明.
伸向远方的火车铁轨 (可看作直线)
激光灯 (可看作射线)
筷子 (可看作线段)
线段、射线、M
Al B
1.判断下列说法是否正确:
(1)直线、射线、线段都有两个端点;
(×)
(2)直线和射线可以延伸,线段不能延伸;
2.请观察图形作出判断:
一个是从A到B的方向,一个是从B到A的方向.
A
B
例如,把一条笔直的自行车专用道看成一 条直线,那么自行车专用道就有两个互为相反的 方向(如图).
做一做
任意画一个点和一条直线,你能发现,点与直线有哪几种位置关系? 点与直线有两种位置关系:点在直线上或点在直线外,
也可以说直线经过这个点或直线不经过这个点.
第4章 图形的认识
4.2 线段、射线、直线
第1课时 线段、射线、直线
1.在现实情境中理解线段、射线、直线的概念及它 们的区别与联系.(重点) 2.会用不同的方法表示线段、射线、直线.(难点) 3.了解“两点确定一条直线”的基本事实.
观察 图中可以近似地看作线段、射线、直线的分别有哪些?
绷紧的钢拉索、笔直的路灯杆等实物都给我 们以线段的形象,线段有两个端点.线段向一端 无限延长形成了射线,射线有一个端点.线段向 两端无限延长形成了直线,直线没有端点.
4.2.1直线射线线段(1)

m
实战演练
往返温州、宁波两地的火车,中途需要停靠 雁荡、台州、奉化三个站点,根据你所学的知 识回答: 需要制定多少种不同的票价?
答:10种
温A州 雁B荡 C台州 O
D 奉化 E 宁波
实际问题
转化为
数学问题
ABCFra bibliotek射线BA与射线AB是同一条射线吗?
概念对比
1.如图,若射线AB上有一点C,下列与射线AB是同一
条射线的是( B )
(A)射线BA (C)射线BC
(B)射线AC
(D)射线CB A B C
2.如图,下列语句表述错误的是( C )
A.点A在直线m上
n
B.直线n经过点A
C.点B在直线n上
B
A
D.直线m不经过B点
概念对比
已知线段AB,你能由线段AB得到射线AB和直线 AB吗?
线段AB
A
B
线段和射线都是直线的一部分.
概念对比
类型 线段 射线 直线
端点
延伸方向
有2个端点 不向任何一方延伸
可不可度量 可度量
有1个端点 向一个方向无限延伸 不可度量
无端点 向两个方向无限延伸 不可度量
例题讲解
如图,共有几条直线?几条线段?几条射线?以B 为端点的射线有几条?分别写出来。
相交
b
交点
A
F
点A在直线b外
点A不在直线b上
直线b不经过点A
B
C E
点E在直线b上 直线b经过点E
小试牛刀
按下列语句画出图形 1.直线AB经过点C 2.点A在直线m外 3.直线c与直线b相交于点D
射线 b
射线EF 射线b
F
4.2.1 直线、射线、线段(分层作业)【原卷版】

4.2.1 直线、射线、线段分层作业1.如图,下列说法正确的是()A.点O在射线BA上B.点B是直线AB的端点C.直线AO比直线BO长D.经过A,B两点的直线有且只有一条2.下列说法中正确的是()A.延长直线ABB.反向延长射线ABC.线段AB与线段BA不是同一条线段D.射线AB与射线BA是同一条射线3.如图,下列说法错误的是()A.点A在直线AC上,点B在直线m外B.射线AC与射线CA不是同一条射线C.直线AC还可以表示为直线CA或直线m D.图中有直线3条,射线2条,线段1条4.如图,王伟同学根据图形写出了四个结论:①图中共有4条直线;②图中共有7条射线;③图中共有6条线段;④图中射线BC与射线CD是同一条射线;其中结论错误的有()A.1个B.2个C.3个D.4个5.下面说法与几何图形相符的是()A.点P在直线n上B.直线OA与OB都经过点OC.1∠D.直线OA和直线m表示同一条直线∠可以表示成O6.如图,小轩同学根据图形写出了四个结论:①图中共有2条直线;②图中共有7条射线;③图中共有6条线段;④图中射线BD与射线CD是同一条射线.其中结论错误的是()A.①③④B.①②③C.②③④D.①②④+等于()7.平面内两两相交的4条直线,其交点个数最少为m个,最多为n个,则m nA.6 B.11 C.7 D.17个端点.9.如图,点P在直线AB ;点Q在直线AB ,也在射线AB ,但在线段AB的上.10.下列说法:①两点确定一条直线;②射线OA和射线AO是同一条射线;③对顶角相等;④三角形任意两边和大于第三边的理由是两点之间线段最短.正确的序号是.11.有下列语句:①在所有连接两点的线中,直线最短;②线段AB是点A与点B的距离;③取直线AB的中点;④反向延长线段AB,得到射线BA,其中正确的是.12.如图所示,共有直线条,射线条,线段条.13.如图,(1)点B在直线AD ,点F在直线上;(2)点C在直线AD ,点E是直线和的交点;(3)经过点C的直线共有条,它们分别是.14.判断下列说法是否正确:(1)线段AB和射线AB都是直线AB的一部分(2)直线AB和直线BA是同一条直线;(3)射线AB和射线BA是同一条射线;(4)把线段向一个方向无限延伸可得到射线,向两个方向无限延伸可得到直线.15.根据下列语句画出图形.(1)点A在直线l上,点B在直线l外;(2)过点N画射线MN;(3)画一条与线段AB相交的直线CA.16.如图,已知A,B,C、D四个点,按要求画出图形.(1)画直线AB,CD相交于点P;(2)画射线AC;(3)连接BD;(4)图中共有几条线段?17.(尺规作图,保留作图痕迹)如图,已知四点A,B,C,D,(1)作线段AB,直线CD,射线CB;(2)反向延长线段AB到E,使AE BC;(3)在图中确定点O,使点O到A,B,C,D距离之和最小.18.往返于甲、乙两市的列车,中途需停靠4个站,如果每两站的路程都不相同,这两地之间有多少种不同的票价()A.15 B.30 C.20 D.1019.数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长2017厘米的线段AB,则线段AB盖住的整点共有()个A.2018或2019 B.2017或2018 C.2016或2017 D.2015或201620.如图,在线段MN上有P、Q两点,PQ长度为2cm,MN长为整数,则以M、P、Q、N为端点的所有线段长度和可能为()A.19cm B.20cm C.21cm D.22cm车票.22.同一平面内有四点A,B,C,D,经过每两点作一条直线,则可以作条直线.23.平面上有n条直线,其中没有两条直线互相平行(即每两条直线都相交),也没有三条或三条以上的直线通过同一点.试求:(1)这n条直线共有多少个交点?(2)这n条直线把平面分割为多少块区域?24.如图,如果直线l上依次有3个点A、B、C,那么(1)在直线l上共有多少射线?多少条线段?(2)在直线l上增加一个点,共增加了多少条射线?多少条线段?(3)如果在直线l上增加到n个点,则共有多少条射线?多少条线段?。
4.2.1 直线、射线、线段的概念

移动的项要变号 (3)移项:
例:方程3X+20=4X-25+5 • 移项正确的是:A、3X--4X=-5-25-20 • B、 3X-4X=-25+5-20
× √
知识归纳:
步骤
去分母
相信你能行
依据 注意事项
具体做法
在方程两边都乘 以各分母的最小 公倍数 一般先去小括号, 再去中括号,最后 去大括号 把含有未知数的
去括号后的符号变化,并且不要漏乘括号中的每一项 (2)去括号:
例:去括号 2X- 5 A、+(2X- 5)= ___________
- 2X+5 B、- (2X- 5)=__________
9X+3 C、3(3X+1)=___________
- 6X+10 D、-2(3X- 5)= _________
成的情况给予评价,并请学生作出自我评价.
活动4:课堂小结 1.提问:直线的性质是什么?如何表示直线、射线、 线段? 2.本节课还学习了根据语句画图,知道了每一个语句 都对应着一个几何图形. 活动5:布置作业 习题4.2第1,2,3,4题.
直线、射线、线段是最简单、最基本的图形,是研究复杂 图形的基础.这节课对于几何的学习起着奠基的作用.通 过学生动手操作,反复比较,总结提炼.让他们经历由感 性到理性,由具体到抽象的思维过程
4.2
直线、射线、线段(3课时)
直线、射线、线段的概念
第1课时
1 . 认识直线、射线、线段的联系和区别 , 逐步掌握它
们的表示方法. 2 . 结合实例 , 了解两点确定一条直线的性质 , 并能初 步应用. 3 . 能根据语句画出相应的图形 , 会用语句描述简单的
4.2.1直线、射线、线段[精选文档]
![4.2.1直线、射线、线段[精选文档]](https://img.taocdn.com/s3/m/6e20db30793e0912a21614791711cc7931b7780c.png)
3.按下列语句画出图形:
(1)、直线EF经过点C;
EF
C
(2)、点A在直线a外;
A a
ab
(3)、经过点O的三条线段a、b、c;
c o
(4)、线段AB、CD相交于点B。
C
A
BD
•练一练 •126页1、3
端点)表示 。 如:线段AB或BA
◆用一个小写字母表示。
如:一想
指出直线、射线、线段三者的区别与联系:
射线、线段都是直线的一部分。直线、射线、线段的 表示方法如下:
类型 直线 射线 线段
端点数
延伸
度量
无端点 1个 2个
向两个方向无限 延伸
向一个方向无限 延伸
不可度量 不可度量
不向任何方向延伸 可度量
做一做
(1) 过一点 A 可以画几条直线? (2) 过两点A、B可以画几条直线? (3) 如果你想将一根细木条固定在墙上,
至少需要几个钉子?
A●
●
●
A
B
性质:经过两点有且只有一条直线
(2) 射线:直线上一点和它一旁 的部分,这一点叫做射线的端点。
★ 用两个大写字母(既端点和射线另 外一点,端点必须写在前面)。 如:射线 OA 或射线l.
ι ι ★用一个小写字母表示。如:射线
●
●
O
A
CAB D
射线AC与射线AB 是同一射线吗?射 线AB与射线AD呢?
怎样判断两条射线是同一射线呢?
必须具备的条件
端点相同 延伸方向相同
画一画:画一条射线BE
B
E
(3)线段:直线上两点及两点之 间的部分。这两个点叫做线段的 端点。 ◆ 用两个大写字母(既线段的两
小学升初中衔接教程 4.2.1、线段、射线、直线
第二节 平面图形的进一步认识一、线段、射线、直线球球的数学功夫小学里学习了线段、射线、直线的概念和基本特征,会用刻度尺分别测量比较线段的长度;用刻度尺画出规定长度的线段;1.线段、射线、直线的表示方法:(1)一条线段用表示两个端点的大写字母来表示,如线段AB 或BA.或一个小写字母表示. (2)一条射线可用端点和射线上的另一点表示,规定把表示端点的字母写在前面. (3)一条直线可用两个大写字母表示,这两个大写字母代表直线上的两个点,如直线AB 或BA ;另外直线还可用一个小写字母表示.要点点拨:在学习直线、射线、线段时,要特别注意三者之间的区别,比如端点、表示方法、延伸性及能否度量等方面.3.点与直线的位置关系:(1)点经过直线,说明点在直线上;(2)点不经过直线,说明点在直线外.例1. 下图中有 条线段. 条射线, 条直线.分析与解答:根据线段、射线、直线的概念求解即可. 答案:6, 8 , 1例2. 在沪宁线上,一列火车(高铁),往返于南京和上海,沿途要经过镇江、常州、无锡、苏州四站,铁路部门要为这趟列车准备印制( )种车票. A .6 B .12 C .15 D .30分析与解答:先考虑从南京开往上海方向的,求出从南京出发的有5种车票,从镇江出发的有4种车票,从常州出发的有3种车票,从无锡出发的有2种车票,从苏州出发的有1种车票,即可得到印制的车票种数为2×(5+4+3+2+1)=30(种).答案:D球球的数学功夫升线初中阶段还要学习线段、射线、直线的表示方法及它们之间的关系,点与直线的位置关系,线段、射线、直线的性质,线段的等分点,用无刻度的直尺和圆规作图.1.基本事实:(1)直线的性质:经过两点有且只有一条直线.简称:两点确定一条直线.(2)线段的性质:两点的所有连线中,可以有无数种连法,如折线、曲线、线段等.这些所有的线中,线段最短.简单说成:两点之间线段最短.2.两点间的距离:连接两点间的线段的长度叫两点间的距离.“∵”读作“因为”,“∴”读作“所以”。
4.2.1直线、射线、线段(1)
B
也可记作线段a。
a
4. 合作交流,再获新知
问题9:填写表格,归纳直线、射线、线段的 联系与区别.
名称 图形
表示
延伸 端点 度量
直线
A·
B· l
1.直线AB (或直线BA) 2.直线l
向两端 无限延 伸
0个
不可 度量
射线 A·
B· l
1.射线AB 2.射线l
向一端 无限延 1个 伸
不可 度量
1.线段AB
义务第教育四教章科书图形数认学 识七初年步级 上册
4.2 直线、射线、线段 (第1课时)
1. 以旧悟新,探求新知
问题1:小学的时候我们已经学习过直线、 射线和线段,请同学们回忆一下他们的形 状并分别画出一条直线、射线和线段.
一、创设情境 引入新知
问题2:如图,经过一点O画直线,能画 几条?经过两点A、B呢?
线段
A· a
B·2(.线或段线a段BA)
不可延 伸
2个
可度 量
4. 合作交流,再获新知
问题10: (1)判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分; ②直线AB与直线BA是同一条直线; ③射线AB和射线BA是同一条射线; ④把线段向一个方向无限延伸可得到射线, 把线段向两个方向无限延伸可得到直线.
4. 合作交流,再获新知
问题10:(2)按下列语句画出图形: ①点A在线段MN上; ③经过O点的三条线段a,b,c;
MA N
ab Oc
②射线AB不经过点P;④线段AB、CD相交于点B.
P ●
D
A
B
A
B
C
指出下列各组图中的线段、射线和直 线,哪些能够相交?哪些不能相交?
-4.2.1 直线、射线、线段
知2-讲
①象国旗的旗杆、绷紧的琴弦都可以近似地看作线段. ②将线段向一个方向无限延长就形成了射线. ③将线段向两个方向无限延长就形成了直线.
想一想:线段、射线、直线之间有何异同?
第十七页,编辑于星期五:十七点 二十分。
线段、射线、直线的区别与联系.
知2-讲
类型 线段 射线 直线
端点数
可否延伸
可否度量
2个 1个
无端点
不能延伸
可度量
向一个方向无限
延伸
不可度量
向两个方向无限 延伸
不可度量
第十八页,编辑于星期五:十七点 二十分。
知2-讲
例4 如图所示,A,B,C是同一直线上的三点,
下列说法正确的是( C)
A.射线AB与射线BA是同一条射线
B.射线AB与射线BC是同一条射线
C.射线AB与射线AC是同一条射线 D.射线BA与射线BC是同一条射线
C.只有一个错误
D.只有一个正确
知2-练
第二十四页,编辑于星期五:十七点 二十分。
3 下列说法正确的是( C ) A.射线可以延长
B.射线的长度可以是5 m C.射线可以反向延长
D.射线不可以反向延长
知2-练
第二十五页,编辑于星期五:十七点 二十分。
知2-练
4 将线段AB延长至C,再将线段AB反向延长至
第十九页,编辑于星期五:十七点 二十分。
知2-讲
导引:一条射线可用表示它的端点和射线上另一点
的两个大写字母来表示,表示端点的字母必
须写在前面,所以只有端点相同,并且延伸 方向也相同的射线才是同一条射线.选项A, B中的两条射线端点不同,所以A,B不正确; 选项D中射线BA与射线BC的延伸方向不同,
人教版数学七年级上册4.2.1直线、射线、线段的概念课件
no
(4) 以点A为端点的射线只有一条;
no
(5)射线AB和射线BA是同一条射线。
no
练一练
2.指出下图中线段、射线、直线分别有多少条?
A
B
C
答: 有3条线段.
有6条射线. 只有一条直线.
练一练
3.下图中给出的直线、射线、线段能相交的是 (2.)
C
A
(1)
D
(2) B
A C (3)
A
B
C
D
(4) D
(1)画直线AB、CD交于点E;
(2)画线段AC、BD交于点F;
(3)画线段EF和射线CB 交于点G 。
A B
FG
CE D
问题
某校总务处为解决下雨天学生雨伞的 存放问题,决定在每个班级教室外横向 钉牢固一根2米长的装有挂钩的木条. 本校共三个年级,每个年级十个班, 问至少需要买几颗钉子? 你能帮总 务处的师傅算一算吗?
表示图形
5.点与直线的位置关系
(1)点在直线上(直线经过点)
P
a 点P在直线a上(直线a经过点P)
(2)点在直线外(直线不经过点)
P a 点P在直线a外(直线a不经过点P)
你画我说
例1.(1)分别说出各图中的点与直线的位
置关系。
m
a
b
n
M
O
A
B (1)
P
c
N
(2)
你画我说
(2)把下面几何图形用几何语言表示
读作:射线 OA
某校总务处为解决下雨天学生雨伞的存放问题,决定在每个班级教室外横向钉牢固一根2米长的装有挂钩的木条.
(2)用一个小写字母表示
a 读作:射线 a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l
m n
直线的基本性质:
经过两点有且只有一条直线
存在性 唯一性
.
即:两点确定一条直线
自学反馈(一)
(1)如果你想将一根细木条固
定在墙上,至少需要几个钉子?
.
(2)经过一个已知点画直线,可以 画多少条? (3)经过两个已知点画直线,可 以画多少条?
. .
(4 )平面内三点可确定
条直线.
...
. ..
(4)线段AB、CD相交于点B
如图,已知三点A、B、C. (1)画直线AB; (2)画射线AC;
C
A B
(3)连接BC.
下图中,有几条直线,几条射线,几条线段?
A
C
D
B
答:有1条直线,8条射线,6条线段。
两点确定一条直线
说一说,这节课 经过两点有且只有一条直线 你有什么收获?
用数学符号表示直线、 射线、线段
两点确定一条直线的应用:
1、植树时,只要定出两个树坑的位置就能确定同 一行的树坑所在的直线。
•
建筑工人在砌墙时经常在两个墙脚的位置分 别插一根木桩,然后拉一条直的参照线, 根据 两点确定一条直线的 道理.
在我们的日常生 活中有哪些有关 “直线”形象的 例子?
怎样用数学符号表示直线?
A
B
l
p
A B 表示:直线 AB(或直线BA) 表示:直线 l B a O A 表示:线段 AB(或线段BA) 表示:线段 a 表示:射线 OA 表示:射线 l
l
A
l
注意问题:(1)线段、直线表示与字母顺序无关 (2)射线表示有方向性,端点在前,射线上任意一点在后
已知线段AB,怎样由线段AB得 到射线AB和直线AB呢?
A
B
线Hale Waihona Puke AB从这一问题你能 发现什么呢?
A
B
射线AB
A
B
直线AB
⑴把线段向一个方向无限延伸可 得到射线; ⑵把线段向两个方向延伸可得到直线。 ⑶线段和射线都是直线的一部分。
(2)直线、射线、线段的联系与区别
图形
线段
A
表示方法
B
端点个数
两个 一个 0
延伸方向
不向任何一方延伸 向一方无限延伸
a a
A B
(C )线段Mn
(D)线段mn
2.如图,若射线AB上有一点C,下列与射线 AB是同一条射线的是(B ) (A)射线BA (B)射线AC A B C (C )射线BC (D)射线CB
A
3.图中的几何体有多 少条棱?请写出这些 表示棱的线段。
B
D
C
A
4.请写出图中以O为 端点的各条射线。
B
O
C
A C D B
2、变形题:往返于甲乙两地的客车中途要 停靠三个车站,有多少种不同的票价?要 准备多少种不同的车票?
下课了!
(5)种树时,只要定出两个树坑的位置, 就能确定同一行的树所在的直线,这是 因为 。
请你把左边对图形的描述和右边相应 的图形用线连起来: 以A为端点,经过点B的射线
A
a
A
B
连结A,B两点的线段
B
l
经过A,B两点的直线
A
B
线段、射线、直线的表示方法
• 线段: (1)用表示端点的两个大写字母表示
(2)用一个小写字母表示 A a B
⑴要把准备好的一根硬纸条固定在 硬纸板上,至少需要几个图钉?
两点确定一条直线
⑵ 经过一点O画直线,能画出几条? 经过两点A、B 呢?
O A B
经过两点有且只有一条直线 存在
唯一
生活中我们常常用到两点确定一条 直线,你能举几个例子吗?
两点确定一条直线的应用:
植树时,只要定出两个树坑的位置就 能确定同一行的树坑所在的直线。
作业:P132习题 4.2 第3、4题
练习
l
A m C B
读下列语句,并分别画出图形: (1)直线 l 经过A、B、C三点, 并且点C在点A与B之间; (2)两条线段m与n相交于点P; (3) p是直线外一点,过点p有一条 直线b与直线a相交于点Q; (4)直线 Q b a
n
p p
l 、m 、n 相交于点Q。
A
3、点A在直线l外
L
. . . . . .
A B D C
a
O
b
当堂检测
1、判断
错) (1)延长直线MN到点C (
(3)三点决定一条直线
错 ( )
错 (2)直线A与直线B交于一点M ( )
(4)无数条直线可能交于一点 (对 )
2、下图(1)中的线段可表示为 线段AB (2)中的直线可表示为 直线EF
请你把左边对图形的描述和右边相应 的图形用线连起来: 以A为端点,经过点B的射线
A B
连结A,B两点的线段
A
B
经过A,B两点的直线
A B
E
F C
练习 按下列语句画出图形:
(1)
(2)
A
l
a
(1)直线EF经过点C; (2) 点A在直线 l 外
(3) c A (4) C B D b
(3)经过点O的三条线段a、b、c;
或 线段m 或
。
直线n 。
(3)中的射线可表示为 射线HE 。
m n
A
B
E
F
E
H
3、按下列语句画出图形 (1)直线EF经过点C (2)点A在直线L外
(3)经过点O的三条线段a、b、c (4)线段AB、CD相交于点B
4、用适当的语言描述下列图
Q A D
O
C B
M
P
N
选做题:
1、如图线段AB上有两点C、 D则共有几条 线段?
点p在直线 l 外(直线 l 不经过点 p)
l
l 上(直线 l 经过 点
点O在直线
O)
一个点在一条直线上,也可以说这条直线经过这个点。
点在一条直线外,也可以说直线不经过这个点。
直线 a 和 b 相交于点O a
交点
b
当两条不同的直线有一个公共点时,我们就称这 两条直线相交,这个公共点叫做它们的交点。
线段AB 或线段a
射线 直线
A
射线AB 或射线a
直线AB 或直线a
a
B
向两方无限延伸
注意:(1)表示线段、射线、直线的时候,都要在字母前 注明“线段” “射线 ” “直线”。 (2)用两个大写字母表示直线或线段时,两个字母可以交 换位置,表示射线的两个大写字母不能交换位置,必须把端 点字母放在前面。
线段 AB(或线段BA) 线段 a
• 直线: (1)用它上面任意两点的大 写字母表示
(2)用一个小写字母表示 • 射线:用它的端点和射线方向上的另 外任意一点的两个大写字母表示 A O A a B
直线 AB(或直线BA) 直线 a
射线 OA(不能记作AO)
自学反馈(二)
1.下列给线段取名正确的是:( B ) (A)线段M (B)线段m
5.用两种方式表示图中的两条直线。
m
o
A
n
B
第一种:直线 AO,
直线 BO 第二种:直线 m ,
直线 n
探究练习:
已知线段AB,你能由线段AB 得到射线和直线吗?动手试一试
A B B A
答案
A
A
B
B
例:按下列语句画图
1、已知A 、B、 C、D四个点
(1)画直线AB
(2)画射线AC (3)连结 DC 2、线段a b相交于点O.
线 段
线段的表示方法
在我们的日常生 活中有哪些有关 “线段”形象的 例子?
a
A B
线段AB (线段BA) 或线段a b
画一画:画出线段b
射线
射段的表示方法
l
O A
在我们的日常生 活中有哪些有关 “射线”形象的 例子?
射段OA 或射段 l
画一画:画出射段OB
O
B
学一学, 议一议
怎样用数学符号表示直线、线段、射线?
