2016年上海市崇明县九年级二模数学试题

合集下载

2016年上海中考二模数学24题图文解析

因此对应的点 P 有两个（如图 6 所示）．
那么求点 D（点 P）的坐标还有更简便的方法：由勾股定理，得 AB2＝AD2＋BD2．
由 A(－1, 0)、B(0, 3)、D(1, 2m)，得 12＋32＝22＋(2m)2＋12＋(3－2m)2．
解得 m＝1，或 m＝ 1 ． 2
例
2016 年上海市虹口区中考模拟第 24 题
例
2015 年上海市奉贤区中考模拟第 24 题
如图 1，在平面直角坐标系中，抛物线 y＝－x2＋bx＋c 与 x 轴交于 A(－1, 0)、C(3, 0)两点，与 y 轴交于点 B，点 P 为 OB 上一点，过点 B 作射线 AP 的垂线，垂足为点 D，射线 BD 交 x 轴于点 E．
（1）求该抛物线的解析式；（2）联结 BC，当点 P 的坐标为 (0, 2) 时，求△EBC 的面积；
如图 1，在平面直角坐标系中，直线 AB 过点 A(3,0)、B(0,m)（m＞0），tan∠BAO＝2．（1）求直线 AB 的表达式；（2）反比例函数 y k1 的图像与直线 AB 交于第一象限内的 C、D 两点（BD＜BC），
x 当 AD＝2DB 时，求 k1 的值；
例
2016 年上海市崇明县中考模拟第 24 题
如图 1，一条抛物线的顶点为 E(－1,4)，且过点 A(－3,0)，与 y 轴交于点 C．点 D 是这条抛物线上一点，它的横坐标为 m，且－3＜m＜－1，过点 D 作 DK⊥x 轴，垂足为 K，DK 分别交线段 AE、AC 于点 G、H．
（1）求这条抛物线的解析式；（2）求证：GH＝HK；（3）当△CGH 是等腰三角形时，求 m 的值．
如图 5，一方面，当点 D 落在抛物线的对称轴上时，D(1, 2m)．

(完整)2017年4月崇明区中考数学二模试卷及答案,推荐文档

OB
∴FEBFOE
∴FEFO1分
∵EFB90，EOBO
∴FEFOEO
∴FOEO1分
∴△EFO是等边三角形∴FEB60
∴CEB601分
∴在Rt△ECB中，ECcot60BC
（2）把BE与CF的交点记为点P
由翻折得BE是CF的垂直平分线
即EPCBPC90，FPCP
∴S△△FC2SEPC，S△BFC2SBPC
1GB=GC
延长BF交CD于点H
∵GB=GC∴∠GBC=∠GCB
∵∠HCB=90°∴∠CHB+∠GBC=90°
∵∠ABC=90°∴∠CAB+∠GCB=90°
∴∠CHB=∠CAB
4
∴sin∠CHB=sin∠CAB=
5
∵∠ABC=90°∴∠ACB+∠CAB=90°，∠ABG+∠GBC=90°
∴∠CAB=∠GBA∴GA=GB
）
(A)160元；(B)180元；(C)200元；(D)220元．
5.如图，直线a与直线b交于点A，与直线c交于点B，1120，245，如果使直线
b与直线c平行，那么可将直线b绕点A逆时针旋转 ……………………………………（▲
）
(A)15；(B)30；(C)45；(D) 60．
6.如图，四边形ABCD是平行四边形，延长BA到点E，使AEAB，联结ED、EC、AC．添加一个条件，能使四边形ACDE成为菱形的是………………………………………（▲
∵CEx∴EFx，HE24xEFBCx1
∵HFEHCB90∴sinCHB
24
20
16
12
8
4
O文学艺体科普其他
九年级数学共 5 页第 2 页

崇明初三二模

崇明初三二模选择题1、下列计算中，正确的是（）A、B、C、D、2、下列方程中，一定有实数解的是（）A、B、C、D、3、对于数据：6，3，4，7，6，0，9，下列判断中正确的是（）A、这组数据的平均数是6，中位数是6B、这组数据的平均数是6，中位数是7C、这组数据的平均数是5，中位数是6D、这组数据的平均数是5，中位数是74、直线不经过（）A、第一象限B、第二象限C、第三象限D、第四象限5、下列命题中，真命题是（）A、对角线相等的四边形是等腰梯形B、两个相邻的内角相等的梯形是等腰梯形C、一组对边平行，另一组对边相等的四边形是等腰梯形D、平行于等腰三角形底边的直线截两腰所得的四边形是等腰梯形6、在直角坐标系平面内，点的坐标为，点的坐标为，圆的半径为2，下列说法不正确的是（）A、当时，点在圆上B、当时，点在圆内C、当时，点在圆外D、当时，点在圆内二、填空题7、4的平方根为8、计算：9、不等式组的整数解是10、已知函数，那么11、方程的解是12、从1，2，3，4，5，6，7，8这八个数中，任意抽取一个数，那么抽到素数的概率是13、已知关于的方程没有实数根，那么的取值范围是14 为了了解全区近3600名初三学生数学学习状况，随机抽取600名学生的测试成绩作为样本，将他们的成绩整理后分组情况如下：（每组数据含最低值，不含最高值）分组40~5050~6060~7070~8080~9090~100频数1218180频率0、160、04根据上表信息，由此样本请你估计全区此次成绩在70~80分的人数大约是15、如图，在△中，、分别在边、上，∥，，，，那么用、表示为：16、如图，在中，点为弧的中点，交弦于，如果，，那么的长为17、如图，在正六边形的上方作正方形，联结，那么的正切值为18、如图，在△中，已知，，将△绕着点逆时针旋转30，记点的对应点为点，、的延长线相交于点，如果线段的长为，那么边的长为三、解答题19、先化简，再求值：，其中、20、解方程组、21、如图，已知△中，，，、（1）求边的长；（2）将△沿直线翻折后点与点重合，直线分别与边、相交于点、，求的值、22、崇明区在创建文明城区的活动中，有两段长度相等的彩色砖路面的铺设任务，分别交给甲、乙两个施工队同时进行施工，如图是反映所铺设的彩色道砖路面的长度（米）与施工时间（时）之间关系的部分图像，请解答下列问题：（1）求乙队在的时段内，与之间的函数关系式；（2）如果甲队施工速度不变，乙队在施工6小时后，施工速度增加到12米/时，结果两队同时完成了任务，求甲队从开始施工到完工所铺设的彩色道砖路面的长度为多少米？23、如图，在直角梯形中，，对角线、相交于点，过点作，交于点、（1）联结，若，求证：∥；（2）若且，求证：、24、如图，抛物线交轴于点和点，交轴于点、（1）求抛物线的解析式；（2）在抛物线上找出点，使，求点的坐标；（3）将直线沿轴的正方向平移，平移后的直线交轴于点，交抛物线于点，当四边形为等腰梯形时，求点、的坐标、25、如图，在梯形中，∥，，，，点为边上一点，且，点是边上的一个动点（与点、点不重合），点在射线上，且，设的长为，的长为、（1）当点在线段上时，求与之间的函数关系式，并写出自变量的取值范围；（2）当以点为圆心，长为半径的与以点为圆心，长为半径的相切时，求线段的长；（3）当△为等腰三角形时，直接写出线段的长、参考答案一、选择题1、A2、 B3、 C4、 C5、 D6、 B二、填空题7、8、9、，0，110、11、12、13、14、16xx、16、317、18、三、解答题19、原式，带入得：、20、，、21、（1）；（2）；22、（1）；（2）甲队从开始施工到完工所铺设的彩色道砖路面的长度为110米、23、（1）证明略；（2）证明略、24、（1）；（2）或；（3）存在，，、25、（1）（或）；（2）2或4或6；（3）或2或、三、解答题（本大题共7题，满分78分）19、（本题满分10分）解：原式= …………………………………………………（2分）……………………………………………………………（2分）、…………………………………………………………………（2分）把代入上式，原式= ……………………………………………………………………（2分）、……………………………………………………………………（2分）20、（本题满分10分）解：由②得：…………………………………………………（2分）所以…………………………………………………（2分）…………………………………………………（2分）……………………………………（4分）21、（本题满分10分，每小题满分各5分）解：（1）过A 作AH⊥BC，垂足为H………………………………………………… (1分)∵AB=6，，AH⊥BC∴AH=3 ………………………………………………………………………(1分)∵∴CH=2…………………………………………………………………………(1分)∴ ……………………………………………………(2分)（2）由翻折得：，AE=BE，∵ ∴ ∴…………………………(1分)∴ …………………………………………………………………( 1分)∴………………………………………………………………… (1分)∴ ……………………………………………… (2分)22、（本题满分10分，每小题满分各5分）解：（1）设乙队在2≤x≤6的时段内y与x之间的函数关系式为:y =kx+b（k≠0），…………………………………………………………… (1分)由图6可知，函数图像过点（2，30）、（6，50），得：………………………………………………………… (1分)解得………………………………………………………………（2分）∴ y =5x＋20、………………………………………………………………（1分）（2）由图6可知，甲队施工速度是：606=10（米/时）、…………………………（1分）设甲队从开始到完工所铺设彩色道砖的长度为z米…………………………（1分）由题意得：………………………………………………………（2分解得：=110、…………………………………………………………（1分）答：甲队从开始到完工所铺设彩色道砖的长度为110米、23、（本题满分12分，每小题满分各6分）证明(1)∵,∴ ………………………………………………………………（1分）∴ ………………………………………………………………（2分）∵∴ ……… ………………………………………………………（2分）∴ …………………………………………………………………（1分）(2)∵，，∴四边形ABED为平行四边形又∵∴四边形ABED 为矩形……………………………………………………（1分）∴，又∵∴∴ …………………………………………………………（1分）∴ ∴…………………………………………………（1分）∴ ∴…………………………………………………………（1分）∵∴…………………………………………………………（1分）∴…………………………………………………………………（1分）24、（本题满分12分，每小题满分各4分）解：（1）∵抛物线过点A（1，0）、C（0，3）∴………………………………………………………………（2分）解得……………………………………………………………（1分）∴抛物线的解析式为………………………………………（1分）（2）过P作，垂足为H∵PO＝OC，∴CH＝OH ………………………………………………………………（1分）∴ ……………………………………………………………（1分）∴ ………………………………………………………………（1分）………………………………………………（1分）ABCOyxMNG（3）连接NA并延长交OC于G ∵四边形ACMN为等腰梯形，且AC∥MN ∴∠ANM＝∠CMN，∠ANM＝∠GAC，∠GCA＝∠CMN ∴∠GAC＝∠GCA，∴GA＝GC 设GA＝x，则GC＝x，OG＝3－x 在Rt△OGA中，OA2＋OG2＝AG2 ∴12＋(3－x )2＝x2，解得x＝∴OG＝3－x＝，∴G（0，）易得直线AG的解析式为y＝－ x＋令－ x＋＝x2－4x＋3，解得x1＝1（舍去），x2＝∴N（，－）………………………………………………………………（2分）∴CM＝AN＝＝∴OM＝OC＋CM＝3＋＝∴M （0，）…………………………………………………………………（2分）∴存在M（0，）、N（，－）使四边形ACMN为等腰梯形25、（本题满分14分，其中第(1)、(2)小题满分各4分，第(3)小题满分6分）解：（1）∵梯形ABCD中，AD∥BC，AB＝DC∴∠B＝∠C∵∠EFC=∠B＋∠BEF＝=∠EFG＋∠GF C，∠EFG＝∠B∴∠GFC＝∠FEB ……………………………………………………………（1分）∴△EBF∽△FCG ……………………………………………………………（1分）∴，∴ ………………………………………………（1分）∴ ………………………………………………………………（1分）自变量x的取值范围为：……………（1分）（2）当，都有①当⊙B与⊙C外切时， BF＋CG＝BC∴，解得x＝2或x＝12（舍去）………………………（2分）②当⊙B与⊙C内切时，CG－BF＝BC∴，解得x＝4或x＝6 ……… …… ……………………（2分）综上所述，当⊙B与⊙C相切时，线段BF的长为：2或4或6（3）当△FCG为等腰三角形时，线段BF的长为：或2或………………（6分）。

(完整版)2017年4月崇明区中考数学二模试卷及答案

九年级数学共5页第1页崇明区2016学年第二学期教学质量调研测试卷九年级数学(测试时间：100分钟，满分：150分)考生注意：1 .本试卷含三个大题，共 25题.答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效.2. 除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤.3. 考试中不能使用计算器.一、选择题(本大题共6题，每题4分，满分24分)1 .下列运算错误的是 ......................................................... (▲)3 26々弓ft 49(A) x 2x 3x; (B) (x ) x ; (C) x x x ;(D) x x x .2.一次函数y 3x 2的图像不经过下列各象限中的 ..................................... (▲)(A)第一象限；(B)第二象限；(C)第三象限；(D)第四象限.3 .在一次引体向上的测试中，小强等 5位同学引体向上的次数分别为： 6,8,9,8,9,那么关于这组数据的说法正确的是 .................................................. (▲)(A )平均数是8.5 ;(B )中位数是8.5;(C )众数是8.5;(D )众数是8和9.4 .商场将某种商品按原价的 8折出售，仍可获利20元.已知这种商品的进价为 140元，那么这种商品的原价是 .......................................................... (▲)(A )160 元；(B ) 180 元；(C )200 元；(D )220 元.5. 如图，直线a 与直线b 交于点A,与直线c 交于点B, 1 120 , 2 45 ,如果使直线b与直线c 平行，那么可将直线 b 绕点A 逆时针旋转 ................................ (▲)(A) 15 ;(B) 30 ;(C) 45 ;(D) 60 .6. 如图，四边形 ABCD 是平行四边形，延长 BA 到点E,使AE AB ,联结ED 、EC 、AC.添加一个条件，能使四边形 ACDE 成为菱形的是 ................................ (▲)(A) AB AD ;(B) AB ED;(C) CD AE ;(D) EC AD.(第6题图)1 cb. B2A(第5题图)九年级数学共5页第2页二、填空题（本大题共12题，每题4分，满分48分） 7.16的平方根是 ▲ .8. 因式分解： x 2 9x ▲. 9 .方程J2x 3 x 的解是 ▲.3X 150 .•八一 10.不等式组的解集是 ▲3x011.已知函数f （x ）亏、，那么自变量x 的取值范围是▲ .12 .已知关于x 的方程x 2 4x m 0有两个不相等的实数根，那么 m 的取值范围是▲ 213 .如果将抛物线 y 3x 5向右平移4个单位后，那么所得新抛物线的顶点坐标是 ▲14.有一枚材质均匀的正方体骰子，它的六个面上分别有1点、2点、…、6点的标记，掷一次骰子，向上的一面出现的点数是素数的概率是 ▲ .15 .某校为了开阔学生的视野，积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如图所示的两幅不完整的统计图，已知该校有名学生，估计全校最喜爱文学类图书的学生有（第15题图）16. 一商场内的一座自动扶梯所在的斜边的坡度为 i 1： 2.4 ,小明站在自动扶梯上，当他沿着斜坡向上方向前进了 13米时，他在铅垂方向升高了 A 米.1200最喜爱的各类图书的人数24 20 12 8 4文学其他16 艺体科普最喜爱的各类图书的人数占总人数的百分比17 .在Rt ABC中，B 90 , BC 3, cosA 4 ,以点A为圆心，J5为半径作圆，再以点5C为圆心，2为半径作圆，那么这两圆的位置关系是▲.九年级数学共5页第3页九年级数学共5页第4页18 .如图，已知 ABC 中， C 90 , BC 3 , AC 4,BD 平分 ABC ，将 ABC 绕着点A 旋转后，点B 、C 的对应点分别记为 B 1、C 1 ,如果点B 1落在射线BD 上,那么CG 的长度为 ▲ 三、解答题（本大题共7题，满分78分）19.（本题满分10分）122计算：273 3 11——2——2 tan 60120.（本题满分10分）22-解方程组：x 3xy 4y 0x 2y 1已知 ABC 中，AD BC ,垂足为 D,且 AD 4 ,以 AD 为直径作圆O,交AB 边于点G,交AC 边于点F,如果点 F 恰好是A D 的中点.（1）求CD 的长度；（2）当BD 3时，求BG 的长度.22. （本题满分10分）地然后立即原路返回到 B 地，如图是两人离 B 地的距离图像.请根据图像回答下列问题：（1） AB 两地的距离是 ,小明行驶的速度是; （2）若两人间的距离不超过 3千米时，能够用无线对讲机保持联系，那么小刚从A 地原路返回到B 地途中，两人能够用无线对讲机保持联系的 x 的取值范围是.23. （本题满分12分，其中每小题各 6分）如图，已知 ABC 是等边三角形，点 D 、E 分别在边BC 、AC 上，且CD CE ,联结DE 并延长至点F,使EF AE ,联结AF , CF ,联结BE 并延长交 CF 于点G .（1）求证：BC DF ;（2）若 BD 2DC ,求证：GF 2EG .21.（本题满分10分，其中每小题各 5分）在一条笔直的公路上有 AB 两地，小明骑自行车从A 地去B 地，小刚骑电动车从 B 地去 A（第18题（第21题y （千米）和行驶时间x （小时）之间的函F（第23题九年级数学共5页第5页24. (本题满分12分，其中每小题各 4分)(1) 求这条抛物线的解析式； (2) 求 tan ABC 的值； (3) 若点D 为抛物线的顶点，点当CDE 与 ABC 相似时,25. (本题满分14分，其中第 ⑴小题4分，第 ⑵小题4分，第 ⑶小题6分)如图，梯形 ABCD 中，AB II CD, ABC 90 , AB 6 , BC 8 , tanD 2,点 E 是射线CD 上一动点(不与点 C 重合)，将 BCE 沿着BE 进行翻折，点 C 的对应点记为点F .(1)如图1,当点F 落在梯形ABCD 的中位线 MN 上时，求CE 的长;(2) 如图2,当点E 在线段CD 上时，设CE x ,去巴 y ，求y 与x 之间的函数关系式，并S EFC写出定义域；如图，已知抛物线 y ax 2 AC II x 轴.2x c 经过 ABC 的三个顶点，其中点 A(0,1)，点B(9,10),E 是直线 AC 上一点,求点E 的坐标.(第24题图)(3)如图3,联结AC,线段BF与射线CA交于点G,当CBG是等腰三角形时，求CE的长.(第25题图1)(第25题图2) (第25题图3)(第25题备用图)九年级数学共5页第6页1分九年级数学共5页第7页崇明区2016学年第二学期教学质量调研测试卷九年级数学答案及评分参考2017.4、选择题：（本大题共6题，每题4分，满分24分）1. D ；2.C;3.D;4.C;5.A ;6.B二、填空题：（本大题12 题，每题4分 '，满分48分）7. 4;8. x(x 9)；9. x=3; 10. 3< xv5 ; 11.3x -； 12.mv 4 ；13. (4,5); 14. 】；2216 W17.外离；15. 480;16. 5;18.5三、解答题：（本大题共7题，满分78分）19.解：原式=3 4 2无4 扼1 .............................................................................................................. 8分AOF ADC ..................................................................................................... 1 分OF // CD ..............................................................................................OFAO 1CDAD (2)OF OA , AD 4CD 4.............................................................................................(2)过点O 作OH AG,垂足为H.在 eO 中，OH AG . . AG 2AH.• ADB 90 AD 2BD 2AB 220.解：由①得：x 4y0, xy 0 ................................................... ................. 2分x原方程组可化为x4y °, 2y 12x 1 3,x x x 2y 02y 11....................................... 2分...................... 6分 21.解：(1) Q AD BCv 1 V2y 16ADB1ADC 90•.•点F 是A D OF AD的中点，OF AOF 是半径 90................................. ................................... 1 二3、一322分分九年级数学共5页第8页BD 3, AD 4••• AB 5 ...................................................... 1分AD 4在 Rt △ ABD 中， cos BADAB 5AH AH 4 在 Rt A AOHcos BADAO 25 (8)八--AH —.............................................................................................................. 1 分 5(2) —V xV 2 .................................................................................................................... 4 分5明：(1) ...△ ABC 是等边三角形证••• AB AC BC , ABC ACB 60 QCD CE CDE 是等边三角形 CDE ABC 60 , CD DEDF // AB ............................................................................................ 2 分Q EF AE , CD DE AE EF二—— ——CE DEAF H BC .............................................................................................. 2 分四边形ABDF 是平行四边形 ... AB DF ............................................ 1分又•. AB BC••• BC DF .....................................................................................CDE 是等边三角形(2)••• CDE DCE 60 , CE CD DE 又.BC DF. . △ BCE^A FDC ........................................................................... ••• CBE DFC ................................................................................ 又.• BED FEG △ BDEs/X FGE .......................................................................................BD DEFG EG又.CD DE , BD 2CDBD GF -:. ---- ..................................................................................................................... 2 CD EG••• GF 2EG ...................................................................................... 解：(1) 抛物线y ax 2 2x c 经过点A(0,1)和点B(9,10)AG2AH16 .................................................1分—5BG16 5 — 9 ..................................................1分55(1) 30千米； 15E /时 ............................................. 各 3分22.23. 24.1分1分 1分 1分 1分1分分九年级数学共5页第9页81a 18 c 101 a —八解得 3 ........................................................................................................................... 2分c 11 2八..•N 条抛物线的解析式为 y — x 2x 1.................................................... 1分3(2)过点B 作BH AC,垂足为HQAC//X 轴，A(0,1), B(9,10)二 H (9,1)BH AH 9 又 Q BHA 90 •••△ HAB 是等腰直角三角形HAB 45........................................................................... 1 分Q AC // x 轴，A(0,1),点C 也在该抛物线上过点C 作CG AB ，垂足为点GDCK BAC.••当△ CDE 与^ ABC 相似时，存在以下两种情况:1 竺 EC .斗葺 ... EC =2 E(4,1)AB CD 9.2 3； 22AC DC . f =瓯 • EC=9 ••• E( 3,1)AB EC 9,2 EC. .CG ACgsin45 AG ACgpos45 又•.在Rt△ ABH 中,BG 9、2 3、23/2 ........................... 3 2BH - AB9.2sin 45 ..•在 Rt△ BCG 中，tan(3)过点D 作DK AC,. .......... ........... 1 2•.•点D 是抛物线y -x3••• K(3,1)CK DK 3 又. ABCCG BG垂足为K2x 1的顶点CKD 9012••- D(3, 2)......................△ CDK1等腰直角三角形25.解：(1)把BE与MN的交点记为点O••梯形ABCD 中，AB// CD , ABC 90C 90九年级数学共5页第10九年级数学共5页第11由翻折得 CEB. MN 是梯形ABCD• •MN // AB// CD-& BPC BC 2 . SZC 住). S A BFC 64• • y= ------- -----S A EFCx(3)当^ CBG 是等腰三角形时，存在以下三种情况: 1 GB=GC延长BF 交CD 于点H. • GB=GC•••/ GBC= / GCB•••/ HCB=90 ° / CHB+ / GBC=90 ° •••/ ABC=90 ° / CAB+ / GCB=90 °Z CHB= Z CAB ______4. .sin / CHB=Sin / CAB=—5 ••• Z ACB+ Z CAB=90 ° , Z ABG+ Z GBC=90 °GA=GBCEB FOE EO ，OB史1 BNFOE.FEB . FE FO-EFB 90 , EO BO . FE FO EO. △ EFO 是等边三角形. CEB 60 ........... •.•FO EO FEB 608“332)把 BE 与CF 的交点记为点 P由翻折得 BE 是CF 的垂直平分线1 FC2即 EPCBPC 90 ,FP CP• • S A EFC2S A EPC ，S Z\ BFC2S /\ BPC-S A BFCSz\ BPCS A EFC.................S z\ EPC. ECP BCP 90 , CBPBCP ECP CBP..•在 Rt△ ECB 中，EC cot 60 gBC390BPC 又.• EPC. ECPs/X CBP90FEB, EFB C 90的中位线64 -2 x(0< xV 10)•••/ ABC=90 / CAB= GA=GC ZGBA九年级数学共5页第12. AB // CD CH . CE xAB EF四1AG x, HE 6 xCH=AB=6九年级数学共5页第13HFE 90 sin CHB -^^ —HE 6 x 5即CE - 3 2° CB=CG 当CB=CG=8 时, . . AB // CD AG=10 CH AB 8=2 CG 4 AG CH=4AB=24 . CE x EF x, HE 24 x HFE HCB 90 sin CHB EF BC HEBH24 x1 ,10解得x 匝J 3 3 ° BC=BG 当BC=BG 时，F 点与G 点重合由翻折可得，BE 垂直平分线段易证 Z CBE= Z CAB 即CE8.10 8 GC •••/ ECB= Z CAB=90 °••• tan CBE tan 4 CAB -3CE 4 8 3 …日 32 解得CE=— 3… … 8 8.10 8 综上所述，CE 的长为—、 ----- -----33323。

上海市崇明县中考数学二模试卷含答案解析

上海市崇明县中考数学二模试卷一、选择题（本大题共6题，每题4分，满分24分）1．（4分）8的相反数是（）A．B．8C．D．﹣82．（4分）下列计算正确的是（）A．B．a+2a=3a C．（2a）3=2a3D．a6÷a3=a23．（4分）今年3月12日，某学校开展植树活动，某植树小组20名同学的年龄情况如下表：年龄（岁）1213141516人数14375那么这20名同龄的众数和中位数分别是（）A．15，14 B．15，15 C．16，14 D．16，154．（4分）某美术社团为练习素描，他们第一次用120元买了若干本相同的画册，第二次用240元在同一家商店买与上一次相同的画册，这次商家每本优惠4元，结果比上次多买了20本．求第一次买了多少本画册？设第一次买了x本画册，列方程正确的是（）A．B．C．D．5．（4分）下列图形中，既是轴对称图形又是中心对称图形的是（）A．等边三角形B．平行四边形C．菱形D．正五边形6．（4分）已知△ABC中，D、E分别是AB、AC边上的点，DE∥BC，点F是BC 边上一点，联结AF交DE于点G，那么下列结论中一定正确的是（）A．B．C．D．二、填空题（本大题共12题，每题4分，满分48分）7．（4分）因式分解：x2﹣9=．8．（4分）不等式组的解集是．9．（4分）函数y=的定义域是．10．（4分）方程的根是x=．11．（4分）已知袋子中的球除颜色外均相同，其中红球有3个，如果从中随机摸得1个红球的概率为，那么袋子中共有个球．12．（4分）如果关于x的方程x2+4x﹣k=0有两个相等的实数根，那么实数k的值是．13．（4分）如果将抛物线y=x2+2x﹣1 向上平移，使它经过点A（1，3），那么所得新抛物线的表达式是．14．（4分）某校组织了主题为“共建生态岛”的电子小报作品征集活动，先从中随机抽取了部分作品，按A，B，C，D 四个等级进行评分，然后根据统计结果绘制了如图两幅不完整的统计图，那么此次抽取的作品中等级为B的作品数为．15．（4分）已知梯形ABCD，AD∥BC，BC=2AD，如果，，那么=（用表示）．16．（4分）如图，正六边形ABCDEF 的顶点B、C 分别在正方形AGHI 的边AG、GH 上，如果AB=4，那么CH的长为．17．（4分）在矩形ABCD中，AB=5，BC=12，点E是边AB上一点（不与A、B重合），以点A为圆心，AE为半径作⊙A，如果⊙C与⊙A外切，那么⊙C的半径r 的取值范围是．18．（4分）如图，△ABC 中，∠BAC=90°，AB=6，AC=8，点D是BC的中点，将△ABD，将△ABD沿AD翻折得到△AED，联结CE，那么线段CE的长等于．三、解答题（本大题共7题，满分78分）19．（10分）计算： +（﹣2）2+9﹣（π﹣3.14）020．（10分）解方程组：21．（10分）已知圆O的直径AB=12，点C是圆上一点，且∠ABC=30°，点P是弦BC上一动点，过点P作PD⊥OP交圆O于点D．（1）如图1，当PD∥AB 时，求PD的长；（2）如图2，当BP平分∠OPD时，求PC的长．22．（10分）温度通常有两种表示方法：华氏度（单位：°F）与摄氏度（单位：℃），已知华氏度数y 与摄氏度数x 之间是一次函数关系，下表列出了部分华氏度与摄氏度之间的对应关系：摄氏度数x （℃）…0…35…100…华氏度数y （℉）…32…95…212…（1）选用表格中给出的数据，求y关于x的函数解析式；（2）有一种温度计上有两个刻度，即测量某一温度时左边是摄氏度，右边是华氏度，那么在多少摄氏度时，温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56？23．（12分）如图，AM 是△ABC的中线，点D是线段AM上一点（不与点A 重合）．DE∥AB交BC 于点K，CE∥AM，联结AE．（1）求证：；（2）求证：BD=AE．24．（12分）已知抛物线经过点A（0，3）、B（4，1）、C（3，0）．（1）求抛物线的解析式；（2）联结AC、BC、AB，求∠BAC的正切值；（3）点P是该抛物线上一点，且在第一象限内，过点P作PG⊥AP交y轴于点G，当点G在点A 的上方，且△APG与△ABC相似时，求点P的坐标．25．（14分）如图，已知△ABC 中，AB=8，BC=10，AC=12，D是AC边上一点，且AB2=AD•AC，联结BD，点E、F分别是BC、AC上两点（点E不与B、C重合），∠AEF=∠C，AE与BD相交于点G．（1）求证：BD平分∠ABC；（2）设BE=x，CF=y，求y与x 之间的函数关系式；（3）联结FG，当△GEF 是等腰三角形时，求BE的长度．上海市崇明县中考数学二模试卷参考答案与试题解析一、选择题（本大题共6题，每题4分，满分24分）1．（4分）8的相反数是（）A．B．8 C．D．﹣8【解答】解：8的相反数是﹣8，故选：D．2．（4分）下列计算正确的是（）A．B．a+2a=3a C．（2a）3=2a3D．a6÷a3=a2【解答】解：A、+，无法计算，故此选项错误；B、a+2a=3a，正确；C、（2a）3=8a3，故此选项错误；D、a6÷a3=a3，故此选项错误；故选：B．3．（4分）今年3月12日，某学校开展植树活动，某植树小组20名同学的年龄情况如下表：年龄（岁）1213141516人数14375那么这20名同龄的众数和中位数分别是（）A．15，14 B．15，15 C．16，14 D．16，15【解答】解：由于15岁出现次数最多，所以众数为15岁，中位数为第10、11个数据的平均数，所以中位数为=15（岁），4．（4分）某美术社团为练习素描，他们第一次用120元买了若干本相同的画册，第二次用240元在同一家商店买与上一次相同的画册，这次商家每本优惠4元，结果比上次多买了20本．求第一次买了多少本画册？设第一次买了x本画册，列方程正确的是（）A．B．C．D．【解答】解：设第一次买了x本画册，根据题意可得：，故选：A．5．（4分）下列图形中，既是轴对称图形又是中心对称图形的是（）A．等边三角形B．平行四边形C．菱形D．正五边形【解答】解：A、等边三角形不是中心对称图形，是轴对称图形，故本选项错误；B、平行四边形是中心对称图形，不是轴对称图形，故本选项错误；C、菱形是中心对称图形，也是轴对称图形，故本选项正确；D、正五边形是轴对称图形，不是中心对称图形，故本选项错误．故选：C．6．（4分）已知△ABC中，D、E分别是AB、AC边上的点，DE∥BC，点F是BC 边上一点，联结AF交DE于点G，那么下列结论中一定正确的是（）A．B．C．D．【解答】解：∵DE∥BC，∴△ADG∽△ABF，△AEG∽△ACF，∴=，∴，二、填空题（本大题共12题，每题4分，满分48分）7．（4分）因式分解：x2﹣9=（x+3）（x﹣3）．【解答】解：原式=（x+3）（x﹣3），故答案为：（x+3）（x﹣3）．8．（4分）不等式组的解集是﹣3＜x＜1．【解答】解：，解不等式①得：x＜1，解不等式②得：x＞﹣3，所以不等式组的解集是﹣3＜x＜1．故答案为：﹣3＜x＜1．9．（4分）函数y=的定义域是x≠2．【解答】解：根据题意得：x﹣2≠0解得：x≠2，故答案为：x≠2．10．（4分）方程的根是x=8．【解答】解：方程两边平方得：x+1=9，解得：x=8，经检验：x=8是方程的解．故答案是：8．11．（4分）已知袋子中的球除颜色外均相同，其中红球有3个，如果从中随机摸得1个红球的概率为，那么袋子中共有24个球．【解答】解：设袋子中共有x个球，∵红球有3个，从中随机摸得1个红球的概率为，∴=，解得：x=24（个）．故答案为：24．12．（4分）如果关于x的方程x2+4x﹣k=0有两个相等的实数根，那么实数k的值是﹣4．【解答】解：∵关于x的方程x2+4x﹣k=0有两个相等的实数根，∴△=0，即42﹣4（﹣k）=0，解得k=﹣4，故答案为：﹣4．13．（4分）如果将抛物线y=x2+2x﹣1 向上平移，使它经过点A（1，3），那么所得新抛物线的表达式是y=x2+2x．【解答】解：∵将抛物线y=x2+2x﹣1 向上平移，使它经过点A（1，3），∴平移后的解析式为：y=x2+2x﹣1+h，则3=1+2﹣1+h，解得：h=1，故所得新抛物线的表达式是：y=x2+2x．故答案为：y=x2+2x．14．（4分）某校组织了主题为“共建生态岛”的电子小报作品征集活动，先从中随机抽取了部分作品，按A，B，C，D 四个等级进行评分，然后根据统计结果绘制了如图两幅不完整的统计图，那么此次抽取的作品中等级为B的作品数为48．【解答】解：∵30÷25%=120（份），∴一共抽取了120份作品，∴此次抽取的作品中等级为B的作品数120﹣36﹣30﹣6=48份，故答案为：48．15．（4分）已知梯形ABCD，AD∥BC，BC=2AD，如果，，那么=﹣（用表示）．【解答】解：∵=，=，∴=﹣=﹣，∵AD∥BC，BC=2AD，∴==（﹣）=﹣．故答案为：﹣．16．（4分）如图，正六边形ABCDEF 的顶点B、C 分别在正方形AGHI 的边AG、GH 上，如果AB=4，那么CH的长为．【解答】解：正六边形的内角的度数==120°，则∠CBG=180°﹣120°=60°，∴∠BCG=30°，∴BG=BC=2，CG=BC=2，∴AG=AB+BG=6，∵四边形AGHI是正方形，∴GH=AG=6，∴CH=HG﹣CG=6﹣2，故答案为：6﹣2．17．（4分）在矩形ABCD中，AB=5，BC=12，点E是边AB上一点（不与A、B重合），以点A为圆心，AE为半径作⊙A，如果⊙C与⊙A外切，那么⊙C的半径r 的取值范围是8＜r＜13．【解答】解：∵四边形ABCD为矩形，∴∠B=90°，AD=BC=12，在Rt△ABC中，AC==13，∵以点A为圆心，AE为半径作⊙A，如果⊙C与⊙A外切，可得：⊙C的半径r的取值范围是8＜r＜13．故答案为：8＜r＜1318．（4分）如图，△ABC 中，∠BAC=90°，AB=6，AC=8，点D是BC的中点，将△ABD，将△ABD沿AD翻折得到△AED，联结CE，那么线段CE的长等于．【解答】解：如图连接BE交AD于O，作AH⊥BC于H．在Rt△ABC中，∵AC=8，AB=6，∴BC==10，∵CD=DB，∴AD=DC=DB=5，∵BC•AH=AB•AC，∴AH=，∵AE=AB，∴点A在BE的垂直平分线上．∵DE=DB=DC，∴点D在BE使得垂直平分线上，△BCE是直角三角形，∴AD垂直平分线段BE，∵AD•BO=BD•AH，∴OB=，∴BE=2OB=，在Rt△BCE中，EC===，故答案为三、解答题（本大题共7题，满分78分）19．（10分）计算： +（﹣2）2+9﹣（π﹣3.14）0【解答】解：原式=3+7﹣4+3﹣1=9﹣．20．（10分）解方程组：【解答】解：由①得：x+3y=0或x﹣3y=0③，由②得：x﹣y=2或x﹣y=﹣2④，由③和④组成方程组，，，，解得：，，，，所以原方程组的解为：，，，．21．（10分）已知圆O的直径AB=12，点C是圆上一点，且∠ABC=30°，点P是弦BC上一动点，过点P作PD⊥OP交圆O于点D．（1）如图1，当PD∥AB 时，求PD的长；（2）如图2，当BP平分∠OPD时，求PC的长．【解答】解：如图1，联结OD∵直径AB=12∴OB=OD=6∵PD⊥OP∴∠DPO=90°∵PD∥AB∴∠DPO+∠POB=180°∴∠POB=90°又∵∠ABC=30°，OB=6∴∵在Rt△POD 中，PO2+PD2=OD2∴∴（2）如图2，过点O 作OH⊥BC，垂足为H ∵OH⊥BC∴∠OHB=∠OHP=90°∵∠ABC=30°，OB=6∴，∵在⊙O 中，OH⊥BC∴∵BP 平分∠OPD∴∴PH=OH•co t45°=3∴．22．（10分）温度通常有两种表示方法：华氏度（单位：°F）与摄氏度（单位：℃），已知华氏度数y 与摄氏度数x 之间是一次函数关系，下表列出了部分华氏度与摄氏度之间的对应关系：摄氏度数x （℃）…0…35…100…华氏度数y （℉）…32…95…212…（1）选用表格中给出的数据，求y关于x的函数解析式；（2）有一种温度计上有两个刻度，即测量某一温度时左边是摄氏度，右边是华氏度，那么在多少摄氏度时，温度计上右边华氏度的刻度正好比左边摄氏度的刻度大56？【解答】（1）解：设y=kx+b（k≠0）把x=0，y=32；x=35，y=95 代入y=kx+b，得，解得∴y 关于x 的函数解析式为（2）由题意得：解得x=30∴在30摄氏度时，温度计右边华氏度的刻度正好比左边摄氏度的刻度大56．23．（12分）如图，AM 是△ABC的中线，点D是线段AM上一点（不与点A 重合）．DE∥AB交BC 于点K，CE∥AM，联结AE．（1）求证：；（2）求证：BD=AE．【解答】证明：（1）∵DE∥AB，∴∠ABC=∠EKC．∵CE∥AM，∴∠AMB=∠ECK，∴△ABM∽△EKC，∴=．∵AM是△ABC的中线，∴BM=CM，∴．（2）证明：∵CE∥AM，∴△KDM∽△KEC，∴=，∴，又∵，∴DE=AB．又∵DE∥AB，∴四边形ABDE是平行四边形，∴BD=AE．24．（12分）已知抛物线经过点A（0，3）、B（4，1）、C（3，0）．（1）求抛物线的解析式；（2）联结AC、BC、AB，求∠BAC的正切值；（3）点P是该抛物线上一点，且在第一象限内，过点P作PG⊥AP交y轴于点G，当点G在点A 的上方，且△APG与△ABC相似时，求点P的坐标．【解答】解：（1）设所求二次函数的解析式为y=ax2+bx+c（a≠0），将A（0，3）、B（4，1），C（3，0）代入，得：，解得：，所以，这个二次函数的解析式为：；（2）∵A（0，3、B（4，1）、C（3，0 ）∴AC=3，BC=，AB=2，∴AC2+BC2=AB2∴∠ACB=90°，∴；（3）过点P作PH⊥y轴，垂足为H设P则H∵A（0，3）∴，PH=x，∵∠ACB=∠APG=90°∴当△APG与△ABC相似时，存在以下两种可能：①∠PAG=∠CAB则tan∠PAG=tan∠CAB=，即∴，解得：x=11，∴点P 的坐标为（11，36）；②∠PAG=∠ABC则tan∠PAG=tan∠ABC=3即∴解得：x=，∴点P 的坐标为，综上所述：点P 的坐标为或（11，36）．25．（14分）如图，已知△ABC 中，AB=8，BC=10，AC=12，D是AC边上一点，且AB2=AD•AC，联结BD，点E、F分别是BC、AC上两点（点E不与B、C重合），∠AEF=∠C，AE与BD相交于点G．（1）求证：BD平分∠ABC；（2）设BE=x，CF=y，求y与x 之间的函数关系式；（3）联结FG，当△GEF 是等腰三角形时，求BE的长度．【解答】解：（1）∵AB=8，AC=12，又∵AB2=AD•AC，∴，∴，∵AB2=AD•AC，∴，又∵∠BAC是公共角，∴△ADB∽△ABC，∴∠ABD=∠C，，∴，∴BD=CD，∴∠DBC=∠C，∴∠ABD=∠DBC，∴BD平分∠ABC；（2）如图，过点A作AH∥BC，交BD的延长线于点H，∵AH∥BC，∴，∵，AH=8，∴，∴BH=12，∵AH∥BC，∴，∴，∴，∵∠BEF=∠C+∠EFC，∴∠BEA+∠AEF=∠C+∠EFC，∵∠AEF=∠C，∴∠BEA=∠EFC，又∵∠DBC=∠C，∴△BEG∽△CFE，∴，∴，∴；（3）当△GEF是等腰三角形时，存在以下三种情况：1°若GE=GF，则∠GEF=∠GFE=∠C=∠DBC，∴△GEF∽△DBC，∵BC=10，DB=DC=，∴==，又∵△BEG∽△CFE，∴，即，又∵，∴x=BE=4；2°若EG=EF，则△BEG与△CFE全等，∴BE=CF，即x=y，又∵，∴x=；3°若FG=FE，则同理可得==，由△BEG∽△CFE，可得，即，又∵，∴x=．。

2016年上海中考二模数学18题图文解析

如图1，在Rt△ABC中，∠ABC＝90°，AB＝BC＝2，将△ABC绕点C逆时针旋转60°，得到△MNC，联结BM，那么BM的长是___________．图1动感体验请打开几何画板文件名“16崇明18”，拖动点M绕点C逆时针旋转，可以体验到，当旋转60°时，AC就是等腰直角三角形ABC和等边三角形ACM的公共边，BM是两个三角形AC边上的高的和．答案如图2，在等腰Rt△ABC中，AB＝BC＝2，高BH在等边三角形AMC中，AC MH．图2如图1，在△ABC 中，∠B ＝45°，∠C ＝30°，AC ＝2，点D 在BC 上，将△ACD 沿直线AD 翻折后，点C 落在点E 处，边AE 交边BC 于点F ，如果DE //AB ，那么CF BF的值是______．图1动感体验请打开几何画板文件名“16奉贤18”，拖动点D 在BC 上运动，可以体验到，当DE //AB 时，△ACF 是顶角为30°的等腰三角形．答案1．思路如下：如图2，作AH ⊥BC 于H ．在Rt △ACH 中，∠C ＝30°，AC ＝2，所以AH ＝1，CH ．在Rt △ABH 中，∠B ＝45°，所以BH ＝AH ＝1．所以BC 1．如图3，当DE //AB 时，∠BAE ＝∠AED ＝∠C ＝30°．此时∠AFC ＝∠B ＋∠BAE ＝75°．在△ACF 中，∠C ＝30°，∠AFC ＝75°，所以∠F AC ＝75°．所以CF ＝CA ＝2．所以BF ＝BC －CF 12-1．所以1CF BF ==．另解：也可以根据△BAF ∽△BCA 先求得BF 的长．由BA 2＝BF ·BA ，得21)BF =⋅．所以1BF =．图2 图3如图1，已知△ABC中，AB＝AC＝5，BC＝6，将△ABC沿射线BC方向平移m个单位得到△DEF，顶点A、B、C分别与D、E、F对应，若以点A、D、E为顶点的三角形是等腰三角形，且AE为腰，则m的值是__________．图1动感体验请打开几何画板文件名“16虹口18”，拖动点E在射线BC上运动，可以体验到，以AE为腰的等腰三角形ADE有两个．答案6或256．思路如下：如图2，四边形ABED保持平行四边形，AM＝EN＝4，BM＝DN＝3，AD＝BE＝m．①如图3，当EA＝ED时，点E在AD的垂直平分线上，此时AD＝2ND＝6．②如图4，当AE＝AD时，根据AE2＝AD2，得m2＝42＋(m－3)2．解得256m ．图2 图3 图4如图1，在Rt△ABC中，∠BAC＝90°，将△ABC绕点C逆时针旋转，旋转后的图形是△A′B′C，点A的对应点A′落在中线AD上，且点A′是△ABC的重心，A′B′与BC相交于点E，那么BE∶CE＝___________．图1动感体验请打开几何画板文件名“16黄浦18”，拖动点A可以改变直角三角形ABC的形状，可以体验到，当点A′落在△ABC的重心时，AD//B′C．答案4∶3．思路如下：根据旋转前后的对应边相等，对应角相等，可知∠ACB＝∠A′CB′，CA＝CA′．所以∠CAA′＝∠CA′A．又因为直角三角形斜边上的中线等于斜边的一半，所以DA＝DC．所以∠CAA′＝∠ACB．所以∠A′CB′＝∠CA′A．所以AD// B′C．根据重心的性质，可得1'3DA DA=．又因为12DA CB=，所以1'6DA CB=．所以'1'6DE DACE CB==．所以71847163BECE+===-．图2如图1，点D 在边长为6的等边三角形ABC 的边AC 上，且AD ＝2，将△ABC 绕点C 顺时针方向旋转60°，若此时点A 和点D 的对应点分别记为点E 和点F ，联结BF 交边AC 于点G ，那么tan ∠AEG ＝__________．图1动感体验请打开几何画板文件名“16嘉定宝山18”，拖动点E 绕点C 顺时针旋转60°，可以体验到，四边形ABCE 是菱形，ME ∶BC ＝1∶2，从而得到AG ∶CG ＝3∶2．这样在△AEG 中，就已知了∠A 及夹∠A 的两边，构造AE 边上的高就可以解△AEG 了．答案 7．思路如下：如图2，将△ABC 绕点C 顺时针方向旋转60°，得到菱形ABCE ．延长AE 交BF 的延长线于M ．因为12ME EF BC CF ==，所以32AG MA CG BC ==．设菱形的边长为10m ，那么AG ＝6m ．如图3，作GH ⊥AE 于H ．在Rt △AGH 中，∠GAH ＝60°，所以AH ＝12AG ＝3m ，GH ＝．在Rt △EGH 中，EH ＝AE －AH ＝7m ，所以tan ∠AEG ＝GH EH ==图2 图3如图1，在△ABC 中，AB ＝AC ＝4，cos C ＝14，BD 是中线，将△CBD 沿直线BD 翻折，点C 落在点E ，那么AE 的长为_______．图1 动感体验请打开几何画板文件名“16静安青浦18”，可以体验到，四边形BCDE 是菱形，四边形AEBD 是平行四边形，AE ＝BD ．答案如图2，作AM 作BC 于M ，DN ⊥BC 于N ．在Rt △ACM 中，AC ＝4，cos C ＝14，所以CM ＝1．所以BC ＝2CM ＝2．已知D 是AC 的中点，所以BC ＝DC ＝2．如图3，由BE ＝BC ，BC ＝DC ，DC ＝DA ，得BE ＝DA ．由∠1＝∠2，∠1＝∠3，得∠2＝∠3．所以EB //AC ．所以四边形AEBD 是平行四边形．所以AE ＝BD ．如图2，在Rt △DCN 中，DC ＝2，CN ＝12，所以DN在Rt △DBN 中，BN ＝32，所以BD AE ．图2 图3如图1，已知在△ABC中，AB＝AC，tan∠B＝13，将△ABC翻折，使点C与点A重合，折痕DE交边BC于点D，交边AC于点E，那么BDDC的值为_________．图1动感体验请打开几何画板文件名“16闵行18”，拖动点C绕着对称轴DE旋转到点A，可以体验到，DE垂直平分AC，DC＝DA．答案135．思路如下：如图2，作AH⊥BC于H，那么BH＝CH．已知tan∠B＝AHBH＝13，设AH＝1，BH＝3．设DC＝DA＝m．在Rt△ADH中，由勾股定理，得m2＝12＋(3－m)2．解得53m=．所以BD＝BC－DC＝563-＝133．所以135BDDC=．图2如图1，在矩形ABCD中，将矩形折叠，使点B落在边AD上，这时折痕与边AD和边BC分别交于点E、F．然后再展开铺平，以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”．如图2，在矩形ABCD中，AB＝2，BC＝4，当“折痕△BEF”的面积最大时，点E的坐标是___________．图1 图2动感体验请打开几何画板文件名“16普陀18”，拖动点G在AD上运动，可以体验到，△BEF 的高AB保持不变，当点与点D重合时，BF最大，△BEF的面积也最大（如图3，图4所示）．答案3(,2)2．思路如下：设菱形BFGD的边长为m．如图4，当G、D重合时，在Rt△ABE中，AB＝2，BE＝m，AE＝4－m．由勾股定理，得m2＝22＋(4－m)2．解得m＝52．此时AE＝4－m＝32，点E的坐标为3(,2)2．图3 图4如图1，在梯形ABCD中，AD//BC，∠B＝90°，AD＝2，BC＝5，E是AB上一点，将△BCE沿着直线CE翻折，点B恰好与点D重合，则BE＝________．图1动感体验请打开几何画板文件名“16松江18”，拖动点E可以改变梯形的上底AD的长，可以体验到，当AD＝2时，直角三角形CDH的三边长为3、4、5．答案52．思路如下：如图2，过点C作AD的垂线，垂足为H．在Rt△CDH中，DC＝BC＝5，DH＝AH－AD＝3，所以HC＝AB＝4．设BE＝DE＝m．在Rt△ADE中，由勾股定理，得m2＝(4－m)2＋22．解得52m ．图2如图1，在△ABC中，∠CAB＝90°，AB＝6，AC＝4，CD是△ABC的中线，将△ABC 沿直线CD翻折，点B′是点B的对应点，点E是线段CD上的点，如果∠CAE＝∠BAB′，那么CE的长是__________．图1动感体验请打开几何画板文件名“16徐汇18”，可以体验到，AE// B′B，AE⊥CD，AE是直角三角形ACD的斜边上的高．答案165．思路如下：如图2，由DA＝DB＝DB′，可知∠AB′B＝90°．由∠CAE＝∠BAB′，∠CAB＝90°，可得∠EAB′＝90°．所以AE//B′B．如图3，在等腰三角形CB′B中，根据三线合一，可知CD⊥B′B．所以AE⊥CD．如图4，在Rt△ACD中，AC＝4，AD＝3，所以CD＝5，cos∠ACD＝45．在Rt△ACE中，CE＝AC·cos∠ACD＝4164=55 ．图2 图3 图4如图1，将平行四边形ABCD 绕点A 旋转到平行四边形AEFG 的位置，其中点B 、C 、D 分别落在点E 、F 、G 处，且点B 、E 、D 、F 在一条直线上．如果点E 恰好是对角线BD的中点，那么ABAD的值是___________．图1动感体验请打开几何画板文件名“16杨浦18”，拖动点B 可以改变平行四边形ABCD 的形状，可以体验到，四边形ECFG 保持平行四边形的形状，当B 、E 、D 、F 四点在一条直线上时，D 是平行四边形ECFG 的对角线的交点，此时△GAD ∽△GCA ．答案 2．思路如下：如图2，旋转前后，AB 与AE 是对应线段，点E 是平行四边形ABCD 的对角线的交点，所以AC ＝2AE ＝2AB ．因为AE 与GF 平行且相等，AE ＝EC ，所以EC 与GF 平行且相等．所以四边形ECFG 保持平行四边形的形状．如图3，当B 、E 、D 、F 四点在一条直线上时，平行四边形ECFG 的对角线交于点D ．设AB ＝m ，AD ＝n ．由△GAD ∽△GCA ，得GA 2＝GD ·GC ．所以n 2＝2m 2．解得m n图2 图3如图1，底角为α的等腰三角形ABC 绕着点B 顺时针旋转，使得点A 与BC 边上的点D重合，点C 与点E 重合，联结AD 、CE ，已知tan α＝34，AB ＝5，则CE ＝_________．图1动感体验请打开几何画板文件名“16闸北18”，拖动点E 绕点B 旋转，可以体验到，当点D 落在BC 上时，△BAD ∽△BCE ．答案如图2，作AH ⊥BC 于H ，那么BH ＝CH ．在Rt △ABH 中，tan ∠B ＝34，AB ＝5，由此可得AH ＝3，BH ＝4．所以BC ＝8．在Rt △ADH 中，DH ＝BD －BH ＝5－4＝1，所以AD =如图3，由△BAD ∽△BCE ，得AD BA CE BC =58=．所以CE =图2 图3例 2016年上海市长宁区金山区中考模拟第18题如图1，在△ABC中，AB＝AC＝5，BC＝8，将△ABC绕着点B旋转得到△A′BC′，点A 的对应点A′落在BC边上，那么点C和点C′之间的距离等于________．图1动感体验请打开几何画板文件名“16长宁金山18”，拖动点C′绕点B旋转，可以体验到，当点A′落在BC上时，C′F是Rt△BC′F和Rt△CC′F的公共直角边．答案如图2，作AH⊥BC于H，那么BH＝CH．在Rt△ABH中，AB＝5，BH＝4，所以AH＝3，sin∠B＝35．如图3，在Rt△BC′F中，sin∠C′BF＝35，BE＝8，由此可得C′F＝245，325BF=．在Rt△CC′F中，328855CF=-=，由勾股定理，得C′C2＝C′F2＋CF2．所以C′C==图2 图3。

上海市2016年二模数学第24题汇编

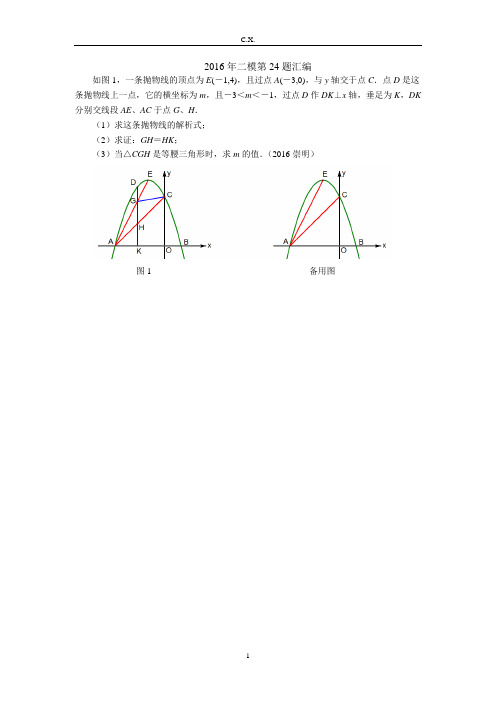
2016年二模第24题汇编如图1，一条抛物线的顶点为E(－1,4)，且过点A(－3,0)，与y轴交于点C．点D是这条抛物线上一点，它的横坐标为m，且－3＜m＜－1，过点D作DK⊥x轴，垂足为K，DK 分别交线段AE、AC于点G、H．（1）求这条抛物线的解析式；（2）求证：GH＝HK；（3）当△CGH是等腰三角形时，求m的值．（2016崇明）图1 备用图如图1，在平面直角坐标系中，抛物线y＝－x2＋bx＋c与x轴交于A(－1, 0)、C(3, 0)两点，与y轴交于点B，点P为OB上一点，过点B作射线AP的垂线，垂足为点D，射线BD 交x轴于点E．（1）求该抛物线的解析式；（2）联结BC，当点P的坐标为2(0,)3时，求△EBC的面积；（3）当点D落在抛物线的对称轴上时，求点P的坐标．（2016奉贤）图1 备用图如图1，在平面直角坐标系中，直线AB 过点A (3,0)、B (0,m )（m ＞0），tan ∠BAO ＝2．（1）求直线AB 的表达式；（2）反比例函数1k y x=的图像与直线AB 交于第一象限内的C 、D 两点（BD ＜BC ），当AD ＝2DB 时，求k 1的值；（3）设线段AB 的中点为E ，过点E 作x 轴的垂线，垂足为点M ，交反比例函数2k y x=的图像于点F ，联结OE 、OF ，当△OEF 与△OBE 相似时，请直接写出满足条件的所有k 2的值．（2016虹口）图1如图1，在直角坐标系中，抛物线y＝ax2＋bx＋c与x轴交于A(1, 0)、B(4, 0)两点，与y 轴交于点C(0, 2)．（1）求抛物线的表达式；（2）求证：∠CAO＝∠BCO；（3）若点P是抛物线上的一点，且∠PCB＋∠ACB＝∠BCO，求直线CP的表达式．（2016黄浦）图1如图1，在平面直角坐标系中，经过点A(－1,0)的抛物线y＝－x2＋bx＋3与y轴交于点C，点B与点A，点D与点C分别关于抛物线的对称轴对称．（1）求b的值以及直线AD与x轴正方向的夹角；（2）如果点E是抛物线上的一个动点，过点E作EF平行x轴交直线AD于点F，且F 在E的右边．过点E作EG⊥AD于点G，设点E的横坐标为m，△EFG的周长为l，试用m 表示l；（3）点M是该抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，如果以A、M、P、Q为顶点的四边形是矩形，求该矩形的顶点Q的坐标．（2016嘉定宝山）图1如图1，在平面直角坐标系中，抛物线y＝ax2＋bx－1经过点A(2,－1)，它的对称轴与x 轴相交于点B．（1）求点B的坐标；（2）如果直线y＝x＋1与此抛物线的对称轴交于点C，与此抛物线在对称轴右侧交于点D，且∠BDC＝∠ACB，求此抛物线的表达式．（2016静安青浦）如图1，已知在平面直角坐标系中，抛物线y＝ax2＋2x＋c与x轴交于点A(－1,0)和点B，与y轴交于点C(0, 3)，抛物线的对称轴为直线l．（1）求这条抛物线的关系式，并写出其对称轴和顶点M的坐标；（2）如果直线y＝kx＋b经过C、M两点，且与x轴交于点D，点C关于直线l的对称点为N，试证明四边形CDAN是平行四边形；（3）点P在直线l上，且以点P为圆心的圆经过A、B两点，并且与直线CD相切，求点P的坐标．（2016闵行）图1如图1，在平面直角坐标系中，二次函数213y x bx c =++的图像与y 轴交于点A ，与双曲线8y x=有一个公共点B ，它的横坐标为4．过点B 作直线l //x 轴，与二次函数图像交于另一点C ，直线AC 的截距是－6．（1）求二次函数的解析式；（2）求直线AC 的表达式；（3）平面内是否存在点D ，使A 、B 、C 、D 为顶点的四边形是等腰梯形，如果存在，求出点D 的坐标；如果不存在，请说明理由．（2016普陀）如图1，平面直角坐标系中，已知B(－1, 0)，一次函数y＝－x＋5的图像与x轴、y轴分别交于A、C两点．二次函数y＝－x2＋bx＋c的图像经过A、B两点．（1）求这个二次函数的解析式；（2）点P是该二次函数图像的顶点，求△APC的面积；（3）如果点Q在线段AC上，且△ABC与△AOQ相似，求点Q的坐标．（2016松江）图1如图1，直线y＝mx＋4与反比例函数kyx（k＞0）的图像交于A、B两点，与x轴、y轴分别交于D、C，tan∠CDO＝2，AC∶CD＝1∶2．（1）求反比例函数的解析式；（2）联结BO，求∠DBO的正切值；（3）点M在直线x＝－1上，点N在反比例函数的图像上，如果以点A、B、M、N为顶点的四边形是平行四边形，求点N的坐标．（2016徐汇）如图1，已知在直角坐标系中，抛物线y＝ax2－8ax＋3（a＜0）与y轴交于点A，顶点为D，其对称轴交x轴于点B，点P在抛物线上，且位于抛物线对称轴的右侧．（1）当AB＝BD时，求抛物线的表达式；（2）在（1）的条件下，当DP//AB时，求点P的坐标；（3）点G在对称轴BD上，且∠AGB＝12∠ABD，求△ABG的面积．（2016杨浦）图1 备用图如图1，矩形OMPN的顶点O在原点，M、N分别在x轴和y轴的正半轴上，OM＝6，ON＝3，反比例函数6yx的图像与PN交于点C，与PM交于点D，过点C作CA⊥x轴于点A，过点D作DB⊥y轴于点B，AC与BD交于点G．（1）求证：AB//CD；（2）在直角坐标平面内是否存在点E，使以B、C、D、E为顶点，BC为腰的梯形是等腰梯形？若存在，求点E的坐标；若不存在，请说明理由．（2016闸北）如图1，在平面直角坐标系中，抛物线y＝x2＋bx＋c与x轴交于A、B两点，已知点A 的坐标为(1,0)，与y轴相交于点C(0,3)，抛物线的顶点为P．（1）求这条抛物线的解析式，并写出顶点P的坐标；（2）如果点D在此抛物线上，DF⊥x轴于点F，DF与直线PB相交于点E，设点D的横坐标为t（t＞3），且DE∶EF＝2∶1，求点D的坐标；（3）在第（2）题的条件下，求证：∠DPE＝∠BDE．（2016长宁金山）图1。