对正弦信号的采样频谱分析
实验二的应用FFT对信号进行频谱分析

实验二的应用FFT对信号进行频谱分析引言:频谱分析是通过将连续信号转换为离散信号,根据信号在频域上的强度分布来分析信号的频谱特性。
其中,FFT(Fast Fourier Transform,快速傅里叶变换)是一种常见的频谱分析算法,可以高效地计算离散信号的傅里叶变换。
实验目的:本实验旨在使用FFT算法来对一个信号进行频谱分析,从而了解FFT 的原理和应用。
实验器材:-计算机-MATLAB软件实验步骤:1.准备信号数据:首先,需要准备一个信号数据用于进行频谱分析。
可以通过MATLAB 自带的函数生成一个简单的信号数据,例如生成一个正弦信号:```Fs=1000;%采样频率T=1/Fs;%采样时间间隔L=1000;%信号长度t=(0:L-1)*T;%时间向量S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 生成信号,包含50Hz和120Hz的正弦波成分```其中,Fs为采样频率,T为采样时间间隔,L为信号长度,t为时间向量,S为生成的信号数据。
2.进行FFT计算:利用MATLAB提供的fft函数,对准备好的信号数据进行FFT计算,得到信号的频谱:```Y = fft(S); % 对信号数据进行FFT计算P2 = abs(Y/L); % 取FFT结果的模值,并归一化P1=P2(1:L/2+1);%取模值前一半P1(2:end-1) = 2*P1(2:end-1); % 对非直流分量进行倍频处理f=Fs*(0:(L/2))/L;%计算对应的频率```其中,Y为FFT计算的结果,P2为对应结果的模值,并进行归一化处理,P1为P2的前一半,f为对应的频率。
3.绘制频谱图:使用MATLAB的plot函数,将频率和对应的功率谱绘制成频谱图:```plot(f,P1)title('Single-Sided Amplitude Spectrum of S(t)')xlabel('f (Hz)')ylabel(',P1(f),')```实验结果与分析:上述实验步骤通过MATLAB实现了对一个信号的频谱分析并绘制成频谱图。
用FFT对信号作频谱分析

用FFT对信号作频谱分析快速傅立叶变换(FFT)是一种在信号处理中常用于频谱分析的方法。
它是傅立叶变换的一种快速算法,通过将信号从时间域转换到频域,可以提取信号的频率信息。
FFT算法的原理是将信号分解为不同频率的正弦波成分,并计算每个频率成分的幅度和相位。
具体而言,FFT将信号划分为一系列时间窗口,每个窗口内的信号被认为是一个周期性信号,然后对每个窗口内的信号进行傅立叶变换。
使用FFT进行频谱分析可以得到信号的频率分布情况。
频谱可以显示信号中各个频率成分的强度。
通过分析频谱可以识别信号中的主要频率成分,判断信号中是否存在特定频率的干扰或噪声。
常见的应用包括音频信号处理、图像处理、通信系统中的滤波和解调等。
使用FFT进行频谱分析的步骤如下:1.首先,获取待分析的信号,并确保信号是离散的,即采样频率与信号中的最高频率成分满足奈奎斯特采样定理。
2.对信号进行预处理,包括去除直流分量和任何不需要的干扰信号。
3.对信号进行分段,分段后的每个窗口长度在FFT算法中通常为2的幂次方。
常见的窗口函数包括矩形窗、汉明窗等。
4.对每个窗口内的信号应用FFT算法,将信号从时间域转换到频域,并计算每个频率成分的幅度和相位。
5.对所有窗口得到的频谱进行平均处理,以得到最终的频谱分布。
在使用FFT进行频谱分析时需要注意的问题有:1.噪声的影响:FFT对噪声敏感,噪声会引入幅度偏差和频率漂移。
可以通过加窗等方法来减小噪声的影响。
2.分辨率的选择:分辨率是指在频谱中能够分辨的最小频率间隔。
分辨率与信号长度和采样频率有关,需要根据需求进行选择。
3.漏泄效应:当信号中的频率不是FFT长度的整数倍时,会出现漏泄效应。
可以通过零填充等方法来减小漏泄效应。
4.能量泄露:FFT将信号限定在一个周期内进行计算,如果信号过长,则可能导致部分频率成分的能量泄露到其他频率上。
总之,FFT作为信号处理中常用的频谱分析方法,能够提取信号中的频率信息,广泛应用于多个领域。
matlab正弦函数的频谱图,【求助】正弦信号序列fft频谱分析!!!

matlab正弦函数的频谱图,【求助】正弦信号序列fft频谱分析该楼层疑似违规已被系统折叠 隐藏此楼查看此楼就是正弦包含频率是20hz,20.5hz,40hz,采样频率fs是100hz,分析栅栏效应,先是128个点fft,补零到512个点进⾏fft,再512个点fft。
程序是这样的:N1=128;N2=512;fs=100;f1=20;f2=20.5;f3=40;n1=0:N1-1;n2=0:N2-1;xn1=sin(2*pi*f1*n1/fs)+sin(2*pi*f2*n1/fs)+sin(2*pi*f3*n1/fs);xk11=fft(xn1,N1)mxk11=abs(xk11(1:N1/2));figure(1);subplot(211);plot(n1,xn1);xlabel('n');title('x(n) 0<=n<127');axis([0,128,-3,3]);k1=(0:N1/2-1)*fs/N1;subplot(212)plot(k1,mxk11);xlabel('频率 单位Hz');title('X1(k)的幅度谱');xn2=[xn1,zeros(1,N2-N1)];xk12=fft(xn2,N2);mxk12=abs(xk12(1:N2/2));figure(2);subplot(211);plot(n2,xn2);xlabel('n');title('x(n) 0<=n<=511');axis([0,512,-3,3]);k2=(0:N2/2-1)*fs/N2;subplot(212);plot(k2,mxk12);xlabel('频率 单位Hz');title('x1(k)补零后的幅度谱');xn3=sin(2*pi*f1*n2/fs)+sin(2*pi*f2*n2/fs)+sin(2*pi*f3*n2/fs);xk2=fft(xn3,N2);mxk3=abs(xk2(1:N2/2));figure(3);subplot(211);plot(n2,xn3);xlabel('n');title('x(n) 0<=n=511');axis([0,512,-3,3]);k3=(0:N2/2-1)*fs/N2;subplot(212);plot(k3,mxk3);xlabel('频率 单位Hz');title('512点有效数据的幅度谱');我看不懂的是xk11=fft(xn1,N1)mxk11=abs(xk11(1:N1/2));(这个是什么意思?)和k1=(0:N1/2-1)*fs/N1;(为什么是⼆分之⼀得N1呢?)。
正弦信号整周期采样

正xx信号整周期采样的fft变换2010-01-28 10:53fs=1;N=100;%频率分辨率为fs/N=0.01Hz,下面信号的频率0.05是0.01的整数倍,即为整周期采样n=0:N-1;t=n/fs;f0=0.05;%设定xx信号频率x=cos(2*pi*f0*t);%生成正弦信号%FFT是余弦类变换,最后得到的初始相位是余弦信号的初时相位,在这里为0。
如果信号figure(1); %为x=sin(2*pi*f0*t);则初时相位应该是-90度而非0度。
subplot(311);plot(t,x);%作余弦信号的时域波形xlabel('t');ylabel('y');title('xx信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y)*2/N;%求幅值乘上后面的2/N得到正确幅值f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换subplot(312);stem(f(1:N/2),mag(1:N/2));%做频谱图xlabel('频率(Hz)');ylabel('幅值');title('xx信号幅频谱图');grid;phase=angle(y);%求幅值乘上后面的2/N得到正确幅值f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换subplot(313);stem(f(1:N/2),phase(1:N/2));%做频谱图xlabel('频率(Hz)');ylabel('相位');title('xx信号相频谱图');grid;angle(y(6))*180/pi %求信号初时相位。
频率坐标f为[0 0.010.020.030.040.050.06 ...],所以谱线y中第6根谱线和信号x对应。
实验二_应用FFT对信号进行频谱分析
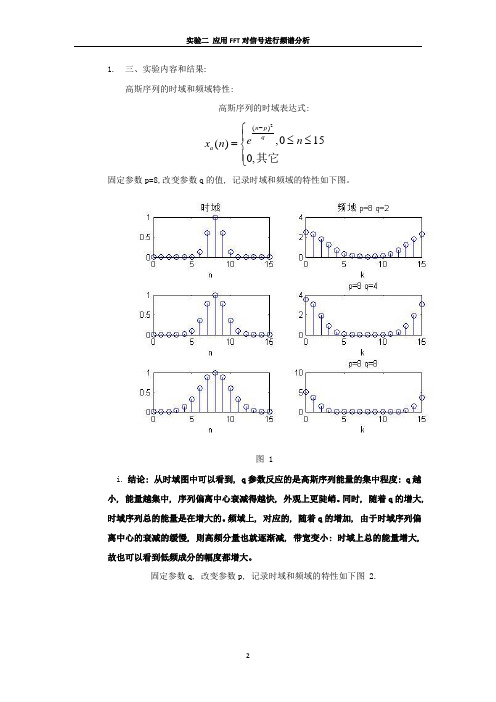
1. 三、实验内容和结果:高斯序列的时域和频域特性:高斯序列的时域表达式:2(),015()0,n p q a e n x n -⎧⎪≤≤=⎨⎪⎩其它固定参数p=8,改变参数q 的值, 记录时域和频域的特性如下图。
图 1i. 结论: 从时域图中可以看到, q 参数反应的是高斯序列能量的集中程度: q 越小, 能量越集中, 序列偏离中心衰减得越快, 外观上更陡峭。
同时, 随着q 的增大, 时域序列总的能量是在增大的。
频域上, 对应的, 随着q 的增加, 由于时域序列偏离中心的衰减的缓慢, 则高频分量也就逐渐减, 带宽变小: 时域上总的能量增大, 故也可以看到低频成分的幅度都增大。
固定参数q, 改变参数p, 记录时域和频域的特性如下图 2.图 22. 结论: p 是高斯序列的对称中心, p 的变化在时域表现为序列位置的变化。
由于选取的矩形窗函数一定, p 值过大时, 会带来高斯序列的截断。
并且随着p 的增大, 截断的越来越多。
对应地, 看频域上的变化: 截断的越多, 高频的成分也在增多, 以至发生谱间干扰, 泄露现象变得严重。
从图中可以看到, 在p=13时, 已经有混叠存在。
当p=14时, 混叠进一步加大, 泄露变得更明显。
衰减正弦序列的时域和幅频特性:sin(2),015()0,n b e fn n x n απ-⎧≤≤=⎨⎩其它改变参数f, 记录时域和幅频特性如下图3.图 33. 结论: 随着f 的增大, 时域上可以看到, 序列的变化明显快多了。
从幅度谱上看, 序列的高频分量逐渐增多, 低频分量逐渐减小, 以至于发生严重的频谱混叠。
当f 增大到一定的程度, 从图中可以看到, f=0.4375和f=0.5625时的幅度谱是非常相似的, 此时已经很难看出其幅度谱的区别。
三角序列的时域表达式和对应的时域和幅频特性如图 4:c 1,03()8,470,n n x n n n n +≤≤⎧⎪=-≤≤⎨⎪⎩其它图 4结论: 随着fft 取点数的增多, 能够看到的幅度谱的频率分量变得丰富, 得到的是高密度更高的谱, 也就是减轻了栅栏效应。
信号分析实验报告总结

一、实验目的本次信号分析实验旨在通过MATLAB软件,对连续信号进行采样、重建、频谱分析等操作,加深对信号处理基本理论和方法的理解,掌握信号的时域、频域分析技巧,并学会使用MATLAB进行信号处理实验。
二、实验内容1. 连续信号采样与重建(1)实验内容:以正弦信号为例,验证采样定理,分析采样频率与信号恢复质量的关系。
(2)实验步骤:a. 定义连续信号y(t) = sin(2π×24t) + sin(2π×20t),包含12Hz和20Hz 两个等幅度分量。
b. 分别以1/4、1/2、1/3Nyquist频率对信号进行采样,其中Nyquist频率为最高信号频率的两倍。
c. 利用MATLAB的插值函数对采样信号进行重建,比较不同采样频率下的信号恢复质量。
(3)实验结果与分析:a. 当采样频率低于Nyquist频率时,重建信号出现失真,频率混叠现象明显。
b. 当采样频率等于Nyquist频率时,重建信号基本恢复原信号,失真较小。
c. 当采样频率高于Nyquist频率时,重建信号质量进一步提高,失真更小。
2. 离散信号频谱分析(1)实验内容:分析不同加窗长度对信号频谱的影响,理解频率分辨率的概念。
(2)实验步骤:a. 定义离散信号x[n],计算其频谱。
b. 分别采用16、60、120点窗口进行信号截取,计算其频谱。
c. 比较不同窗口长度对频谱的影响。
(3)实验结果与分析:a. 随着窗口长度的增加,频谱分辨率降低,频率混叠现象减弱。
b. 频率分辨率与窗口长度成反比,窗口长度越长,频率分辨率越高。
3. 调频信号分析(1)实验内容:搭建调频通信系统,分析调频信号,验证调频解调原理。
(2)实验步骤:a. 搭建调频通信系统,包括信号源、调制器、解调器等模块。
b. 产生调频信号,并对其进行解调。
c. 分析调频信号的频谱,验证调频解调原理。
(3)实验结果与分析:a. 调频信号具有线性调频特性,其频谱为连续谱。
[重点]对正弦信号的采样频谱分析
![[重点]对正弦信号的采样频谱分析](https://img.taocdn.com/s3/m/4f2f80ccac51f01dc281e53a580216fc700a530f.png)
一、题目要求:给定采样频率fs,两个正弦信号相加,两信号幅度不同、频率不同。
要求给定正弦信号频率的选择与采样频率成整数关系和非整数关系两种情况,信号持续时间选择多种情况分别进行频谱分析。
二、题目原理与分析:本题目要对正弦信号进行抽样,并使用fft对采样信号进行频谱分析。
因此首先对连续正弦信号进行离散处理。
实际操作中通过对连续信号间隔相同的抽样周期取值来达到离散化的目的。
根据抽样定理,如果信号带宽小于奈奎斯特频率(即采样频率的二分之一),那么此时这些离散的采样点能够完全表示原信号。
高于或处于奈奎斯特频率的频率分量会导致混叠现象。
设抽样周期为TS(抽样角频率为ωS),则可见抽样后的频谱是原信号频谱的周期性重复,当信号带宽小于奈奎斯特频率的二分之一时不会产生频谱混叠现象。
因此,我们对采样频率的选择采取fs>2fo,fs=2fo,fs<2fo三种情况进行分析。
对信号采样后,使用fft函数对其进行频谱分析。
为了使频谱图像更加清楚,更能准确反映实际情况并接近理想情况,我们采用512点fft。
取512点fft不仅可以加快计算速度,而且可以使频谱图更加精确。
若取的点数较少,则会造成频谱较大的失真。
三、实验程序:本实验采用matlab编写程序,实验中取原信号为ft=sin(2πfXt)+2sin(10πfXt),取频率f=1kHz,实验程序如下:f=1000;fs=20000;Um=1;N=512;T=1/fs;t=0:1/fs:0.01;ft=Um*sin(2*pi*f*t)+2*Um*sin(10*pi*f*t);subplot(3,1,1);plot(t,ft);grid on;axis([0 0.01 1.1*min(ft) 1.1*max(ft)]);xlabel('t'),ylabel('ft');title('抽样信号的连续形式');subplot(3,1,2);stem(t,ft);grid on;axis([0 0.01 1.1*min(ft) 1.1*max(ft)]);xlabel('t'),ylabel('ft');title('实际抽样信号');k=0:N-1;Fw=fft(ft,N);subplot(3,1,3);plot(k,abs(Fw));grid on;axis([0 550 -0.2 65*pi]);title('抽样信号幅度谱')在实际操作过程中,对于信号频率与采样频率所成整数倍与非整数倍关系时,信号持续时间不同时,只需改变程序中的相关语句即可。
FFT频谱分析

%*************************************************************************%% FFT实践及频谱分析%%*************************************************************************%%***************1.正弦波****************%fs=100;%设定采样频率N=128;n=0:N-1;t=n/fs;f0=10;%设定正弦信号频率x=sin(2*pi*f0*t); %生成正弦信号figure(1);subplot(231);plot(t,x);%作正弦信号的时域波形xlabel('t');ylabel('y');title('正弦信号y=2*pi*10t时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换figure(1);subplot(232);plot(f,mag);%做频谱图axis([0,100,0,80]);xlabel('频率(Hz)');ylabel('幅值');title('正弦信号y=2*pi*10t幅频谱图N=128');grid;%求均方根谱sq=abs(y);figure(1);subplot(233);plot(f,sq);xlabel('频率(Hz)');ylabel('均方根谱');title('正弦信号y=2*pi*10t均方根谱');grid;%求功率谱power=sq.^2;figure(1);subplot(234);plot(f,power);xlabel('频率(Hz)');ylabel('功率谱');title('正弦信号y=2*pi*10t功率谱');grid;%求对数谱ln=log(sq);figure(1);subplot(235);plot(f,ln);xlabel('频率(Hz)');ylabel('对数谱');title('正弦信号y=2*pi*10t对数谱');grid;%用IFFT恢复原始信号xifft=ifft(y);magx=real(xifft);ti=[0:length(xifft)-1]/fs;figure(1);subplot(236);plot(ti,magx);xlabel('t');ylabel('y');title('通过IFFT转换的正弦信号波形');grid;FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
给定采样频率fs,两个正弦信号相加,两信号幅度不同、频率不同。
要求给定正弦信号频率的选择与采样频率成整数关系和非整数关系两种情况,信号持续时间选择多种情况分别进行频谱分析。
二、题目原理与分析:
本题目要对正弦信号进行抽样,并使用fft对采样信号进行频谱分析。
因此首先对连续正弦信号进行离散处理。
实际操作中通过对连续信号间隔相同的抽样周期取值来达到离散化的目的。
根据抽样定理,如果信号带宽小于奈奎斯特频率(即采样频率的二分之一),那么此时这些离散的采样点能够完全表示原信号。
高于或处于奈奎斯特频率的频率分量会导致混叠现象。
设抽样周期为TS(抽样角频率为ωS),则
可见抽样后的频谱是原信号频谱的周期性重复,当信号带宽小于奈奎斯特频率的二分之一时不会产生频谱混叠现象。
因此,我们对采样频率的选择采取fs>2fo,fs=2fo,fs<2fo三种情况进行分析。
对信号采样后,使用fft函数对其进行频谱分析。
为了使频谱图像更加清楚,更能准确反映实际情况并接近理想情况,我们采用512点fft。
取512点fft不仅可以加快计算速度,而且可以使频谱图更加精确。
若取的点数较少,则会造成频谱较大的失真。
三、实验程序:
本实验采用matlab编写程序,实验中取原信号为
ft=sin(2πfXt)+2sin(10πfXt) ,取频率f=1kHz,实验程序如下:
f=1000;fs=20000;Um=1;
N=512;T=1/fs;
t=0:1/fs:;
ft=Um*sin(2*pi*f*t)+2*Um*sin(10*pi*f*t);
subplot(3,1,1);
plot(t,ft);grid on;
axis([0 *min(ft) *max(ft)]);
xlabel('t'),ylabel('ft');
title('抽样信号的连续形式');
subplot(3,1,2);
stem(t,ft);grid on;
axis([0 *min(ft) *max(ft)]);
xlabel('t'),ylabel('ft');
title('实际抽样信号');
k=0:N-1;
Fw=fft(ft,N);
subplot(3,1,3);
plot(k,abs(Fw));grid on;
axis([0 550 65*pi]);
title('抽样信号幅度谱')
在实际操作过程中,对于信号频率与采样频率所成整数倍与非整数倍关系时,信号持续时间不同时,只需改变程序中的相关语句即可。
既t=0:1/fs:to;语句控制信号持续时间,改变to即可。
改变抽样频率只需对fs取不同的值即可。
四、实验过程及图示:
1.信号持续时间为,信号频率与采样频率成整数关系:
(1)fs>2fo,取fs=20kHz,得到频谱图:
(2)fs=2fo,取fs=10kHz,得到频谱图:
(3)fs<2fo,取fs=5kHz,得到频谱图:
通过比较三个图形发现当抽样信号频率大于原信号频率的二倍时抽样信号能较好的反应原信号,并且抽样信号频谱呈现两个峰值,与正弦信号的理想频谱既冲击函数较为接近。
但是由于实际信号的持续时间是有限的,因此频谱不可能完全表现为冲击函数的情况,会有尾部延伸。
当抽样频率等于原信号频率的二倍时,抽样信号只能表现为单个正弦信号的形式,因此频谱只能表现为单峰情况,且幅度也较前者有较大的下降。
当抽样信号频率小于原信号频率的两倍时,抽样信号波形有较大的失真,且幅度有更大的下降,频谱的尾部所占比例更大,失真较为严重。
2.持续时间为,信号频率与采样频率成非整数关系:
(1)fs>2fo,取fs为,得到频谱为:
(2)fs=2fo的情况同1,省略。
(3)fs<2fo,取fs为,得到频谱为:
通过观察频谱图发现,对抽样频率取三种情况时频谱的规律与成整数关系时的规律基本相同,但是纵向比较时,抽样信号的波形与原信号波形有较大的失真,这是由于抽样信号的频率不为原信号的整数倍造成的,反应到频率谱上,导致出现的峰值下降,较为弱的趋向理想冲击函数。
3.持续时间为,信号频率与采样频率成整数倍关系:
(1)fs>2fo,取fs=20kHz,得到频谱图为:(2)fs=2fo,去fs为10kHz,得到频谱图为:(3)fs<2fo,取fs=5kHz,得到频谱图为:
4.持续时间为,信号频率与采样频率成非整数关系:(1)fs>2fo,取fs=,得到频谱图为:
(2)fs=2fo,略
(3)fs<2fo,取fs=,得到频谱图为:
5.持续时间为,采样频率与信号频率成整数关系:(1)fs>2fo,取fs=20kHz,得到频谱图为:
(2)fs=2fo,取fs=10kHz,得到频谱图为:
(3)fs<2fo,取fs=5kHz,得到频谱图为:
6.持续时间为,采样频率与信号频率成非整数关系:(1)fs>2fo,取fs=,得到频谱图为:
(2)fs=2fo,略
(3)fs<2fo,取fs=,得到频谱图为:
通过观察持续时间为和时的时域图形和频谱图我们发现,对于每个不同的持续时间,随抽样信号的频率不同,分别满足抽样定理的要求,这同持续时间为是得到的结论是一样的。
但是随着持续时间的增加,意味着抽样得到的点数增多,
反应到频谱图中即为信号峰值增大,更加接近于冲击函数。
五、结果分析:
本试验中我们讨论了对连续正弦信号进行抽样,并讨论抽样信号的频谱与抽样信号频率和信号持续时间的关系。
这里使用控制变量法来讨论,一下是具体分析。
(1)抽样信号频率:通过比较图形发现当抽样信号频率大于原信号频率的二倍时抽样信号能较好的反应原信号,并且抽样信号频谱呈现两个峰值,与正弦信号的理想频谱既冲击函数较为接近。
当抽样频率等于原信号频率的二倍时,因此频谱只能表现为单峰情况,且幅度也较前者有较大的下降,这是由于抽样信号有较大失真造成的。
当抽样信号频率小于原信号频率的两倍时,抽样信号波形有更大的失真,且幅度有更大的下降。
这个结论对抽样信号频率为原信号的整数倍和非整数倍时均适用。
当抽样信号频率为原信号的非整数倍时,与整数倍的情况相比较,可以发现抽样信号有一定的失真,导致频谱有一定的失真,即为频谱更严重的偏离冲击函数,尾部展宽,幅度下降。
(2)信号持续时间:对于抽样信号频率为原信号频率的整数倍和非整数倍的情况,当信号持续时间增加时,也就是抽样的点数增多时,抽样信号的频谱函数更加趋近于冲击函数,尾部缩小,峰值增加。
因为理想正弦信号的频谱图即为冲击函数,但是实际信号持续时间不能趋于无穷大,是有限的,因此频谱图不是冲击函数,随着持续时间的增加,频谱图趋近于冲击函数。
