电网络理论-第二章
电网络理论考点 - 副本

.供用电网络考试内容第一章绪论第一节电力系统概述理解掌握 1 电力系统的构成包括:答:电力系统是由发电机,变压器,输配电线路和电力用户的电器装置连接而成的整体,他完成了发电,输电,变电,配电,用电的任务。
电力系统的概念答:什么是电力网、电力系统、动力系统答:电路系统各种电压的变电所及输配电线路组成的统一体,称为电力网。
电力网的主要任务是输电与分配电能。
2为发电厂和用户架起一座桥梁,用于传输电能,这边是电力系统。
2电力系统运行的特点(1)、电能生产,运输,使用的同时性(2)与生产及人们生活密切相关性、(3)过渡过程的瞬时性3对电力系统的基本要求(1)满足用电要求、(2)、安全可靠用电(3)保证电能质量,保证电力系统运行的经济性---以及1类~3类负荷的定义答:,电能质量指标—电压(正负百分五)、频率(正负百分之零点二到五)、波形(正弦波)一类负荷,在正常的运行和故障情况下,系统接线方式必须有足够的可靠性和灵和性,保证对用户的连续供电。
二类负荷,需双回路线路供电,三类负荷,允许停电较长,但不可以随意停电。
第二节发电厂类型熟悉1发电厂的种类;理解掌握1水电厂发电机容量大小由上下游的落差和流量决定2根据地形地质水能资源特点的不同,水电厂的分类;水力发电厂按其运行方式可分为无调节水电厂和有调节水电厂)3各类电厂的结构和特点第三节变电所类型熟悉变电所的类型和分类1按在电网的地位和作用划分:升压变压器和降压变压器按电压高低划分,大型变电所,中型变电说,小型变电所,按变电所的结构型式划分,屋外是变电所,屋内是变电所,地下变电所和箱式变电所第四节电力网的电压理解掌握1我国电力的额定电压022. 0.38 3 6 10 35 60 110 220 330 500 750KV第五节供配电系统的接地理解熟练掌握1按接地的目的不同,接地可以分为什么?答:工作接地,保护接地。
防雷接地2工作接地,中性点直接接地优点:单相接地时,其中性点电位不变,非故障相对电压接近相电压,因此降低电力网绝缘的投资,而且电压越高,其经济效益也越大,所以,目前我国对110千伏以上的电力网一般采用中性点直接接地。
电网络理论 第二章图论

电网络理论第二章图论第二章图论图论是电网络理论的重要分支,主要研究对象是图。
图是由节点和边构成的一种抽象模型,被广泛应用于计算机科学、数学和其他相关领域。
本章将介绍图论的基本概念、常用算法以及在电网络中的应用。
1. 图的定义和表示方式图由节点(也称为顶点)和边组成。
节点表示图中的元素,边表示节点之间的关联关系。
图可以分为有向图和无向图两种类型。
有向图中的边有方向性,表示从一个节点到另一个节点的单向关系。
无向图中的边没有方向性,表示节点之间的无序关系。
图可以用邻接矩阵或邻接表来表示。
邻接矩阵是一个二维数组,用于表示节点之间的关系。
邻接表则是由链表构成的数组,每个节点对应一条链表,链表中记录了该节点与其他节点的关系。
2. 图的基本术语和性质图论中有一些基本的术语和性质,包括:- 路径:指从一个节点到达另一个节点所经过的一系列边和节点。
- 简单路径:路径中不含有重复节点的路径。
- 环:起点和终点相同的路径。
- 连通图:图中任意两个节点之间都存在路径的图。
- 强连通图:有向图中任意两个节点之间都存在路径的图。
- 子图:由图中部分节点和对应的边组成的图。
- 度:节点所连接的边的数量。
- 入度和出度:有向图中节点的入边和出边的数量。
3. 常用图论算法图论中有许多重要的算法,下面介绍其中几个常用算法:- 广度优先搜索(BFS):用于查找图中从起点到终点的最短路径,同时可以用于遍历图的所有节点。
- 深度优先搜索(DFS):用于遍历图的所有节点,通过递归的方式沿着路径向前搜索,直到没有未访问的节点。
- 最小生成树(MST):通过连接图中的所有节点,使得生成的树具有最小的总权重。
- 最短路径算法:例如迪杰斯特拉算法和贝尔曼-福特算法,用于查找图中两个节点之间的最短路径。
- 拓扑排序:用于对有向无环图进行排序,使得图中的节点满足一定的顺序关系。
4. 图论在电网络中的应用图论在电网络领域有广泛的应用,包括:- 网络拓扑分析:通过图论算法可以对电网络的拓扑结构进行分析,了解网络中节点之间的连接关系。
电网络理论

电网络理论电网络理论是电力系统的基础理论,通过对电路中电流、电压、功率和能量等参数的分析和研究,以及电路中的元件如电阻、电容和电感等的特性和相互关系,来研究电路中的电能传输、控制和转换问题。
本文将从电网络的基本原理、电路分析方法、交直流电路、三相电路和磁电路等方面来介绍电网络理论。
一、电网络的基本原理电网络是由电路元件按照一定的连接方式组成,在电路中产生或传输电能的一种电学系统。
它包含基本电路、复合电路和控制电路等三种基本类型。
其中,基本电路只由一种电路元件构成,例如电阻、电容和电感等单元,例子如图1所示。
图1:基本电路复合电路由多种电路元件组合而成,可以分为串联、并联、树型等不同结构,例子如图2所示。
图2:复合电路控制电路则在复合电路的基础上增加了逻辑控制包括开关、计算机等,在实现空间、时间、功能上高度复杂,例子如图3所示。
图3:控制电路每种电路元件都有其对电能的特性消耗、储存、转换的贡献,而每种电路结构规则所连接的电路元件也影响了电路的性能特征。
因此,电网络理论的基本任务是分析和预测电路中电信号之间的关系和影响。
二、电路分析方法为了研究电路中的各种性质,需要采用适当的方法来分析电路。
电路分析方法主要分为两大类,即基本法和派生法。
1.基本法基本法是指对简单电路采用基本关系式和物理学原理求解电路中的电压、电流和功率各种参数的方法。
其中包括:(1)基尔霍夫电压定律法和基尔霍夫电流定律法,用于求解电路中各节点的电压和电流。
(2)欧姆定律法,用于求解电路中电阻元件的电流和电压。
(3)功率方程法,用于求解电路中的功率分配和传输。
(4)电荷守恒定律法,用于求解电路中的电荷分布和电场特性等。
如图4所示的简单电路,可以采用基本法来计算其中的电路参数。
图4:简单电路2.派生法派生法是指通过用已知电路中的节点电压、电流或电阻替换未知元件来简化复杂电路求解问题的方法。
其中的常用方法有:(1)串并联电路转换,用于求解串联、并联电路特性和电路等效性分析。
第二章 电网络分析与综合

图1-5 基本回路
对图所示的基本回路列写KVL方程,并表达成矩阵形式:
4
5
l1
2
3
l2
6
l3
图1-5 基本回路
u1 u 2 0 1 1 1 0 0 1 1 1 0 1 0 u3 u 4 1 1 0 0 0 1 u 5 u6
(b)
2.三端元件的线图
可用三个节点和两条支路表示
i1 i2 i3 0 u12 u 23 u13 0
依此类推,对n端元件,如果存在 m个独立的端 子电流 或 m个独立的端对电压,则可抽象成 m条支 路 n个节点的线图。
二、 网络的线图(linear graph)
①
②
说明连支电压可以用树支电压的线性组合表示。 在全部支路电压中,树支电压是一组独立变量, (n 1) 个数等于树支数 取基本回路是列写独立KVL方程的一个充分非 必要条件 。
u 6 u1 u 2
推广到一般情况:在基本回路上列写的基尔霍夫 电压定律方程是一组独立方程,方程的数目等于 连支数,基本回路是一组独立回路。
u 回路l1 u 回路l2 u l3 回路
0 0 0
BU=0
对图1-4所示的基本割集依次列写KCL方程并写成矩阵形式得
c3
4 2
5 3 6 c1
0 1 1 i4 i1 1 1 1 i i 5 2 1 1 0 i3 i6
§2.2独立的基尔霍夫定律方程
一、独立的基尔霍夫电流定律方程
基尔霍夫电流定律表述成:集中参数电路中,流入任意割集各 支路电流的代数和恒等于零。
王勤电网络理论第二章

⎧ 1, 若 ⎪ a jk = ⎨ − 1 , 若 ⎪ 0, 若 ⎩
j j j
k k k
② b1 ① b4 b5 ⑤ b7 b6 ④
b1 b2 b3 0 0 1 -1 0 b4 1 0 0 -1 0 b5 -1 0 0 0 1 b6 0 0 0 -1 1 b7 0⎤ 0⎥ ⎥ -1⎥ ⎥ 0⎥ 1⎥ ⎦ 0 ① ⎡1 ⎢− 1 - 1 ② ⎢ 1 ③ ⎢0 ⎢ 0 ④ ⎢0 0 ⑤ ⎢0 ⎣
一般规定: ① 支路的编号采用先连支后树支的顺序; ② 各单连支回路的绕向与相应连支的方向一致; ③ 回路的序号与连支的序号要一致且顺次列写。 Bf=[1l | Bt ] Bt 1l (b-n)×n矩阵 b-n阶单位矩阵 基本回路与树支的关联关系 基本回路与连支的关联关系
② b1 ① b2 b5 ⑤ b7 b6 ④ b3 ③
0 ⎡ 1 ⎢− 1 - 1 A= ⎢ ⎢ 0 1 ⎢ 0 ⎣0
① 按“Aa每一列中只有两个非零元素,一个为+1, 另一个为–1”的关系,可由A还原成Aa 。 ② 故A也与有向图G一一对应。即已知G可唯一地写 出A;已知A也可唯一地画出G 。 ③ 通常采用的是A,且A也简称为关联矩阵。 定理5:连通图G的A的n×n子阵非奇异的充分必 要条件是:此子阵的列所对应的支路形成G的一 个树,且该子阵的行列式之值为±1 定理6:连通图G满足: 秩(Aa )= 秩(A )=n= nt –1
§2—3
一、关联矩阵Aa和A
图的矩阵表示
增广关联矩阵Aa表示G的节点和支路的关联关系 (augmented incidence matrix) Aa=[ajk]是一个nt × b的矩阵。
+1第k条支路与第j个节点相关联,且支路方向离开节点j;
电网络 - 第二章电网络简单电路

i2
R2 + 1V _
i3
R3 + 4V _
+ u3 _
i1+i2+i3=0 u1+u25+u33=0
u-2+(u-1)5+(u-4) 3=0
u
例
G1、G2为线性电导,非线性电阻为压控电阻
i2
U n1 i3
G2
U n 2 i4 u3 +
i3 5u
+
u5
3 3
+
u4
U n3
13 i4 10u4 15 i5 15u5
o
i
•非线性电阻的并联
i + u
i1
+ i2
u1
+
u2
i ( u)
i i1 i2 u u1 u2
i
i' ' i2
i '1
i1 ( u) i 2 ( u)
同一电压下电流相加得 相应的DP特性。
i1' o
u'
u
(3)曲线相交法(负载线法)可求工作点,可求TC(如电子学 三极管的转移特性) 若已知:u1-i1,u2-i2,u1=u2=u,i1=-i2=i,求工作点。
+ u6 _
R0 U0 _ +
º + u _ º
i + u _
将线性部分作戴维南等效,非线性部分用一个非线电阻等效
得出 u , i。 图中i 4= g (u4 ), u 5= f 1(i5 ), u 6= f 2(i6 ),则 曲线 i - i4 u (u4) → i4 → i5
u5(i - i4)
电网络理论第2章课件.ppt
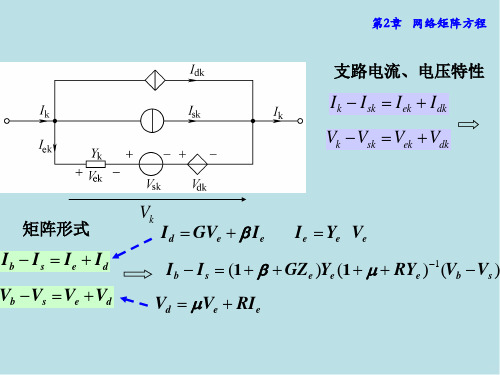
第2章 网络矩阵方程
Vk nVj 0
Ik
1 n
I
j
0
Vk rI j 0
Vj rIk 0
I j Ik 0
第2章 网络矩阵方程
Vj rIk 0 Ik 0
I j gVk 0
Vj Vk 0
Vk 0
2.6.2 多端元件的伏安特性的描述
第2章 网络矩阵方程
V1 r11 r12 r13 r14 I1
Vws 2
VT ws3
Y nVn J n N
Jn
Iws1 Iws1
第2章 网络矩阵方程
Iw2 Iw2
Iw3 Iw3
T
Jn Aw Iw
Aw
00 0 0
i 1 0 0
j 1 0
0
k0 1 0
l
0
1
0
m
0
0
1
n 0 0 1
第2章 网络矩阵方程
Y nVn J n Aw Iw
附加方程
Ac
零值器关联节点短接后网络 Nc 的关联矩阵
Jn ArYbVs Ar Is
第2章 网络矩阵方程
2.6 表格法
含多端口器件的计算
待求变量 支路电压、支路电流 2b 个
方程 AI 0 BfU 0 FU KI S
F K
S
B
f
0
A0 UI
0 0
元件伏 安特性
第2章 网络矩阵方程
Zl Il El
回路电压 源向量
第2章 网络矩阵方程
网络含q 条纯电流源支路时
阻抗
已知信息描述为
Il
Il1
I
l
2
1 Bf 0
电网络理论第二章

子图
二、回路(Loop) 路径的起点和终点重合 用支路表示 l(1,3,6), l(1,2,4) 用节点表示 l(a,d,c,a), l(a,d,b,a) 三、树(Tree) 包含所有节点;是连通的;不包含任何回路 树支:nt
a
4
6
a
4
b
2
5
c
3
1
d
6
b
2
5
c
a
4
b
2 3
c
a
1
b
2
c
连支: l
d d
可用(n-1)×b阶矩阵Q表示,其中元素qij定义如下:
1 支路j与割集i关联且方向一致 qij = -1 支路j与割集i关联且方向相反 0 支路j与割集i不关联
1 2 3 4 5 6 b
1
3
2 5
1 0 1 Q f = c2 0 1 1 1 0 1 c3 0 0 1 0 1 1
A= i ai1 n-1 a( n 1)1
a1b a2b aib a( n 1) b
2
……
b
b12 b11 b22 2 b21 Bf = bj2 i b j1 b-n+1 b(b n 1)1 a(b n 1)2
k 1
b
(1)回路j不通过节点i
a 、若支路k与回路j有关联,则必与节点i无关联
k j i j i j
i
即bjk 0, aik 0 即aik 0, bjk 0
aik bjk 0 aik bjk 0
b 、若支路k与节点i有关联,则必与回路j无关联
k
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-25
QB i 0
T l
Q B
T f f
T
0 or
T t
B Q
0
T
0
T t
对同一有向图,任选一树,按先树枝后连枝顺序有:
Q B
B 1 Ql 1
Ql B
§2-3 图的基本矩阵形式
A与Qf 之间的关系 对同一有向图,任选一树,按先树枝后连 枝顺序写出矩阵:
2-26
A At Al B f Bt 1 Q 1 Q l f
§2-3 图的基本矩阵形式
结 支 ② 1 -1 0 1 0 2 3 -1 1 0 -1 0 0 1 0 4 0 -1 1 0 5 0 0 1 -1
2-10
1 Aa= 2 3 4
6 3 4 0 6 ③ 1 ① 5 0 2 -1 ④ 1
降阶关联矩阵A
支路b
A=
结 点 n-1
(n-1) b
§2-3 图的基本矩阵形式
矩阵形式的KVL:[ Qf ]T[ut ]=[u]
§2-3 图的基本矩阵形式 注意 连支电压可以用树支电压表示。 ut 1 T [u ] Qf ut T ut ul Ql ul QlT ut 小结
A KCL KVL B [B ] T [ il ] =[i] Q [Qf][i]=0
un1 un un2 un3
矩阵阵形式KVL
[u ] [ A] [un ]
T
§2-3 图的基本矩阵形式 2. 回路矩阵B
2-13
[B]=
独 立 回 路
支路b
注意
每一行对应一个独立回路, 每一列对应一条支路。
l b
l
矩阵B的每一个元素定义为: 1 支路 j 在回路 i 中,且方向一致;
矩阵形式的KCL:[ Qf ][i ]=0
§2-3 图的基本矩阵形式
②用[Qf]T表示矩阵形式的KVL方程
2-22
设树枝电压(或基本割集电压):ut=[ u1 u2 u3 ]T
ut1 u1 1 0 0 ut 2 u2 0 1 0 ut1 0 0 1 ut 3 u3 T Q f ut 1 0 1 ut 2 u u u u t1 t3 4 u 1 1 0 t 3 u u u t1 t 2 5 0 1 1 ut2 ut 3 u6
§1 网络的图和图论基本术语
分类 无向图:未赋以方向的图。G=(V,E) 混合图:只有部分支路赋以方向的图。 有向图:所有支路都赋以方向的图。Gd=(V,A)
注:图并不反映支路间的耦合关系。 相关联 若e=[vi,vj],则称边e与顶点vi和vj相关联。
相邻接 若顶点vi和vj之间至少存在一条边,则为相邻接的点。
独立回路电流
§2-3 图的基本矩阵形式
②
1 0 0 1 1 0 0 0 1 0 il1 0 1 il 2 1 0 il 3 0 1 1 1
2-17
il1 i1 i i 3 4 3 l2 3 6 i 2 il 3 4 ① ③ 5 il1 il 2 i2 2 1 il1 il 3 i5 ④ i i 1 l 2 l 3 i6
2-18
[Q ] =
割 集 数
注意
每一行对应一个基本割集, 每一列对应一条支路.
(n-1)b
矩阵Q的每一个元素定义为:
1
支路 j 在割集 i 中,且与割集方向一致;
qij
-1 支路 j 在割集 i中,且与割集方向相反; 0 支路 j 不在割集 i 中。
§2-3 图的基本矩阵形式 规定 基本割集矩阵[Qf]
2-2
若边ei和ej之间至少存在一个公共顶点,则为相邻接的边。
§1 网络的图和图论基本术语
径
2-3
( V3 ) e ( V4 ) e ( V2 ) e 2 V2 3 V3 1 V1
V p 1 V1
若图 自环
,…, p
e(V p V p1 )
回路 子图
G1
的点和边是图 G 的子集
§1 网络的图和图论基本术语
第二章 网络图论和网络方程
2-1
§1 网络的图和图论基本术语 §2-3 图的基本矩阵形式 §4-8 几种网络方程的系统方法 §补充 改进节点方程的直接形成方法 §9 撕裂法
§1 网络的图和图论基本术语
图 点和边的集合,边连于两点
2-2
图 G 为线形图、拓扑图或称线图 孤点 点集 边集
Va Vb Vc Vd V f e ( Vd ) 1 Va
2-20
6
5
③
2
④ 1
Qt
Ql
基本割集矩阵[Qf]的作用 ①用基本割集矩阵[Qf]表示矩阵形式的KCL方程。 设
[1 Ql ]
[i] [i1 i2 i3 i4 i5 i6 ]
T
§2-3 图的基本矩阵形式
2-21
i1 ② 1 0 0 1 1 0 i 2 4 [ Qf ][i ]= 0 1 0 0 -1 -1 3 i 6 0 0 1 1 0 -1 3 ① ③ 5 i 4 2 i i1 i 4 i5 5 ④ 1 i 2 i5 i6 0 i 6 i3 i 4 i6 n-1个独立 KCL方程
bij
-1 支路 j 在回路 i中,且方向相反; 0 支路 j 不在回路 i 中。
§2-3 图的基本矩阵形式
取网孔为独立回路,顺时针方向 支1 2 回 3 4 5 6 3 1 [B] = 2 3
2-14
②
4
2 6 1 ① ③ 5 2 3 ④ 1 注意 给定B可以画出对应的有向图。 0 1 1 0 0 1 0 0 0 -1 1 -1 1 -1 0 0 -1 0
§1 网络的图和图论基本术语
基本割集 只含有一个树枝的割集。割集数 = n-1
1 9 2 6 3 4 7 5
2-7
8
基本回路
只含有一个连枝的回路。回路数 =b-(n-1)
§2-3 图的基本矩阵形式
2-8
1. 图的矩阵表示
图的矩阵表示是指用矩阵描述图的拓扑性质, 即KCL和KVL的矩阵形式。有三种矩阵形式: 结点 回路 割集 支路 支路 支路 关联矩阵 回路矩阵 割集矩阵
2-19
①割集方向为树支方向; ②支路排列顺序先树支后连支; ② ③割集顺序与树支次序一致。 3 选 1、2、3支路为树 6 ①
4 5 1 ③
Q1: {1, 4, 5} Q2: {2, 5, 6} Q3: {3, 4 , 6}
2
④
§2-3 图的基本矩阵形式
支
割集 1 2 3 4 5 6 3 ① Q1 1 0 0 1 1 0 [Qf]=Q2 0 1 0 0 -1 -1 Q3 0 0 1 1 0 -1 ② 4
2-23
[A][ i ]=0
B i it
T t l
it Ql il
T l
A u u
T n
[B][u]=0 ul= - Btut
[Q]T [ ut]=[u]
ul Q ut
§2-3 图的基本矩阵形式
矩阵A、Bf 、Qf 之间的关系 三个矩阵从不同角度表示同一网络的连接性 质,它们之间自然存在着一定的关系。 A与B 之间的关系
n-1个独立 方程
i i i i i i i i i
矩阵形式的KCL: [ A ][ i ]= 0
§2-3 图的基本矩阵形式
②用矩阵[A]T表示矩阵形式的KVL方程。 设:
2-12
u u1 u2 u3 u4 u5 u6
T
1 0 1 un1 un3 u u1 1 0 0 n1 u 2 un1 T 1 1 0 un1 un 2 u 3 A un un 2 un2 un 3 u 4 0 1 1 u n 3 u 5 u 0 1 0 n 3 u 6 u 1 0 0 n 2
度 有向图 顶点关联的边数 di 4 连通图 非连通图
②
2-4
断点
①
2 3 5 6
4
③
④
1
可分图
完备图
§1 网络的图和图论基本术语
树
树余
2-5
连通图的一个子图且满足下列条件:
a. 连通 b. 包含所有结点 c. 不含闭合路径 树 不 是 树 单连支回路
树支:构成树的支路
连支:属于G而不属于T的支路
矩阵形式的KCL: [ B ]T[ il ]=[ i ]
注意 树支电流可以用连支电流表出。
1 [Bf ] T Bt
T
1 il BT [il ] i t t
B i it
T t l
§2-3 图的基本矩阵形式 3. 基本割集矩阵[Qf]
支路b
1
l个独立 KVL方程
1 0 0 -1 -1 0 [ B ][ u ]= 0 1 0 1 0 1 0 0 1 0 -1 1
u1 u 2 u5 0 u3 u 2 u 6 u 4 u5 u 6
矩阵形式的KVL:[ B ][ u ]= 0
§2-3 图的基本矩阵形式
§2-3 图的基本矩阵形式 2. 关联矩阵A
支路b
2-9
Aa=
结 点 n
