浙大数据结构课件-update_hqm_DS05_Ch04b
合集下载
DS-数据结构概述PPT课件

算法的基本特征
有穷性:算法中的操作步骤为有限个,且每个步骤都能在有限时
间内完成。
确定性:组成算法的操作必须清晰无二义性。
可行性:算法中的所有操作都必须足够基本,都可以通过已经实
现的基本操作运算有限次实现之。
输入:作为算法加工对象的量值,通常体现为算法中的一组变量
。些算法的字面上可以没有输入,实际上已被嵌入算法之中。
入学成绩 561 512 532 509
所在班级 00计算机2 00计算机1 00计算机2 00计算机3
说明:在此类文档管理中,可以有查找、修改、插入、删 除等操作。
结论4:在某种数据结构上可以定义一组运算。
2021
软件学院 李媛媛9
1.2 数据结构的有关概念和术语
1、数据:对客观事物的符号表示,信息的载体,能被计算机识别、存 储和加工处理。如整数,实数,字符串、图象、声音等都是数据。 2、数据元素:数据的基本单位,又可称为元素、结点、顶点、记录等。 3、数据项: 是数据不可分割的最小单位。如学号、姓名等。
① 计算机处理的数据量越来越大。
② 数据类型越来越多。
③ 数据的结构越来越复杂。
2021
软件学院 李媛媛5
例1 已知数据如下:
19850700163172978233000340304195902261011
工号:1985070016 电话号码:3172978 邮编:233000 身份证号码:340304195902261011
第1章
1.1 为什么要学习数据结构 1.2 数据结构的基本概念和术语 1.3 算法和算法描述 1.4 算法时空效率分析方法
2021
软件学院 李媛媛1
本章重点难点
重点: ①数据结构的逻辑结构、存储结构以及基本操
浙江大学数据库系统概念PPT第十六章-精品文档28页

A locking protocol is a set of rules followed by all transactions while requesting and releasing locks. Locking protocols restrict the set of possible schedules.
Database System Concepts 3rd Edition
16.1
©Silberschatz, Korth and Sudarshan, Bo Zhou
Lock-Based Protocols
A lock is a mechanism to control concurrent access to a data item Data items can be locked in two modes :
Basically, how to generate a correct (serializable) schedule?
Database System Concepts 3rd Edition
16.4
©Silberschatz, Korth and Sudarshan, Bo Zhou
Pitfalls of Lock-Based Protocols
T2: lock-S(A); read (A); unlock(A); lock-S(B); read (B); unlock(B); display(A+B)
Locking as above is not sufficient to guarantee serializability — if A and B get updated in-between the read of A and B, the displayed sum would be wrong.
Database System Concepts 3rd Edition
16.1
©Silberschatz, Korth and Sudarshan, Bo Zhou
Lock-Based Protocols
A lock is a mechanism to control concurrent access to a data item Data items can be locked in two modes :
Basically, how to generate a correct (serializable) schedule?
Database System Concepts 3rd Edition
16.4
©Silberschatz, Korth and Sudarshan, Bo Zhou
Pitfalls of Lock-Based Protocols
T2: lock-S(A); read (A); unlock(A); lock-S(B); read (B); unlock(B); display(A+B)
Locking as above is not sufficient to guarantee serializability — if A and B get updated in-between the read of A and B, the displayed sum would be wrong.
浙大数据结构课件-hqm_DS04_Ch04a
Unix directory with file sizes
static int SizeDir ( DirOrFile D ) {
int TotalSize; TotalSize = 0; if ( D is a legitimate entry ) {
+a b *c d * +e
T2 T2 a + b
cT1d * + e T1 T1
a
bT2 T2 c d + e T1
d
e
8/16
Tree Traversals —— visit each node exactly once
§2 Binary Trees
❖ Preorder Traversal
❖ Postorder Traversal
Note: ➢ Subtrees must not connect together. Therefore every
node in the tree is the root of some subtree. ➢ There are N 1 edges in a tree with N nodes. ➢ Normally the root is drawn at the top.
B
E
K
F
L
A
C
G
H
M
D
I
J
5/16
❖ FirstChild-NextSibling Representation
Element
A
N
FirstChild NextSibling
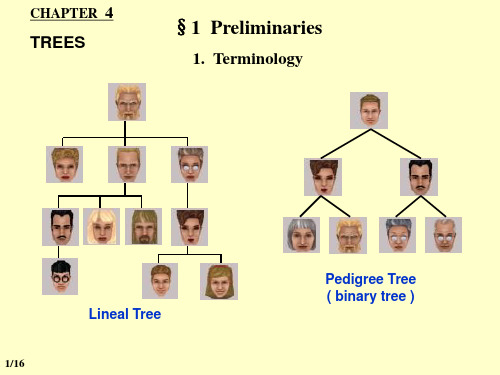
§1 Preliminaries
A BC D E F G HI J
KL
数据结构浙江工业大学(ppt)

8
Main Index
Contents
2. Creating a Linked List
将1,2,3,4,5顺序插入链表(正向插入) node<int> *nodeptr1,*nodeptr2; for(int i=1;i<6;i++) {
nodeptr1=new node<int>(i,null); nodeptr1? } nodeptr1=new node<int>(1,null); for(int i=2;i<6;i++) { nodeptr2=new node<int>(i,null); nodeptr1->next=nodeptr2; nodeptr1=nodeptr1->next; }
Before
After front
front
back item
Before
front
(a)
newNode
20
55
front
After
front
(b)
item
20
55
front
12
Main Index
Contents
3.2 Handling the Back of the List
top D
C B A
public: T nodeValue; // data held by the node node<T> *next; // next node in the list
node() : next(NULL) {}
node(const T& item, node<T> *nextNode = NULL) : nodeValue(item), next(nextNode)
数据结构课件第5章-PPT文档资料

(a) 非紧缩方式; (b) 紧缩方式
第5章 串
5.2.2
和线性表的链式存储结构相类似,串的存储结构也可采用链 式存储结构,即用线性链表来存储串值。在这种存储结构下,存 储空间被分成一系列大小相同的结点,每个结点用data域存放字 符, link域存放指向下一个结点的指针。 这样, 一个串就可以用 一个线性链表来表示。
private { private declaration }
public { public declaration }
end;
第5章 串
这一段程序可看作一个字符串:“type private
Tstring = class
{private declaration } public {public declaration } end;
”, 其中“ ”表示换行符。Delphi的源程序编辑器提供了字符 串的查找与替换功能。 选择“Search”菜单中的“Replace”项, 在对话框中输入要查找字符串‘private’及替代串‘protected’, 如 图 5.1 所 示 , 则 执 行 命 令 后 以 上 程 序 中 的 关 键 字 ‘ private’ 被 ‘protected’替代。
第5章 串 串中任意个连续的字符组成的子序列称为该串的子串。包含 子串的串称为主串。通常称字符在序列中的序号为该字符在串中 的位置。子串在主串中的位置可以用子串的第一个字符在主串中 的位置来表示。
例如, 假设a、 b、 c、 d为如下的四个串:
a =‘Data’
b =‘Structure’
c =‘Data Structure’ d =‘Data Structure’
const maxlen = 允许的串最大长度;
第5章 串
5.2.2
和线性表的链式存储结构相类似,串的存储结构也可采用链 式存储结构,即用线性链表来存储串值。在这种存储结构下,存 储空间被分成一系列大小相同的结点,每个结点用data域存放字 符, link域存放指向下一个结点的指针。 这样, 一个串就可以用 一个线性链表来表示。
private { private declaration }
public { public declaration }
end;
第5章 串
这一段程序可看作一个字符串:“type private
Tstring = class
{private declaration } public {public declaration } end;
”, 其中“ ”表示换行符。Delphi的源程序编辑器提供了字符 串的查找与替换功能。 选择“Search”菜单中的“Replace”项, 在对话框中输入要查找字符串‘private’及替代串‘protected’, 如 图 5.1 所 示 , 则 执 行 命 令 后 以 上 程 序 中 的 关 键 字 ‘ private’ 被 ‘protected’替代。
第5章 串 串中任意个连续的字符组成的子序列称为该串的子串。包含 子串的串称为主串。通常称字符在序列中的序号为该字符在串中 的位置。子串在主串中的位置可以用子串的第一个字符在主串中 的位置来表示。
例如, 假设a、 b、 c、 d为如下的四个串:
a =‘Data’
b =‘Structure’
c =‘Data Structure’ d =‘Data Structure’
const maxlen = 允许的串最大长度;
浙教版(2019)高中信息技术选修一1.2数据与数据结构(二)课件(18张PPT)

Data and data structure
常见的数据结构——队列
先进先出
队列 栈 树
用计算机程序处理数据时,有时也需要将数据进行“排队”,并遵循现实中排队的规律,对数 据进行“先进先出” FIFO(First In First Out)且中间不能“插队”的组织和操作,计算机科学家 由此发明了“队列”这种数据结构。
Data and data structure
队列 栈 树
数据与数据结构(二)
队列
栈
树
Data and data structure
课前回顾
队列 栈 树
➢ 数组的特点?
不仅需要描述数据对象本身,还需要描述数据所处的位置或者数据之间的前后顺 序关系
➢ 链表的特点?
只需知道数据之间相互链接的顺序
Data and data structure
Data and data structure
常见的数据结构——队列
先进先出
队列 栈 树
Data and data structure
常见的数据结构——栈
先进后出、后进先出
队列 栈 树
弹匣的装弹过程(入栈)
栈的示例—弹匣
子弹进出弹匣的过程具有下列特点: ①整个装置只有一端开放(最上端),而 且进、出只能在这一端进行。 ②弹匣中的子弹成一纵队排列。 ③任何子弹进出弹匣的规律是“先进后出、 后进先出”,即最先装入弹匣的子弹最后 才能被弹出,而最后装入弹匣的子弹则最 先被弹出。
活动一:快递拿取
队列 栈 树
栈 2
Data and data structure
队列 栈 树
常见的数据结构——树
一个元素前面(或上面)只有一个元素,而后面(或下面)却有多个(0个或多个)元素相邻,所 有的数据元素之间的特征就像一棵倒放的树。
基本数据结构课件高中信息技术浙教版(2019)必修1(20张PPT)

小组中小明的学习成绩的表达式为( D)
A.student[4] B.student[3] C.student{”小明”} D.student[”小明”]
例题
3.“回文”是古今中外都有的一种修辞方式和文字游戏,如“我为人人,人人为
我”等。在数学中也存在这样一类数具有这样的特征,称为回文数。例如:
123454321为回文数。
a[7:-9:-2] a[-2:-9:-2] 切片 a[开始索引:结束元素索引的后一个:步长]
1、从空间上看,一般切片从左往右 2、步长为负,从右往左
基本数据结构
由多个数据元素共同组成的序列组合
-9 -8 -7 -6 -5 -4 -3-2 -1
a=“你 好 , P y t h o n”
0 1 2 3 4 567 8
“hy,你”
a[索引] “P” a[3] a[-3] =“h” a[9] × a[6::-2] a[-3::-2]
切片 a[开始索引:结束元素索引的后一个:步长]
1、从空间上看,一般切片从左往右 2、步长为负,索引不变,整体倒置 3、开始索引、结束索引、步长均可为空
基本数据结构
由多个数据元素共同组成的序列组合
C2
D3
例题 已知列表a=[6,5],b=[6,5,4,3],则a*2+b的结果为( )
例题
某班级组建研究性学习小组,小组成员的情况以及学员成绩用Python存 储在student中。若student={”小红”:90,”小明”:80,”小张 ”:75,”小黄”:86,”小霞”:70,”小斌”:89},则访问学习
。要
访问小明的学习成绩的表达式为 scores[0][""]小[0明] "] 。
A.student[4] B.student[3] C.student{”小明”} D.student[”小明”]
例题
3.“回文”是古今中外都有的一种修辞方式和文字游戏,如“我为人人,人人为
我”等。在数学中也存在这样一类数具有这样的特征,称为回文数。例如:
123454321为回文数。
a[7:-9:-2] a[-2:-9:-2] 切片 a[开始索引:结束元素索引的后一个:步长]
1、从空间上看,一般切片从左往右 2、步长为负,从右往左
基本数据结构
由多个数据元素共同组成的序列组合
-9 -8 -7 -6 -5 -4 -3-2 -1
a=“你 好 , P y t h o n”
0 1 2 3 4 567 8
“hy,你”
a[索引] “P” a[3] a[-3] =“h” a[9] × a[6::-2] a[-3::-2]
切片 a[开始索引:结束元素索引的后一个:步长]
1、从空间上看,一般切片从左往右 2、步长为负,索引不变,整体倒置 3、开始索引、结束索引、步长均可为空
基本数据结构
由多个数据元素共同组成的序列组合
C2
D3
例题 已知列表a=[6,5],b=[6,5,4,3],则a*2+b的结果为( )
例题
某班级组建研究性学习小组,小组成员的情况以及学员成绩用Python存 储在student中。若student={”小红”:90,”小明”:80,”小张 ”:75,”小黄”:86,”小霞”:70,”小斌”:89},则访问学习
。要
访问小明的学习成绩的表达式为 scores[0][""]小[0明] "] 。
浙大数据结构课件-hqm_DS08_Ch06b
5/14
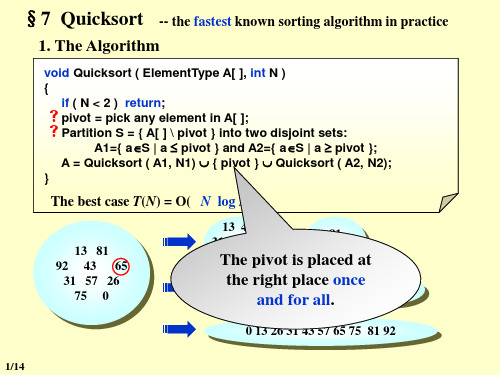
§7 Quicksort
void Qsort( ElementType A[ ], int Left, int Right ) { int i, j;
ElementType Pivot; if ( Left + Cutoff <= Right ) { /* if the sequence is not too short */
31 57 26 75 0
13 43 31 57 26 65
Th0e pivot is
81 92 75
placed
at
0
the right
13 26 31 43
5p7lace6o5 nce75
81 92
and for all.
0 13 26 31 43 57 65 75 81 92
1/14
2. Picking the Pivot
3/14
4. Small Arrays
§7 Quicksort
Problem: Quicksort is slower than insertion sort for small N ( 20 ).
Solution: Cutoff when N gets small ( e.g. N = 10 ) and use other efficient algorithms (such as insertion sort).
Swap( &A[ Left ], &A[ Center ] ); if ( A[ Left ] > A[ Right ] )
Swap( &A[ Left ], &A[ Right ] ); if ( A[ Center ] > A[ Right ] )
§7 Quicksort
void Qsort( ElementType A[ ], int Left, int Right ) { int i, j;
ElementType Pivot; if ( Left + Cutoff <= Right ) { /* if the sequence is not too short */
31 57 26 75 0
13 43 31 57 26 65
Th0e pivot is
81 92 75
placed
at
0
the right
13 26 31 43
5p7lace6o5 nce75
81 92
and for all.
0 13 26 31 43 57 65 75 81 92
1/14
2. Picking the Pivot
3/14
4. Small Arrays
§7 Quicksort
Problem: Quicksort is slower than insertion sort for small N ( 20 ).
Solution: Cutoff when N gets small ( e.g. N = 10 ) and use other efficient algorithms (such as insertion sort).
Swap( &A[ Left ], &A[ Center ] ); if ( A[ Left ] > A[ Right ] )
Swap( &A[ Left ], &A[ Right ] ); if ( A[ Center ] > A[ Right ] )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
if ( T->Left == NULL ) return T; /* found left most */
else return FindMin( T->Left ); /* keep moving to left */
}
FindMax
Position FindMax( SearchTree T ) {
}
7/13
Insert
§3 Binary Search Trees
Sketch of the idea:
30
Insert 80
check if 80 is already in the tree
5
40
80 > 40, so it must be the right child
2 25 35 80 of 40
return T; /* Do not forget this line!! */
}
9/13
Delete
§3 Binary Search Trees
❖ Delete a leaf nodeNo: tRe:eTshetesites kpianrdesntolfinnkodtoesNULL. ❖ Delete a degree 1 nohdavee: dReegprelaecaettmheosnto1d.e by its single child.
{ Position TmpCell;
if ( T == NULL ) Error( "Element not found" );
else if ( X < T->Element ) /* Go left */
T->Left = Delete( X, T->Left );
else if ( X > T->Element ) /* Go right */
the key in the root of the subtree. (4) The left and right subtrees are also binary search trees.
30
60
20
5
40
70
15 25
2
65 80
12 10
22
3/13
2. ADT
§3 Binary Search Trees
TmpCell = FindMin( T->Right );
T->Element = TmpCell->Element;
if ( X < T->Element ) T = T->Left ; /*move down along left path */
else T = T-> Right ; /* move down along right path */
} /* end while-loop */ return NULL ; /* not found */ }
【Definition】A binary search tree is a binary tree. It may be
empty. If it is not empty, it satisfies the following properties: (1) Every node has a key which is an integer, and the keys are
distinct. (2) The keys in a nonempty left subtree must be smaller than
the key in the root of the subtree. (3) The keys in a nonempty right subtree must be larger than
TH(aNnd)le=dOup( ldic)ated Keys?
if ( X < T->Element )
T->Left = Insert( X, T->Left );
else
if ( X > T->Element )
T->Right = Insert( X, T->Right );
/* Else X is in the tree already; we'll do nothing */
Proof: Let n1 be the number of nodes of degree 1, and n the
total number of nodes. Then
n = n0 n1 n2 1
Let B be the number of branches. Then nn=~ BB?+ 1. 2
B
B
Skewed Binary Trees
A
A
B
B
C
C
D
D
Skewed to the left Skewed to the right
1/13
Complete Binary Tree A
B
C
D EF G
HI
All the leaf nodes are on two adjacent levels
Properties of Binary Trees
Since all e out of nodes of degree 1 or 2, we have B
~ n1 & n2 ? B = n1 + 2 n2. 3
n0 = n2 + 1
2/13
§3 The Search Tree ADT -- Binary Search Trees
1. Definition
〖Example〗 Delete 60
40
Solution 1: reset left subtree. Solution 2: reset right subtree.
20
6505
10 30 50 70
45 552
52
10/13
§3 Binary Search Trees
SearchTree Delete( ElementType X, SearchTree T )
Insert 35 chTechkisifis3t5hieslaalsrteandoydien the tree when35se<a4rw0c,hesfoeonritctomhuuensktteebryenthuemlebfetrc.hild of 40
Insert 25
chIetcwkiilfl b25e itshealpreaardeynitn the tree of the new node.
Objects: A finite ordered list with zero or more elements.
Operations:
SearchTree MakeEmpty( SearchTree T ); Position Find( ElementType X, SearchTree T ); Position FindMin( SearchTree T ); Position FindMax( SearchTree T ); SearchTree Insert( ElementType X, SearchTree T ); SearchTree Delete( ElementType X, SearchTree T ); ElementType Retrieve( Position P );
not ) /*
iffosumndallienratnhaenmrpotoytt*r/eteaiT*l /rheecsuerasiroens.
return Find( X, T->Left ); /* search left subtree */
else
if ( X > T->Element ) /* if larger than root */
❖ Delete a degree 2 node :
Replace the node by the largest one in its left subtree or
the smallest one in its right subtree.
Delete the replacing node from the subtree.
§2 Binary Trees
The maximum number of nodes on level i is 2 i1, i 1.
The maximum number of nodes in a binary tree of depth k is
2 k 1, k 1.
For any nonempty binary tree, n0 = n2 + 1 where n0 is the number of leaf nodes and n2 the number of nodes of degree 2.
return Find( X, T->Right ); /* search right subtree */
else /* if X == root */
return T; /* found */
} T( N ) = S ( N ) = O( d ) where d is the depth of X
4/13
3. Implementations
Find
§3 Binary Search Trees
Must this test be performed first?
Position Find( ElementType X, SearchTreeT == NULL ) return NULL; /* ( X < T->Element
